A Finite Element Solution of Lateral Periodic Poisson–Boltzmann Model for Membrane Channel Proteins
Abstract
1. Introduction
2. Results and Discussion
2.1. Validation for the Treatments of Fixed Singular Charge
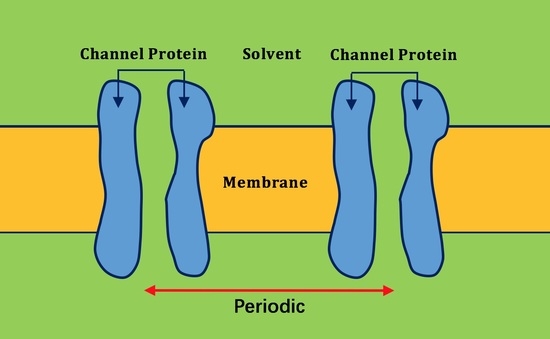
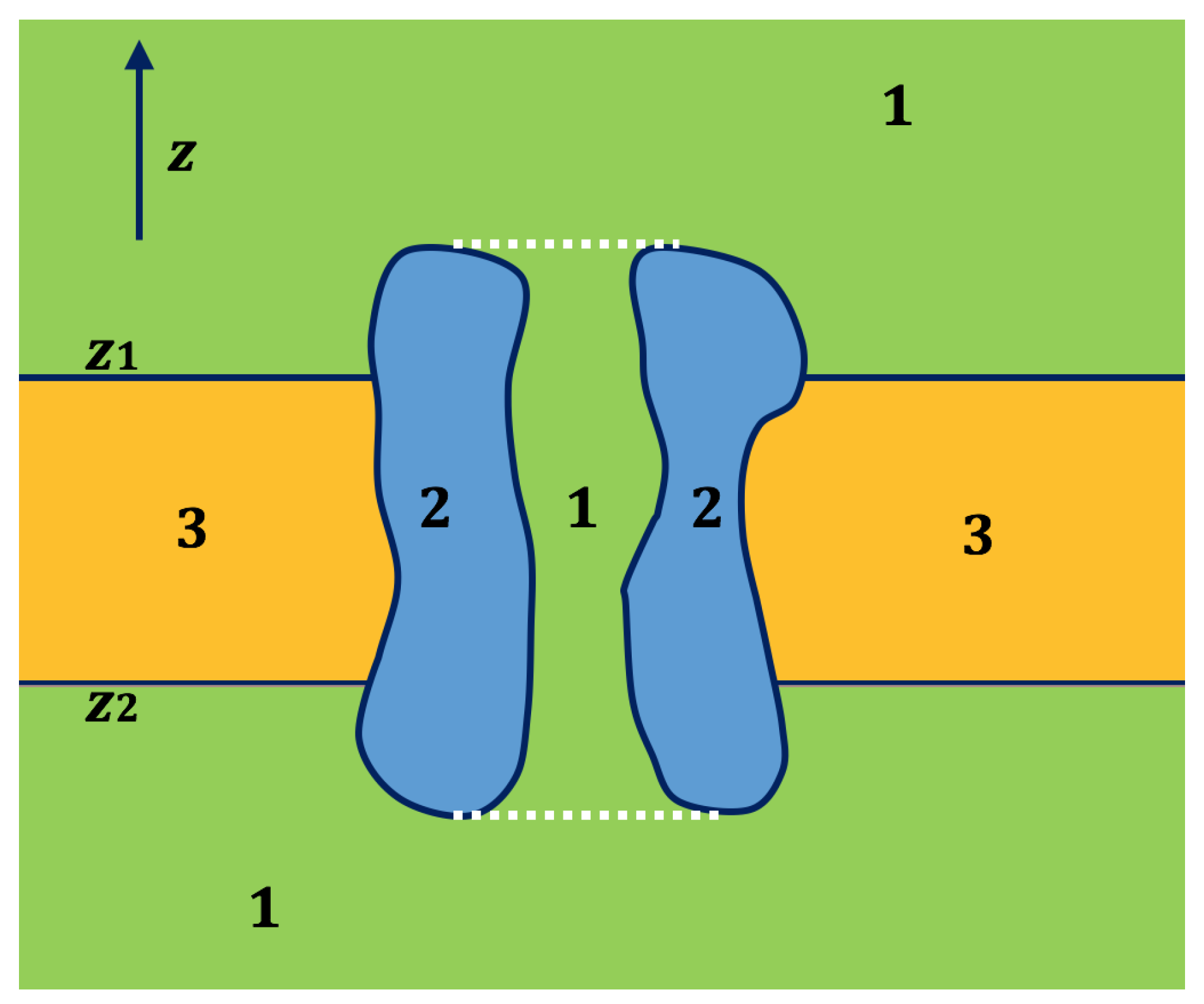
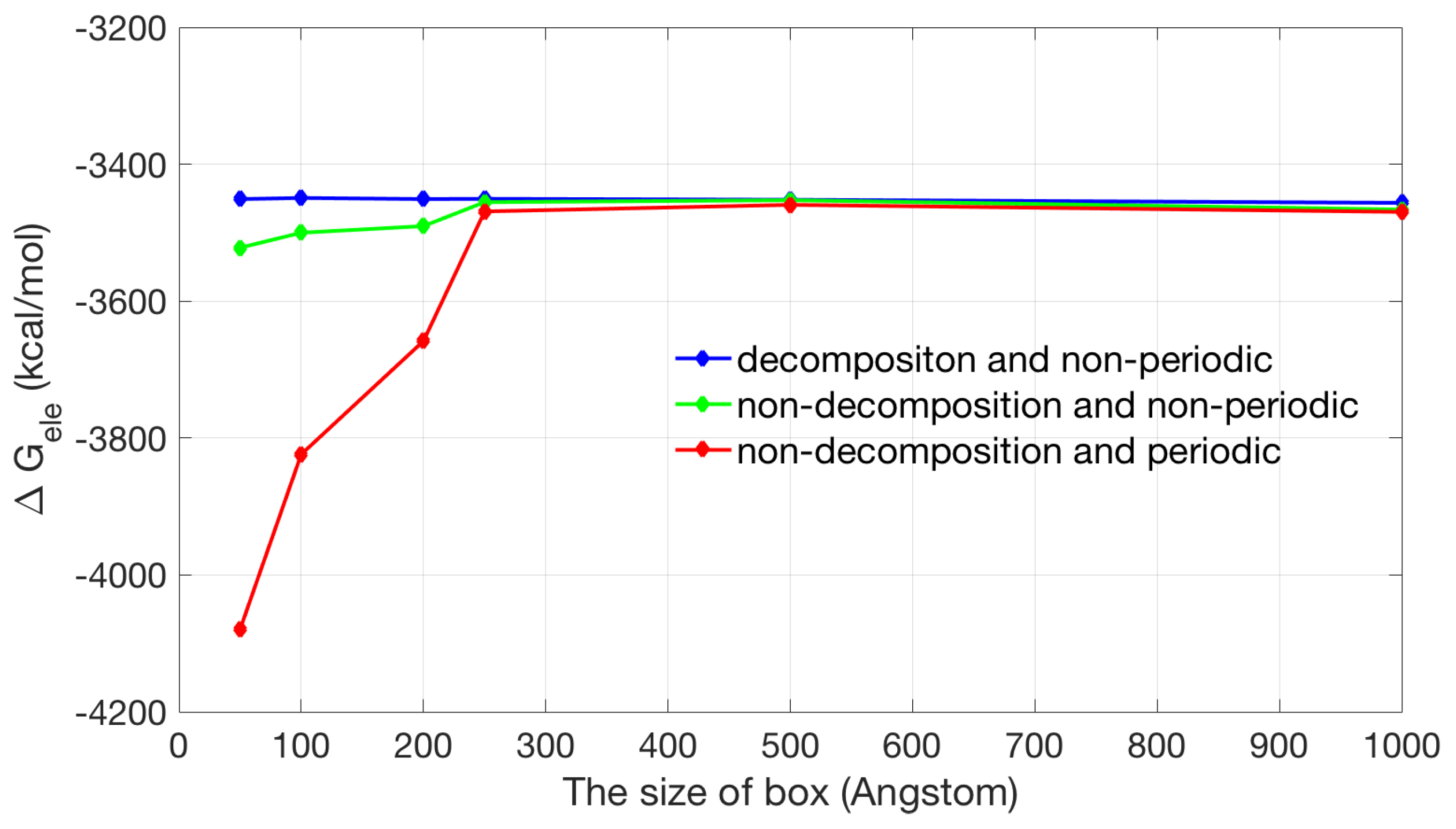
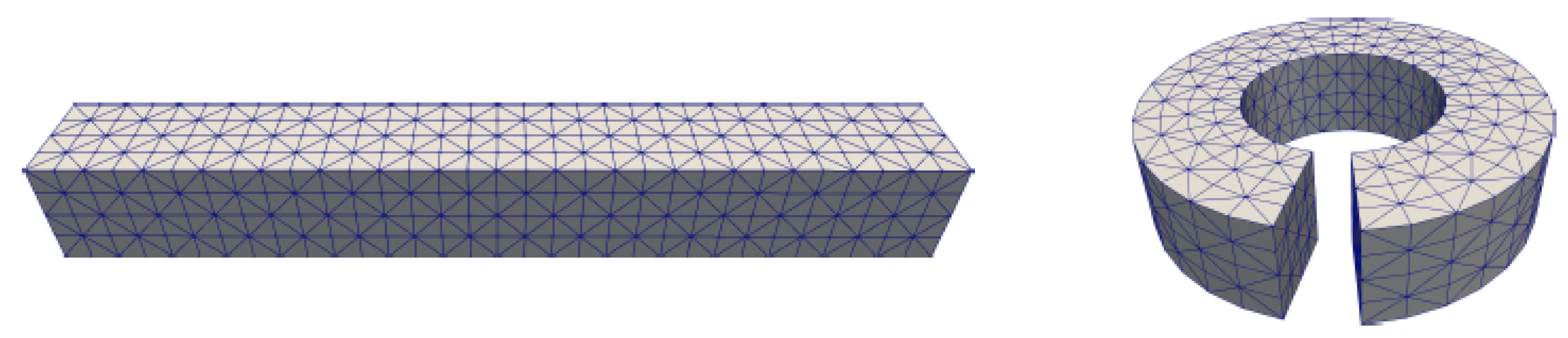
2.2. Application of Lateral Periodic Boundary Condition
2.2.1. Validation of Lateral Periodic Boundary Conditions
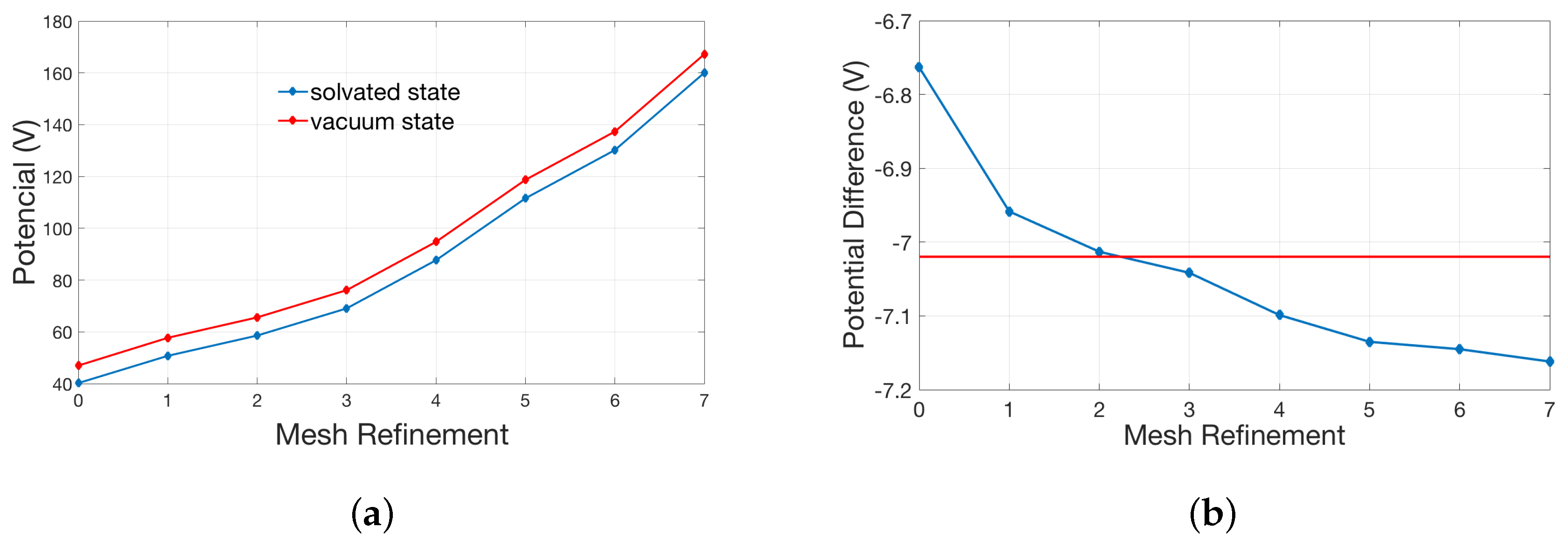
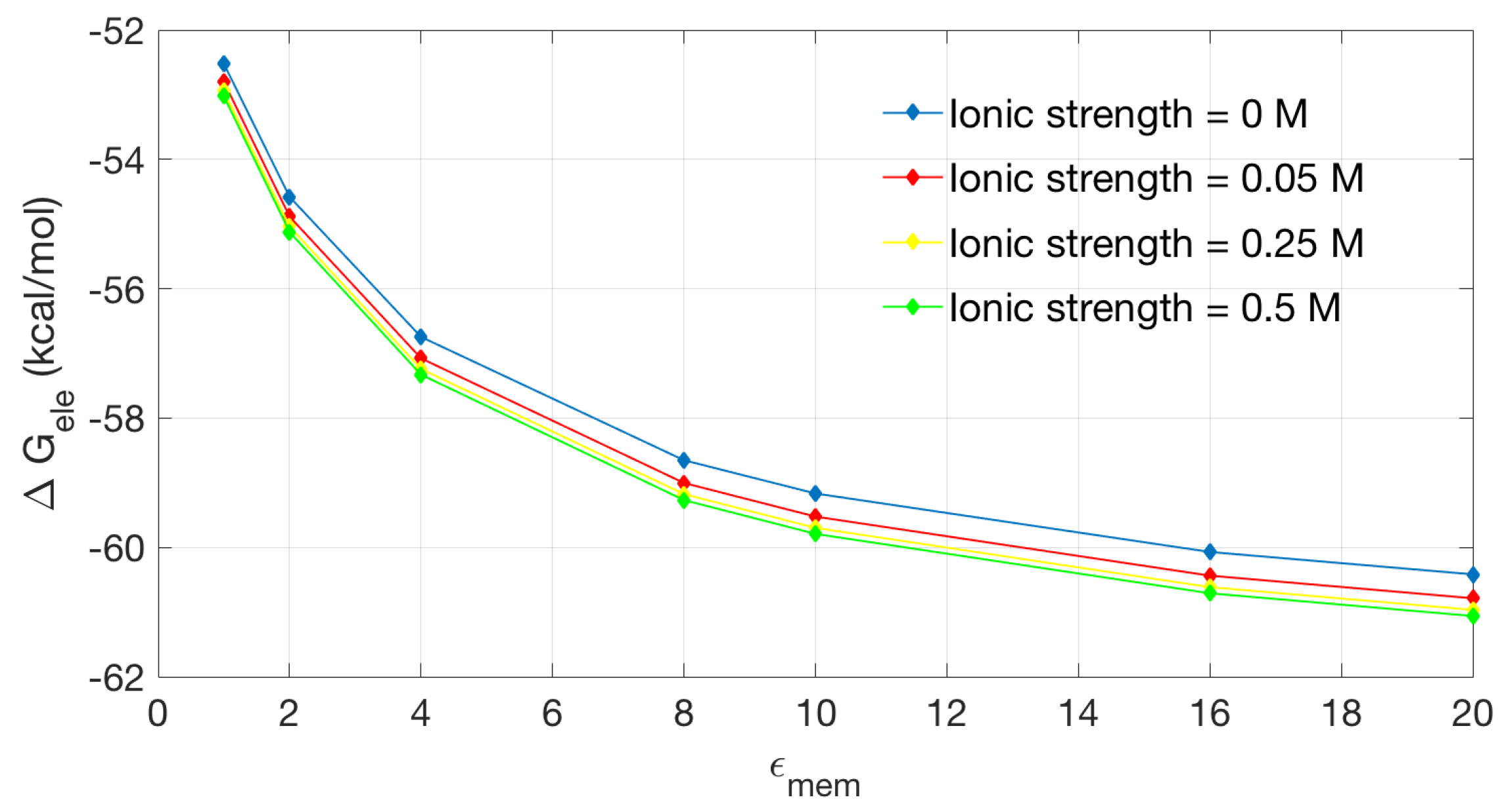
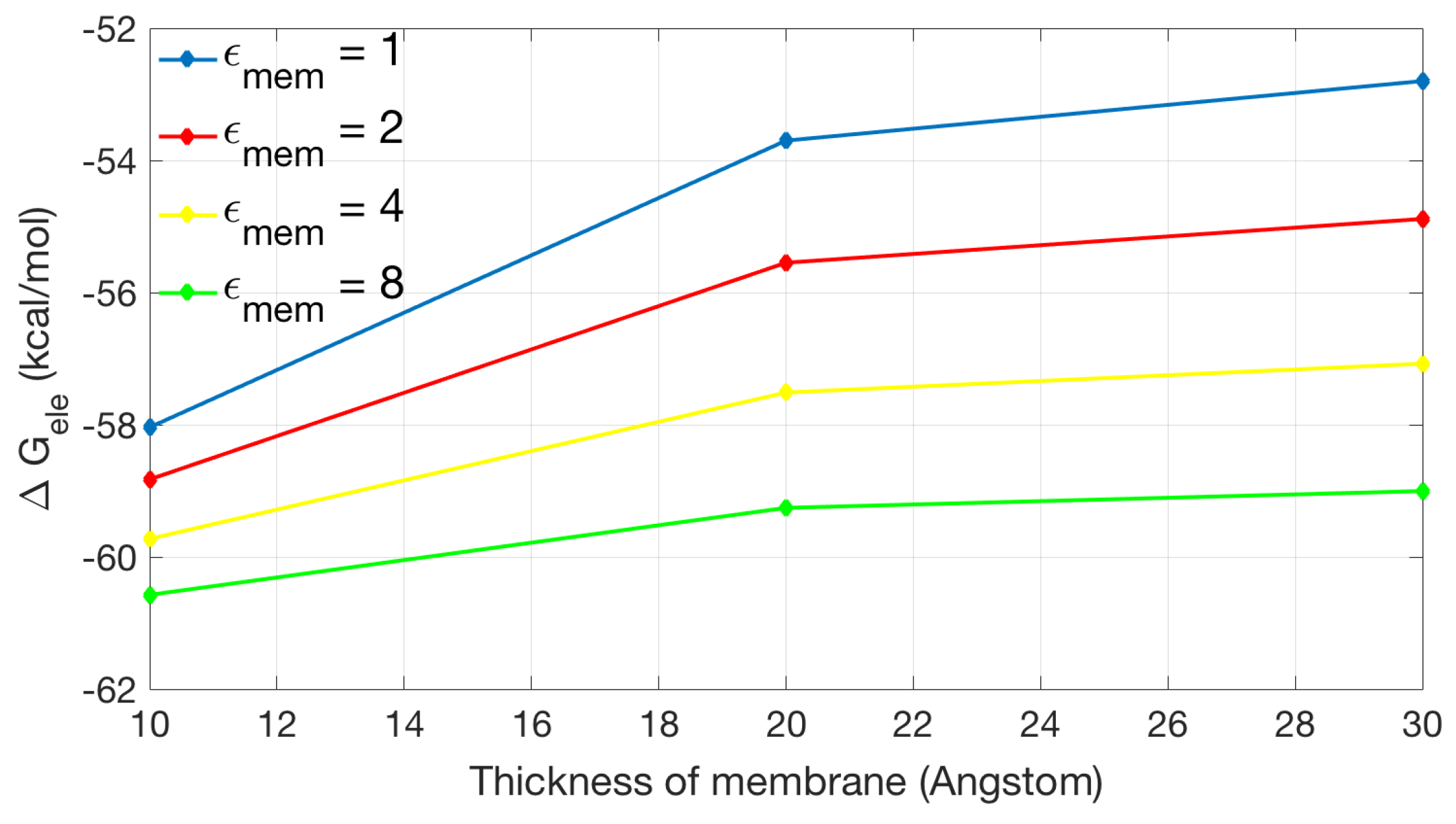
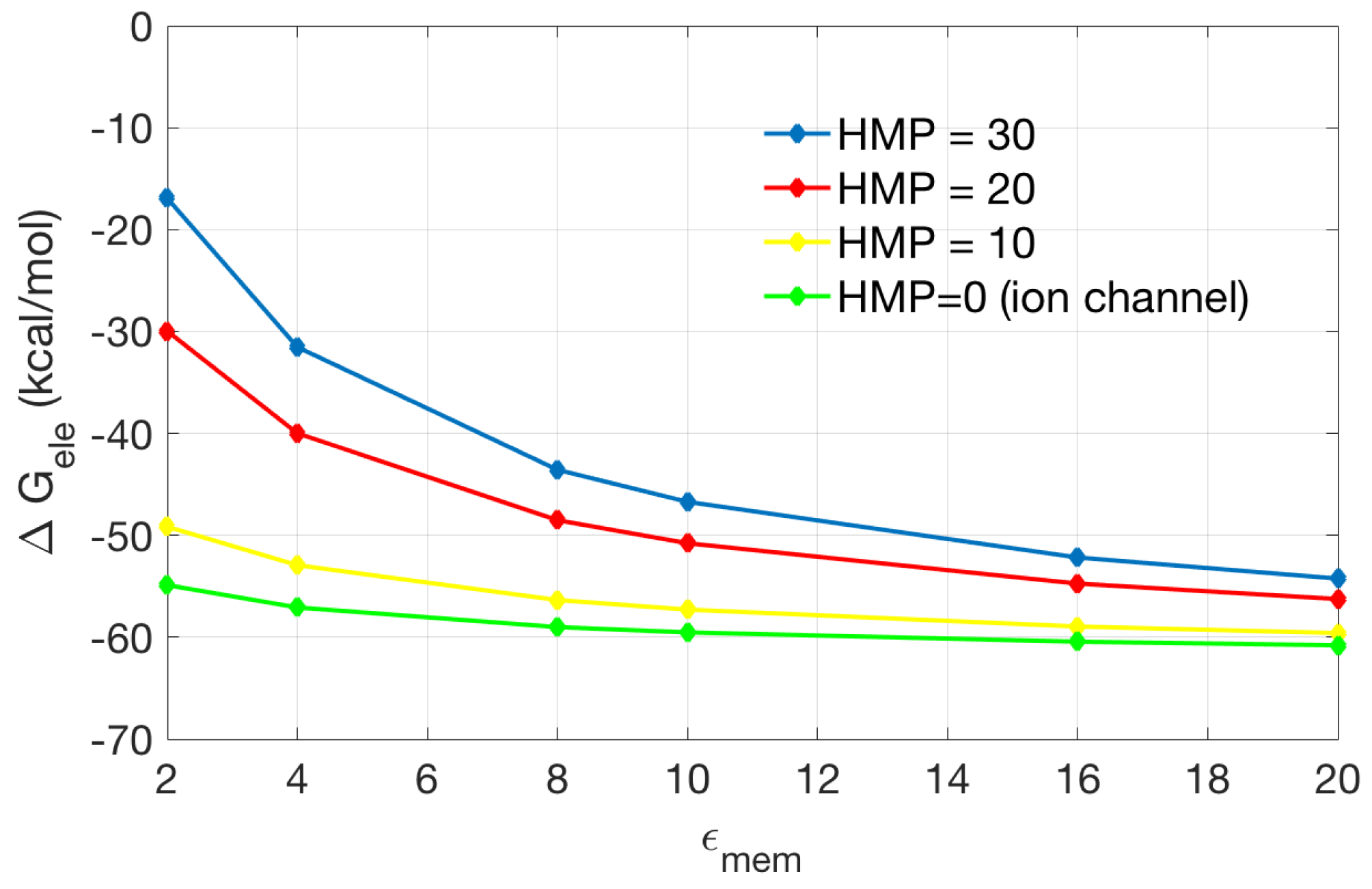
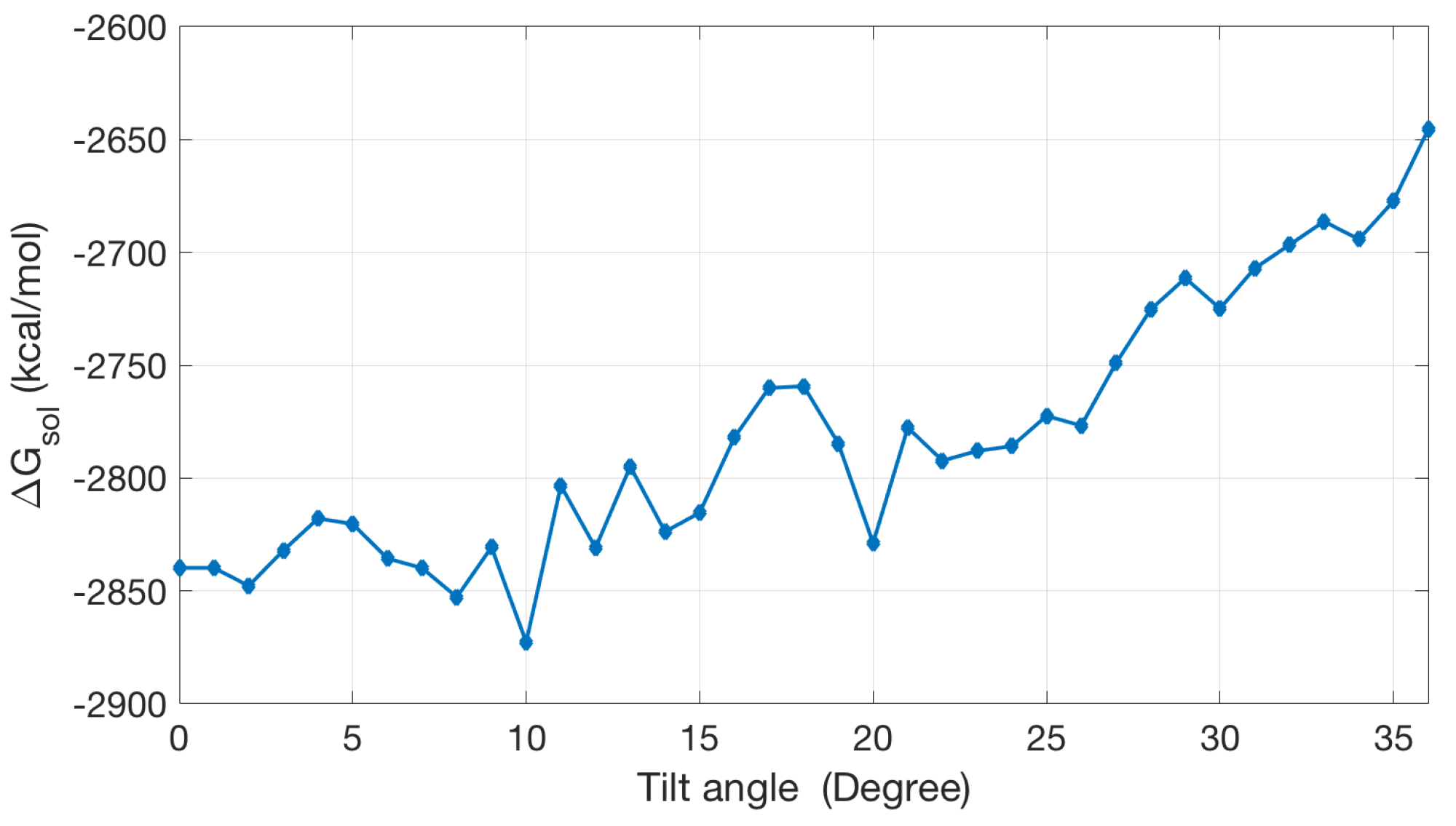
2.2.2. Application to the Channel Protein
2.2.3. Non-Polar Contribution to Solvation Energy
3. Materials and Methods
3.1. Finite Element Method of Poisson–Boltzmann Equation
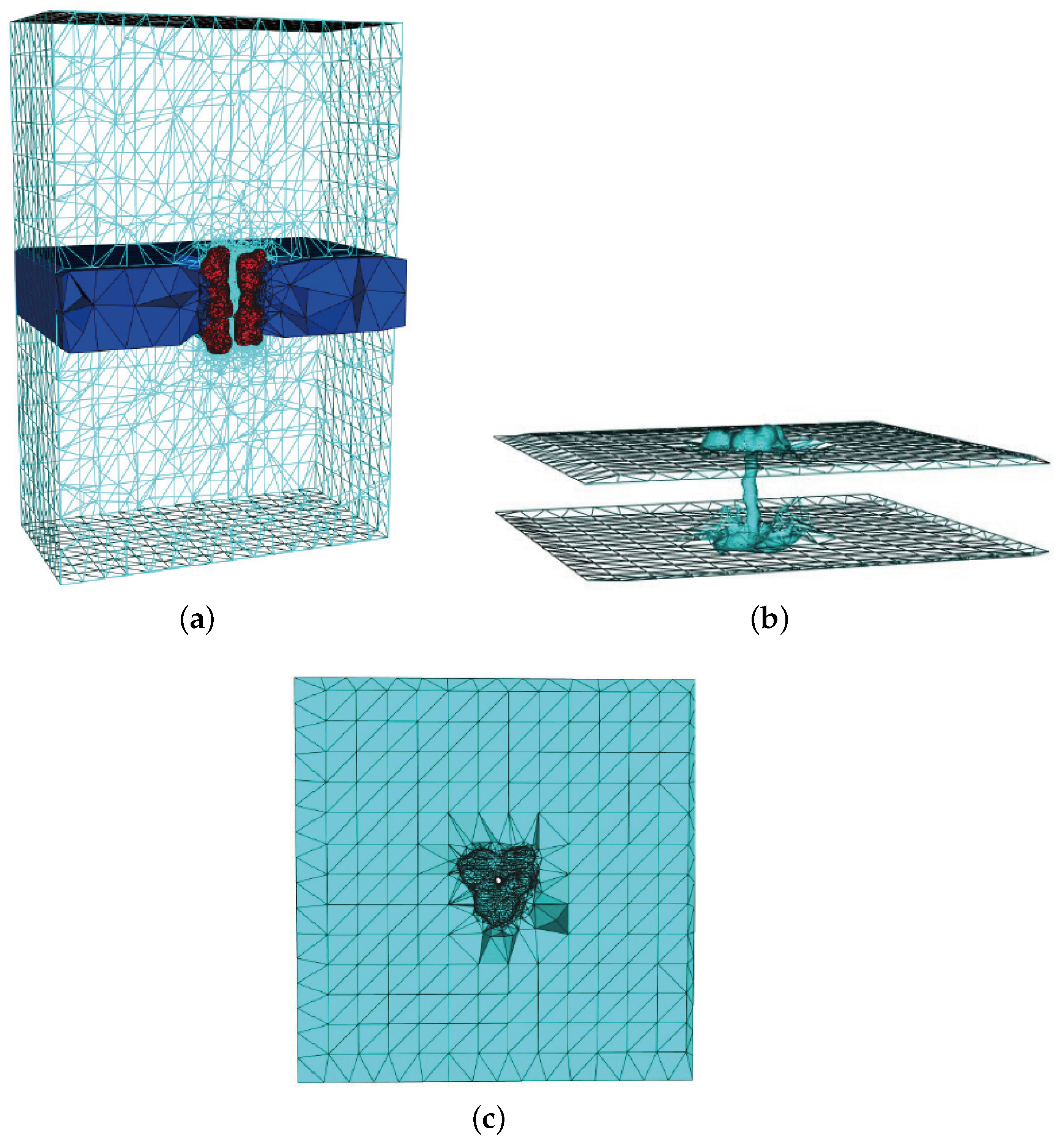
3.2. Mesh Construction for Membrane Protein System
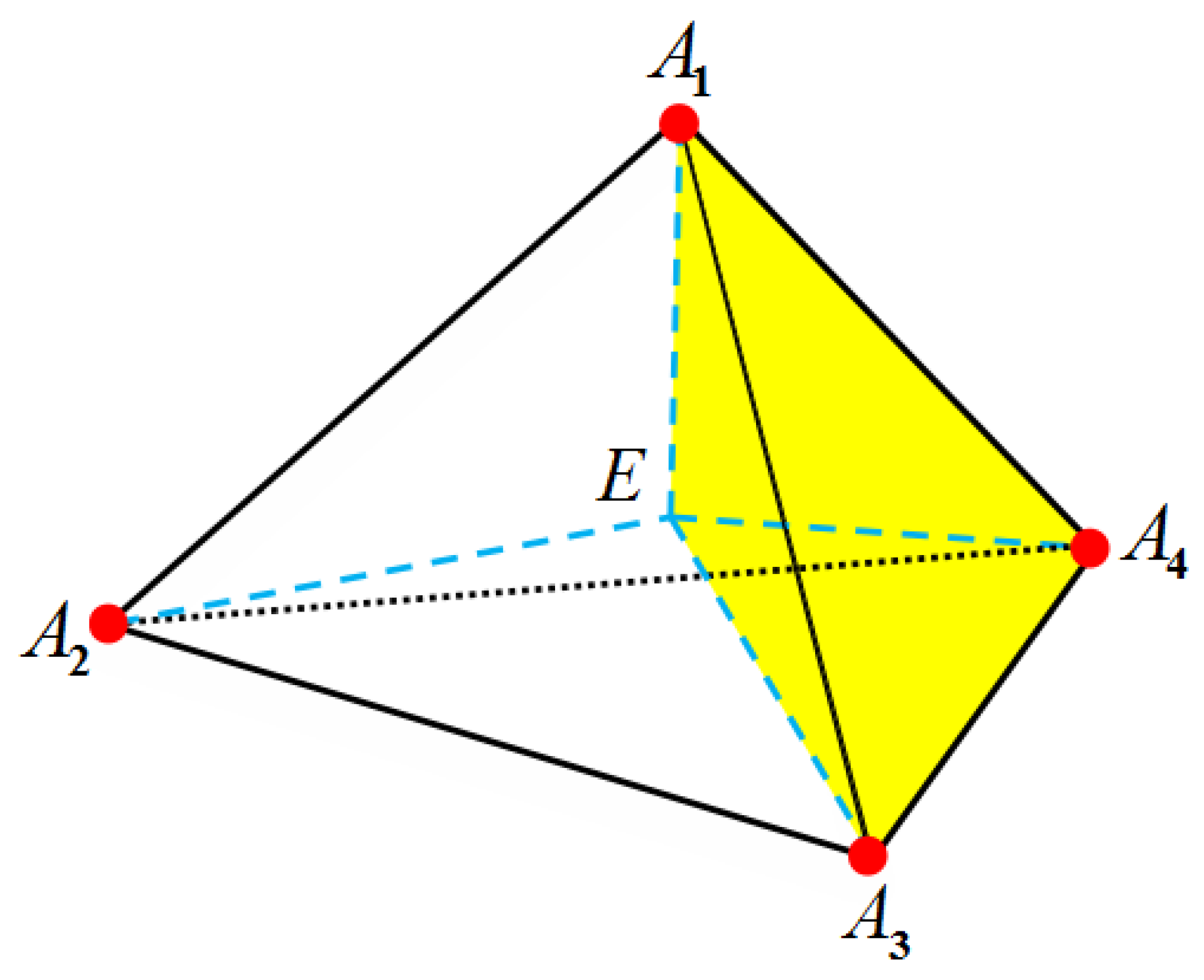
3.3. Treatments of Fixed Singular Charges
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PB | Poisson–Boltzmann |
| FEM | Finite element method |
| FDM | Finite difference method |
| BEM | Boundary element method |
| FEPB | FEM for PB electrostatics calculations of the membrane channel systems with periodical boundary conditions |
| TPM | The thickness of the filled membrane in the pore region |
References
- Sharp, K.A.; Honig, B. Electrostatic interactions in macromolecules: Theory and applications. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 301–332. [Google Scholar] [CrossRef] [PubMed]
- Honig, B.; Sharp, K.; Yang, A.S. Macroscopic models of aqueous solutions: Biological and chemical applications. J. Phys. Chem. 1993, 97, 1101–1109. [Google Scholar] [CrossRef]
- Honig, B.; Nicholls, A. Classical electrostatics in biology and chemistry. Science 1995, 268, 1144–1149. [Google Scholar] [CrossRef] [PubMed]
- Beglov, D.; Roux, B. Solvation of complex molecules in a polar liquid: An integral equation theory. J. Chem. Phys. 1996, 104, 8678–8689. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999, 99, 2161–2200. [Google Scholar] [CrossRef] [PubMed]
- Bashford, D.; Case, D.A. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000, 51, 129–152. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.A. Improving implicit solvent simulations: A Poisson-centric view. Curr. Opin. Struct. Biol. 2005, 15, 137–143. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Im, W.; Brooks, C.L. Balancing solvation and intramolecular interactions: Toward a consistent generalized Born force field. J. Am. Chem. Soc. 2006, 128, 3728–3736. [Google Scholar] [CrossRef] [PubMed]
- Feig, M.; Chocholoušová, J.; Tanizaki, S. Extending the horizon: Towards the efficient modeling of large biomolecular complexes in atomic detail. Theor. Chem. Acc. 2006, 116, 194–205. [Google Scholar] [CrossRef]
- Koehl, P. Electrostatics calculations: Latest methodological advances. Curr. Opin. Struct. Biol. 2006, 16, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Im, W.; Chen, J.; Rd, B.C. Peptide and Protein Folding and Conformational Equilibria: Theoretical Treatment of Electrostatics and Hydrogen Bonding with Implicit Solvent Models. Adv. Protein Chem. 2005, 72, 173–198. [Google Scholar] [PubMed]
- Lu, B.Z.; Zhou, Y.C.; Holst, M.J.; McCammon, J.A. Recent progress in numerical methods for the Poisson-Boltzmann equation in biophysical applications. Commun. Comput. Phys. 2008, 37060, 973–1009. [Google Scholar]
- Georgescu, R.E.; Alexov, E.; Gunner, M.R. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys. J. 2002, 83, 1731–1748. [Google Scholar] [CrossRef]
- Greene, D.; Botellosmith, W.M.; Follmer, A.; Li, X.; Lambros, E.; Luo, R. Modeling Membrane Protein–Ligand Binding Interactions: The Human Purinergic Platelet Receptor. J. Phys. Chem. B 2016, 120, 12293. [Google Scholar] [CrossRef] [PubMed]
- Swanson, J.M.J.; Henchman, R.H.; McCammon, J.A. Revisiting Free Energy Calculations: A Theoretical Connection to MM/PBSA and Direct Calculation of the Association Free Energy. Biophys. J. 2004, 86, 67–74. [Google Scholar] [CrossRef]
- Luo, R.; Head, M.S.; Given, J.A.; Gilson, M.K. Nucleic acid base-pairing and N-methylacetamide self-association in chloroform: Affinity and conformation. Biophys. Chem. 1999, 78, 183–193. [Google Scholar] [CrossRef]
- Holst, M.; Baker, N.A.; Wang, F. Adaptive multilevel finite element solution of the Poisson-Boltzmann equation I. Algorithms and examples. J. Comput. Chem. 2000, 21, 1319–1342. [Google Scholar] [CrossRef]
- Baker, N.A.; Holst, M.; Wang, F. Adaptive multilevel finite element solution of the Poisson-Boltzmann equation II. Refinement at solvent-accessible surfaces in biomolecular systems. J. Comput. Chem. 2015, 21, 1343–1352. [Google Scholar] [CrossRef]
- Chen, L.; Holst, M.J.; Xu, J. The Finite Element Approximation of the Nonlinear Poisson-Boltzmann Equation. SIAM J. Numer. Anal. 2007, 45, 2298–2320. [Google Scholar] [CrossRef]
- Xie, D. New solution decomposition and minimization schemes for Poisson–Boltzmann equation in calculation of biomolecular electrostatics. J. Comput. Phys. 2014, 275, 294–309. [Google Scholar] [CrossRef]
- Ulmschneider, M.B.; Ulmschneider, J.P.; Sansom, M.S.P.; Nola, A.D. A Generalized Born Implicit-Membrane Representation Compared to Experimental Insertion Free Energies. Biophys. J. 2007, 92, 2338–2349. [Google Scholar] [CrossRef] [PubMed]
- Ulmschneider, J.P.; Ulmschneider, M.B. Folding Simulations of the Transmembrane Helix of Virus Protein U in an Implicit Membrane Model. J. Chem. Theory Comput. 2007, 3, 2335–2346. [Google Scholar] [CrossRef] [PubMed]
- Spassov, V.Z.; Yan, L.; Szalma, S. Introducing an implicit membrane in generalized born/solvent accessibility continuum solvent models. J. Phys. Chem. B 2002, 106, 8726–8738. [Google Scholar] [CrossRef]
- Im, W.; Feig, M.; Brooks, C.L. An Implicit Membrane Generalized Born Theory for the Study of Structure, Stability, and Interactions of Membrane Proteins. Biophys. J. 2003, 85, 2900–2918. [Google Scholar] [CrossRef]
- Sakalli, I.; Schöberl, J.; Knapp, E.W. mFES: A Robust Molecular Finite Element Solver for Electrostatic Energy Computations. J. Chem. Theory Comput. 2014, 10, 5095–51112. [Google Scholar] [CrossRef] [PubMed]
- Callenberg, K.M.; Choudhary, O.P.; de Forest, G.L.; Gohara, D.W.; Baker, N.A.; Grabe, M. APBSmem: A Graphical Interface for Electrostatic Calculations at the Membrane. PLoS ONE 2010, 5, e12722. [Google Scholar] [CrossRef] [PubMed]
- Botellosmith, W.M.; Luo, R. Applications of MMPBSA to Membrane Proteins I: Efficient Numerical Solutions of Periodic Poisson-Boltzmann Equation. J. Chem. Inf. Model. 2015, 55, 2187–2199. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Diao, J.; Greene, D.; Wang, J.; Luo, R. A Continuum Poisson-Boltzmann Model for Membrane Channel Proteins. J. Chem. Theory Comput. 2017, 13, 3398–3412. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Bai, S.; Tu, B.; Chen, M.; Lu, B. Membrane-Channel Protein System Mesh Construction for Finite Element Simulations. Mol. Based Math. Biol. 2015, 3, 128–139. [Google Scholar] [CrossRef]
- Sharp, K.A.; Nicholls, A.; Fine, R.; Honig, B. Reconciling the magnitude of the microscopic and macroscopic hydrophobic effects. Science 1991, 252, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, D.; Mclachlan, A.D. Solvation energy in protein folding and binding. Nature 1986, 319, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. An SCF Solvation Model for the Hydrophobic Effect and Absolute Free Energies of Aqueous Solvation. Science 1992, 256, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Tanizaki, S.; Feig, M. A generalized Born formalism for heterogeneous dielectric environments: Application to the implicit modeling of biological membranes. J. Chem. Phys. 2005, 122, 124706. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.A.; Sept, D.; Joseph, S.; Holst, M.; McCammon, J.A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar] [CrossRef] [PubMed]
- Si, H. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 2015, 41, 11. [Google Scholar] [CrossRef]
- Song, C.; Weichbrodt, C.; Salnikov, E.S.; Dynowski, M.; Forsberg, B.O.; Bechinger, B.; Steinem, C.; de Groot, B.L.; Zachariae, U.; Zeth, K. Crystal structure and functional mechanism of a human antimicrobial membrane channel. Proc. Natl. Acad. Sci. USA 2013, 110, 4586–4591. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Lu, B. TMSmesh: A Robust Method for Molecular Surface Mesh Generation Using a Trace Technique. J. Chem. Theory Comput. 2011, 7, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Tu, B.; Lu, B. Triangulated manifold meshing method preserving molecular surface topology. J. Mol. Graph. Model. 2012, 38, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Decherchi, S.; Rocchia, W. A general and Robust Ray-Casting-Based Algorithm for Triangulating Surfaces at the Nanoscale. PLoS ONE 2013, 8, e59744. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, C.L.; Xu, G.L.; Zhang, Q. Bio-molecule Surfaces Construction via a Higher-Order Level-Set Method. J. Comput. Sci. Technol. 2008, 23, 1026–1036. [Google Scholar] [CrossRef] [PubMed]
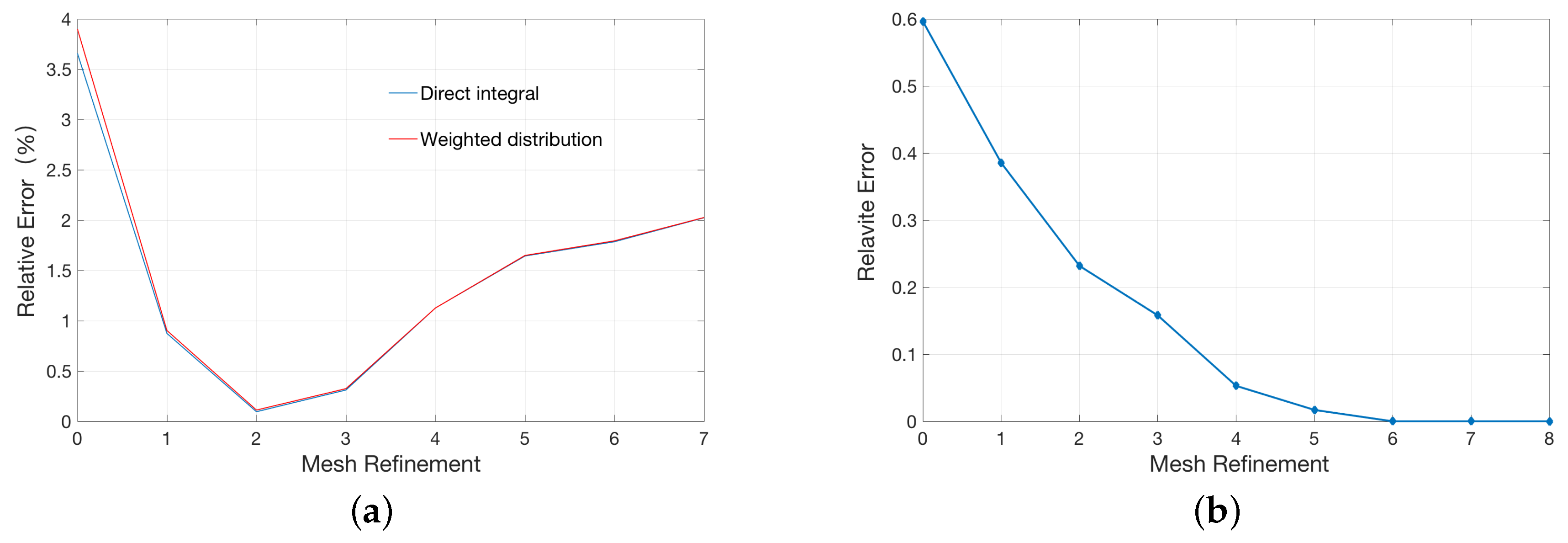

| Singular Charges Treatments | Elements | DOFs | (kcal/mol) | |
|---|---|---|---|---|
| Average assignment method | 22614 | 3745 | −77.01 | %4.9 |
| 92595 | 17037 | −80.11 | %1.03 | |
| Weighted assignment method | 22614 | 3745 | −77.79 | %3.9 |
| 92595 | 17037 | −80.21 | %0.90 | |
| Direct integral method | 22614 | 3745 | −77.98 | %3.6 |
| 92595 | 17037 | −80.23 | %0.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, N.; Liu, T.; Xu, J.; Shen, L.Q.; Lu, B. A Finite Element Solution of Lateral Periodic Poisson–Boltzmann Model for Membrane Channel Proteins. Int. J. Mol. Sci. 2018, 19, 695. https://doi.org/10.3390/ijms19030695
Ji N, Liu T, Xu J, Shen LQ, Lu B. A Finite Element Solution of Lateral Periodic Poisson–Boltzmann Model for Membrane Channel Proteins. International Journal of Molecular Sciences. 2018; 19(3):695. https://doi.org/10.3390/ijms19030695
Chicago/Turabian StyleJi, Nan, Tiantian Liu, Jingjie Xu, Longzhu Q. Shen, and Benzhuo Lu. 2018. "A Finite Element Solution of Lateral Periodic Poisson–Boltzmann Model for Membrane Channel Proteins" International Journal of Molecular Sciences 19, no. 3: 695. https://doi.org/10.3390/ijms19030695
APA StyleJi, N., Liu, T., Xu, J., Shen, L. Q., & Lu, B. (2018). A Finite Element Solution of Lateral Periodic Poisson–Boltzmann Model for Membrane Channel Proteins. International Journal of Molecular Sciences, 19(3), 695. https://doi.org/10.3390/ijms19030695