iRSpot-TNCPseAAC: Identify Recombination Spots with Trinucleotide Composition and Pseudo Amino Acid Components
Abstract
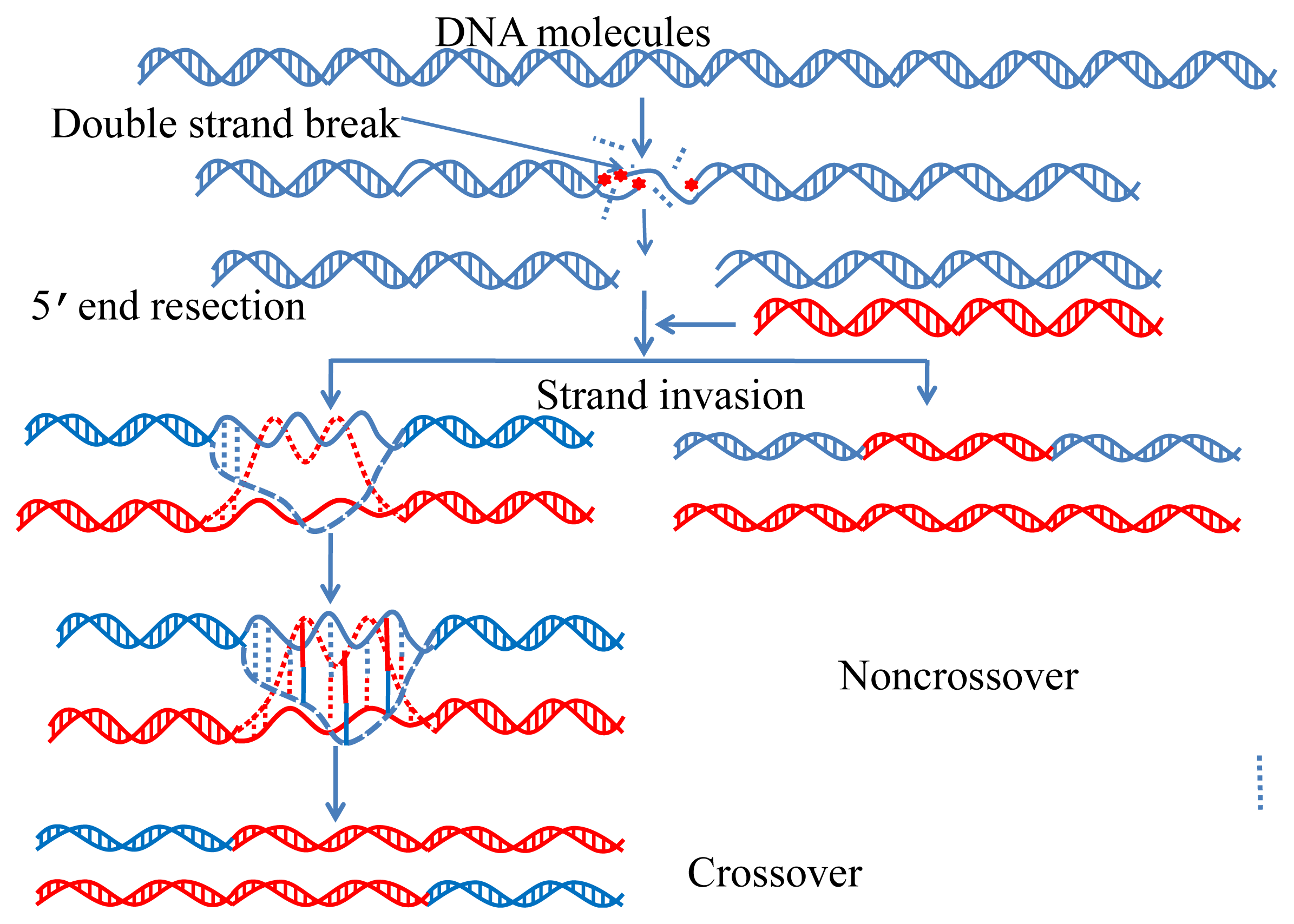
:1. Introduction
2. Results and Discussion
2.1. Benchmark Dataset
2.2. Formulate DNA Samples by Combining Trinucleotide Composition and Pseudo Amino Acid Components
2.3. Use Support Vector Machine as an Operation Engine
2.4. Four Different Metrics for Measuring the Prediction Quality
2.5. Evaluate the Anticipated Success Rates by Jackknife Tests
3. Experimental Section
4. Conclusions
5. Web Server and User Guide
Supplementary Information
Acknowledgments
Conflicts of Interest
References
- Hansen, L.; Kim, N.K.; Marino-Ramirez, L.; Landsman, D. Analysis of biological features associated with meiotic recombination hot and cold spots in Saccharomyces cerevisiae. PLoS One 2011, 6, e29711. [Google Scholar]
- Keeney, S. Spo11 and the formation of DNA double-strand breaks in meiosis. Genome Dyn. Stab 2008, 2, 81–123. [Google Scholar]
- Ferguson, K.A.; Wong, E.C.; Chow, V.; Nigro, M.; Ma, S. Abnormal meiotic recombination in infertile men and its association with sperm aneuploidy. Hum. Mol. Genet 2007, 16, 2870–2879. [Google Scholar]
- Griffin, J.; Emery, B.R.; Christensen, G.L.; Carrell, D.T. Analysis of the meiotic recombination gene REC8 for sequence variations in a population with severe male factor infertility. Syst. Biol. Reprod. Med 2008, 54, 163–165. [Google Scholar]
- Hann, M.C.; Lau, P.E.; Tempest, H.G. Meiotic recombination and male infertility: From basic science to clinical reality? Asian J. Androl 2011, 13, 212–218. [Google Scholar]
- Baudat, F.; Nicolas, A. Clustering of meiotic double-strand breaks on yeast chromosome III. Proc. Natl. Acad. Sci. USA 1997, 94, 5213–5218. [Google Scholar]
- Klein, S.; Zenvirth, D.; Dror, V.; Barton, A.B.; Kaback, D.B.; Simchen, G. Patterns of meiotic double-strand breakage on native and artificial yeast chromosomes. Chromosoma 1996, 105, 276–284. [Google Scholar]
- Zenvirth, D.; Arbel, T.; Sherman, A.; Goldway, M.; Klein, S.; Simchen, G. Multiple sites for double-strand breaks in whole meiotic chromosomes of Saccharomyces cerevisiae. EMBO J 1992, 11, 3441–3447. [Google Scholar]
- Petes, T.D. Meiotic recombination hot spots and cold spots. Nat. Rev. Genet 2001, 2, 360–369. [Google Scholar]
- Kohl, K.P.; Sekelsky, J. Meiotic and mitotic recombination in meiosis. Genetics 2013, 194, 327–334. [Google Scholar]
- Lichten, M.; Goldman, A.S. Meiotic recombination hotspots. Ann. Rev. Genet 1995, 29, 423–444. [Google Scholar]
- Jeffreys, A.J.; Holloway, J.K.; Kauppi, L.; May, C.A.; Neumann, R.; Slingsby, M.T.; Webb, A.J. Meiotic recombination hot spots and human DNA diversity. Philos. Trans. R. Soc. Lond. Ser. B 2004, 359, 141–152. [Google Scholar]
- Wahls, W.P. Meiotic recombination hotspots: Shaping the genome and insights into hypervariable minisatellite DNA change. Curr. Top. Dev. Biol 1998, 37, 37–75. [Google Scholar]
- Liu, G.; Liu, J.; Cui, X.; Cai, L. Sequence-dependent prediction of recombination hotspots in Saccharomyces cerevisiae. J. Theor. Biol 2012, 293, 49–54. [Google Scholar]
- Chen, W.; Lin, H.; Feng, P.M.; Ding, C.; Zuo, Y.C.; Chou, K.C. iNuc-PhysChem: A sequence-based predictor for identifying nucleosomes via physicochemical properties. PLoS One 2012, 7, e47843. [Google Scholar]
- Chou, K.C. Prediction of G-protein-coupled receptor classes. J. Proteome Res 2005, 4, 1413–1418. [Google Scholar]
- Chou, K.C.; Elrod, D.W. Prediction of enzyme family classes. J. Proteome Res 2003, 2, 183–190. [Google Scholar]
- Wang, M.; Yang, J.; Xu, Z.J.; Chou, K.C. SLLE for predicting membrane protein types. J. Theor. Biol 2005, 232, 7–15. [Google Scholar]
- Xiao, X.; Wang, P.; Chou, K.C. Predicting protein structural classes with pseudo amino acid composition: An approach using geometric moments of cellular automaton image. J. Theor. Biol 2008, 254, 691–696. [Google Scholar]
- Chou, K.C. A novel approach to predicting protein structural classes in a 20–1-d amino acid composition space. Proteins: Struct. Funct. Genet 1995, 21, 319–344. [Google Scholar]
- Feng, K.Y.; Cai, Y.D.; Chou, K.C. Boosting classifier for predicting protein domain structural class. Biochem. Biophys. Res. Commun 2005, 334, 213–217. [Google Scholar]
- Cai, Y.D.; Chou, K.C. Artificial neural network for predicting alpha-turn types. Anal. Biochem 1999, 268, 407–409. [Google Scholar]
- Thompson, T.B.; Chou, K.C.; Zheng, C. Neural network prediction of the HIV-1 protease cleavage sites. J. Theor. Biol 1995, 177, 369–379. [Google Scholar]
- Feng, P.M.; Chen, W.; Lin, H.; Chou, K.C. iHSP-PseRAAAC: Identifying the heat shock protein families using pseudo reduced amino acid alphabet composition. Anal. Biochem 2013, 442, 118–125. [Google Scholar]
- Chen, W.; Feng, P.M.; Lin, H.; Chou, K.C. iRSpot-PseDNC: Identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Res 2013, 41, e69. [Google Scholar]
- Xiao, X.; Wang, P.; Chou, K.C. iNR-PhysChem: A sequence-based predictor for identifying nuclear receptors and their subfamilies via physical-chemical property matrix. PLoS One 2012, 7, e30869. [Google Scholar]
- Lin, W.Z.; Fang, J.A.; Xiao, X.; Chou, K.C. iDNA-Prot: Identification of DNA binding proteins using random forest with grey model. PLoS One 2011, 6, e24756. [Google Scholar]
- Kandaswamy, K.K.; Chou, K.C.; Martinetz, T.; Moller, S.; Suganthan, P.N.; Sridharan, S.; Pugalenthi, G. AFP-Pred: A random forest approach for predicting antifreeze proteins from sequence-derived properties. J. Theor. Biol 2011, 270, 56–62. [Google Scholar]
- Xu, Y.; Ding, J.; Wu, L.Y.; Chou, K.C. iSNO-PseAAC: Predict cysteine S-nitrosylation sites in proteins by incorporating position specific amino acid propensity into pseudo amino acid composition. PLoS One 2013, 8, e55844. [Google Scholar]
- Cai, Y.D.; Chou, K.C. Predicting subcellular localization of proteins in a hybridization space. Bioinformatics 2004, 20, 1151–1156. [Google Scholar]
- Chou, K.C.; Cai, Y.D. Prediction of protease types in a hybridization space. Biochem. Biophys. Res. Commun 2006, 339, 1015–1020. [Google Scholar]
- Chou, K.C.; Shen, H.B. Predicting eukaryotic protein subcellular location by fusing optimized evidence-theoretic K-nearest neighbor classifiers. J. Proteome Res 2006, 5, 1888–1897. [Google Scholar]
- Chou, K.C.; Shen, H.B. Hum-PLoc: A novel ensemble classifier for predicting human protein subcellular localization. Biochem. Biophys. Res. Commun 2006, 347, 150–157. [Google Scholar]
- Chou, K.C.; Shen, H.B. Large-scale predictions of Gram-negative bacterial protein subcellular locations. J. Proteome Res 2006, 5, 3420–3428. [Google Scholar]
- Chou, K.C.; Shen, H.B. Euk-mPLoc: A fusion classifier for large-scale eukaryotic protein subcellular location prediction by incorporating multiple sites. J. Proteome Res 2007, 6, 1728–1734. [Google Scholar]
- Chou, K.C.; Shen, H.B. Signal-CF: A subsite-coupled and window-fusing approach for predicting signal peptides. Biochem. Biophys. Res. Commun 2007, 357, 633–640. [Google Scholar]
- Shen, H.B.; Chou, K.C. Using optimized evidence-theoretic K-nearest neighbor classifier and pseudo amino acid composition to predict membrane protein types. Biochem. Biophys. Res. Commun 2005, 334, 288–292. [Google Scholar]
- Shen, H.B.; Chou, K.C. A top-down approach to enhance the power of predicting human protein subcellular localization: Hum-mPLoc 2.0. Anal. Biochem 2009, 394, 269–274. [Google Scholar]
- Xiao, X.; Wang, P.; Chou, K.C. GPCR-2L: Predicting G protein-coupled receptors and their types by hybridizing two different modes of pseudo amino acid compositions. Mol. Biosyst 2011, 7, 911–919. [Google Scholar]
- Shen, H.B.; Yang, J.; Chou, K.C. Fuzzy KNN for predicting membrane protein types from pseudo amino acid composition. J. Theor. Biol 2006, 240, 9–13. [Google Scholar]
- Xiao, X.; Min, J.L.; Wang, P.; Chou, K.C. iGPCR-Drug: A web server for predicting interaction between GPCRs and drugs in cellular networking. PLoS One 2013, 8, e72234. [Google Scholar]
- Xiao, X.; Min, J.L.; Wang, P.; Chou, K.C. iCDI-PseFpt: Identify the channel-drug interaction in cellular networking with PseAAC and molecular fingerprints. J. Theor. Biol 2013, 337C, 71–79. [Google Scholar]
- Xiao, X.; Wang, P.; Lin, W.Z.; Jia, J.H.; Chou, K.C. iAMP-2L: A two-level multi-label classifier for identifying antimicrobial peptides and their functional types. Anal. Biochem 2013, 436, 168–177. [Google Scholar]
- Chou, K.C. Prediction of protein cellular attributes using pseudo amino acid composition. Proteins: Struct. Funct. Genet 2001, 43, 246–255. [Google Scholar]
- Chou, K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics 2005, 21, 10–19. [Google Scholar]
- Lin, S.X.; Lapointe, J. Theoretical and experimental biology in one—A symposium in honour of Professor Kuo-Chen Chou’s 50th anniversary and Professor Richard Giegé’s 40th anniversary of their scientific careers. J. Biomed. Sci. Eng 2013, 6, 435–442. [Google Scholar]
- Nanni, L.; Lumini, A.; Gupta, D.; Garg, A. Identifying bacterial virulent proteins by fusing a set of classifiers based on variants of Chou’s pseudo amino acid composition and on evolutionary information. IEEE/ACM Trans. Comput. Biol. Bioinform 2012, 9, 467–475. [Google Scholar]
- Khosravian, M.; Faramarzi, F.K.; Beigi, M.M.; Behbahani, M.; Mohabatkar, H. Predicting antibacterial peptides by the concept of Chou’s pseudo-amino acid composition and machine learning methods. Protein Pept. Lett 2013, 20, 180–186. [Google Scholar]
- Yu, L.; Guo, Y.; Li, Y.; Li, G.; Li, M.; Luo, J.; Xiong, W.; Qin, W. SecretP: Identifying bacterial secreted proteins by fusing new features into Chou’s pseudo-amino acid composition. J. Theor. Biol 2010, 267, 1–6. [Google Scholar]
- Zou, D.; He, Z.; He, J.; Xia, Y. Supersecondary structure prediction using Chou’s pseudo amino acid composition. J. Comput. Chem 2011, 32, 271–278. [Google Scholar]
- Zhang, S.W.; Zhang, Y.L.; Yang, H.F.; Zhao, C.H.; Pan, Q. Using the concept of Chou’s pseudo amino acid composition to predict protein subcellular localization: An approach by incorporating evolutionary information and von Neumann entropies. Amino Acids 2008, 34, 565–572. [Google Scholar]
- Kandaswamy, K.K.; Pugalenthi, G.; Moller, S.; Hartmann, E.; Kalies, K.U.; Suganthan, P.N.; Martinetz, T. Prediction of apoptosis protein locations with genetic algorithms and support vector machines through a new mode of pseudo amino acid composition. Protein Pept. Lett 2010, 17, 1473–1479. [Google Scholar]
- Mei, S. Predicting plant protein subcellular multi-localization by Chou’s PseAAC formulation based multi-label homolog knowledge transfer learning. J. Theor. Biol 2012, 310, 80–87. [Google Scholar]
- Chang, T.H.; Wu, L.C.; Lee, T.Y.; Chen, S.P.; Huang, H.D.; Horng, J.T. EuLoc: A web-server for accurately predict protein subcellular localization in eukaryotes by incorporating various features of sequence segments into the general form of Chou’s PseAAC. J. Comput.-Aided Mol. Des 2013, 27, 91–103. [Google Scholar]
- Fan, G.L.; Li, Q.Z. Predict mycobacterial proteins subcellular locations by incorporating pseudo-average chemical shift into the general form of Chou’s pseudo amino acid composition. J. Theor. Biol 2012, 304, 88–95. [Google Scholar]
- Huang, C.; Yuan, J. Using radial basis function on the general form of Chou’s pseudo amino acid composition and PSSM to predict subcellular locations of proteins with both single and multiple sites. Biosystems 2013, 113, 50–57. [Google Scholar]
- Lin, H.; Wang, H.; Ding, H.; Chen, Y.L.; Li, Q.Z. Prediction of subcellular localization of apoptosis protein using Chou’s pseudo amino acid composition. Acta Biotheor 2009, 57, 321–330. [Google Scholar]
- Wan, S.; Mak, M.W.; Kung, S.Y. GOASVM: A subcellular location predictor by incorporating term-frequency gene ontology into the general form of Chou’s pseudo-amino acid composition. J. Theor. Biol 2013, 323, 40–48. [Google Scholar]
- Huang, C.; Yuan, J.Q. Predicting protein subchloroplast locations with both single and multiple sites via three different modes of Chou’s pseudo amino acid compositions. J. Theor. Biol 2013, 335, 205–212. [Google Scholar]
- Chen, Y.K.; Li, K.B. Predicting membrane protein types by incorporating protein topology, domains, signal peptides, and physicochemical properties into the general form of Chou’s pseudo amino acid composition. J. Theor. Biol 2013, 318, 1–12. [Google Scholar]
- Huang, C.; Yuan, J.Q. A Multilabel model based on Chou’s pseudo-amino acid composition for identifying membrane proteins with both single and multiple functional types. J. Membr. Biol 2013, 246, 327–334. [Google Scholar]
- Hayat, M.; Khan, A. Discriminating outer membrane proteins with fuzzy K-nearest neighbor algorithms based on the general form of Chou’s PseAAC. Protein Pept. Lett 2012, 19, 411–421. [Google Scholar]
- Mohabatkar, H.; Beigi, M.M.; Abdolahi, K.; Mohsenzadeh, S. Prediction of allergenic proteins by means of the concept of Chou’s pseudo amino acid composition and a machine learning approach. Med. Chem 2013, 9, 133–137. [Google Scholar]
- Mohammad Beigi, M.; Behjati, M.; Mohabatkar, H. Prediction of metalloproteinase family based on the concept of Chou’s pseudo amino acid composition using a machine learning approach. J. Struct. Funct. Genomics 2011, 12, 191–197. [Google Scholar]
- Sahu, S.S.; Panda, G. A novel feature representation method based on Chou’s pseudo amino acid composition for protein structural class prediction. Comput. Biol. Chem 2010, 34, 320–327. [Google Scholar]
- Zia Ur, R.; Khan, A. Identifying GPCRs and their types with Chou’s pseudo amino acid composition: An approach from multi-scale energy representation and position specific scoring matrix. Protein Pept. Lett 2012, 19, 890–903. [Google Scholar]
- Xie, H.L.; Fu, L.; Nie, X.D. Using ensemble SVM to identify human GPCRs N-linked glycosylation sites based on the general form of Chou’s PseAAC. Protein Eng. Des. Sel 2013, 26, 735–742. [Google Scholar]
- Zhang, S.W.; Chen, W.; Yang, F.; Pan, Q. Using Chou’s pseudo amino acid composition to predict protein quaternary structure: A sequence-segmented PseAAC approach. Amino Acids 2008, 35, 591–598. [Google Scholar]
- Sun, X.Y.; Shi, S.P.; Qiu, J.D.; Suo, S.B.; Huang, S.Y.; Liang, R.P. Identifying protein quaternary structural attributes by incorporating physicochemical properties into the general form of Chou’s PseAAC via discrete wavelet transform. Mol. BioSyst 2012, 8, 3178–3184. [Google Scholar]
- Nanni, L.; Lumini, A. Genetic programming for creating Chou’s pseudo amino acid based features for submitochondria localization. Amino Acids 2008, 34, 653–660. [Google Scholar]
- Fan, G.L.; Li, Q.Z. Predicting protein submitochondria locations by combining different descriptors into the general form of Chou’s pseudo amino acid composition. Amino Acids 2012, 43, 545–555. [Google Scholar]
- Mei, S. Multi-kernel transfer learning based on Chou’s PseAAC formulation for protein submitochondria localization. J. Theor. Biol 2012, 293, 121–130. [Google Scholar]
- Zeng, Y.H.; Guo, Y.Z.; Xiao, R.Q.; Yang, L.; Yu, L.Z.; Li, M.L. Using the augmented Chou’s pseudo amino acid composition for predicting protein submitochondria locations based on auto covariance approach. J. Theor. Biol 2009, 259, 366–372. [Google Scholar]
- Esmaeili, M.; Mohabatkar, H.; Mohsenzadeh, S. Using the concept of Chou’s pseudo amino acid composition for risk type prediction of human papillomaviruses. J. Theor. Biol 2010, 263, 203–209. [Google Scholar]
- Mohabatkar, H. Prediction of cyclin proteins using Chou’s pseudo amino acid composition. Protein Pept. Lett 2010, 17, 1207–1214. [Google Scholar]
- Mohabatkar, H.; Mohammad Beigi, M.; Esmaeili, A. Prediction of GABA(A) receptor proteins using the concept of Chou’s pseudo-amino acid composition and support vector machine. J. Theor. Biol 2011, 281, 18–23. [Google Scholar]
- Georgiou, D.N.; Karakasidis, T.E.; Nieto, J.J.; Torres, A. Use of fuzzy clustering technique and matrices to classify amino acids and its impact to Chou’s pseudo amino acid composition. J. Theor. Biol 2009, 257, 17–26. [Google Scholar]
- Zhang, G.Y.; Fang, B.S. Predicting the cofactors of oxidoreductases based on amino acid composition distribution and Chou’s amphiphilic pseudo amino acid composition. J. Theor. Biol 2008, 253, 310–315. [Google Scholar]
- Zhou, X.B.; Chen, C.; Li, Z.C.; Zou, X.Y. Using Chou’s amphiphilic pseudo-amino acid composition and support vector machine for prediction of enzyme subfamily classes. J. Theor. Biol 2007, 248, 546–551. [Google Scholar]
- Liu, B.; Wang, X.; Zou, Q.; Dong, Q.; Chen, Q. Protein remote homology detection by combining Chou’s pseudo amino acid composition and profile-based protein representation. Mol. Informa 2013, 32, 775–782. [Google Scholar]
- Georgiou, D.N.; Karakasidis, T.E.; Megaritis, A.C. A short survey on genetic sequences, Chou’s pseudo amino acid composition and its combination with fuzzy set theory. Open Bioinforma. J 2013, 7, 41–48. [Google Scholar]
- Hajisharifi, Z.; Piryaiee, M.; Mohammad Beigi, M.; Behbahani, M.; Mohabatkar, H. Predicting anticancer peptides with Chou’s pseudo amino acid composition and investigating their mutagenicity via Ames test. J. Theor. Biol 2014, 341, 34–40. [Google Scholar]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition (50th Anniversary Year Review). J. Theor. Biol 2011, 273, 236–247. [Google Scholar]
- Li, B.Q.; Huang, T.; Liu, L.; Cai, Y.D.; Chou, K.C. Identification of colorectal cancer related genes with mRMR and shortest path in protein-protein interaction network. PLoS One 2012, 7, e33393. [Google Scholar]
- Huang, T.; Wang, J.; Cai, Y.D.; Yu, H.; Chou, K.C. Hepatitis C virus network based classification of hepatocellular cirrhosis and carcinoma. PLoS One 2012, 7, e34460. [Google Scholar]
- Jiang, Y.; Huang, T.; Lei, C.; Gao, Y.F.; Cai, Y.D.; Chou, K.C. Signal propagation in protein interaction network during colorectal cancer progression. BioMed Res. Int 2013, 2013, 287019. [Google Scholar]
- Du, P.; Wang, X.; Xu, C.; Gao, Y. PseAAC-Builder: A cross-platform stand-alone program for generating various special Chou’s pseudo-amino acid compositions. Anal. Biochem 2012, 425, 117–119. [Google Scholar]
- Cao, D.S.; Xu, Q.S.; Liang, Y.Z. Propy: A tool to generate various modes of Chou’s PseAAC. Bioinformatics 2013, 29, 960–962. [Google Scholar]
- Shen, H.B.; Chou, K.C. PseAAC: A flexible web-server for generating various kinds of protein pseudo amino acid composition. Anal. Biochem 2008, 373, 386–388. [Google Scholar]
- Min, J.L.; Xiao, X.; Chou, K.C. iEzy-Drug: A web server for identifying the interaction between enzymes and drugs in cellular networking. BioMed Res. Int 2013, 2013, 701317. [Google Scholar]
- Xu, Y.; Shao, X.J.; Wu, L.Y.; Deng, N.Y.; Chou, K.C. iSNO-AAPair: Incorporating amino acid pairwise coupling into PseAAC for predicting cysteine S-nitrosylation sites in proteins. PeerJ 2013, 1, e171. [Google Scholar]
- Liu, B.; Zhang, D.; Xu, R.; Xu, J.; Wang, X.; Chen, Q.; Dong, Q.; Chou, K.C. Combining evolutionary information extracted from frequency profiles with sequence-based kernels for protein remote homology detection. Bioinformatics 2013. [Google Scholar] [CrossRef]
- Lin, H.; Ding, H. Predicting ion channels and their types by the dipeptide mode of pseudo amino acid composition. J. Theor. Biol 2011, 269, 64–69. [Google Scholar]
- Liu, W.; Chou, K.C. Protein secondary structural content prediction. Protein Eng 1999, 12, 1041–1050. [Google Scholar]
- Lin, H.; Li, Q.Z. Using pseudo amino acid composition to predict protein structural class: Approached by incorporating 400 dipeptide components. J. Comput. Chem 2007, 28, 1463–1466. [Google Scholar]
- Chou, K.C. Using pair-coupled amino acid composition to predict protein secondary structure content. J. Protein Chem 1999, 18, 473–480. [Google Scholar]
- Lin, H.; Ding, C.; Yuan, L.F.; Chen, W.; Ding, H.; Li, Z.Q.; Guo, F.B.; Hung, J.; Rao, N.N. Predicting subchloroplast locations of proteins based on the general form of Chou’s pseudo amino acid composition: Approached from optimal tripeptide composition. Int. J. Biomath 2013, 6, 1350003. [Google Scholar] [CrossRef]
- Tanford, C. Contribution of hydrophobic interactions to the stability of the globular conformation of proteins. J. Am. Chem. Soc 1962, 84, 4240–4274. [Google Scholar]
- Hopp, T.P.; Woods, K.R. Prediction of protein antigenic determinants from amino acid sequences. Proc. Natl. Acad. Sci. USA 1981, 78, 3824–3828. [Google Scholar]
- Robert, C.W. CRC Handbook of Chemistry and Physics, 66th ed.; CRC Press: Boca Raton, FL, USA, 1985. [Google Scholar]
- Dawson, R.M.C.; Elliott, D.C.; Elliott, W.H.; Jones, K.M. Data for Biochemical Research, 3rd ed.; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Chen, J.; Liu, H.; Yang, J.; Chou, K.C. Prediction of linear B-cell epitopes using amino acid pair antigenicity scale. Amino Acids 2007, 33, 423–428. [Google Scholar]
- Chou, K.C.; Cai, Y.D. Using functional domain composition and support vector machines for prediction of protein subcellular location. J. Biol. Chem 2002, 277, 45765–45769. [Google Scholar]
- Lin, W.Z.; Fang, J.A.; Xiao, X.; Chou, K.C. Predicting secretory proteins of malaria parasite by incorporating sequence evolution information into pseudo amino acid composition via grey system model. PLoS One 2012, 7, e49040. [Google Scholar]
- Wang, S.Q.; Yang, J.; Chou, K.C. Using stacked generalization to predict membrane protein types based on pseudo amino acid composition. J. Theor. Biol 2006, 242, 941–946. [Google Scholar]
- Cai, Y.D.; Zhou, G.P.; Chou, K.C. Support vector machines for predicting membrane protein types by using functional domain composition. Biophys. J 2003, 84, 3257–3263. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol 2011, 2, 1–27. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000; p. 189. [Google Scholar]
- Chou, K.C. Some remarks on predicting multi-label attributes in molecular biosystems. Mol. Biosyst 2013, 9, 1092–1100. [Google Scholar]
- Chou, K.C. Using subsite coupling to predict signal peptides. Protein Eng 2001, 14, 75–79. [Google Scholar]
- Chou, K.C. Prediction of protein signal sequences and their cleavage sites. Proteins: Struct. Funct. Genet 2001, 42, 136–139. [Google Scholar]
- Chou, K.C.; Wu, Z.C.; Xiao, X. iLoc-Euk: A multi-label classifier for predicting the subcellular localization of singleplex and multiplex eukaryotic proteins. PLoS One 2011, 6, e18258. [Google Scholar]
- Wu, Z.C.; Xiao, X.; Chou, K.C. iLoc-Plant: A multi-label classifier for predicting the subcellular localization of plant proteins with both single and multiple sites. Mol. BioSyst 2011, 7, 3287–3297. [Google Scholar]
- Wu, Z.C.; Xiao, X.; Chou, K.C. iLoc-Gpos: A multi-layer classifier for predicting the subcellular localization of singleplex and multiplex gram-positive bacterial proteins. Protein Pept. Lett 2012, 19, 4–14. [Google Scholar]
- Xiao, X.; Wu, Z.C.; Chou, K.C. iLoc-Virus: A multi-label learning classifier for identifying the subcellular localization of virus proteins with both single and multiple sites. J. Theor. Biol 2011, 284, 42–51. [Google Scholar]
- Xiao, X.; Wu, Z.C.; Chou, K.C. A multi-label classifier for predicting the subcellular localization of gram-negative bacterial proteins with both single and multiple sites. PLoS One 2011, 6, e20592. [Google Scholar]
- Chou, K.C.; Wu, Z.C.; Xiao, X. iLoc-Hum: Using accumulation-label scale to predict subcellular locations of human proteins with both single and multiple sites. Mol. Biosyst 2012, 8, 629–641. [Google Scholar]
- Lin, W.Z.; Fang, J.A.; Xiao, X.; Chou, K.C. iLoc-Animal: A multi-label learning classifier for predicting subcellular localization of animal proteins. Mol. Biosyst 2013, 9, 634–644. [Google Scholar]
- Chen, L.; Zeng, W.M.; Cai, Y.D.; Feng, K.Y.; Chou, K.C. Predicting Anatomical Therapeutic Chemical (ATC) classification of drugs by integrating chemical-chemical interactions and similarities. PLoS One 2012, 7, e35254. [Google Scholar]
- Chou, K.C.; Zhang, C.T. Review: Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol 1995, 30, 275–349. [Google Scholar]
- Fan, G.L.; Li, Q.Z. Discriminating bioluminescent proteins by incorporating average chemical shift and evolutionary information into the general form of Chou’s pseudo amino acid composition. J. Theor. Biol 2013, 334, 45–51. [Google Scholar]
- Qiu, J.D.; Huang, J.H.; Liang, R.P.; Lu, X.Q. Prediction of G-protein-coupled receptor classes based on the concept of Chou’s pseudo amino acid composition: an approach from discrete wavelet transform. Anal. Biochem 2009, 390, 68–73. [Google Scholar]
- Chou, K.C. Pseudo amino acid composition and its applications in bioinformatics, proteomics and system biology. Curr. Proteomics 2009, 6, 262–274. [Google Scholar]
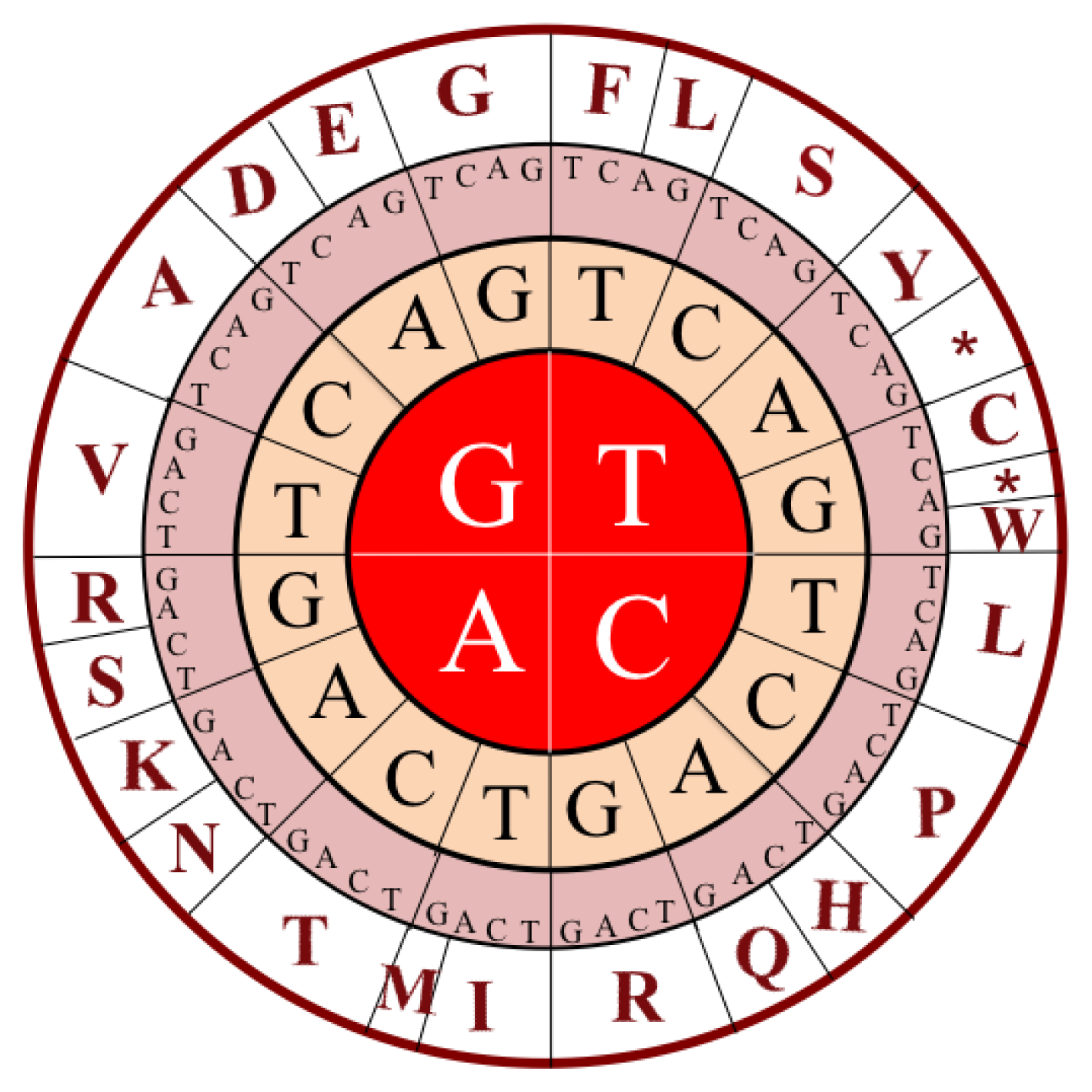

| Trinucleotide | Amino acid |
|---|---|
| AAA | Lys (K) |
| AAC | Asn (N) |
| AAG | Lys (K) |
| AAT | Asn (N) |
| ACA | Thr (T) |
| ACC | |
| ACG | |
| ACT | |
| AGA | Arg (R) |
| AGC | Ser (S) |
| AGG | Arg (R) |
| AGT | Ser (S) |
| ATA | Ile (I) |
| ATC | |
| ATG | Met (M) |
| ATT | Ile (I) |
| CAA | Gln (Q) |
| CAC | His (H) |
| CAG | Gln (Q) |
| CAT | His (H) |
| CCA | Pro (P) |
| CCC | |
| CCG | |
| CCT | |
| CGA | Arg (R) |
| CGC | |
| CGG | |
| CGT | |
| CTA | Leu (L) |
| CTC | |
| CTG | |
| CTT | |
| GAA | Glu (E) |
| GAC | Asp (D) |
| GAG | Glu (E) |
| GAT | Asp (D) |
| GCA | Ala (A) |
| GCC | |
| GCG | |
| GCT | |
| GGA | Gly (G) |
| GGC | |
| GGG | |
| GGT | |
| GTA | Val (V) |
| GTC | |
| GTG | |
| GTT | |
| TAA | Stop! |
| TAC | Tyr (Y) |
| TAG | Stop! |
| TAT | Tyr (Y) |
| TCA | Ser (S) |
| TCC | |
| TCG | |
| TCT | |
| TGA | Stop! |
| TGC | Cys (C) |
| TGG | Trp (W) |
| TGT | Cys (C) |
| TTA | Leu (L) |
| TTC | Phe (F) |
| TTG | Leu (L) |
| TTT | Phe (F) |
| Amino acid | Hydro-phobicity a | Hydro-philicity b | Side-chain mass c | pK1 d | pK2 e | PI f |
|---|---|---|---|---|---|---|
| A | 0.62 | −0.5 | 15 | 2.35 | 9.87 | 6.11 |
| C | 0.29 | −1.00 | 47 | 1.71 | 10.78 | 5.02 |
| D | −0.90 | 3.00 | 59 | 1.88 | 9.60 | 2.98 |
| E | −0.74 | 3.00 | 73 | 2.19 | 9.67 | 3.08 |
| F | 1.19 | −2.50 | 91 | 2.58 | 9.24 | 5.91 |
| G | 0.48 | 0.00 | 1 | 2.34 | 9.60 | 6.06 |
| H | −0.40 | −0.50 | 82 | 1.78 | 8.97 | 7.64 |
| I | 1.38 | −1.80 | 57 | 2.32 | 9.76 | 6.04 |
| K | −1.50 | 3.00 | 73 | 2.20 | 8.90 | 9.47 |
| L | 1.06 | −1.80 | 57 | 2.36 | 9.60 | 6.04 |
| M | 0.64 | −1.30 | 75 | 2.28 | 9.21 | 5.74 |
| N | −0.78 | 0.20 | 58 | 2.18 | 9.09 | 10.76 |
| P | 0.12 | 0.00 | 42 | 1.99 | 10.60 | 6.30 |
| Q | −0.85 | 0.20 | 72 | 2.17 | 9.13 | 5.65 |
| R | −2.53 | 3.00 | 101 | 2.18 | 9.09 | 10.76 |
| S | −0.18 | 0.30 | 31 | 2.21 | 9.15 | 5.68 |
| T | −0.05 | −0.40 | 45 | 2.15 | 9.12 | 5.60 |
| V | 1.08 | −1.50 | 43 | 2.29 | 9.74 | 6.02 |
| W | 0.81 | −3.40 | 130 | 2.38 | 9.39 | 5.88 |
| Y | 0.26 | −2.30 | 107 | 2.20 | 9.11 | 5.63 |
| Amino acid | H1 | H2 | H3 | H4 | H5 | H6 |
|---|---|---|---|---|---|---|
| A | 0.62 | −0.15 | −1.55 | 0.78 | 0.77 | −0.10 |
| C | 0.29 | −0.41 | −0.52 | −2.27 | 2.57 | −0.64 |
| D | −0.90 | 1.67 | −0.13 | −1.46 | 0.24 | −1.65 |
| E | −0.74 | 1.67 | 0.33 | 0.01 | 0.37 | −1.61 |
| F | 1.19 | −1.19 | 0.91 | 1.87 | −0.48 | −0.20 |
| G | 0.48 | 0.11 | −2.00 | 0.73 | 0.24 | −0.13 |
| H | −0.40 | −0.15 | 0.62 | −1.94 | −1.01 | 0.65 |
| I | 1.38 | −0.82 | −0.19 | 0.63 | 0.55 | −0.14 |
| K | −1.50 | 1.67 | 0.33 | 0.06 | −1.15 | 1.56 |
| L | 1.06 | −0.82 | −0.19 | 0.82 | 0.24 | −0.14 |
| M | 0.64 | −0.56 | 0.39 | 0.44 | −0.54 | −0.29 |
| N | −0.78 | 0.22 | −0.16 | −0.03 | −0.77 | 2.20 |
| P | 0.12 | 0.11 | −0.68 | −0.94 | 2.21 | −0.01 |
| Q | −0.85 | 0.22 | 0.29 | −0.08 | −0.69 | −0.33 |
| R | −2.53 | 1.67 | 1.23 | −0.03 | −0.77 | 2.20 |
| S | −0.18 | 0.27 | −1.03 | 0.11 | −0.65 | −0.32 |
| T | −0.05 | −0.10 | −0.58 | −0.18 | −0.71 | −0.36 |
| V | 1.08 | −0.67 | −0.65 | 0.49 | 0.51 | −0.15 |
| W | 0.81 | −1.65 | 2.17 | 0.92 | −0.18 | −0.22 |
| Y | 0.26 | −1.08 | 1.43 | 0.06 | −0.73 | −0.34 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Qiu, W.-R.; Xiao, X.; Chou, K.-C. iRSpot-TNCPseAAC: Identify Recombination Spots with Trinucleotide Composition and Pseudo Amino Acid Components. Int. J. Mol. Sci. 2014, 15, 1746-1766. https://doi.org/10.3390/ijms15021746
Qiu W-R, Xiao X, Chou K-C. iRSpot-TNCPseAAC: Identify Recombination Spots with Trinucleotide Composition and Pseudo Amino Acid Components. International Journal of Molecular Sciences. 2014; 15(2):1746-1766. https://doi.org/10.3390/ijms15021746
Chicago/Turabian StyleQiu, Wang-Ren, Xuan Xiao, and Kuo-Chen Chou. 2014. "iRSpot-TNCPseAAC: Identify Recombination Spots with Trinucleotide Composition and Pseudo Amino Acid Components" International Journal of Molecular Sciences 15, no. 2: 1746-1766. https://doi.org/10.3390/ijms15021746
APA StyleQiu, W.-R., Xiao, X., & Chou, K.-C. (2014). iRSpot-TNCPseAAC: Identify Recombination Spots with Trinucleotide Composition and Pseudo Amino Acid Components. International Journal of Molecular Sciences, 15(2), 1746-1766. https://doi.org/10.3390/ijms15021746




