Multiscale Models of the Antimicrobial Peptide Protegrin-1 on Gram-Negative Bacteria Membranes
Abstract
:1. Introduction
2. Results and Discussion
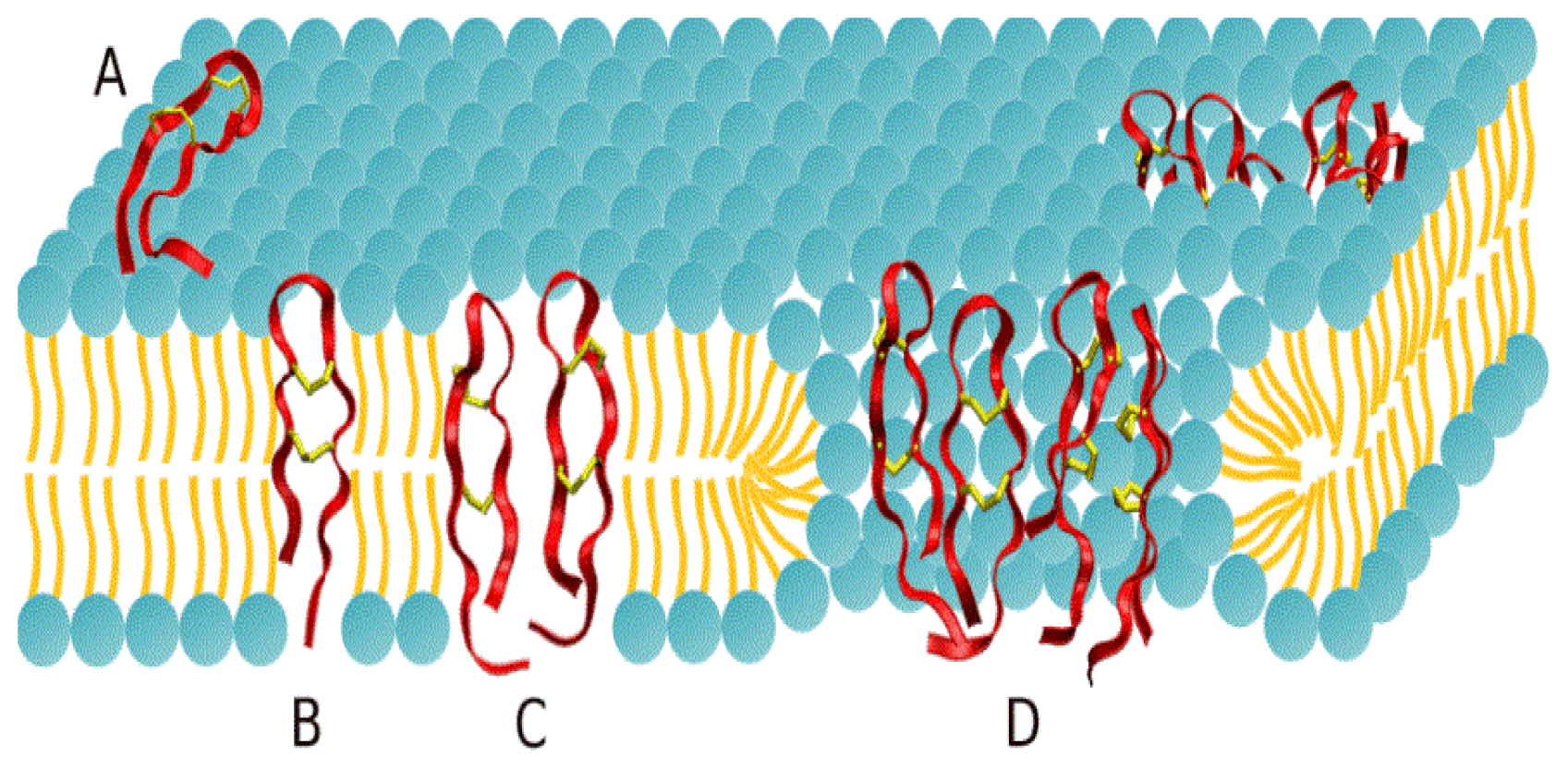
2.1. Potential of Mean Force Calculations
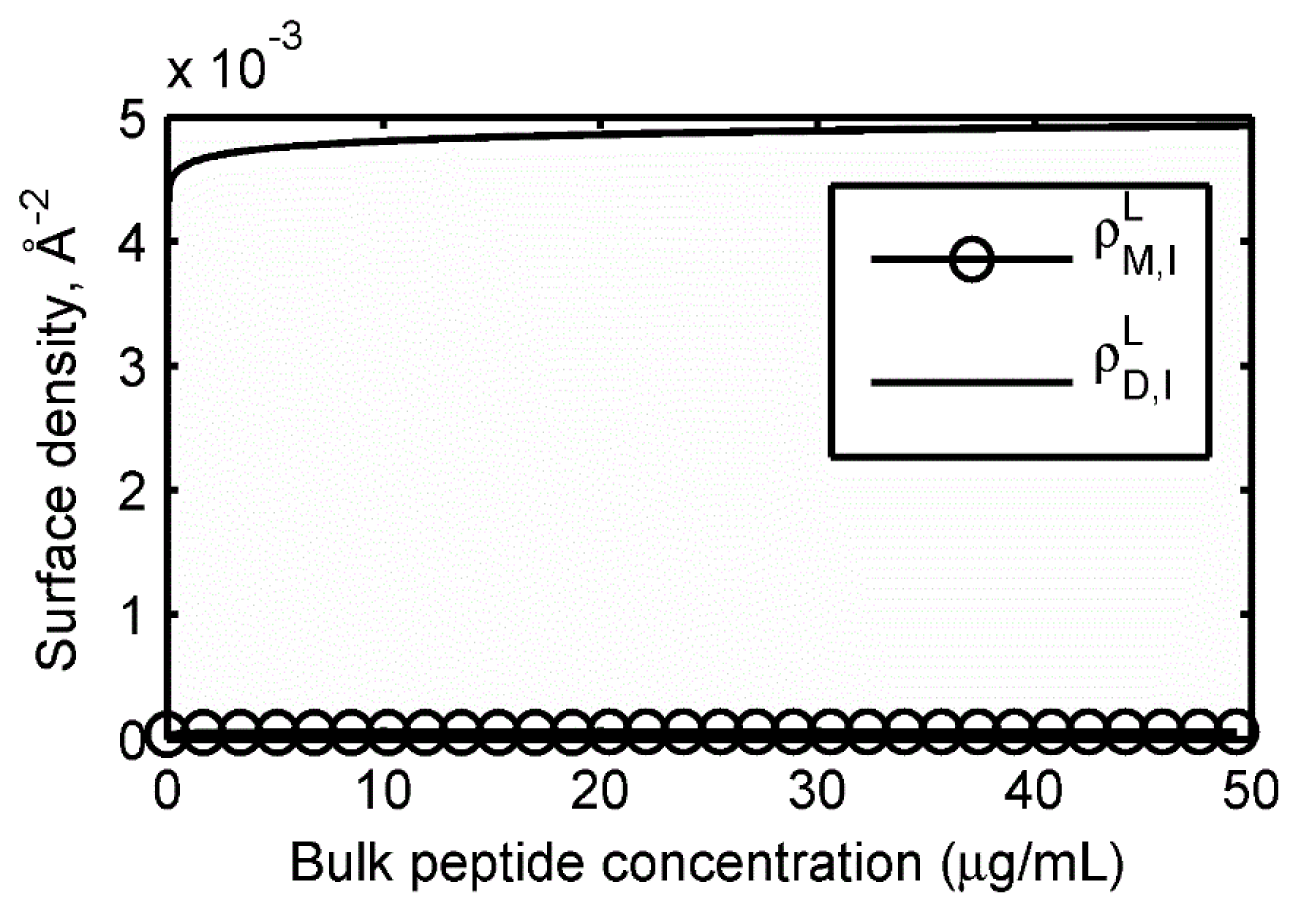
2.2. Adsorption Isotherms
2.3. Protegrin Pores and Ion Transport Models
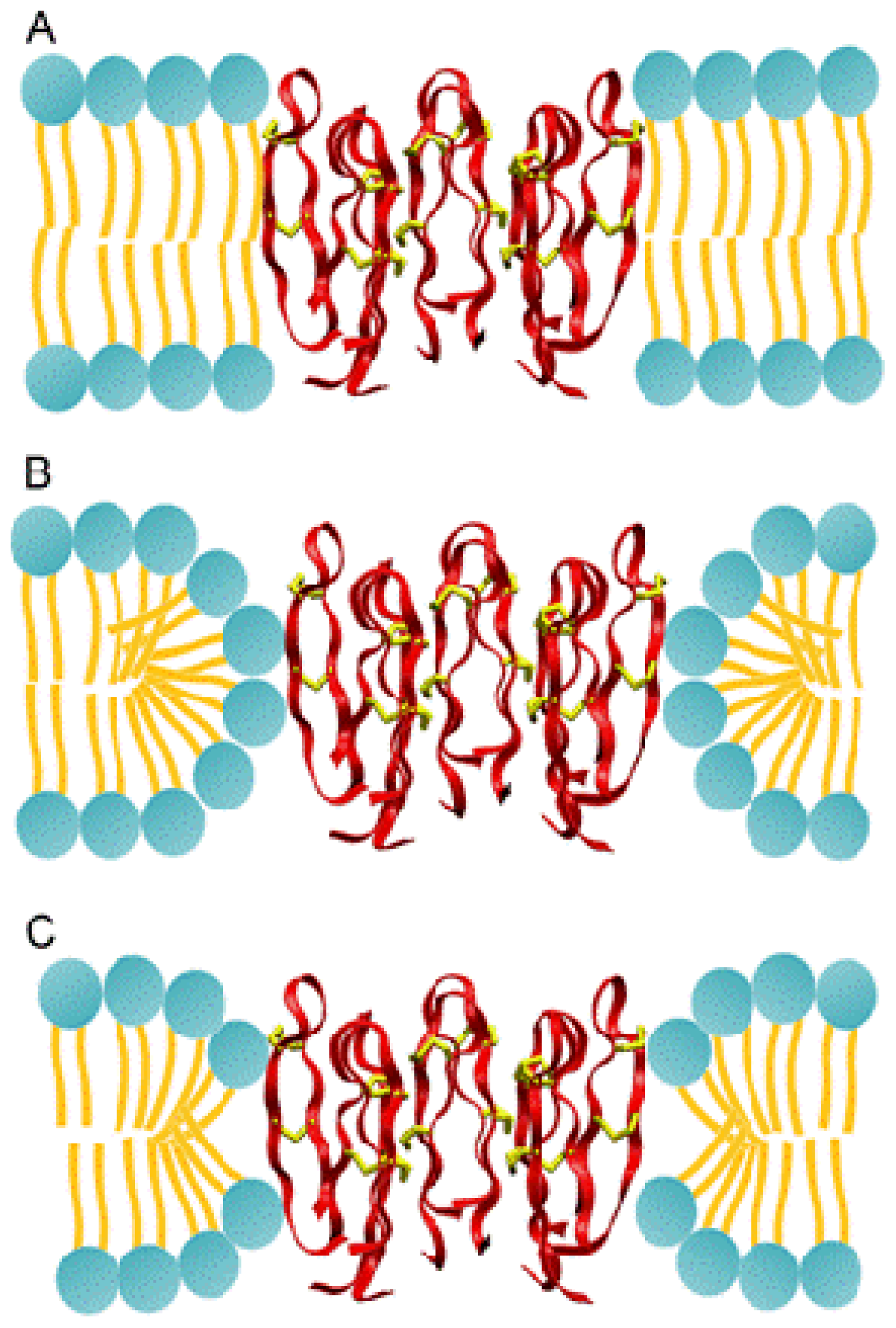
2.3.1. Molecular Simulations of Protegrin Pores
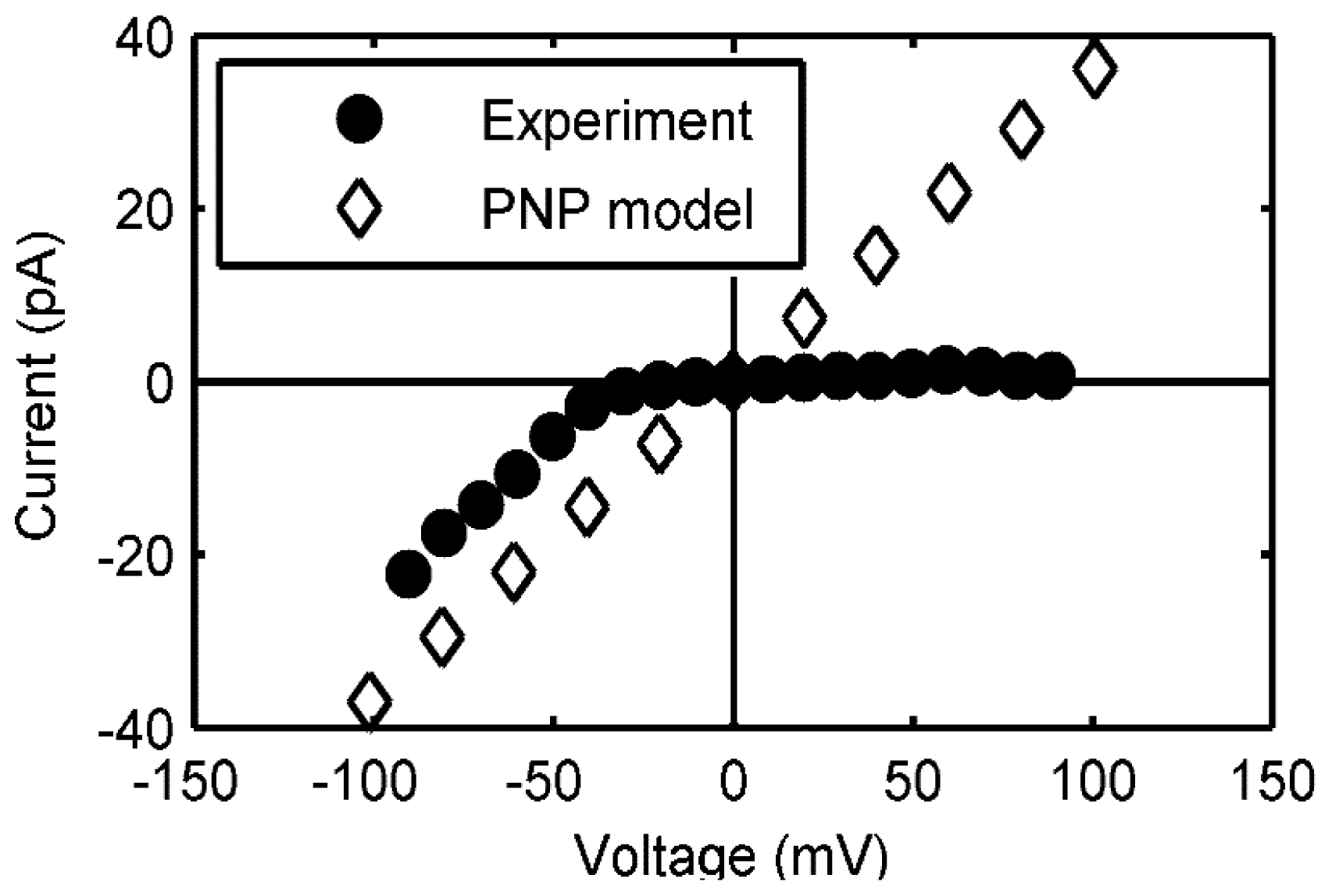
2.3.2. Continuum Electrodiffusion Models
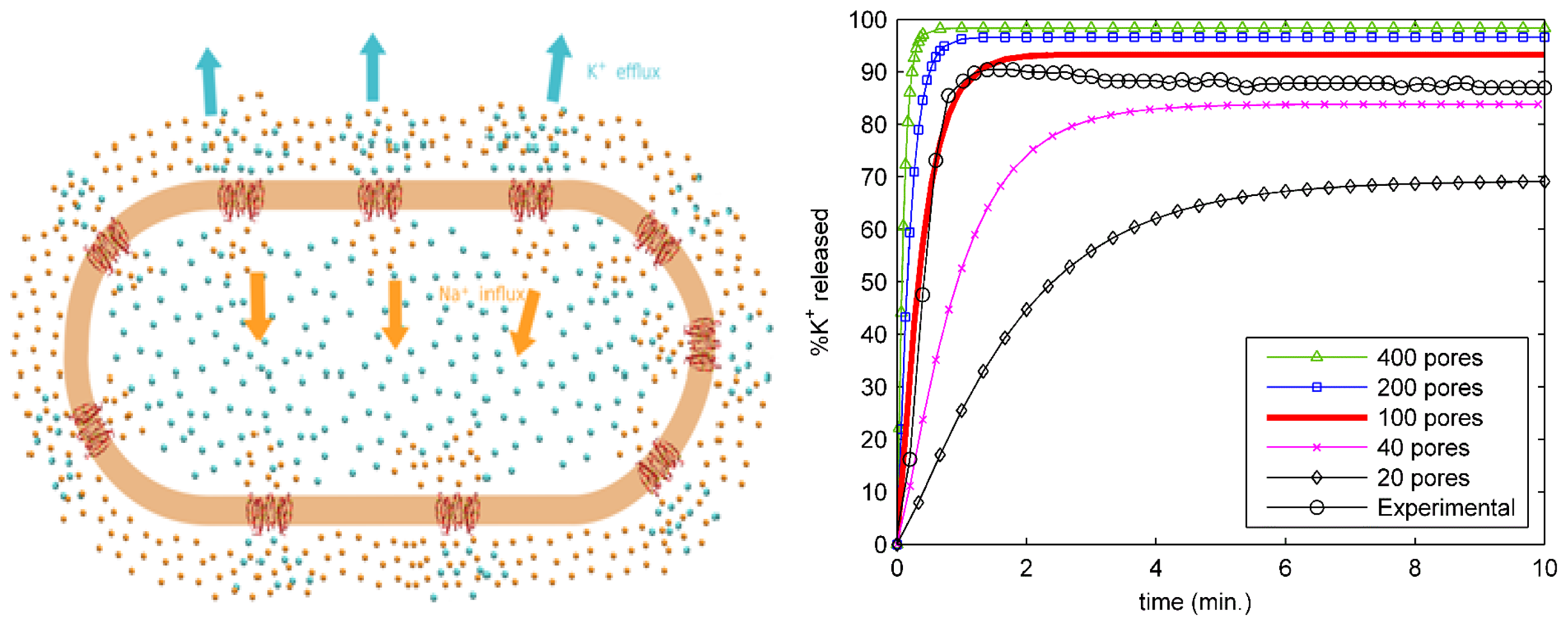
2.4. Ion Transport from an Entire Bacterial Cell
3. Conclusions
Acknowledgments
References
- Boucher, H.W.; Talbot, G.H.; Bradley, J.S.; Edwards, J.E.; Gilbert, D.; Rice, L.B.; Scheld, M.; Spellberg, B.; Bartlett, J. Bad bugs, no drugs: No ESKAPE! An update from the infectious diseases society of america. Clin. Infect. Dis 2009, 48, 1–12. [Google Scholar]
- Zasloff, M. Antimicrobial peptides of multicellular organisms. Nature 2002, 415, 389–395. [Google Scholar]
- Brogden, K.A. Antimicrobial peptides: Pore formers or metabolic inhibitors in bacteria? Nat. Rev. Microbiol 2005, 3, 238–250. [Google Scholar]
- Kokryakov, N.V.; Harwig, S.S.L.; Panyutich, E.A.; Shevchenko, A.A.; Aleshina, G.M.; Shamova, O.V.; Korneva, H.A.; Lehrer, R.I. Protegrins: Leukocyte antimicrobial peptides that combine features of corticostatic defensins and tachyplesins. FEBS Lett 1993, 327, 231–236. [Google Scholar]
- Mangoni, M.E.; Aumelas, A.; Charnet, P.; Roumestand, C.; Chiche, L.; Despaux, E.; Grassy, G.; Calas, B.; Chavanieu, A. Change in membrane permeability induced by protegrin 1: Implication of disulphide bridges for pore formation. FEBS Lett 1996, 383, 93–98. [Google Scholar]
- Sokolov, Y.; Mirzabekov, T.; Martin, D.W.; Lehrer, R.I.; Kagan, B.L. Membrane channel formation by antimicrobial protegrins. Biochim. Biophys. Acta 1999, 1420, 23–29. [Google Scholar]
- Neville, F.; Ishitsuka, Y.; Hodges, C.S.; Konovalov, O.; Waring, A.J.; Lehrer, R.; Lee, K.Y.; Gidalevitz, D. Protegrin interaction with lipid monolayers: Grazing incidence X-ray diffraction and X-ray reflectivity study. Soft Matter 2008, 4, 1665–1674. [Google Scholar]
- Gidalevitz, D.; Ishitsuka, Y.; Muresan, A.S.; Konovalov, O.; Waring, A.J.; Lehrer, R.I.; Lee, K.Y. Interaction of antimicrobial peptide protegrin with biomembranes. Proc. Natl. Acad Sci. USA 2003, 100, 6302–6307. [Google Scholar]
- Langham, A.A.; Ahmad, A.S.; Kaznessis, Y.N. On the nature of antimicrobial activity: A model for protegrin-1 pores. J. Am. Chem. Soc 2008, 130, 4338–4346. [Google Scholar]
- Bolintineanu, D.S.; Hazrati, E.; Davis, H.T.; Lehrer, R.I.; Kaznessis, Y.N. Antimicrobial mechanism of pore-forming protegrin peptides: 100 pores to kill E. coli. Peptides 2010, 31, 1–8. [Google Scholar]
- Bolintineanu, D.S.; Kaznessis, Y.N. Computational studies of protegrin antimicrobial peptides: A review. Peptides 2011, 32, 188–201. [Google Scholar]
- Vivcharuk, V.; Kaznessis, Y. Free energy profile of the interaction between a monomer or a dimer of protegrin-1 in a specific binding orientation and a model lipid bilayer. J. Phys. Chem. B 2010, 114, 2790–2797. [Google Scholar]
- Vivcharuk, V.; Kaznessis, Y.N. Dimerization of protegrin-1 in different environments. Int. J. Mol. Sci 2010, 11, 3177–3194. [Google Scholar]
- Vivcharuk, V.; Kaznessis, Y. Thermodynamic Analysis of Protegrin-1 Insertion and Permeation through a Lipid Bilayer. 2011, 115, 14704–14712. [Google Scholar]
- Kaznessis, Y.N. Statistical Thermodynamics and Stochastic Kinetics; Cambridge University Press: Cambridge, UK; p. 2012.
- Talbot, J. Molecular thermodynamics of binary mixture adsorption: A scaled particle theory approach. J. Chem. Phys 1997, 106, 4696–4706. [Google Scholar]
- Zuckermann, M.J.; Heimburg, T. Insertion and pore formation driven by adsorption of proteins onto lipid bilayer membrane-water interfaces. Biophys. J 2001, 81, 2458–2472. [Google Scholar]
- Reiss, H.; Frisch, H.L.; Lebowitz, J.L. Statistical mechanics of rigid spheres. J. Chem. Phys 1959, 31, 369–380. [Google Scholar]
- Matsuzaki, K.; Murase, O.; Fujii, N.; Miyajima, K. An antimicrobial peptide, magainin 2, induced rapid flip-flop of phospholipids coupled with pore formation and peptide translocation. Biochemistry 1996, 35, 11361–11368. [Google Scholar]
- Huang, H.W.; Chen, F.Y.; Lee, M.T. Molecular mechanism of peptide-induced pores in membranes. Phys. Rev. Lett 2004, 92, 198304. [Google Scholar]
- Mani, R.; Cady, S.D.; Tang, M.; Waring, A.J.; Lehrer, R.I.; Hong, M. Membrane-dependent oligomeric structure and pore formation of a beta-hairpin antimicrobial peptide in lipid bilayers from solid-state NMR. Proc. Natl. Acad Sci. USA 2006, 103, 16242–16247. [Google Scholar]
- Bolintineanu, D.S.; Sayyed-Ahmad, A.; Davis, H.T.; Kaznessis, Y.N. Poisson-Nernst-Planck models of nonequilibrium ion electrodiffusion through a protegrin transmembrane pore. PLoS Comput. Biol 2009, 5, e1000277. [Google Scholar]
- Langham, A.; Kaznessis, Y.N. Molecular simulations of antimicrobial peptides. Methods Mol. Biol 2010, 618, 267–285. [Google Scholar]
- Sayyed-Ahmad, A.; Kaznessis, Y.N. Determining the orientation of protegrin-1 in DLPC bilayers using an implicit solvent-membrane model. PLoS One 2009, 4, e4799. [Google Scholar]
- Langham, A.A.; Khandelia, H.; Schuster, B.; Waring, A.; Lehrer, R.; Kaznessis, Y. Correlation between simulated physicochemical properties and hemolycity of protegrin-like antimicrobial peptides: Predicting experimental toxicity. Peptides 2008, 29, 1085–1093. [Google Scholar]
- Bolintineanu, D.S.; Langham, A.; Davis, T.H.; Kaznessis, Y. Molecular dynamics simulations of three protegrin-type anti-microbial peptides: interplay between charges at the termini, beta-sheet structure and amphiphilic interactions. Mol. Simul 2007, 33, 809–819. [Google Scholar]
- Langham, A.A.; Waring, A.J.; Kaznessis, Y. Comparison of interactions between beta-hairpin decapeptides and SDS/DPC micelles from experimental and simulation data. BMC Biochem 2007, 8, 11. [Google Scholar]
- Khandelia, H.; Kaznessis, Y. Structure of the antimicrobial beta-hairpin peptide protegrin-1 in a DLPC lipid bilayer investigated by molecular dynamics Simulation. Biochim. Biophys. Acta 2007, 1768, 509–520. [Google Scholar]
- Khandelia, H.; Kaznessis, Y. Cation-π Interactions stabilize the structure of the antimicrobial peptide indolicidin near membranes: Molecular dynamics simulations. J. Phys. Chem. B 2007, 111, 242–250. [Google Scholar]
- Langham, A.A.; Kaznessis, Y. Effects of mutations on the C-terminus of protegrin-1: A molecular dynamics simulation study. Mol. Simul 2006, 32, 193–201. [Google Scholar]
- Khandelia, H.; Langham, A.; Kaznessis, Y. Driving engineering of novel antimicrobial peptides from simulations of peptide-micelle interactions. Biochim. Biophys. Acta 2006, 1758, 1224–1234. [Google Scholar]
- Khandelia, H.; Kaznessis, Y. Molecular dynamics investigation of the influence of anionic and zwitterionic interfaces on antimicrobial peptides’ structure: Implications on peptide toxicity and activity. Peptides 2006, 27, 1192–1200. [Google Scholar]
- Langham, A.A.; Khandelia, H.; Kaznessis, Y. How can protegrin-1 be both a potent antimicrobial and harmfully toxic? Molecular dynamics simulations of a beta-sheet antimicrobial peptide in micelles. Biopolym. Pept. Sci 2006, 84, 219–231. [Google Scholar]
- Khandelia, H.; Kaznessis, Y. Molecular dynamics simulations of helical antimicrobial peptides in SDS micelles: What do point mutations achieve? Peptides 2005, 26, 2037–2049. [Google Scholar]
- Sayyed-Ahmad, A.; Khandelia, H.; Kaznessis, Y.N. Relative free energy of binding between antimicrobial peptides and SDS or DPC micelles. Mol. Simul 2009, 35, 986–997. [Google Scholar]
- Langham, A.; Kaznessis, Y. Molecular dynamics simulations of the N-terminus of HIV GP-41 fusion peptide in SDS micelles. J. Pept. Sci 2005, 14, 316–328. [Google Scholar]
- Ostberg, N.; Khandelia, H.; Kaznessis, Y. Protegrin structure activity relationships: Using homology models of synthetic sequences to determine structural characteristics important for activity. Peptides 2005, 26, 297–306. [Google Scholar]
- Mulakala, C.; Lambris, J.D.; Kaznessis, Y. A simple, yet highly accurate, QSAR model captures the complement inhibitory activity of compstatin. Bioorg. Med. Chem 2007, 15, 1638–1644. [Google Scholar]
- Wang, W.; Mulakala, C.; Ward, S.C.; Jung, G.; Luong, H.; Pham, D.; Waring, A.J.; Kaznessis, Y.; Lu, W.; Bradley, K.A.; et al. Retrocyclins kill bacilli and germinating spores of Bacillus anthracis and inactivate anthrax lethal toxin. J. Biol. Chem 2006, 281, 32755–32764. [Google Scholar]
- Chiu, T.-L.; Mulakala, C.; Lambris, J.D.; Kaznessis, Y.N. Development of a new pharmacophore model that discriminates active compstatin analogs. Chem. Biol. Drug Des 2008, 72, 249–256. [Google Scholar]



© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bolintineanu, D.S.; Vivcharuk, V.; Kaznessis, Y.N. Multiscale Models of the Antimicrobial Peptide Protegrin-1 on Gram-Negative Bacteria Membranes. Int. J. Mol. Sci. 2012, 13, 11000-11011. https://doi.org/10.3390/ijms130911000
Bolintineanu DS, Vivcharuk V, Kaznessis YN. Multiscale Models of the Antimicrobial Peptide Protegrin-1 on Gram-Negative Bacteria Membranes. International Journal of Molecular Sciences. 2012; 13(9):11000-11011. https://doi.org/10.3390/ijms130911000
Chicago/Turabian StyleBolintineanu, Dan S., Victor Vivcharuk, and Yiannis N. Kaznessis. 2012. "Multiscale Models of the Antimicrobial Peptide Protegrin-1 on Gram-Negative Bacteria Membranes" International Journal of Molecular Sciences 13, no. 9: 11000-11011. https://doi.org/10.3390/ijms130911000



