Förster Resonance Energy Transfer (FRET) Correlates of Altered Subunit Stoichiometry in Cys-Loop Receptors, Exemplified by Nicotinic α4β2
Abstract
:1. Introduction
2. Results and Discussion
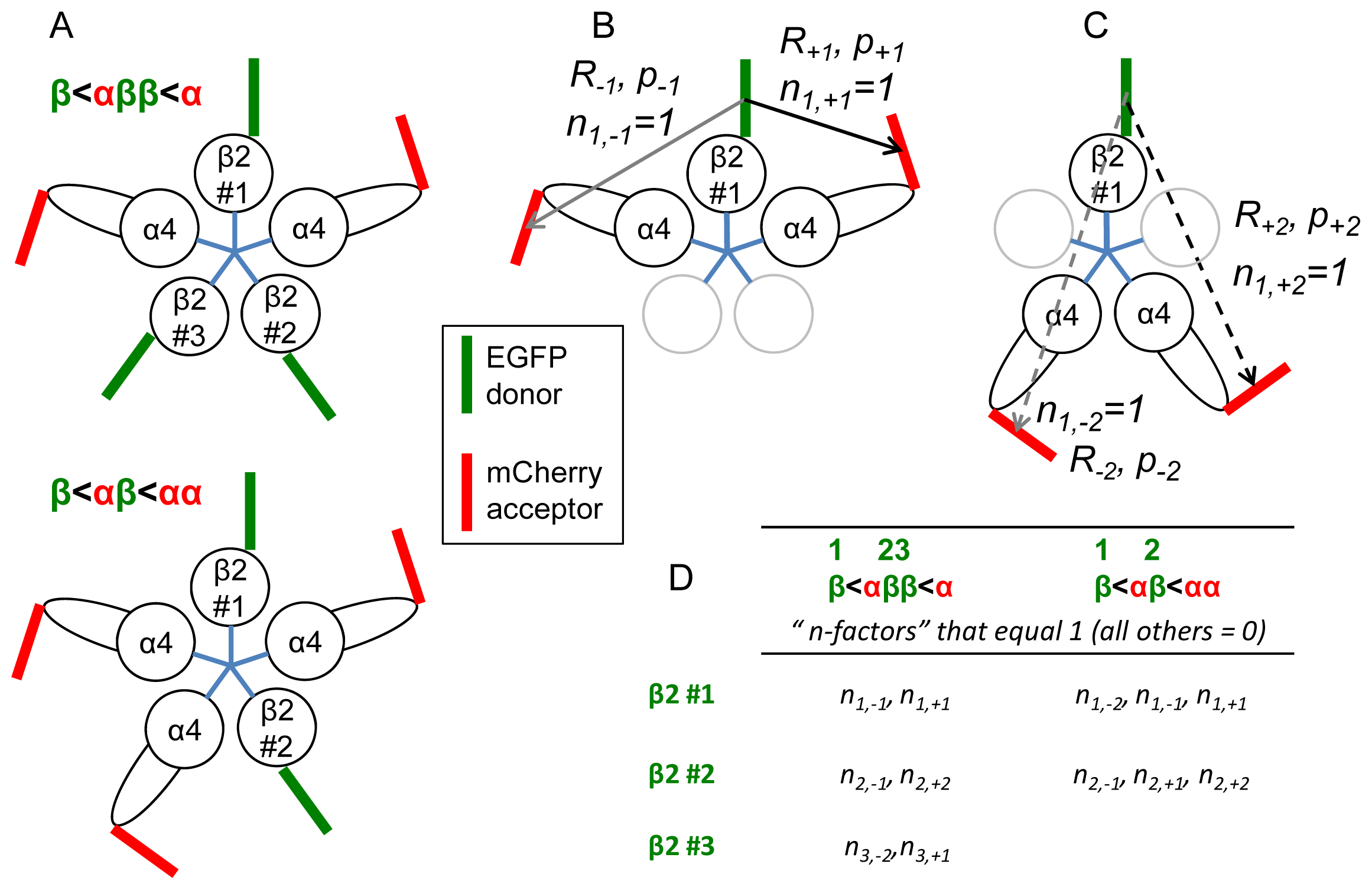
2.1. Simulations
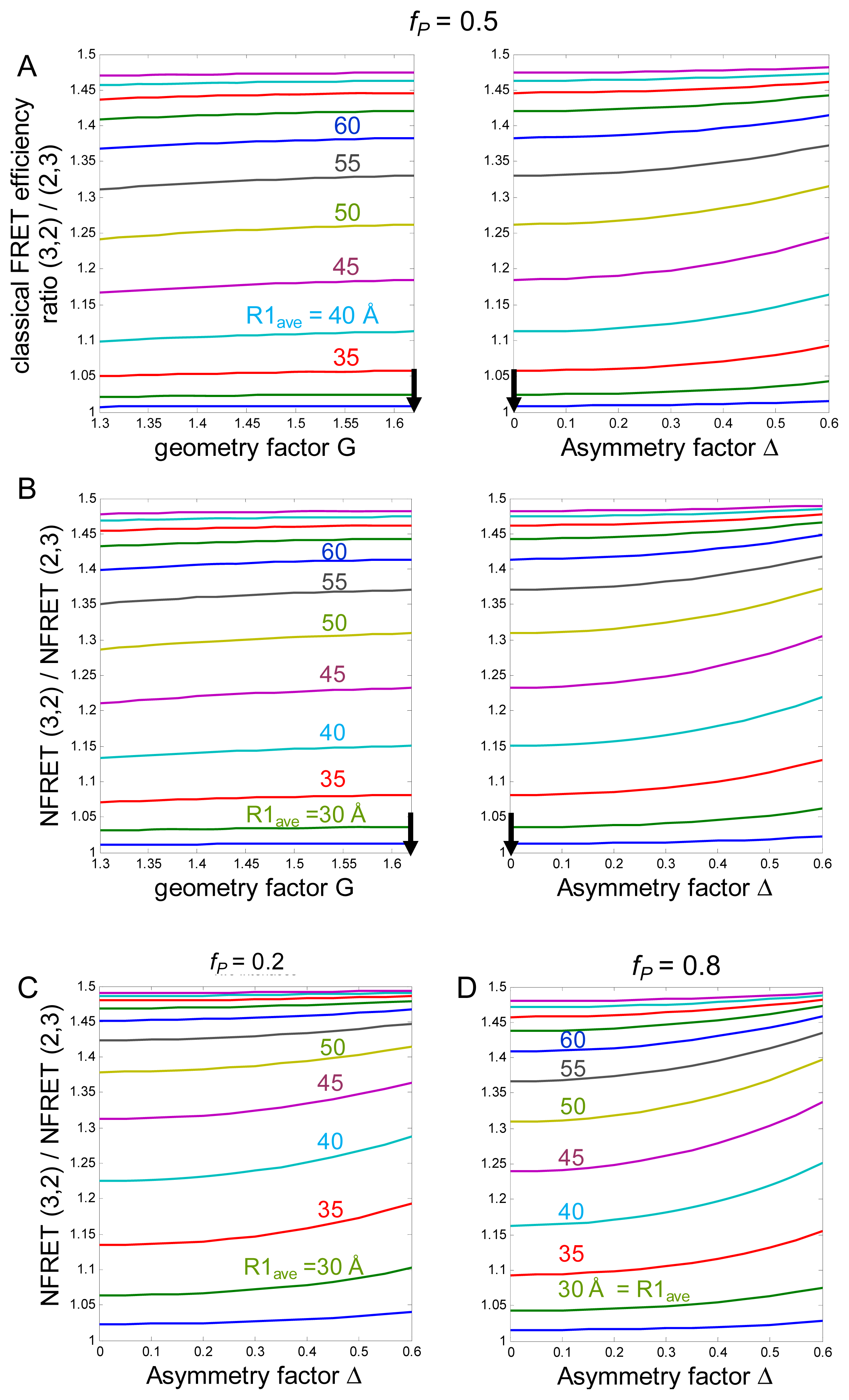
2.1.1. Calculations of NFRET
2.1.2. Summary of the Predictions
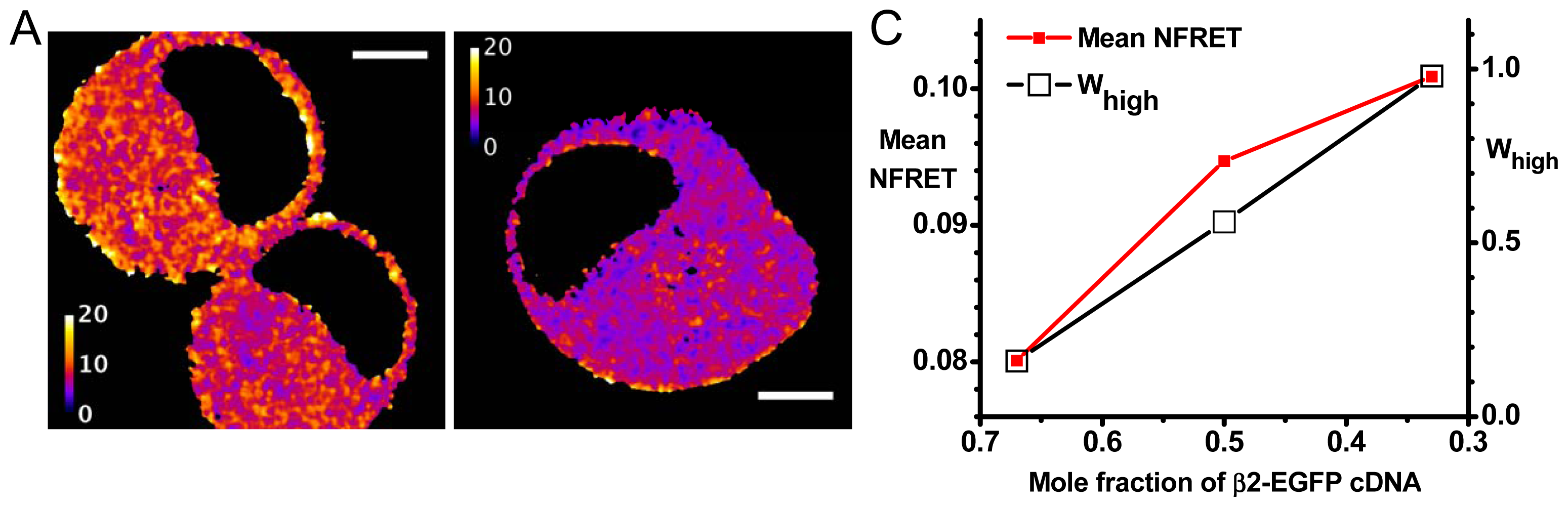
2.2. Agreement with Biased Transfection Experiments
2.2.1. Further Analysis Based on Distinct Populations
2.2.2. Variations in Stoichiometry among Pixels and among Cells
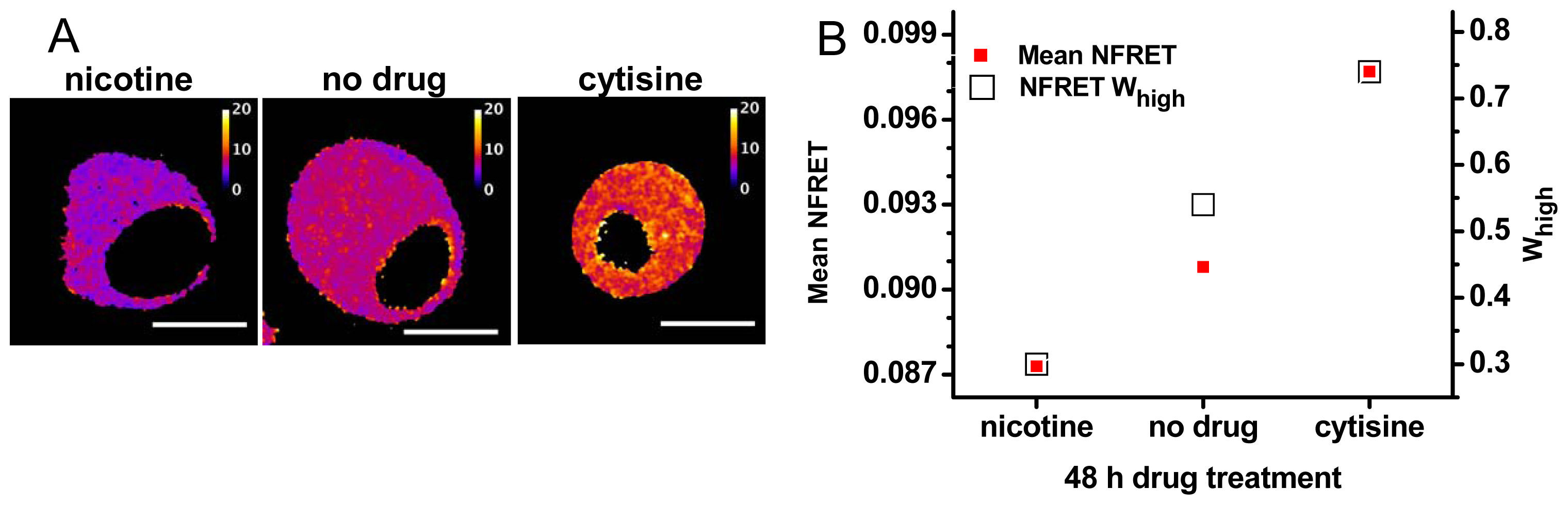
2.3. Pharmacological Chaperoning Stabilizes Alternative α4β2 Stoichiometries
2.4. One vs. Two β2 < α4 Subunit Interfaces
2.5. Requirements for the Procedure
3. Conclusions
3.1. Investigations that Might Use the Procedures
3.2. Other Cys-Loop Receptors
Supplementary Materials
ijms-13-10022-s001.pdfAcknowledgments
Abbreviations
| EGFP | enhanced green fluorescent protein |
| ER | endoplasmic reticulum |
| FRET | Förster resonance energy transfer |
| nAChR | neuronal nicotinic acetylcholine receptors |
| mCherry | monomeric cherry fluorescent protein |
| NFRET | normalized Förster resonance energy transfer |
References
- Zwart, R.; Vijverberg, H.P. Four pharmacologically distinct subtypes of α4β2 nicotinic acetylcholine receptor expressed in Xenopus laevis oocytes. Mol. Pharmacol 1998, 54, 1124–1131. [Google Scholar]
- Moroni, M.; Zwart, R.; Sher, E.; Cassels, B.K.; Bermudez, I. α4β2 nicotinic receptors with high and low acetylcholine sensitivity: Pharmacology, stoichiometry, and sensitivity to long-term exposure to nicotine. Mol. Pharmacol 2006, 70, 755–768. [Google Scholar]
- Xiu, X.; Puskar, N.L.; Shanata, J.A.; Lester, H.A.; Dougherty, D.A. Nicotine binding to brain receptors requires a strong cation-π interaction. Nature 2009, 458, 534–537. [Google Scholar]
- Tapia, L.; Kuryatov, A.; Lindstrom, J. Ca2+ permeability of the (α4)3(β2)2 stoichiometry greatly exceeds that of (α4)2(β2)3 human acetylcholine receptors. Mol. Pharmacol 2007, 71, 769–776. [Google Scholar]
- Nelson, M.E.; Kuryatov, A.; Choi, C.H.; Zhou, Y.; Lindstrom, J. Alternate stoichiometries of α4β2 nicotinic acetylcholine receptors. Mol. Pharmacol 2003, 63, 332–341. [Google Scholar]
- Srinivasan, R.; Pantoja, R.; Moss, F.J.; Mackey, E.D.W.; Son, C.; Miwa, J.; Lester, H.A. Nicotine upregulates α4β2 nicotinic receptors and ER exit sites via stoichiometry-dependent chaperoning. J. Gen. Physiol 2011, 137, 59–79. [Google Scholar]
- Commons, K.G. α4 containing nicotinic receptors are positioned to mediate postsynaptic effects on 5-HT neurons in the rat dorsal raphe nucleus. Neuroscience 2008, 153, 851–859. [Google Scholar]
- Shapiro, M.S.; Hille, B. Substance P and somatostatin inhibit calcium channels in rat sympathetic neurons via different G protein pathways. Neuron 1993, 10, 11–20. [Google Scholar]
- Sallette, J.; Pons, S.; Devillers-Thiery, A.; Soudant, M.; de Carvalho, L.P.; Changeux, J.P.; Corringer, P.J. Nicotine upregulates its own receptors through enhanced intracellular maturation. Neuron 2005, 46, 595–607. [Google Scholar]
- Kuryatov, A.; Luo, J.; Cooper, J.; Lindstrom, J. Nicotine acts as a pharmacological chaperone to up-regulate human α4β2 acetylcholine receptors. Mol. Pharmacol 2005, 68, 1839–1851. [Google Scholar]
- Lester, H.A.; Xiao, C.; Srinivasan, R.; Son, C.; Miwa, J.; Pantoja, R.; Dougherty, D.A.; Banghart, M.R.; Goate, A.M.; Wang, J.C. Nicotine is a selective pharmacological chaperone of acetylcholine receptor number and stoichiometry. Implications for drug discovery. AAPS J 2009, 11, 167–177. [Google Scholar]
- Miwa, J.M.; Freedman, R.; Lester, H.A. Neural systems governed by nicotinic acetylcholine receptors: Emerging hypotheses. Neuron 2011, 70, 20–33. [Google Scholar]
- Gopalakrishnan, M.; Molinari, E.J.; Sullivan, J.P. Regulation of human α4β2 neuronal nicotinic acetylcholine receptors by cholinergic channel ligands and second messenger pathways. Mol. Pharmacol 1997, 52, 524–534. [Google Scholar]
- Whiteaker, P.; Sharples, C.G.; Wonnacott, S. Agonist-induced up-regulation of α4β2 nicotinic acetylcholine receptors in M10 cells: Pharmacological and spatial definition. Mol. Pharmacol 1998, 53, 950–962. [Google Scholar]
- Kishi, M.; Steinbach, J.H. Role of the agonist binding site in up-regulation of neuronal nicotinic α4β2 receptors. Mol. Pharmacol 2006, 70, 2037–2044. [Google Scholar]
- Nashmi, R.; Dickinson, M.E.; McKinney, S.; Jareb, M.; Labarca, C.; Fraser, S.E.; Lester, H.A. Assembly of α4β2 nicotinic acetylcholine receptors assessed with functional fluorescently labeled subunits: Effects of localization, trafficking, and nicotine-induced upregulation in clonal mammalian cells and in cultured midbrain neurons. J. Neurosci 2003, 23, 11554–11567. [Google Scholar]
- Drenan, R.M.; Nashmi, R.; Imoukhuede, P.I.; Just, H.; McKinney, S.; Lester, H.A. Subcellular trafficking, pentameric assembly and subunit stoichiometry of neuronal nicotinic ACh receptors containing Fluorescently-Labeled α6 and β3 subunits. Mol. Pharmacol 2008, 73, 27–41. [Google Scholar]
- Son, C.D.; Moss, F.J.; Cohen, B.N.; Lester, H.A. Nicotine normalizes intracellular subunit stoichiometry of nicotinic receptors carrying mutations linked to autosomal dominant nocturnal frontal lobe epilepsy. Mol. Pharmacol 2009, 75, 1137–1148. [Google Scholar]
- Moss, F.J.; Imoukhuede, P.I.; Scott, K.; Hu, J.; Jankowsky, J.L.; Quick, M.W.; Lester, H.A. GABA transporter function, oligomerization state, and anchoring: Correlates with subcellularly resolved FRET. J. Gen. Physiol 2009, 134, 489–521. [Google Scholar]
- Corry, B.; Jayatilaka, D.; Rigby, P. A flexible approach to the calculation of resonance energy transfer efficiency between multiple donors and acceptors in complex geometries. Biophys. J 2005, 89, 3822–3836. [Google Scholar]
- Corry, B.; Jayatilaka, D.; Martinac, B.; Rigby, P. Determination of the orientational distribution and orientation factor for transfer between membrane-bound fluorophores using a confocal microscope. Biophys. J 2006, 91, 1032–1045. [Google Scholar]
- Raicu, V. Efficiency of resonance energy transfer in homo-oligomeric complexes of proteins. J. Biol. Phys 2007, 33, 109–127. [Google Scholar]
- Deplazes, E.; Jayatilaka, D.; Corry, B. ExiFRET: Flexible tool for understanding FRET in complex geometries. J. Biomed. Opt 2012, 17, 011005. [Google Scholar]
- Wlodarczyk, J.; Woehler, A.; Kobe, F.; Ponimaskin, E.; Zeug, A.; Neher, E. Analysis of FRET signals in the presence of free donors and acceptors. Biophys. J 2008, 94, 986–1000. [Google Scholar]
- Akrap, N.; Seidel, T.; Barisas, B.G. Forster distances for fluorescence resonant energy transfer between mCherry and other visible fluorescent proteins. Anal. Biochem 2010, 402, 105–106. [Google Scholar]
- Wolber, P.K.; Hudson, B.S. An analytic solution to the Forster energy transfer problem in two dimensions. Biophys. J 1979, 28, 197–210. [Google Scholar]
- Srinivasan, R.; Richards, C.I.; Xiao, C.; Rhee, D.; Pantoja, R.; Dougherty, D.A.; Miwa, J.M.; Lester, H.A. Pharmacological chaperoning of nicotinic acetylcholine receptors reduces the ER stress response. Mol. Pharmacol 2012, 81, 759–769. [Google Scholar]
- Hoppe, A.; Christensen, K.; Swanson, J.A. Fluorescence resonance energy transfer-based stoichiometry in living cells. Biophys. J 2002, 83, 3652–3664. [Google Scholar]
- Nashmi, R.; Xiao, C.; Deshpande, P.; McKinney, S.; Grady, S.R.; Whiteaker, P.; Huang, Q.; McClure-Begley, T.; Lindstrom, J.M.; Labarca, C.; et al. Chronic nicotine cell specifically upregulates functional α4* nicotinic receptors: Basis for both tolerance in midbrain and enhanced long-term potentiation in perforant path. J. Neurosci 2007, 27, 8202–8218. [Google Scholar]
- Raicu, V.; Stoneman, M.; Fung, R.; Melnichuk, M.; Jansma, D.; Pisterzi, L.; Rath, S.; Fox, M.; Wells, J.; Saldin, D. Determination of supramolecular structure and spatial distribution of protein complexes in living cells. Nat. Photonics 2009, 3, 107–113. [Google Scholar]
- Singh, D.R.; Raicu, V. Comparison between whole distribution- and average-based approaches to the determination of fluorescence resonance energy transfer efficiency in ensembles of proteins in living cells. Biophys. J 2010, 98, 2127–2135. [Google Scholar]
- Tadross, M.R.; Park, S.A.; Veeramani, B.; Yue, D.T. Robust approaches to quantitative ratiometric FRET imaging of CFP/YFP fluorophores under confocal microscopy. J. Microsc 2009, 233, 192–204. [Google Scholar]
- Xia, Z.; Liu, Y. Reliable and global measurement of fluorescence resonance energy transfer using fluorescence microscopes. Biophys. J 2001, 81, 2395–2402. [Google Scholar]
- Kuryatov, A.; Onksen, J.; Lindstrom, J. Roles of accessory subunits in α4β2α5 nicotinic receptors. Mol. Pharmacol 2008, 74, 132–143. [Google Scholar]
- Zhou, Y.; Nelson, M.E.; Kuryatov, A.; Choi, C.; Cooper, J.; Lindstrom, J. Human α4β2 acetylcholine receptors formed from linked subunits. J. Neurosci 2003, 23, 9004–9015. [Google Scholar]
- Khakh, B.S.; Fisher, J.A.; Nashmi, R.; Bowser, D.N.; Lester, H.A. An angstrom scale interaction between plasma membrane ATP-gated P2×2 and α4β2 nicotinic channels measured with FRET and TIRF microscopy. J. Neurosci 2005, 25, 6911–6920. [Google Scholar]
- Richards, C.I.; Srinivasan, R.; Xiao, C.; Mackey, E.D.W.; Miwa, J.M.; Lester, H.A. Trafficking of α4* nicotinic receptors revealed by superecliptic phluorin: Effects of a β4 ALS-associated mutation and chronic exposure to nicotine. J. Biol. Chem 2011, 286, 31241–31249. [Google Scholar]
- Chiu, C.S.; Kartalov, E.; Unger, M.; Quake, S.; Lester, H.A. Single-molecule measurements calibrate green fluorescent protein surface densities on transparent beads for use with ‘knock-in’ animals and other expression systems. J. Neurosci. Methods 2001, 105, 55–63. [Google Scholar]
- Chiu, C.S.; Jensen, K.; Sokolova, I.; Wang, D.; Li, M.; Deshpande, P.; Davidson, N.; Mody, I.; Quick, M.W.; Quake, S.R.; et al. Number, density, and surface/cytoplasmic distribution of GABA transporters at presynaptic structures of knock-in mice carrying GABA transporter subtype 1-green fluorescent protein fusions. J. Neurosci 2002, 22, 10251–10266. [Google Scholar]
- Pantoja, R.; Rodriguez, E.A.; Dibas, M.I.; Dougherty, D.A.; Lester, H.A. Single-molecule imaging of a fluorescent unnatural amino Acid incorporated into nicotinic receptors. Biophys. J 2009, 96, 226–237. [Google Scholar]
- Richards, C.I.; Luong, K.; Srinivasan, R.; Turner, S.W.; Dougherty, D.A.; Korlach, J.; Lester, H.A. Live-cell imaging of single receptor composition using zero-mode waveguides nanostructures. Nano Lett 2012, 12, 3690–3694. [Google Scholar]
- Fabian, A.I.; Rente, T.; Szollosi, J.; Matyus, L.; Jenei, A. Strength in numbers: Effects of acceptor abundance on FRET efficiency. Chemphyschem 2010, 11, 3713–3721. [Google Scholar]
- Brejc, K.; van Dijk, W.J.; Klaassen, R.V.; Schuurmans, M.; van der Oost, J.; Smit, A.B.; Sixma, T.K. Crystal structure of an ACh-binding protein reveals the ligand-binding domain of nicotinic receptors. Nature 2001, 411, 269–276. [Google Scholar]
- Unwin, N. Refined structure of the nicotinic acetylcholine receptor at 4A resolution. J. Mol. Biol 2005, 346, 967–989. [Google Scholar]
- Hibbs, R.E.; Gouaux, E. Principles of activation and permeation in an anion-selective Cys-loop receptor. Nature 2011, 474, 54–60. [Google Scholar]
- Ormo, M.; Cubitt, A.B.; Kallio, K.; Gross, L.A.; Tsien, R.Y.; Remington, S.J. Crystal structure of the Aequorea victoria green fluorescent protein. Science 1996, 273, 1392–1395. [Google Scholar]

© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Srinivasan, R.; Richards, C.I.; Dilworth, C.; Moss, F.J.; Dougherty, D.A.; Lester, H.A. Förster Resonance Energy Transfer (FRET) Correlates of Altered Subunit Stoichiometry in Cys-Loop Receptors, Exemplified by Nicotinic α4β2. Int. J. Mol. Sci. 2012, 13, 10022-10040. https://doi.org/10.3390/ijms130810022
Srinivasan R, Richards CI, Dilworth C, Moss FJ, Dougherty DA, Lester HA. Förster Resonance Energy Transfer (FRET) Correlates of Altered Subunit Stoichiometry in Cys-Loop Receptors, Exemplified by Nicotinic α4β2. International Journal of Molecular Sciences. 2012; 13(8):10022-10040. https://doi.org/10.3390/ijms130810022
Chicago/Turabian StyleSrinivasan, Rahul, Christopher I. Richards, Crystal Dilworth, Fraser J. Moss, Dennis A. Dougherty, and Henry A. Lester. 2012. "Förster Resonance Energy Transfer (FRET) Correlates of Altered Subunit Stoichiometry in Cys-Loop Receptors, Exemplified by Nicotinic α4β2" International Journal of Molecular Sciences 13, no. 8: 10022-10040. https://doi.org/10.3390/ijms130810022




