Dynamic Rheological Studies of Poly(p-phenyleneterephthalamide) and Carbon Nanotube Blends in Sulfuric Acid
Abstract
:1. Introduction
2. Results and Discussion
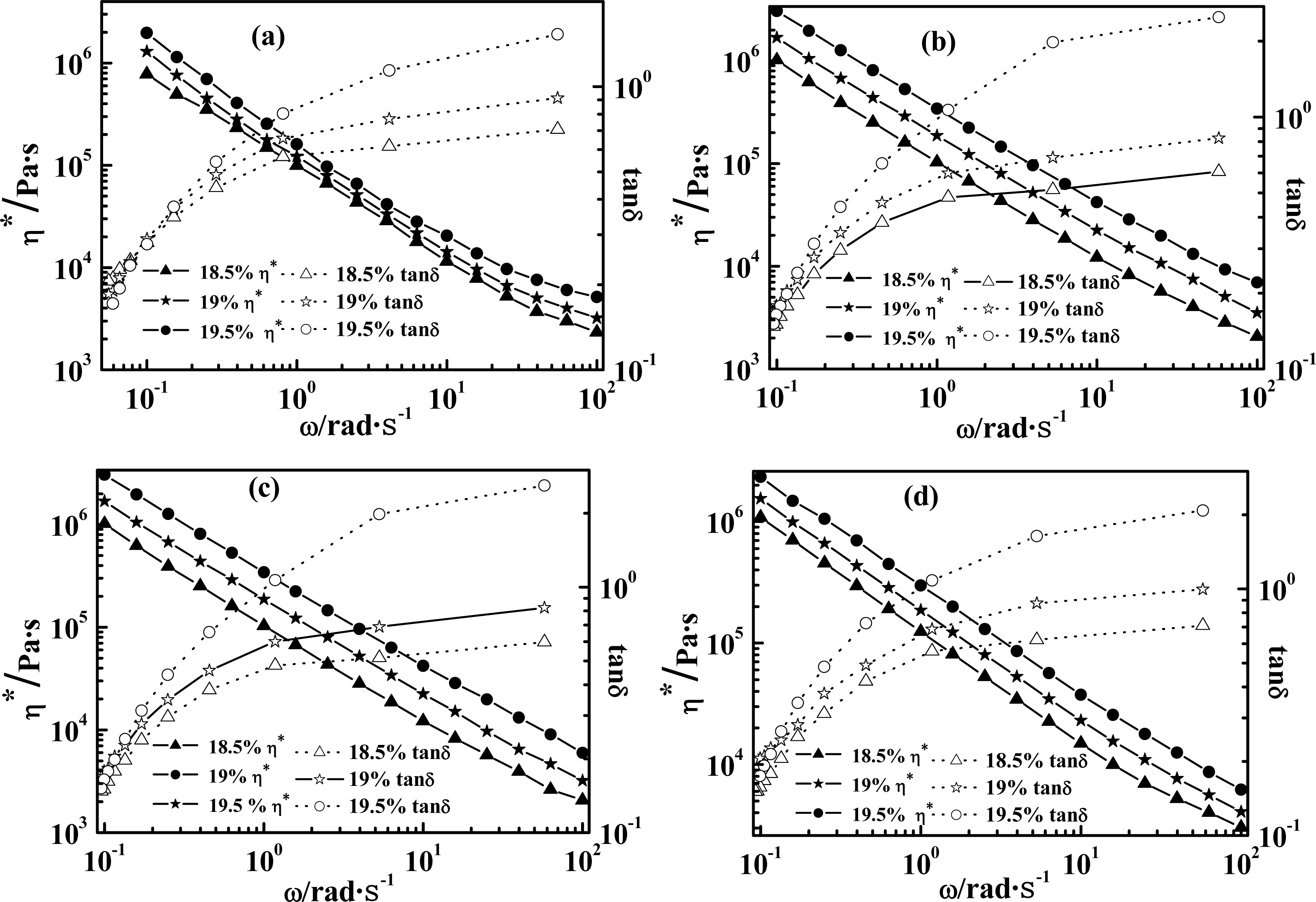
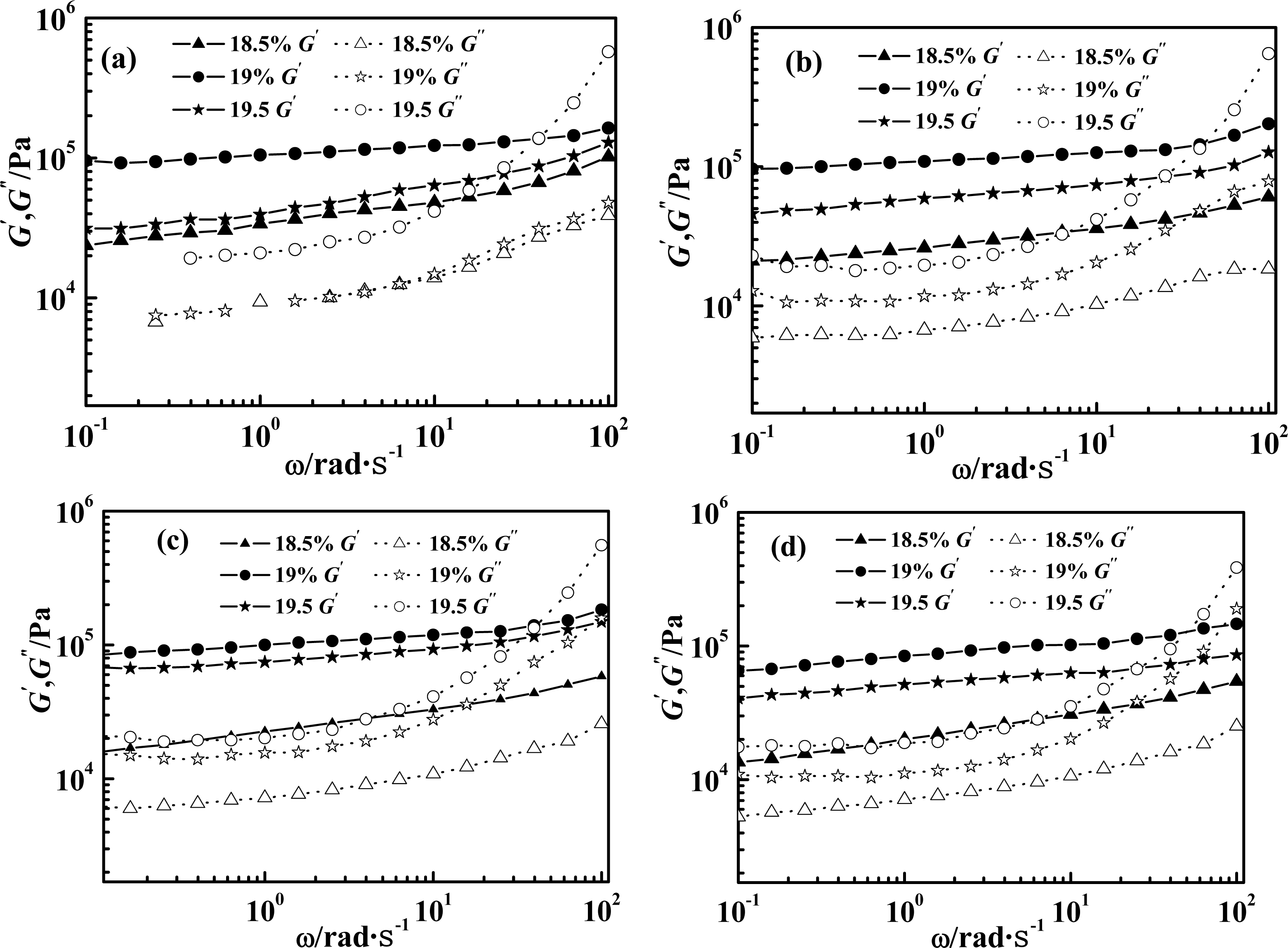
2.1. Effect of Weight Concentration of PPTA on Rheological Behaviors
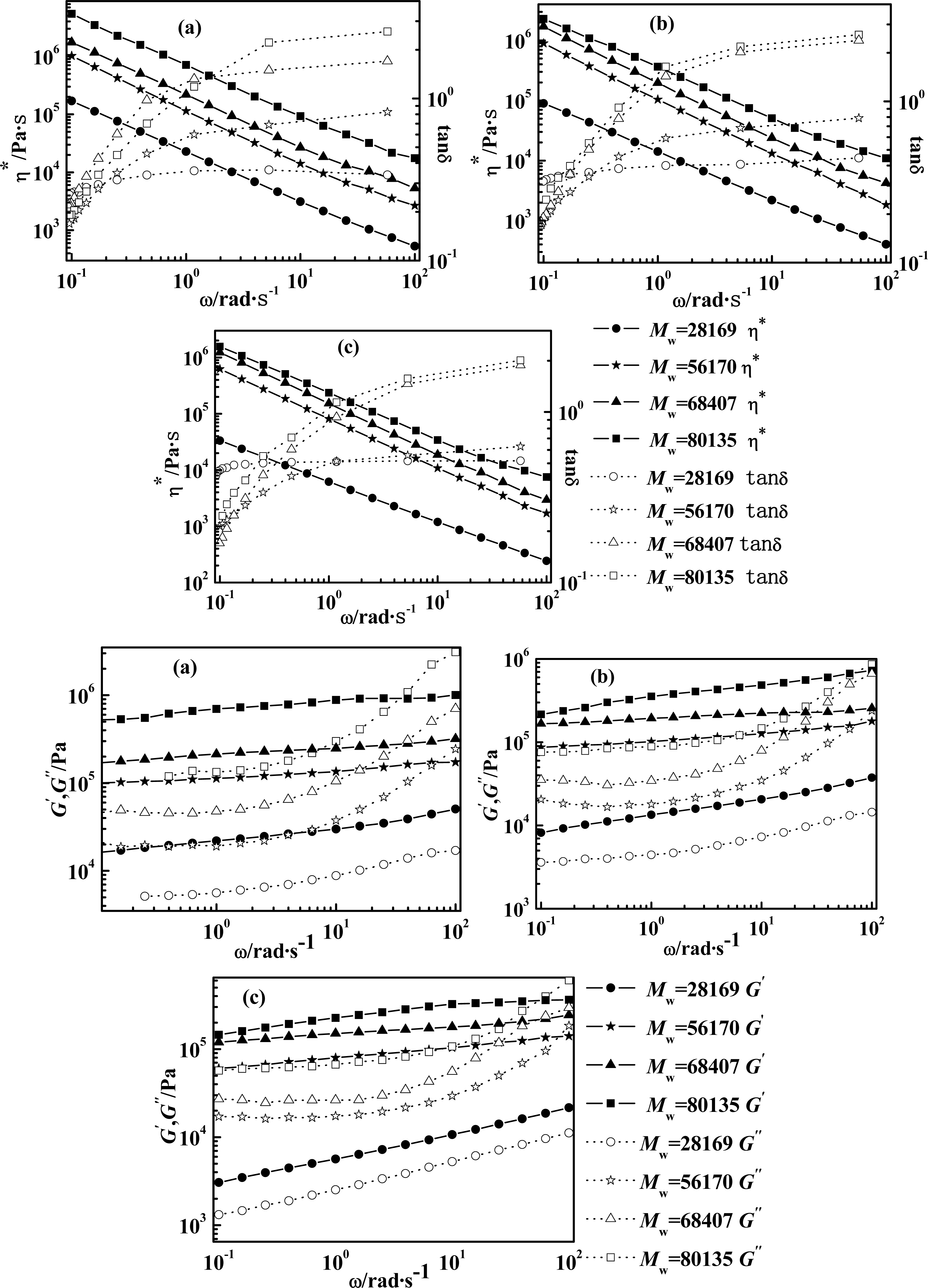
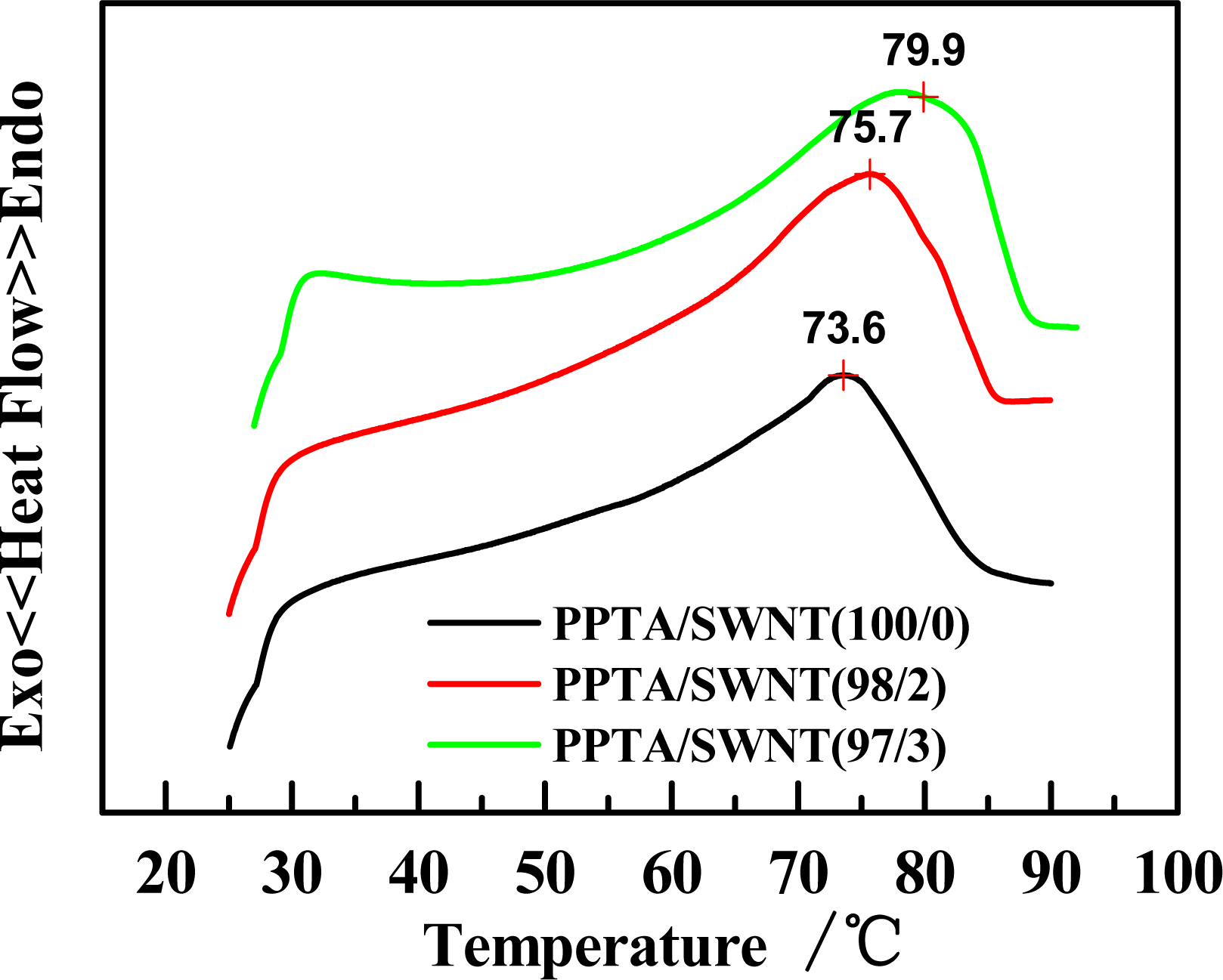
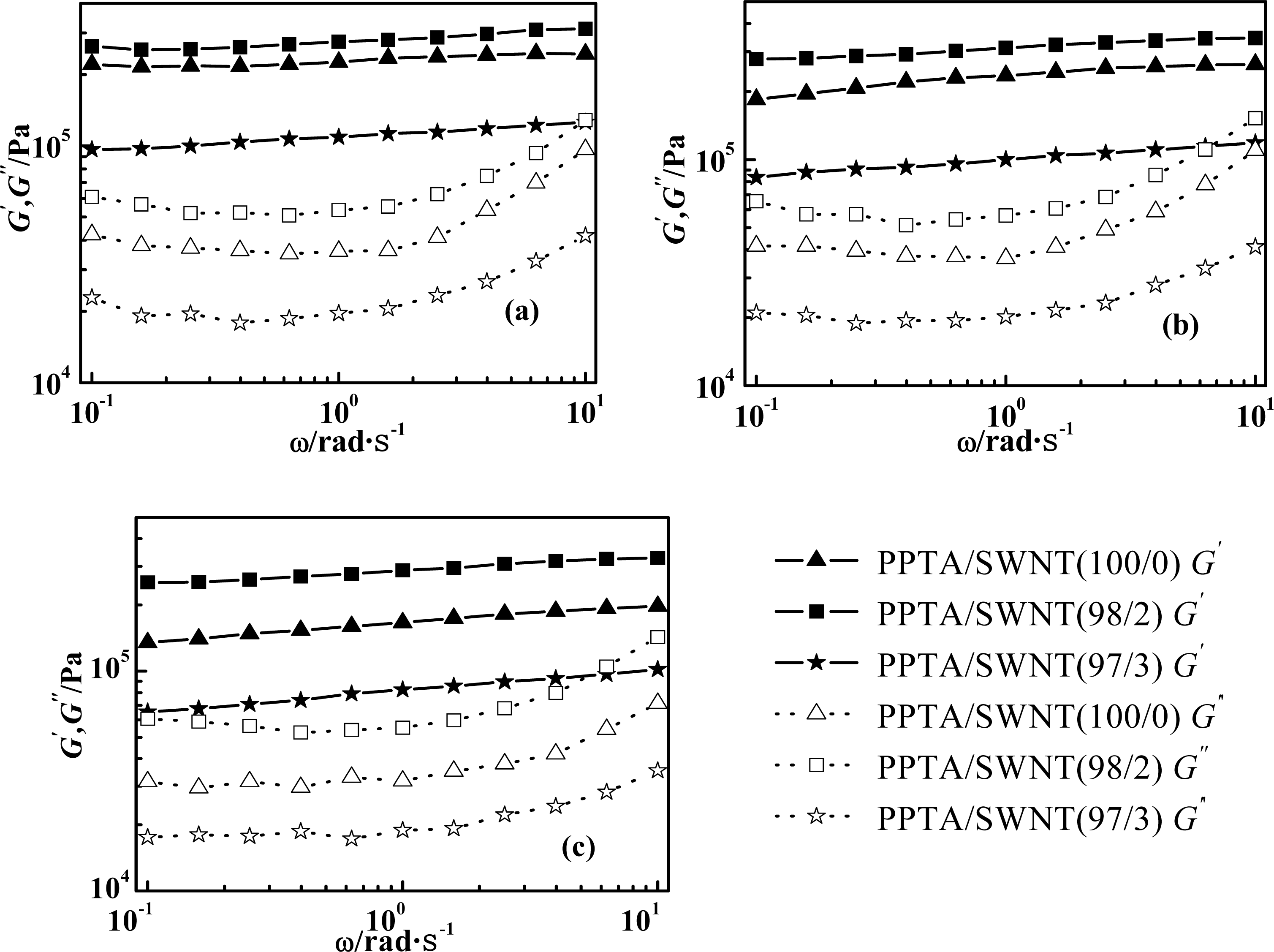
2.2. Effect of Molecular Weight of PPTA on Rheological Behaviors
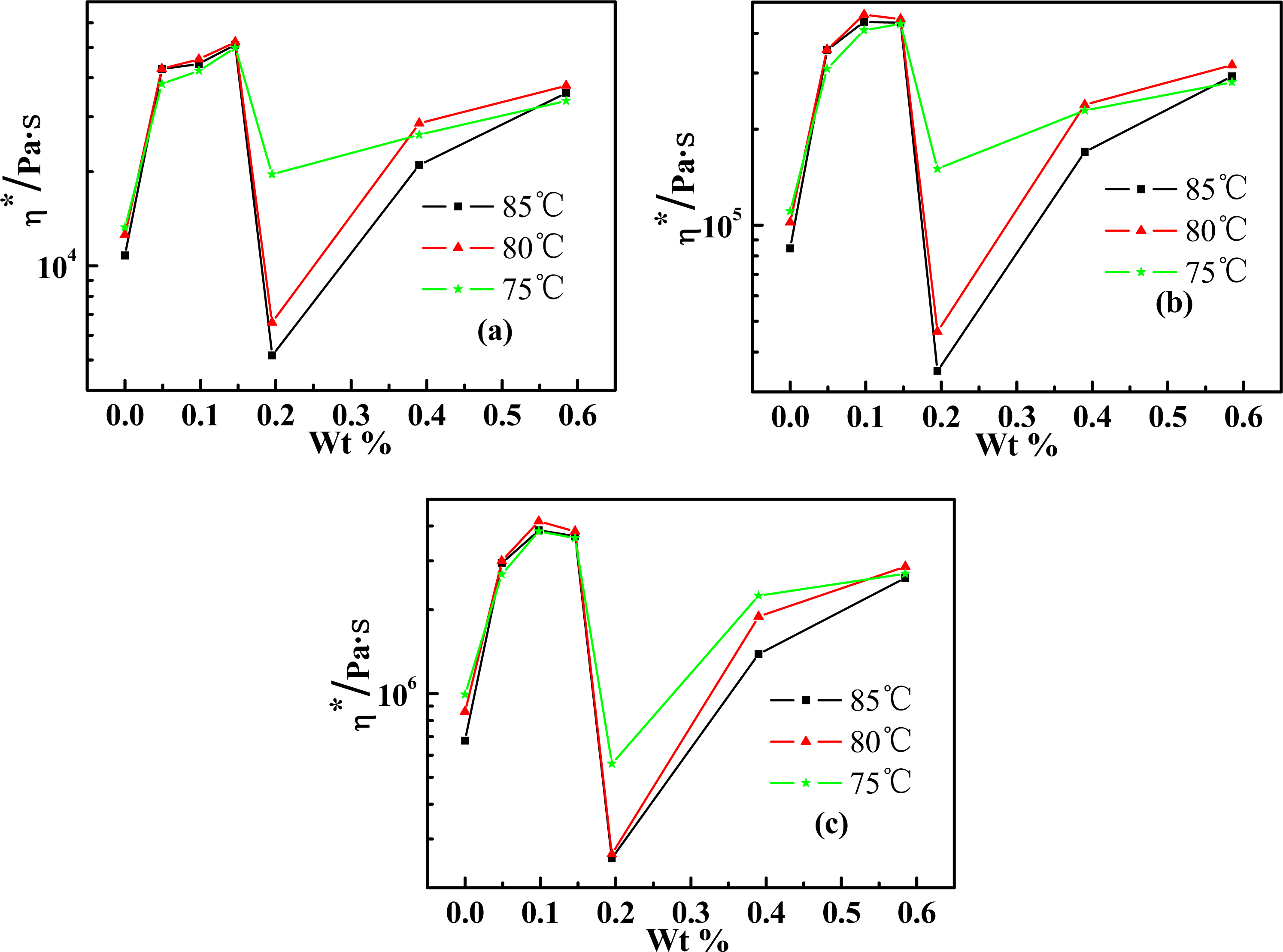
2.3. Effect of Weight Concentration of SWNT on Rheological Behaviors
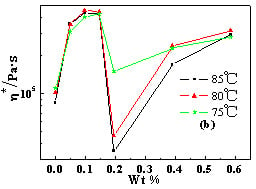
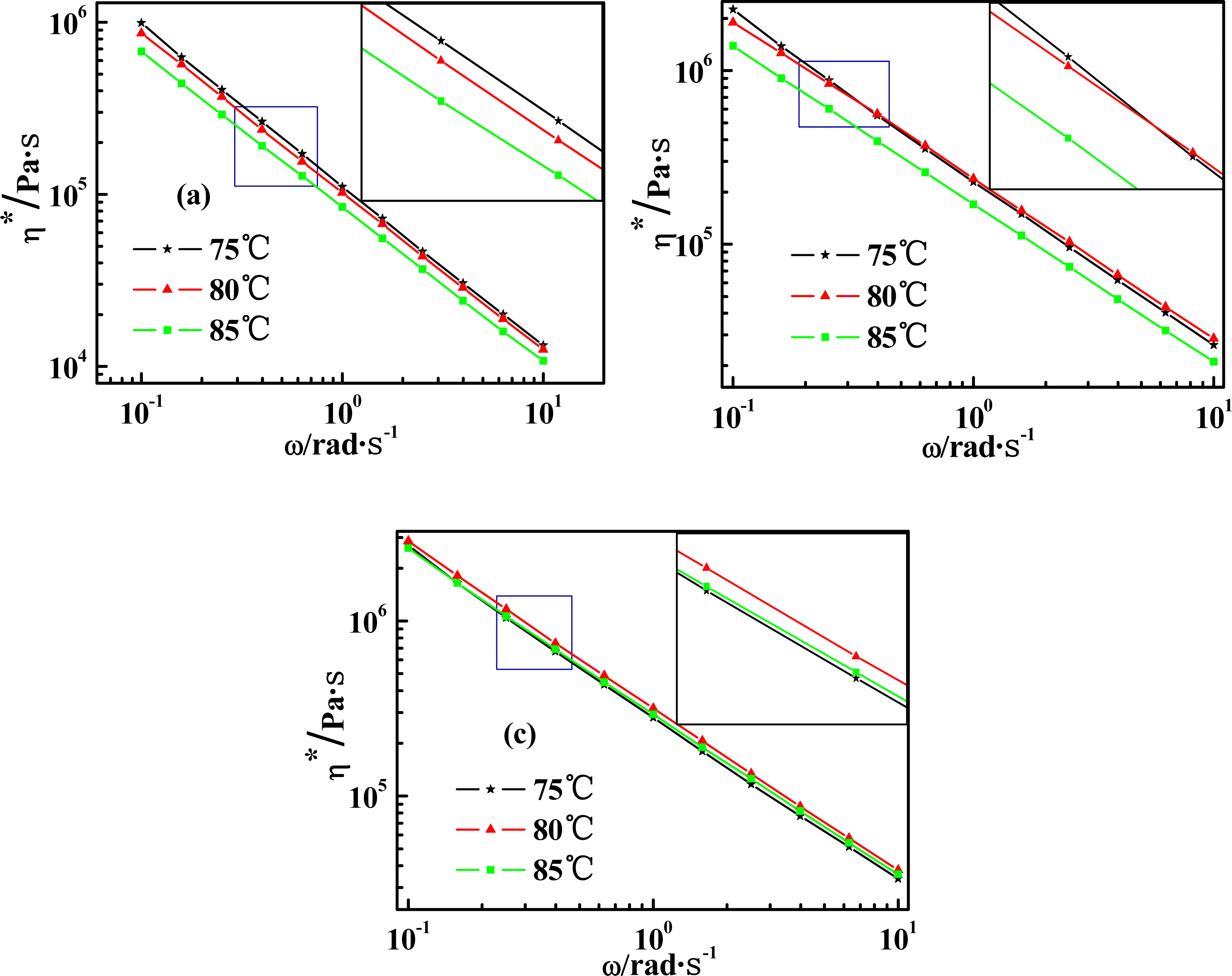
2.4. Temperature Dependence of Rheological Behaviors
3. Experimental Section
3.1. Materials and Preparation
3.2. Rheological Properties
3.3. Characterization
4. Conclusions
Acknowledgments
References
- Friedel, G. Mesomorphic states of matter. Ann. Phys 1922, 18, 273–474. [Google Scholar]
- Yang, HH. Aromatic High-Strength Fibers, 1st ed; Wiley-VCH: New York, NY, USA, 1989; pp. 207–289. [Google Scholar]
- Zhou, M; Frydman, V; Frydman, L. On the Molecular organization of PPTA in sulfuric acid: an NMR study. J. Phys. Chem 1996, 100, 19280–19288. [Google Scholar]
- Kiyo-Oglu, VN; Rozhdestvenskaya, TA; Serova, LD. Rheological properties of liquid-crystalline solutions of poly(p-phenylene terephthalamide) and behavior of the jet in spinning through an air space. Fibre Chem 1997, 29, 81–86. [Google Scholar]
- Picken, SJ; Zwaag, SV; Northolt, MG. Molecular and macroscopic orientational order in aramid solutions: a model to explain the influence of some spinning parameters on the modulus of aramid yarns. Polymer 1992, 33, 2998–3006. [Google Scholar]
- Slugin, IV; Sklyarova, GB; Kashirin, AI; Tkacheva, LV; Komissarov, SV. Rusar microfilament yarn for ballistic protection. Fibre Chem 2006, 38, 22–24. [Google Scholar]
- Picken, SJ; Aerts, J; Doppert, HL; Reuvers, AJ; Northolt, MG. Structure and rheology of aramid solutions: transient rheological and rheo-optical measurements. Macromolecules 1991, 24, 1366–1375. [Google Scholar]
- Doppert, HL; Picken, SJ. Rheological properties of aramid solutions: transient flow and rheooptical measurements. Mol. Cryst. Liq. Cryst 1987, 153, 109–116. [Google Scholar]
- Picken, SJ. Phase transitions and rheology of aramid solutions. Liq. Cryst 1989, 5, 1635–1643. [Google Scholar]
- Picken, SJ; Aerts, J; Visser, R; Northolt, MG. Structure and rheology of aramid solutions: X-ray scattering measurements. Macromolecules 1990, 23, 3849–3854. [Google Scholar]
- Baird, DG; Ballman, RL. Comparison of the rheological properties of concentrated solutions of a rodlike and a flexible chain polyamide. J. Rheol 1979, 23, 505–524. [Google Scholar]
- Baughman, RH; Zakhidov, AA; De Heer, WA. Carbon nanotubes--the route toward applications. Science 2002, 297, 787–792. [Google Scholar]
- Wong, EW; Sheehan, PE; Lieber, CM. Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar]
- Tans, SJ; Devoret, MH; Dai, HJ; Thess, A; Smalley, RE; Geerligs, LJ; Dekker, C. Individual single-wall carbon nanotubes as quantum wires. Nature 1977, 386, 474–477. [Google Scholar]
- Treact, MMJ; Ebbesen, TW; Gibson, JM. Exceptionally high Young’s modulus observed for individual carbon nanotubes. Nature 1996, 381, 678–680. [Google Scholar]
- Lee, HK; Pejanovic, S; Mondragon, I; Mijovic, J. Dynamics of single-walled carbon nanotube (SWNT)/polyisoprene (PI) nanocomposites in electric and mechanical fields. Polymer 2007, 48, 7345–7355. [Google Scholar]
- Kinloch, IA; Roberts, SA; Windle, AH. A rheological study of concentrated aqueous nanotube dispersions. Polymer 2002, 43, 7483–7491. [Google Scholar]
- Andrews, R; Jacques, D; Rao, AM; Rantell, T; Derbyshire, F. Nanotube composite carbon fibers. Appl. Phys. Lett 1999, 75, 1329–1331. [Google Scholar]
- Kumar, S; Dang, TD; Arnold, FE; Bhattacharyya, AR; Min, BG; Zhang, X; Vaia, RA; Park, C; Adams, WW; Hauge, RH; Smalley, RE; Ramesh, S; Willis, PA. Synthesis, structure, and properties of PBO/SWNT composites. Macromolecules 2002, 35, 9039–9043. [Google Scholar]
- Streekumar, TV; Liu, T; Min, BG; Gao, H; Kumar, S; Hauge, RH; Smalley, RE. Polyacrylonitrile single-walled carbon nanotube composite fibers. Adv. Mater 2004, 16, 58–62. [Google Scholar]
- Davis, VA; Ericson, LM; Parra-Vasquez, ANG; Fan, H; Wang, Y; Prieto, V; Longoria, JA; Ramesh, S; Saini, RK; Kittrell, C; Billups, WE; Adams, WW; Hauge, RH; Smalley, RE; Pasquali, M. Phase behavior and rheology of SWNTs in superacids. Macromolecules 2004, 37, 154–160. [Google Scholar]
- Lin, JP; Wu, HR; Li, SJ. Kinetics of phase transition in lyotropic liquid crystalline polymers. Polym. Int 1993, 32, 339–342. [Google Scholar]
- Gupta, RK. Polymer and Composite Rheology, 2nd ed; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Schaefgen, JR; Foldi, VS; Logullo, FM; Good, VH; Gulrich, LW; Killian, FL. Viscosity-molecular weight relationshios in stiff-chain aromatic polyamides. Polym. Prepr 1976, 17, 69–74. [Google Scholar]
- Arpin, M; Strazielle, C. Conformation de polyamides aromatiques en solution diluée dans l’acide sulfurique concentré. 1. Étude par viscosité et diffusion de la lumière. Makromol. Chem 1976, 177, 581–584. [Google Scholar]
- Ramesh, S; Ericson, LM; Davis, VA; Saini, RK; Kittrell, C; Pasquali, M; Billups, WE; Adams, WW; Hauge, RH; Smalley, RE. Dissolution of pristine single walled carbon nanotubes in superacids by direct protonation. J. Phys. Chem. B 2004, 108, 8794–8798. [Google Scholar]
- Rommel, H; Forster, G. Topology of the ternary phase system poly(p-phenylene terephthalamide)-sulfuric acid-water. Macromolecules 1994, 27, 4570–4576. [Google Scholar]
- Picken, SJ. Orientational order in aramid solutions determined by diamagnetic susceptibility and birefringence measurements. Macromolecules 1990, 23, 464–470. [Google Scholar]
- Li, L; Li, CY; Ni, C; Rong, L; Hsiao, B. Structure and crystallization behavior of Nylon 66/multi-walled carbon nanotube nanocomposites at low carbon nanotube contents. Polymer 2007, 48, 3452–3460. [Google Scholar]
- Vlasveld, DPN; Fischer, HR; Swierenga, E; Picken, SJ. Interaction of SWCNT and PPTA with sulfuric acid—compatibilization of two materials in a common solvent. J. Polym. Sci. Part B: Polym. Phys 2008, 46, 1914–1922. [Google Scholar]
- Ferry, JD. Viscoelastic Properties of Polymers, 3rd ed; Wiley-VCH: New York, NY, USA, 1980. [Google Scholar]
- Piau, JM; Agassant, JF. Rheology for Polymer Melt Processing, 1st ed; Elsevier: Amsterdam, The Netherland, 1996. [Google Scholar]
- Hsieh, T; Tiu, C; Simon, GP. Rheology and miscibility of thermotropic liquid crystalline polymer blends. J. Non-Newtonian Fluid Mech 1999, 86, 15–35. [Google Scholar]
- Kim, JY; Han, SI; Hong, S. Effect of modified carbon nanotube on the properties of aromatic polyester nanocomposites. Polymer 2008, 49, 3335–3345. [Google Scholar]
- Chiang, IW; Brinson, BE; Huang, AY; Willis, PA; Bronikowski, MJ; Margrave, JL; Smalley, RE; Hauge, RH. Purification and characterization of single-wall carbon nanotubes (SWNTs) obtained from the gas-phase decomposition of CO (HiPco Process). J. Phys. Chem. B 2001, 105, 8297–8301. [Google Scholar]
- Morgan, PW. Synthesis and properties of aromatic and extended chain polyamides. Macromolecules 1977, 10, 1381–1390. [Google Scholar]
- Kwolek, SL; Morgan, PW; Schaefgen, JR; Gulrich, LW. Synthesis, anisotropic solutions, and fibers of poly(1,4-benzamide). Macromolecules 1977, 10, 1390–1396. [Google Scholar]
- Frey, MW; Cuculo, JA; Khan, SA. Rheology and gelation of cellulose/ammonia/ammonium thiocyanate solutions. J. Polym. Sci. Part B: Polym. Phys 1996, 34, 2375–2381. [Google Scholar]
- Kim, SO; Shin, WJ; Cho, H; Kim, BC; Chung, IJ. Rheological investigation on the anisotropic phase of cellulose–MMNO/H2O solution system. Polymer 1999, 40, 6443–6450. [Google Scholar]

© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cao, Y.; Liu, Z.; Gao, X.; Yu, J.; Hu, Z.; Liang, Z. Dynamic Rheological Studies of Poly(p-phenyleneterephthalamide) and Carbon Nanotube Blends in Sulfuric Acid. Int. J. Mol. Sci. 2010, 11, 1352-1364. https://doi.org/10.3390/ijms11041352
Cao Y, Liu Z, Gao X, Yu J, Hu Z, Liang Z. Dynamic Rheological Studies of Poly(p-phenyleneterephthalamide) and Carbon Nanotube Blends in Sulfuric Acid. International Journal of Molecular Sciences. 2010; 11(4):1352-1364. https://doi.org/10.3390/ijms11041352
Chicago/Turabian StyleCao, Yutong, Zhaofeng Liu, Xianghua Gao, Junrong Yu, Zuming Hu, and Ziqi Liang. 2010. "Dynamic Rheological Studies of Poly(p-phenyleneterephthalamide) and Carbon Nanotube Blends in Sulfuric Acid" International Journal of Molecular Sciences 11, no. 4: 1352-1364. https://doi.org/10.3390/ijms11041352