A Review on Progress in QSPR Studies for Surfactants
Abstract
:1. Introduction
2. Studies on Relationships between CMC and Molecular Structures
2.1. QSPR Studies on CMC of Surfactants Based on Molecular Connectivity Index
2.2. QSPR Studies of CMC of Surfactants Based on Quantum Mechanical Descriptors
2.3. QSPR Studies of CMC of Surfactants Using Neural Network
2.4. QSPR Studies of CMC of Surfactants Using Other Methods
3. Charge Distribution of Surfactants and Its Influence on Their Properties
3.1. Computation of Charge Distribution in Ionic Surfactant Molecules and Their Effects
3.2. Descriptors Related to Molecular Surface Area—CPSA
4. Surface Tension Prediction Models
5. Qsar Studies on Cloud Point of Nonionic Surfactants
6. Studies on Degradation of Surfactants
7. QSPR Studies on Other Properties of Surfactants
8. Conclusions and Prospects
Acknowledgments
References
- Li, GZ; Sui, H; Zhu, WZ. Progress of surfactant study [in Chinese]. China Surfact. Deterg. Cosm 1999, 1, 24–26. [Google Scholar]
- William, AE; the Committee on Fetus and Newborn. Surfactant-replacement therapy for respiratory distress in the preterm and term neonate. Pediatrics 2008, 121, 419–432. [Google Scholar]
- Riviere, JE; Baynes, RE; Xia, XR. Membrane-coated fiber array approach for predicting skin permeability of chemical mixtures from different vehicles. Toxicol. Sci 2007, 99, 153–161. [Google Scholar]
- Wolf, S; Lohbrunner, H; Busch, T; Sterner-Kock, A; Deja, M; Sarrafzadeh, A; Neumann, U; Kaisers, U. Small dose of exogenous surfactant combined with partial liquid ventilation in experimental acute lung injury: effects on gas exchange, haemodynamics, lung mechanics, and lung pathology. Br. J. Anaesth 2001, 87, 593–601. [Google Scholar]
- Fendler, JH. Atomic and molecular clusters in membrane mimetic chemistry. Chem. Rev 1987, 87, 877–899. [Google Scholar]
- Zhang, XY; Zhu, HW; Li, L; Li, GZ; Wang, ZW. The progress of qsar/qspr for surfactants [in Chinese]. Prog. Chem 2003, 15, 351–360. [Google Scholar]
- Eibl, H. Phospholipids as functional constituents of biomembranes. Angew. Chem. Int. Ed. Engl 1984, 23, 257–271. [Google Scholar]
- Jiang, ZL; Xiao, D; Wang, KM; Xia, SX. Bilayer lipid membrane and biosensors [in Chinese]. Chem. Sensors 1995, 15, 161–167. [Google Scholar]
- Crivori, P; Morelli, A; Pezzetta, D; Rocchetti, M; Poggesi, I. Development and validation of in silico models for estimating drug preformulation risk in PEG400/water and Tween80/water systems. Eur. J. Pharm. Sci 2007, 32, 169–181. [Google Scholar]
- Stevens, TP; Sinkin, RA. Surfactant replacement therapy. Chest 2007, 131, 1577–1582. [Google Scholar]
- Zhang, PF; Avudzega, DM; Bowman, RS. Removal of perchlorate from contaminated waters using surfactant-modified zeolite. J. Environ. Qual 2007, 36, 1069–1075. [Google Scholar]
- Wang, LS. Organic Pollutant Chemistry [in Chinese]; Science Press: Beijing, China, 1991. [Google Scholar]
- Lehmler, HJ. Synthesis of environmentally relevant fluorinated surfactants—A review”. Chemosphere 2005, 58, 1471–1496. [Google Scholar]
- Salager, JL. FIRP Booklet # 300-A: Surfactants-Types and Uses; University of the Andes, Laboratory of Formulation, Interfaces Rheology and Processes: Merida, Venezuela, 2002; p. 44. [Google Scholar]
- Mason Chemical Company. Fluorosurfactant—Structure/Function.
- Kardanpour, Z; Hemmateenejad, B; Khayamian, T. Wavelet neural network-based QSPR for prediction of critical micelle concentration of Gemini surfactants. Anal. Chim. Acta 2005, 531, 285–291. [Google Scholar]
- Zhao, GX. Physical Chemistry of Surfactants (revised edition) [in Chinese]; Beijing University Press: Beijing, China, 1991. [Google Scholar]
- Wang, ZW; Feng, JL; Wang, HJ; Cui, ZG; Li, GZ. Effectiveness of surface tension reduction by nonionic surfactants with quantitative structure-property relationship approach. J. Dispersion Sci. Technol 2005, 26, 441–447. [Google Scholar]
- Katritzky, AR; Pacureanu, LM; Slavov, SH; Dobchev, DA; Karelson, M. QSPR study of critical micelle concentrations of nonionic surfactants. Ind. Eng. Chem. Res 2008, 47, 9687–9695. [Google Scholar]
- Chen, ML; Wang, ZW; Wang, HJ; Zhang, GX; Tao, FM. Investigation of adsorption of surfactant at the air-water interface with quantum chemistry method. Chin. Sci. Bull 2007, 52, 1451–1455. [Google Scholar]
- Wang, ZW; Feng, JL; Wang, ZN; Li, GZ; Lou, AJ. Quantitative structure-property relationship on prediction of the interaction parameters of organic compounds. J. Dispersion Sci. Technol 2006, 27, 11–14. [Google Scholar]
- Wang, LS; Han, SK; Kong, LR. Molecular Structure, Properties and Activity [in Chinese]; Chemical Industry Press: Beijing, China, 1997. [Google Scholar]
- Katritzky, AR; Lobanov, VS; Karelson, M. QSPR-The correlation and quantitative prediction of chemical and physical properties from structure. Chem. Soc. Rev 1995, 24, 279–287. [Google Scholar]
- Theil, W; Voityuk, AA. Extension of MNDO to d-orbitals: parameters and results for the second-row elements and for the zinc group. J. Phys. Chem 1996, 100, 616–626. [Google Scholar]
- Becher, P. Hydrophile lipophile balance: history and recent developments (Langmuir lecture, 1983). J. Dispersion Sci. Technol 1984, 5, 81–96. [Google Scholar]
- Karelson, M; Maran, U; Wang, YL; Katritzky, AR. QSPR and QSAR models derived using large molecular descriptor spaces. A review of CODESSA applications. Collec. Czechoslovak Chem. Commun 1999, 64, 1551–1571. [Google Scholar]
- Wang, ZW; Li, GZ; Zhang, XY; Li, L. Prediction on critical micelle concentration of anionic surfactants in aqueous solution: quantitative structure-property relationship approach [in Chinese]. Acta Chim. Sinica 2002, 60, 1548–1552. [Google Scholar]
- Li, L; Zhang, XY; Wang, ZW; Li, GZ; Zhu, HW; Zhang, YS. Study of quantitative structure-property relationship of nonionic surfactants [in Chinese]. China Surfact. Deterg. Cosm 2003, 33, 343–345. [Google Scholar]
- Li, XF; Zhang, GY; Dong, JF; Zhou, XH; Yan, XC; Luo, MD. Estimation of critical micelle concentration of anionic surfactants with QSPR approach. J. Mol. Struct 2004, 710, 119–126. [Google Scholar]
- Huibers, PDT; Lobanov, VS; Katritzky, AR; Shah, DO; Karelson, M. Prediction of critical micelle concentration using a quantitative structure-property relationship approach: 1. nonionic surfactants. Langumir 1996, 12, 1462–1470. [Google Scholar]
- Huibers, PDT; Lobanov, VS; Katritzky, AR; Shah, DO; Karelson, M. Prediction of critical micelle concentration using a quantitative structure property relationship approach: 2. anionic surfactants. J. Colloid Interface Sci 1997, 187, 113–120. [Google Scholar]
- Kier, LB; Hall, LH. Molecular Connectivity in Structure-activity Analysis; John Wiley and Sons: New York, USA, 1986. [Google Scholar]
- Stankevich, MI; Stankevich, IV; Zefirov, NS. Topological indices in organic chemistry. Russ. Chem. Rev 1988, 57, 191–208. [Google Scholar]
- Stewart, JJP. MOPAC 6.0: A General Purpose Molecular Orbital Package; QCPE No. 455, Frank J. Seiler Research Laboratory, U.S. Air Force Academy: Colorado Springs, CO, USA, 1989. [Google Scholar]
- Wang, ZW; Li, GZ; Zhang, XY; Wang, RK; Lou, AJ. A quantitative structure-property relationship study for the prediction of critical micelle concentration of nonionic surfactants. Colloids Surf. A: Physicochem. Eng. Aspects 2002, 197, 37–45. [Google Scholar]
- Katritzky, AR; Pacureanu, L; Dobchev, D; Karelson, M. QSPR study of critical micelle concentration of anionic surfactants using computational molecular descriptors. J. Chem. Inf. Model 2007, 47, 782–793. [Google Scholar]
- Wang, ZW; Huang, DY; Gong, SP; Li, GZ. Prediction on critical micelle concentration of nonionic surfactants in aqueous solution: Quantitative structure-property relationship approach. Chin. J. Chem 2003, 21, 1573–1579. [Google Scholar]
- Wang, ZN; Wang, ZW; Gao, YA; Zhen, LQ; Liu, J; Li, GZ; Zhang, GY. QSPR cmc calculations for AE3SO3 and the contribution of EO in micellization [in Chinese]. Acta Chim. Sinica 2004, 62, 2391–2397. [Google Scholar]
- Roberts, DW. Application of octanol/water partition coefficients in surfactant science: a quantitative structure-property relationship for micellization of anionic surfactants. Langmuir 2002, 18, 345–352. [Google Scholar]
- Leo, AJ; Hansch, C. Substituent Constants for Correlation Analysis in Chemistry and Biology; John Wiley and Sons: New York, NY, USA, 1979. [Google Scholar]
- Roberts, DW. Aquatic toxicity of linear alkyl benzene sulphonates (LAS)-A QSAR approach. J. Com. Esp. Deterg 1989, 20, 35–43. [Google Scholar]
- Puvvada, S; Blankschtein, D. Molecular-thermodynamic approach to predict micellization, phase behavior, and phase separation of micellar solutions. I. Application to nonionic surfactants. J. Chem. Phys 1990, 92, 3710–3724. [Google Scholar]
- Nagarajan, R; Ruckenstein, E. Theory of surfactant self-assembly: a predictive molecular thermodynamics approach. Langumir 1991, 7, 2934–2969. [Google Scholar]
- Zhang, B; Liu, HL; Hu, Y. Attraction between like-charge particles [in Chinese]. Prog. Chem 2001, 13, 1–9. [Google Scholar]
- Huibers, PDT. Quantum-chemical calculations of the charge distribution in ionic surfactants. Langumir 1999, 15, 7546–7550. [Google Scholar]
- Gadre, SR; Pingale, SS. An electrostatic investigation: how polar are ionic surfactant hydrocarbon tails? Chem. Commun 1996, 5, 595–596. [Google Scholar]
- Jiang, YB; Xu, JG; Chen, GZ. Molecular structure of ionic surfactants in water solution. Sci. China Ser. B 1991, 10, 1028–1034. [Google Scholar]
- Thiel, W; Voityuk, AA. Extension of MNDO to d orbitals: parameters and results for the second-row elements and for the zinc group. J. Phys. Chem 1996, 100, 616–626. [Google Scholar]
- Heidl, A; Kohler, HH. Rod formation of ionic surfactants: a thermodynamic model. Langmuir 1996, 12, 2464–2474. [Google Scholar]
- Zhao, J; Fung, BM. NMR study of the transformation of sodium dodecyl sulfate micelles. Langmuir 1993, 9, 1228–1231. [Google Scholar]
- Jacobs, PT; Anacker, EW. The effect of polar head charge delocalization on micellar aggregation numbers of decylpyridinium salts. J. Collid Interface Sci 1973, 44, 505–508. [Google Scholar]
- Huibers, PDT; Jacobs, PT. The effect of polar head charge delocalization on micellar aggregation numbers of decylpyridinium salts, revisited. J. Colloid Interface Sci 1998, 206, 342–344. [Google Scholar]
- Villamagna, F; Whitehead, MA; Chattopadyay, AKJ. A molecular modelling approach to the analysis of present and design of future surfactants for water-in-oil emulsions. J. Mol. Struct. (THEOCHEM) 1995, 343, 77–103. [Google Scholar]
- Camilleri, P; Watts, A; Boraston, JA. A surface area approach to determination of partition coefficients. J. Chem. Soc. Perkin Trans 1988, 2, 1699–1708. [Google Scholar]
- Koehler, MG; Grigoras, S; Dunn, WJ, III. The Relationship between chemical structure and the logarithm of the partition coefficient. Quant. Struc.—Act. Relat 1988, 7, 150–159. [Google Scholar]
- Grigoras, S. A structural approach to calculate physical properties of pure organic substances: the critical temperature, critical volume and related properties. J. Comput. Chem 1990, 11, 493–510. [Google Scholar]
- Stanton, DT; Jurs, PC. Development and use of charged partial surface area structural descriptors in computer-assisted quantitative structure-property relationship studies. Anal. Chem 1990, 62, 2323–2329. [Google Scholar]
- Pearlman, RS. Physical Chemical Properties of Drugs; Yalkowsky, SH, Sinkula, AA, Valvani, SC, Marcel, D, Eds.; Marcel Dekker Inc: New York, NY, USA, 1980; p. 331. [Google Scholar]
- Abraham, RJ; Smith, PE. Charge calculations in molecular mechanics iv: A general method for conjugated systems. J. Comput. Chem 1988, 9, 288–297. [Google Scholar]
- Wang, ZW; Li, GZ; Mu, JH; Zhang, XY; Lou, AJ. Quantitative structure-property relationship on prediction of surface tension of nonionic surfactants. Chin. Chem. Lett 2002, 13, 363–366. [Google Scholar]
- Wang, ZW; Feng, JL; Wang, HJ; Cui, ZG; Li, GZ. Effectiveness of surface tension reduction by nonionic surfactants with quantitative structure-property relationship approach. J. Dispersion Sci. Technol 2005, 26, 441–447. [Google Scholar]
- Wang, ZW; Li, GZ; Zhang, XY; Liao, LL. Prediction on the effectiveness in surface tension reduction of anionic surfactants in aqueous solution: quantitative structure-property relationship approach. Proceeding of 2002 International Conference on Surfactants & Detergents, Shenzhen, China, July 28–August 1, 2002; pp. 66–70.
- Wang, ZW; Huang, DY; Li, GZ; Zhang, XY; Liao, LL. Effectiveness of surface tension reduction by anionic surfactants, a quantitative structure-property relationship. J. Dispersion Sci. Technol 2003, 24, 653–658. [Google Scholar]
- Stanton, DT; Jurs, PC; Hicks, MG. Computer-assisted prediction of normal boiling points of furans, tetrahydrofurans, and thiophenes. J. Chem. Inf. Comput. Sci 1991, 31, 301–310. [Google Scholar]
- Stanton, DT; Jurs, PC. Computer-assisted study of the relationship between molecular structure and surface tension of organic compounds. J. Chem. Inf. Comput. Sci 1992, 32, 109–115. [Google Scholar]
- Ghasemi, J; Ahmadi, S. Combination of genetic algorithm and partial least squares for cloud point prediction of nonionic surfactants from molecular structures. Anal. Chim 2007, 97, 69–83. [Google Scholar]
- Chen, ML; Wang, ZW; Zhang, GX; Gu, J; Cun, Z; Tao, FM. Studies on the cloud points of nonionic surfactants with QSPR. Chem. Res. Chinese U 2007, 23, 715–719. [Google Scholar]
- Mitchell, DJ; Tiddy, GJT; Waring, L; Bostock, T; McDonald, MP. Phase behaviour of polyoxyethylene surfactants with water. J. Chem. Soc. Faraday Trans 1983, 79, 975–1000. [Google Scholar]
- Ren, YY; Liu, HX; Yao, XJ; Liu, MC; Hu, ZD; Fan, BT. The accurate QSPR models for the prediction of nonionic surfactant cloud point. J. Colloid Interface Sci 2006, 302, 669–672. [Google Scholar]
- Bünz, AP; Braun, B; Janowsky, R. Application of quantitative structure performance relationship and neural network models for the prediction of physical properties from molecular structure. Ind. Eng. Chem. Res 1998, 37, 3043–3051. [Google Scholar]
- Huibers, PDT; Shah, DO; Katritzky, AR. Predicting surfactant cloud point from molecular structure. J. Colloid Interface Sci 1997, 193, 132–136. [Google Scholar]
- Yuan, SL; Cai, ZT; Xu, GY; Wang, W. Prediction of cloud poiont of nonionic surfactants using quantitative structure-property relationship method. Acta Phys. Chim. Sin 2003, 19, 334–337. [Google Scholar]
- Guan, JQ; Li, JS. Biodegradation of surfactants in the environment [in Chinese]. Environ. Sci 1994, 15, 81–85. [Google Scholar]
- Schöbel, P; Marl, FRG. Basic principles of LAS degradation. Tenside Surfactants Detergents 1989, 26, 86–94. [Google Scholar]
- Qu, FP; Yang, YY; Feng, XD; Qi, J; Dai, YY. Research principle and progress of QSBR (Quantitative Structure Biodegradability Relationships) [in Chinese]. China Environ. Sci 1999, 19, 18–21. [Google Scholar]
- European Parliament Regulation (EC) No 648/2004 of the European Parliament and of the Council of 31 March 2004 on detergents. EC No 684/2004. In Official Journal of the European Union, published in Luxembourg, 8 April 2004.
- Merrettig-Bruns, U; Jelen, E. Anaerobic biodegradation of detergent surfactants. Materials 2009, 2, 181–206. [Google Scholar]
- Siwiski, P; Szymaski, A; Lukaszewski, Z. Biodegradability of detergent powder surfactants in the river water die-away test. Polish J. Environ. Stud 1998, 7, 251–256. [Google Scholar]
- Sales, D; Perales, JA; Manzano, MA; Quiroga, JM. Anionic surfactant biodegradation in seawater. Bol. Inst. Esp. Oceanogr 1999, 15, 517–522. [Google Scholar]
- Li, L; Zhang, XY; Wang, ZW; Li, GZ. Structure-biodegradation relationship study of commercial linear alkylbenzene sulfonates. Internet Electr. J. Mol. Des 2003, 2, 383–391. [Google Scholar]
- Schultz, MM; Barofsky, DF; Field, JA. Fluorinated alkyl surfactants. Environ. Eng. Sci 2003, 20, 487–501. [Google Scholar]
- Nabb, DL; Szostek, B; Himmelstein, MW; Mawn, MP; Gargas, ML; Sweeney, LM; Stadler, JC; Buck, RC; Fasano, WJ. In Vitro metabolism of 8-2 fluorotelomer alcohol: interspecies comparisons and metabolic pathway refinement. Toxicol. Sci 2007, 100, 333–344. [Google Scholar]
- Parsons, JR; Sáez, M; Dolfing, J; Voogt, P. Biodegradation of perfluorinated compounds. Rev. Environ. Contam. Toxicol 2008, 196, 53–71. [Google Scholar]
- Guruge, KS; Yeung, LWY; Yamanaka, N; Miyazaki, S; Lam, PKS; Giesy, JP; Jones, PD; Yamashita, N. Gene expression profiles in rat liver treated with perfluorooctanoic acid (PFOA). Toxicol. Sci 2006, 89, 93–107. [Google Scholar]
- Dimitrov, S; Kamenska, V; Walker, JD; Windle, W; Purdy, R; Lewis, M; Mekenyan, O. Predicting the biodegradation products of perfluorinated chemicals using catabol. SAR QSAR Environ. Res 2004, 15, 69–82. [Google Scholar]
- Fei, CY; McLaughlin, JK; Lipworth, L; Olsen, J. Maternal levels of perfluorinated chemicals and subfecundity. Hum. Reprod 2009, 24, 1200–1205. [Google Scholar]
- Dimitrov, S; Kamenska, V; Walker, JD; Windle, W; Purdy, R; Lewis, M; Mekenyan, O. Predicting the biodegradation products of perfluorinated chemicals using catabol. SAR QSAR Environ. Res 2004, 15, 69–82. [Google Scholar]
- Torres, FJ; Ochoa-Herrera, V; Blowers, P; Sierra-Alvarez, R. Ab initio study of the structural, electronic, and thermodynamic properties of linear perfluorooctane sulfonate (PFOS) and its branched isomers. Chemosphere 2009, 76, 1143–1149. [Google Scholar]
- Chen, ML; Wang, ZW; Zhang, GX; Wang, WD; Wang, ZN. Prediction on hydrophile-lipophile balance values of anionic surfactants with QSPR method [in Chinese]. Acta Chim. Sinica 2007, 65, 1265–1272. [Google Scholar]
- Davies, JA; Hockensmith, CM; Kukushkin, VY; Kukushkin, YN. Synthetic Coordination Chemistry; World Scientific Publishing Co Pte Ltd: River Edge, NJ, USA, 1996; pp. 37–38. [Google Scholar]
- Liu, SL; Tong, JB; Li, YF. QSPR Study on hydrophile-lipophile balance values of anionic surfactant [in Chinese]. Guangdong Chem 2009, 36, 64–65. [Google Scholar]
- Ghasemi, J; Abdolmaleki, A; Asadpour, S; Shiri, F. Prediction of solubility of nonionic solutes in anionic micelle (SDS) using a QSPR model. QSAR Comb. Sci 2008, 27, 338–346. [Google Scholar]
- Campbell, P; Strinivasan, R; Knoell, T; Phipps, D; Ishida, K; Safarik, J. Quantitative structure-activity relationship (QSAR) analysis of surfactants influencing attachment of a Mycobacterium sp. to cellulose acetate and aromatic polyamide reverse osmosis membranes. Biotechnol. Bioeng 1999, 64, 527–544. [Google Scholar]
- Biz, S; Occelli, ML. Synthesis and characterization of mesostructured material. Catal. Rev. Sci. Eng 1998, 40, 329–407. [Google Scholar]
- Missel, PJ; Mazer, NA; Benedek, GB; Young, CY; Carey, MC. Thermodynamic analysis of the growth of sodium dodecyl sulfate micelles. J. Phys. Chem 1980, 84, 1044–1057. [Google Scholar]
- You, H; Zhao, B; Wang, ZW. Mesoscopic simulation on phase behavior of sodium polyoxyethylene fatty alcohol sulfate in aqueous solution. Acta Phys.—Chim 2009, 25, 67–73. [Google Scholar]
- Lindgren, A; Sjostrom, M; Wold, S. Quantitative-structure-effect relationship for some technical nonionic surfactants. J. Amer. Oil Chem. Soc 1996, 73, 863–875. [Google Scholar]
- Warszynski, P; Lunkenheimer, K. Influence of conformational free energy of hydrocarbon chains on adsorption of nonionic surfactants at the air/solution interface. J. Phys. Chem. B 1999, 103, 4404–4411. [Google Scholar]
- Wang, ZW; Yi, XZ. Calculation of the molecular exchanging energy of binary surfactants system on the surface monolayer of aqueous solution. Sci. China Ser. B 2007, 50, 468–475. [Google Scholar]
- Vitha, MF; Carr, PW. A linear solvation energy relationship study of the effects of surfactant chain length on the chemical interactions governing retention and selectivity in micellar electrokinetic capillary chromatography using sodium alkyl sulfate buffers. Sep. Sci. Technol 1998, 33, 2075–2100. [Google Scholar]
- Rosen, MJ. Surfactants and Interfacial Phenomena; John Wiley and Sons: New York, NY, USA, 1987; pp. 393–421. [Google Scholar]
- Andreea, PB; Muriel, B; Maura, B; Emile, P; Christophe, M; Isabelle, RL; Thomas, L; Reiko, O. Spontaneous vesicles of single-chain sugar-based fluorocarbon surfactants. J. Fluor. Chem 2005, 126, 33–38. [Google Scholar]
- Tu, GY; Wang, ZW; Wang, ZN; Liu, F; Xiao, JY. Theoretical expression and experiment on surface tension in ideal binary mixtures of surfactants [in Chinese]. Acta Phys.—Chim. Sin 2008, 24, 400–404. [Google Scholar]
- Wang, ZW; Yu, HX; Wang, ZN; Li, GZ. Theoretical further study on synergisms of binary surfactant mixtures in aqueous solution. J. Dispersion Sci. Technol 2006, 27, 723–726. [Google Scholar]
- Lü, Q; Gong, HF; Liu, MH. Progress in bolaamphiphile [in Chinese]. Prog. Chem 2001, 13, 161–166. [Google Scholar]
- McGregor, C; Perrin, C; Monck, M; Camilleri, P; Kirby, AJ. Rational approaches to the design of cationic gemini surfactants for gene deliver. J. Am. Chem. Soc 2001, 123, 6215–6220. [Google Scholar]
- Tomasi, J; Persico, M. Molecular interactions in solution: An overview of methods based on continuous distributions of the solvent jacopo tomasi, maurizio persico. Chem. Rev 1994, 94, 2027–2094. [Google Scholar]
- Karelson, MM; Zerner, MC. Theoretical treatment of solvent effects on electronic spectroscopy. J. Phys. Chem 1992, 96, 6949–6957. [Google Scholar]
- Szafran, M; Karelson, MM; Katritzky, AR; Koput, J; Zerner, MC. Reconsideration of solvent effects calculated by semiempirical quantum chemical methods. J. Comput. Chem 1993, 14, 371–377. [Google Scholar]
- Wong, MW; Frisch, MJ; Wiberg, KB. Solvent effects. 1. The mediation of electrostatic effects by solvents. J. Am. Chem. Soc 1991, 113, 4776–4781. [Google Scholar]
- Dykstra, CE. Electrostatic interaction potentials in molecular force fields. Chem. Rev 1993, 93, 2339–2353. [Google Scholar]
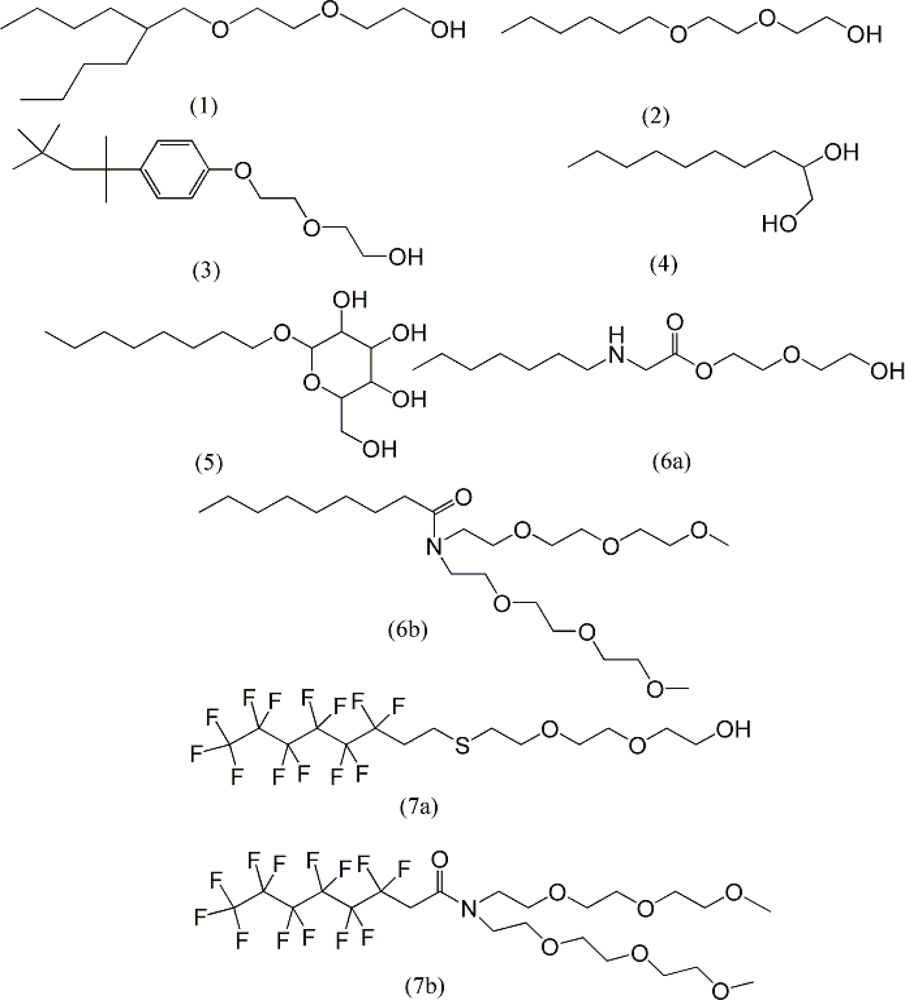
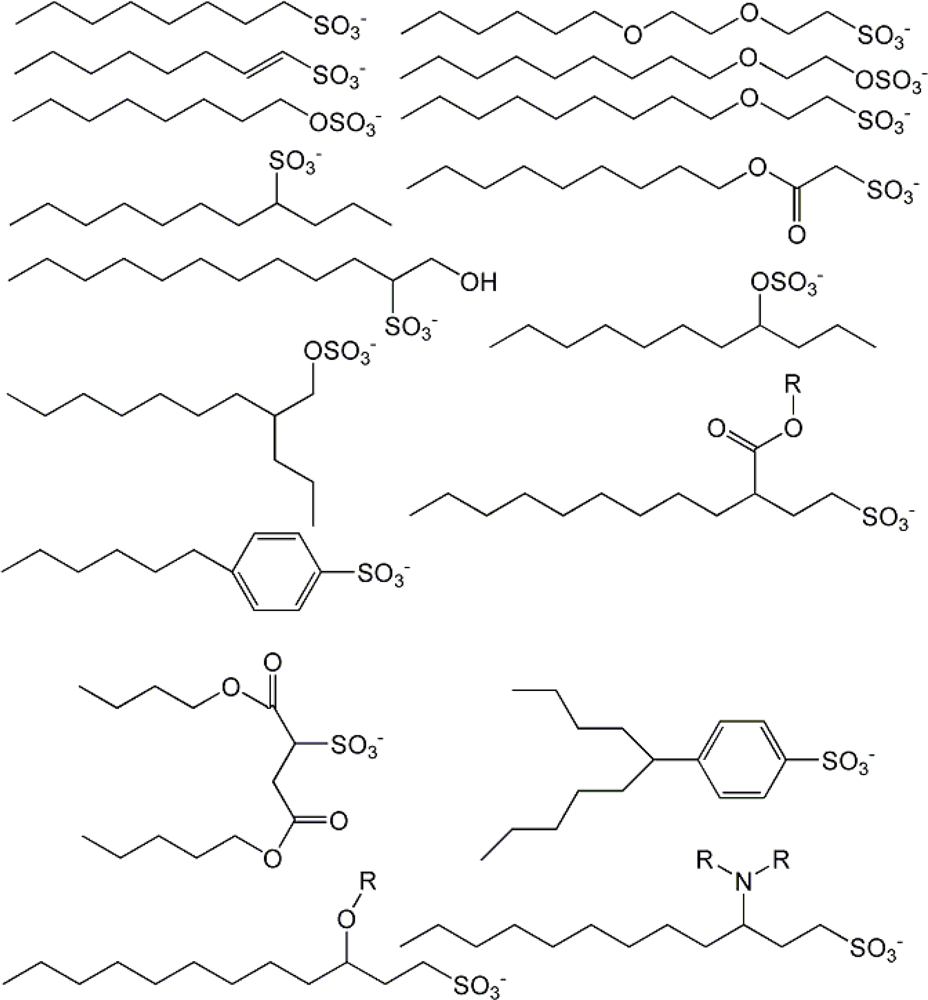
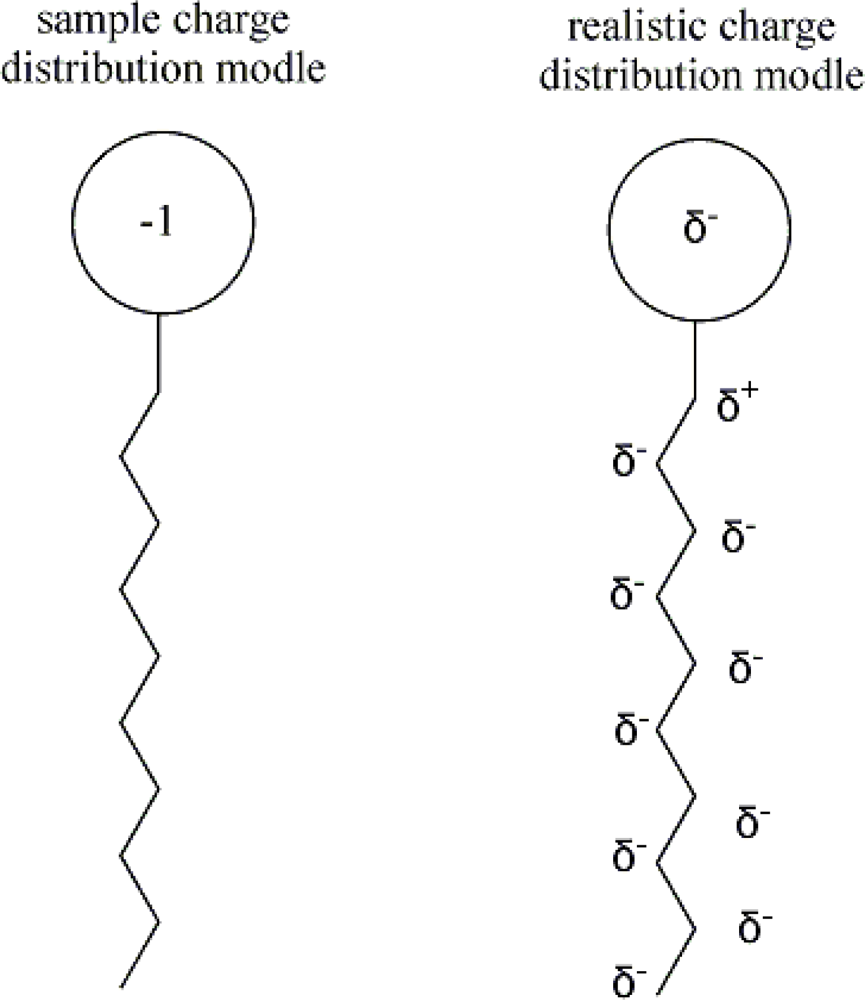
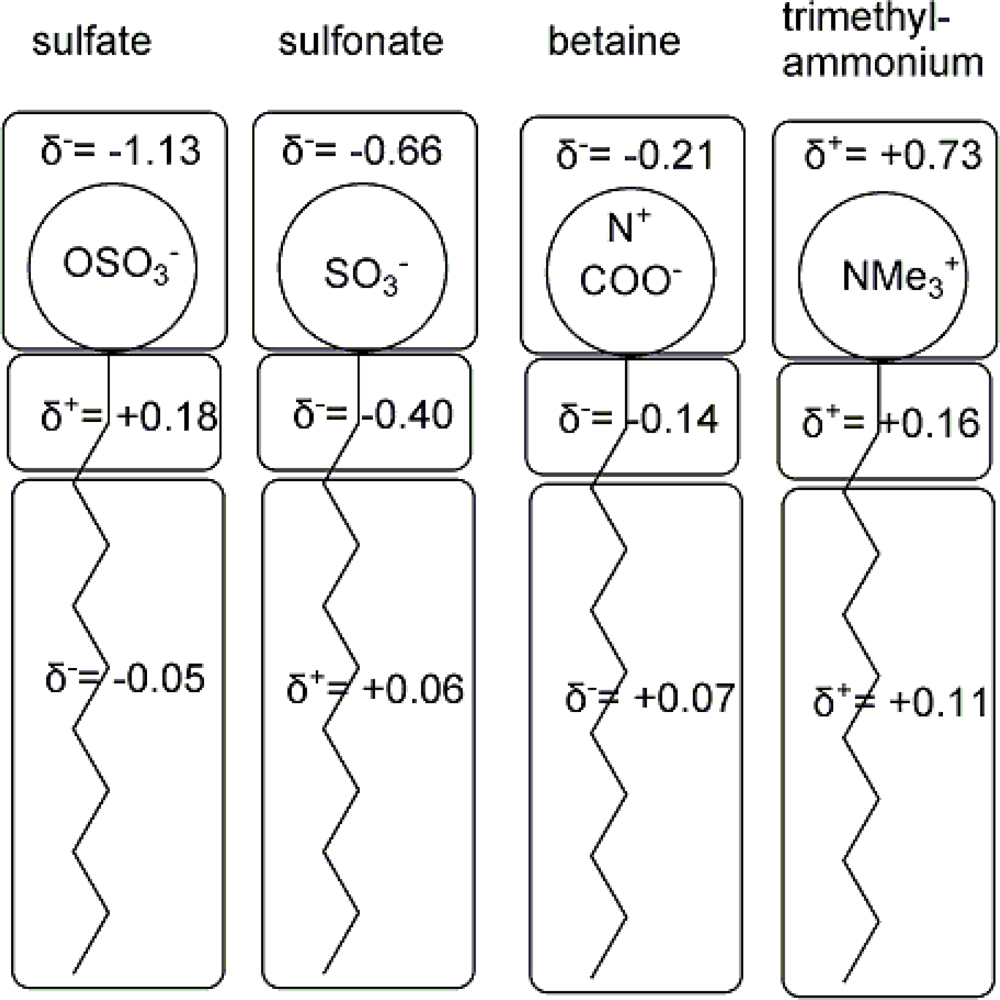
| descriptor | No. | X | DX | t-test | R2 | F | S2 |
|---|---|---|---|---|---|---|---|
| intercept | 0 | –7.03E + 02 | 1.91E + 01 | –36.7455 | |||
| relative molecular weight | 1 | 1.77E + 02 | 4.33E + 00 | 40.9502 | 0.2983 | 8.08 | 313.55 |
| average information content (order 2) | 2 | –4.53E + 01 | 2.56E + 00 | –17.7164 | 0.6445 | 16.32 | 167.67 |
| relative number of rings | 3 | –5.53E + 03 | 1.68E + 02 | –32.8383 | 0.8516 | 32.51 | 74.14 |
| Kier shape index (order 3) | 4 | –2.81E + 00 | 1.34E – 01 | –21.0049 | 0.9948 | 765.99 | 2.75 |
| 1 | Introduction |
| 2 | Studies on Relationships between CMC And Molecular Structures |
| 2.1 | QSPR Studies on CMC of Surfactants Based on Molecular Connectivity Index |
| 2.2 | QSPR Studies of CMC of Surfactants Based on Quantum Mechanical Descriptors |
| 2.3 | QSPR Studies of CMC of Surfactants Using Neural Network |
| 2.4 | QSPR Studies of CMC of Surfactants Using Other Methods |
| 3 | Charge Distribution of Surfactants and Its Influence on Their Properties |
| 3.1 | Computation of Charge Distribution in Ionic Surfactant Molecules and Their Effects |
| 3.2 | Descriptors Related to Molecular Surface Area — CPSA |
| 4 | Surface Tension Prediction Models |
| 5 | QSAR Studies on Cloud Point of Nonionic Surfactants |
| 6 | Studies on Degradation of Surfactants |
| 7 | QSPR Studies on Other Properties of Surfactants |
| 8 | Conclusions and Prospects |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hu, J.; Zhang, X.; Wang, Z. A Review on Progress in QSPR Studies for Surfactants. Int. J. Mol. Sci. 2010, 11, 1020-1047. https://doi.org/10.3390/ijms11031020
Hu J, Zhang X, Wang Z. A Review on Progress in QSPR Studies for Surfactants. International Journal of Molecular Sciences. 2010; 11(3):1020-1047. https://doi.org/10.3390/ijms11031020
Chicago/Turabian StyleHu, Jiwei, Xiaoyi Zhang, and Zhengwu Wang. 2010. "A Review on Progress in QSPR Studies for Surfactants" International Journal of Molecular Sciences 11, no. 3: 1020-1047. https://doi.org/10.3390/ijms11031020





