Active Polymer Gel Actuators
Abstract
:1. Introduction
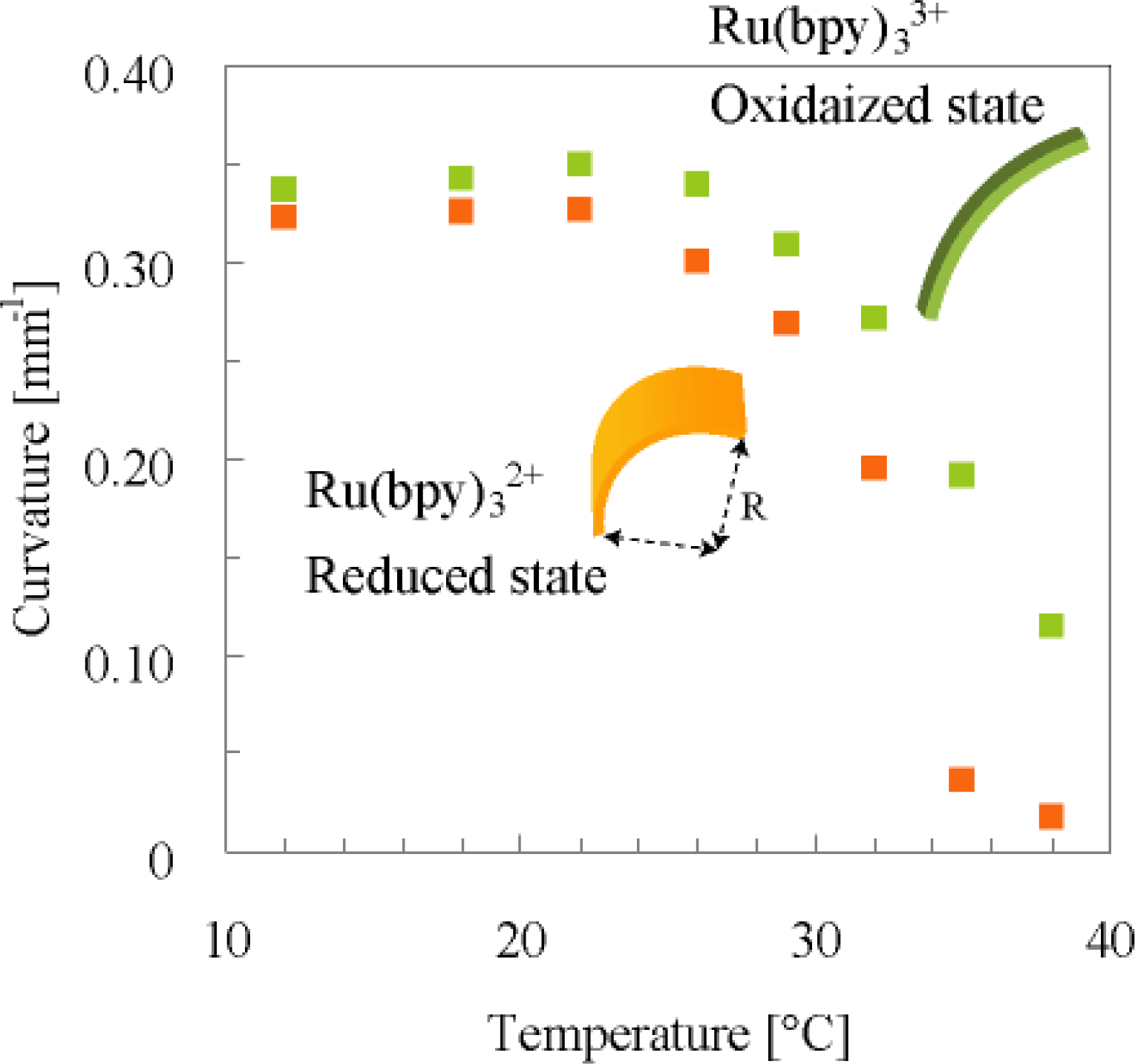
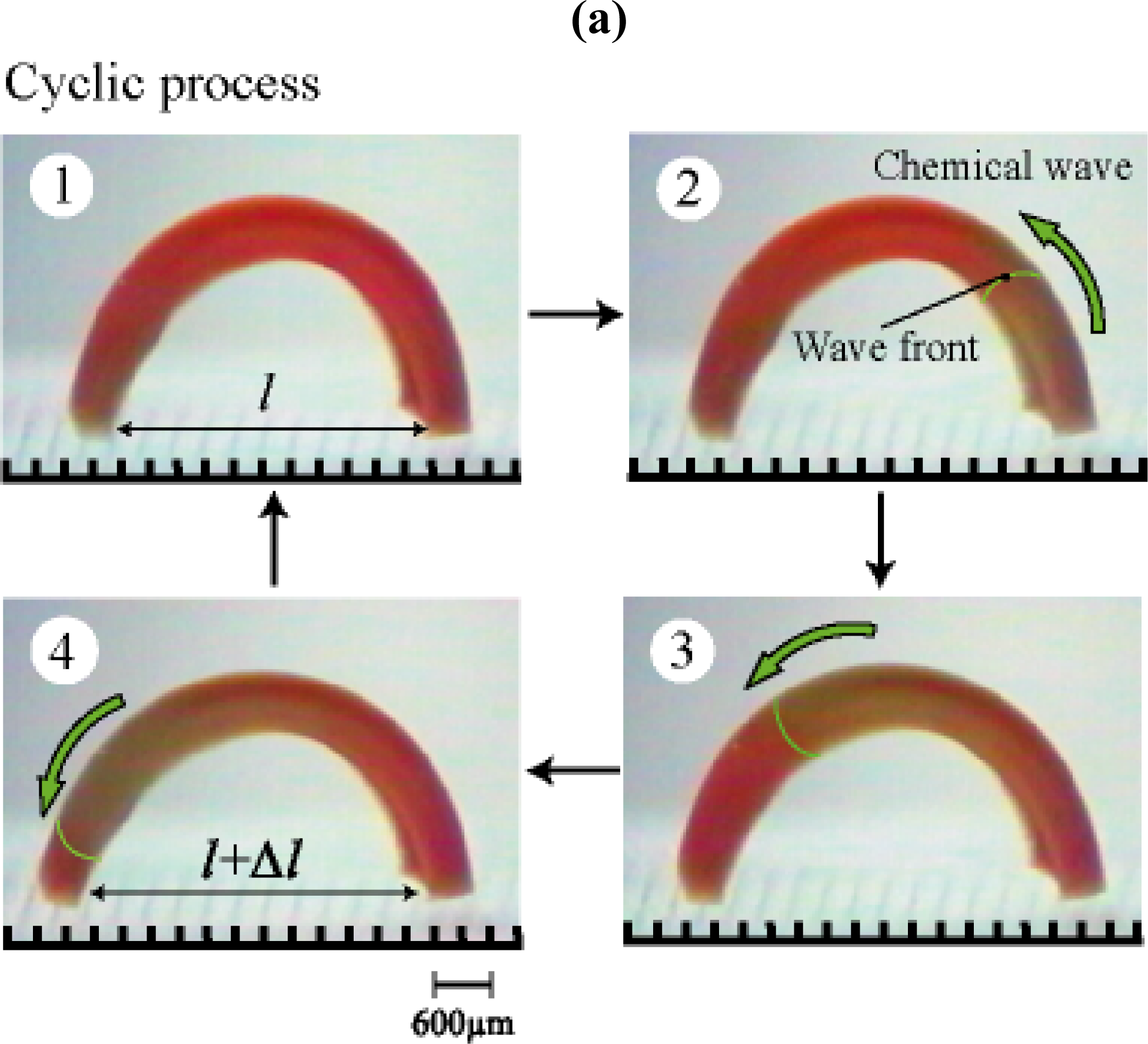
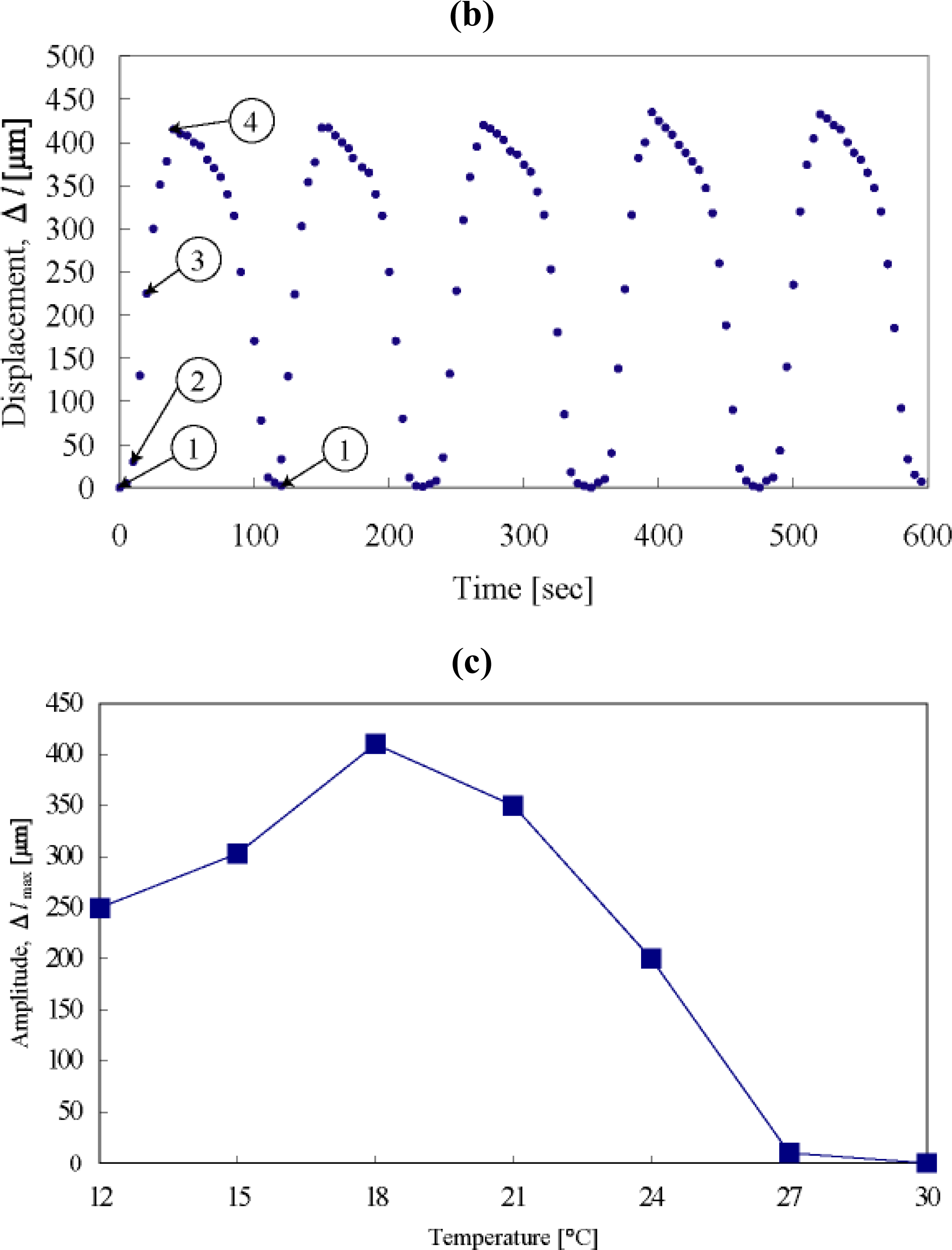
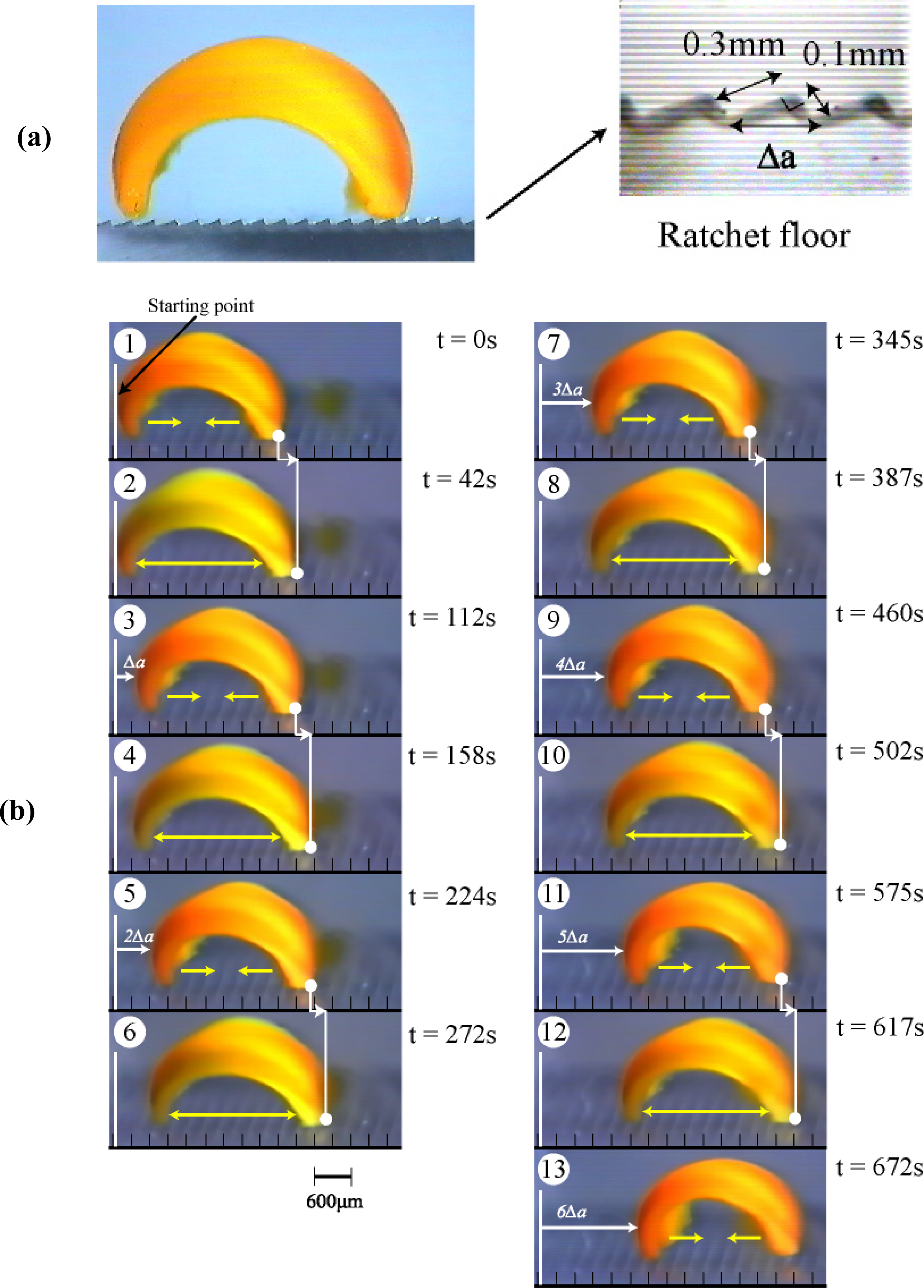
2. Design of Self-walking Gel
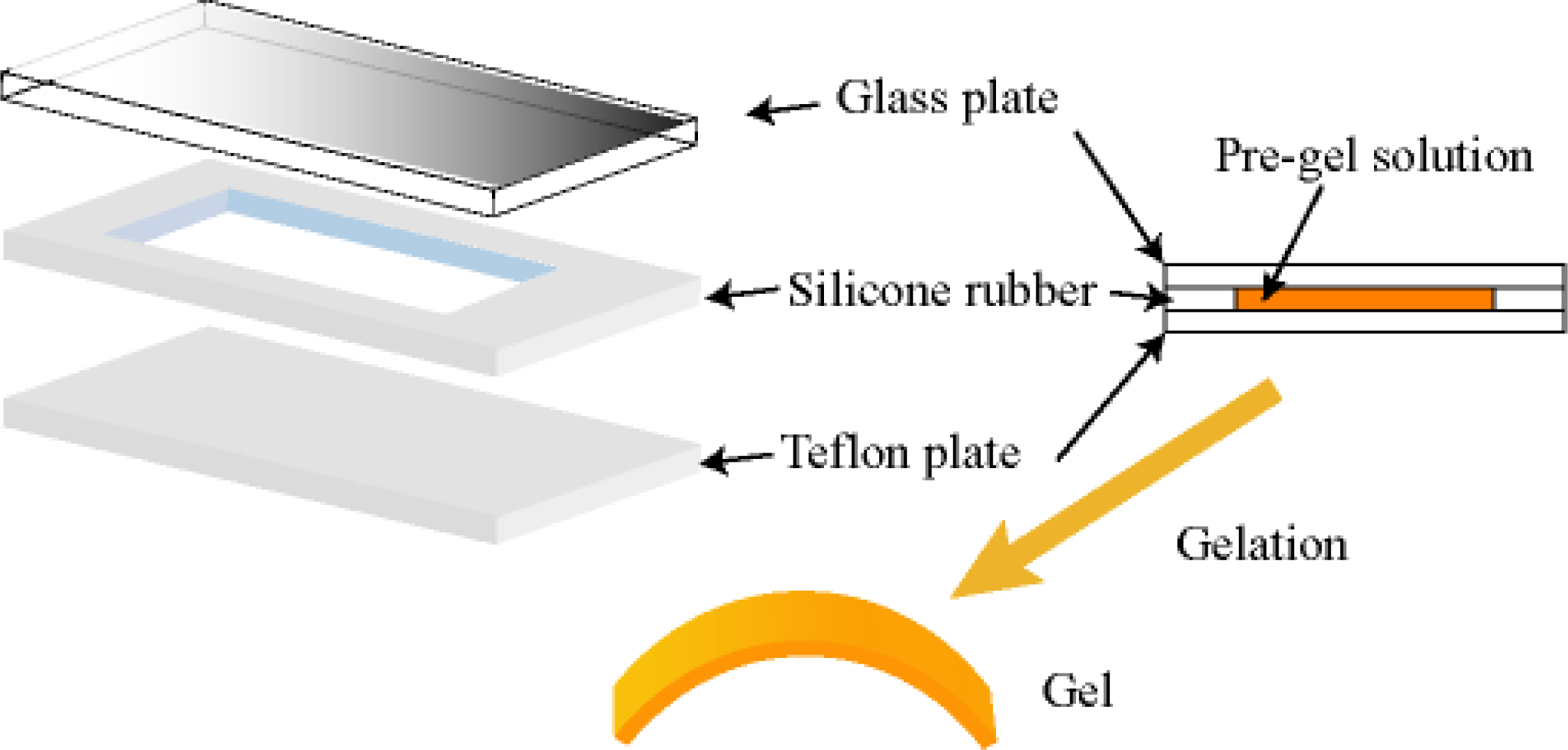
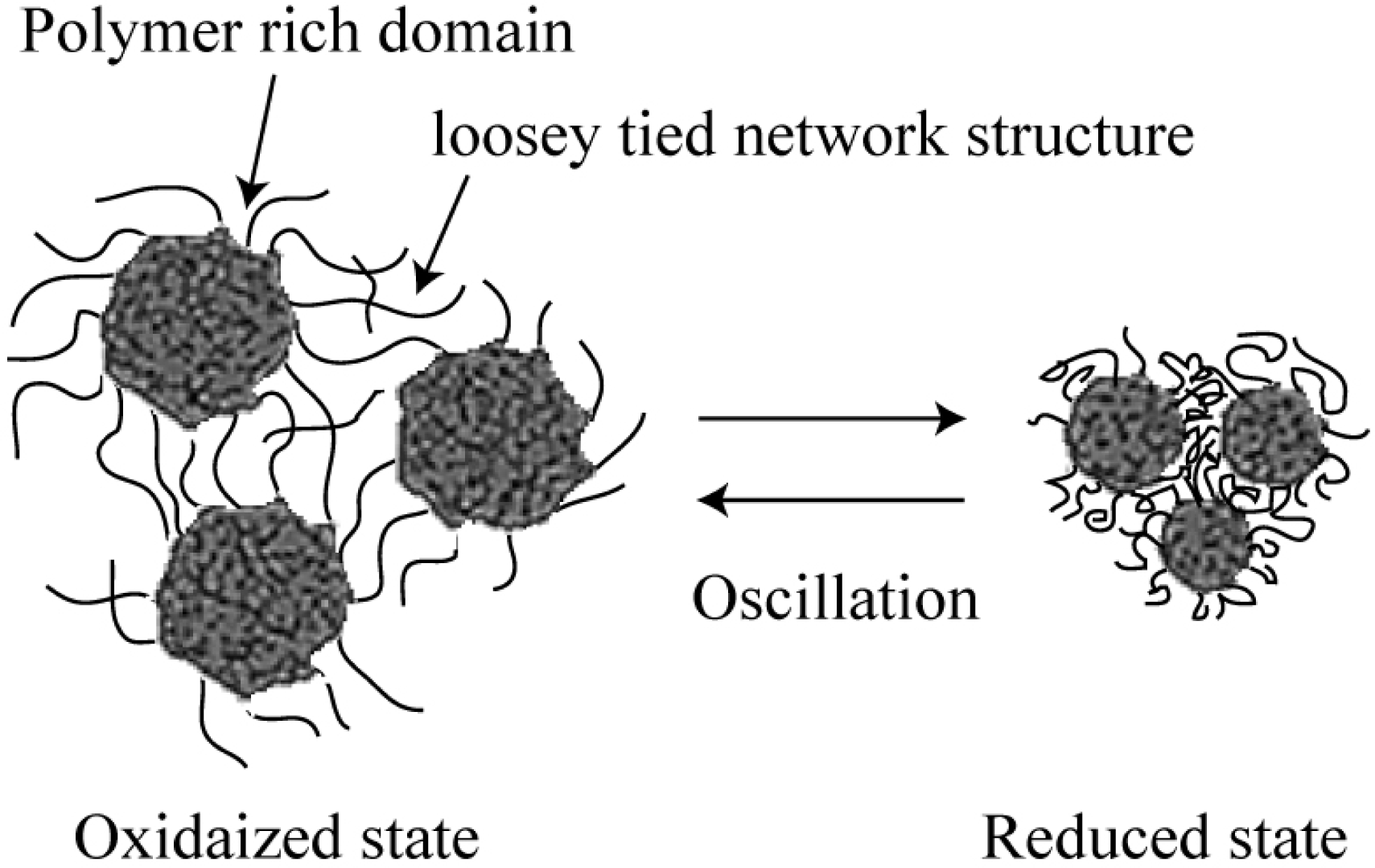
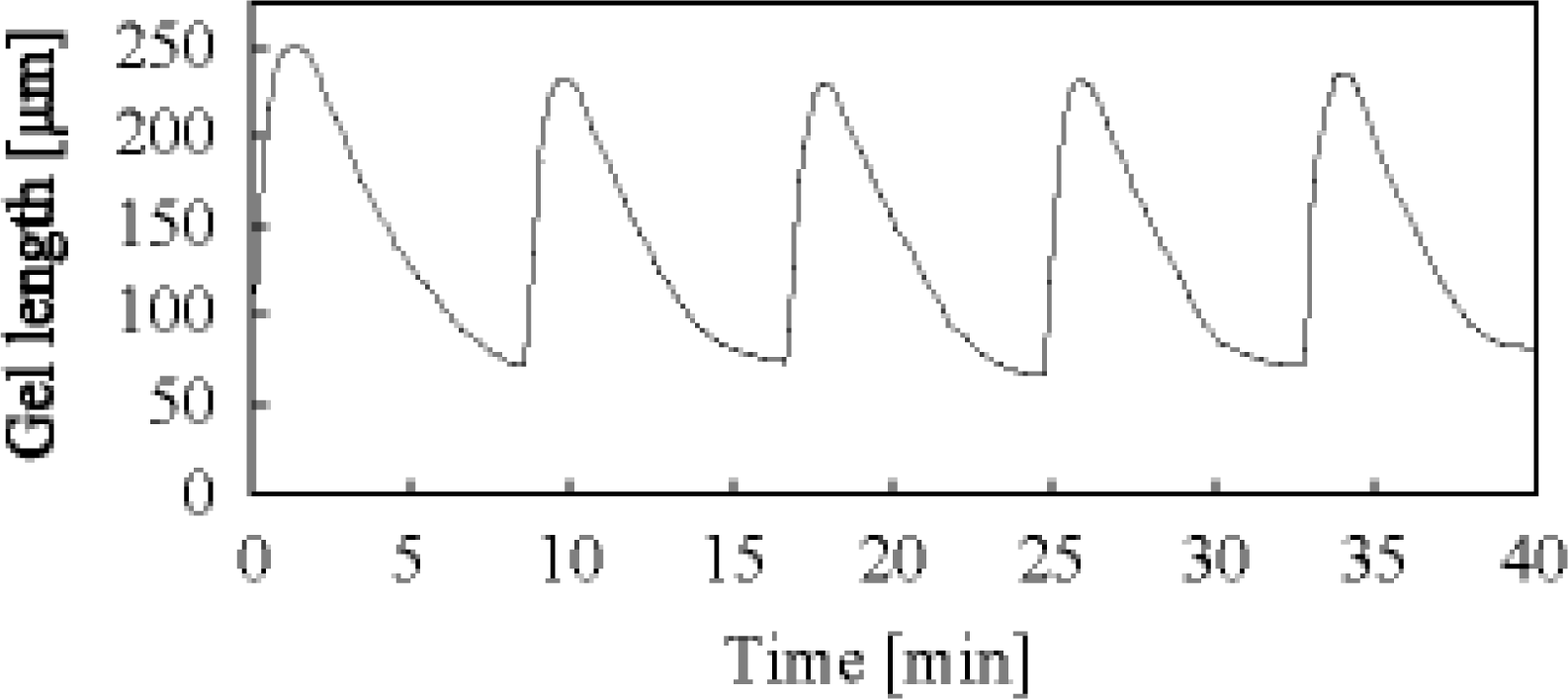
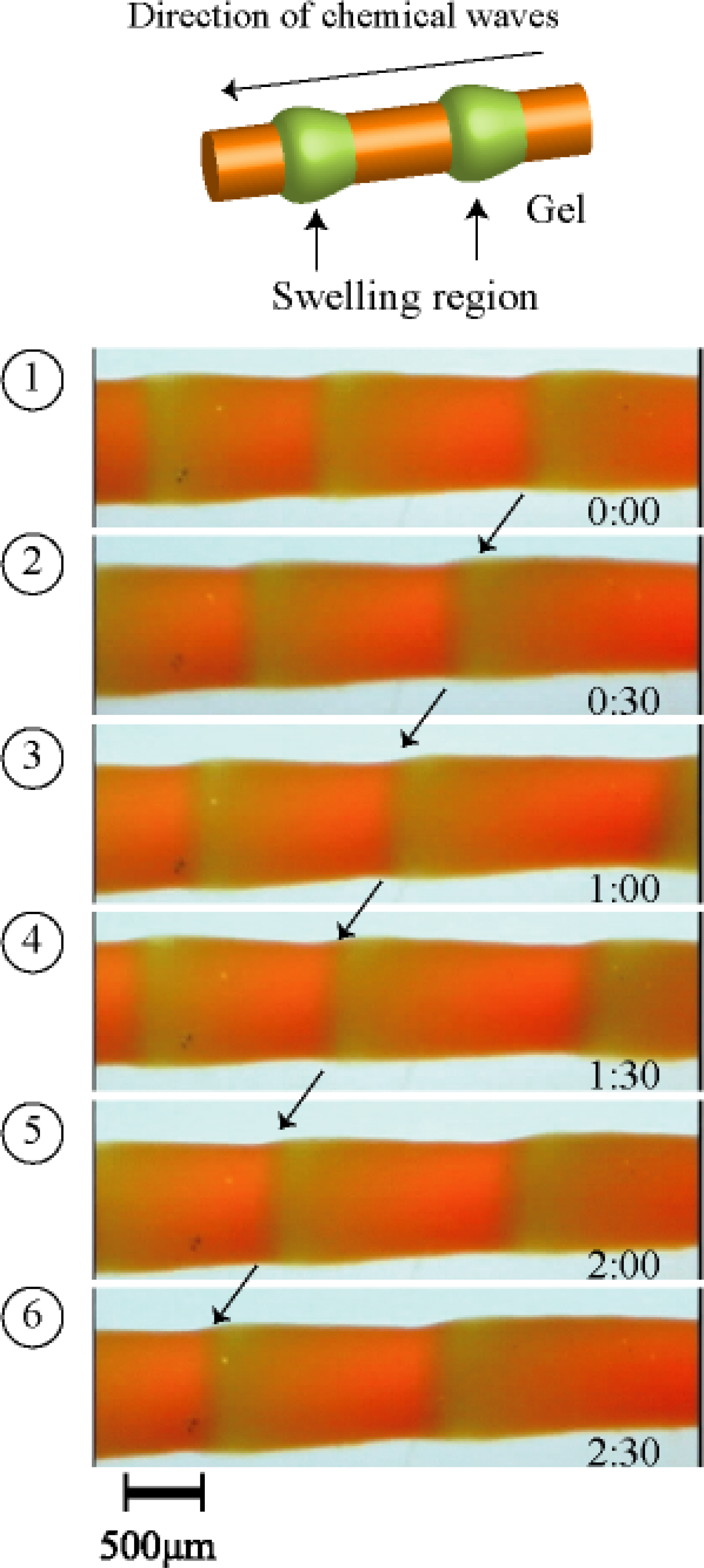
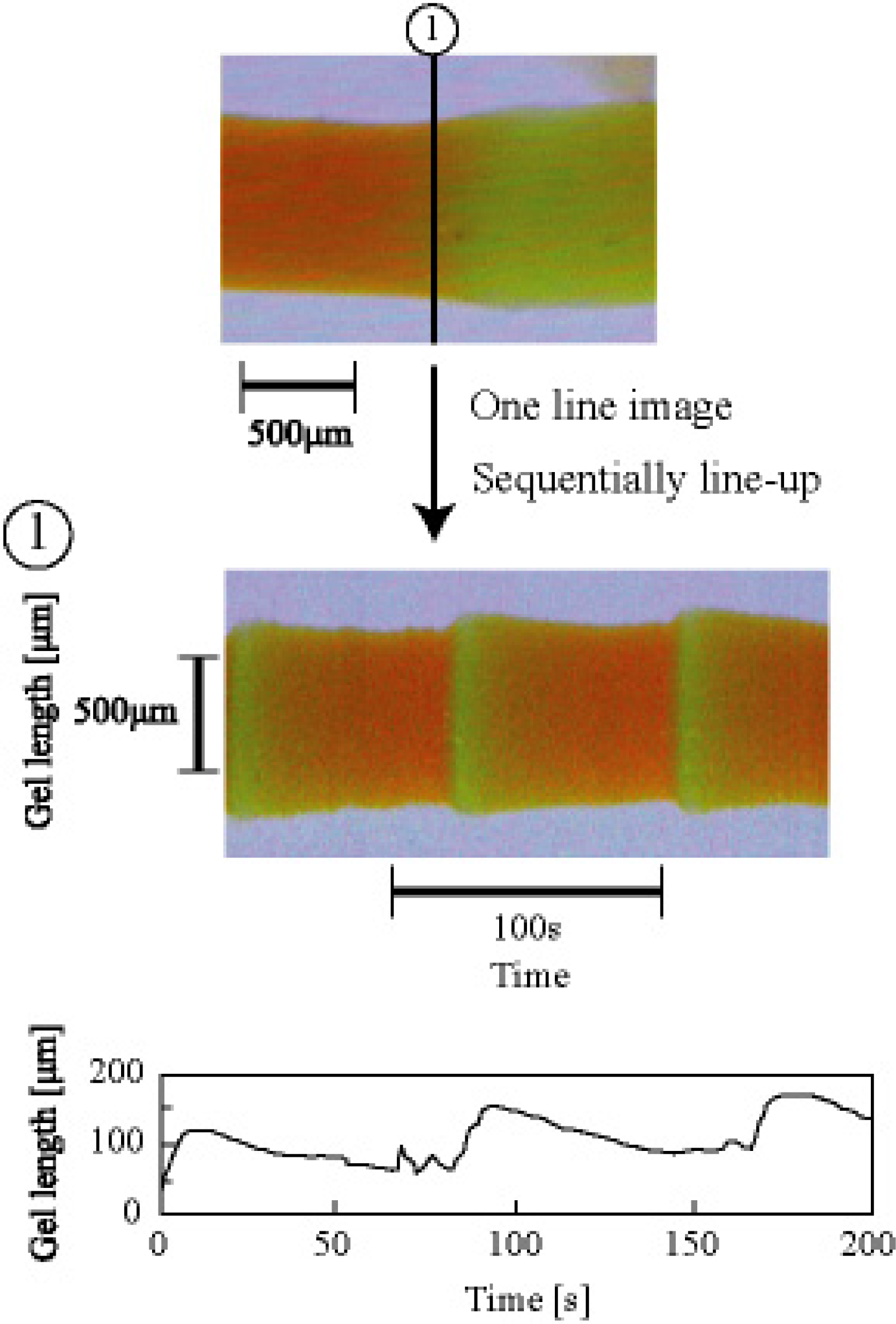
3. Design of Peristaltic Motion of a Polymer Gel
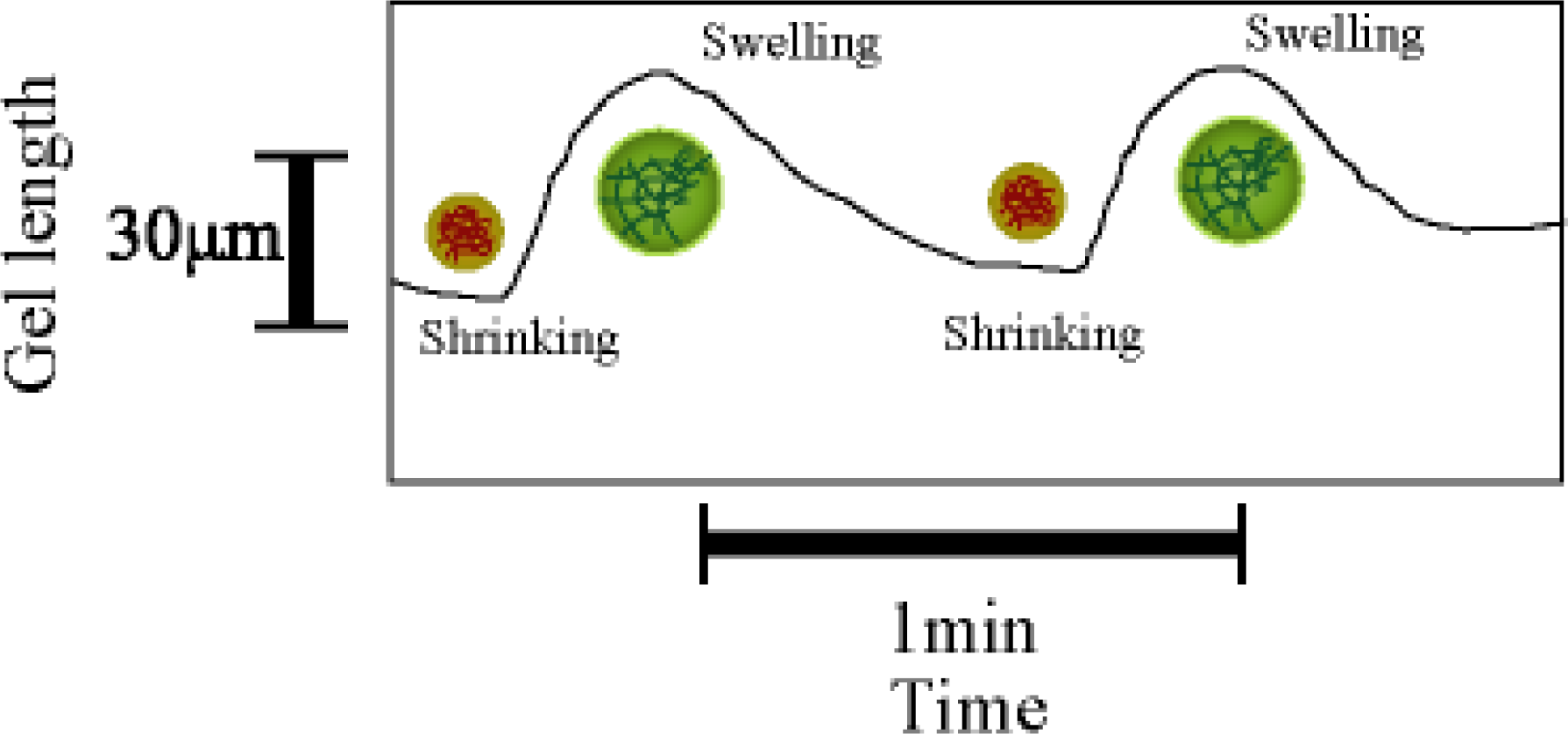
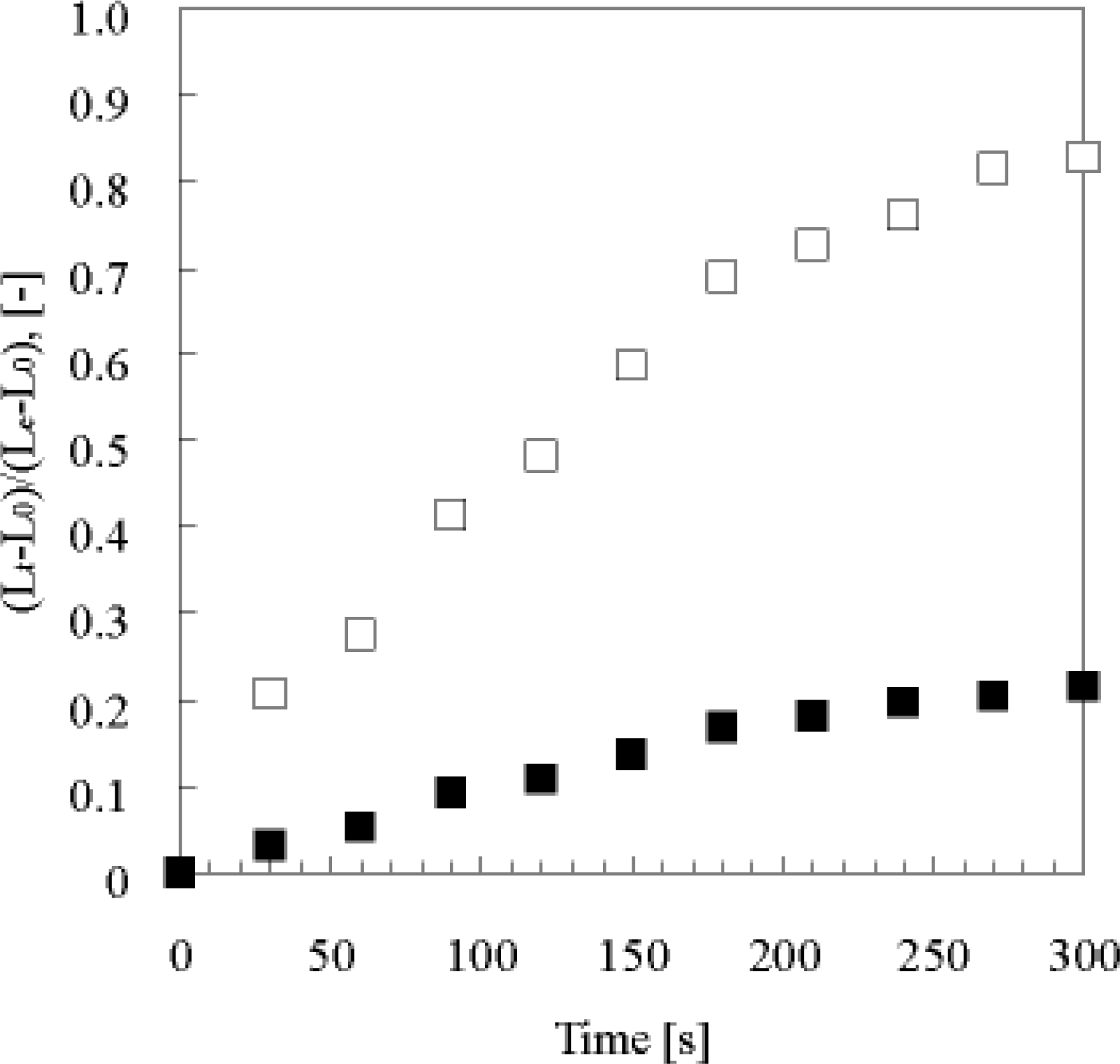
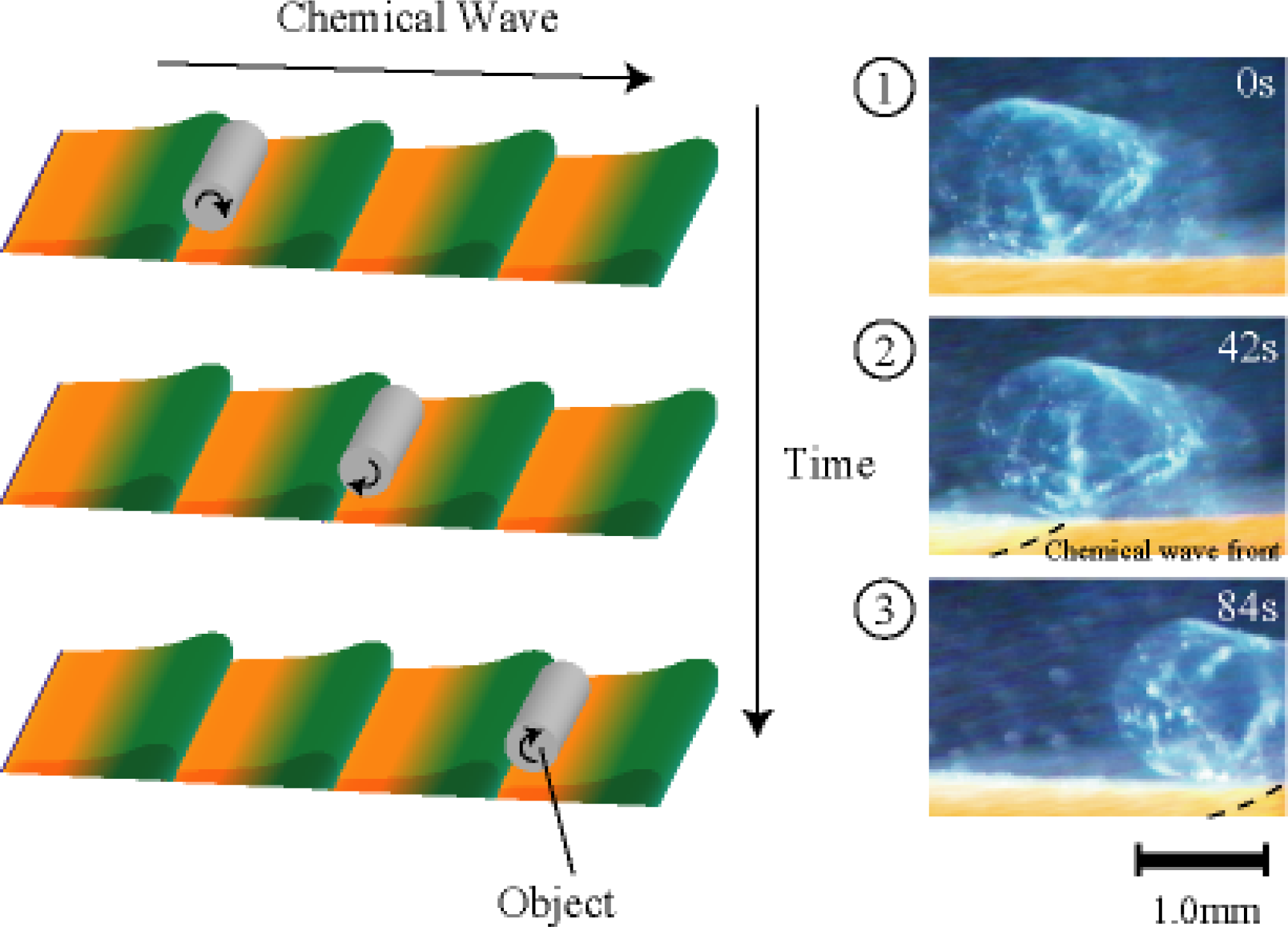
4. Matter Transport
5. Conclusions
Acknowledgments
References
- Hirokawa, Y; Tanaka, T. Volume phase transition in a non ionic gel. J. Chem. Phys 1984, 81, 6379–6380. [Google Scholar]
- Tanaka, T. Collapse of gels and critical endpoint. Phys. Rev. Lett 1978, 40, 820–823. [Google Scholar]
- Suzuki, A; Tanaka, T. Phase transition in a polymer gels induced by visible-light. Nature 1990, 346, 345–347. [Google Scholar]
- Ilmain, F; Tanaka, T; Kokufuta, E. Volume transition in a gel by hydrogen bonding. Nature 1991, 349, 400–401. [Google Scholar]
- Tanaka, T; Nishio, I; Sun, ST; Uenoshio, S. Collapse of gels in an electric field. Science 1982, 218, 467–469. [Google Scholar]
- Oguro, K; Kawami, Y; Takenaka, H. An actuator element of polyelectrotyte gel membrane-electrode composite. Bull. Gov. Ind. Res. Inst 1992, 43, 21–24. [Google Scholar]
- Fukushima, T; Asaka, K; Kosaka, A; Aida, T. Fully plastic actuator through layer-by-layer casting with ionic-liquid-based bucky gel. Angew. Chem. Int. Ed 2005, 44, 2410–2413. [Google Scholar]
- Steinberg, IZ; Oplatka, A; Kachalsky, A. Mechanochemnical engines. Nature 1966, 210, 568–571. [Google Scholar]
- Tanaka, T. Gels. Sci. Am 1981, 244, 110–116. [Google Scholar]
- Yoshida, R; Sakai, K; Okano, T; Sakurai, Y. Modern hydrogel delivery systems. Adv. Drug Delivery Rev 1993, 11, 85–108. [Google Scholar]
- Hu, Z; Zhang, X; Li, Y. Synthesis and application of modulated polymer gels. Science 1995, 269, 525–527. [Google Scholar]
- Yeghiazarian, L; Mahajan, S; Montemagno, C; Cohen, C; Wiesner, U. Directed motion and cargo transport through propagation of polymer-gel volume phase transitions. Adv. Mater 2005, 17, 1869–1873. [Google Scholar]
- Huber, DL; Manginell, RP; Samara, MA; Kim, B; Bunker, BC. Programmed adsorption and released of proteins in a microfluidic device. Science 2003, 301, 352–354. [Google Scholar]
- Feinberg, AW; Feigel, A; Shevkoplyas, SS; Sheehy, S; Whitesides, GM; Parker, KK. Muscular thin films for building actuators and powering devices. Science 2007, 317, 1366–1370. [Google Scholar]
- Crook, CJ; Smith, A; Jones, AL; Ryan, AJ. Chemically induced oscillations in a pH-responsive hydrogel. Phys. Chem. Chem. Phys 2002, 4, 1367–1369. [Google Scholar]
- Lerox, JC; Siegel, RA. Autonomous gel/enzyme oscillator fueled by glucose: Preliminary evidence for oscillations. Chaos 1999, 9, 267–275. [Google Scholar]
- Labrot, V; De Kepper, P; Boissonade, J; Szalai, I; Gauffre, F. Wave patterns driven by chemomechanical instabilities in responsive gels. J. Phys. Chem. B 2005, 109, 21476–21480. [Google Scholar]
- Yoshida, R; Takahashi, T; Yamaguchi, T; Ichijo, H. Self-oscillating gel. J. Am. Chem. Soc 1996, 118, 5134–5135. [Google Scholar]
- Zaikin, AN; Zhabotinsky, AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature 1970, 225, 535–537. [Google Scholar]
- Noszticzius, Z; Horsthemke, W; Mccormick, WD; Swinney, HL; Tam, WY. Sustained chemical waves in an annular gel reactor: A chemical pinwheel. Nature 1987, 329, 619–621. [Google Scholar]
- Yamaguchi, T; Kuhnert, L; Nagy-Ungvarai, Z; Muller, SC; Hess, B. Gel systems for the Belousov-Zhabotinskii reaction. J. Phys. Chem 1991, 95, 5831–5837. [Google Scholar]
- Ishiwatari, T; Kawaguchi, M; Mitsuishi, M. Oscillatry reactions in polymer systems. J. Polym. Sci. Part. A: Polm. Chem 1984, 22, 2699–2704. [Google Scholar]
- Yoshida, R; Sakai, T; Ito, S; Yamaguchi, T. Self-oscillation of polymer chains with rhythmical soluble-insoluble changes. J. Am. Chem. Sci 2002, 124, 8095–8098. [Google Scholar]
- Maeda, S; Hara, Y; Yoshida, R; Hashimoto, S. Control of the dynamic motion of a gel actuator driven by the Belousov-Zhabotinsky reaction, Macromol. Rapid Commun 2008, 29, 401–405. [Google Scholar]
- Maeda, S; Hara, Y; Sakai, T; Yoshida, R; Hashimoto, S. Self-walking gel. Adv. Mater 2007, 19, 3480–3484. [Google Scholar]
- Yashin, VV; Balazs, AC. Pattern formation and shape changes in self-oscillating polymer gels. Science 2006, 314, 798–801. [Google Scholar]
- Yashin, VV; Balazs, AC. Theoretical and computational modeling of self-oscillating polymer gels. J Chem Phys 2007, 126, 124707:1–124707:17. [Google Scholar]
- Takeoka, Y; Watanabe, M; Yoshida, R. Self-sustaining peristaltic motion on the surface of a porous gel. J. Am. Chem. Soc 2003, 125, 13320–13321. [Google Scholar]
- Maeda, S; Hara, Y; Yoshida, R; Hashimoto, S. Peristaltic motion of polymer gels. Angew. Chem. Int. Ed 2008, 47, 6690–6693. [Google Scholar]
- Tanaka, T; Hocker, L; Benedek, GB. Spectrum of light scattered from a viscoelastic gel. J. Chem. Phys 1973, 53, 5151–5159. [Google Scholar]
- Kabra, BG; Gehrke, SH. Synthesis of fast response, temperature-sensitive poly(N-isopropylacrylamide) gels. Polym. Commun 1991, 32, 322–323. [Google Scholar]
- Hirotsu, S. Phase Transition of a Polymer Gel in Pure and Mixed Solvent Media. J. Phys. Soc. Jpn 1986, 56, 233–242. [Google Scholar]
- Tanaka, F; Koga, T; Kojima, H; Winnik, MF. Temperature- and tension-induced coil–globule transition of Poly(N-isopropylacrylamide) chains in water and mixed solvent of water/methanol. Macromolecules 2009, 42, 1321–1330. [Google Scholar]
- Hara, Y; Yoshida, R. Self-oscillating polymer fueled by organic acid. J. Phys. Chem. B 2008, 112, 8427–8429. [Google Scholar]
- Hara, Y; Yoshida, R. Self-oscillation of polymer chains induced by the Belousov-Zhabotinsky reaction under acid-free conditions. J. Phys. Chem. B 2005, 109, 9451–9454. [Google Scholar]
- Hara, Y; Sakai, T; Maeda, S; Hashimoto, S; Yoshida, R. Self-oscillating soluble-insoluble changes of polymer chain including an oxidizing agent induced by the Belousov-Zhabotinsky reaction. J. Phys. Chem. B 2005, 109, 23316–23319. [Google Scholar]
- Nakamaru, S; Maeda, S; Hara, Y; Hashimoto, S. Control of autonomous swelling-deswelling behavior for a polymer gel. J. Phys. Chem. B 2009, 113, 4609–4613. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Maeda, S.; Hara, Y.; Yoshida, R.; Hashimoto, S. Active Polymer Gel Actuators. Int. J. Mol. Sci. 2010, 11, 52-66. https://doi.org/10.3390/ijms11010052
Maeda S, Hara Y, Yoshida R, Hashimoto S. Active Polymer Gel Actuators. International Journal of Molecular Sciences. 2010; 11(1):52-66. https://doi.org/10.3390/ijms11010052
Chicago/Turabian StyleMaeda, Shingo, Yusuke Hara, Ryo Yoshida, and Shuji Hashimoto. 2010. "Active Polymer Gel Actuators" International Journal of Molecular Sciences 11, no. 1: 52-66. https://doi.org/10.3390/ijms11010052




