Self-Assembly of Diamondoid Molecules and Derivatives (MD Simulations and DFT Calculations)
Abstract
:1. Introduction
2. Density Functional Theory (DFT) Calculations
3. Molecular Dynamic (MD) Simulation Procedures and Results
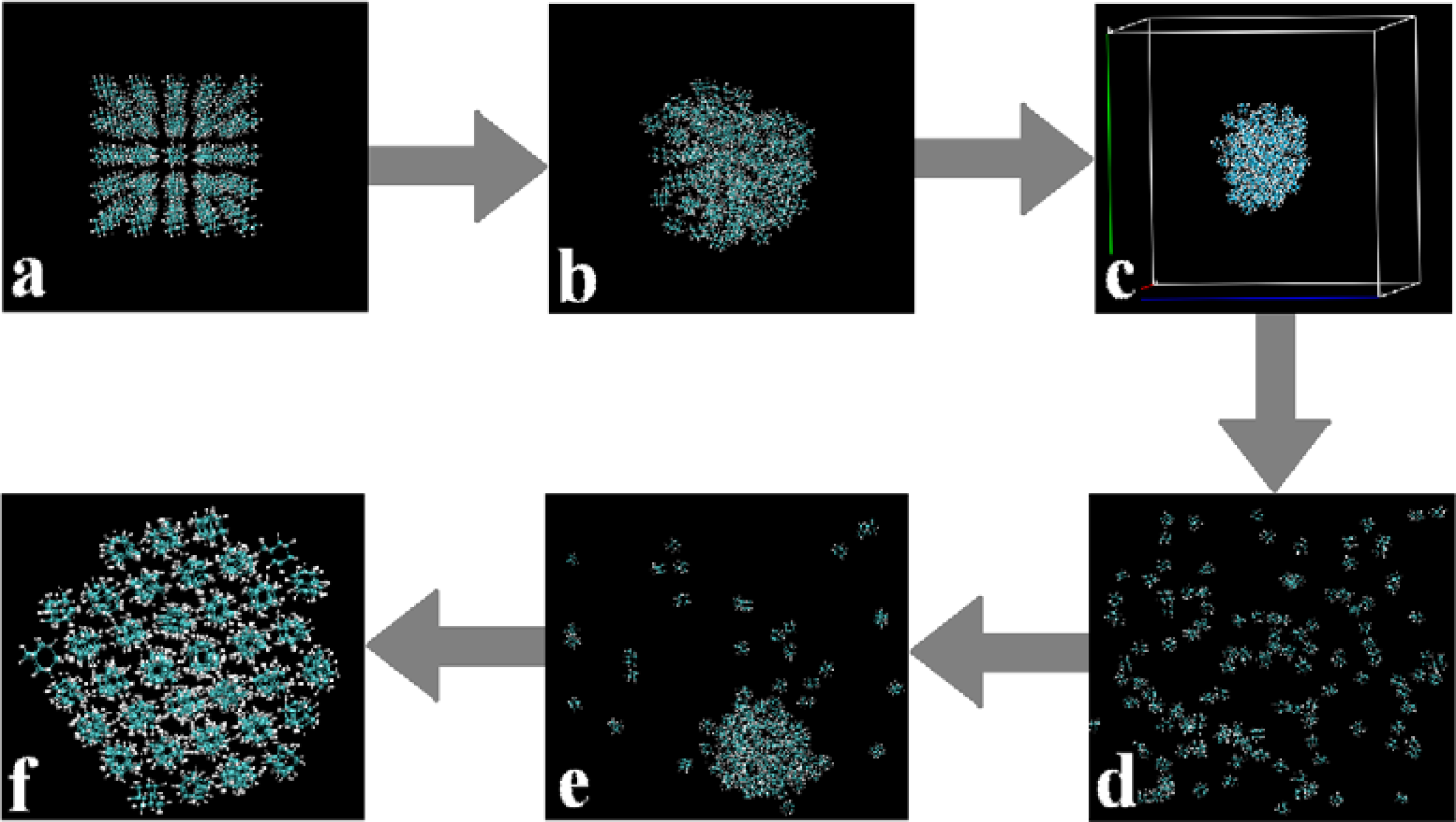
- A MD simulation box with 5 × 5 × 5 = 125 molecules was built by the intrinsic tools in the Gromacs software, as shown in Figure 2a.
- We boxed those stable structures and set the distances from molecules to the boundaries of the simulation boxes to about +3 nm. In this manner we could build simulation systems with reasonable densities which were in the range of their gas states and also made the systems isolated from the adjacent simulation boxes under the periodic boundary conditions, as shown in Figure 2c.
- Longer (more than 1,000 picoseconds) equilibrating simulations were performed in the NVT ensembles, and we applied the PME method with the cut-off at 2.0 nm and high temperatures (in the range of 500–700 K) in order to make sure the entire system went to the gaseous state, i.e., all the molecules separated from each other and distributed randomly in the simulation box as shown in Figure 2d.By applying the above four-step procedure we could equilibrate the system in a gas state. As a result, we eliminated the problem due to directly equilibrating the initially prepared molecular system, Figure 2a, at high temperatures. The equilibrated and stable-structure gaseous state, Figure 2d, was then ready for cooling down towards the self-assembly.
- Further cooling down of the system resulted in the complete self-assembly of all the molecules (to solid state) as shown in Figure 2f.
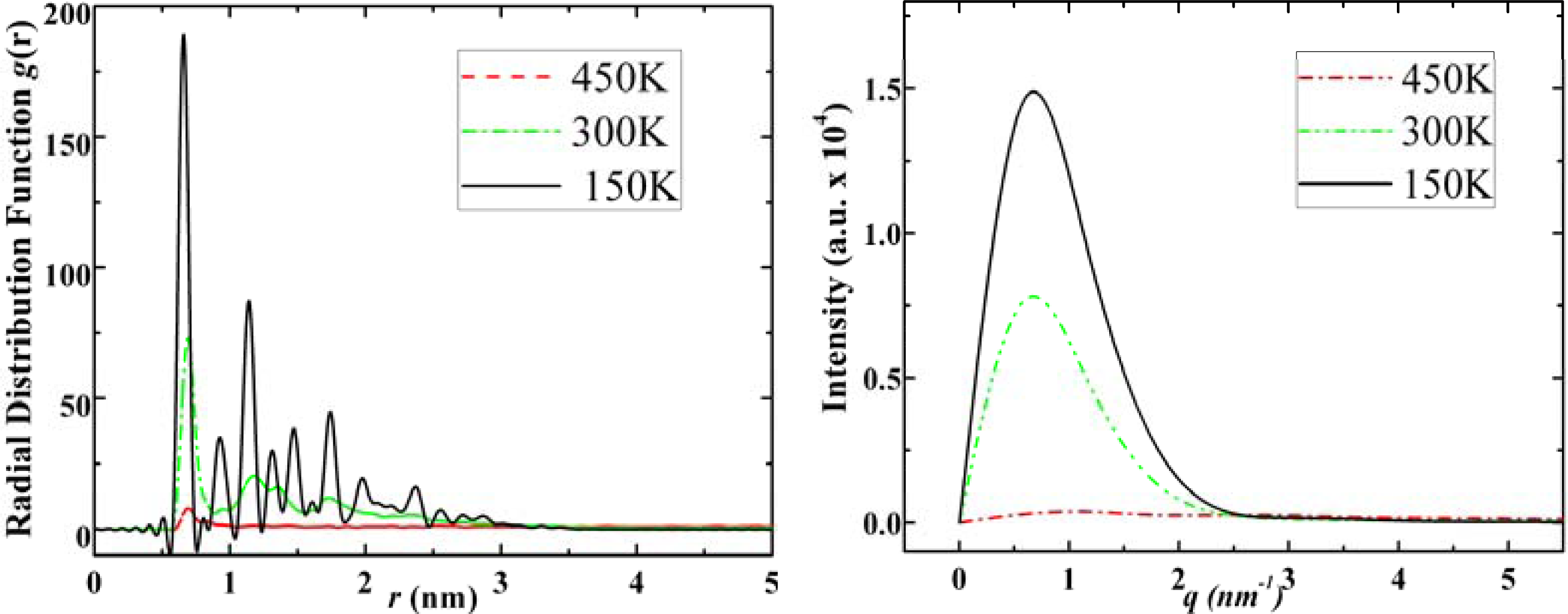
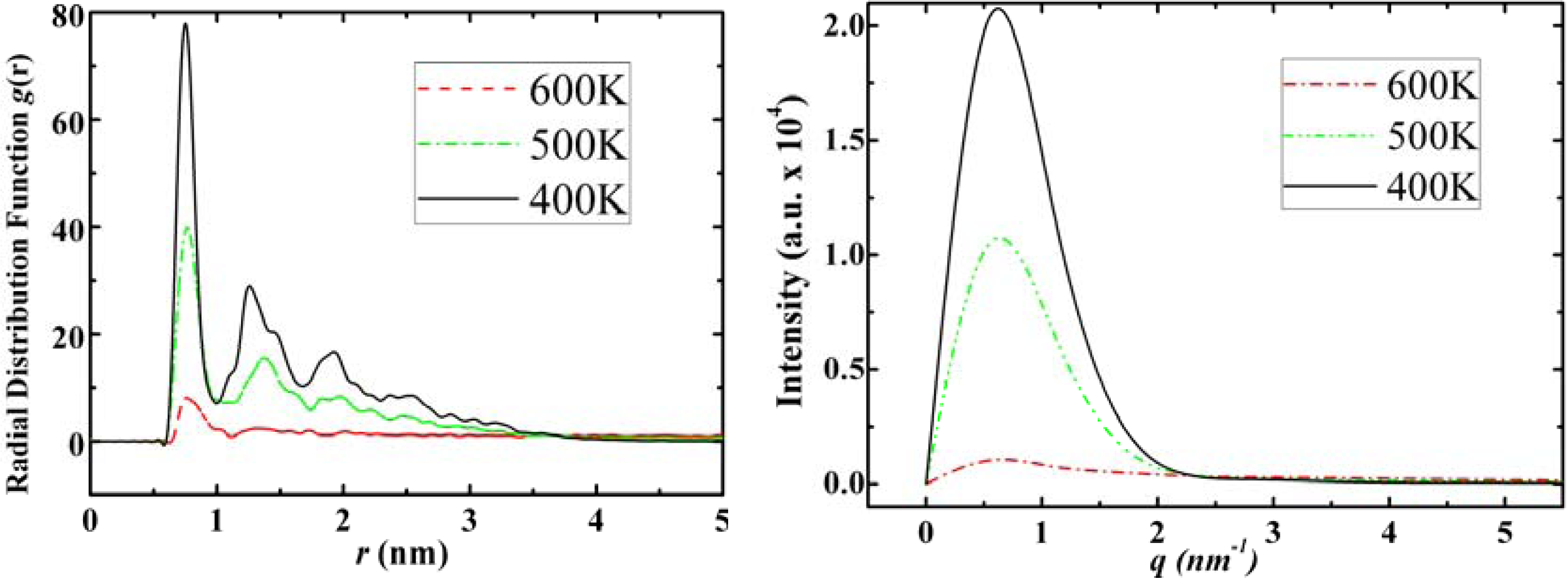
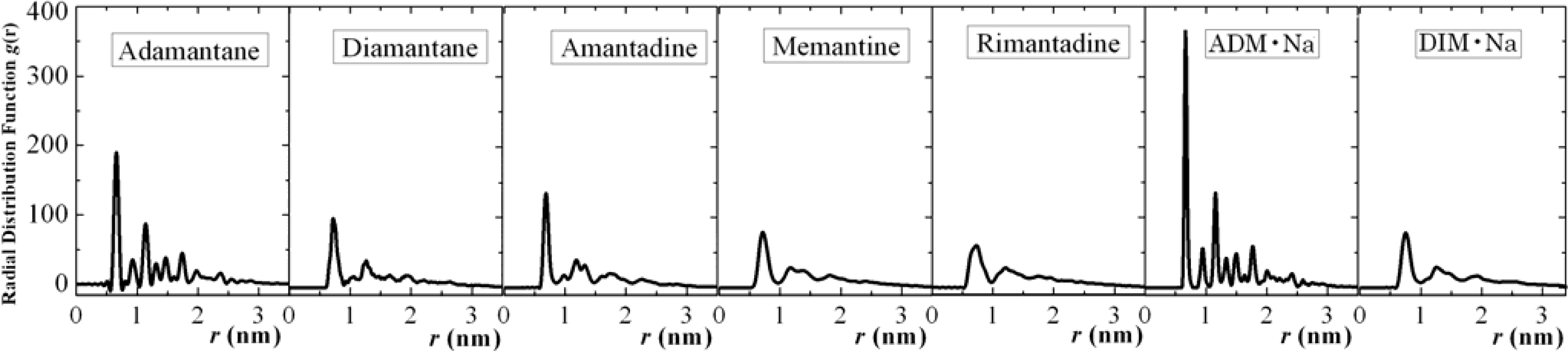
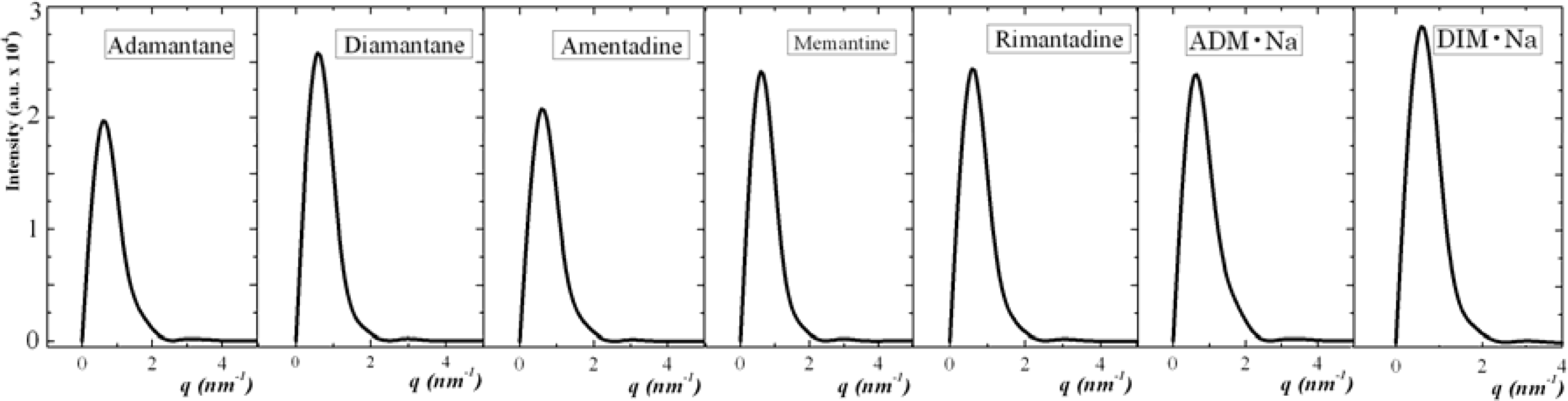
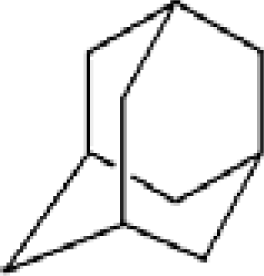
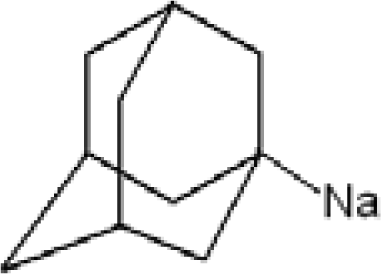
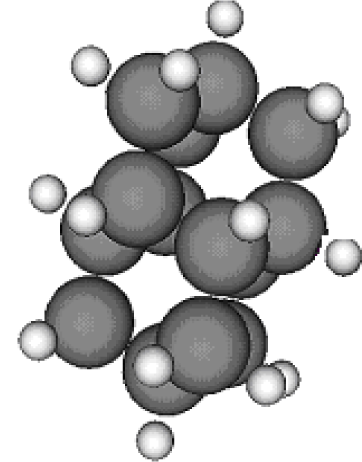
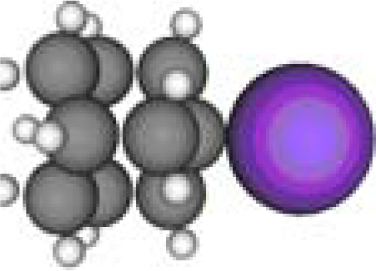
3.1. Adamantane and ADM•Na
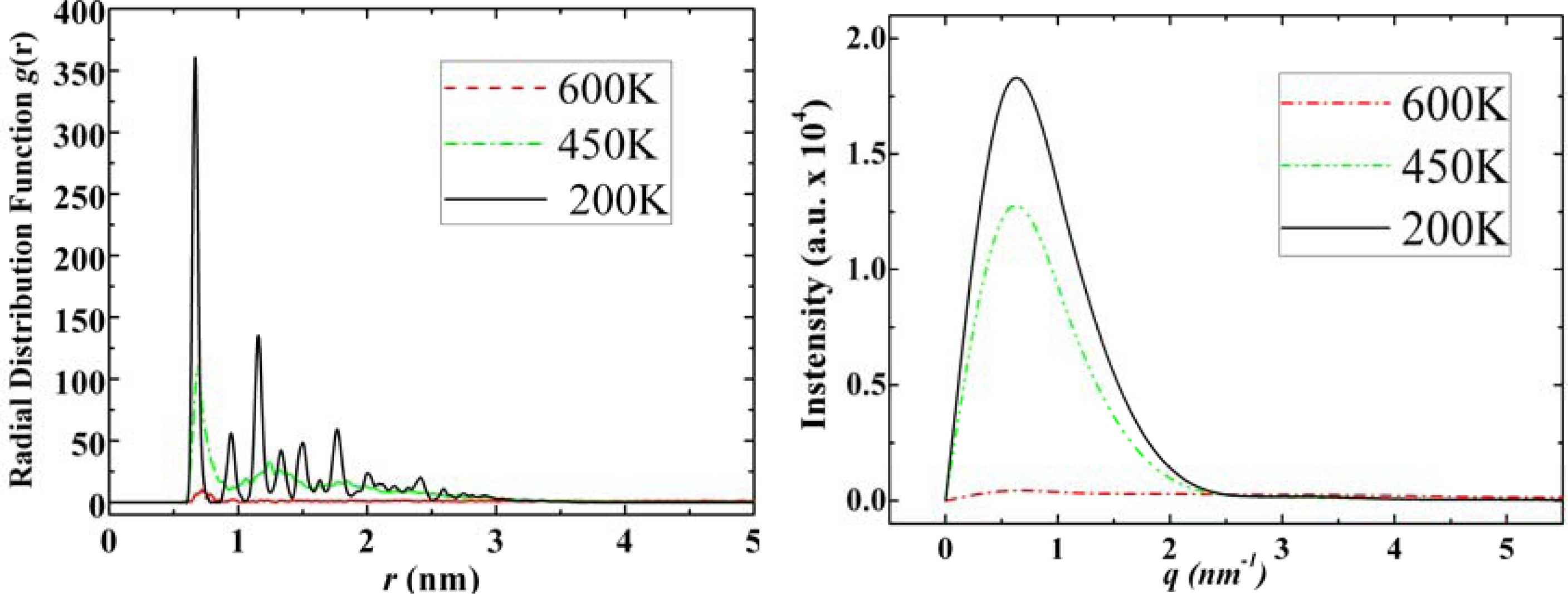
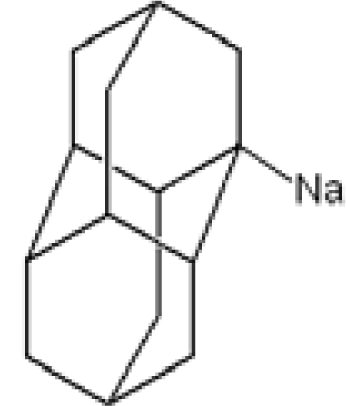
3.2. Diamantane and DIM•Na
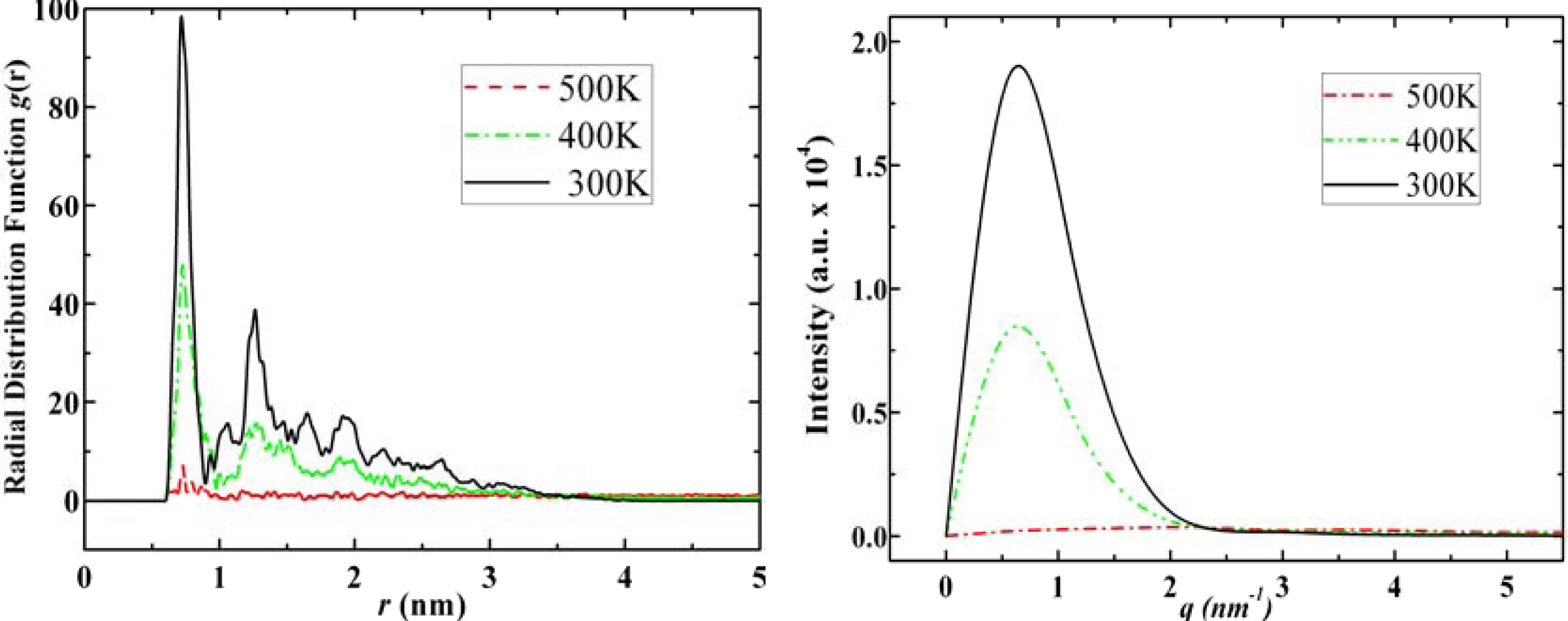
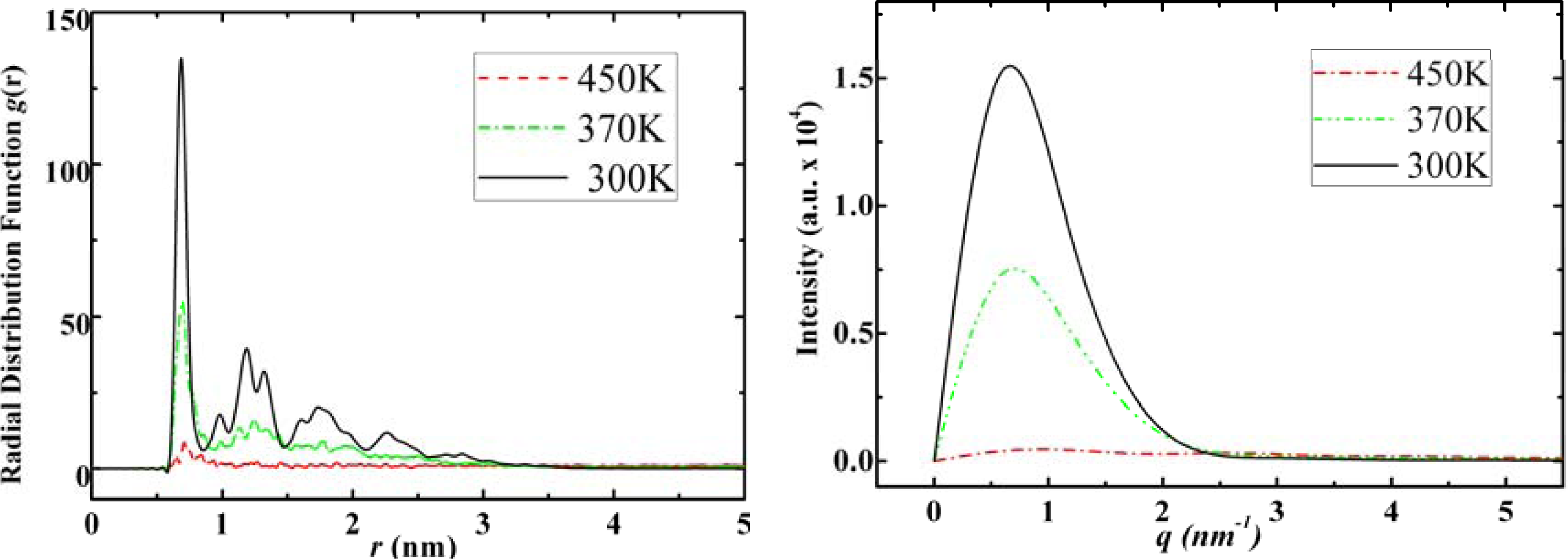
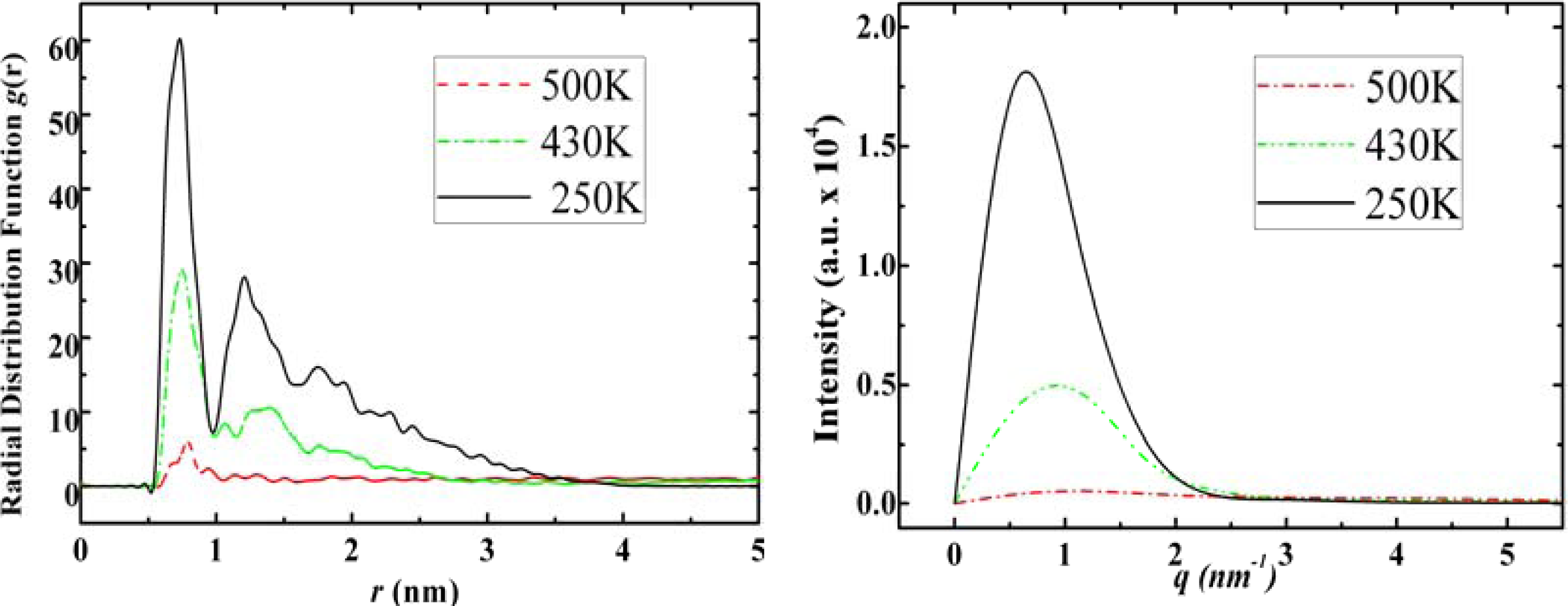
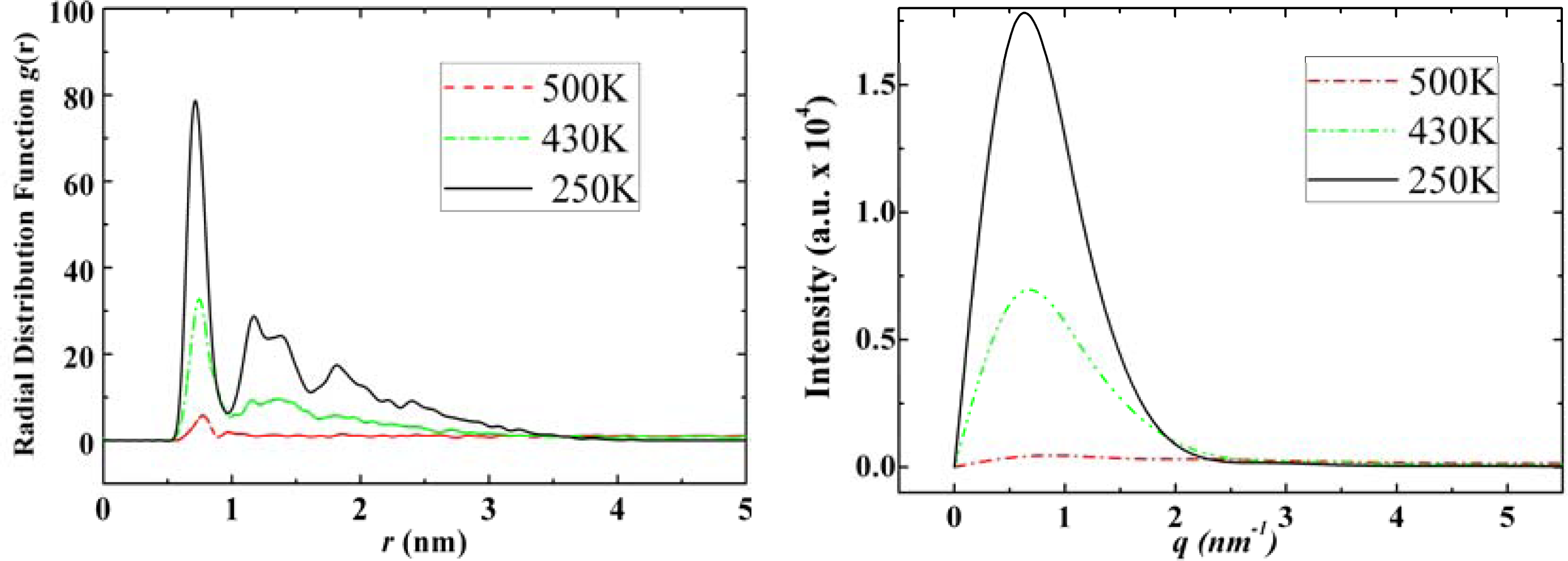
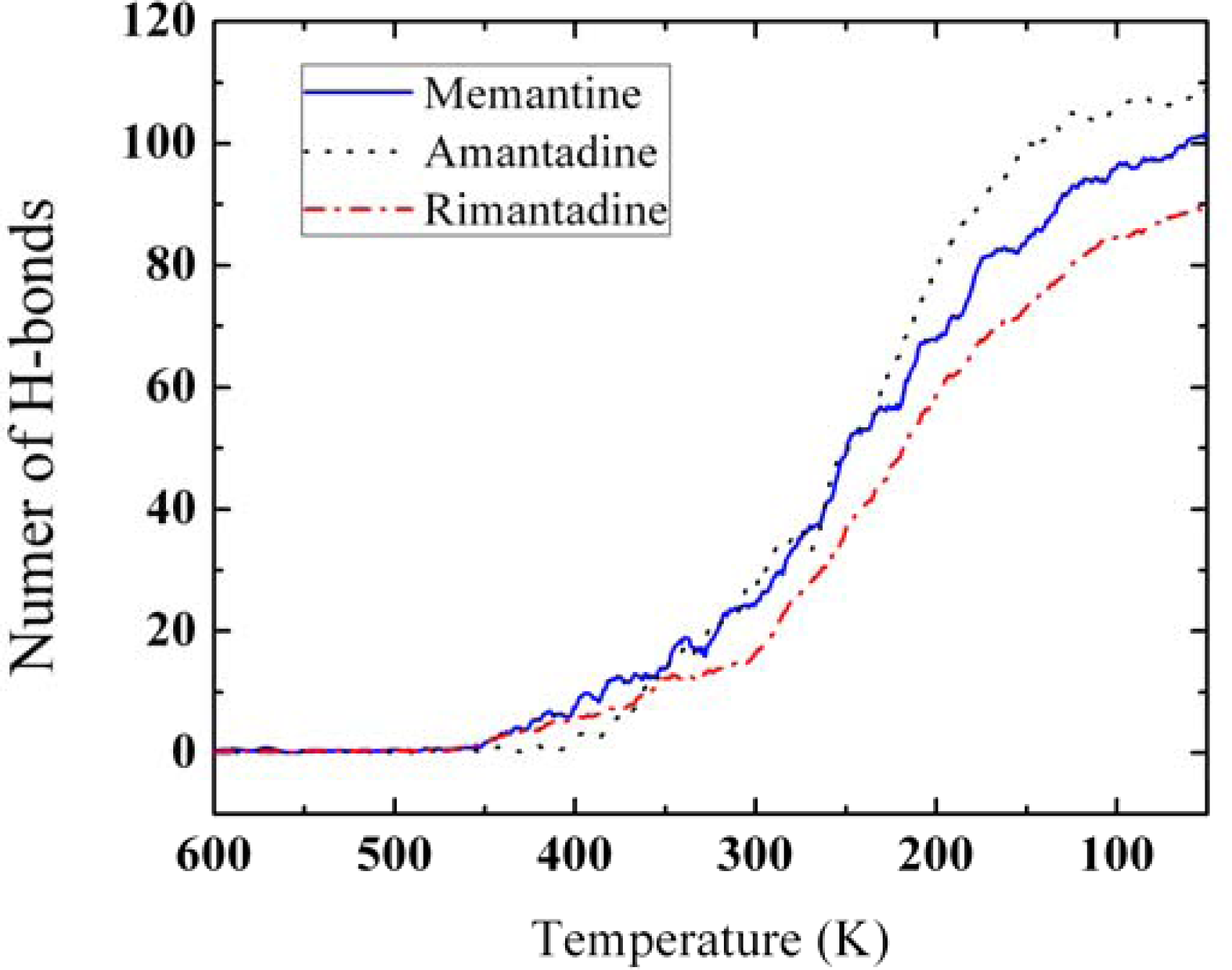
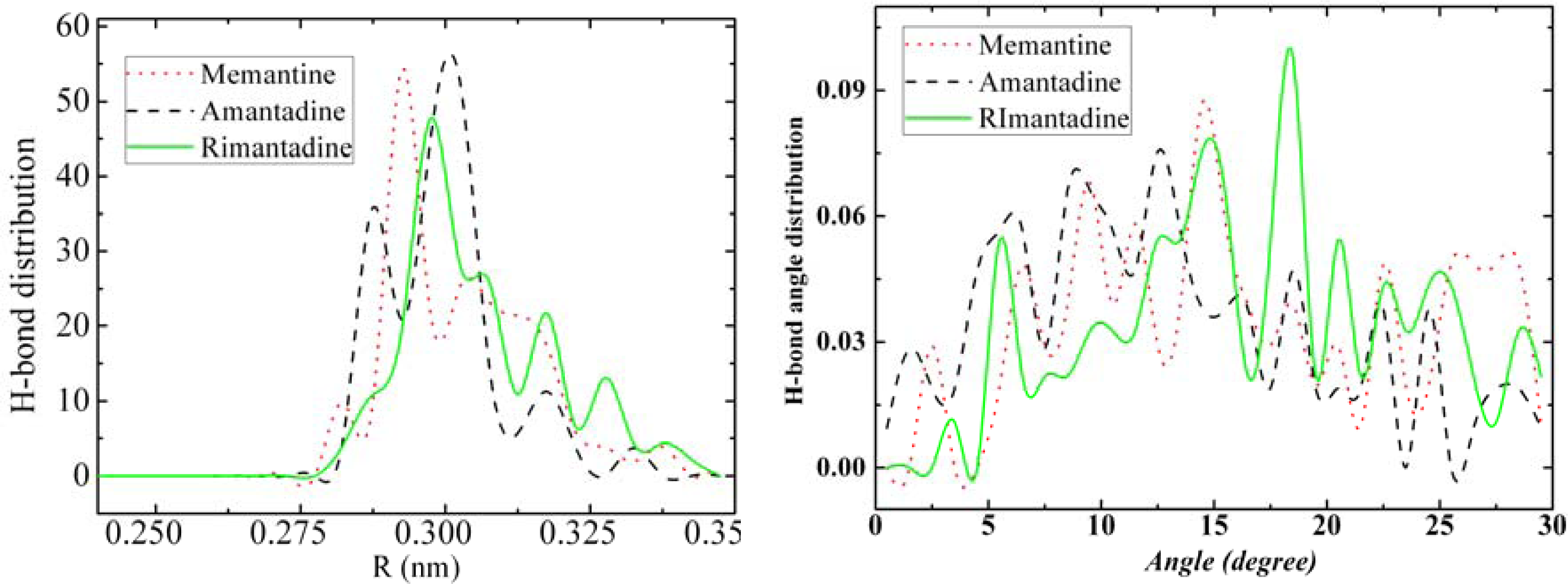
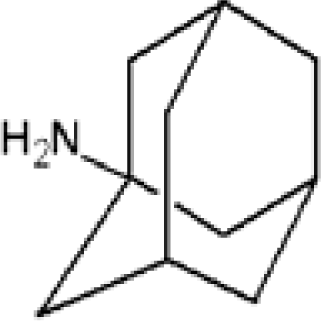
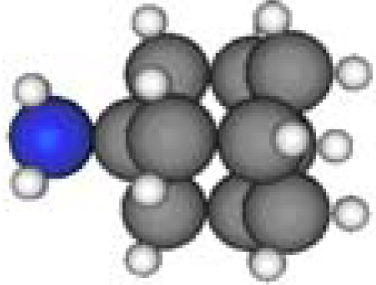
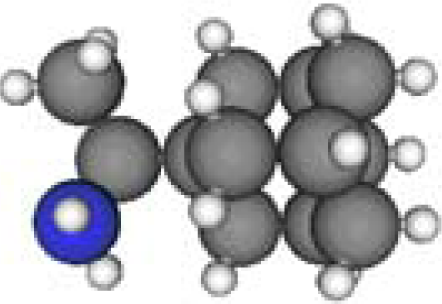
3.3. Amantadine, Rimantadine and Memantine
- . Since there are nitrogen ions in the structure of amantadine, rimantadine and memantine, which makes their attractive intermolecular forces much larger than that of adamantane, higher temperatures should be applied to these systems in order to obtain initial gas state structures in the step d of Figure 2.
- . During the cooling down process of amantadine, rimantadine and memantine, hydrogen-bonds are formed which, as expected, increases their phase transition temperatures compared to that of adamantane.
4. Conclusion
Acknowledgments
References
- Mansoori, GA. Principles of Nanotechnology—Molecular-Based Study of Condensed Matter in Small Systems; World Scientific Pub. Co: Hackensack, NJ, USA, 2005. [Google Scholar]
- Mansoori, GA. Diamondoid molecules. Adv. Chem. Phys 2007, 136, 207–258. [Google Scholar]
- Zhang, GP; George, TF; Assoufid, L; Mansoori, GA. First-principles simulation of the interaction between adamantane and an atomic-force microscope tip. Phys Rev B 2007, 75. [Google Scholar]
- Ramezani, H; Mansoori, GA; Saberi, MR. Diamondoids-DNA nanoarchitecture: From nanomodules design to self-assembly. J. Comput. Theory Nanosci 2007, 4, 96–10. [Google Scholar]
- Mansoori, GA; George, TF; Zhang, GP; Assoufid, L. Molecular Building Blocks for Nanotechnology: From Diamondoids to Nanoscale Materials and Applications (Topics in Applied Physics); Springer: New York, NY, USA, 2007; Volume 109, pp. 44–71. [Google Scholar]
- Ramezani, H; Mansoori, GA. Molecular Building Blocks for Nanotechnology: Diamondoids as Molecular Building Blocks for Nanotechnology (Topics in Applied Physics); Springer: New York, NY, USA, 2007; Volume 109, pp. 44–71. [Google Scholar]
- Ramezani, H; Saberi, MR; Mansoori, GA. Diamondoids and DNA nanotechnologies. Int. J. Nanosci. Nanotechnol 2007, 3, 21–35. [Google Scholar]
- Xue, Y; Mansoori, GA. Quantum Conductance and Electronic Properties of Lower Diamondoids and their Derivatives. Int. J. Nanosci 2008, 7, 63–72. [Google Scholar]
- Marsusi, F; Mirabbaszadeh, K; Mansoori, GA. Opto-electronic properties of adamantane and hydrogen-terminated sila- and germa-adamantane: A comparative study. Phys. E 2009, 41, 1151–1156. [Google Scholar]
- Mansoori, GA; George, TF; Zhang, GP; Assoufid, L. Structure and opto-electronic behavior of diamondoids, with applications as mems and at the nanoscale level. In Progress Nanotechnology Research; Springer: New York, NY, USA, 2009; ; Chapter 1, pp. 1–19. [Google Scholar]
- Kohn, W; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, B37, 785–789. [Google Scholar]
- Woon, DE; Dunning, TH, Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys 1993, 98, 1358–1371. [Google Scholar]
- Curtiss, LA; McGrath, MP; Blaudeau, J-P; Davis, NE; Binning, RC, Jr; Radom, L. Extension of Gaussian-2 theory to molecules containing third-row atoms Ga-Kr. J. Chem. Phys 1995, 103, 6104–6113. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR; Montgomery, JA, Jr; Vreven, T; Kudin, KN; Burant, M; Gill, PMW; Johnson, B; Chen, W; Wong, MW; Gonzalez, C; Pople, JA. Gaussian 03, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Carpenter, JE; Weinhold, FJ. Analysis of the geometry of the hydroxyl radical by the ldquo. Mol. Struct. (Theochem.) 1988, 169, 41–62. [Google Scholar]
- Jorgensen, WL; Maxwell, DS; Tirado-Rives, J. Development and testing of the opls all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc 1996, 118, 11225–11236. [Google Scholar]
- Damm, W; Frontera, A; Tirado-Rives, J; Jorgensen, WL. OPLS all-atom force field for carbohydrates. J. Comput. Chem 1997, 18, 1955–1970. [Google Scholar]
- Lindahl, E; Hess, B; van der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Mod 2001, 7, 306–317. [Google Scholar]
- van der Spoel, D; Lindahl, E; Hess, B; Groenhof, G; Mark, AE; Berendsen, HJC. GROMACS: Fast, flexible and free. J. Comp. Chem 2005, 26, 1701–1718. [Google Scholar]
- Hess, B; Kutzner, C; van der Spoel, D; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput 2008, 4, 435–447. [Google Scholar]
- Greig, DW; Pawley, GS. Molecular dynamics simulations of the order-disorder phase transition in adamantane. Mol. Phys 1996, 89, 677–689. [Google Scholar]
- Ciccotti, G; Ferrario, M; Memeo, E; Meyer, M. Structural transition on cooling of plastic adamantane: A molecular-dynamics study. Phys. Rev. Lett 1987, 59, 2574–2577. [Google Scholar]
- Humphrey, W; Dalke, A; Schulten, K. VMD-visual molecular dynamics. J. Mol. Graph 1996, 14, 33–38. [Google Scholar]




| Group 1 | Group 2 | Group 3 | ||||
|---|---|---|---|---|---|---|
| Adamantane | Diamantane | Amantadine | Rimantadine | Memantine | Optimized ADM•Na | Optimized DIM•Na |
| C10H16 | C14H20 | C10H17N | C11H20N | C12H21N | C10H15Na | C14H19Na |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xue, Y.; Mansoori, G.A. Self-Assembly of Diamondoid Molecules and Derivatives (MD Simulations and DFT Calculations). Int. J. Mol. Sci. 2010, 11, 288-303. https://doi.org/10.3390/ijms11010288
Xue Y, Mansoori GA. Self-Assembly of Diamondoid Molecules and Derivatives (MD Simulations and DFT Calculations). International Journal of Molecular Sciences. 2010; 11(1):288-303. https://doi.org/10.3390/ijms11010288
Chicago/Turabian StyleXue, Yong, and G. Ali Mansoori. 2010. "Self-Assembly of Diamondoid Molecules and Derivatives (MD Simulations and DFT Calculations)" International Journal of Molecular Sciences 11, no. 1: 288-303. https://doi.org/10.3390/ijms11010288




