Binding and Docking Interactions of NO, CO and O2 in Heme Proteins as Probed by Density Functional Theory
Abstract
:1. Introduction
1.1. Inner Cavity Interactions
1.2. The Bound Interactions
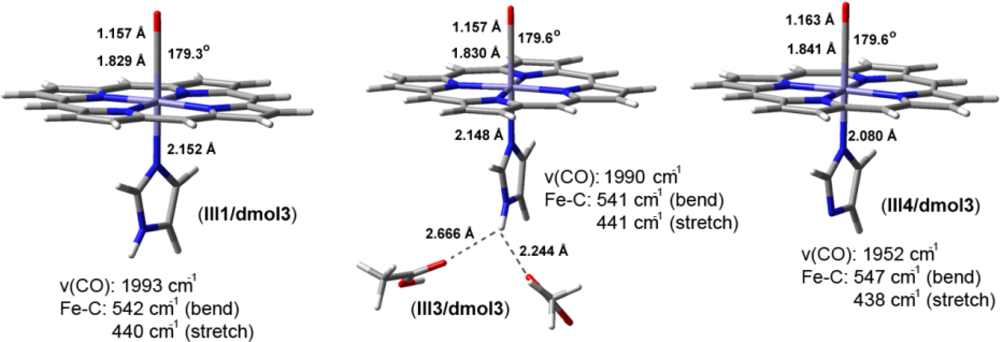
2. Results and Discussion
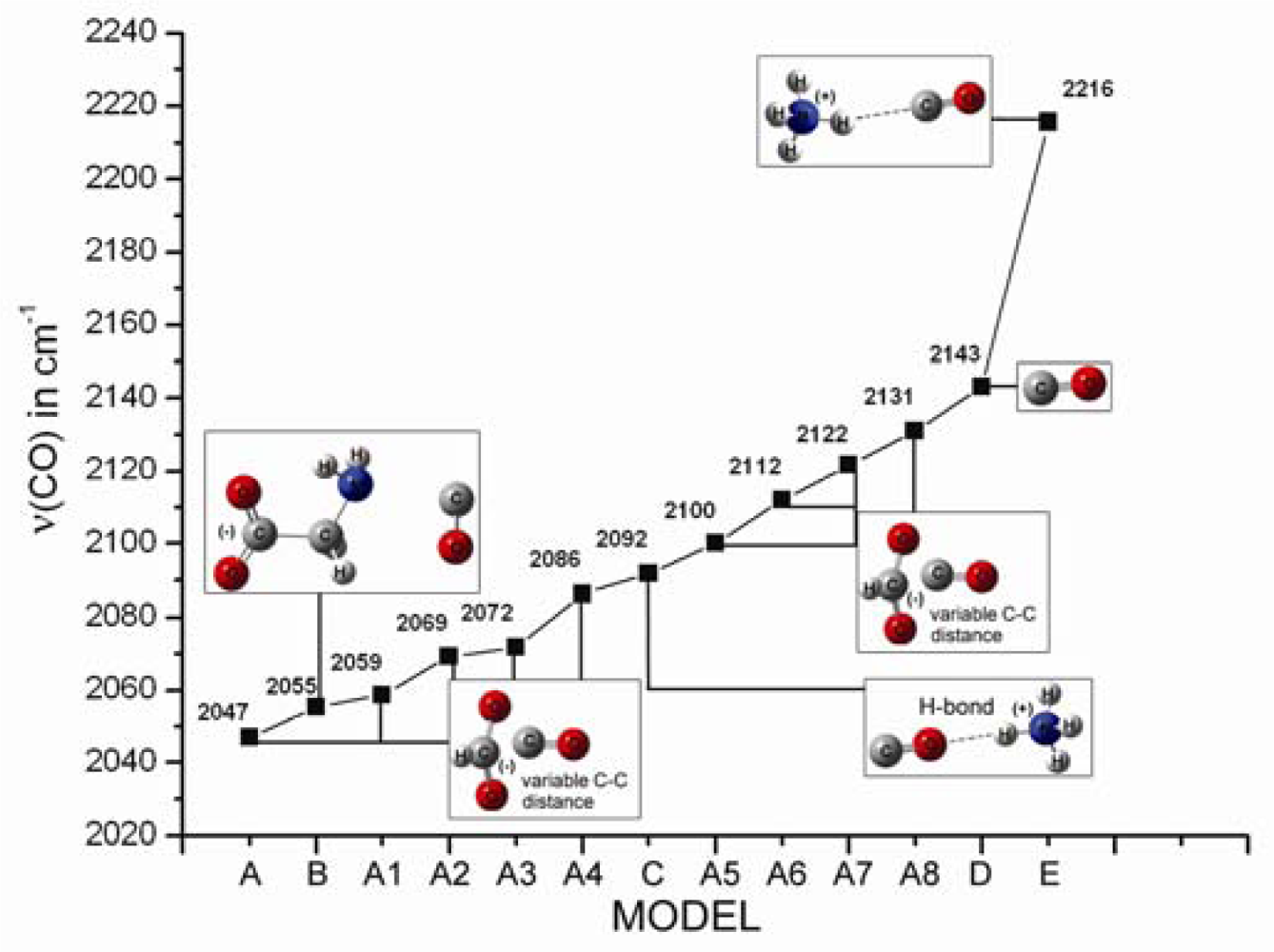
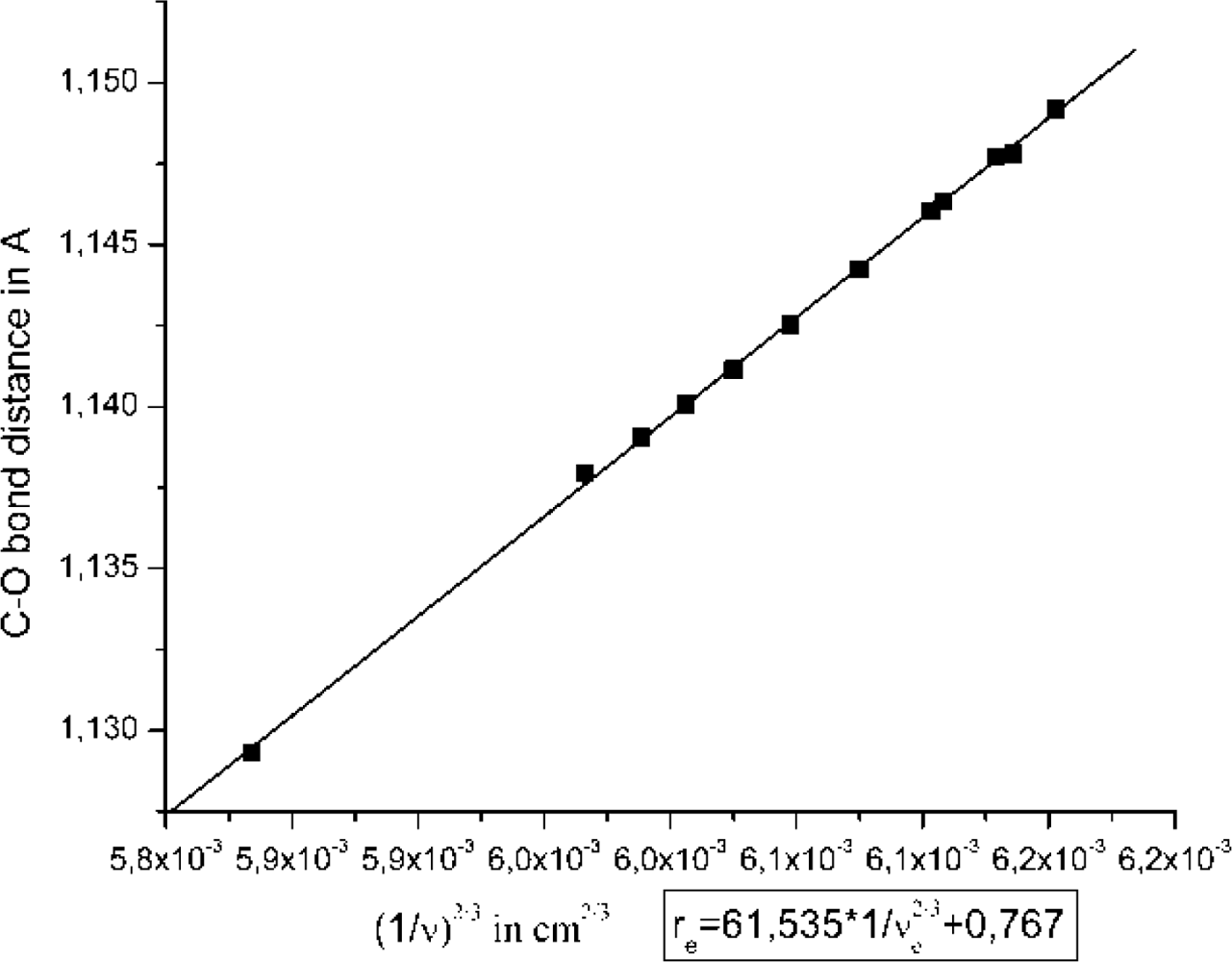
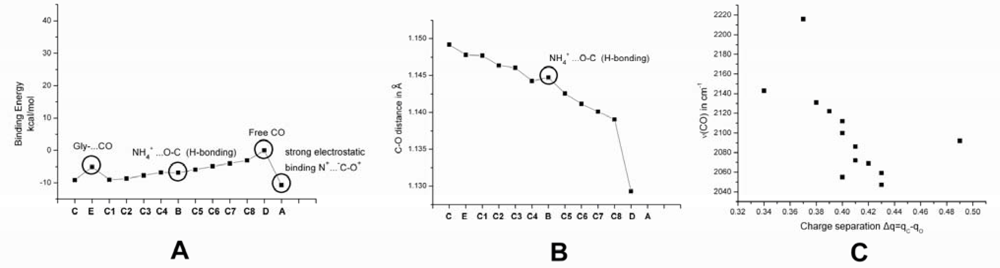
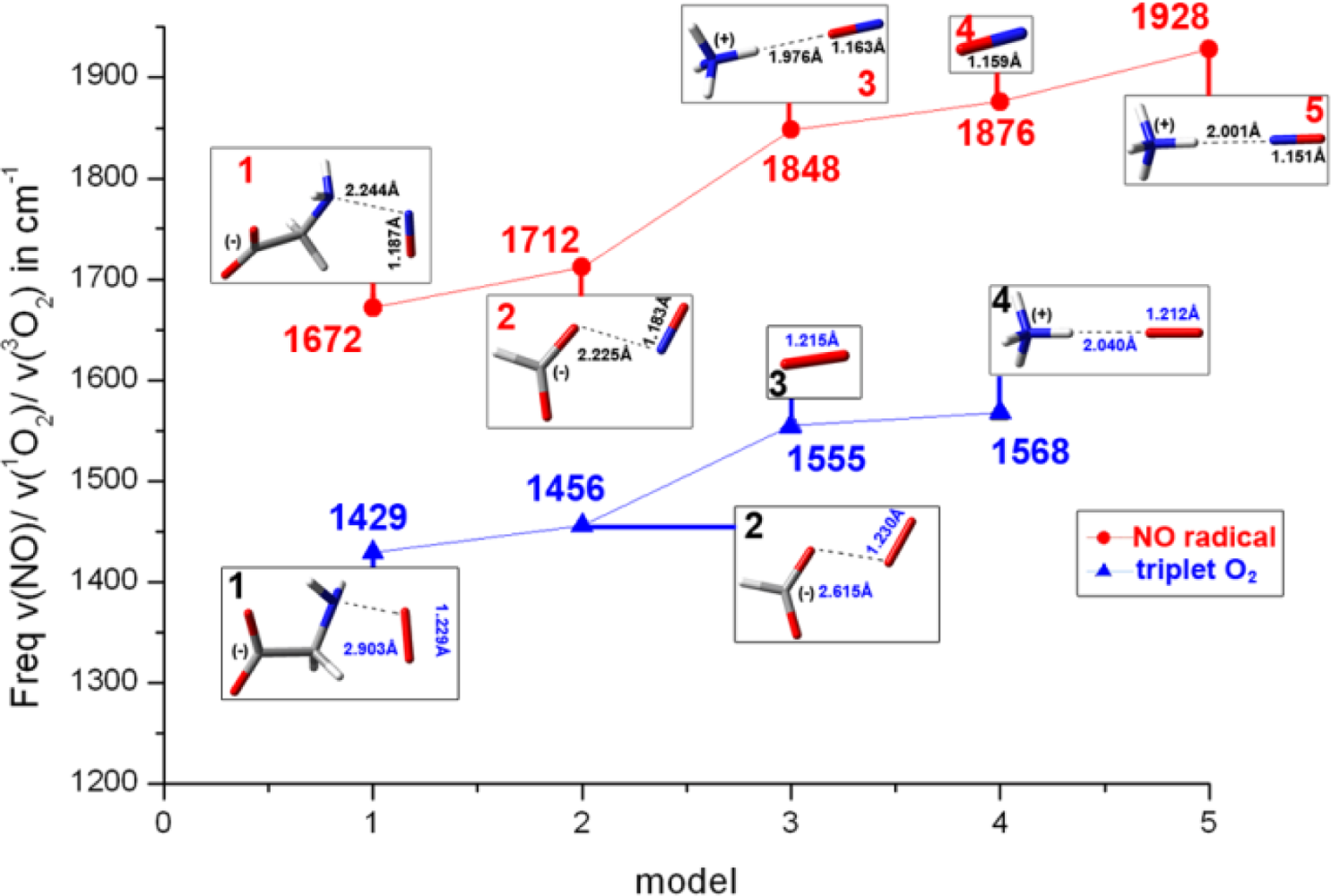
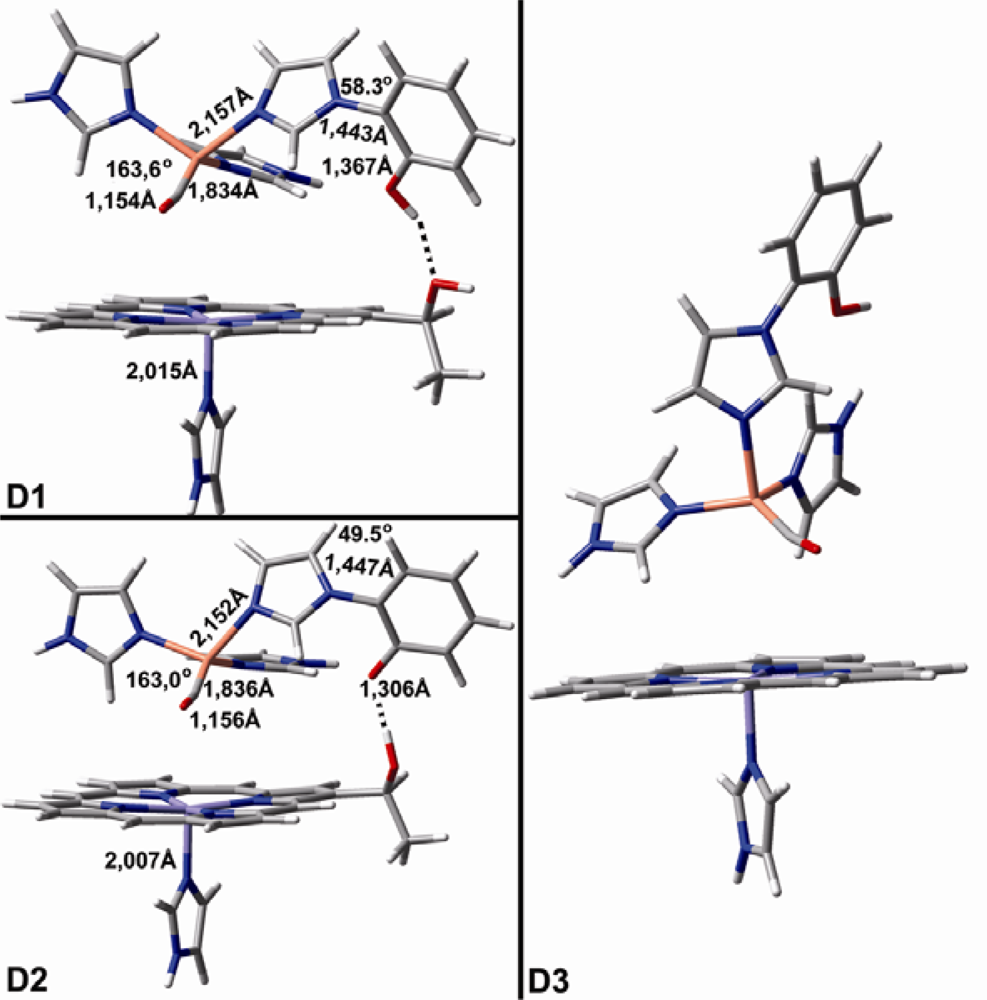
2.1. The Unbound Interactions inside Cavities
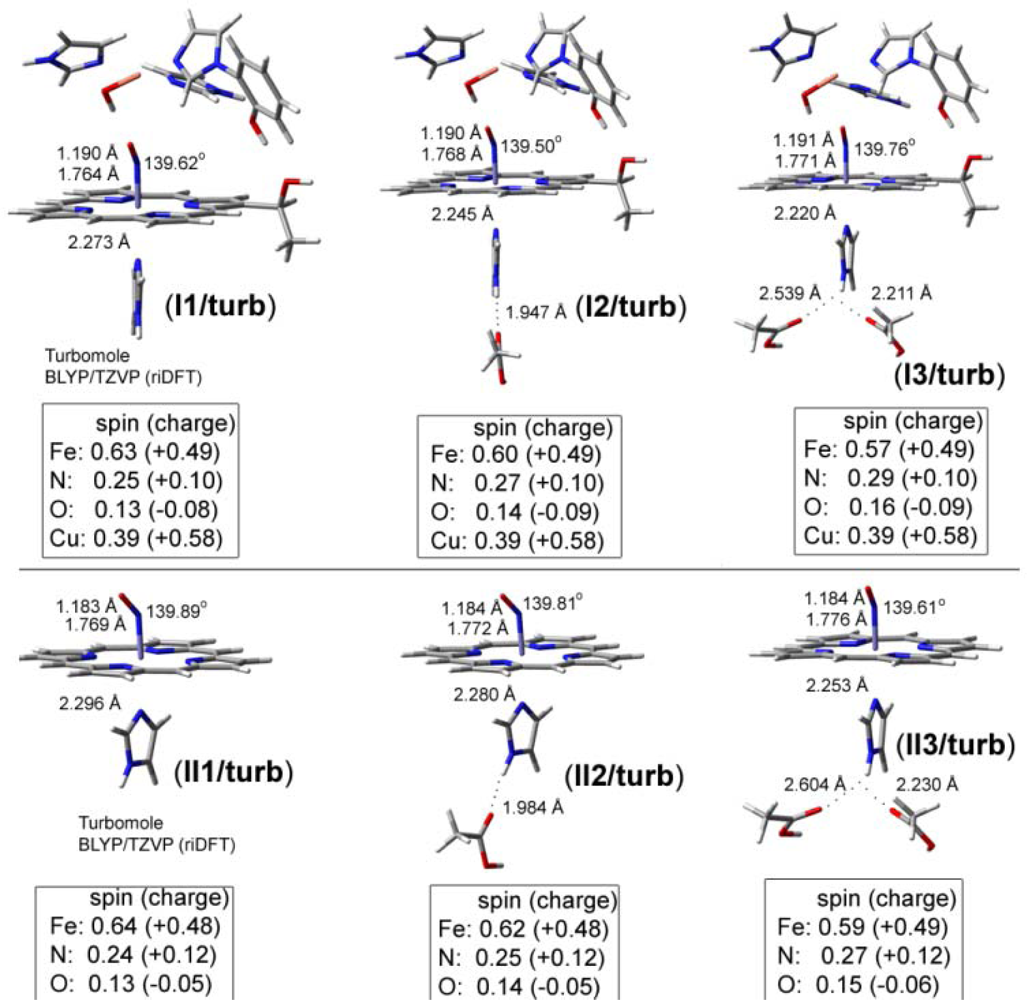
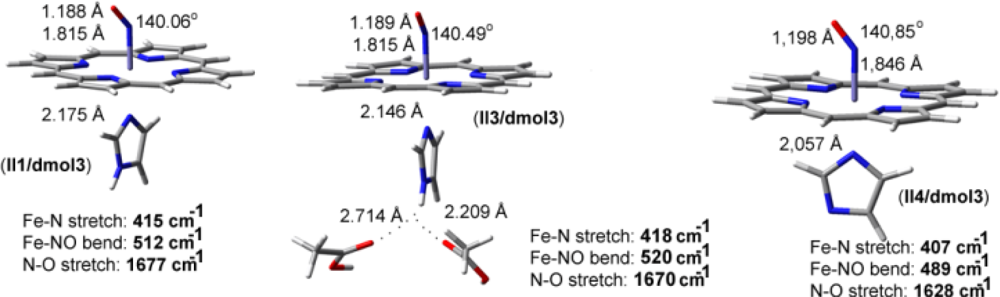
2.2. The Bound Interactions
3. Calculation Methods
4. Conclusions
References and Notes
- Blomberg, LM; Blomberg, MRA; Siegbahn, PEM. A theoretical study on the binding of O2, NO and CO to heme proteins. J. Inorg. Biochem 2005, 99, 949–958. [Google Scholar]
- Rovira, C; Kunc, K; Hutter, J; Ballone, P; Parrinello, M. Equilibrium geometries and electronic structure of iron-porphyrin complexes: A density functional study. J. Phys. Chem. A 1997, 101, 8914–8925. [Google Scholar]
- Rovira, C; Kunc, K; Hutter, J; Ballone, P; Parrinello, M. A comparative study of O2, CO, and NO binding to iron-porphyrin. Int. J. Quant. Chem 1998, 69, 31–35. [Google Scholar]
- Sigfridsson, E; Ryde, U. On the significance of hydrogen bonds for the discrimination between CO and O2 by myoglobin. J. Biol. Inorg. Chem 1999, 4, 99–110. [Google Scholar]
- Harvey, JN. DFT computation of the intrinsic barrier to CO geminate recombination with heme compounds. J. Am. Chem. Soc 2000, 122, 12401–12402. [Google Scholar]
- Sigfridsson, E; Ryde, U. Theoretical study of the discrimination between O2 and CO by myoglobin. J. Inorg. Biochem 2002, 91, 101–115. [Google Scholar]
- Jensen, KP; Roos, BO; Ryde, U. O2-binding to heme: Electronic structure and spectrum of oxyheme, studied by multiconfigurational methods. J. Inorg. Biochem 2005, 99, 45–54. [Google Scholar]
- Jensen, KP; Roos, BO; Ryde, U. Erratum to “O2-binding to heme: Electronic structure and spectrum of oxyheme, studied by multiconfigurational methods”. J. Inorg. Biochem 2005, 99, 978. [Google Scholar]
- Rutkowska-Zbik, DMW; Stochel, G. Theoretical density functional theory studies on interactions of small biologically active molecules with isolated heme group. J. Comput. Chem 2007, 28, 825–831. [Google Scholar]
- Strickland, N; Harvey, JN. Spin-forbidden ligand binding to the ferrous-heme group: Ab initio and DFT studies. J. Phys. Chem. B 2007, 111, 841–852. [Google Scholar]
- Ribas-Ariño, J; Novoa, JJ. The mechanism for the reversible oxygen addition to heme. A theoretical CASPT2 study. Chem. Commun 2007, 30, 3160–3162. [Google Scholar]
- Nienhaus, K; Olson, JS; Franzen, S; Nienhaus, GU. The origin of stark splitting in the initial photoproduct state of MbCO. J. Am. Chem. Soc 2005, 127, 40–41. [Google Scholar]
- Lim, M; Jackson, T; Anfinrud, P. Binding of CO to myoglobin from a heme pocket docking site to form nearly linear Fe-C-O. Science 1995, 269, 962–966. [Google Scholar]
- Frauenfelder, H; Sligar, S; Wolynes, P. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar]
- Ansari, A; Jones, CM; Henry, ER; Hofrichter, J; Eaton, WA. Conformational relaxation and ligand binding in myoglobin. Biochemistry 1994, 33, 5128–5145. [Google Scholar]
- Lim, M; Jackson, TA; Anfinrud, PA. Nonexponential protein relaxation: Dynamics of conformational change in myoglobin. Proc. Natl. Acad. Sci. USA 1993, 90, 5801–5804. [Google Scholar]
- Nienhaus, K; Deng, P; Kriegl, JM; Nienhaus, GU. Structural dynamics of myoglobin: Effect of internal cavities on ligand migration and binding. Biochemistry 2003, 42, 9647–9658. [Google Scholar]
- Koutsoupakis, C; Soulimane, T; Varotsis, C. Docking site dynamics of ba3-cytochrome c oxidase from thermus thermophilus. J. Biol. Chem 2003, 278, 36806–36809. [Google Scholar]
- Case, DA; Karplus, M. Dynamics of ligand binding to heme proteins. J. Mol. Biol 1979, 132, 343–368. [Google Scholar]
- Tilton, RF; Singh, UC; Weiner, SJ; Connolly, ML; Kuntz, ID; Kollman, PA; Max, N; Case, DA. Computational studies of the interaction of myoglobin and xenon. J. Mol. Biol 1986, 192, 443–456. [Google Scholar]
- Elber, R; Karplus, M. Enhanced sampling in molecular dynamics: Use of the time-dependent Hartree approximation for a simulation of carbon monoxide diffusion through myoglobin. J. Am. Chem. Soc 1990, 112, 9161–9175. [Google Scholar]
- Bossa, C; Anselmi, M; Roccatan, D; Amadei, A; Vallone, B; Brunori, M; Di Nola, A. Extended molecular dynamics simulation of the carbon monoxide migration in sperm whale myoglobin. Biophys. J 2004, 86, 3855–3862. [Google Scholar]
- Agmon, N. Coupling of protein relaxation to ligand binding and migration in myoglobin. Biophys. J 2004, 87, 1537–1543. [Google Scholar]
- Nutt, DR; Meuwly, M. CO migration in native and mutant myoglobin: Atomistic simulations for the understanding of protein function. Proc. Natl. Acad. Sci. USA 2004, 101, 5998–6002. [Google Scholar]
- Banushkina, P; Meuwly, M. Free-energy barriers in MbCO rebinding. J. Phys. Chem. B 2005, 109, 16911–16917. [Google Scholar]
- Olson, JS; Phillips, GN, Jr. Kinetic pathways and barriers for ligand binding to myoglobin. J. Biol. Chem 1996, 271, 17593–17596. [Google Scholar]
- Ostermann, A; Waschipky, R; Parak, FG; Nienhaus, UG. Ligand binding and conformational motions in myoglobin. Nature 2000, 404, 205–208. [Google Scholar]
- Carver, TE; Rohlfs, RJ; Olson, JS; Gibson, QH; Blackmore, RS; Springer, BA; Sligar, SG. Analysis of the kinetic barriers for ligand binding to sperm whale myoglobin using site-directed mutagenesis and laser photolysis techniques. J. Biol. Chem 1990, 265, 20007–20020. [Google Scholar]
- Vojtechovský, J; Chu, K; Berendzen, J; Sweet, RM; Schlichting, I. Crystal structures of myoglobin-ligand complexes at near-atomic resolution. Biophys. J 1999, 77, 2153–2174. [Google Scholar]
- Hou, S; Larsen, RW; Boudko, D; Riley, CW; Karatan, E; Zimmer, M; Ordal, GW; Alam, M. Myoglobin-like aerotaxis transducers in Archaea and Bacteria. Nature 2000, 403, 540–544. [Google Scholar]
- Pinakoulaki, E; Yoshimura, H; Daskalakis, D; Yoshioka, S; Aono, S; Varotsis, C. Two ligand-binding sites in the O2-sensing signal transducer HemAT: Implications for ligand recognition/discrimination and signaling. Proc. Natl. Acad. Sci. USA 2006, 103, 14796–14801. [Google Scholar]
- Ischiropoulos, H. Biological tyrosine nitration: A pathophysiological function of nitric oxide and reactive oxygen species. Arch. Biochem. Biophys 1998, 356, 1–11. [Google Scholar]
- Radi, R; Beckman, JS; Bush, KM; Freeman, BA. Peroxynitrite oxidation of sulfhydryls. The cytotoxic potential of superoxide and nitric oxide. J. Biol. Chem 1991, 266, 4244–4250. [Google Scholar]
- King, PA; Anderson, VE; Edwards, JO; Gustafson, G; Plumb, RC; Suggs, JW. A stable solid that generates hydroxyl radical upon dissolution in aqueous solutions: Reaction with proteins and nucleic acid. J. Am. Chem. Soc 1992, 114, 5430–5432. [Google Scholar]
- Goodin, DB; McRee, DE. The Asp-His-iron triad of cytochrome c peroxidase controls the reduction potential electronic structure, and coupling of the tryptophan free radical to the heme. Biochemistry 1993, 32, 3313–3324. [Google Scholar]
- Vogel, KM; Spiro, TG. Resonance raman evidence for a novel charge relay activation mechanism of the CO-dependent heme protein transcription factor CooA. Biochemistry 1999, 38, 2679–2687. [Google Scholar]
- Daskalakis, V; Farantos, SC; Varotsis, C. Assigning vibrational spectra of ferryl-oxo intermediates of cytochrome c oxidase by periodic orbits and molecular dynamics. J. Am. Chem. Soc 2008, 130, 12385–12393. [Google Scholar]
- Crane, BR; Siegel, LM; Getzoff, ED. Structures of the siroheme- and Fe4S4-containing active center of sulfite reductase in different states of oxidation: Heme activation via reduction-gated exogenous ligand exchange. Biochemistry 1997, 36, 12101–12119. [Google Scholar]
- Decatur, SM; Belcher, KL; Rickert, PK; Franzen, S. Hydrogen bonding modulates binding of exogenous ligands in a myoglobin proximal cavity mutant. Biochemistry 1999, 38, 11086–11092. [Google Scholar]
- Franzen, S. Effect of a charge relay on the vibrational frequencies of carbonmonoxy iron porphine adducts: The coupling of changes in axial ligand bond strength and porphine core size. J. Am. Chem. Soc 2001, 123, 12578–12589. [Google Scholar]
- Hu, C; Noll, BC; Schulz, CE; Scheidt, WR. Proton-mediated electron configuration change in high-spin iron(II) porphyrinates. J. Am. Chem. Soc 2005, 127, 15018–15019. [Google Scholar]
- Daskalakis, V; Pinakoulaki, E; Stavrakis, S; Varotsis, C. Probing the environment of CuB in Heme-copper oxidases. J. Phys. Chem. B 2007, 111, 10502–10509. [Google Scholar]
- Redfern, PC; Zapol, P; Curtiss, LA. Assessment of Gaussian-3 and density functional theories for a larger experimental test set. J. Phys. Chem 2000, 112, 7374–7383. [Google Scholar]
- Straub, JE; Karplus, M. Molecular dynamics study of the photodissociation of carbon monoxide from myoglobin: Ligand dynamics in the first 10 ps. Chem. Phys 1991, 158, 221–248. [Google Scholar]
- Nutt, DR; Meuwly, M. Theoretical investigation of infrared spectra and pocket dynamics of photodissociated carbonmonoxy myoglobin. Biophys. J 2003, 85, 3612–3623. [Google Scholar]
- Badger, RM. The relation between the internuclear distances and force constants of molecules and its application to polyatomic molecules. J. Chem. Phys 1935, 3, 710–714. [Google Scholar]
- Brewer, SH; Franzen, S. A quantitative theory and computational approach for the vibrational Stark effect. J. Chem. Phys 2003, 119, 851–858. [Google Scholar]
- Das, TK; Pecoraro, C; Tomson, FL; Gennis, RB; Rousseau, DL. The post-translational modification in cytochrome c oxidase is required to establish a functional environment of the catalytic site. Biochemistry 1998, 37, 14471–14476. [Google Scholar]
- Proshlyakov, DA; Pressler, MA; Babcock, GT. Dioxygen activation and bond cleavage by mixed-valence cytochrome c oxidase. Proc. Natl. Acad. Sci. USA 1998, 95, 8020–8025. [Google Scholar]
- Pinakoulaki, E; Pfitzner, U; Ludwig, B; Varotsis, C. The role of the cross-link His-Tyr in the functional properties of the binuclear center in cytochrome c oxidase. J. Biol. Chem 2002, 277, 13563–13568. [Google Scholar]
- Pinakoulaki, E; Pfitzner, U; Ludwig, B; Varotsis, C. Direct detection of Fe(IV)=O intermediates in the cytochrome aa3 oxidase from Paracoccus denitrificans/H2O2 reaction. J. Biol. Chem 2003, 278, 18761–18766. [Google Scholar]
- Hoffmann, R; Chen, MML; Thorn, DL. Qualitative discussion of alternative coordination modes of diatomic ligands in transition metal complexes. Inorg. Chem 1977, 16, 503–511. [Google Scholar]
- Spiro, TG; Kozlowski, PM. Will the real FeCO please stand up? J. Biol. Inorg. Chem 1997, 2, 516–520. [Google Scholar]
- Spiro, TG; Kozlowski, PM. Is the CO adduct of myoglobin bent, and does it matter? Acc. Chem. Res 2001, 34, 137–144. [Google Scholar]
- Müller, JD; McMahon, BH; Chien, EY; Sligar, SG; Nienhaus, GU. Connection between the taxonomic substates and protonation of histidines 64 and 97 in carbonmonoxy myoglobin. Biophys. J 1999, 77, 1036–1051. [Google Scholar]
- Ghosh, A. Mettaloporphyrin-NO bonding: Building bridges with organometallic chemistry. Acc. Chem. Res 2005, 38, 943–954. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR; Montgomery, JA, Jr; Vreven, T; Kudin, KN; Burant, JC; Millam, JM; Iyengar, SS; Tomasi, J; Barone, V; Mennucci, B; Cossi, M; Scalmani, G; Rega, N; Petersson, GA; Nakatsuji, H; Hada, M; Ehara, M; Toyota, K; Fukuda, R; Hasegawa, J; Ishida, M; Nakajima, T; Honda, Y; Kitao, O; Nakai, H; Klene, M; Li, X; Knox, JE; Hratchian, HP; Cross, JB; Bakken, V; Adamo, C; Jaramillo, J; Gomperts, R; Stratmann, RE; Yazyev, O; Austin, AJ; Cammi, R; Pomelli, C; Ochterski, JW; Ayala, PY; Morokuma, K; Voth, GA; Salvador, P; Dannenberg, JJ; Zakrzewski, VG; Dapprich, S; Daniels, AD; Strain, MC; Farkas, O; Malick, DK; Rabuck, AD; Raghavachari, K; Foresman, JB; Ortiz, JV; Cui, Q; Baboul, AG; Clifford, S; Cioslowski, J; Stefanov, BB; Liu, G; Liashenko, A; Piskorz, P; Komaromi, I; Martin, RL; Fox, DJ; Keith, T; Al-Laham, MA; Peng, CY; Nanayakkara, A; Challacombe, M; Gill, PMW; Johnson, B; Chen, W; Wong, MW; Gonzalez, C; Pople, JA. Gaussian 03, Revision C02; Gaussian, Inc: Wallingford CT, USA, 2004. [Google Scholar]
- Pople, JA; Scott, AP; Wong, MW; Radom, L. Scaling factors for obtaining fundamental vibrational frequencies and zero-point energies from HF/6–31G* and MP2/6–31G* harmonic frequencies. Isr. J. Chem 1993, 33, 345–350. [Google Scholar]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys 1990, 92, 508–517. [Google Scholar]
- Dolg, M; Wedig, U; Stoll, H; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys 1987, 86, 866–872. [Google Scholar]
- Pinakoulaki, E; Stavrakis, S; Urbani, A; Varotsis, C. Resonance raman detection of a ferrous five-coordinate nitrosylheme b3 complex in cytochrome cbb3 from Pseudomonas stutzeri. J. Am. Chem. Soc 2002, 124, 9378–9379. [Google Scholar]
- Stavrakis, S; Pinakoulaki, E; Urbani, A; Varotsis, C. Fourier transform infrared evidence for a ferric six-coordinate nitrosylheme b3 complex of cytochrome cbb3 oxidase from Pseudomonas stutzeri at ambient temperature. J. Phys. Chem. B 2002, 106, 12860–12862. [Google Scholar]
- Pinakoulaki, E; Varotsis, C. Time-resolved resonance Raman and time-resolved step-scan FTIR studies of nitric oxide reductase from Paracoccus denitrificans: Comparison of the heme b3-FeB site to that of the Heme-CuB in oxidases. Biochemistry 2003, 42, 14856–14861. [Google Scholar]
- Ohta, T; Pinakoulaki, E; Soulimane, T; Kitagawa, T; Varotsis, C. Detection of a photostable five-coordinate heme a3-Fe-CO species and functional implications of His384/a10 in CO-bound ba3-cytochrome c oxidase from Thermus thermophilus. J. Phys. Chem. B 2004, 108, 5489–5491. [Google Scholar]
- Pinakoulaki, E; Koutsoupakis, C; Stavrakis, S; Aggelaki, M; Papadopoulos, G; Daskalakis, V; Varotsis, C. Structural dynamics of Heme-copper oxidases and nitric oxide reductases: Time-resolved step-scan FTIR and time-resolved resonance Raman studies. J. Raman Spectrosc 2005, 36, 337–349. [Google Scholar]
- Pinakoulaki, E; Ohta, T; Soulimane, T; Kitagawa, T; Varotsis, C. Detection of the primary His-heme Fe2+-NO intermediate in the reduction of NO to N2O by ba3-oxidase from Thermus thermophilus. J. Am. Chem. Soc 2005, 127, 15161–15167. [Google Scholar]
- Pinakoulaki, E; Yoshimura, H; Yoshioka, S; Aono, S; Varotsis, C. Recognition and discrimination of gases by the oxygen-sensing signal transducer protein HemAT as revealed by FTIR spectroscopy. Biochemistry 2006, 45, 7763–7766. [Google Scholar]
- Varotsis, C; Ohta, T; Kitagawa, T; Soulimane, T; Pinakoulaki, E. The structure of the hyponitrite species in a heme Fe-Cu binuclear center. Angew. Chem. Int 2007, 46, 2210–2214. [Google Scholar]
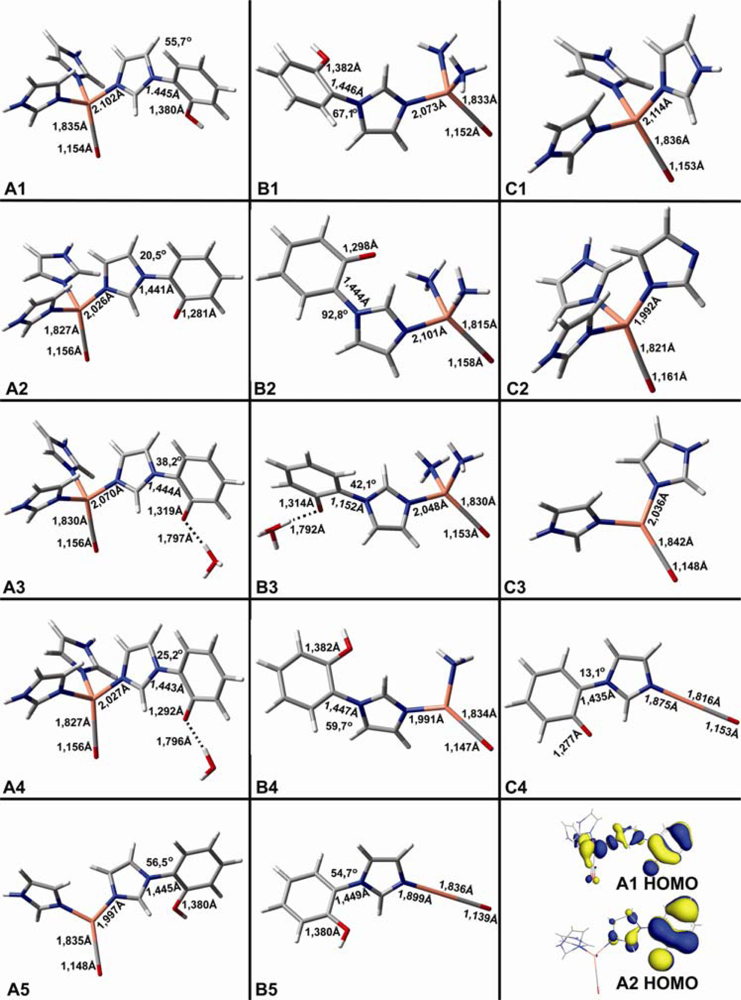
| CuB-CO models | Theoretical vibrations in cm−1 (dmol3-BLYP/DND) | ||
|---|---|---|---|
| ν(C-O) | ν(Cu-C) | δ(Cu-C-O | |
| A1 | 2031 | 414 | 326 |
| A2 | 2020 | 425 | |
| A3 | 2020 | 420 | |
| A4 | 2023 | 421 | |
| A5 | 2072 | 421 | |
| B1 | 2049 | 419 | |
| B2 | 2011 | 442 | |
| B3 | 2040 | 421 | |
| B4 | 2083 | 422 | |
| B5 | 2147 | 444 | |
| C1 | 2035 | 411 | 324 |
| C2 | 1992 | 431 | |
| C3 | 2078 | 411 | |
| C4 | 2026 | 468 | |
| Fe-NO models | ν(N-O) in cm−1 | ν(Fe-N) in cm−1 | δ(Fe-N-O) in cm−1 |
|---|---|---|---|
| II1/dmol3 | 1677 | 415 | 512 |
| II3/dmol3 | 1670 | 418 | 520 |
| II4/dmol3 | 1628 | 407 | 489 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Daskalakis, V.; Varotsis, C. Binding and Docking Interactions of NO, CO and O2 in Heme Proteins as Probed by Density Functional Theory. Int. J. Mol. Sci. 2009, 10, 4137-4156. https://doi.org/10.3390/ijms10094137
Daskalakis V, Varotsis C. Binding and Docking Interactions of NO, CO and O2 in Heme Proteins as Probed by Density Functional Theory. International Journal of Molecular Sciences. 2009; 10(9):4137-4156. https://doi.org/10.3390/ijms10094137
Chicago/Turabian StyleDaskalakis, Vangelis, and Constantinos Varotsis. 2009. "Binding and Docking Interactions of NO, CO and O2 in Heme Proteins as Probed by Density Functional Theory" International Journal of Molecular Sciences 10, no. 9: 4137-4156. https://doi.org/10.3390/ijms10094137




