Ordering and Reverse Ordering Mechanisms of Triblock Copolymers in the Presence of Solvent
Abstract
:1. Introduction
2. Self-Consistent Field Theory
3. Results and Discussion
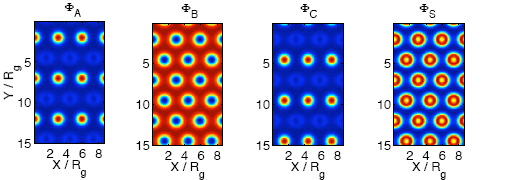
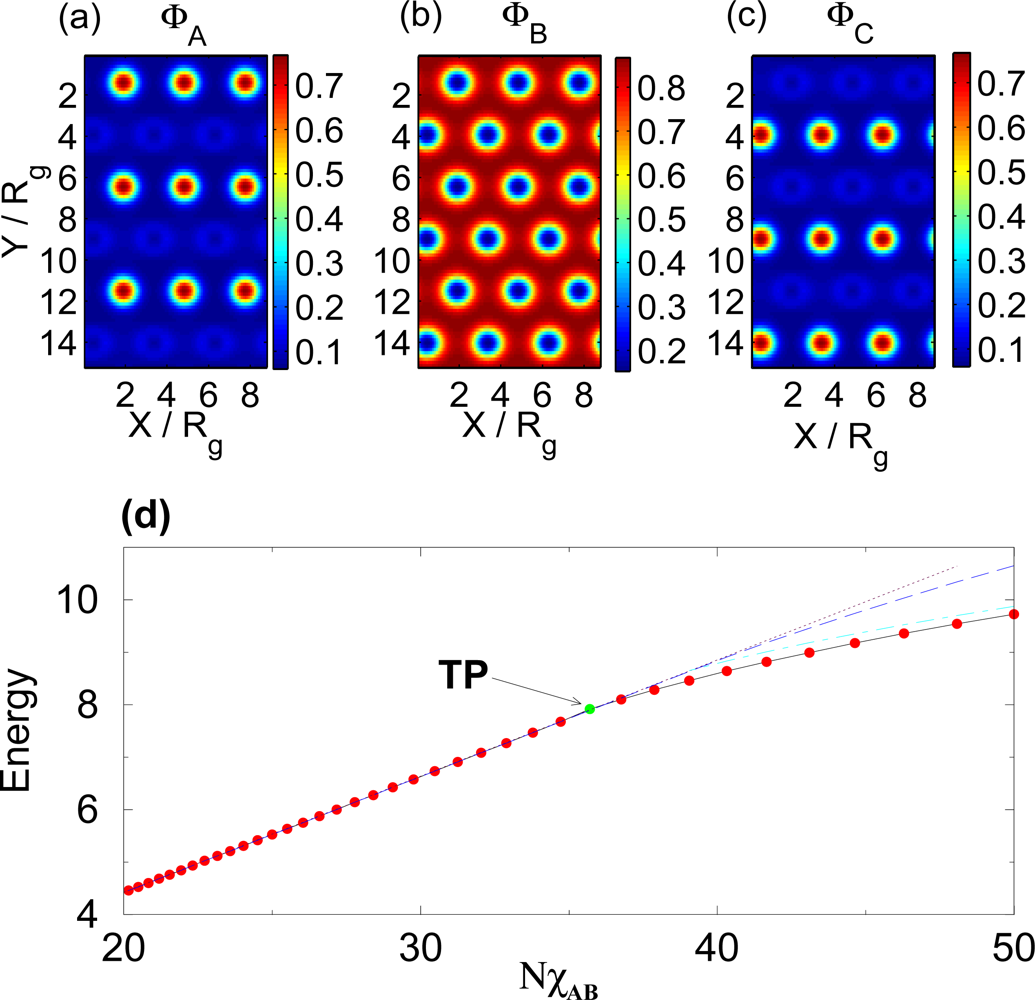
3.1. Temperature Dependence
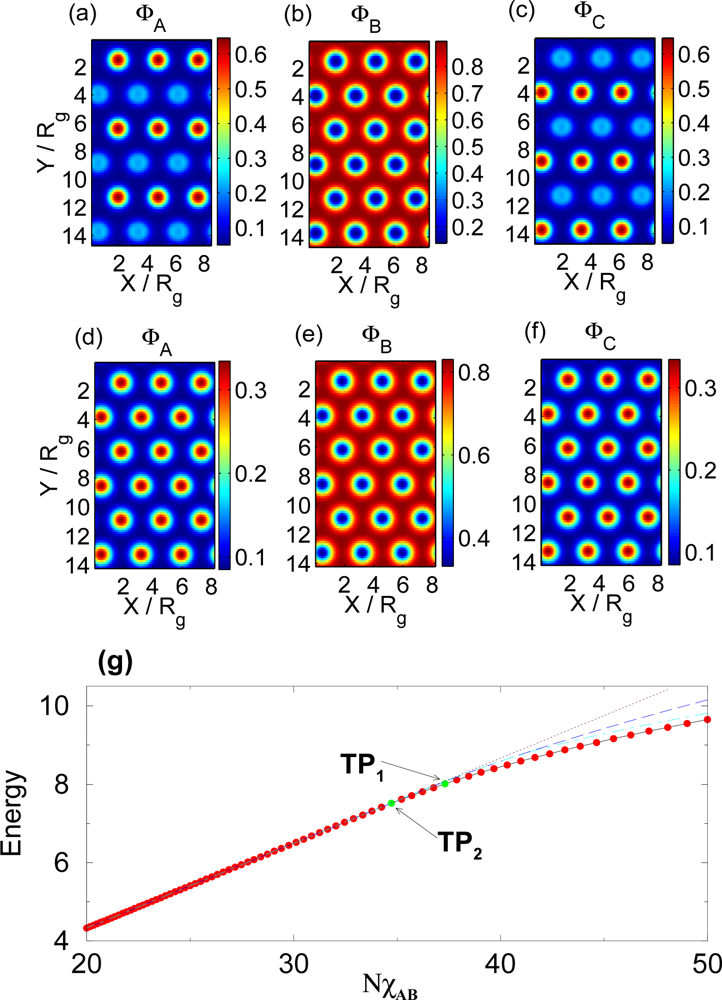
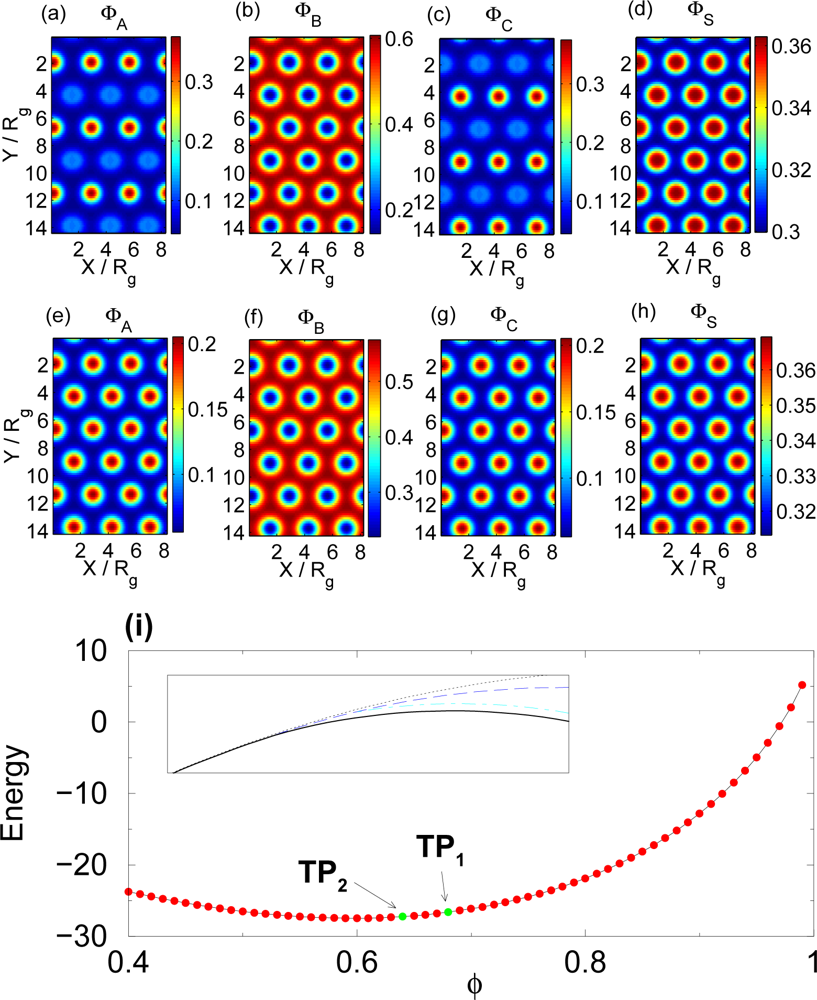
3.2. Non-selective Solvent
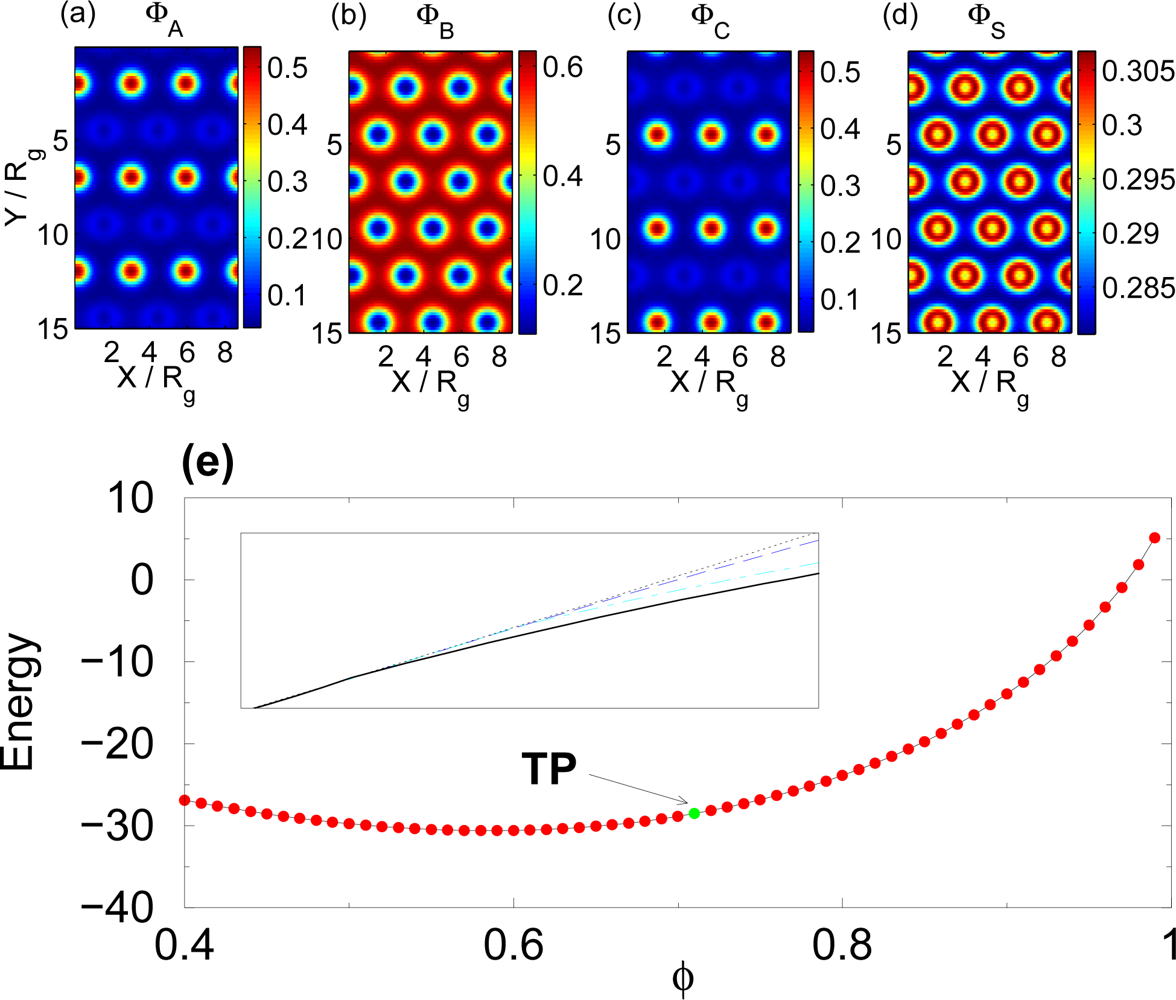
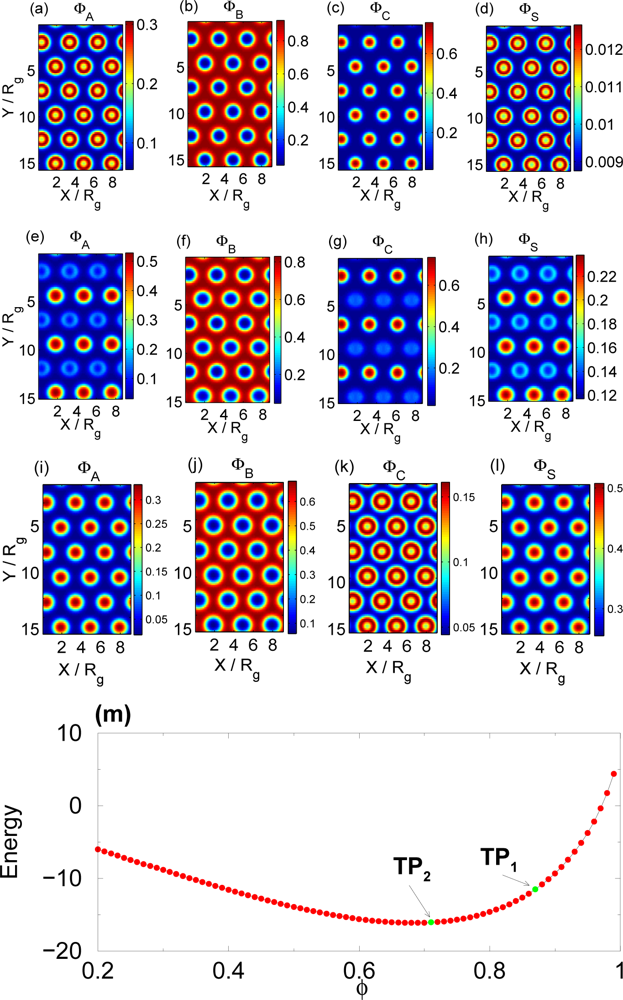
3.3. Selective Solvent
4. Conclusions
Acknowledgments
References and Notes
- Yamauchi, K; Hasegawa, H; Hashimoto, T; Köhler, N; Knoll, K. Synthesis and morphological studies of polyisoprene-block-polystyrene-block-poly(vinyl methyl ether) triblock terpolymer. Polymer 2002, 43, 3563–3570. [Google Scholar]
- Yamauchi, K; Hasegawa, H; Hashimoto, T; Nagao, M. Complex microphase separation and microdomain structures in poly(isoprene)-block-poly(D-8-styrene)-block-poly(vinyl methyl ether) triblock terpolymer. J. Appl. Cryst 2003, 36, 708–712. [Google Scholar]
- Maniadis, P; Thompson, RB; Rasmussen, KØ; Lookman, T. Ordering mechanisms in triblock copolymers. Phys Rev E 2004, 69. [Google Scholar]
- Vavasour, JD; Whitmore, MD. Self-consistent field theory of block copolymers with conformational asymmetry. Macromolecules 1993, 26, 7070–7075. [Google Scholar]
- Naughton, JR; Matsen, MW. Limitations of the dilution approximation for concentrated block copolymer/solvent mixtures. Macromolecules 2002, 35, 5688–5696. [Google Scholar]
- Tzeremes, G; Rasmussen, KØ; Lookman, T; Saxena, A. Efficient computation of the structural phase behavior of block copolymers. Phys Rev E 2002, 65, 1806–1806. [Google Scholar]
- Rasmussen, KØ; Kalosakas, G. Improved numerical algorithm for exploring block copolymer mesophases. J. Polymer Sci. Part B: Polymer Phys 2002, 40, 1777–1783. [Google Scholar]
- Doi, M. Introduction to Polymer Physics; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Mai, S-M; Fairclough, JPA; Terrill, NJ; Turner, SC; Hamley, IW; Matsen, MW; Ryan, AJ; Booth, C. Microphase separation in poly(oxyethylene)-poly(oxybutylene) diblock copolymers. Macromolecules 1998, 31, 8110–8116. [Google Scholar]
- Mai, S-M; Mingvanish, W; Turner, SC; Chaibundit, C; Fairclough, JPA; Heatley, F; Matsen, MW; Ryan, AJ; Booth, C. Microphase-separation behavior of triblock copolymer melts. Comparison with diblock copolymer melts. Macromolecules 2000, 33, 5124–5130. [Google Scholar]
- It is important to note that all our simulations are performed in two-dimensions, which excludes certain morphologies than can only be realized in three-dimensions. It is therefore possible that, as large amounts of solvent is added, we may be missing low energy, high-curvature morphologies that are only realizable in three-dimensions. However, this does not change the phenomenology this paper describes.
- Whitmore, MD; Noolandi, J. Self-consistent theory of block copolymer blends: neutral solvent. J. Chem. Phys 1990, 93, 2946–2955. [Google Scholar]
- Whitmore, MD; Vavasour, JD. Self-consistent mean field-theory of the microphase diagram of block copolymer neutral blends. Macromolecules 1992, 25, 2041–2045. [Google Scholar]
- Huang, C-I; Lodge, TP. Self-consistent calculations of block copolymer solution phase behavior. Macromolecules 1998, 31, 3556–3565. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Maniadis, P.; Rasmussen, K.O.; Thompson, R.B.; Kober, E.M. Ordering and Reverse Ordering Mechanisms of Triblock Copolymers in the Presence of Solvent. Int. J. Mol. Sci. 2009, 10, 805-816. https://doi.org/10.3390/ijms10030805
Maniadis P, Rasmussen KO, Thompson RB, Kober EM. Ordering and Reverse Ordering Mechanisms of Triblock Copolymers in the Presence of Solvent. International Journal of Molecular Sciences. 2009; 10(3):805-816. https://doi.org/10.3390/ijms10030805
Chicago/Turabian StyleManiadis, Panagiotis, Kim O. Rasmussen, Russell B. Thompson, and Edward M. Kober. 2009. "Ordering and Reverse Ordering Mechanisms of Triblock Copolymers in the Presence of Solvent" International Journal of Molecular Sciences 10, no. 3: 805-816. https://doi.org/10.3390/ijms10030805