An Algorithm for Emulsion Stability Simulations: Account of Flocculation, Coalescence, Surfactant Adsorption and the Process of Ostwald Ripening
Abstract
:1. Introduction
2. Brownian Dynamics (BD) Simulations
3. Emulsion Stability Simulations (ESS)
3.1. Equation of Motion
3.2. Interaction Forces and the surface excess
3.3. Surfactant Distribution (Evaluation of the surface excess)
3.3.1. Homogeneous Surfactant Distribution with fast and irreversible surfactant adsorption
3.3.2. Homogeneous Surfactant Distribution with time-dependent surfactant adsorption
3.3.3. Equilibrium Surfactant Distribution (Gibbs)
3.4. Ostwald Ripening
3.5. The Algorithm of ESS
4. Results
4.1. Low surfactant concentration
4.2. Intermediate surfactant concentration. Insufficient surfactant molecules to prevent the initial coalescence of drops
4.3. High surfactant concentrations
4.4. Time-dependent adsorption
4.5. Ostwald Ripening
- The particles are fixed in space.
- The system is infinitely dilute (implying the absence of interactions).
- The molecules of the internal phase are transported from one particle to another by molecular diffusion.
- The concentration of oil is the same through the whole system except in a direct neighbourhood of the particles, where it is given by the Kelvin equation.
5. Modifications of ESS for the Calculation of Deformable Drops
5.1. Regions of deformation
5.2. Interaction forces between deformable droplets
5.3. Calculation of the diffusion constant for deformable droplets
5.4. Coalescence criteria for deformable drops
- τij is counted continuously from the moment a doublet enters Regions II or III until either h = hcrit (coalescence occurs) or the double separates: rij >Ri + Rj + h0. If the doublet separates τij is made equal to zero (its starting value at the beginning of the simulation).
- τij is estimated from the total number of time steps accumulated every time particles i and j enter zones II and III. In this case τij ≠ 0 after a couple of particles enter Regions II or III the first time.
5.5. Preliminary Results
6. Conclusions
Acknowledgments
References and Notes
- Bancroft, WD. Theory of Emulsification. J. Phys. Chem 1913, 17, 501–519. [Google Scholar]
- Shinoda, K. The Correlation between the Dissolution State of Nonionic Surfactant and the Type of Dispersion Stabilized with the Surfactant. J. Colloid Interface Sci 1967, 24, 4–9. [Google Scholar]
- Miñana-Perez, M; Gutron, C; Zundel, C; Anderez, JM; Salager, JL. Miniemulsion Formation by Transitional Inversion. J. Disp. Sci. Tech 1999, 20, 893–905. [Google Scholar]
- Salager, JL; Morgan, JC; Schechter, RS; Wade, WH. Vasquez, E. Optimum Formulation of Surfactant/Water/Oil Systems for Minimum Interfacial Tension or Phase Behavior. Soc. Petrol. Eng. J 1979, 19, 107–115. [Google Scholar]
- Salager, JL. Phase Transformation and Emulsion Inversion on the Basis of Catastrophe Theory. In Encyclopedia of Emulsion Technology, 1st Ed; Becher, P, Ed.; Marcel Dekker: New York, USA, 1988; Volume 3, pp. 79–134. [Google Scholar]
- Ivanov, IB; Danov, KD; Kralchevsky, PA. Flocculation and Coalescence of Micron-Size Emulsion Droplets. Colloids and Surfaces A: Physicochem. Eng. Aspects 1999, 152, 161–182. [Google Scholar]
- Vrij, A; Overbeek, JThG. Rupture of Thin Liquid Films due to Spontaneous Fluctuations in Thickness. J. Ame. Chem. Soc 1968, 90, 3074–3078. [Google Scholar]
- Vrij, A. Light Scattering by Soap Films. J. Colloid Interface Sci 1964, 19, 1–27. [Google Scholar]
- Kashchiev, D; Exerowa, D. Nucleation Mechanism of Rupture of Newton Black Films: I. Theory. J. Colloid Interface Sci 1980, 77, 501–511. [Google Scholar]
- Nikolova, A; Exerowa, D. Rupture of Common Black Films. Experimental Study. Colloid Surfaces A: Physicochem. Eng. Aspects 1999, 149, 185–191. [Google Scholar]
- Einstein, A. Investigations on the theory of the Brownian movement, 2nd Ed; Fürth, R, Ed.; Dover Publications Inc: New York, USA, 1956; pp. 1–35. [Google Scholar]
- Mazo, RM. Brownian Motion Fluctuation, Dynamics and Applications, 1st Ed ed; Oxford University Press: New York, USA, 2002; pp. 46–59. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics, 1st Ed ed; McGraw-Hill: Singapore, Singapore, 1985; pp. 560–582. [Google Scholar]
- Van de Ven, TGM. Colloidal Hydrodynamics, 1st Ed ed; Academic Press: Padstow, Great Britain, 1989; pp. 51–126. [Google Scholar]
- Ermak, D; McCammon, JA. Brownian Dynamics with Hydrodynamic Interactions. J. Chem. Phys 1978, 69, 1352–1360. [Google Scholar]
- Batchelor, GK. Sedimentation in a Dilute Polydisperse System of Interacting Spheres. Part 1. General Theory. J. Fluid Mech 1982, 119, 379–408. [Google Scholar]
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP. Numerical Recipes in Fortran 77, 2nd Ed ed; Cambridge University Press: New York, USA, 1996. [Google Scholar]
- Bacon, J; Dickinson, E.; Parker, R. Simulation of Particle Motion and Stability in Concentrated Dispersions. Faraday Discuss. Chem. Soc 1983, 76, 165–178. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M.; Toro-Mendoza, J. Influence of Polydispersity and Thermal Exchange on the Flocculation Rate of O/W Emulsions. Mol. Simul 2003, 29, 393–404. [Google Scholar]
- Verwey, EJW; Overbeek, JThG. Theory of the stability of lyophobic colloids, 2nd Ed ed; Dover Publications Inc: New York, USA, 1948; pp. 100–185. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M. Role of the Secondary Minimum on the Flocculation Rate of Nondeformable Droplets. Langmuir 2005, 21, 6675–6687. [Google Scholar]
- Chandrasekar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys 1943, 15, 1–89. [Google Scholar]
- Kramer, HA. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica 1940, VII, 284–304. [Google Scholar]
- Fuchs, N. Über die Stabilität und Aufladung der Aerosole. Z. Physik 1936, 89, 736–743. [Google Scholar]
- McGown, DN.L.; Parfitt, GD. Improved Theoretical Calculation of the Stability Ratio for Colloidal Systems. J. Phys. Chem 1967, 71, 449–450. [Google Scholar]
- Prieve, D; Ruckenstein, E. Role of Surface Chemistry in Primary and Secondary Coagulation and Heterocoagulation. J. Colloids Interface Sci 1980, 73, 539–555. [Google Scholar]
- von Smoluchowski, M. Versuch einer Mathematischen Theorie der Koagulationskinetik Kolloider Losungen. Z. Phys. Chem 1917, 92, 129–168. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M. Brownian Dynamics Simulation of Emulsion Stability. Langmuir 2000, 16, 7975–7985. [Google Scholar]
- Urbina-Villalba, G; Toro-Mendoza, J; Lozsán, A; García-Sucre, M. Brownian dynamics simulations of emulsion stability. In Emulsions: Structure, Stability and Interactions, 1st Ed; Petsev, DN, Ed.; Elsevier Ltd: Amsterdam, The Netherlands, 2004; pp. 677–719. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M.; Toro-Mendoza, J. Average Hydrodynamic Correction for the Brownian Dynamics Calculation of Flocculation Rates in Concentrated Dispersions. Phys. Rev. E 2003, 68, 061408. [Google Scholar]
- Honig, EP; Roebersen, GJ; Wiersema, PH. Effect of Hydrodynamic Interaction on the Coagulation Rate of Hydrophobic Colloids. J. Colloid Interface Sci 1971, 36, 97–109. [Google Scholar]
- Hamaker, HC. The London-Van der Waals Attraction between Spherical Particles. Physica (Amsterdam) 1937, IV, 1058–1072. [Google Scholar]
- Hough, DB; White, LR. The Calculation of Hamaker Constants from Lifshitz Theory with Applications to Wetting Phenomena. Adv. Colloid Interface Sci 1980, 14, 3–41. [Google Scholar]
- Reddy, SR; Melik, DH; Fogler, HS. Emulsion Stability. Theoretical Studies on Simultaneous Flocculation and Creaming. J. Colloid Interface Sci 1981, 82, 117–127. [Google Scholar]
- Sakai, T; Kamogawa, K.; Harusawa, F.; Momozawa, N.; Sakai, H.; Abe, M. Direct Observation of Flocculation/Coalescence of Metastable Oil Droplets in Surfactant-Free Oil/Water Emulsion by Freeze-Fracture Electron Microscopy. Langmuir 2001, 23, 255–259. [Google Scholar]
- Rosen, MJ. Surfactants and Interfacial Phenomena, 2nd Ed ed; John Wiley & Sons: New York, USA, 1989; pp. 33–107. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M. Role of the Secondary Minimum on the Flocculation Rate of Non-deformable Droplets (Correction). Langmuir 2006, 22, 6675–6687. [Google Scholar]
- Danov, KD; Petsev, DN; Denkov, ND; Borwankar, R. Pair Interaction Energy between Deformable Drops and Bubbles. J. Chem. Phys 1993, 99, 7179–7189. [Google Scholar]
- Sader, JE. Accurate Analytical Formulae for the Far Field Effective Potential and Surface Charge Density of a Uniformly Charged Sphere. J. Colloids Interface Sci 1997, 188, 508–510. [Google Scholar]
- Oberholzer, MR; Stankovich, JM; Carnie, SL; Chan, DYC; Lenhoff, AM. 2-D and 3-D Interactions in Random Sequential Adsorption of Charged Particles. J. Colloid Interface Sci 1997, 194, 138–153. [Google Scholar]
- Sader, JE; Carnie, SL; Chan, DYC. Accurate Analytic Formulas for the Double-Layer Interaction between Spheres. J. Colloid Interface Sci 1995, 171, 46–54. [Google Scholar]
- Derjaguin, B. On the Repulsive Forces between Charged Colloid Particles and on the Theory of Slow Coagulation and Stability of Lyophobe Sols. Trans. Faraday Soc 1940, 36, 203–211. [Google Scholar]
- Lozsán, A; García-Sucre, M.; Urbina-Villalba, G. Steric Interaction between Spherical Colloidal Particles. Phys. Rev. E 2005, 72, 061405. [Google Scholar]
- Lozsan, A; García-Sucre, M.; Urbina-Villalba, G. Theoretical Estimation of Stability Ratios for Hexadecane-in-Water (h/w) Emulsions Stabilized with Nonylphenol Ethoxylated Surfactants. J. Colloid Interface Sci 2006, 299, 366–377. [Google Scholar]
- Vincent, B; Edwards, J.; Emmett, S.; Jones, A. Depletion Flocculation in Dispersions of Sterically-Stabilised Particles (“soft spheres”). Colloids Surf 1986, 18, 261–281. [Google Scholar]
- Bagchi, P. Theory of Stabilization of Spherical Colloidal Particles by Non-ionic Polymers. J. Colloid Interface Sci 1974, 47, 86–99. [Google Scholar]
- Israelachvilli, J. Intermolecular and surface forces, 2nd Ed ed; Academic Press: London, United Kingdom, 2002; pp. 161–164. [Google Scholar]
- Flory, PJ; Krigbaum, WR. Statistical Mechanics of Dilute Polymer Solutions II. J. Chem. Phys 1950, 18, 1086–1094. [Google Scholar]
- Flory, PJ. Principles of Polymer Chemistry, 1st Ed ed; Cornell University Press: New York, USA, 1971; pp. 495–539. [Google Scholar]
- De Gennes, PG. Polymers at the Interface; a Simplified View. Adv. Colloid Interface Sci 1987, 27, 189–209. [Google Scholar]
- Marquez, N; Graciaa, A.; Lachaise, J.; Salager, JL. Partioning of Ethoxylated Alkylphenol Surfactants in Microemulsion-Oil-Water Systems: Influence of Physicochemical Formulation variables. Langmuir 2002, 18, 6021–6024. [Google Scholar]
- Svitova, TF; Radke, CJ. AOT and Pluronic F68 Coadsorption at Fluid/Fluid Interfaces: A Continuous-Flow Tensiometry Study. Ind. Eng. Chem 2005, 44, 1129–1138. [Google Scholar]
- Miller, R. On the Solution of Diffusion Controlled Adsorption Kinetics for Any Adsorption Isotherms. Colloid Polymer Sci 1981, 375–381. [Google Scholar]
- Urbina-Villalba, G. Influence of Surfactant Distribution on the Stability of Oil/Water Emulsions towards Flocculation and Coalescence. Colloids and Surfaces A: Physicochem. Eng. Aspects 2001, 190, 111–116. [Google Scholar]
- Urbina-Villalba, G. Effect of Dynamic Surfactant Adsorption on Emulsion Stability. Langmuir 2004, 20, 3872–3881. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M. Effect of Non-Homogeneous Spatial Distributions of Surfactants on the Stability of High-Content Bitumen-in-Water Emulsions. Interciencia 2000, 25, 415–422. [Google Scholar]
- Urbina-Villalba, G; García-Sucre, M. A Simple Computational Technique for the Systematic Study of Adsorption Effects in Emulsified Systems. Influence of Inhomogeneous Surfactant Distributions on the Coalescence rate of a Bitumen-in-Water Emulsion. Mol. Simul 2001, 22, 75–97. [Google Scholar]
- Ward, AFH; Tordai, L. Time-Dependence of Boundary Tensions of Solutions I. The Role of Diffusion in Time-Effects. J. Chem. Phys 1946, 14, 453–461. [Google Scholar]
- Liggieri, L; Ravera, F.; Passerone, A. A Diffusion-Based Approach to Mixed Adsorption Kinetics. Colloids and Surfaces A: Physicochem. Eng. Aspects 1996, 114, 351–359. [Google Scholar]
- Hua, XY; Rosen, MJ. Dynamic Surface Tension of Aqueous Surfactant Solutions. 1. Basic Parameters. J. Colloid Interface Sci 1988, 124, 652–659. [Google Scholar]
- Rosen, MJ; Hua, XY. Dynamic Surface Tension of Aqueous Surfactant Solutions. 2. Parameters at 1 s and at Mesoequilibrium. J. Colloid Interface Sci 1990, 139, 397–407. [Google Scholar]
- Yao, JH; Elder, KR; Guo, H; Grant, M. Theory and Simulation of Ostwald Ripening. Phys. Rev. B 1993, 47, 14110–14125. [Google Scholar]
- Yarranton, HW; Masliyah, JH. Numerical Simulation of Ostwald Ripening in Emulsions. J. Colloid Interface Sci 1997, 196, 157–169. [Google Scholar]
- Parbhakar, K; Lewandowski, J.; Dao, LH. Simulation Model for Ostwald Ripening in Liquids. J. Colloid Interface Sci 1995, 174, 142–147. [Google Scholar]
- Stevens, RN; Davies, CK. Self Consistent Forms of the Chemical Rate Theory of Ostwald Ripening. J. Materials. Sci 2002, 37, 765–779. [Google Scholar]
- Wang, KG; Glicksman, ME; Rajan, K. Modelling and Simulation for Phase Coarsening: A Comparison with Experiment. Phys. Rev. E 2004, 69, 0615071–0615079. [Google Scholar]
- De Smet, Y; Deriemaeker, L; Finsy, R. A Simple Computer Simulation of Ostwald Ripening. Langmuir 1997, 13, 6884–6888. [Google Scholar]
- De Smet, Y; Danino, D; Deriemaeker, L; Talmon, Y; Finsy, R. Ostwald Ripening in the Transient Regime. A Cryo-TEM Study. Langmuir 2000, 16, 961–967. [Google Scholar]
- De Smet, Y; Deriemaeker, L; Parloo, E; Finsy, R. On the Determination of Ostwald Ripening Rates from Dynamic Light Scattering Measurements. Langmuir 1999, 15, 2327–2332. [Google Scholar]
- Finsy, R. On the Critical Radius in Ostwald Ripening. Langmuir 2004, 20, 2975–2976. [Google Scholar]
- Urbina-Villalba, G; Forgiarini, A; Rahn, K; Lozsán, A. Is a Linear Slope ofr3 vs t an Unmistakable Signature of Ostwald Ripening? In Proceedia Chemistry; Adamczyk, Z, Warszyński, P, Eds.; Elsevier: Cracow, 2008; under review. [Google Scholar]
- Urbina–Villalba, G; Toro-Mendoza, J.; Lozsán, A.; García-Sucre, M. Effect of the Volume Fraction on the Average Flocculation Rate. J. Phys. Chem 2004, 108, 5416–5423. [Google Scholar]
- Urbina-Villalba, G; Toro-Mendoza, J.; García-Sucre, M. Calculation of Flocculation and Coalescence Rates for Concentrated Dispersions Using Emulsion Stability Simulations. Langmuir 2005, 21, 1719–1728. [Google Scholar]
- Urbina-Villalba, G; Lozsán, A.; Toro-Mendoza, J.; Rahn, K.; García-Sucre, M. Aggregation Dynamics in Systems of Coalescing Non-Deformables Droplets. J. Molec. Struct: Theochem 2006, 769, 171–181. [Google Scholar]
- Danov, KD; Ivanov, IB; Gurkov, TD; Borwankar, RP. Kinetic Model for the Simultaneous Processes of Flocculation and Coalescence in Emulsion Systems. J. Colloid Interface Sci 1994, 167, 8–17. [Google Scholar]
- Sonntag, H; Strenge, K. Coagulation Kinetics and structure formation, 1st Ed ed; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1987; pp. 48–125. [Google Scholar]
- Kuznar, ZA; Elimelech, M. Direct Microscopic Observation of Particle Deposition in Porous Media. Role of the Secondary Energy Minimum. Colloid and Surfaces A: Physicochem. Eng. Aspects 2007, 294, 156–162. [Google Scholar]
- Tufenkji, N; Elimelech, M. Breakdown of Colloid Filtration Theory: Role of the Secondary Energy Minimum and Surface Charge Heterogeneities. Langmuir 2005, 21, 841–852. [Google Scholar]
- Puertas, AM; de las Nieves, FJ. A New Method for Calculating Kinetic Constants Within the Rayleigh-Gans-Debye Approximation from Turbidity Measurements. J. Phys. Condens. Matter 1997, 9, 3313–3320. [Google Scholar]
- Puertas, AM; Maroto, JA; Fernández-Barbero, A; de las Nieves, FJ. Particle Interactions in Colloidal Aggregation by Brownian Dynamics Simulation. Phys. Rev. E 1999, 59, 1943–1947. [Google Scholar]
- Bonfillon, A; Sicoli, F.; Langevin, D. Dynamic Surface Tension of Ionic Surfactant Solutions. J. Colloid Interface Sci 1994, 168, 497–504. [Google Scholar]
- Diamand, H; Andelman, D. Kinetics of Surfactant Adsorption at Fluid/Fluid Interfaces: Non Ionic Surfactant. Europhys. Lett 1996, 34, 575–580. [Google Scholar]
- Salou, M; Siffert, B.; Jada, A. Study of the Stability of Bitumen Emulsions by Application of DLVO Theory. Colloid Surfaces A: Physicochem. Eng. Aspects 1998, 142, 9–16. [Google Scholar]
- Lifshitz, IM; Slezov, VV. The Kinetics of Precipitation from Supersaturated Solid Solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar]
- Wagner, C. Theorie der Alterung von Niederschlägen durch Umlösen. Z. Elektrochemie 1961, 65, 581–591. [Google Scholar]
- Sakai, T; Kamogawa, K; Nishiyama, K; Sakai, H; Abe, M. Molecular Difusion of Oil/Water Emulsions in Surfactant-Free Conditions. Langmuir 2002, 18, 1985–1990. [Google Scholar]
- Sakai, T; Kamogawa, K.; Harusawa, F.; Momozawa, N.; Sakai, H.; Abe, M. Direct observation of flocculation/coalescence of metastable oil droplets in surfactant-free oil/water emulsion by freeze-fracture electron microscopy. Langmuir 2001, 23, 255–259. [Google Scholar]
- Ju, RT.C.; Frank, C.W.; Gast, AP. Contin analysis of colloidal aggregates. Langmuir 1992, 8, 2165–2171. [Google Scholar]
- Feder, J; Jössang, T.; Roserqvist, E. Scaling Behavior and Cluster Fractal Dimension Determined by Light Scattering from Aggregating Proteins. Phys. Rev. Lett 1984, 53, 1403–1406. [Google Scholar]
- Lin, MY; Lindsay, HM; Weitz, DA; Ball, RC; Klein, R; Meakin, P. Universality in Colloid Aggregation. Nature 1989, 339, 360–362. [Google Scholar]
- Velikov, KP; Velev, OD; Marinova, KG; Constantinides, GN. Effect of the Surfactant Concentration on the Kinetic Stability of Thin Foam and Emulsion Films. J. Chem. Soc. Faraday Trans 1997, 93, 2069–2075. [Google Scholar]
- Toro-Mendoza, J. Simulationes de estabilidad de emulsiones de gotas deformables, Doctoral Thesis, IVIC, 2007.
- Toro-Mendoza, J; García-Sucre, M; Castellanos, AJ; Urbina-Villalba, G. Emulsion Stability Simulations of Deformable Droplets, 2008. submitted to J. Colloid Interface Sci.
- Denkov, ND; Petsev, DN; Danov, KD. Flocculation of Deformable Emulsion Droplets. I. Droplet Shape and Line-Tension Effects. J. Colloid Interface Sci 1995, 176, 189–200. [Google Scholar]
- Petsev, DN; Denkov, ND; Kralchevsky, PA. Flocculation of Deformable Emulsion Droplets. II. Interaction Energy. J. Colloid Interface Sci 1995, 176, 201–213. [Google Scholar]
- Helfrich, W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. Naturforsch 1973, 28, 693–703. [Google Scholar]
- Danov, KD; Denkov, ND; Petsev, DN; Borwankar, R. Coalescence Dynamics of Deformable Brownian Droplets. Langmuir 1993, 9, 1731–1740. [Google Scholar]
- Scheludko, A. Thin Liquid Films. Adv. Colloids and Interface Sci 1967, 1, 391–464. [Google Scholar]
- Ivanov, IB; Radoev, B; Manev, E; Scheludko, A. The Theory of Critical Thickness of Rupture of Thin Liquid Films. Trans. Faraday Soc 1970, 66, 1262–1273. [Google Scholar]
- Manev, ED; Nguyen, AV. Critical Thickness of Microscopic Thin Liquid Films. Adv Colloid Interface Sci 2005, 114–115, 133–146. [Google Scholar]
- Manev, ED; Angarska, JK. Critical Thickness of Thin Liquid Films: Comparison of Theory and Experiment. Colloids Surfaces A: Physicochem. Eng. Aspects 2005, 263, 250–257. [Google Scholar]
- Gurkov, TD; Basheva, ES. Hydrodynamic Behaviour and Stability of Approaching Deformable Drops. In Encyclopedia of Surface and Colloid Science, 1st Ed; Hubbard, AT, Ed.; Marcel Dekker: New York, USA, 2002; Volume 1, pp. 2349–2363. [Google Scholar]
- Tsekov, R. The R4/5 Problem in the Drainage of Dimpled Thin Liquid Films. Colloids Surfaces A: Physicochem. Eng. Aspects 1998, 141, 161–164. [Google Scholar]
- Ivanov, IB. Effect of Surface Mobility on the Dynamic Behaviour of Thin Liquid Films. Pure App. Chem 1980, 52, 1241–1262. [Google Scholar]
- Vrij, A. Possible Mechanism for the Spontaneous Rupture of Thin, Free Liquid Films. Discuss. Faraday Soc 1966, 42, 23–33. [Google Scholar]
- Dickinson, E; Murray, B.S.; Stainsby, G. Coalescence Stability of Emulsion-sized Droplets at a Planar Oil-Water Interface and the Relationship to Protein Film Surface Rheology. J. Chem. Soc. Faraday Trans 1988, 84, 871–883. [Google Scholar]
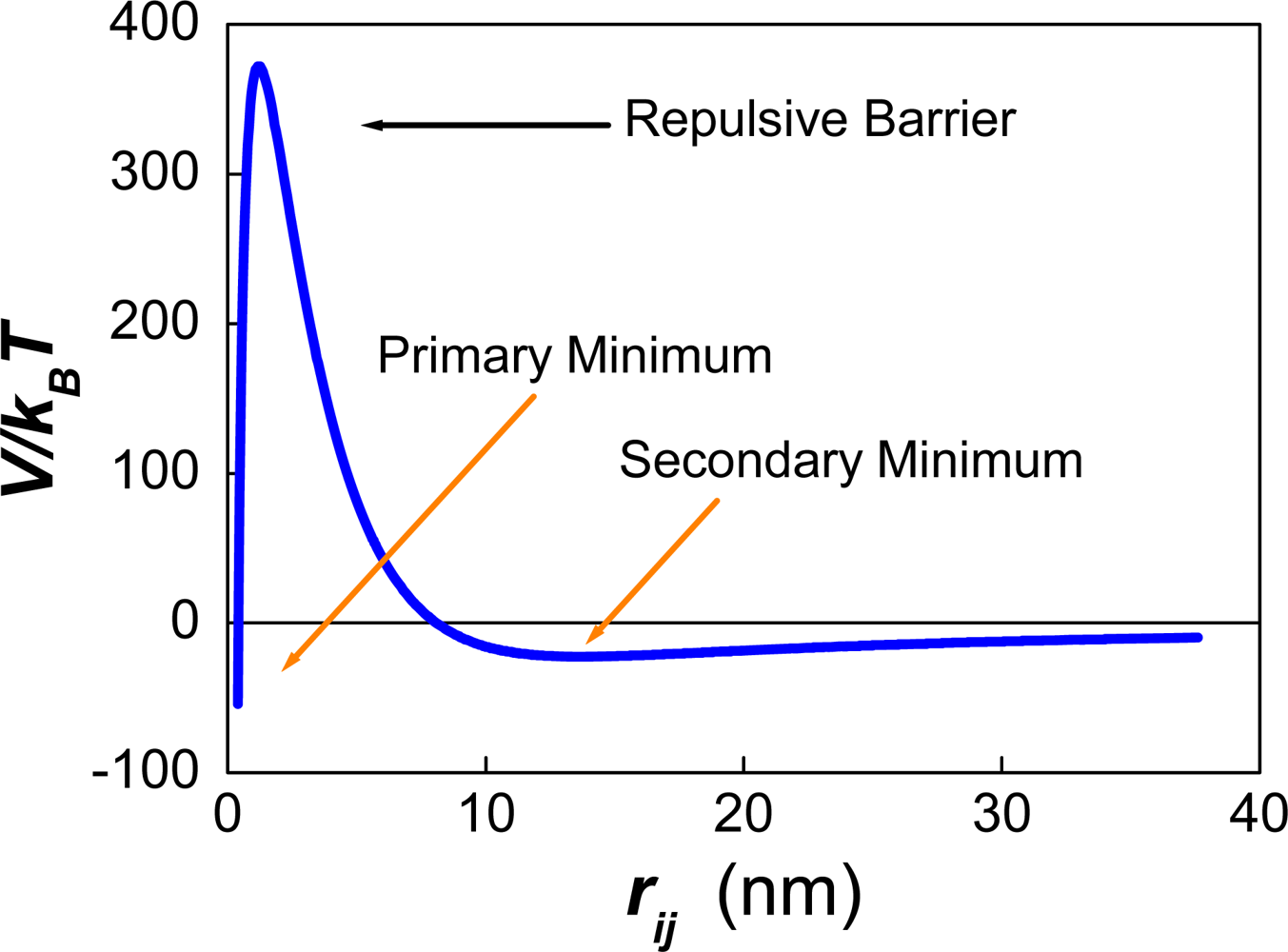
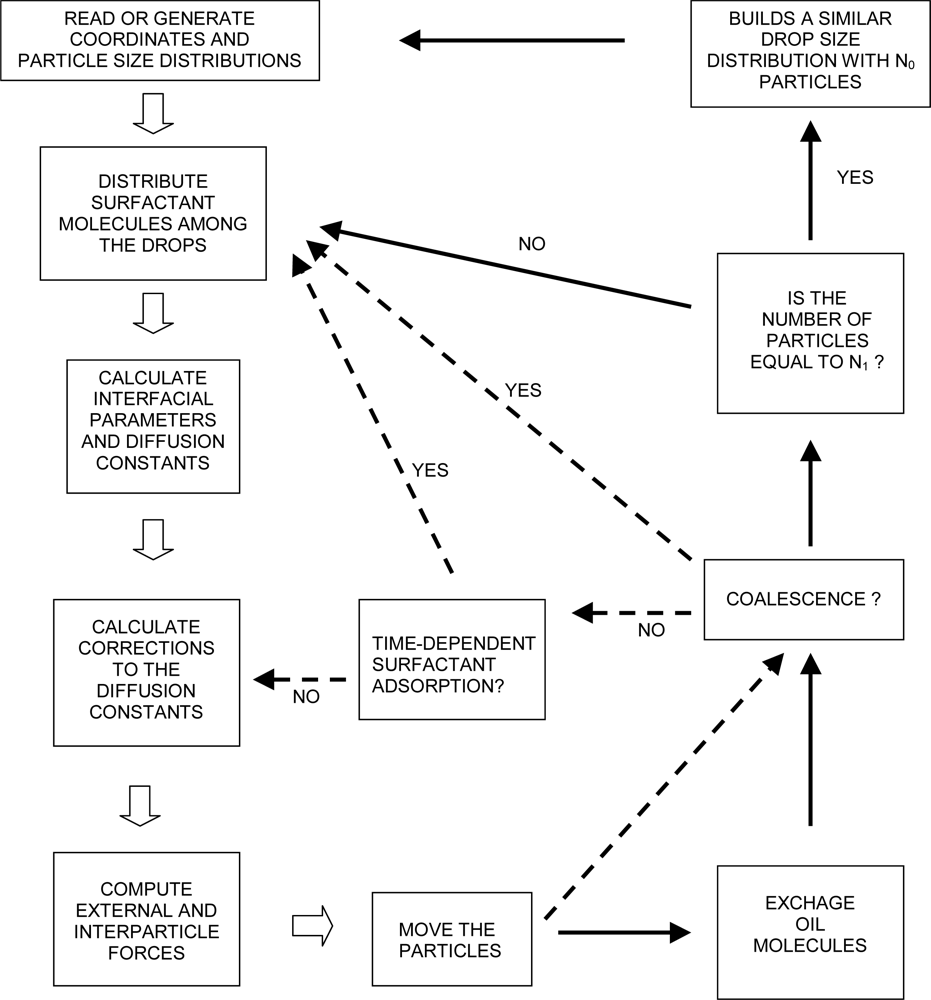
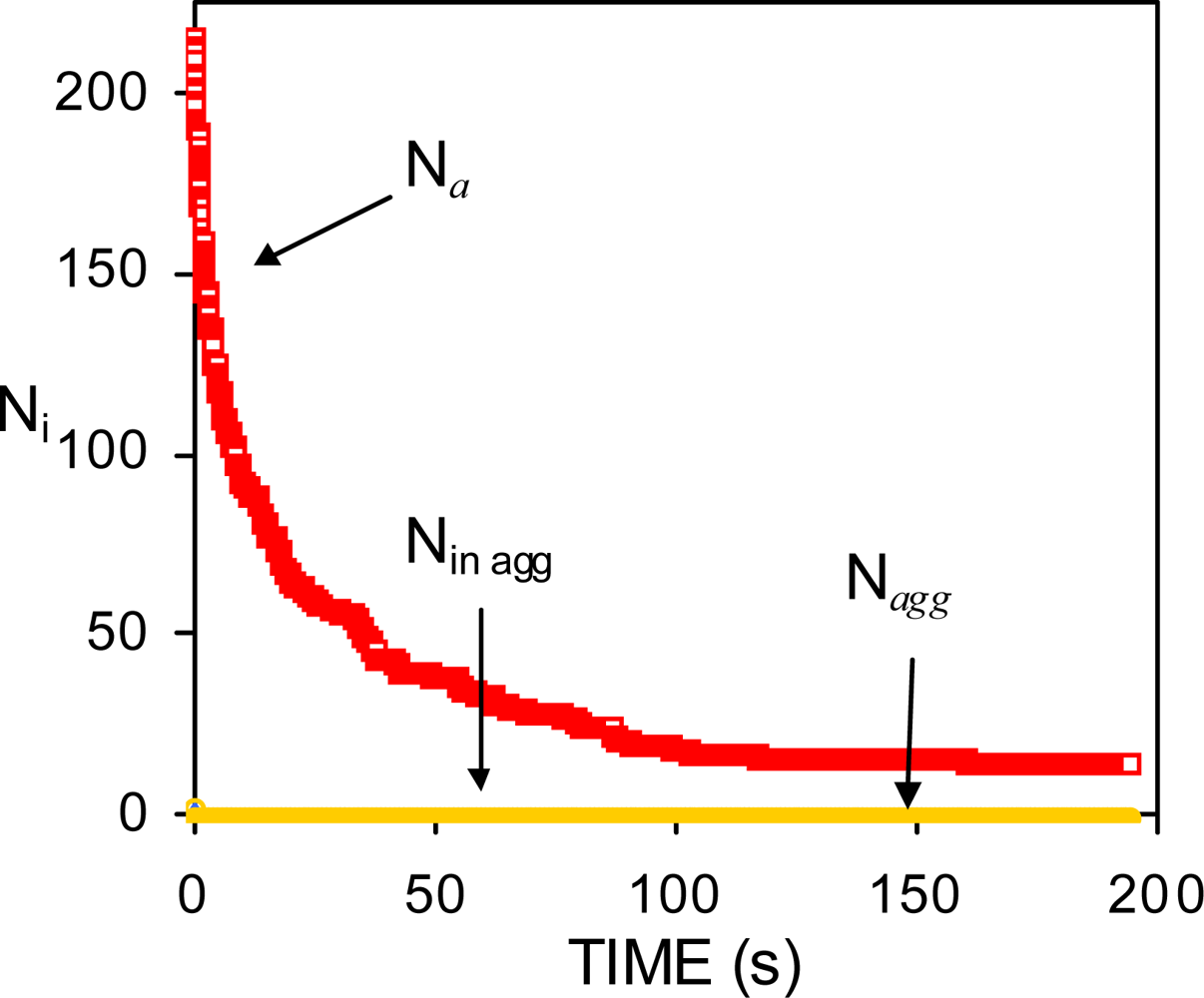
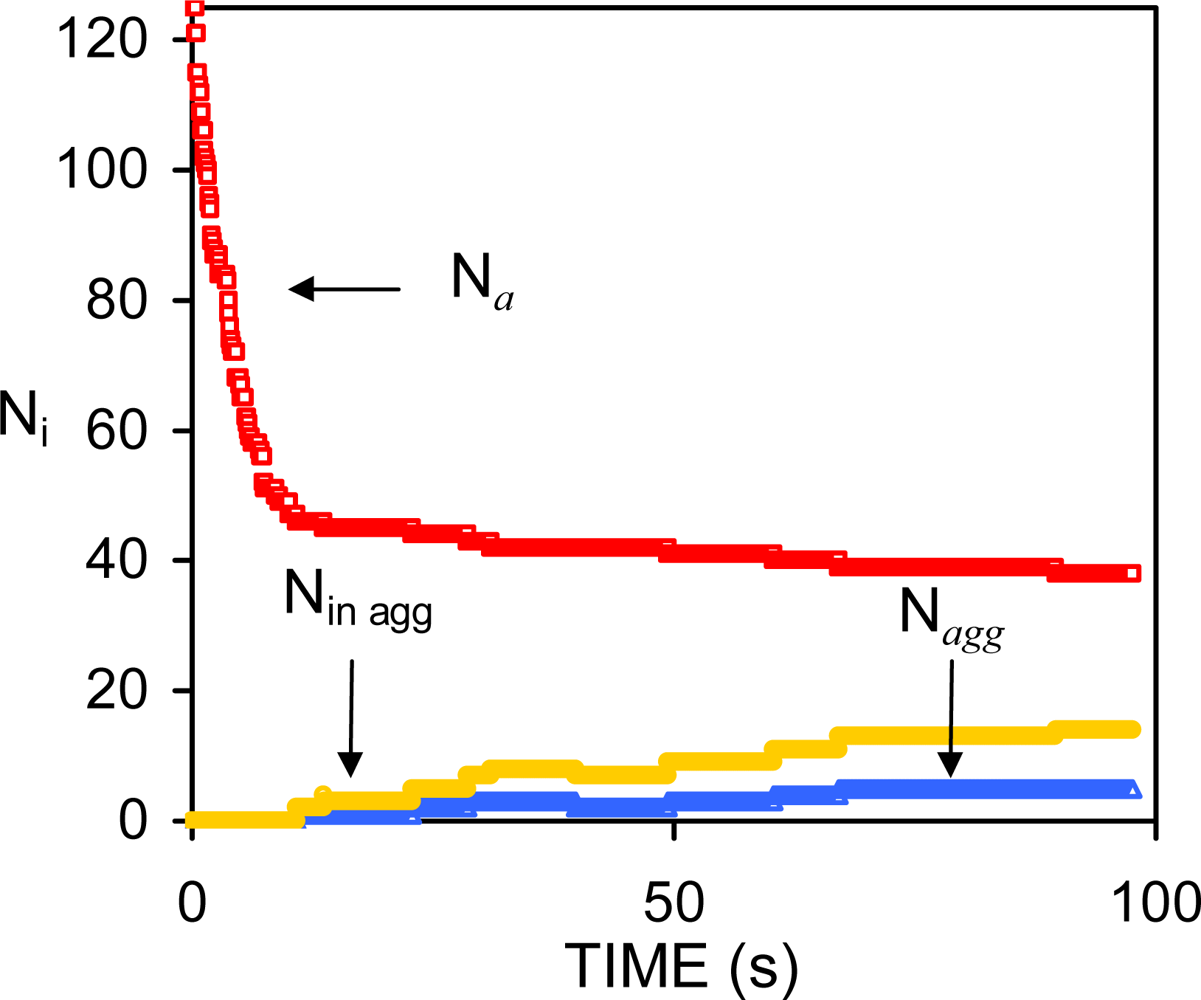
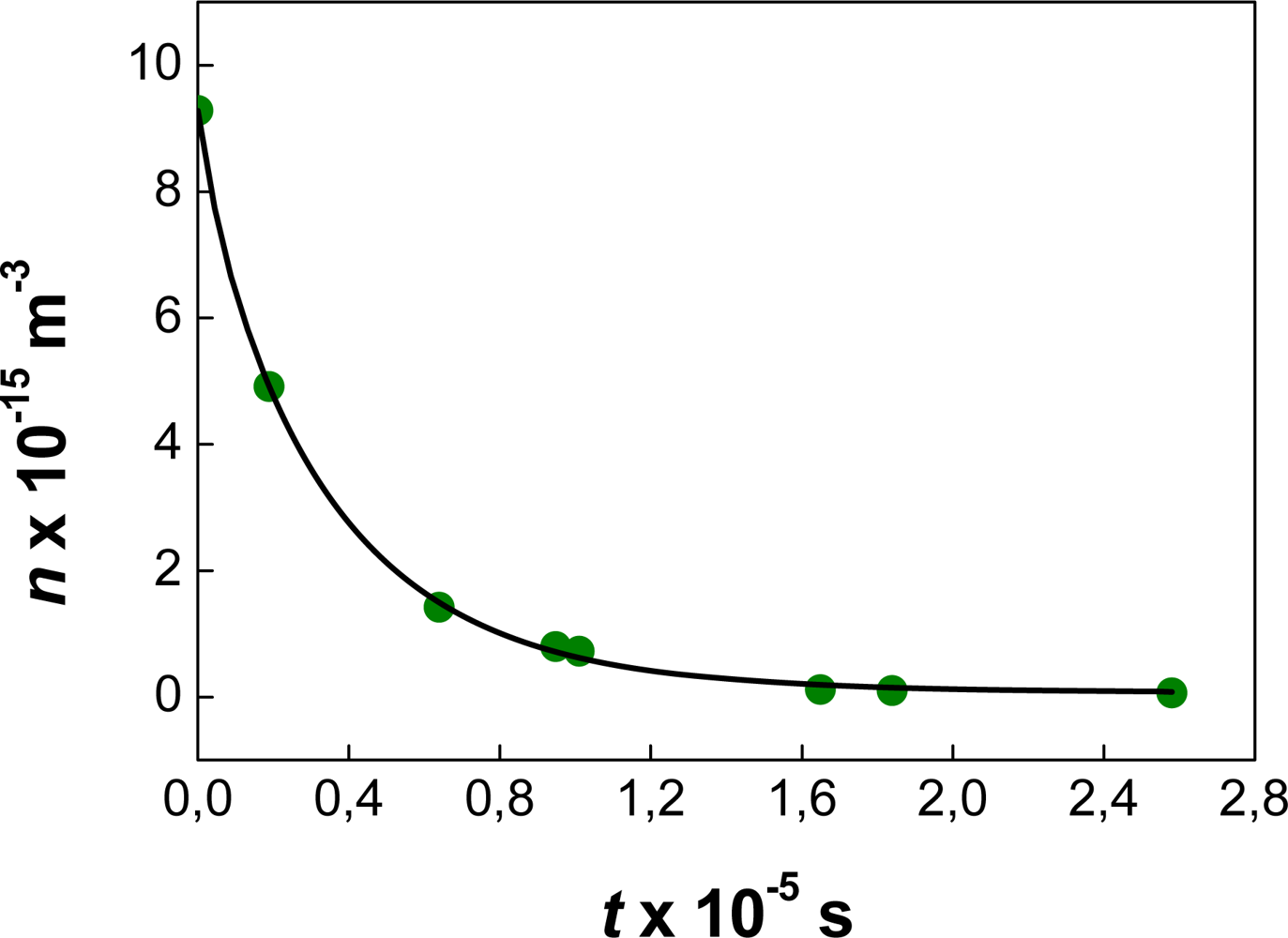
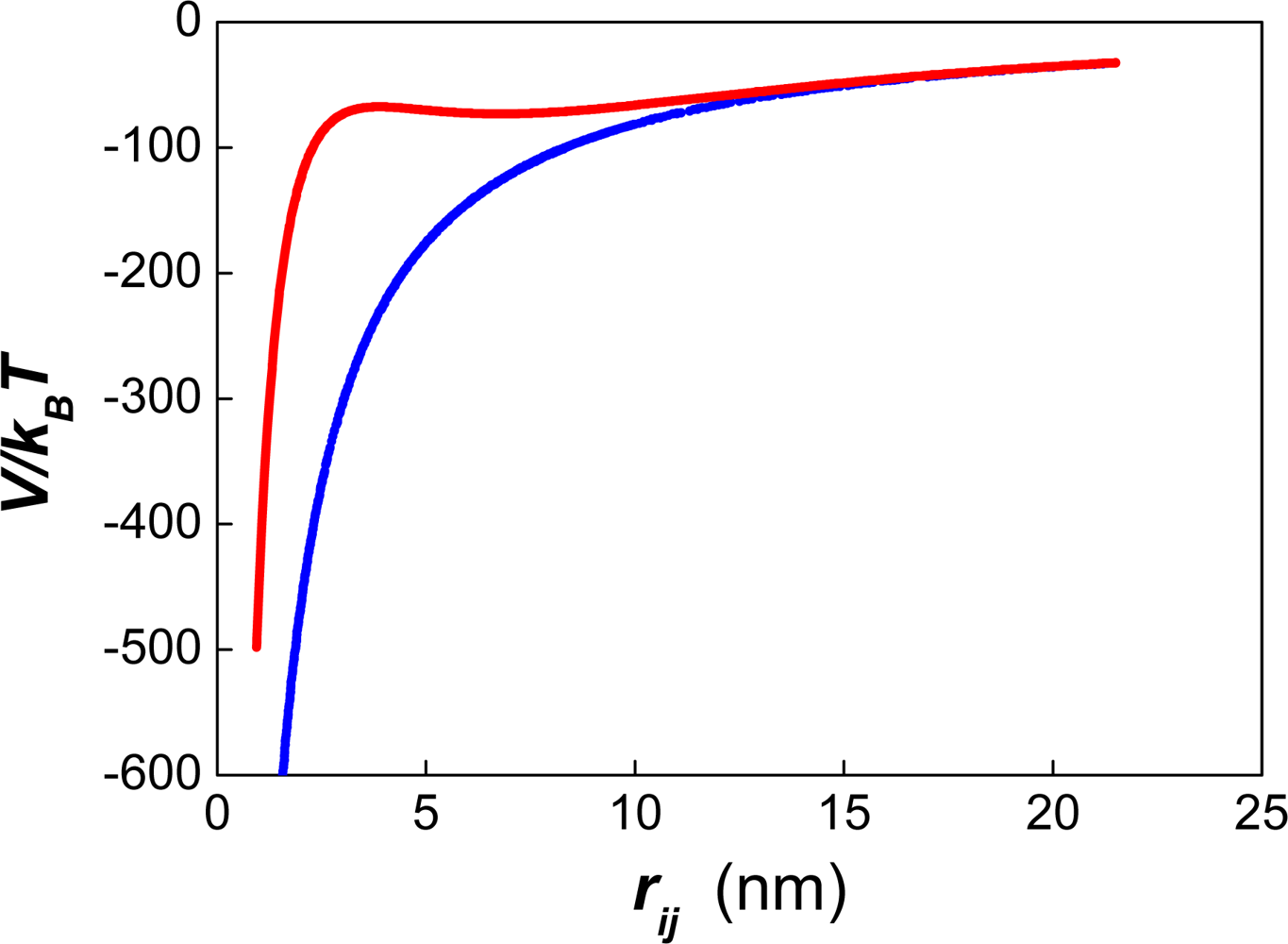
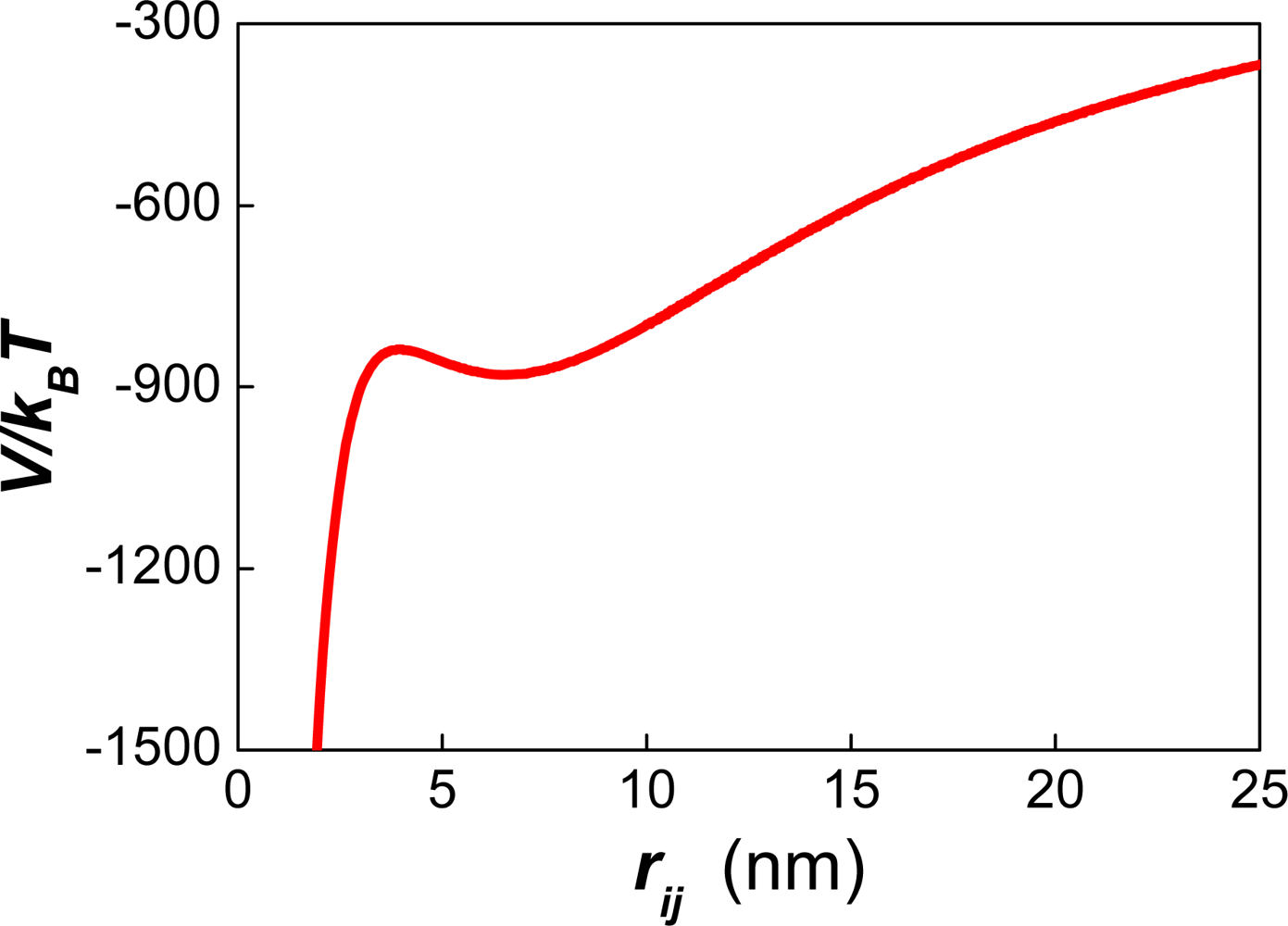
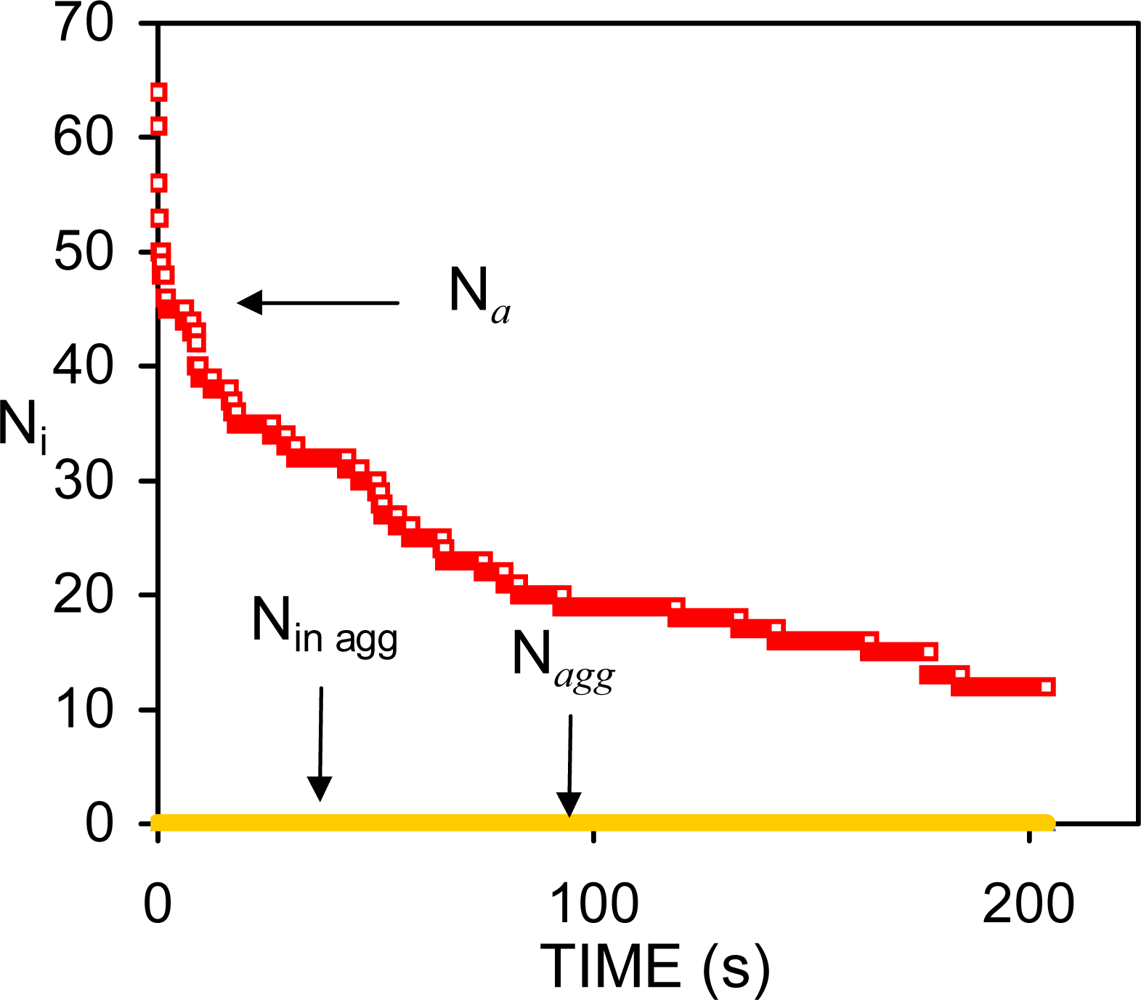
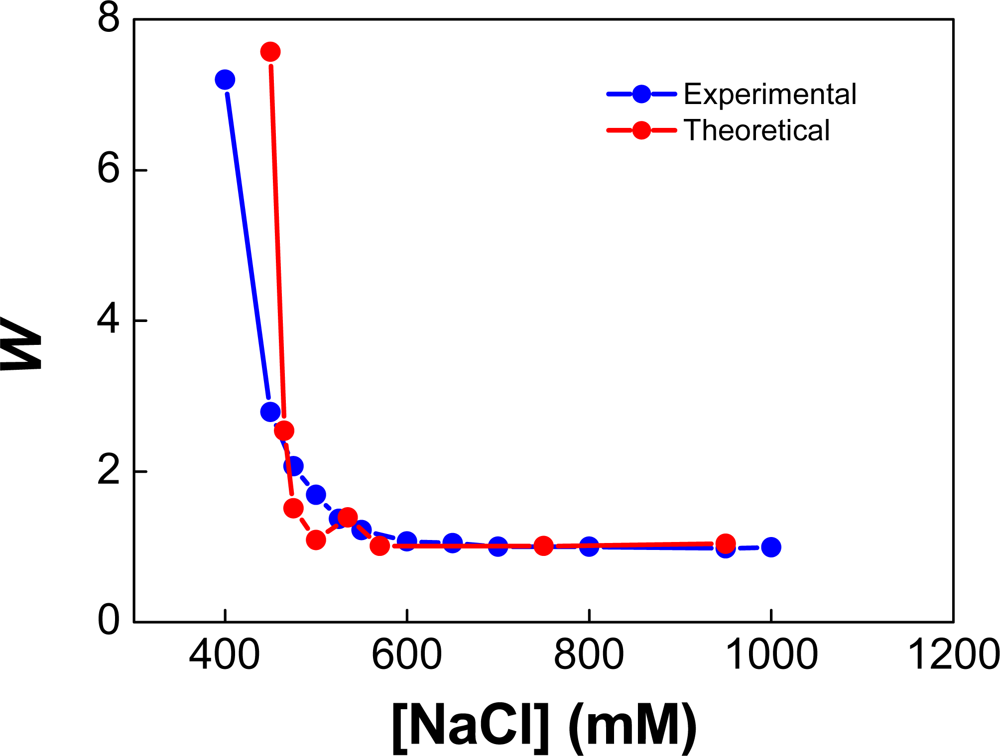
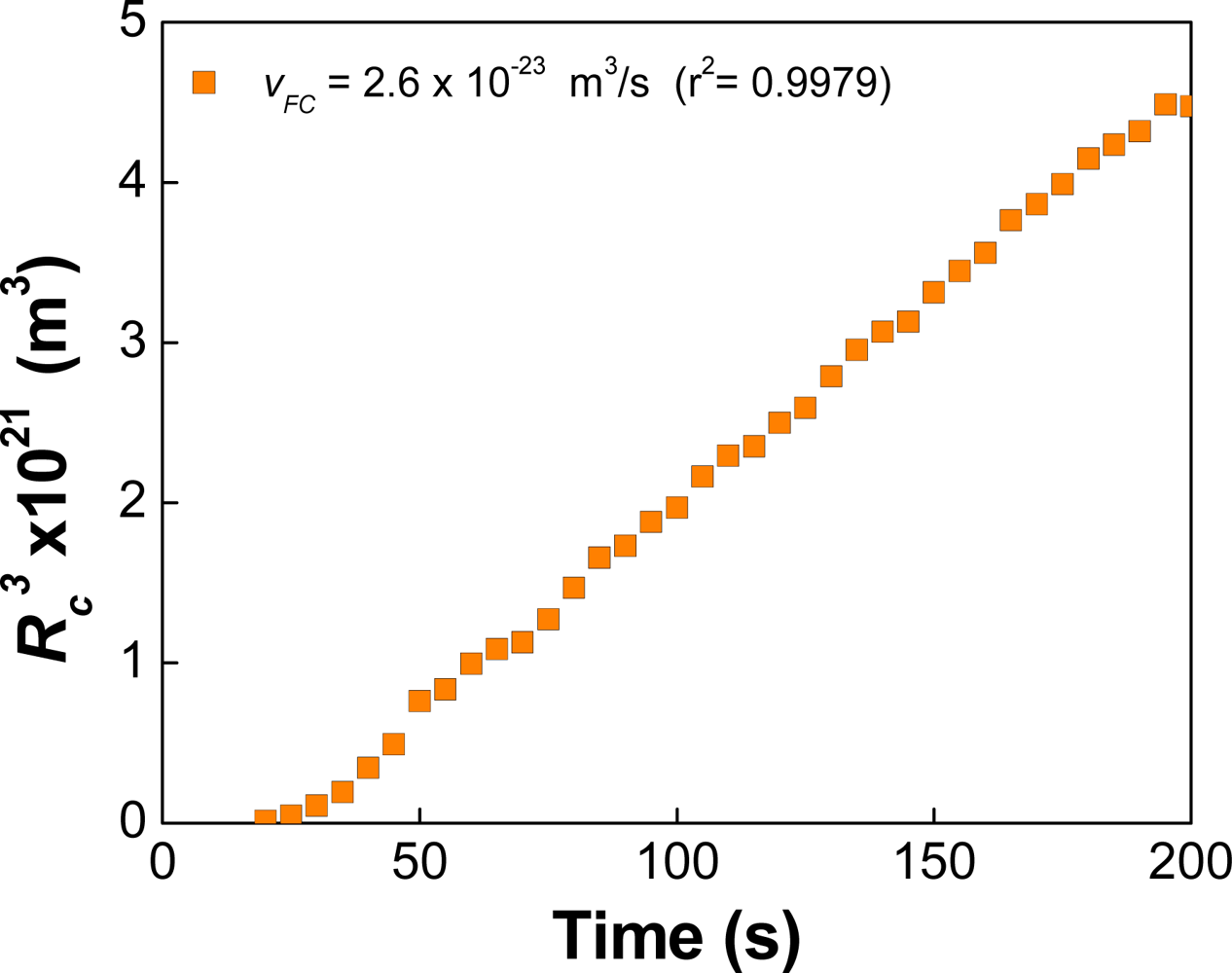
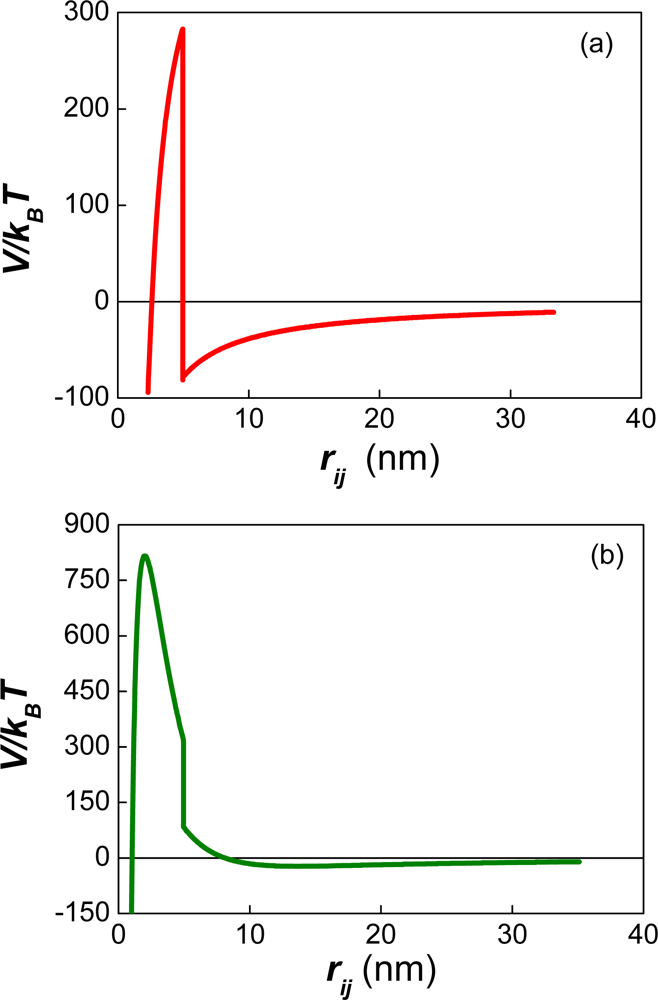
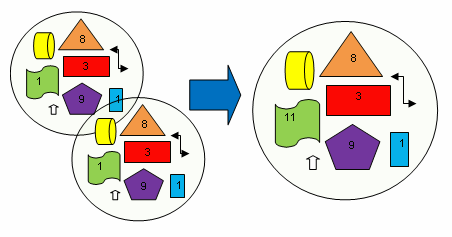
| Dapp (m2/s) | CT (M) | tmsa (s) |
|---|---|---|
| 1 × 10−9 | 5 × 10−4 | 0.03 |
| 1 × 10−9 | 1 × 10−4 | 0.87 |
| 1 × 10−10 | 5 × 10−4 | 0.35 |
| 1 × 10−10 | 1 × 10−4 | 8.67 |
| 1 × 10−12 | 5 × 10−4 | 34.7 |
| 1 × 10−12 | 1 × 10−4 | 867 |
| System | kf (m3/s) | VF (m3/s) | 3 p |
|---|---|---|---|
| Dodecane/Water | 7.37 × 10−18 | 3.11 × 10−22 | 0.78 |
| Octane/Water | 6.62 × 10−18 | 2.58 × 10−22 | 0.72 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Urbina-Villalba, G. An Algorithm for Emulsion Stability Simulations: Account of Flocculation, Coalescence, Surfactant Adsorption and the Process of Ostwald Ripening. Int. J. Mol. Sci. 2009, 10, 761-804. https://doi.org/10.3390/ijms10030761
Urbina-Villalba G. An Algorithm for Emulsion Stability Simulations: Account of Flocculation, Coalescence, Surfactant Adsorption and the Process of Ostwald Ripening. International Journal of Molecular Sciences. 2009; 10(3):761-804. https://doi.org/10.3390/ijms10030761
Chicago/Turabian StyleUrbina-Villalba, German. 2009. "An Algorithm for Emulsion Stability Simulations: Account of Flocculation, Coalescence, Surfactant Adsorption and the Process of Ostwald Ripening" International Journal of Molecular Sciences 10, no. 3: 761-804. https://doi.org/10.3390/ijms10030761