Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life
Abstract
:1. Introduction
2. Methods
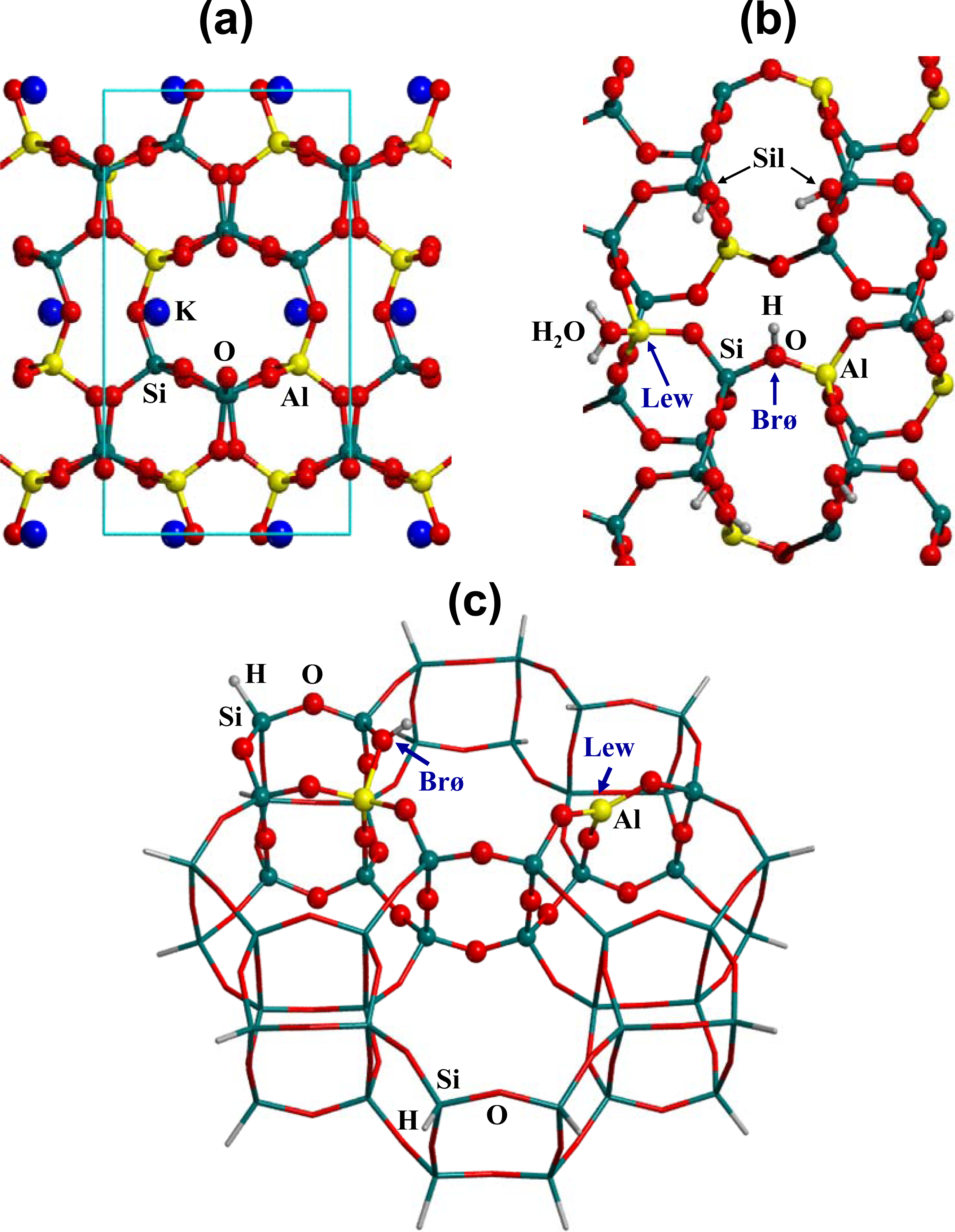
2.1. Surface Model
2.2. Computational Details
3. Results and Discussion
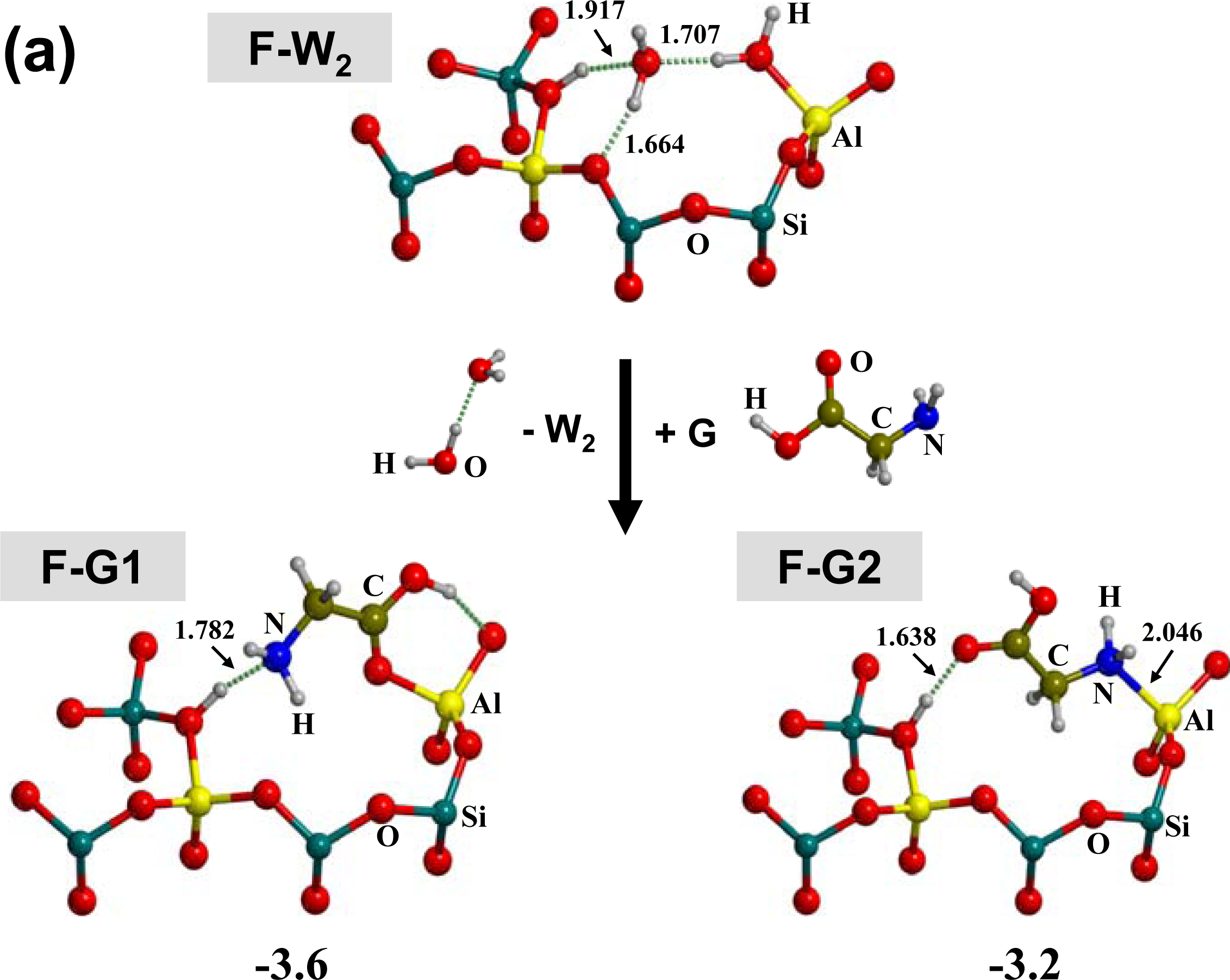
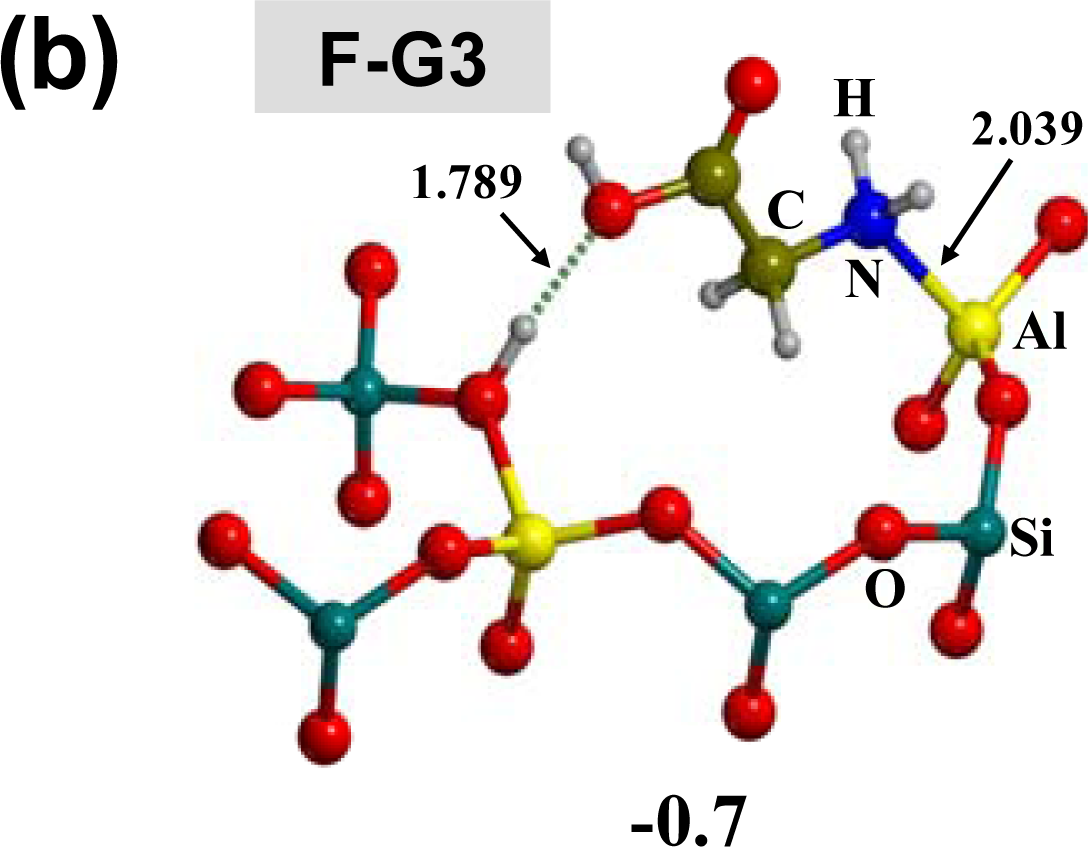
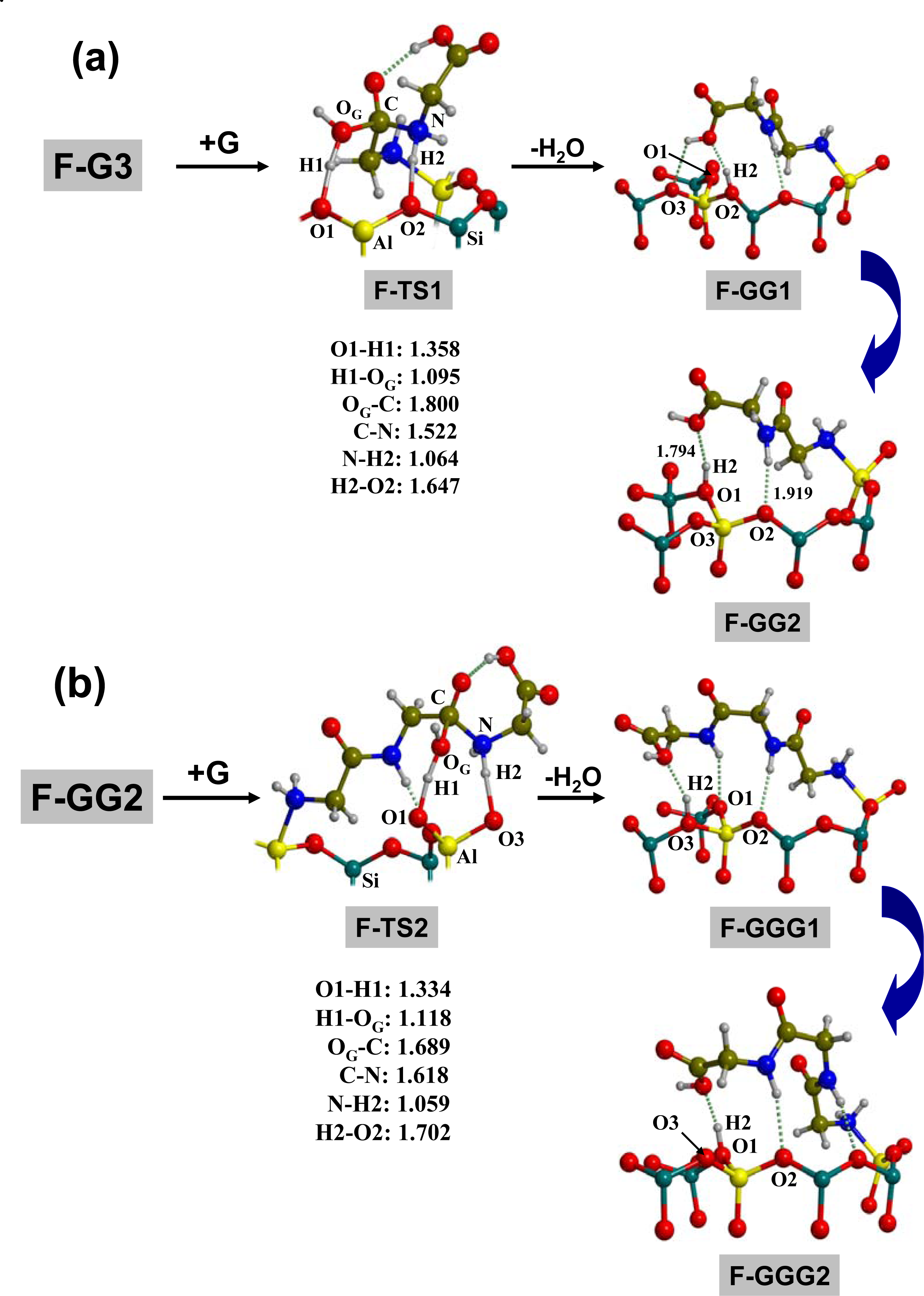
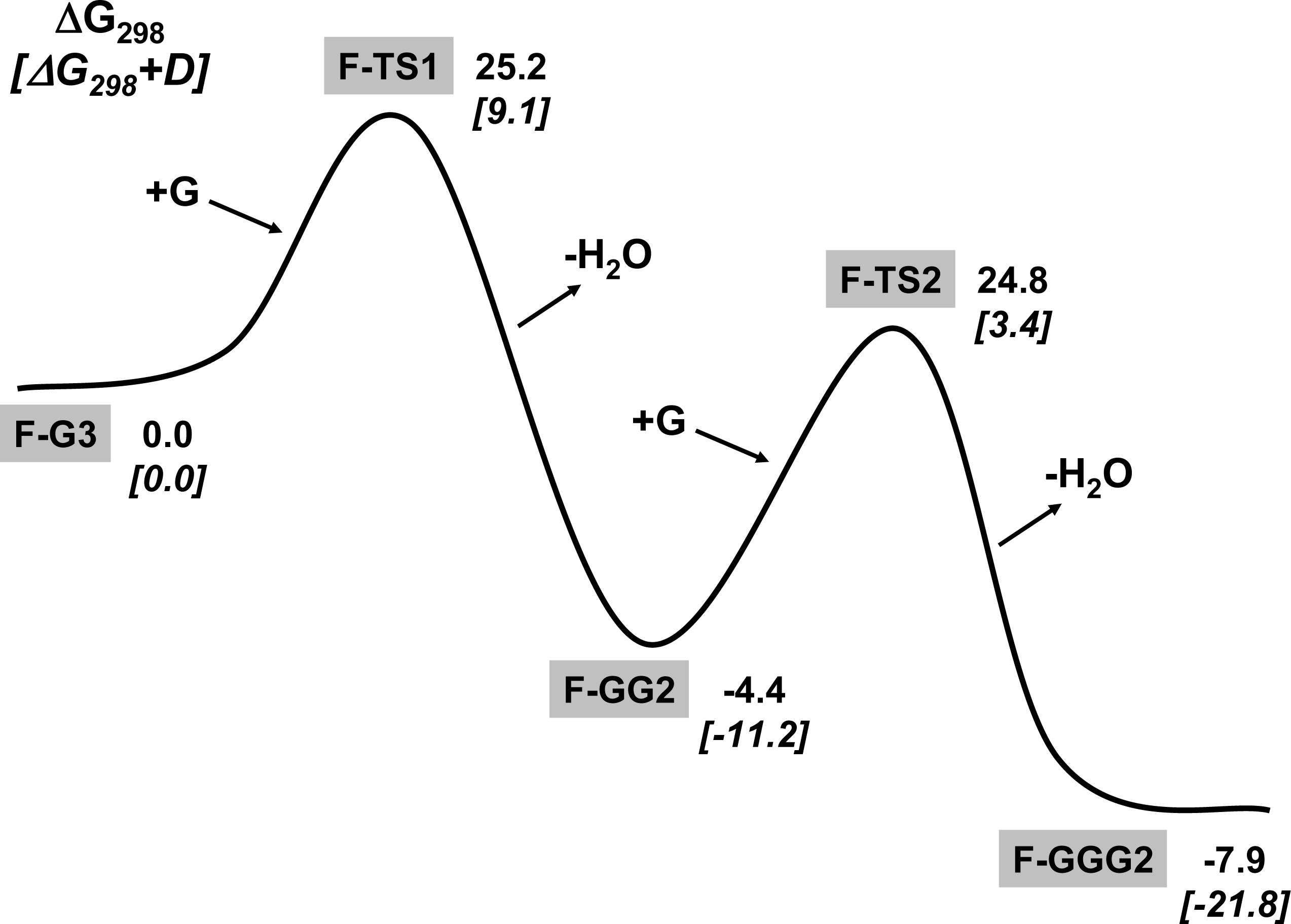
3.1. Amino acid polymerization
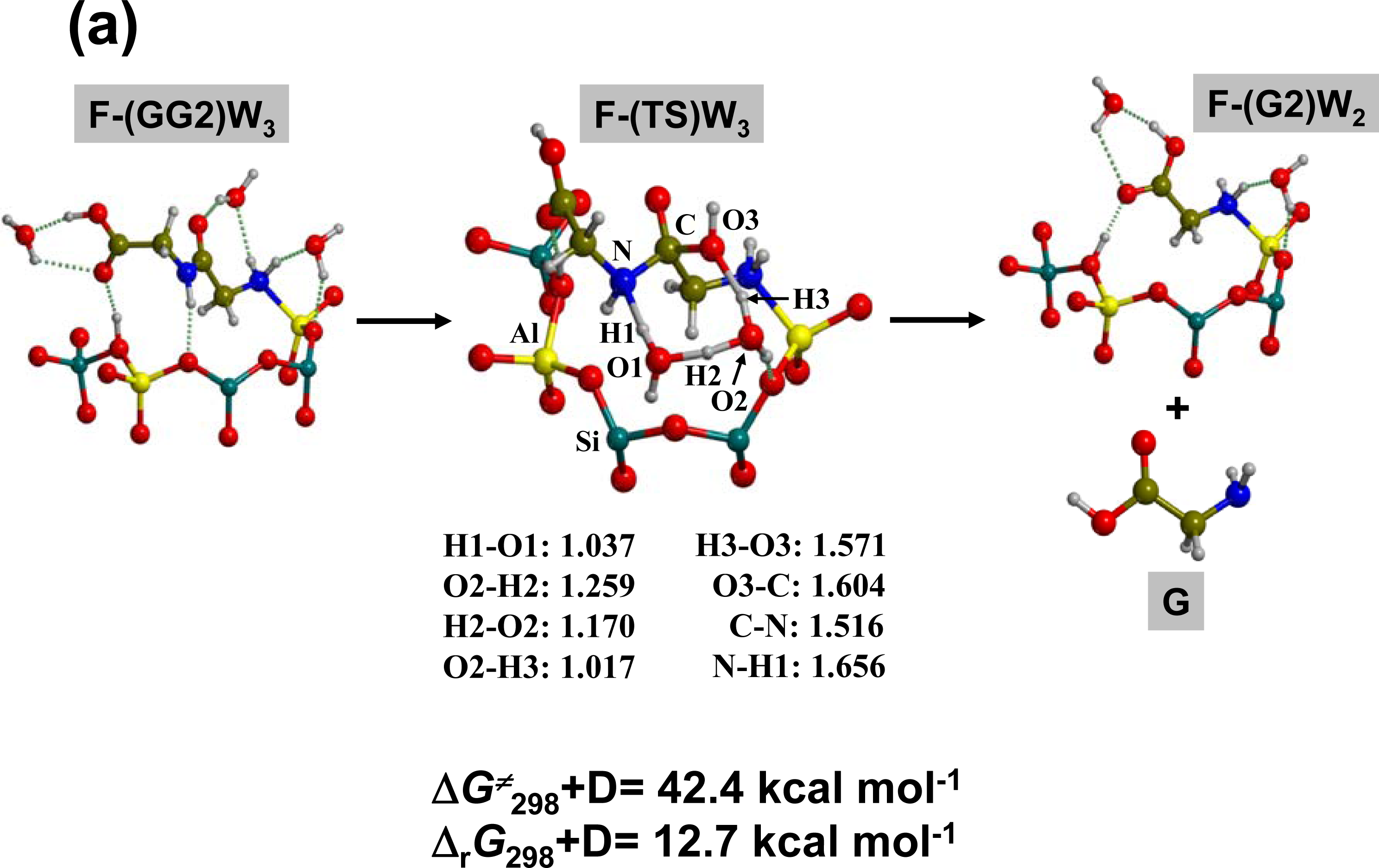
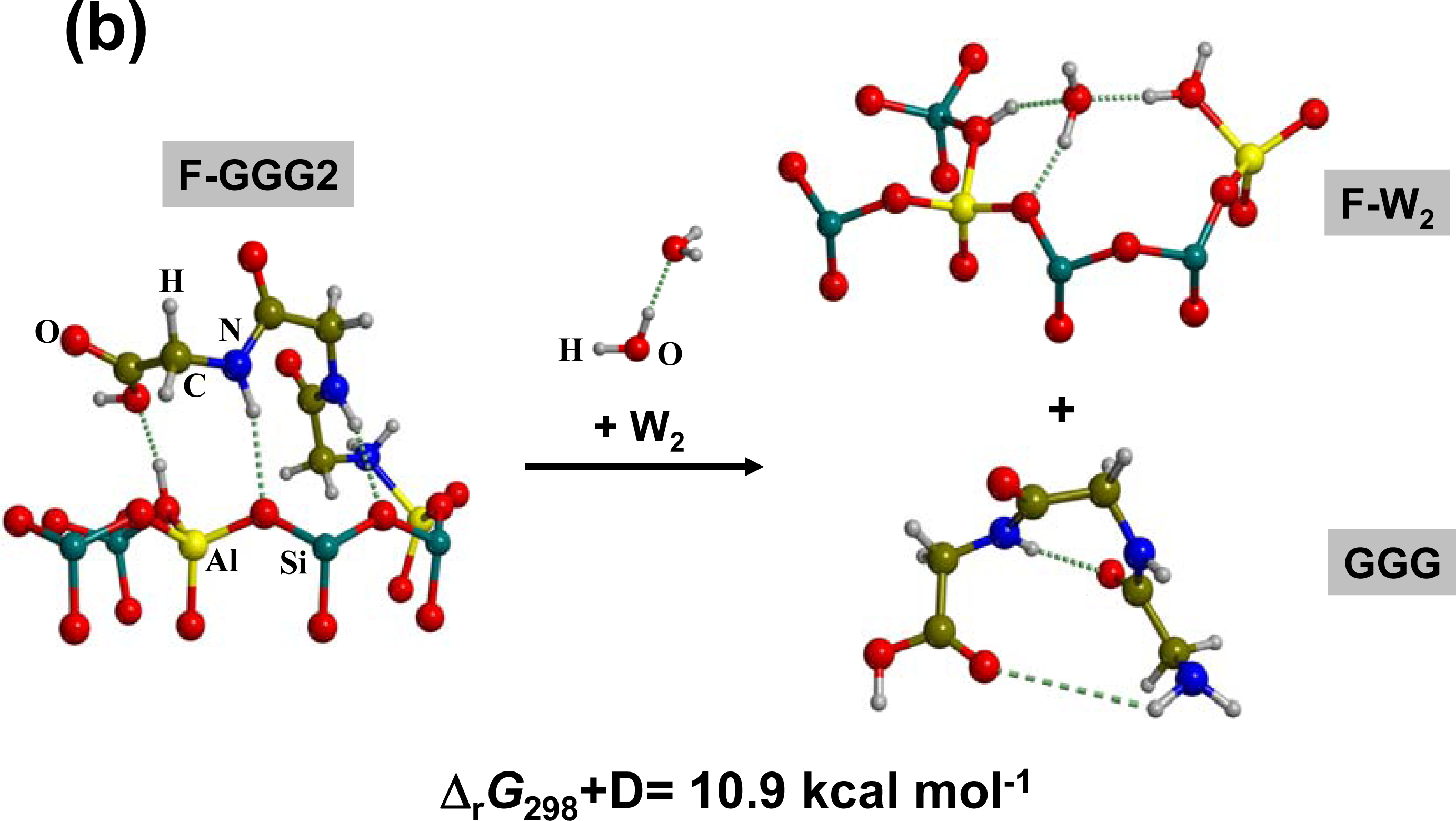
3.2. Peptide hydrolysis
4. Concluding Remarks
Acknowledgments
References and Notes
- Miller, SL. A production of amino acids under possible primitive earth conditions. Science 1953, 117, 528–529. [Google Scholar]
- Hazen, RM. Genesis: The Scientific Quest for Life’s Origins, 1st Ed. ed; Joseph Henry Press: Washington, DC, 2005. [Google Scholar]
- Miller, SL. Production of some organic compounds under possible primitive earth conditions. J. Am. Chem. Soc 1955, 77, 2351–2666. [Google Scholar]
- Miller, SL; Urey, HC. Organic compound synthesis on the primitive earth. Science 1959, 130, 245–251. [Google Scholar]
- Oró, J. Mechanism of synthesis of adenine from hydrogen cyanide under possible primitive earth conditions. Nature 1961, 191, 1193–1194. [Google Scholar]
- Sutherland, JD; Whitfield, JN. Prebiotic chemistry: A bioorganic perspective. Tetrahedron 1997, 53, 11493–11527. [Google Scholar]
- Schlesinger, G; Miller, SL. Prebiotic synthesis in atmospheres containing CH4, CO, and CO2. J. Mol. Evol 1983, 19, 376–382. [Google Scholar]
- Miyakawa, S; Yamanashi, H; Kobayashi, K; Cleaves, HJ; Miller, SL. Prebiotic synthesis from CO atmospheres: Implications for the origins of life. Proc. Natl. Acad. Sci. USA 2002, 99, 14628–14631. [Google Scholar]
- Cleaves, HJ; Chalmers, JH; Lazcano, A; Miller, SL; Bada, JL. A reassessment of prebiotic organic synthesis in neutral planetary atmospheres. Orig. Life Evol. Biosph 2008, 38, 105–115. [Google Scholar]
- Bernstein, MP; Dworkin, JP; Sandford, SA; Cooper, GW; Allamandola, LJ. Racemic amino acids from the ultraviolet photolysis of interstellar ice analogues. Nature 2002, 416, 401–403. [Google Scholar]
- Muñoz-Caro, GM; Meierhenrich, UJ; Schutte, WA; Barbier, B; Segovia, AA; Rosenbauer, H; Thiemann, WH-P; Brack, A; Greenberg, JM. Amino acids from ultraviolet irradiation of interstellar ice analogues. Nature 2002, 416, 403–406. [Google Scholar]
- Nuevo, M; Auger, G; Blanot, D; d’Hendecourt, L. A detailed study of the amino acids produced from the vacuum UV irradiation of interstellar ice analogs. Orig. Life Evol. Biosph 2008, 38, 37–56. [Google Scholar]
- Kuan, Y-J; Charnley, SB; Huang, H-C; Tseng, W-L; Kisiel, Z. Interstellar glycine. Astrophys. J 2004, 593, 848–867. [Google Scholar]
- Snyder, LE; Lovas, FJ; Hollis, JM; Friedel, DN; Jewell, PR; Remijan, A; Ilyushin, VV; Alekseev, EA; Dyubko, SF. A rigorous attempt to verify interstellar glycine. Astrophys. J 2005, 619, 914–930. [Google Scholar]
- Pizzarello, S. The chemistry of life’s origin: A carbonaceous meteorite perspective. Acc. Chem. Res 2006, 39, 231–237. [Google Scholar]
- Ehrenfreund, P; Sephton, MA. Carbon molecules in space: From astrochemistry to astrobiology. Faraday Discuss 2006, 133, 277–288. [Google Scholar]
- Wächtershäuser, G. Before enzymes and templates: theory of surface metabolism. Microbiol. Rev 1988, 52, 452–484. [Google Scholar]
- Huber, C; Wächtershäuser, G. Activated acetic acid by carbon fixation on (Fe,Ni)S under primordial conditions. Science 1997, 276, 245–247. [Google Scholar]
- Cody, GD; Boctor, NZ; Filley, TR; Hazen, RM; Scott, JH; Sharma, A; Yoder, HS, Jr. Primordial carbonylated iron-sulfur compounds and the synthesis of pyruvate. Science 2000, 289, 5483. [Google Scholar]
- Rimola, A; Sodupe, M; Ugliengo, P. Aluminosilicate surfaces as promoters for peptide bond formation: An assessment of Bernal’s hypothesis by ab Initio methods. J. Am. Chem. Soc 2007, 129, 8333–8344. [Google Scholar]
- Brack, A. From interstellar amino acids to prebiotic catalytic peptides: A review. Chem. Biodiv 2007, 4, 665–679. [Google Scholar]
- Bernal, JD. The physical basis of life. Proc. Phys. Soc. B 1949, 62, 597–618. [Google Scholar]
- Lambert, J-F. Adsorption and Polymerization of Amino Acids on Mineral Surfaces: A Review. Orig. Life Evol. Biosph 2008, 38, 211–242. [Google Scholar]
- Ferris, JP; Ertem, G. Oligomerization of ribonucleotides on montmorillonite: reaction of the 5′-phosphorimidazolide of adenosine. Science 1992, 257, 1387–1389. [Google Scholar]
- Ferris, JP; Hill, AR, Jr; Liu, R; Orgel, LE. Synthesis of long prebiotic oligomers on mineral surfaces. Nature 1996, 381, 59–61. [Google Scholar]
- Ferris, JP. Montmorillonite-catalysed formation of RNA oligomers: The possible role of catalysis in the origins of life. Phil. Trans. R. Soc. B 2006, 361, 1777–1786. [Google Scholar]
- Huber, C; Wächtershäuser, G. Peptides by activation of amino acids with CO on (Ni,Fe)S surfaces: Implications for the origin of life. Science 1998, 281, 670–672. [Google Scholar]
- Huber, C; Eisenreich, W; Hecht, S; Wächtershäuser, G. A possible primordial peptide cycle. Science 2003, 301, 938–940. [Google Scholar]
- Boehme, C; Marx, D. Glycine on a Wet Pyrite Surface at extreme conditions. J. Am. Chem. Soc 2003, 125, 13362–13363. [Google Scholar]
- Pollet, R; Boehme, C; Marx, D. Ab initio simulations of desorption and reactivity of glycine at water-pyrite interface at “iron-sulfur world” prebiotic conditions. Orig. Life Evol. Biosph 2006, 36, 363–379. [Google Scholar]
- Nair, NN; Schreiner, E; Marx, D. Glycine at the pyrite-water interface: The role of surface defects. J. Am. Chem. Soc 2006, 128, 13815–13826. [Google Scholar]
- Schreiner, E; Nair, NN; Marx, D. Influence of extreme thermodynamic conditions and pyrite surfaces on peptide synthesis in aqueous media. J. Am. Chem. Soc 2008, 130, 2768–2770. [Google Scholar]
- Nair, NN; Schreiner, E; Marx, D. Peptide synthesis in aqueous environments: The role of extreme conditions on amino acid activation. J. Am. Chem. Soc 2008, 130, 14148–14160. [Google Scholar]
- Rimola, A; Tosoni, S; Sodupe, M; Ugliengo, P. Does silica surface catalyse peptide bond formation? New insights from first-principles calculations. ChemPhysChem 2006, 7, 157–163. [Google Scholar]
- Rimola, A; Tosoni, S; Sodupe, M; Ugliengo, P. Peptide bond formation activated by the interplay of Lewis and Bronsted catalysts. Chem. Phys. Lett 2005, 408, 295–301. [Google Scholar]
- Smith, JV. Biochemical evolution. I. Polymerization on internal, organophilic silica surfaces of dealuminated zeolites and feldspars. Proc. Natl. Acad. Sci. USA 1998, 95, 3370–3375. [Google Scholar]
- Maseras, F; Morokuma, K. IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J. Comput. Chem 1995, 16, 1170. [Google Scholar]
- Becke, AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648. [Google Scholar]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Slavetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar]
- Dewar, MJS; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc 1977, 99, 4899–4907. [Google Scholar]
- Roggero, I; Civalleri, B; Ugliengo, P. Modeling physisorption with the ONIOM method: The case of NH3 at the isolated hydroxyl group of the silica surface. Chem. Phys. Lett 2001, 341, 625–632. [Google Scholar]
- Solans-Monfort, X; Sodupe, M; Branchadell, V; Sauer, J; Orlando, R; Ugliengo, P. Adsorption of NH3 and H2O in Acidic Chabazite. Comparison of ONIOM Approach with Periodic Calculations. J. Phys. Chem. B 2005, 109, 3539–3545. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR; Montgomery, JJA; Vreven, T; Kudin, KN; Burant, JC; Millam, JM; Iyengar, SS; Tomasi, J; Barone, V; Mennucci, B; Cossi, M; Scalmani, G; Rega, N; Petersson, GA; Nakatsuji, H; Hada, M; Ehara, M; Toyota, K; Fukuda, R; Hasegawa, J; Ishida, M; Nakajima, T; Honda, Y; Kitao, O; Nakai, H; Klene, M; Li, X; Knox, JE; Hratchian, HP; Cross, JB; Bakken, V; Adamo, C; Jaramillo, J; Gomperts, R; Stratmann, RE; Yazyev, O; Austin, AJ; Cammi, R; Pomelli, C; Ochterski, JW; Ayala, PY; Morokuma, K; Voth, GA; Salvador, P; Dannenberg, JJ; Zakrzewski, VG; Dapprich, S; Daniels, AD; Strain, MC; Farkas, O; Malick, DK; Rabuck, AD; Raghavachari, K; Foresman, JB; Ortiz, JV; Cui, Q; Baboul, AG; Clifford, S; Cioslowski, J; Stefanov, BB; Liu, G; Liashenko, A; Piskorz, P; Komaromi, I; Martin, RL; Fox, DJ; Keith, T; Al-Laham, MA; Peng, CY; Nanayakkara, A; Challacombe, M; Gill, PMW; Johnson, B; Chen, W; Wong, MW; Gonzalez, C; Pople, JA. Gaussian 03, Revision C.02; Gaussian, Inc: Wallingford, CT, 2004. [Google Scholar]
- McQuarrie, D. Statistical Mechanics; Harper and Row: New York, NY, 1986. [Google Scholar]
- Grimme, S. Semiempirical GGA-Type density functional constructed with a long-range dispersion correction. J. Comp. Chem 2006, 27, 1787–1799. [Google Scholar]
- Ugliengo, P. 2005.
- Sarv, P; Tuherm, T; Lippmaa, E; Keskinen, K; Root, A. Mobility of the acidic proton in broensted sites of H-Y, H-Mordenite, and H-ZSM-5 zeolites, studied by high-temperature 1H MAS NMR. J. Phys. Chem 1995, 99, 13763–13768. [Google Scholar]
- Baba, T; Komatsu, N; Ono, Y. Mobility of the acidic protons in H ZSM-5 as studied by variable temperature 1H MAS NMR. J. Phys. Chem. B 1998, 102, 804–808. [Google Scholar]
- Sierka, M; Sauer, J. Proton mobility in Chabazite, Faujasite, and ZSM-5 Zeolite catalysts. Comparison based on ab initio calculations. J. Phys. Chem. B 2001, 105, 1603–1613. [Google Scholar]
- Orgel, LE. Polymerization on the rocks: Theoretical introduction. Orig. Life Evol. Biosph 1998, 28, 227–234. [Google Scholar]
- Orgel, LE. Prebiotic chemistry and the origin of the RNA world. Critical Rev. Biochem. Mol. Biol 2004, 39, 99–123. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rimola, A.; Ugliengo, P.; Sodupe, M. Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life. Int. J. Mol. Sci. 2009, 10, 746-760. https://doi.org/10.3390/ijms10030746
Rimola A, Ugliengo P, Sodupe M. Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life. International Journal of Molecular Sciences. 2009; 10(3):746-760. https://doi.org/10.3390/ijms10030746
Chicago/Turabian StyleRimola, Albert, Piero Ugliengo, and Mariona Sodupe. 2009. "Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life" International Journal of Molecular Sciences 10, no. 3: 746-760. https://doi.org/10.3390/ijms10030746





