Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding
Abstract
:1. Introduction
2. Translational-Entropy Gain of Water upon Protein Folding
2.1. Statistical-mechanical calculation
2.2. Morphometric approach
2.3. Isochoric and isobaric processes
2.4. Comparison between experimental and theoretical results
2.5. On the previously reported thermodynamic data for protein folding
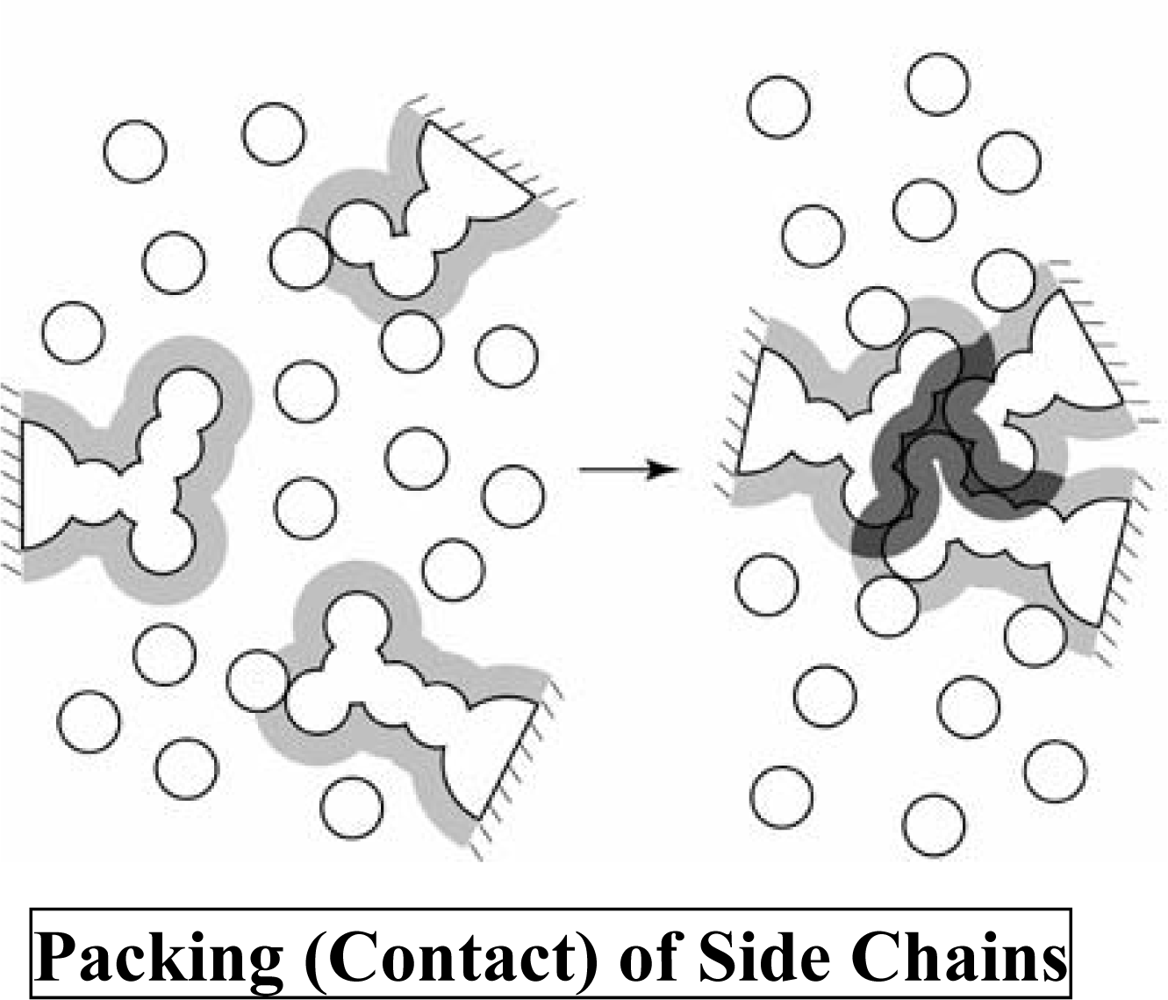
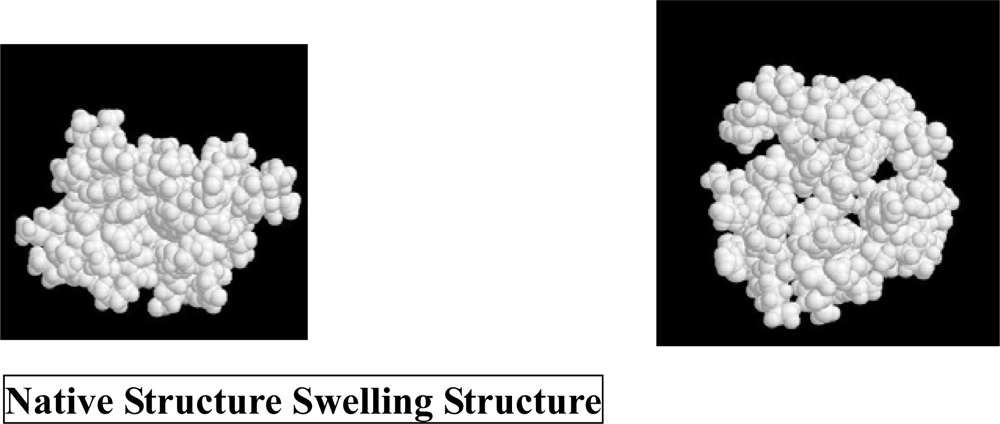
3. Molecular Mechanism of Denaturation of Proteins
3.1. Pressure denaturation
3.2. Cold denaturation
3.3. Heat denaturation
4. Novel Method for Predicting the Native Structure
4.1. Free-energy function based on all-atom model for a protein
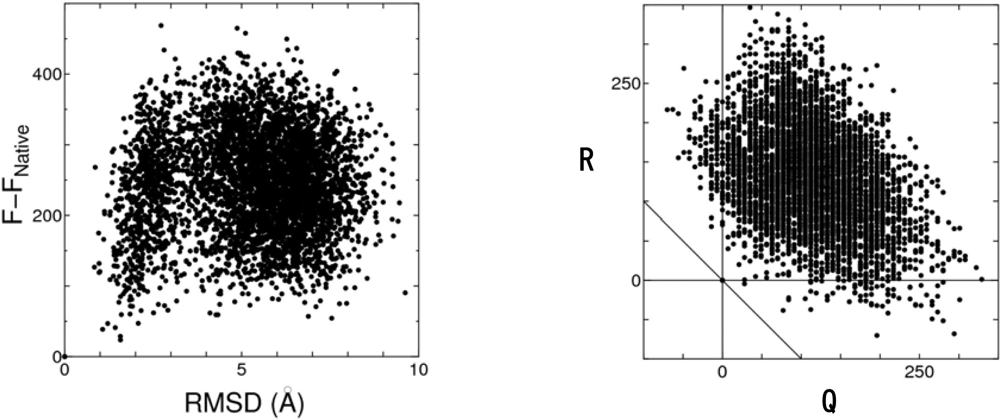
4.2. Discrimination of the native fold from misfolded decoys
4.3. Toward development of a reliable tool for predicting the native structure of proteins
5. Conclusions
Acknowledgments
References and Notes
- Harano, Y; Kinoshita, M. Large gain in translational entropy of water is a major driving force in protein folding. Chem. Phys. Lett 2004, 399, 342–348. [Google Scholar]
- Harano, Y; Kinoshita, M. Translational-entropy gain of solvent upon protein folding. Biophys. J 2005, 89, 2701–2710. [Google Scholar]
- Kinoshita, M; Oguni, T. Depletion effects on the lock and key steric interactions between macromolecules. Chem. Phys. Lett 2002, 351, 79–84. [Google Scholar]
- Kinoshita, M. Spatial distribution of a depletion potential between a big solute of arbitrary geometry and a big sphere immersed in small spheres. J. Chem. Phys 2002, 116, 3493–3501. [Google Scholar] [Green Version]
- Kinoshita, M. Roles of entropic excluded-volume effects in colloidal and biological systems: Analyses using the three-dimensional integral equation theory. Chem. Eng. Sci 2006, 61, 2150–2160. [Google Scholar]
- Kinoshita, M. Interaction between big bodies with high asphericity immersed in small spheres. Chem. Phys. Lett 2004, 387, 47–53. [Google Scholar]
- Kinoshita, M. Ordered aggregation of big bodies with high asphericity in small spheres: A possible mechanism of the amyloid fibril formation. Chem. Phys. Lett 2004, 387, 54–60. [Google Scholar]
- Kauzmann, W. Some factors in the interpretation of protein denaturation. Adv. Protein Chem 1959, 14, 1–63. [Google Scholar]
- Dill, KA. Dominant forces in protein folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar]
- Yoshidome, T; Kinoshita, M; Hirota, S; Baden, N; Terazima, M. Thermodynamics of apoplastocyanin folding: comparison between experimental and theoretical results. J Chem Phys 2008, 128 225104. (1–9). [Google Scholar]
- Harano, Y; Kinoshita, M. On the physics of pressure denaturation of proteins. J. Phys. Condens. Matt 2006, 18, L107–L113. [Google Scholar]
- Harano, Y; Kinoshita, M. Crucial importance of translational entropy of water in pressure denaturation of proteins. J Chem Phys 2006, 125 024910. (1–10). [Google Scholar]
- Harano, Y; Yoshidome, T; Kinoshita, M. Molecular mechanism of pressure denaturation of proteins. J Chem Phys 2008, 129 145103. (1–9). [Google Scholar]
- Yoshidome, T; Harano, Y; Kinoshita, M. Pressure effects on structures formed by the entropically driven self-assembly: Illustration for denaturation of proteins. Phys Rev E 2009, 79 011912. (1–10). [Google Scholar]
- Yoshidome, T; Kinoshita, M. Hydrophobicity at low temperatures and cold denaturation of a protein. Phys Rev E. in press.
- Harano, Y; Roth, R; Kinoshita, M. On the energetics of protein folding in aqueous solution. Chem. Phys. Lett 2006, 432, 275–280. [Google Scholar]
- Harano, Y; Roth, R; Sugita, Y; Ikeguchi, M; Kinoshita, M. Physical basis for characterizing native structures of proteins. Chem. Phys. Lett 2007, 437, 112–116. [Google Scholar]
- Asakura, S; Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys 1954, 22, 1255–1256. [Google Scholar]
- Asakura, S; Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polymer Sci 1958, 33, 183–192. [Google Scholar]
- Roth, R; Harano, Y; Kinoshita, M. Morphometric approach to the solvation free energy of complex molecules. Phys Rev Lett 2006, 97 078101. (1–4). [Google Scholar]
- Kusalik, PG; Patey, GN. On the molecular theory of aqueous electrolyte solutions. I. The solution of the RHNC approximation for models at finite concentration. J. Chem. Phys 1988, 88, 7715–7738. [Google Scholar]
- Kusalik, PG; Patey, GN. The solution of the reference hypernetted-chain approximation for water-like models. Mol. Phys 1988, 65, 1105–1119. [Google Scholar]
- Kinoshita, M; Harada, M. Numerical solution of the RHNC theory for water-like fluids near a macroparticle and a planar wall. Mol. Phys 1994, 81, 1473–1488. [Google Scholar]
- Kinoshita, M; Bérard, DR. Analysis of the bulk and surface-induced structure of electrolyte solutions using integral equation theories. J. Comput. Phys 1996, 124, 230–241. [Google Scholar]
- Cann, NM; Patey, GN. An investigation of the influence of solute size and insertion conditions on solvation thermodynamics. J. Chem. Phys 1997, 106, 8165–8195. [Google Scholar]
- Kinoshita, M. Molecular origin of the hydrophobic effect: Analysis using the angle-dependent integral equation theory. J Chem Phys 2008, 128 024507. (1–14). [Google Scholar]
- Kinoshita, M; Suzuki, M. A statistical-mechanical analysis on the hyper-mobile water around a large solute with high surface charge density. J Chem Phys 2009, 130 014707. (1–11). [Google Scholar]
- Kinoshita, M; Harano, Y; Akiyama, R. Changes in thermodynamic quantities upon contact of two solutes in solvent under isochoric and isobaric conditions. J Chem Phys 2006, 125 244504. (1–7). [Google Scholar]
- Imai, T; Harano, Y; Kinoshita, M; Kovalenko, A; Hirata, F. A theoretical analysis on hydration thermodynamics of proteins. J Chem Phys 2006, 125 024911. (1–7). [Google Scholar]
- Baden, N; Hirota, S; Takabe, T; Funasaki, N; Terazima, M. Thermodynamical properties of reaction intermediates during apoplastocyanin folding in time-domain. J Chem Phys 2007, 127 175103. (1–12). [Google Scholar]
- Liu, L; Yang, C; Guo, Q-X. A study on the enthalpy-entropy compensation in protein unfolding. Biophys. Chem 2000, 84, 239–251. [Google Scholar]
- Kardos, J; Yamamoto, K; Hasegawa, K; Naiki, H; Goto, Y. Direct measurement of the thermodynamic parameters of amyloid formation by isothermal titration calorimetry. J. Biol. Chem 2004, 279, 55308–55314. [Google Scholar]
- Bonafe, CFS; Vital, CMR; Telles, RCB; Gonçalves, MC; Matsuura, MSA; Pessine, FBT; Freitas, DRC; Vega, J. Tabacco mosaic virus disassembly by high hydrostatic pressure in combination with urea and low temperature. Biochemistry 1998, 37, 11097–11105. [Google Scholar]
- Kasai, M; Asakura, S; Oosawa, F. G-F equilibrium in actin solutions under various conditions. Biochim. Biophys. Acta 1962, 57, 13–21. [Google Scholar]
- Fitter, J. A measure of conformational entropy change during thermal protein unfolding using neutron spectroscopy. Biophys. J 2003, 84, 3924–3930. [Google Scholar]
- Amano, K; Yoshidome, T; Harano, Y; Oda, K; Kinoshita, M. Theoretical analysis on thermal stability of a protein focused on the water entropy. Chem. Phys. Lett. submitted.
- Sneddon, SF; Tobias, DJ; Brooks, CL, III. Thermodynamics of amide hydrogen bond formation in polar and apolar solvents. J. Mol. Biol 1989, 209, 817–820. [Google Scholar]
- Yoshidome, T; Oda, K; Harano, Y; Roth, R; Sugita, Y; Ikeguchi, M; Kinoshita, M. Free-energy function based on all-atom model for proteins. J. Mol. Biol. submitted.
- Yoda, T; Sugita, Y; Okamoto, Y. Comparisons of force fields for proteins by generalized-ensemble simulations. Chem. Phys. Lett 2004, 386, 460–467. [Google Scholar]
- Lee, B. The physical origin of the low solubility of nonpolar solutes in water. Biopolymers 1985, 24, 813–823. [Google Scholar]
- Soda, K. Solvent exclusion effect predicted by the scaled particle theory as an important factor of the hydrophobic effect. J. Phys. Soc. Jpn 1993, 62, 1782–1793. [Google Scholar]
- Madan, B; Lee, B. Role of hydrogen bonds in hydrophobicity: the free energy of cavity formation in water models with and without the hydrogen bonds. Biophys. Chem 1994, 51, 279–289. [Google Scholar]
- Graziano, G; Lee, B. Hydration entropy change from the hard sphere model. Biophys. Chem 2002, 101, 173–185. [Google Scholar]
- Graziano, G. Comment on “Reevaluation in interpretation of hydrophobicity by scaled particle theory”. J. Phys. Chem. B 2002, 106, 7713–7716. [Google Scholar]
- Kinoshita, M. Roles of translational motion of water molecules in sustaining life. Front. Biosci 2009, 14, 3419–3454. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kinoshita, M. Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding. Int. J. Mol. Sci. 2009, 10, 1064-1080. https://doi.org/10.3390/ijms10031064
Kinoshita M. Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding. International Journal of Molecular Sciences. 2009; 10(3):1064-1080. https://doi.org/10.3390/ijms10031064
Chicago/Turabian StyleKinoshita, Masahiro. 2009. "Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding" International Journal of Molecular Sciences 10, no. 3: 1064-1080. https://doi.org/10.3390/ijms10031064



