1. Introduction
Diverse studies have reported spatio-temporal organization properties in natural languages. Two representative findings of universal features of natural language are the Zipf and Heaps laws, which are based on word frequency and number of different words, respectively [
1,
2,
3,
4]. From a more basic perspective, human language can also be considered as a sequence of symbols which contains information encoded in the patterns (words) needed to communicate. For instance, the frequency rate of appearance of the symbols is different for every language, and so are the declension and verbal conjugation rules. There are also restrictions in the order of appearance of bigrams, trigrams and, in general,
n-grams; for example, in English and Spanish the letter “q” is always followed by “u”. The way these restrictions and other factors modulate the structure and randomness of the language can be potentially evaluated by means of concepts like entropy, as proposed by Shannon [
5,
6]. The use of entropy-related algorithms to estimate orderliness in natural language have revealed that language is not regular nor random, but the direct quantification of the presence of randomness is not an easy task. Diverse studies have used the concept of entropy by means of a
n-gram analysis [
7], a binary simplification [
8], nonparametric entropy estimation [
9], mutual information of letters [
10], information-based energy [
11], complexity quantification [
12] and entropy-word approach [
13]. However, entropy-information measures based on regularity of pattern statistics has not been widely employed to evaluate the “complexity” of natural language. A straightforward way to quantify the propinquity of two words is to count the number of letters that they have in common; the words coming from the same root, diminutives, augmentatives or the “functional shift” of certain words are good examples of these similarities. In the context of dynamical systems, there are well known methods to measure the repetition pattern in a time series: the approximate entropy (
) and its derivatives [
14,
15]. The
quantifies the regularity in a time series, a lower value of
indicates a more regular behavior whereas a high value is assigned to more irregular sequences. This method has been successfully applied to analyze time series from several sources [
16,
17,
18,
19,
20]. Here we adopt a similar approach based on the
algorithm in order to evaluate the levels of complexity in four language families (Romance, Germanic, Slavic and Uralic). Our goal is to determine the dominance of regularities in written texts, which are considered as finite time series. Our method was applied to several texts from different languages. The results reveal that, for texts belonging to the same family, it is observed that the
decreases as the length of the word pattern increases in similar fashion. Moreover, we also extend our study to evaluate the multiscale behavior of entropy for the assessment of regularities based on different scales as it was suggested by Costa et al. [
21]. Additionally, we also apply our methodology to two synthetic sequences, which are the randomized versions of the original text and a text written in Esperanto. We found significant differences between real and synthetic texts, observing a higher complexity for the real sequences compared to the randomized ones through different scales. The paper is organized as follows: First, we present the methodology used throughout the article, including the modified method to calculate the
for the cases of sequences of symbols. Next, the main results of the study are described; and finally, we provide some final remarks.
2. Approximate Entropy of a Text
Within the context of information theory, the entropy of a sequence of symbols (from an alphabet with
L elements) is given in terms of the so-called Shannon entropy
, with
the probability of the symbol
j. The Shannon entropy measures the average uncertainty of a discrete variable and represents the average information content [
6]. For sequences composed of blocks with
n symbols, the entropy
measures the uncertainty assigned to a word of length
n [
22,
23]. The difference entropy
represents the uncertainty related to the appearance of the
symbol given that the
n preceding symbols are known [
22]. For dynamical systems, the estimation of the mean rate of creation of information is given by the Kolmogorov–Sinai (KS) entropy and KS measures the unpredictability of systems changing with time [
24]. However, numerical calculations of KS requires very large sequences, therefore it is not practical to apply to real sequences. In order to overcome this limitation, Grassberger et al. [
25] proposed the
entropy to evaluate the dimensionality of chaotic systems as a lower bound of the KS entropy. Later, as an extension of the
entropy, Pincus [
14] introduced the Approximate Entropy (
) to evaluate the regularity in a given time series. The
provides a direct measure of the degree of irregularity or randomness in a time series and, in the context of physiological signals, as a measure of system complexity: smaller values indicate greater regularity, and greater values convey more disorder or randomness [
14,
17]. Here we introduce a modified
algorithm for the regularity analysis of a written text. Our method considers a similar procedure as the
proposed by Pincus [
14] and it can be summarized as follows: for a given text,
of
N elements, where an element can be a letter or symbol (including the space), we define a set of patterns of length
m,
for
, where
is the pattern of
m elements or symbols, from
to
. Next, we look for matches occurring between two patterns if the “distance” is smaller than a given value. We impose a restriction to the “distance” between two such patterns, i.e., we set a number
r representing the maximum number of positions at which the corresponding symbols are different. This distance is known as the Hamming distance [
26]. Next, we calculate the number
of patterns
with
such that
, with
the Hamming distance. Then, the quantity
is defined, representing the probability of having patterns within the distance
r from the template pattern
.
Following Pincus [
14] we define the Approximate Entropy in the case of texts as,
where
and
are given by
and
, respectively. As in the context of time series, the statistic represented by
quantifies the degree of regularity/irregularity in a given text, and it is conceived as approximately equal to the negative average natural logarithm of the conditional probability that two patterns that are similar for
m symbols remain similar for
elements [
14]. Although
is very useful for distinguishing a variety of deterministic/stochastic processes, it has been reported that there is a bias in
because the method counts each pattern as matching itself. The existence of this bias, under particular circunstances, causes
to substimate or to provide a faulty value for a given time series. Therefore, the development of an alternative method was desirable to overcome the limitations of
. On the basis of
and
algorithms, Richman and Moorman [
15] introduced the so-called sample entropy (
) to reduce the bias in
. One of the advantages of
is that it does not count self-matches and is not based on a template-wise approach. Discounting the self-matches is justified since the entropy is conceived as a measure of the rate of information production; then, self-matches do not add new information [
15]. Following the definition of Richman and Moorman [
15], we can also define the
in the case of texts as,
where
and
are the probabilities that two patterns will match (with a tolerance of
r) for
and
m symbols, respectively [
27]. As in the case of
,
is conceived as the negative natural logarithm of the conditional probability that two sequences similar for
m points remain similar at the next point, with a tolerance of
r, without counting the self-matches; and a lower value of
indicates a more regular behavior of a symbol sequence whereas high values are assigned to more irregular sequences. We remark that both
and
represent family statistics that depend on the sequence length
N, the tolerance parameter
r and the pattern length
m.
3. Results and Discussion
Prior to the description of our results, we briefly explain the main steps of our method for a simple case of a very short text. Lets consider the beginning of the famously acknowledged Hamlet’s soliloquy:
To-be-or-not-to-be. The length of the sentence is 18, and the average length of words in this sentence is 2, i.e., approximately every three symbols the space mark repeats, then a natural value for
m is 3, and we set the tolerance value
(33% of the pattern length). Starting with the first letter from the left, the 16 subseries we can built are
,
, ...,
. After performing all the procedure described in the previous section, we find that, for the Hamlet’s soliloquy beginning, the statistics Equation (
1) results in
. This is a relatively intermediate value, which indicates that the sentence is moderately predictable compared to the case where the position of symbols was randomized (
in average for five independent realizations).
First, we analyze literary texts from each of the 14 languages which are described in
Table 1 for an extended dataset, which includes two more books of each language, please refer to the supporting information online at [
28]. The texts were downloaded from the website of the Gutenberg Project (
http://www.gutenberg.org). In order to avoid finite size effects and to validate our method for relatively short sequences, we restrict ourselves to segments with 5000 symbols and repeat the calculations for 10 segments this length [
29]. In our case we have kept the punctuation marks and the space mark as symbols. In what follows, we will only refer to
values since we obtain the same qualitative results using either
or
algorithms and particular differences will be discussed elsewhere.
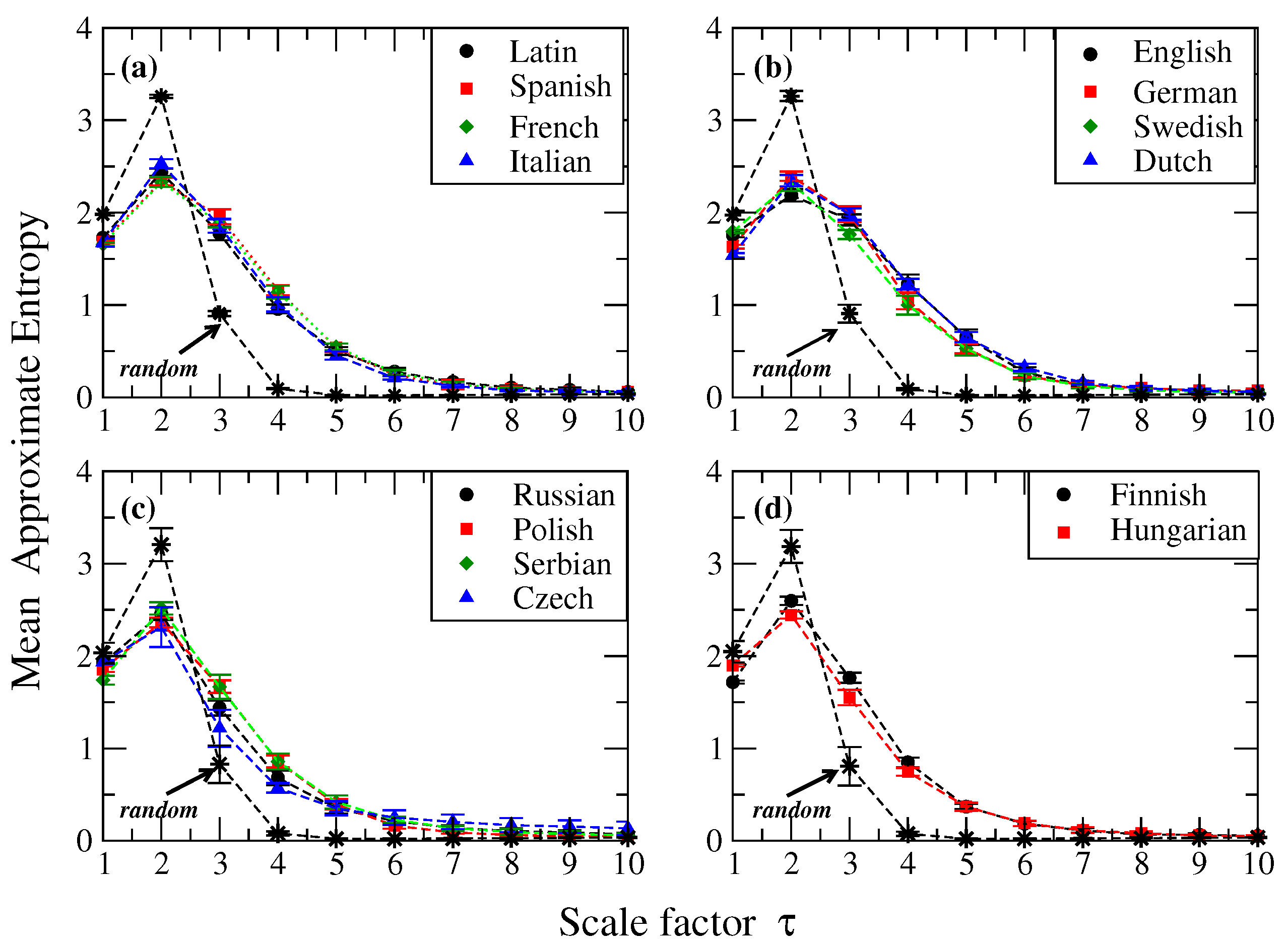
Figure 1 shows the calculations of the average
for several values of
m and a fixed value
. We notice that for
, the
values obtained for each language tend to be close when they are grouped according to the family to which they belong, allowing a comparison between families (see
Table 1). For this
m value, the Romance family exhibits the highest value of
, followed by the Uralic, Germanic and Slavic families, indicating that different levels of regularity/irregularity are observed in the analyzed family languages (
Figure 1a–d). It is also worth to mention that languages that belong to the same family display a similar profile as the pattern length increases, while the value of entropy for Romance, Slavic and Uralic families almost monotonically decreases; for the Germanic one the entropy exhibits a small change between
and
, revealing that the level of irregularity remains approximately constant for these pattern length scales, which roughly corresponds to the mean word length of these languages [
7]. Notably, all the Romance languages are much more overlapped compared to ApEn curves for the other families.
To further compare the
profiles in texts, we also studied two artificial cases: Esperanto and randomized versions of the original sequences. Invented languages like Esperanto are attempts to simplify natural languages by suppressing, for example, irregular verbs and including words from different languages to make it universal. For the randomized version, we consider a text which is randomly generated with identical symbol and space probabilities as observed in a real text and ten independent realizations were constructed. The results of
-values for the randomized versions are shown in
Figure 1f. In
Figure 1e we also show the behavior of entropy in terms of
m for Esperanto. For
, we observe that at
, the entropy value is close to the values observed in the majority of natural languages, and a rapid decay is observed between
and
, being this decline much faster than the one observed in real texts (see
Figure 1a–d). We note that for values between
and
, a higher value of
is observed for random texts than for real texts, and then the entropy decreases dramatically for larger values of the pattern length. We remark that for short length patterns the
is high due to the fact that the frequency of
m and
length patterns is quite different, indicating a high irregularity in the text, as expected for random sequences. When the entropy values (corresponding to pattern lengths 3–10) from the different languages were pairwise compared with their corresponding random version, we found significant differences in almost all cases (
p-value
by Student’s test, see
Table 2 for details).
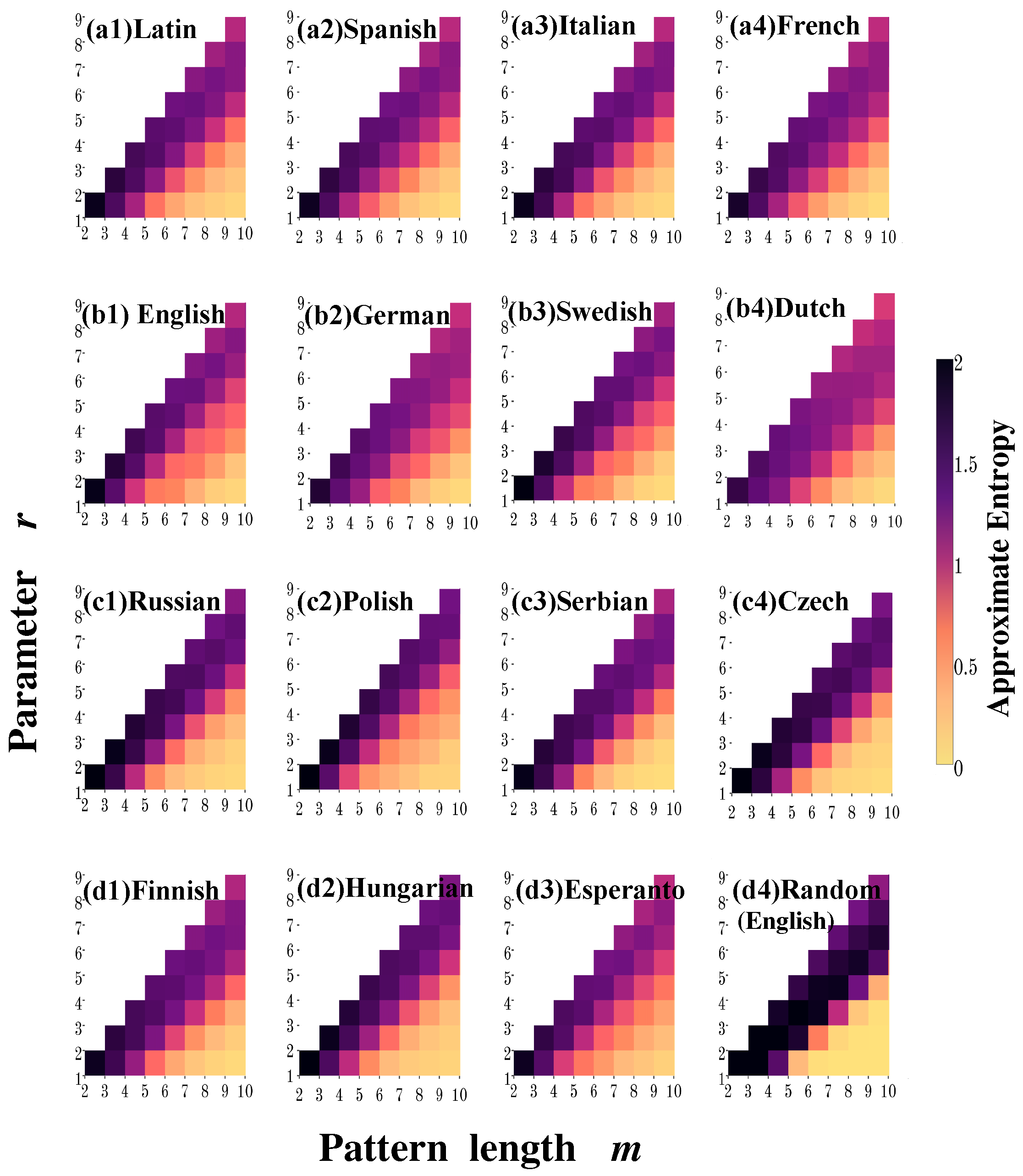
In order to further characterize the effects of the parameters
m and
r on the entropy values, in
Figure 2 we show the calculations of
for 36 pairs of values of the parameter
r and the pattern length
m. Recall that the
r value represents the similarity criterion based on the Hamming distance, i.e., the number of positions at which the corresponding symbols may differ. Thus,
r takes values between 1 and
. As shown in
Figure 2, we find that in most cases the entropy increases as the parameter
r increases for a fixed value of the pattern length
m, whereas for a fixed
r the entropy value tends to decrease as
m increases. Note that, for Germanic languages this general behavior is not observed as
m increases (
Figure 2(b1)). As a general remark of the dependence of entropy on parameters
m and
r, we notice that an acceptable value of
r is given by the level of discrepancies between the two patterns (a factor of the pattern length), since for larger
m values and small values of
r, a higher concordance is required every time, i.e., almost a perfect match, and larger sequences are required to get a reliable statistic.
Finally, to compare the behavior of the entropy values, we applied the Fisher’s linear discriminant [
30] to the data showed in
Figure 1a–d. This technique is very useful to determine if the
profiles could potentially classify languages into the Romance, Germanic, Slavic and Uralic families. Results for the 14 languages are presented in
Figure 3. For this analysis we considered the
values (corresponding to pattern lengths 3–10) from ten segments of 5000 symbols for each language. Then, the data were projected down to a two-dimensional scatter plot presented in
Figure 3. We observe a separation between clusters formed by languages that belong to the same linguistic family.
Multiscale Entropy Analysis of Texts
In the context of biological signals, Costa et al. [
21] introduced the multiscale entropy analysis (MSE) to evaluate the relative complexity of time series across multiple scales. This method was introduced to give an explanation to the fact that, in the context of biological signals, single-scale entropy methods (such as
) assign higher values to random sequences from certain pathologic conditions whereas an intermediate value is assigned to signals from healthy systems [
17,
21]. It has been argued that these results may lead to erroneous conclusions about the level of complexity displayed by these systems. Here we adopt a similar approach with the idea of evaluating the complexity of written texts by accounting multiple time scales. We explain the main steps of the modified MSE for the analysis of texts. Given the original sequence
, a coarse-graining process is applied. A scale factor
is considered to generate new sequences with elements formed by repeated concatenation of symbols from non-overlapping segments of length
. Thus, the coarse-graining sequences for a scale factor
are given by
, with
,
and the dots denote concatenation. We observe that for
, the original sequence is recovered, whereas for
the length of the new sequences is reduced to
. We note that for each scale factor
, there are
coarse-grained sequences derived from the original one, as it was recently pointed out in the composite MSE [
31,
32]. Next, to complete the MSE steps the
algorithm is applied to the sequence
for each scale to evaluate the regularity/irregularity in the new block-sequences. In order to improve the statistics, the entropy was calculated for all the
jth coarse-grained time series for a given
and the MSE value is given in terms of the average value of the entropies. Finally, the entropy value is plotted against the scale factor. A very simple example of the coarse-graining procedure can be illustrated for the Hamlet’s soliloquy:
“To-be-or-not-to-be”. For
we obtain
,
, ...,
and
,
, ...,
. We note that these new sequences have components formed by two-letter blocks which are the input for the modified
algorithm described in the previous Section. In practice, each new
-block component is assumed as a single character for calculation purposes.
Figure 4 presents the results of the MSE analysis for the real and synthetic texts described in the previous Section. The value of the entropy for scales one and two is higher for random texts than for real ones (
Figure 4a–d). It is noticeable that for texts from natural language, as the scale factor increases, the entropy value decreases moderately compared to the rapid decreasing observed for synthetic random data such that for scales larger than 3, the entropy values for random sequences are smaller than the ones from original texts. Similar conclusions were obtained for Esperanto and its random version (data not shown). As it has been identified when MSE was applied to biological signals, it is observed signals that exhibit long-range correlated behavior are more complex than the uncorrelated ones. When applied to natural language, our results show that the temporal organization of natural languages (with some differences between them) exhibits more complex structure than the sequences constructed by randomizations. These results are also concordant with previous studies, which report the presence of long-range correlations in written texts [
33,
34].