Figure 1.
Equivalent fraction as the central quantity from which all other formulas follow.
Figure 1.
Equivalent fraction as the central quantity from which all other formulas follow.
Figure 2.
Relationships between 1-, 2-, and 3-component systems.
Figure 2.
Relationships between 1-, 2-, and 3-component systems.
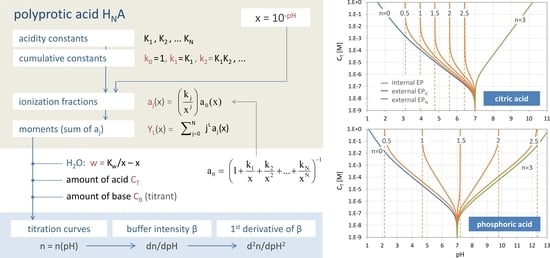
Figure 3.
pH dependence of ionization fractions for four acids (small circles mark equivalence points).
Figure 3.
pH dependence of ionization fractions for four acids (small circles mark equivalence points).
Figure 4.
Each ionization fraction aj has its own domain in the pH interval between two adjacent pKj values. (HA—acetic acid, H2A—carbonic acid, H3A—phosphoric acid).
Figure 4.
Each ionization fraction aj has its own domain in the pH interval between two adjacent pKj values. (HA—acetic acid, H2A—carbonic acid, H3A—phosphoric acid).
Figure 5.
Construction of Y1 (blue curve in bottom diagram) from summation over weighted ionization fraction aj. (Example: phosphoric acid as a triprotic acid).
Figure 5.
Construction of Y1 (blue curve in bottom diagram) from summation over weighted ionization fraction aj. (Example: phosphoric acid as a triprotic acid).
Figure 6.
pH dependence of the moments Y1 to Y4 for four acids. In the case of monoprotic acids (top-left diagram), all YL are equal, i.e., the four curves cover each other.
Figure 6.
pH dependence of the moments Y1 to Y4 for four acids. In the case of monoprotic acids (top-left diagram), all YL are equal, i.e., the four curves cover each other.
Figure 7.
Titration curve n = n(pH) of the “closed” carbonate system (100 mM H2CO3).
Figure 7.
Titration curve n = n(pH) of the “closed” carbonate system (100 mM H2CO3).
Figure 8.
Titration curves for 1, 10, and 100 mM H2CO3. (Left): n = n(pH); (right): pH = pH(n).
Figure 8.
Titration curves for 1, 10, and 100 mM H2CO3. (Left): n = n(pH); (right): pH = pH(n).
Figure 9.
Set of equations describing the 3-component acid–base system (H2O, HNA, strong base). The three components are coupled via the charge-balance equation.
Figure 9.
Set of equations describing the 3-component acid–base system (H2O, HNA, strong base). The three components are coupled via the charge-balance equation.
Figure 10.
Titration curves (i.e., buffer capacities) for four acids with different amounts of CT (including the high-CT limit n(pH) = Y1). Plots are based on Equation (41).
Figure 10.
Titration curves (i.e., buffer capacities) for four acids with different amounts of CT (including the high-CT limit n(pH) = Y1). Plots are based on Equation (41).
Figure 11.
Functional relationship between pH and CT for four acids (and n = 0). (Left): calculation based on Equation (43); (right): calculation based on the polynomial (44).
Figure 11.
Functional relationship between pH and CT for four acids (and n = 0). (Left): calculation based on Equation (43); (right): calculation based on the polynomial (44).
Figure 12.
Equivalence points of a triprotic acid—the common approach.
Figure 12.
Equivalence points of a triprotic acid—the common approach.
Figure 13.
Equivalence points of a triprotic acid H3A arranged on the pH scale.
Figure 13.
Equivalence points of a triprotic acid H3A arranged on the pH scale.
Figure 14.
pH–CT diagrams for a diprotic and triprotic acid—the common approach.
Figure 14.
pH–CT diagrams for a diprotic and triprotic acid—the common approach.
Figure 15.
Relationship EPn ⇔ pHn. EPs and semi-EPs are located at integer and half-integer values of n on the titration curve. Calculation for 100 mM H2CO3.
Figure 15.
Relationship EPn ⇔ pHn. EPs and semi-EPs are located at integer and half-integer values of n on the titration curve. Calculation for 100 mM H2CO3.
Figure 16.
Two approaches to equivalence points.
Figure 16.
Two approaches to equivalence points.
Figure 17.
Normalized [ANC]n and [BNC]n for carbonic acid with CT = 10 mM.
Figure 17.
Normalized [ANC]n and [BNC]n for carbonic acid with CT = 10 mM.
Figure 18.
Optimal buffer range of the H2CO3 system with CT = 100 mM.
Figure 18.
Optimal buffer range of the H2CO3 system with CT = 100 mM.
Figure 19.
Normalized buffer capacity (blue), buffer intensity (green), and dβ/dpH (red) for four acids and CT → ∞.
Figure 19.
Normalized buffer capacity (blue), buffer intensity (green), and dβ/dpH (red) for four acids and CT → ∞.
Figure 20.
Same as
Figure 19, but for C
T = 100 mM.
Figure 20.
Same as
Figure 19, but for C
T = 100 mM.
Figure 21.
Micro- and macrostates of a triprotic acid and the corresponding (cumulative) equilibrium constants.
Figure 21.
Micro- and macrostates of a triprotic acid and the corresponding (cumulative) equilibrium constants.
Figure 22.
Ionization fractions aj (dashed curves) and probability density functions f0 and fN.
Figure 22.
Ionization fractions aj (dashed curves) and probability density functions f0 and fN.
Figure 23.
Interrelation between different types of equilibrium constants of a polyprotic acid HNA.
Figure 23.
Interrelation between different types of equilibrium constants of a polyprotic acid HNA.
Figure 24.
Undissociated fraction a0 for strong and weak acids. Strong acids are completely dissociated in the pH range above pH ≈ 0.
Figure 24.
Undissociated fraction a0 for strong and weak acids. Strong acids are completely dissociated in the pH range above pH ≈ 0.
Figure 25.
Weak/strong vs. diluted/concentrated acids.
Figure 25.
Weak/strong vs. diluted/concentrated acids.
Figure 26.
Y1 and aj for a system composed of phosphoric and carbonic acid.
Figure 26.
Y1 and aj for a system composed of phosphoric and carbonic acid.
Figure 27.
pH–CT diagrams with trajectories of EPs and semi-EPs for four acids. Calculations are based on Equation (117).
Figure 27.
pH–CT diagrams with trajectories of EPs and semi-EPs for four acids. Calculations are based on Equation (117).
Figure 28.
Trajectories of EPs and semi-EPs for phosphoric acid (H3PO4) for the uncoupled (top) and coupled system (bottom).
Figure 28.
Trajectories of EPs and semi-EPs for phosphoric acid (H3PO4) for the uncoupled (top) and coupled system (bottom).
Figure 29.
Ionization fractions for phosphoric acid in two approximations (dashed lines) vs. exact description based on Equation (17).
Figure 29.
Ionization fractions for phosphoric acid in two approximations (dashed lines) vs. exact description based on Equation (17).
Figure 30.
Titration curve n = n(pH) for carbonic acid (CT = 10 mM) with equivalence points and the corresponding types of alkalinity and acidity.
Figure 30.
Titration curve n = n(pH) for carbonic acid (CT = 10 mM) with equivalence points and the corresponding types of alkalinity and acidity.
Figure 31.
Species distribution of H2CO3 as a function of pH for var A (left) and var B (right). Top diagrams: concentrations in linear scale; bottom diagrams: logarithmic scale.
Figure 31.
Species distribution of H2CO3 as a function of pH for var A (left) and var B (right). Top diagrams: concentrations in linear scale; bottom diagrams: logarithmic scale.
Figure 32.
Species distribution of H2CO3 as a function of pH for var A (left) and var C (right). Top diagrams: concentrations in linear scale; bottom diagrams: logarithmic scale.
Figure 32.
Species distribution of H2CO3 as a function of pH for var A (left) and var C (right). Top diagrams: concentrations in linear scale; bottom diagrams: logarithmic scale.
Figure 33.
pH–CT diagrams of the carbonic-acid system. (Left): H2CO3 in pure water (solid lines) vs. H2CO3 in seawater (dashed lines). (Right): closed-form expression (117) vs. numerical model (dots).
Figure 33.
pH–CT diagrams of the carbonic-acid system. (Left): H2CO3 in pure water (solid lines) vs. H2CO3 in seawater (dashed lines). (Right): closed-form expression (117) vs. numerical model (dots).
Figure 34.
Ionization fractions of two diprotic acids: glycine (left) vs. carbonic acid (right).
Figure 34.
Ionization fractions of two diprotic acids: glycine (left) vs. carbonic acid (right).
Figure 35.
Titration curves n = n(pH) for the amino acid glycine. (Left): calculations based on Equation (138) for four amounts of CT. (Right): comparison with numerical program PhreeqC (dots).
Figure 35.
Titration curves n = n(pH) for the amino acid glycine. (Left): calculations based on Equation (138) for four amounts of CT. (Right): comparison with numerical program PhreeqC (dots).
Figure 36.
Structural formula of four zwitterionic acids.
Figure 36.
Structural formula of four zwitterionic acids.
Figure 37.
Titration curves n(pH), buffer capacity β and its derivative dβ/dpH for four zwitterionic acids (from
Table 12). Calculations for C
T → ∞.
Figure 37.
Titration curves n(pH), buffer capacity β and its derivative dβ/dpH for four zwitterionic acids (from
Table 12). Calculations for C
T → ∞.
Figure 38.
Same as
Figure 37, but for C
T = 500 mM.
Figure 38.
Same as
Figure 37, but for C
T = 500 mM.
Figure 39.
(Left): Ionization fractions of EDTA in linear scale (top) and logarithmic scale (bottom). (Right): Titration curves of EDTA for three values of CT based on Equation (138). The red dots represent numerical calculations with PhreeqC. [Note: Complexation with Na is ignored.]
Figure 39.
(Left): Ionization fractions of EDTA in linear scale (top) and logarithmic scale (bottom). (Right): Titration curves of EDTA for three values of CT based on Equation (138). The red dots represent numerical calculations with PhreeqC. [Note: Complexation with Na is ignored.]
Figure 40.
Titration curve of glycine with EPs and semi-EPs located at integer and half-integer n.
Figure 40.
Titration curve of glycine with EPs and semi-EPs located at integer and half-integer n.
Figure 41.
(Left) pH–CT diagrams for glycine. (Right): enlarged section around EP0 showing the isoelectric and isoionic points as a function of CT.
Figure 41.
(Left) pH–CT diagrams for glycine. (Right): enlarged section around EP0 showing the isoelectric and isoionic points as a function of CT.
Figure 42.
Ionization fractions representing the surface-species distribution on kaolinite (in the absence of Coulomb interactions).
Figure 42.
Ionization fractions representing the surface-species distribution on kaolinite (in the absence of Coulomb interactions).
Figure 43.
pH dependence of surface charge for four surfaces (in the absence of Coulomb interactions).
Figure 43.
pH dependence of surface charge for four surfaces (in the absence of Coulomb interactions).
Figure 44.
Three mathematically equivalent descriptions of the N-protic acid–base system. The algebraic set of N + 3 equations is defined in Equations (27)–(32).
Figure 44.
Three mathematically equivalent descriptions of the N-protic acid–base system. The algebraic set of N + 3 equations is defined in Equations (27)–(32).
Figure 45.
Building-block hierarchy of the acid–base model.
Figure 45.
Building-block hierarchy of the acid–base model.
Table 1.
pK values for four N-protic acids at 25 °C. (The composite carbonic acid is the sum of the unionized species CO2(aq) and the pure acid: H2CO3* = CO2(aq) + H2CO3; to simplify the notation, we omit the asterisk (*) on H2CO3* throughout the paper).
Table 1.
pK values for four N-protic acids at 25 °C. (The composite carbonic acid is the sum of the unionized species CO2(aq) and the pure acid: H2CO3* = CO2(aq) + H2CO3; to simplify the notation, we omit the asterisk (*) on H2CO3* throughout the paper).
| N | Acid | Formula | Type | pK1 | pK2 | pK3 | Ref. |
|---|
| 1 | acetic acid | CH3COOH | HA | 4.76 | | | [35] |
| 2 | (composite) carbonic acid | H2CO3 | H2A | 6.35 | 10.33 | | [36] |
| 3 | phosphoric acid | H3PO4 | H3A | 2.15 | 7.12 | 12.35 | [35] |
| 3 | citric acid | C6H8O7 | H3A | 3.13 | 4.76 | 6.4 | [35] |
Table 2.
Two types of ionization fractions.
Table 2.
Two types of ionization fractions.
| | Type 1 (S Shaped) | Type 2 (Bell Shaped) |
|---|
| ionization fraction | a0 and aN | a1, a2, … aN−1
(does not exist for 1-protic acids) |
| domain (pH interval) | pH < pK1 (for a0)
pH > pKN (for aN) | pKj < pH < pKj+1 |
| maximum at pH | −∞ (for a0)
+∞ (for aN) | ½ (pKj + pKj+1) |
strongly acidic (pH → 0)
strongly alkaline (pH → 14) | a0 = 1, aN = 0
a0 = 0, aN = 1 | aj = 0
aj = 0 |
| integral (area below curve) | infinite | finite |
statistical meaning
(see Section 2.5.3) | cumulative distribution function | – |
associated
equivalence points | two external EPs:
EP0 and EPN | N − 1 internal EPs:
EP1, EP2, … EPN-1 |
Table 3.
Internal equivalence points (based on pK values in
Table 1).
Table 3.
Internal equivalence points (based on pK values in
Table 1).
| N | Acid | pH1/2 | pH1 | pH3/2 | pH2 | pH5/2 |
|---|
| 1 | acetic acid | 4.76 | | | | |
| 2 | (composite) carbonic acid | 6.35 | 8.34 | 10.33 | | |
| 3 | phosphoric acid | 2.15 | 4.68 | 7.21 | 9.78 | 12.35 |
| 3 | citric acid | 3.13 | 3.94 | 4.76 | 5.58 | 6.4 |
Table 4.
Macroscopic and microscopic acidity constants.
Table 4.
Macroscopic and microscopic acidity constants.
| N Acidity Constants | N + 1 Cumulative Constants for | N Simms Constants | 2N − 1 Microscopic Constants |
|---|
| Dissociation | Association |
|---|
| K1, K2, …, KN | k0 = 1 | β0 = 1 | g1, g2, …, gN | g1, g2, g3, …
g1g2, g2g3, …
g1g2g3, …
g1g2⋯gN |
| | (implicit functions of Equations (101) and (102)) |
Table 5.
Strong vs. weak acids (greatly simplified).
Table 5.
Strong vs. weak acids (greatly simplified).
| | Strong Acid | Weak Acid |
|---|
| acidity constant | Ka ≫ 1 | Ka ≤ 1 |
| pKa = −lg Ka | pKa < 0 | pKa > 0 |
| [H+] ≈ {H+} = 10−pH | [H+] ≈ CT | [H+] ≪ CT |
| undissociated acid | [HA] ≈ 0 or a0 ≈ 0 | [HA] ≈ CT or a0 ≈ 1 |
| dissociated acid | [A−] ≈ CT or a1 ≈ 1 | [A−] ≪ CT or a1 ≪ 1 |
Table 6.
Degree of strength vs. degree of dilution.
Table 6.
Degree of strength vs. degree of dilution.
| | Degree of Strength | Degree of Dilution |
|---|
| determined by | acidity constant Ka | amount of acid CT |
| relationships | weak acid
small Ka
(positive pKa | ↔
↔
↔ | strong acid
large Ka
negative pKa) | diluted acid
small CT | ↔
↔ | concentr. Acid
large CT |
| compares | two different acids | dilution of the same acid |
| describes | release of H+ | dilution of H+ |
| type | fundamental property
(cannot be changed) | control parameter
(can be changed) |
Table 7.
Equivalence points as local extrema and inflection points.
Table 7.
Equivalence points as local extrema and inflection points.
| Function/Curve | semi-EPn
(half-integer n = j − ½)
at pKj | EPn
(integer n = j)
at pHj |
|---|
titration curve n = n(pH)
(normalized buffer capacity) | inflection points | inflection points |
| buffer intensity β = dn/dpH | maxima | minima |
| dβ/dpH = d2n/dpH2 | zeros | zeros |
| ionization fraction aj | inflection point | maximum |
Table 8.
Thermodynamic and conditional equilibrium constants for H
2CO
3 in pure water and seawater (at 25 °C, 1 atm);
cK values from [
39].
Table 8.
Thermodynamic and conditional equilibrium constants for H
2CO
3 in pure water and seawater (at 25 °C, 1 atm);
cK values from [
39].
| | Thermodynamic K
(Pure Water, I = 0) | Conditional cK
(Seawater, I = 0.7 M) |
|---|
| pK1 | 5.18 | 6.0 |
| pK2 | 10.33 | 9.1 |
| pKw | 14.0 | 13.9 |
Table 9.
Diprotic acids (N = 2): ordinary acid vs. zwitterion (simplest amino acid).
Table 9.
Diprotic acids (N = 2): ordinary acid vs. zwitterion (simplest amino acid).
| | Diprotic Acid | Zwitterion
(Simplest Amino Acid) |
|---|
| 1st dissociation | H2A = H+ + HA− | K1 | H2A+ = H+ + HA | K1 |
| 2nd dissociation | HA− = H+ + A−2 | K2 | HA = H+ + A− | K2 |
| species | H2A | HA− | A−2 | H2A+ | HA | A− |
| abbreviation | [0] | [1] | [2] | [0] | [1] | [2] |
| ionic fraction aj | a0 | a1 | a2 | a0 | a1 | a2 |
| charge zj | 0 | −1 | -2 | 1 | 0 | −1 |
| average charge zav | (0·[H2A] − 1·[HA−] − 2·[A−2])/CT | (1·[H2A+] − 0·[HA] − 1·[A−])/CT |
Table 10.
The three species of an ordinary diprotic acid vs. the simplest zwitterion.
Table 10.
The three species of an ordinary diprotic acid vs. the simplest zwitterion.
| | Diprotic Acid (Z = 0) | Zwitterion (Z = 1) | |
|---|
| [0]: | [H2A] | (neutral) | [H2A+] | (cation) | highest protonation |
| [1]: | [HA−] | (anion) | [HA] | (neutral) | |
| [2]: | [A−2] | (anion) | [A−] | (anion) | fully deprotonated |
Table 11.
Three exceptional cases out of N + 1 acid species.
Table 11.
Three exceptional cases out of N + 1 acid species.
| | | | Ordinary Acid
Z = 0 | Zwitterion
1 ≤ Z < N |
|---|
| j = 0 | [0] = [HNA+Z] | highest protonation | neutral | cation |
| j = Z | [Z] = [HN-ZA] | undissociated acid | neutral, [Z] = [0] | neutral |
| j = N | [N] = [A−(N−Z)] | fully deprotonated | anion | anion |
Table 12.
Acidity constants for carbonic acid and zwitterionic acids (the pK values for EDTA are taken from [
5]; they differ slightly from those in [
17]).
Table 12.
Acidity constants for carbonic acid and zwitterionic acids (the pK values for EDTA are taken from [
5]; they differ slightly from those in [
17]).
| Acid | N | Z | pK1 | pK2 | pK3 | pK4 | pK5 | pK6 | [j = 0] | [j = Z] | [j = N] |
|---|
| carbonic acid | 2 | 0 | 6.35 | 11.33 | | | | | H2A | H2A | A−2 |
| glycine | 2 | 1 | 2.35 | 9.778 | | | | | H2A+ | HA | A−1 |
| glutamic acid | 3 | 1 | 2.16 | 4.30 | 9.96 | | | | H3A+ | H2A | A−2 |
| NTA | 4 | 1 | 1.0 | 2.0 | 2.942 | 10.28 | | | H4A+ | H3A | A−3 |
| EDTA | 6 | 2 | 0 | 1.5 | 2.16 | 3.119 | 6.281 | 10.94 | H6A+2 | H4A | A−4 |
Table 13.
Isoionic vs. isoelectric point.
Table 13.
Isoionic vs. isoelectric point.
| Isoionic Point | Isoelectric Point (pI) |
|---|
| pH of pure acid | pH at which the net charge of all acid species is zero |
depends on CT
(approaches pI-value for CT → ∞
and pH = 7 for CT → 0) | independent of CT |
| Z − Y1(pH) = w(pH)/CT | Z − Y1(pH) = 0 |
| exists for ordinary acids and zwitterions | exists only for zwitterions |
Table 14.
Intrinsic pK values and pH
pzc for surface complexation on four (clay) minerals [
40].
Table 14.
Intrinsic pK values and pH
pzc for surface complexation on four (clay) minerals [
40].
| | Kaolinite | Mica | Goethite | Gibbsite |
|---|
| pK1 | 2.52 | 6.01 | 7.13 | 7.53 |
| pK2 | 5.88 | 7.65 | 9.60 | 9.87 |
| pHpzc = ½ (pK1+pK2) | 4.20 | 6.83 | 8.37 | 8.70 |