1. Introduction
The use of project work has a long history in education; it has formed part of the American education system for over 100 years. However, project-based learning as a teaching method has developed into its present form only in the 21st century. There are a few important reasons for this development: a revolution in learning theory from behaviorism to social constructivism, and the requirements of the modern work environment. Nowadays, everyone needs 21st century skills, such as collaborating, problem solving, scheduling, perseverance, and IT skills, in addition to actual knowledge [
1]. The article focuses on critical thinking, problem solving, collaboration, communication, and self-management, which are highly valuated 21st century skills by the American public and essential parts of project work [
2].
Project-based learning is
a systematic teaching method that engages students in learning knowledge and skills through an extended inquiry process structured around complex, authentic questions and carefully designed products and tasks [
1] (p. 4). Pupils have two central learning objectives: (1) to understand the contents of the subject and (2) to develop their 21st century skills. In addition to the learning objectives, there are some essential project design elements, such as a challenging problem or question, pupils’ voice and choice, varied assessment and feedback, and the public product. Pupils’ project work is typically presented to their classmates in the classroom. On the other hand, a public product outside their own school can increase the pupils’ involvement, since they would not wish to appear ill-prepared [
2]. It is crucial to remember that it is the working process itself that is more significant for learning, than the final output [
3]. If the project work is planned well, some advantage will be gained in addition to the learning objectives alone: it can motivate pupils to study the subject [
4,
5], and helps to instill a feeling for mathematics [
4]. Good project design is important; a badly planned project may lead to pupils’ frustration [
2]. The concept of project work treated in this article is understood to mean an organizing method of teaching that is adapted from project-based learning.
The Finnish national core curriculum for basic education 2014 requires the inclusion of
at least one multidisciplinary learning module for every school year [
6] (p. 33). The aim of the modules is
to link knowledge of and skills in various fields and, in interaction with others, to structure them as meaningful entities. Examination of wholes and exploratory work periods that link different fields of knowledge guide the pupils to apply their knowledge and produce experiences of participation in the communal building of knowledge. This allows the pupils to perceive the significance of topics they learn at school for their own life and community, and for the society and humankind [
6] (p. 32). Mathematics in the curriculum also raises the significance of mathematics in pupils’ personal life and in the surrounding society and highlights the practice of the different 21st century skills [
6].
LUMA Centre Finland organizes a new project-based learning and phenomenon-based learning integrated project competition called StarT, in support of the new curriculum. All pupils, from kindergarten to high school, can participate in the StarT competition, both in Finland and abroad. StarT includes different themes, such as Mathematics around us, Well-being, and Technology around us; participating teams choose one of these themes around which they design their project work. A StarT competition is organized every year. Participation begins in the schools or other learning communities with project work, after which it continues on four levels: local (for example in schools), regional (StarT festivals in ten big cities in Finland), national (StarT gala) and international (StarT gala). The realization of project work in the schools is free but the projects must be connected to at least one StarT theme. LUMA Centre Finland provides lots of project ideas and other materials. However, teachers can create their own projects with their pupils [
7].
In this article, we are interested in examining the attainment of pupils’ learning objectives in the mathematical project work, using the context of the StarT competition. In addition to the Finnish core curriculum, Judith Moschkovich’s academic literacy [
8] is used as a framework for the research, because it provides a tool for examining both learning mathematics and 21st century skills.
4. Results
4.1. Description of the Projects
Different pedagogical approaches to project work in mathematics were found among the teams examined. The project processes resembled design-based learning, collaborative learning, and inquiry-based learning. Design-based learning is a form of project-based learning in which pupils design something concretely [
17]. Using collaborative learning, two or more pupils work together on a task [
18]. Inquiry-based learning is based on a scientific research process in which pupils work with problems by forming and answering questions. Pupils can define the problems themselves or try to solve a given problem [
19]. Teamwork is a central part of working in every approach. All the 16 projects with further information are shown in
Table 3. The information is based on project reports and the researcher’s view of them.
The most popular pedagogical approach was the design-based project (7 of 16). In the projects of that type, pupils designed and built for example a game or a miniature. It is interesting that nearly all the design projects were done by primary pupils. In the secondary schools, the most common approach was the inquiry-based project (5 of 16). Teams studied some interesting mathematical phenomenon or topic, such as the Monty Hall problem, the sum of two dice and the Pythagorean Theorem. The third category of pedagogical approach was collaborative learning (4 of 16).
In addition to the pedagogical approaches, the final products of the projects were varied: physical objects, computer models, posters, videos, diaries, and collections of solutions to exercises. All the primary pupils’ final products (5 of 16) included a physical object and a video or a diary of the building process. The most common output in the secondary pupils’ project work was a poster and a video in which the team presented their study. Some teams also made a computer model, a PowerPoint, or they had only a big collection of answers to the exercises under the theme.
Figure 1 shows some examples of the final products. The marble ball game in the first picture is included in the project Ball path. Pictures 2 and 3 are both parts of the project work on the Fibonacci sequence. The final product includes a poster and a painting. In the fourth picture, there is a miniature of a house.
The Finnish national core curriculum also requires the inclusion of multidisciplinary learning modules every year, and there were many interdisciplinary projects in the competition. Mathematics was combined especially with art and mother tongue. Programming, which is a part of mathematics education in Finland, was included in two projects: the design of the chair, and the modelling of the classroom.
4.2. Description of Mathematical Content
Based on the teachers’ questionnaire answers, and on the reports of the project, we examined what kind of mathematics the projects included, that were in accordance with the national core curriculum. The types of mathematics were classified according to the key content areas of the curriculum (
Table 4). Some projects contained several areas.
More than half of the projects had geometric contents. Some teams acquainted themselves with geometric concepts, such as the golden mean or non-periodic tiling, whereas others used geometry as a tool. Geometry seems to be a content area with which project work readily connects. Thinking skills and methods include for example reasoning, argumentation and using computer programs, that lend themselves to project work. In half of the projects, their role became especially prominent, because algorithmic thinking, programming, and proofing were parts of these projects.
Mathematics is often used as a tool in multidisciplinary projects. The teams especially needed basic arithmetic operations, fractions, percentages, and algebraic skills, such as solving first-degree equations. In one project, pupils had to handle statistics as part of the project. Another team needed a knowledge of probability to solve their problem. Six final products also contained types of mathematics usually studied later. For example, 12-year-old pupils used powers and calculated the scales of the area and the volume.
In addition to the teachers, we also asked the pupils about mathematics during the project, with open-ended questions in the questionnaire; the answers are also shown at
Table 4. Their responses were similar to the teachers’. The pupils’ answers show that it is easier to specify contents such as geometry or mention basic arithmetic; very few understood that for example practicing their thinking skills might also form part of the project.
4.3. Growth of Mathematical Proficiency
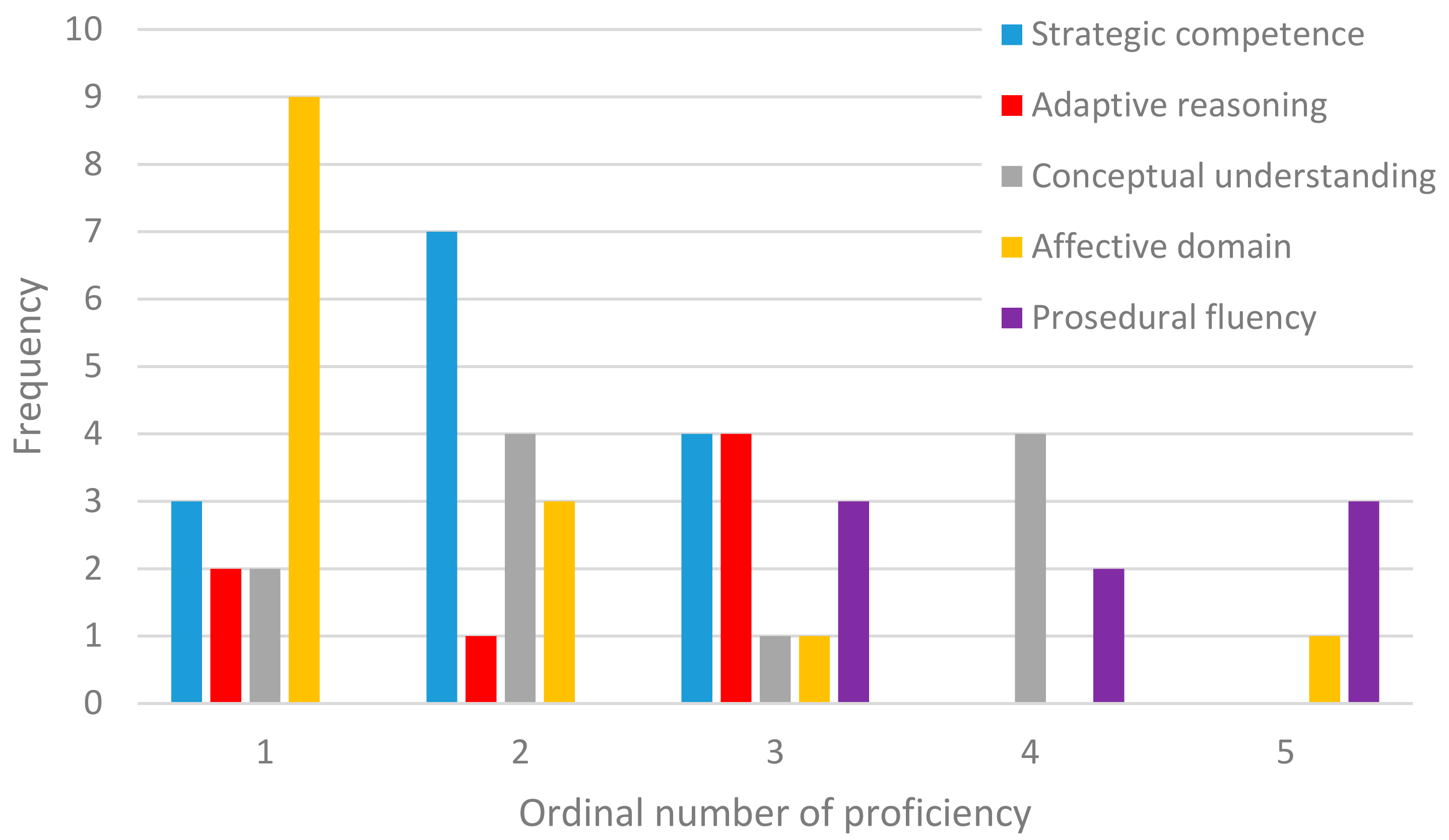
Mathematical proficiency was studied using the teachers’ answers and the teams’ project reports. Teachers were asked to choose from a list of what kinds of proficiencies the project developed, and to place these proficiencies in order of which were most developed. In that case, ordinal number 1 means that project develops this proficiency most in a teacher’s opinion et cetera. The lower the ordinal number, the more important this proficiency was in the project. The researcher also analyzed the project reports from the perspective of mathematical proficiency. The results are based on researcher’s view on a combination of project reports and teacher’s opinion. The frequencies of proficiencies in ordinal numbers are shown in
Figure 2. Additionally, we counted the averages of the ordinal numbers to every proficiency in such a way that number six means researcher did not choose this proficiency from the list. The lower the average, the more important this proficiency was as a whole.
Affective domain was obviously placed first the most (9 out of 16) and its average was clearly the lowest (avg 2.2, SD 1.8). In the open-ended question, teachers firstly explained that pupils used mathematics with math problems in everyday life. Secondly, persistence, patience and diligent work are important in the mathematical project work and the teams really practice these qualities. The next proficiency placed first was strategic competence (3 of 16). It was placed second in seven of the projects, and the average was low (avg 2.6, SD 1.5). Pupils had to formulate original problems using mathematical symbolic language. In some projects, pupils concentrated particularly on conceptual understanding (avg 3.7, SD 1.9). The projects of that kind started by familiarizing the participants with some mathematical concept. Adaptive reasoning was part of the projects in which pupils had to argue their results mathematically (avg 4.5, SD 2.0). Procedural fluency featured in only seven projects, and it was just after other proficiencies in those projects (avg 5.1, SD 1.2).
As a whole, project work usually seems to develop especially pupils’ affective domain and strategic competence, whereas the practice of procedural fluency is only a minor part of the project. On the other hand, mathematical projects are often very varied and some proficiencies, such as conceptual understanding, can be emphasized in a project.
4.4. Mathematical Practices
The questionnaire also enquired about the experience of teachers with the mathematical practices during StarT. According to their answers (
Table 5), project work is a good way to practice them. In their opinion, all or nearly all the projects developed the pupils’ ability to make sense of problems, to persevere in problem solving, to construct viable arguments, to use appropriate tools strategically, attend to precision, look for structures and make use of them.
Pupils had the most challenges with abstract reasoning, reflecting of alternative solutions, and mathematical modelling. On the other hand, about half of the teachers observed pupils also to have made progress in these practices.
Mathematical practices seem to be an essential part of project work in every project. Pupils must understand verbal problems, be able to write them using mathematical symbols, and choose reasonable tools. It is important to think abstractly and work persistently. The exact impression and critical attitude to alternative solutions are an integral part of working. Pupils also must be able to exploit structures.
4.5. The Role of Mathematical Discourse
We asked both teachers and pupils about languaging (
Table 6) during the project work. The question seems to have been a little difficult, because many teachers and pupils answered “I don’t know”, but this could be the result of the teacher not being able to observe every team all the time, or the pupils not always knowing what their teammates were doing.
Mathematical discourse is examined using a multisemiotic approach in which natural language, mathematical symbolic language, pictorial language, and tangible language are connected. Each of these four languages is generally found in StarT project work. Both teachers’ and pupils’ responses to the questionnaire were similar. About three quarters of the teams discussed solutions together and argued their claims (oral languaging). Additionally, teams presented their final products orally to the judges in StarT festivals. Written languaging is found clearly in four of the research reports. For example, in the project Pythagorean Theorem, pupils wrote their proofs to the theorem using natural language.
Most teams used some degree of pictorial language—they drew charts and outlined their thoughts with pictures. In the project work, pupils might need mathematical symbolic language actually less than in the mathematics lesson normally; only about 60% of pupils (N = 79) reported using symbols. According to 56% of the teachers (N = 9), pupils utilized hands on materials, such as ten rods and a thousand cubes.
The project in
Figure 3 is a good example of using the four languages. The team examined a right rectangular prism as a part of the project. Pupils clearly used mathematical symbolic language, pictorial language, and tangible language. Additionally, they presented their work orally.
5. Discussion
The objectives of successful project work are learning mathematics and 21st century skills [
2]. The Finnish StarT competition provides an excellent way to practice both objectives. Firstly, project work on the theme “Mathematics around us” included mathematics diversely. Every mathematical key content area in the Finnish core curriculum [
6] can be found in at least two of the project work; geometry especially was strongly represented. In addition to the key content areas, the projects contained plenty of subject matter, outside of what pupils usually study in mathematics, and also subjects from higher classes.
The project work in the context of StarT seems especially to develop the affective domain of pupils’ mathematical proficiency, because all the projects were concerned with everyday-life mathematics. Pupils saw tangibly how significant mathematics is in our society. In addition to the affective domain, strategic competence played a central part in nearly all the project work. Pupils were usually required to express an ordinary problem in mathematical form. The project work in the competition also showed that all the mathematical proficiencies [
9] could be practiced during project work. It is possible to design a project totally around concepts where the role of conceptual understanding is essential. Adaptive reasoning and procedural fluency can be used as a tool in the project work.
The second learning objective, 21st century skills, were examined using Moschkovich’s mathematical practices and discourse [
13]. Both practices and discourse are found in the Finnish core curriculum, and the practice of them is a task of instruction in mathematics in Finland. Project work seems to provide a good environment to develop all pupils’ mathematical practices as a natural part of working—not as a separate bonus. Problem solving, critical thinking and self-management relate to mathematical content. It is also possible to utilize all the fields of the multisemiotic approach in languaging during project work. Many projects included some written output, in which the team explained their phenomenon or solutions to a problem using natural language, mathematical symbols and pictures. Additionally, some teams illustrated their ideas by hands on materials such as thousand cubes or cardboard models. Project work provides an excellent method to practice oral languaging. Because pupils work in groups, they must communicate with each other in a mathematical context. In the project competition, teams also present their work orally to the judge. The public output is one of the seven essential project design elements in project-based learning [
2].
Project work creates opportunities for teaching in accordance with the Finnish core curriculum. Many projects in the StarT competition were multidisciplinary; the curriculum encourages the use of multidisciplinary learning modules every year [
6]. The mathematical project work included very different pedagogical approaches and outputs. Primary pupils especially made design projects, in which they built for example the miniature of a house; secondary pupils mostly made inquiry-based projects. In this kind of project, the final outputs were mainly posters and videos of the research process. Handicraft, art, and mother tongue connect with mathematics as natural parts of the working.
A few limitations of the study should be mentioned. The data was collected in a specific educational context in Finland, and the sample was small and indented, but on the other hand, we studied just mathematical project work in the Finnish StarT competition.
To conclude, project work provides an opportunity to practice very important 21st century skills as a part of mathematics teaching and implementing the Finnish core curriculum. Similar results have been obtained for example in American education [
2]. Further research is needed into the extent of mathematics learning. At present, this study suggests what kind of mathematics the pupils utilize, and which mathematical proficiencies are developed during the project work, but we do not have an exact knowledge of the depth of learning.