A Review of Gravitational Waves from Cosmic Domain Walls
Abstract
:1. Introduction
2. Domain Walls and Cosmology
2.1. Field Theory
2.2. Cosmological Evolution
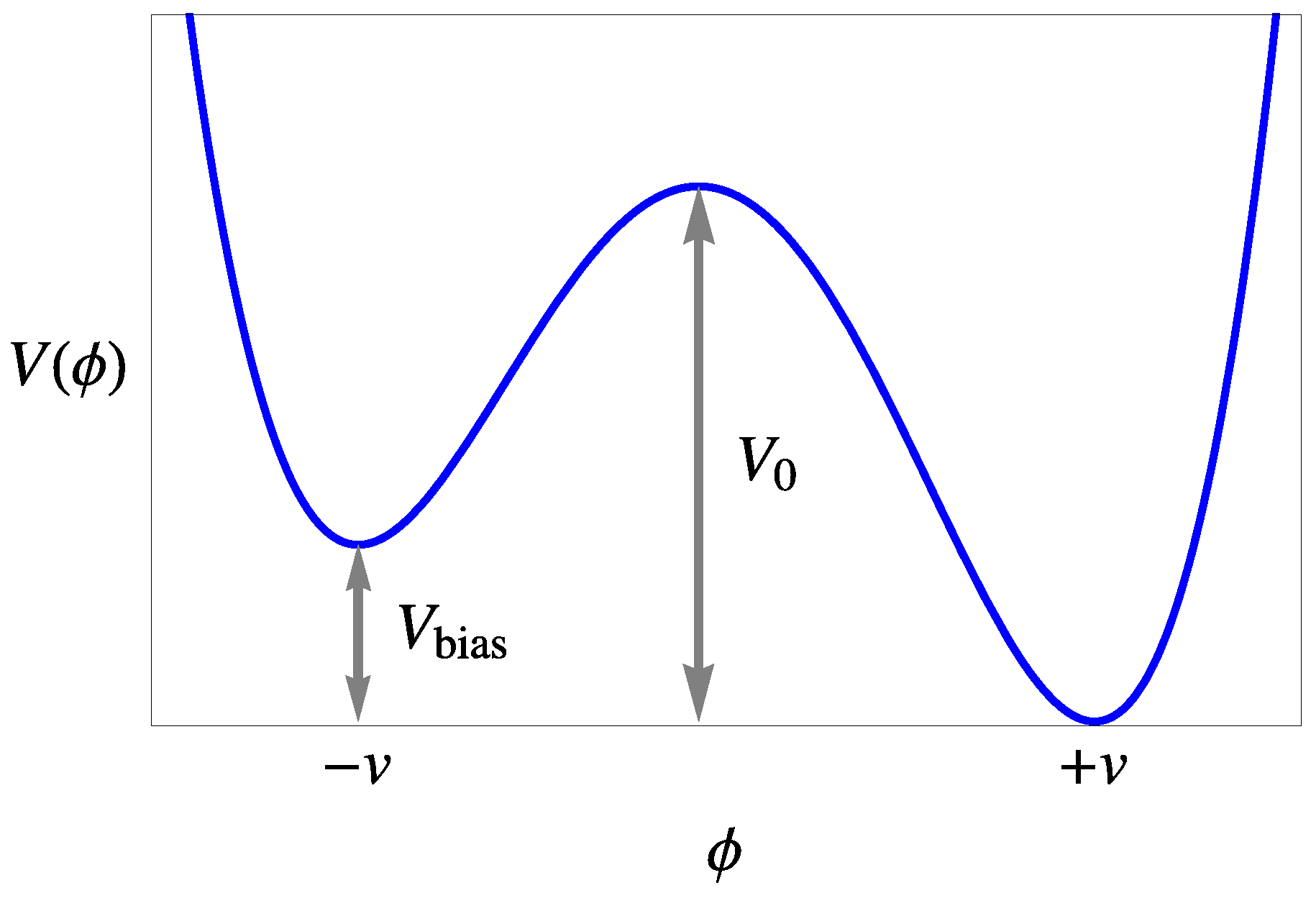
2.3. Biased Domain Walls
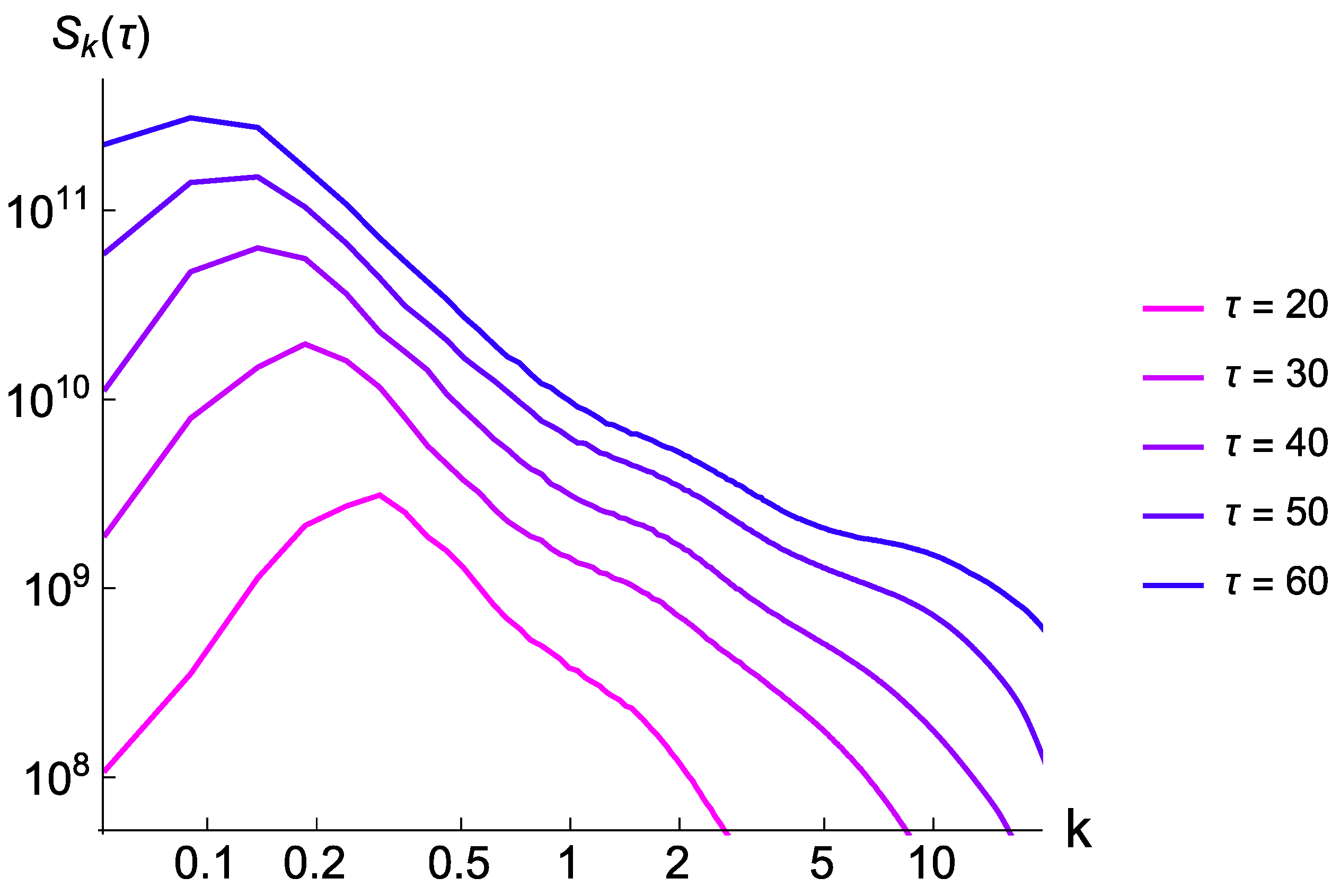
3. Estimation of Gravitational Waves from Domain Walls
4. Particle Physics Models
4.1. Standard Model Higgs Field
4.2. Axion Models
4.3. Supersymmetric Models
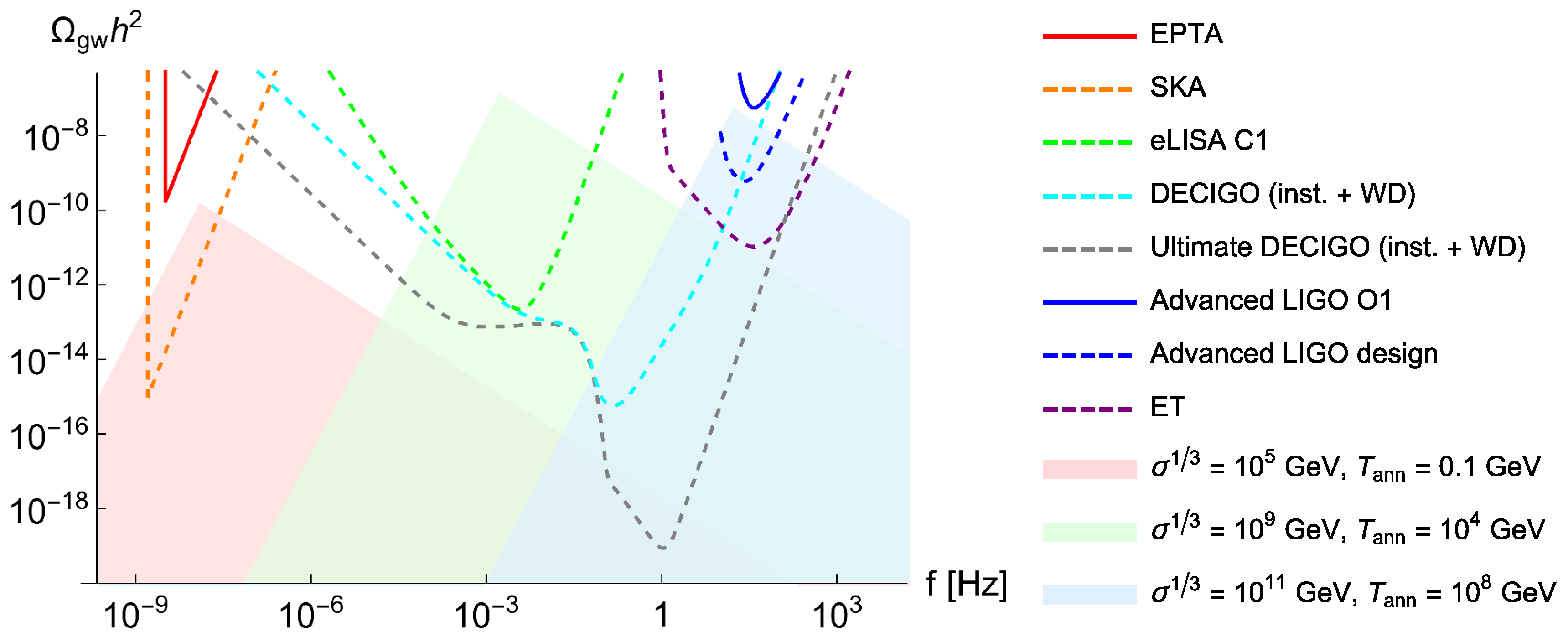
5. Implications for Present and Future Observations
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Maggiore, M. Gravitational Waves. Volume 1: Theory and Experiments; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Maggiore, M. Gravitational wave experiments and early universe cosmology. Phys. Rep. 2000, 331, 283–367. [Google Scholar] [CrossRef]
- Grishchuk, L.P. Amplification of gravitational waves in an isotropic universe. Sov. J. Exp. Theor. Phys. 1975, 40, 409–415. [Google Scholar]
- Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
- Smith, T.L.; Kamionkowski, M.; Cooray, A. Direct detection of the inflationary gravitational wave background. Phys. Rev. D 2006, 73, 023504. [Google Scholar] [CrossRef]
- Zhao, W.; Baskaran, D.; Coles, P. Detecting relics of a thermal gravitational wave background in the early Universe. Phys. Lett. B 2009, 680, 411–416. [Google Scholar] [CrossRef]
- Corda, C. Information on the inflaton field from the spectrum of relic gravitational waves. Gen. Relativ. Gravit. 2010, 42, 1323–1333. [Google Scholar] [CrossRef]
- Zhao, W.; Grishchuk, L.P. Relic gravitational waves: Latest revisions and preparations for new data. Phys. Rev. D 2010, 82, 123008. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837–2851. [Google Scholar] [CrossRef]
- Vilenkin, A. Gravitational radiation from cosmic strings. Phys. Lett. 1981, 107, 47–52. [Google Scholar] [CrossRef]
- Accetta, F.S.; Krauss, L.M. The stochastic gravitational wave spectrum resulting from cosmic string evolution. Nucl. Phys. B 1989, 319, 747–764. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Allen, B. Cosmological constraints on cosmic string gravitational radiation. Phys. Rev. D 1992, 45, 3447–3486. [Google Scholar] [CrossRef]
- Khlebnikov, S.Y.; Tkachev, I.I. Relic gravitational waves produced after preheating. Phys. Rev. D 1997, 56, 653–660. [Google Scholar] [CrossRef]
- Easther, R.; Lim, E.A. Stochastic gravitational wave production after inflation. J. Cosmol. Astropart. Phys. 2006, 2006, 10. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Figueroa, D.G.; Sastre, A. A Gravitational Wave Background from Reheating after Hybrid Inflation. Phys. Rev. D 2008, 77, 043517. [Google Scholar] [CrossRef]
- Dufaux, J.F.; Felder, G.; Kofman, L.; Navros, O. Gravity Waves from Tachyonic Preheating after Hybrid Inflation. J. Cosmol. Astropart. Phys. 2009, 2009. [Google Scholar] [CrossRef]
- Kawasaki, M.; Saikawa, K.; Takeda, N. Gravitational waves from smooth hybrid new inflation. Phys. Rev. D 2013, 87, 103521. [Google Scholar] [CrossRef]
- Corda, C. Interferometric detection of gravitational waves: The definitive test for General Relativity. Int. J. Mod. Phys. D 2009, 18, 2275–2282. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of Cosmic Domains and Strings. J. Phys. A 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Kobzarev, I.Y.; Okun, L.B. Cosmological Consequences of the Spontaneous Breakdown of Discrete Symmetry. Zh. Eksp. Teor. Fiz. 1974, 67, 3–11. [Google Scholar]
- Vilenkin, A. Gravitational Field of Vacuum Domain Walls and Strings. Phys. Rev. D 1981, 23, 852–857. [Google Scholar] [CrossRef]
- Gelmini, G.B.; Gleiser, M.; Kolb, E.W. Cosmology of Biased Discrete Symmetry Breaking. Phys. Rev. D 1989, 39, 1558–1566. [Google Scholar] [CrossRef]
- Larsson, S.E.; Sarkar, S.; White, P.L. Evading the cosmological domain wall problem. Phys. Rev. D 1997, 55, 5129–5135. [Google Scholar] [CrossRef]
- Grojean, C.; Servant, G. Gravitational Waves from Phase Transitions at the Electroweak Scale and Beyond. Phys. Rev. D 2007, 75, 043507. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Mazumdar, A. Probing the Scale of New Physics by Advanced LIGO/VIRGO. Phys. Rev. D 2016, 93, 104001. [Google Scholar] [CrossRef]
- Balazs, C.; Fowlie, A.; Mazumdar, A.; White, G. Gravitational waves at aLIGO and vacuum stability with a scalar singlet extension of the Standard Model. Phys. Rev. D 2017, 95, 043505. [Google Scholar] [CrossRef]
- Ivanov, I.P. Building and testing models with extended Higgs sectors. Prog. Part. Nucl. Phys. 2017. [Google Scholar] [CrossRef]
- Vilenkin, A.; Ford, L.H. Gravitational Effects upon Cosmological Phase Transitions. Phys. Rev. D 1982, 26, 1231–1241. [Google Scholar] [CrossRef]
- Linde, A.D. Scalar Field Fluctuations in Expanding Universe and the New Inflationary Universe Scenario. Phys. Lett. 1982, 116, 335–339. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Harigaya, K.; Ibe, M.; Kawasaki, M.; Yanagida, T.T. Dynamics of Peccei-Quinn Breaking Field after Inflation and Axion Isocurvature Perturbations. J. Cosmol. Astropart. Phys. 2015, 2015, 3. [Google Scholar] [CrossRef]
- Mazumdar, A.; Saikawa, K.I.; Yamaguchi, M.; Yokoyama, J.I. Possible resolution of the domain wall problem in the NMSSM. Phys. Rev. D 2016, 93, 025002. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shellard, E.P. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Press, W.H.; Ryden, B.S.; Spergel, D.N. Dynamical Evolution of Domain Walls in an Expanding Universe. Astrophys. J. 1989, 347, 590–604. [Google Scholar] [CrossRef]
- Garagounis, T.; Hindmarsh, M. Scaling in numerical simulations of domain walls. Phys. Rev. D 2003, 68, 103506. [Google Scholar] [CrossRef]
- Oliveira, J.C.; Martins, C.J.; Avelino, P.P. The Cosmological evolution of domain wall networks. Phys. Rev. D 2005, 71, 083509. [Google Scholar] [CrossRef]
- Avelino, P.P.; Martins, C.J.; Oliveira, J.C. One-scale model for domain wall network evolution. Phys. Rev. D 2005, 72, 083506. [Google Scholar] [CrossRef]
- Leite, A.M.; Martins, C.J. Scaling Properties of Domain Wall Networks. Phys. Rev. D 2011, 84, 103523. [Google Scholar] [CrossRef]
- Leite, A.M.; Martins, C.J.; Shellard, E.P. Accurate Calibration of the Velocity-dependent One-scale Model for Domain Walls. Phys. Lett. B 2013, 718, 740–744. [Google Scholar] [CrossRef]
- Martins, C.J.; Rybak, I.Y.; Avgoustidis, A.; Shellard, E.P. Extending the velocity-dependent one-scale model for domain walls. Phys. Rev. D 2016, 93, 043534. [Google Scholar] [CrossRef]
- Hindmarsh, M. Analytic scaling solutions for cosmic domain walls. Phys. Rev. Lett. 1996, 77, 4495–4498. [Google Scholar] [CrossRef] [PubMed]
- Hindmarsh, M. Level set method for the evolution of defect and brane networks. Phys. Rev. D 2003, 68, 043510. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K. On the estimation of gravitational wave spectrum from cosmic domain walls. J. Cosmol. Astropart. Phys. 2014, 2014, 31. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K.I.; Sekiguchi, T. Axion cosmology with long-lived domain walls. J. Cosmol. Astropart. Phys. 2013, 2013, 1. [Google Scholar] [CrossRef]
- Kawasaki, M.; Saikawa, K.I.; Sekiguchi, T. Axion dark matter from topological defects. Phys. Rev. D 2015, 91, 065014. [Google Scholar] [CrossRef]
- Coulson, D.; Lalak, Z.; Ovrut, B. Biased domain walls. Phys. Rev. D 1996, 53, 4237–4246. [Google Scholar] [CrossRef]
- Stauffer, D. Scaling theory of percolation clusters. Phys. Rep. 1979, 54, 1–74. [Google Scholar] [CrossRef]
- Kawasaki, M.; Takahashi, F. Late-time entropy production due to the decay of domain walls. Phys. Lett. B 2005, 618, 1–6. [Google Scholar] [CrossRef]
- Hattori, H.; Kobayashi, T.; Omoto, N.; Seto, O. Entropy production by domain wall decay in the NMSSM. Phys. Rev. D 2015, 92, 103518. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T. Hadronic decay of late—Decaying particles and Big-Bang Nucleosynthesis. Phys. Lett. B 2005, 625, 7–12. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T. Big-Bang nucleosynthesis and hadronic decay of long-lived massive particles. Phys. Rev. D 2005, 71, 083502. [Google Scholar] [CrossRef]
- Preskill, J.; Trivedi, S.P.; Wilczek, F.; Wise, M.B. Cosmology and broken discrete symmetry. Nucl. Phys. B 1991, 363, 207–220. [Google Scholar] [CrossRef]
- Chang, S.; Hagmann, C.; Sikivie, P. Studies of the motion and decay of axion walls bounded by strings. Phys. Rev. D 1999, 59, 023505. [Google Scholar] [CrossRef]
- Gleiser, M.; Roberts, R. Gravitational waves from collapsing vacuum domains. Phys. Rev. Lett. 1998, 81, 5497–5500. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K.I. Gravitational Waves from Collapsing Domain Walls. J. Cosmol. Astropart. Phys. 2010, 2010, 32. [Google Scholar] [CrossRef]
- Kawasaki, M.; Saikawa, K.I. Study of gravitational radiation from cosmic domain walls. J. Cosmol. Astropart. Phys. 2011, 2011, 8. [Google Scholar] [CrossRef]
- Dufaux, J.F.; Bergman, A.; Felder, G.; Kofman, L.; Uzan, J.P. Theory and Numerics of Gravitational Waves from Preheating after Inflation. Phys. Rev. D 2007, 76, 123517. [Google Scholar] [CrossRef]
- Nakayama, K.; Takahashi, F.; Yokozaki, N. Gravitational waves from domain walls and their implications. arXiv 2016. [Google Scholar]
- Caprini, C.; Durrer, R.; Konstandin, T.; Servant, G. General Properties of the Gravitational Wave Spectrum from Phase Transitions. Phys. Rev. D 2009, 79, 083519. [Google Scholar] [CrossRef]
- Giudice, G.F.; Kolb, E.W.; Riotto, A. Largest temperature of the radiation era and its cosmological implications. Phys. Rev. D 2001, 64, 023508. [Google Scholar] [CrossRef]
- Kitajima, N.; Takahashi, F. Gravitational waves from Higgs domain walls. Phys. Lett. B 2015, 745, 112–117. [Google Scholar] [CrossRef]
- Buttazzo, D.; Degrassi, G.; Giardino, P.P.; Giudice, G.F.; Sala, F.; Salvio, A.; Strumia, A. Investigating the near-criticality of the Higgs boson. J. High Energy Phys. 2013, 2013, 89. [Google Scholar] [CrossRef]
- Andreassen, A.; Frost, W.; Schwartz, M.D. Consistent Use of the Standard Model Effective Potential. Phys. Rev. Lett. 2014, 113, 241801. [Google Scholar] [CrossRef] [PubMed]
- Krajewski, T.; Lalak, Z.; Lewicki, M.; Olszewski, P. Domain walls and gravitational waves in the Standard Model. J. Cosmol. Astropart. Phys. 2016, 2016, 36. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong p and t Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String Axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Cicoli, M.; Goodsell, M.D.; Ringwald, A. The type IIB string axiverse and its low-energy phenomenology. J. High Energy Phys. 2012, 2012, 146. [Google Scholar] [CrossRef]
- Sikivie, P. Axion Cosmology. Lect. Notes Phys. 2008, 741, 19–50. [Google Scholar]
- Ringwald, A. Exploring the Role of Axions and Other WISPs in the Dark Universe. Phys. Dark Univ. 2012, 1, 116–135. [Google Scholar] [CrossRef]
- Kawasaki, M.; Nakayama, K. Axions: Theory and Cosmological Role. Ann. Rev. Nucl. Part. Sci. 2013, 63, 69–95. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Sikivie, P. Of Axions, Domain Walls and the Early Universe. Phys. Rev. Lett. 1982, 48, 1156–1159. [Google Scholar] [CrossRef]
- Di Vecchia, P.; Veneziano, G. Chiral Dynamics in the Large N Limit. Nucl. Phys. B 1980, 171, 253–272. [Google Scholar] [CrossRef]
- Di Cortona, G.G.; Hardy, E.; Vega, J.P.; Villadoro, G. The QCD axion, precisely. J. High Energy Phys. 2016, 2016, 34. [Google Scholar] [CrossRef]
- Daido, R.; Kitajima, N.; Takahashi, F. Domain Wall Formation from Level Crossing in the Axiverse. Phys. Rev. D 2015, 92, 063512. [Google Scholar] [CrossRef]
- Daido, R.; Kitajima, N.; Takahashi, F. Level crossing between the QCD axion and an axionlike particle. Phys. Rev. D 2016, 93, 075027. [Google Scholar] [CrossRef]
- Huang, M.C.; Sikivie, P. The Structure of Axionic Domain Walls. Phys. Rev. D 1985, 32, 1560–1568. [Google Scholar] [CrossRef]
- Vilenkin, A.; Everett, A.E. Cosmic Strings and Domain Walls in Models with Goldstone and PseudoGoldstone Bosons. Phys. Rev. Lett. 1982, 48, 1867–1870. [Google Scholar] [CrossRef]
- Ghigna, S.; Lusignoli, M.; Roncadelli, M. Instability of the invisible axion. Phys. Lett. B 1992, 283, 278–281. [Google Scholar] [CrossRef]
- Barr, S.M.; Seckel, D. Planck scale corrections to axion models. Phys. Rev. D 1992, 46, 539–549. [Google Scholar] [CrossRef]
- Kamionkowski, M.; March-Russell, J. Planck scale physics and the Peccei-Quinn mechanism. Phys. Lett. B 1992, 282, 137–141. [Google Scholar] [CrossRef]
- Holman, R.; Hsu, S.D.; Kephart, T.W.; Kolb, E.W.; Watkins, R.; Widrow, L.M. Solutions to the strong CP problem in a world with gravity. Phys. Lett. B 1992, 282, 132–136. [Google Scholar] [CrossRef]
- Dine, M. Problems of naturalness: Some lessons from string theory. arXiv 1992. [Google Scholar]
- Dobrescu, B.A. The Strong CP problem versus Planck scale physics. Phys. Rev. D 1997, 55, 5826–5833. [Google Scholar] [CrossRef]
- Baker, C.A.; Doyle, D.D.; Geltenbort, P.; Green, K.; Van der Grinten, M.G.; Harris, P.G.; Iaydjiev, P.; Ivanov, S.N.; May, D.J.; Pendlebury, J.M. An Improved experimental limit on the electric dipole moment of the neutron. Phys. Rev. Lett. 2006, 97, 131801. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.S.; Nilles, H.P.; Ramos-Sànchez, S.; Vaudrevange, P.K. Accions. Phys. Lett. B 2009, 675, 381–386. [Google Scholar] [CrossRef]
- Dias, A.G.; Machado, A.C.; Nishi, C.C.; Ringwald, A.; Vaudrevange, P. The Quest for an Intermediate-Scale Accidental Axion and Further ALPs. J. High Energy Phys. 2014, 2014, 37. [Google Scholar] [CrossRef]
- Ringwald, A.; Saikawa, K.I. Axion dark matter in the post-inflationary Peccei-Quinn symmetry breaking scenario. Phys. Rev. D 2016, 93, 085031. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K.I. Evolution of String-Wall Networks and Axionic Domain Wall Problem. J. Cosmol. Astropart. Phys. 2011, 2011, 30. [Google Scholar] [CrossRef]
- Daido, R.; Kitajima, N.; Takahashi, F. Axion domain wall baryogenesis. J. Cosmol. Astropart. Phys. 2015, 2015, 46. [Google Scholar] [CrossRef]
- Higaki, T.; Jeong, K.S.; Kitajima, N.; Takahashi, F. Quality of the Peccei-Quinn symmetry in the Aligned QCD Axion and Cosmological Implications. J. High Energy Phys. 2016, 2016, 150. [Google Scholar] [CrossRef]
- Higaki, T.; Jeong, K.S.; Kitajima, N.; Sekiguchi, T.; Takahashi, F. Topological Defects and nano-Hz Gravitational Waves in Aligned Axion Models. J. High Energy Phys. 2016, 2016, 44. [Google Scholar] [CrossRef]
- Farina, M.; Pappadopulo, D.; Rompineve, F.; Tesi, A. The photo-philic QCD axion. J. High Energy Phys. 2017, 2017, 95. [Google Scholar] [CrossRef]
- Kaplan, D.E.; Rattazzi, R. Large field excursions and approximate discrete symmetries from a clockwork axion. Phys. Rev. D 2016, 93, 085007. [Google Scholar] [CrossRef]
- Takahashi, F.; Yanagida, T.T.; Yonekura, K. Gravitational Waves as a Probe of the Gravitino Mass. Phys. Lett. B 2008, 664, 194–198. [Google Scholar] [CrossRef]
- Dine, M.; Takahashi, F.; Yanagida, T.T. Discrete R Symmetries and Domain Walls. J. High Energy Phys. 2010, 2010, 3. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum Theory of Fields. Vol. 3: Supersymmetry; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dvali, G.; Shifman, M. Domain walls in strongly coupled theories. Phys. Lett. B 1997, 396, 64–69. [Google Scholar] [CrossRef]
- Kovner, A.; Shifman, M.; Smilga, A. Domain walls in supersymmetric Yang-Mills theories. Phys. Rev. D 1997, 56, 7978–7989. [Google Scholar] [CrossRef]
- Kim, J.E.; Nilles, H.P. The mu Problem and the Strong CP Problem. Phys. Lett. 1984, 138, 150–154. [Google Scholar] [CrossRef]
- Maniatis, M. The Next-to-Minimal Supersymmetric extension of the Standard Model reviewed. Int. J. Mod. Phys. A 2010, 25, 3505–3602. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hugonie, C.; Teixeira, A.M. The Next-to-Minimal Supersymmetric Standard Model. Phys. Rep. 2010, 496, 1–77. [Google Scholar] [CrossRef]
- Kadota, K.; Kawasaki, M.; Saikawa, K.I. Gravitational waves from domain walls in the next-to-minimal supersymmetric standard model. J. Cosmol. Astropart. Phys. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Abel, S.A.; Sarkar, S.; White, P.L. On the cosmological domain wall problem for the minimally extended supersymmetric standard model. Nucl. Phys. B 1995, 454, 663–681. [Google Scholar] [CrossRef]
- Panagiotakopoulos, C.; Tamvakis, K. Stabilized NMSSM without domain walls. Phys. Lett. B 1999, 446, 224–227. [Google Scholar]
- Hamaguchi, K.; Nakayama, K.; Yokozaki, N. NMSSM in gauge-mediated SUSY breaking without domain wall problem. Phys. Lett. B 2012, 708, 100–106. [Google Scholar] [CrossRef]
- Moroi, T.; Nakayama, K. Domain Walls and Gravitational Waves after Thermal Inflation. Phys. Lett. B 2011, 703, 160–166. [Google Scholar] [CrossRef]
- Lyth, D.H.; Stewart, E.D. Cosmology with a TeV mass GUT Higgs. Phys. Rev. Lett. 1995, 75, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Lyth, D.H.; Stewart, E.D. Thermal inflation and the moduli problem. Phys. Rev. D 1996, 53, 1784–1798. [Google Scholar] [CrossRef]
- Banks, T.; Kaplan, D.B.; Nelson, A.E. Cosmological implications of dynamical supersymmetry breaking. Phys. Rev. D 1994, 49, 779–787. [Google Scholar] [CrossRef]
- De Carlos, B.; Casas, J.A.; Quevedo, F.; Roulet, E. Model independent properties and cosmological implications of the dilaton and moduli sectors of 4-d strings. Phys. Lett. B 1993, 318, 447–456. [Google Scholar] [CrossRef]
- Asaka, T.; Hashiba, J.; Kawasaki, M.; Yanagida, T. Cosmological moduli problem in gauge mediated supersymmetry breaking theories. Phys. Rev. D 1998, 58, 083509. [Google Scholar] [CrossRef]
- Asaka, T.; Kawasaki, M. Cosmological moduli problem and thermal inflation models. Phys. Rev. D 1999, 60, 123509. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quant. Gravity 2015, 32, 074001. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X. Upper Limits on the Stochastic Gravitational-Wave Background from Advanced LIGO’s First Observing Run. Phys. Rev. Lett. 2017, 118, 121101. [Google Scholar] [CrossRef] [PubMed]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T. Improved Upper Limits on the Stochastic Gravitational-Wave Background from 2009–2010 LIGO and Virgo Data. Phys. Rev. Lett. 2014, 113, 231101. [Google Scholar] [CrossRef] [PubMed]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Klein, A.; Barausse, E.; Sesana, A.; Petiteau, A.; Berti, E.; Babak, S.; Gair, J.; Aoudia, S.; Hinder, I.; Ohme, F.; et al. Science with the space-based interferometer eLISA: Supermassive black hole binaries. Phys. Rev. D 2016, 93, 024003. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 2016, 2016, 1. [Google Scholar] [CrossRef]
- Kawamura, S.; Nakamura, T.; Ando, M.; Seto, N.; Tsubono, K.; Numata, K.; Takahashi, R.; Nagano, S.; Ishikawa, T.; Musha, M.; et al. The Japanese space gravitational wave antenna DECIGO. Class. Quant. Gravity 2006, 23, S125. [Google Scholar] [CrossRef]
- Lentati, L.; Taylor, S.R.; Mingarelli, C.M.; Sesana, A.; Sanidas, S.A.; Vecchio, A.; Caballero, R.N.; Lee, K.J.; Van Haasteren, R.; Babak, S.; et al. European Pulsar Timing Array Limits On An Isotropic Stochastic Gravitational-Wave Background. Mon. Not. R. Astron. Soc. 2015, 453, 2576–2598. [Google Scholar] [CrossRef]
- Jenet, F.A.; Hobbs, G.B.; van Straten, W.; Manchester, R.N.; Bailes, M.; Verbiest, J.P.; Edwards, R.T.; Hotan, A.W.; Sarkissian, J.M.; Ord, S.M. Upper bounds on the low-frequency stochastic gravitational wave background from pulsar timing observations: Current limits and future prospects. Astrophys. J. 2006, 653, 1571–1576. [Google Scholar] [CrossRef]
- Van Haasteren, R.; Levin, Y.; Janssen, G.H.; Lazaridis, K.; Kramer, M.; Stappers, B.W.; Desvignes, G.; Purver, M.B.; Lyne, A.G.; Ferdman, R.D. Placing limits on the stochastic gravitational-wave background using European Pulsar Timing Array data. Mon. Not. R. Astron. Soc. 2011, 414, 3117–3128. [Google Scholar] [CrossRef]
- Demorest, P.B.; Ferdman, R.D.; Gonzalez, M.E.; Nice, D.; Ransom, S.; Stairs, I.H.; Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.J.; et al. Limits on the Stochastic Gravitational Wave Background from the North American Nanohertz Observatory for Gravitational Waves. Astrophys. J. 2013, 762, 94. [Google Scholar] [CrossRef]
- Janssen, G.H.; Hobbs, G.; McLaughlin, M.; Bassa, C.G.; Deller, A.T.; Kramer, M.; Lee, K.J.; Mingarelli, C.M.; Rosado, P.A.; Sanidas, S. Gravitational wave astronomy with the SKA. arXiv 2014. [Google Scholar]
- Nan, R.; Li, D.; Jin, C.; Wang, Q.; Zhu, L.; Zhu, W.; Zhang, H.; Yue, Y.; Qian, L. The Five-Hundred-Meter Aperture Spherical Radio Telescope (FAST) Project. Int. J. Mod. Phys. D 2011, 20, 989–1024. [Google Scholar] [CrossRef]
- Base Sensitivity. Available online: https://workarea.et-gw.eu/et/WG4-Astrophysics/base-sensitivity (accessed on 27 April 2017).
- Kuroyanagi, S.; Nakayama, K.; Yokoyama, J.I. Prospects of determination of reheating temperature after inflation by DECIGO. Prog. Theor. Exp. Phys. 2015, 2015, 013E02. [Google Scholar] [CrossRef]
- Barack, L.; Cutler, C. LISA capture sources: Approximate waveforms, signal-to-noise ratios, and parameter estimation accuracy. Phys. Rev. D 2004, 69, 082005. [Google Scholar] [CrossRef]
- Nishizawa, A.; Yagi, K.; Taruya, A.; Tanaka, T. Cosmology with space-based gravitational-wave detectors: Dark energy and primordial gravitational waves. Phys. Rev. D 2012, 85, 044047. [Google Scholar] [CrossRef]
- Gravitational Wave Detectors and Sources. Available online: http://rhcole.com/apps/GWplotter (accessed on 27 April 2017).
- Moore, C.J.; Cole, R.H.; Berry, C.P. Gravitational-wave sensitivity curves. Class. Quant. Gravity 2015, 32, 015014. [Google Scholar] [CrossRef]
| 1. | We emphasize that the condition is not robust, and we can consider several loopholes depending on the details of the models. For instance, if the field never thermalizes, domain walls may not be formed even when is satisfied. We can also consider the case where the effective mass during inflation is different from the bare mass . In such a case, it is possible to avoid the formation of domain walls even when is satisfied [34,35]. |
| 2. | We note that the results of numerical simulations imply , where the exponent slightly deviates from . At this point, it is unclear whether this deviation represents some physical effect or just a numerical artifact which could be removed if we improve the dynamical range of the simulation. In this article, we carry out the analysis by assuming that the evolution of domain walls is described by the exact scaling law [Equation (17)]. |
| 3. | It is also possible to avoid the domain wall problem by assuming an asymmetric probability distribution for initial field fluctuations [49] instead of introducing the energy bias in the potential. Here, we do not consider such a scenario, since it depends on the models of the evolution of the early universe, which must produce an appropriate initial field distribution. |
| 4. | The domain wall domination does not directly imply a cosmological disaster. In principle, it can happen in the early universe without causing any trouble with the standard cosmology if such domain walls are annihilated before the epoch of Big Bang nucleosynthesis (BBN). For instance, the possibilities of diluting unwanted relics in the domain wall dominated universe are discussed in Refs. [51,52]. However, little is known about the detailed dynamics of domain walls in the domain wall dominated universe, and their behavior in such a scenario is uncertain. Therefore, in this work, we just focus on the case in which the energy density of domain walls never dominates the critical energy density of the universe, and use the condition of the domain wall domination to indicate the potential uncertainties. |
| 5. | |
| 6. | This assumption is not rigorous since the collapse of domain walls is not instantaneous, and they may continue to produce GWs until they completely disappear. This ambiguity can be incorporated into the definition of or the uncertainty of the parameter in Equation (28). |
| 7. | In some exceptional cases, domain walls may be formed even if strings do not exist. For instance, if the initial value of the axion field is tuned to the location which is very close to the top of the cosine potential (7) and its fluctuations are sufficiently large, domain walls without strings can be formed around the time of QCD phase transition. Domain walls without strings can also be formed due to the level crossing between the axion and an ALP [84,85], if there exists an ALP whose mass is comparable to the axion mass around the epoch of QCD phase transition. |
| 8. | String-wall systems may eventually collapse into a single string bundle, since the vacuum may not be disconnected along the direction of the unbroken U(1). However, such a collapse is not likely to occur if is large and is sufficiently small, since in this case strings obey the scaling solution, i.e., the number of strings per horizon remains , before the formation of domain walls and the size of the hybrid object, which evolves toward the bundle and contains exponentially large number of strings, is far outside the horizon [101]. |
| 9. | From Equation (11), we see that the choice corresponds to , which is satisfied in the toy model given by Equations (1) and (2) if . We also note that the condition (26) is always satisfied for domain walls in axion models [Equation (7)], since Equations (9), (11), (26), and (27) imply , which holds after the formation of domain walls. |

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saikawa, K. A Review of Gravitational Waves from Cosmic Domain Walls. Universe 2017, 3, 40. https://doi.org/10.3390/universe3020040
Saikawa K. A Review of Gravitational Waves from Cosmic Domain Walls. Universe. 2017; 3(2):40. https://doi.org/10.3390/universe3020040
Chicago/Turabian StyleSaikawa, Ken’ichi. 2017. "A Review of Gravitational Waves from Cosmic Domain Walls" Universe 3, no. 2: 40. https://doi.org/10.3390/universe3020040