Nonsingular Black Holes in ƒ (R) Theories
Abstract
:1. Introduction
2. Field Equations and Matter Source
3. Structure Equations
4. Wormhole geometry
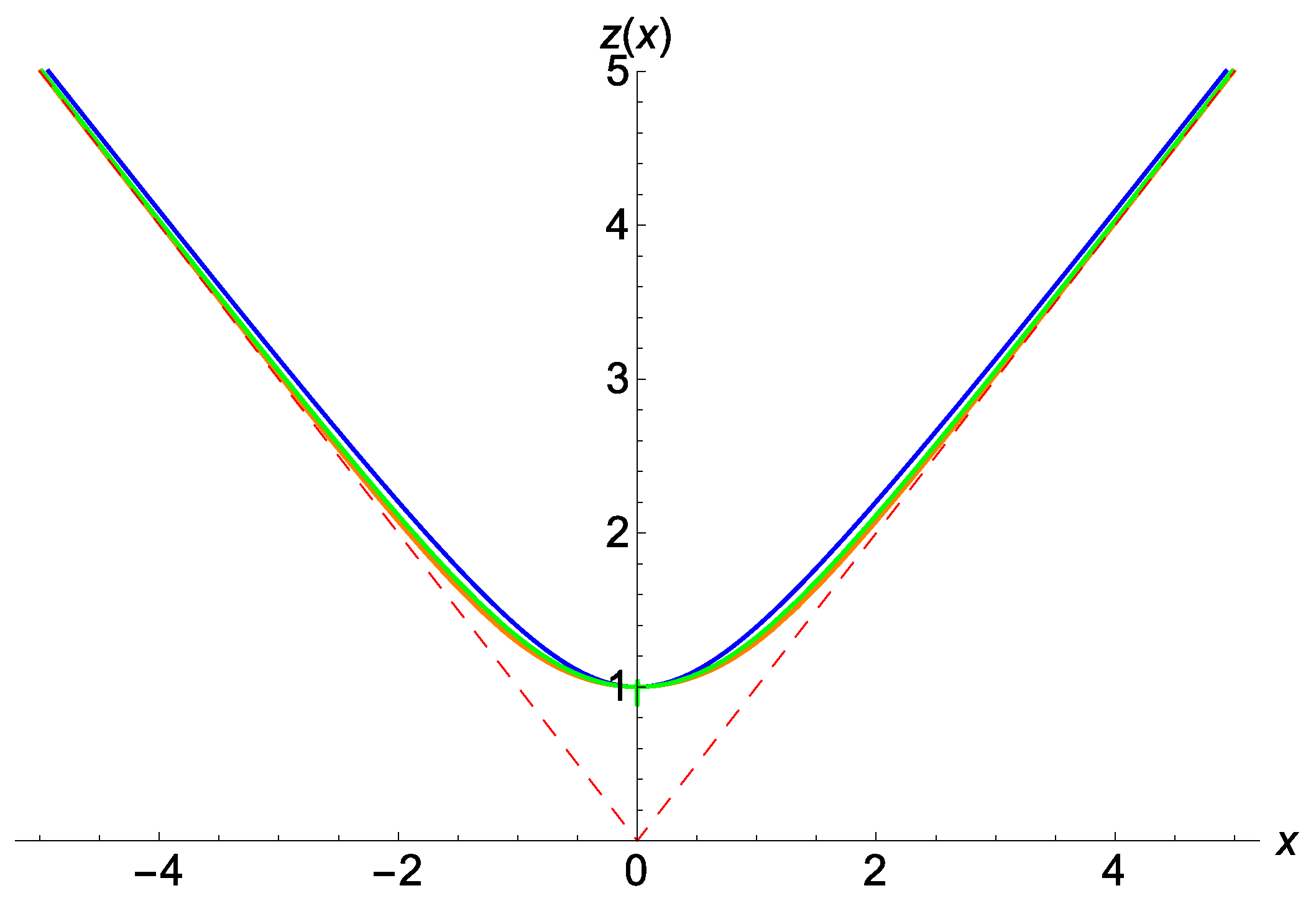
5. Geodesics

6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cimento 1969, 1, 252–276. [Google Scholar]
- Carter, B. Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 1971, 26, 331–333. [Google Scholar] [CrossRef]
- Hawking, S. Black-hole evaporation. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Fabbri, A.; Navarro-Salas, J. Modeling Black Hole Evaporation; Imperial College Press: London, UK, 2005. [Google Scholar]
- Zanelli, J. Lecture notes on Chern-Simons (super-) gravities. 2005; arXiv:hep-th/0502193. [Google Scholar]
- Olmo, G.J. Introduction to Palatini theories of gravity and nonsingular cosmologies. In Open Questions in Cosmology; Gonzalo, J.O., Ed.; InTech Publishing: Rijeka, Croatia, 2012. [Google Scholar]
- Lobo, F.S.N.; Olmo, G.J.; Rubiera-Garcia, D. Crystal clear lessons on the microstructure of spacetime and modified gravity. Phys. Rev. D 2015, 91, 124001. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Actions and Quantum Gravity Phenomenology. J. Cosmol. Astropart. Phys. 2011, 2011, 018. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Reissner-Nordström black holes in extended Palatini theories. Phys. Rev. D 2012, 86, 044014. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Nonsingular charged black holes à la Palatini. Int. J. Mod. Phys. D 2012, 21, 1250067. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Nonsingular black holes in quadratic Palatini gravity. Eur. Phys. J. C 2012, 72, 2098. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Semiclassical geons at particle accelerators. J. Cosmol. Astropart. Phys. 2014, 2014, 010. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Olmo, G.J.; Rubiera-Garcia, D. Semiclassical geons as solitonic black hole remnants. J. Cosmol. Astropart. Phys. 2013, 2013, 011. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Palatini Black Holes in Nonlinear Electrodynamics. Phys. Rev. D 2011, 84, 124059. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. Lond. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchis-Alepuz, H. Geonic black holes and remnants in Eddington-inspired Born-Infeld gravity. Eur. Phys. J. C 2014, 74, 2804. [Google Scholar] [CrossRef] [PubMed]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Classical resolution of black hole singularities via wormholes. 2015; arXiv:1504.07015, [hep-th]. [Google Scholar]
- Visser, M. Lorentzian Wormholes; Springer-Verlarg: New York, NY, USA, 1996. [Google Scholar]
- Ayón-Beato, E.; García, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. Nonsingular charged black hole solution for nonlinear source. Gen. Relativ. Gravit. 1999, 31, 629–633. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef]
- Ansoldi, S. Spherical black holes with regular center: A review of existing models including a recent realization with Gaussian sources. 2008; arXiv:0802.0330, [gr-qc]. [Google Scholar]
- Dymnikova, I. Cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725–740. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini approach to modified gravity: f(R) theories and beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef]
- Geroch, R.P. What is a singularity in general relativity? Ann. Phys. 1968, 48, 526. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Wald, R.M. General Relativity; University Press: Chicago, IL, USA, 1984. [Google Scholar]
- Curiel, E.; Bokulich, P. Singularities and Black Holes; Zalta, E.N., Ed.; Available online: http://plato.stanford.edu/archives/fall2012/entries/spacetime-singularities/ (accessed on 29 January 2009).
- Makarenko, A.N.; Odintsov, S.D.; Olmo, G.J. Born-Infeld- gravity. Phys. Rev. D 2014, 90, 024066. [Google Scholar] [CrossRef]
- Makarenko, A.N.; Odintsov, S.D.; Olmo, G.J. Little Rip, ΛCDM and singular dark energy cosmology from Born-Infeld- gravity. Phys. Lett. B 2014, 734, 36–40. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Olmo, G.J.; Rubiera-Garcia, D. Born-Infeld gravity and its functional extensions. Phys. Rev. D 2014, 90, 044003. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Olmo, G.J. Tensor perturbations in a general class of Palatini theories. J. Cosmol. Astropart. Phys. 2014, 2014, 004. [Google Scholar] [CrossRef]
- Olmo, G.J.; Sanchis-Alepuz, H.; Tripathi, S. Dynamical Aspects of Generalized Palatini Theories of Gravity. Phys. Rev. D 2009, 80, 024013. [Google Scholar] [CrossRef]
- Shaikh, R. Lorentzian wormholes in Eddington-inspired Born-Infeld gravity. 2015; arXiv:1505.01314, [gr-qc]. [Google Scholar]
- Deser, S.; Gibbons, G.W. Born-Infeld-Einstein actions? Class. Quantum Gravity 1998, 15, L35. [Google Scholar] [CrossRef]
- Bañados, M.; Ferreira, P.G. Eddington's theory of gravity and its progeny. Phys. Rev. Lett. 2010, 105, 011101. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K.; Sushkov, S.V. Wormhole geometries in Eddington-inspired Born-Infeld gravity. 2013; arXiv:1307.1883, [gr-qc]. [Google Scholar]
- Boonserm, P.; Ngampitipan, T.; Visser, M. Modelling anisotropic fluid spheres in general relativity. 2015; arXiv:1501.07044, [gr-qc]. [Google Scholar]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Electrostatic spherically symmetric configurations in gravitating nonlinear electrodynamics. Phys. Rev. D 2010, 81, 064021. [Google Scholar] [CrossRef]
- Diaz-Alonso, J.; Rubiera-Garcia, D. Asymptotically anomalous black hole configurations in gravitating nonlinear electrodynamics. Phys. Rev. D 2010, 82, 085024. [Google Scholar] [CrossRef]
- Hassaine, M.; Martinez, C. Higher-dimensional black holes with a conformally invariant Maxwell source. Phys. Rev. D 2007, 75, 027502. [Google Scholar] [CrossRef]
- Hassaine, M.; Martinez, C. Higher-dimensional charged black holes solutions with a nonlinear electrodynamics source. Class. Quantum Gravity 2008, 25, 195023. [Google Scholar] [CrossRef]
- Hendi, S.H. Topological black holes in Gauss-Bonnet gravity with conformally invariant Maxwell source. Phys. Lett. B 2009, 677, 123–132. [Google Scholar] [CrossRef]
- Hendi, S.H.; Rastegar-Sedehi, H.R. Ricci flat rotating black branes with a conformally invariant Maxwell source. Gen. Relativ. Gravit. 2009, 41, 1355–1366. [Google Scholar] [CrossRef]
- Gonzalez, H.A.; Hassaine, M.; Martinez, C. Thermodynamics of charged black holes with a nonlinear electrodynamics source. Phys. Rev. D 2009, 80, 104008. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511–536. [Google Scholar] [CrossRef]
- Barragan, C.; Olmo, G.J. Isotropic and Anisotropic Bouncing Cosmologies in Palatini Gravity. Phys. Rev. D 2010, 82, 084015. [Google Scholar] [CrossRef]
- Barragan, C.; Olmo, G.J.; Sanchis-Alepuz, H. Avoiding the Big Bang Singularity with Palatini f(R) Theories. 2010; arXiv:1002.3919, [gr-qc]. [Google Scholar]
- Barragan, C.; Olmo, G.J.; Sanchis-Alepuz, H. Bouncing Cosmologies in Palatini f(R) Gravity. Phys. Rev. D 2009, 80, 024016. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Brane-world and loop cosmology from a gravity-matter coupling perspective. Phys. Lett. B 2015, 740, 73–79. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Geodesic completeness in a wormhole space-time with horizons. 2015; in preparation. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmo, G.J.; Rubiera-Garcia, D. Nonsingular Black Holes in ƒ (R) Theories. Universe 2015, 1, 173-185. https://doi.org/10.3390/universe1020173
Olmo GJ, Rubiera-Garcia D. Nonsingular Black Holes in ƒ (R) Theories. Universe. 2015; 1(2):173-185. https://doi.org/10.3390/universe1020173
Chicago/Turabian StyleOlmo, Gonzalo J., and Diego Rubiera-Garcia. 2015. "Nonsingular Black Holes in ƒ (R) Theories" Universe 1, no. 2: 173-185. https://doi.org/10.3390/universe1020173





