1. Introduction
The importance of observing the West Antarctic Ice Sheet has been increasing following a number of alarming scientific results of its potential vulnerability due to its exposure to relatively warmer sea water [
1,
2,
3]. In particular, observation of surface topography change can be important information for glacial remote sensing research and most glaciologists to study ice mass balance and its contribution to sea level. In addition, the marginal region requires continuous surface observation to understand the significant dynamic changes such as faster flow velocity and larger thinning rates [
4].
In Antarctica, the surface height of glaciers and ice sheets is measured by satellite radar and laser altimeters, such as ERS-1/2, Envisat RA-2 and ICESat. These satellite altimeters have measured the surface height data from the early 1990s to present. The typical methods to utilize the accumulated altimeter data to extract the surface height variation are cross-track altimetry and along-track repeat altimetry [
5,
6]. These methods have limitations that may be potentially addressed using other methods such as radar interferometry. For example, studies that used radar altimeters rejected elevation data in the marginal regions of ice sheets where rough surfaces with crevasses and rapid slope variations were present because satellite radar altimeters have a tendency to lose their accuracy in regions of complex topography [
7]. Laser altimeters have greater vertical precision with smaller footprint sizes than radar altimeter but large gaps between each track must be filled by interpolation. The GLAS/ICESat 500 m Laser Altimetry Digital Elevation Model of Antarctica is an example of an interpolated grid from laser point measurements and has a spatial spacing of 500 m and 1 km [
8]. Besides, the DEM, especially in the marginal regions of glaciers with fast flow velocity and high thinning rate, might contain errors caused by the surface height variations during the data acquisition between 2003 and 2005. Thus, space-borne altimetry has mostly been effective in terms of measuring relative variation of the polar surface.
Synthetic aperture radar interferometry is another effective tool for measuring surface topography for an extended area. Generation of surface topography using interferometry is not a new approach for the Antarctic ice bodies. However, the main limitation of radar interferometry for ice sheets and glaciers has been the temporal decorrelation effect seen from low interferometric coherence. Low interferometric coherence can decrease the accuracy of generated surface topography. Thus, special tandem missions to reduce the repeat cycle between data acquisitions had been carried out a number of times. For example, COSMO-SkyMed (Constellation of small Satellites for the Mediterranean basin Observation), conducted by the Italian Space Agency (ASI), is a constellation system using four satellites to reduce the repeat cycle to a single day to minimize the temporal decorrelation. TanDEM-X (TerraSAR-X add-on for Digital Elevation Measurement) is a twin satellite of TerraSAR-X that almost completely eradicates the temporal difference between data acquisition [
9,
10]. Another major limitation of achieving the accurate elevation grid in high resolution in the marginal region of Antarctica is the lack of coincident ground reference at the time of SAR acquisition due to its continuously moving state. To generate precise digital elevation model (DEM) using radar interferometry, accurate ground truth data, known as ground control points (GCP), are necessary as reference. It is difficult to obtain these reference data over continuously flowing and changing ice and snow surfaces. A previous study by Baek et al. has combined ERS tandem mission data and ICESat laser altimetry to generate a DEM over King Edward VII Peninsula in West Antarctica [
11]. However, the time gap between ERS and ICESat was eight years, thus the bias had to be compensated by assuming average thinning rate of the region. Although this technique provided the preliminary reference of the surface at the time, it can hardly be used when measuring the surface height variations and corresponding volume changes over time.
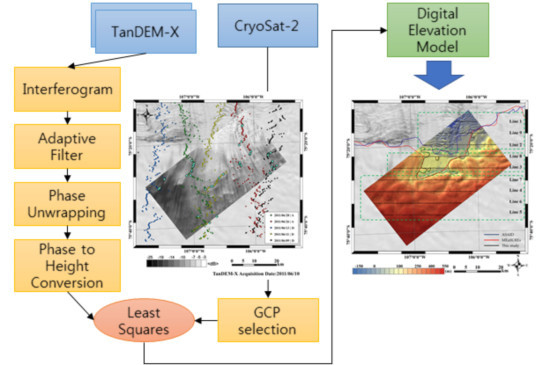
Thus, in this study, we overcome the mentioned limitations by combined usage of single-pass synthetic aperture radar interferometry (TanDEM-X/TerraSAR-X, denoted as TDM) and near-coincident radar altimetry (CryoSat-2, denoted as CS-2) for the first time. The basic idea of combining interferometry and altimetry is not completely new as in other studies such as Zhou et al. [
12] in which utilized ICESat and 35-day repeat-pass interferometry to compensate the ice motion and atmospheric phase; single-pass bi-static configuration of TanDEM-X/TerraSAR-X easily solves the mentioned interferometric problem. Besides, Groh et al. [
13] presented DEM analysis over Thwaites Glacier with near-coincident lidar altimeter; however, airborne campaign at every data acquisition is impossible. Therefore, CryoSat-2 in SAR Interferometric mode (SARIn) point measurements are used as ground control points (GCPs) to calculate absolute height offset. CryoSat-2 is the only available radar altimeter with an ability to provide near-coincident surface height measurements along with TanDEM-X/TerraSAR-X as discussed later in
Section 2.1.2. The accuracy assessment is carried out with the Airborne Topographic Mapper (ATM) from the Operation IceBridge by NASA, acquired five months after the SAR acquisition. Finally, the generated high resolution DEM is used to estimate grounding line location of the ice shelf by utilizing hydrostatic equilibrium theorem.
Section 2 gives detailed information about generating a DEM, datasets and study area.
Section 3 shows result and its assessment.
Section 4 and
Section 5 follow with the discussion, and conclusions are in
Section 6.
3. Results
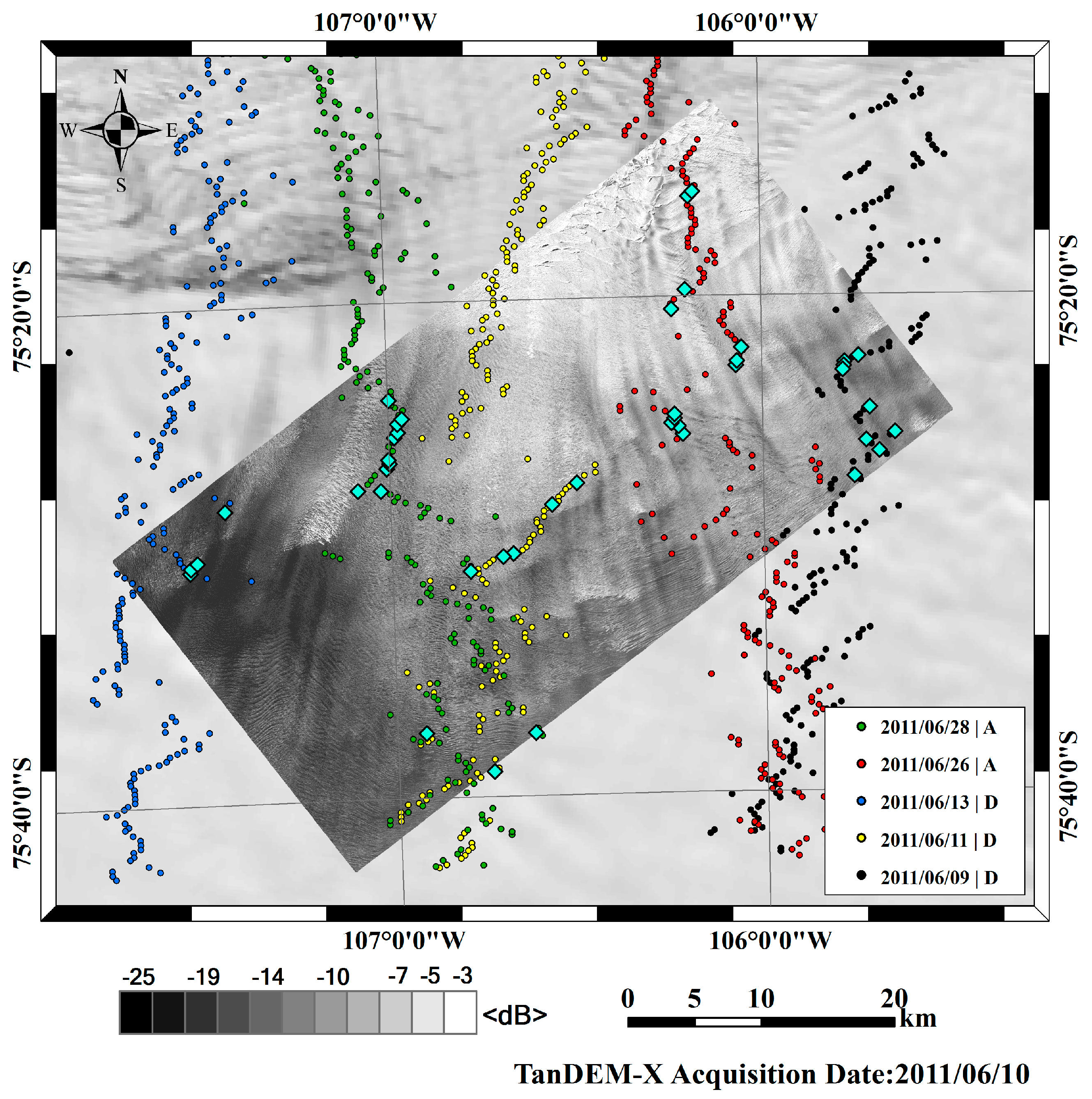
Figure 2 illustrates the generated high resolution DEM using a composite of monthly CS-2 data as reliable GCPs after a selection process. ENVI SARScape is used to generate and unwrap interferograms of TanDEM-X data. After converting it to the uncorrected height and geocoding, the absolute height estimation as well as GCP selection is done using Matlab. GCPs are selected when correlation coefficient is greater than 0.95 with RMS less than 10 m. The number of points within a segment is 5 not only to maintain enough sample number of GCPs, but also to consider that a segment makes azimuth length of around 1.5 km which is nearly the length of azimuth footprint.
More than 1/3 of GCP candidates have higher than 0.95 correlation coefficients where high correlation was originally expected owing to high accuracy of CryoSat-2 data. Besides, RMS height plays a significant role in picking out bad candidates with large biases, dramatically decreasing the number of GCP candidates. Finally, a selected RMS height from the center of 1.5 km represents a slope of 0.76 degrees, indicating selected candidates are from relatively flatter regions.
Out of 368 GCP candidates, a total of 44 points are qualified under the criteria with the mean correlation coefficient of 0.97. They are mostly located over a grounded area of ice sheet; and a couple of points from floating area are seemed to be from relatively smoother area (
Figure 1). The sampling space of the generated DEM is 5 m × 5 m, precise enough to show crevasses and large scale surface undulations over the ice shelf.
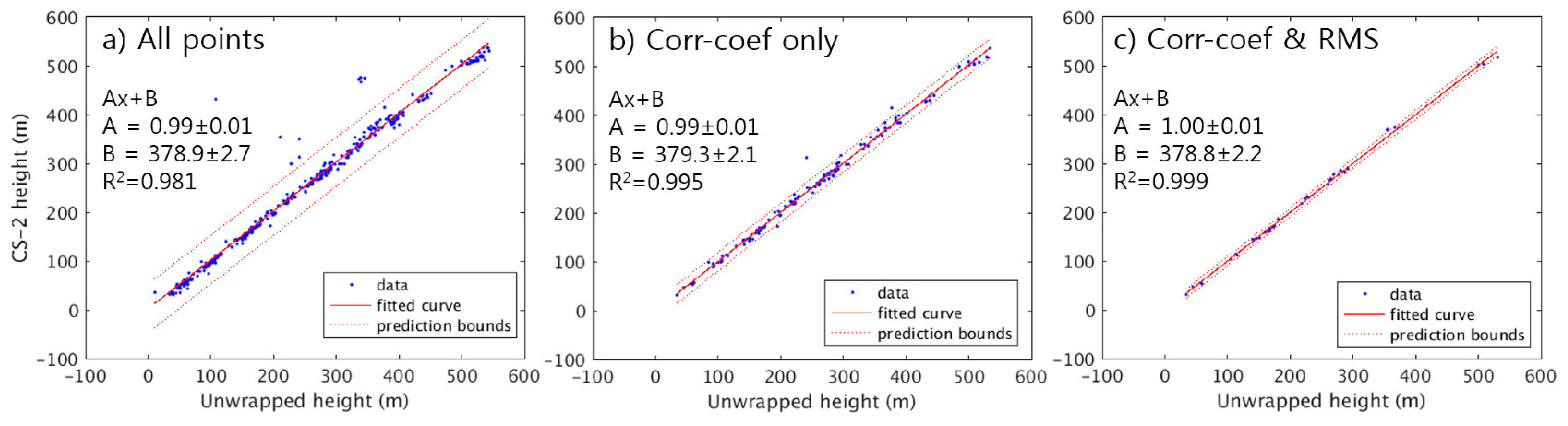
Figure 3 shows the scatter plots between the CS-2 heights, used as GCPs, and the corrected unwrapped heights using linear least-squares approach. The fitted curve of the unbiased estimators is shown in red along with the prediction bounds in dotted red. For each figure, the number of GCPs used in the estimation differs such that in
Figure 3a, all of the available CS-2 heights were used as GCPs and the total number was 334. The R-square value of the fitted result was 0.98; however, the RMS error was 18.57 m.
Figure 3b,c represents the cases when the correlation coefficient was the sole threshold and the coefficients and RMS heights both are combined, respectively. The width of the prediction bounds is the minimum when the correlation coefficients and RMS heights are used with the RMS error of 5.81 m. The mean difference between the CS-2 heights and the corrected unwrapped heights is nearly zero in all cases. This shows that the inclusion of the RMS height as the second threshold practically increases the accuracy of the absolute height estimation although the number of GCPs decreases.
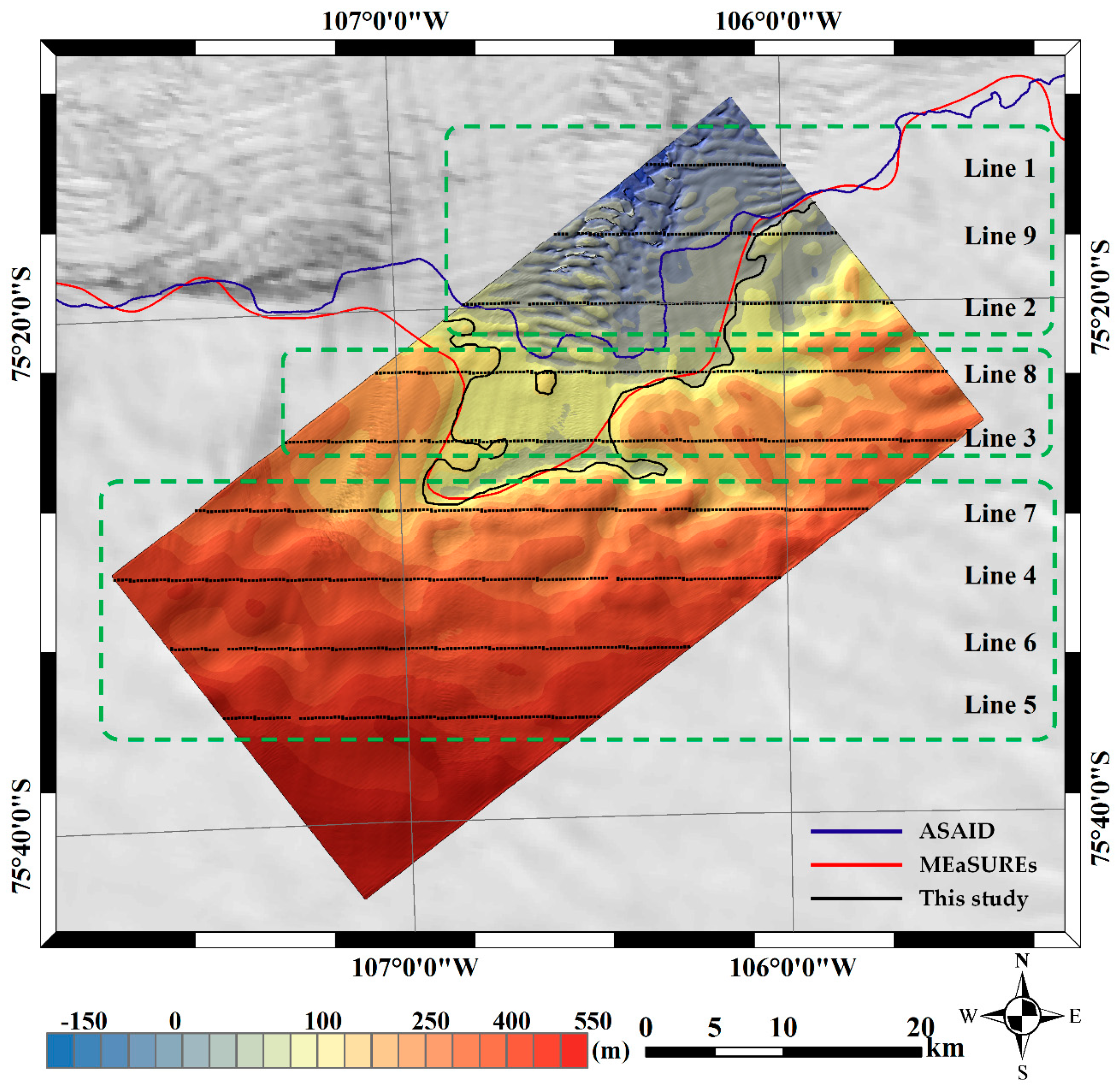
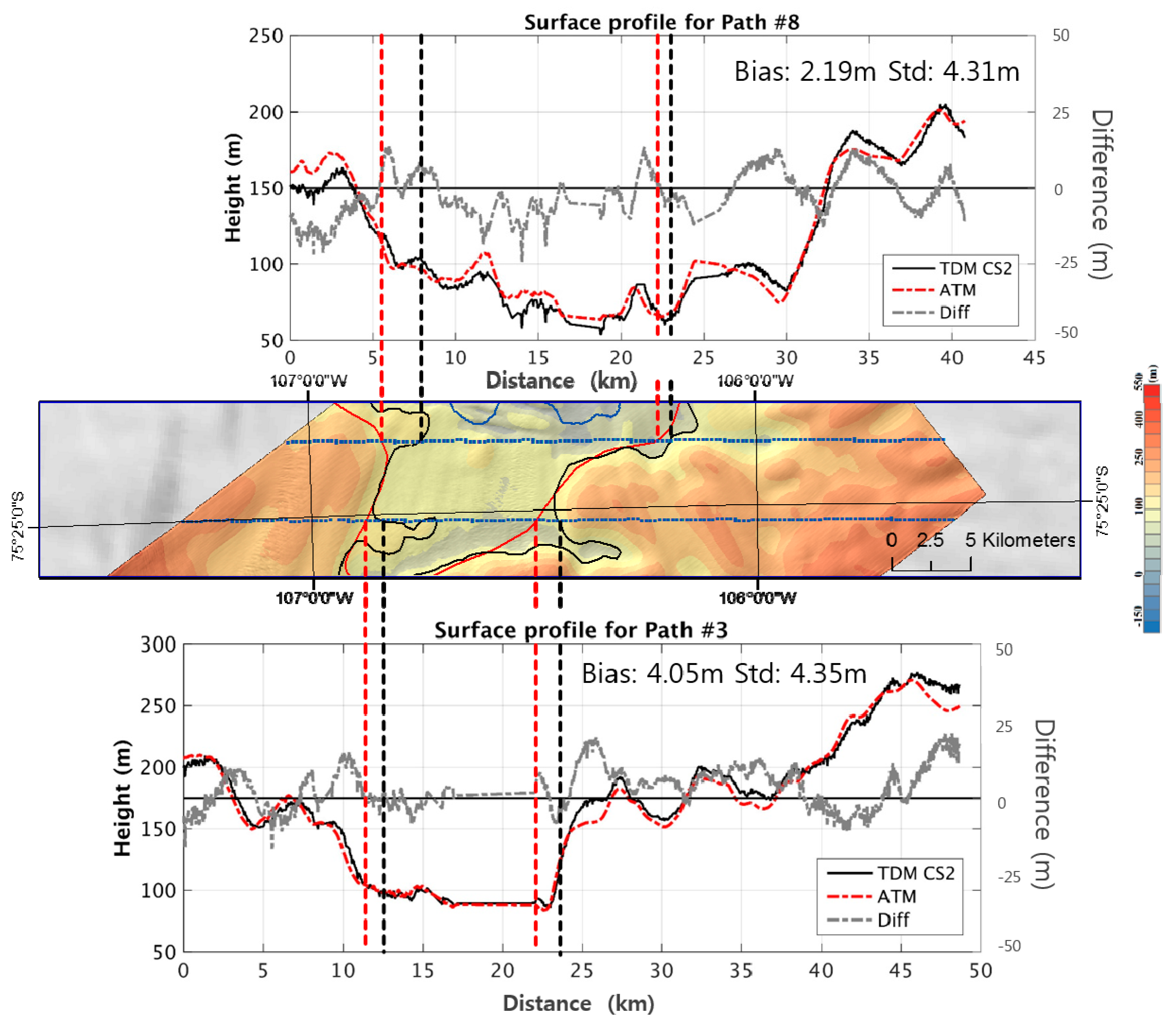
The generated DEM is directly compared with nine ATM flight lines intersecting in longitudinal direction, west-to-east and east-to-west.
Figure 2 shows locations of each flight line, numbered in the order of its acquisition time, shown on the right side of each box. Originally provided with nadir profile plus three off-nadir profiles per time stamp, surface elevation acquired only from nadir direction of ATM flight lines are extracted for a single height profile with a spatial resolution 80 m; and the profile is re-processed to provide an elevation point at every 283 m, which is close to the along-track footprint size of CryoSat-2. Since altimeter points are not located in the middle of each corresponding pixel of the DEM, the surface elevation of the generated DEM is bi-linearly interpolated to match exact locations of the ATM measurements.
Table 2 shows the mean height differences between TDM_CS2 and ATM (TDM_CS2 minus ATM) of each flight line as well as of three sub-sites of the study area: (1) ice sheet; (2) grounding zone; and (3) ice shelf (ice tongue) with respect to the grounding line from the MEaSUREs project.
3.1. Ice Sheet
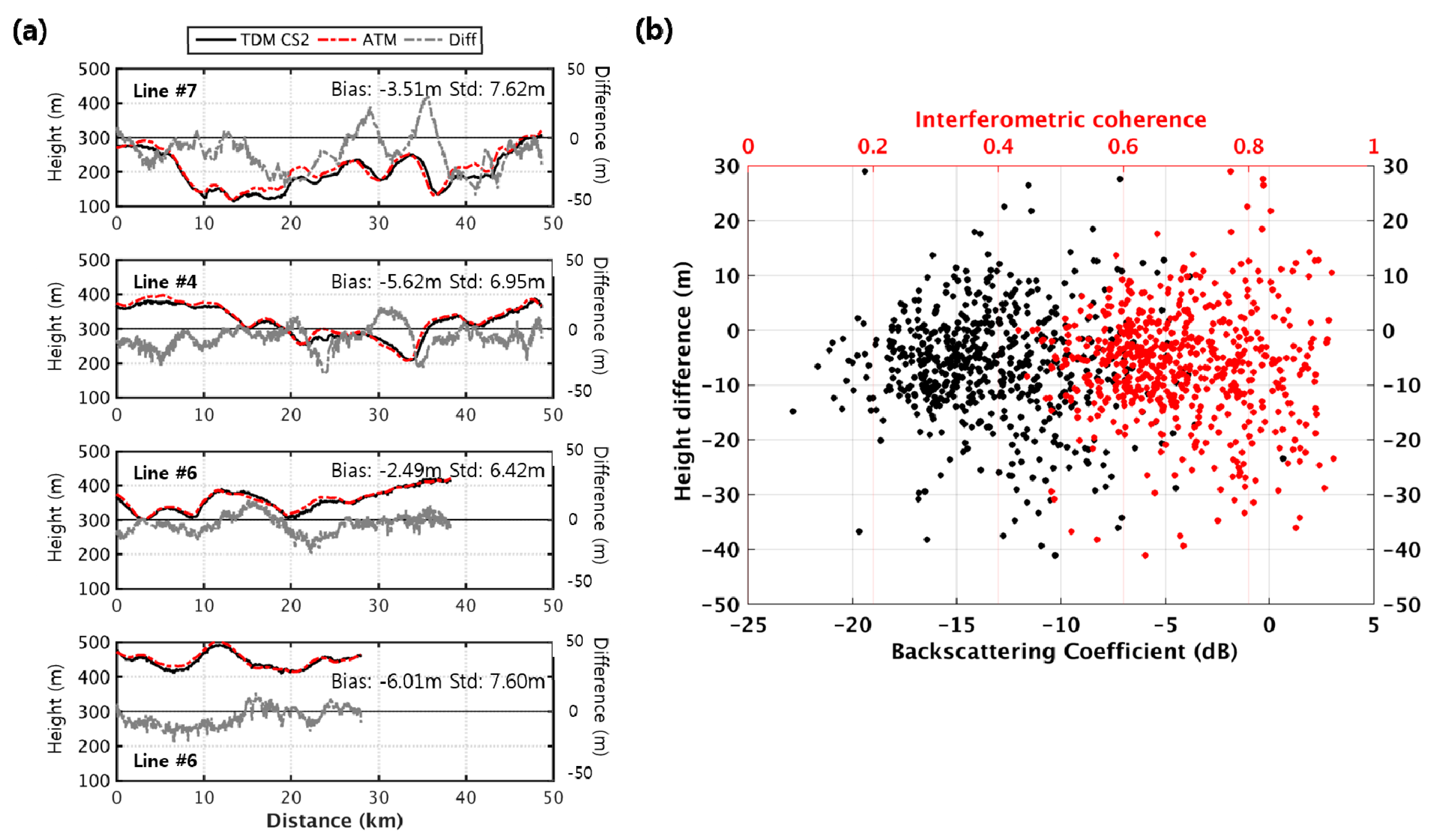
The first site contains the lines 7, 4, 6 and 5 (in order from North to South), representing the grounded ice sheet (
Figure 4a). The profiles with an odd flight number were flown in east-to-west direction and are re-projected to represent topographic profiles in west-to-east direction for easier visualization.
On average, TDM_CS2 shows lower elevation (negative bias) suggesting 4.31 m of the radar penetration if the surface had not changed during five months. The profiles of TDM_CS2 and ATM are also well correlated with some noticeable local height differences.
Higher penetration is usually expected with lower surface density, which can be associated with fresh snow or dryer conditions. In SAR images, it can be observed as low SAR backscattering coefficients. Besides, low backscattering also leads to low coherence decreasing accuracy of interferometry.
Figure 4b illustrates a scatter plot of the height difference versus (black) backscattering coefficients in dB and (red) interferometric coherence. More values are plotted in the negative sign, as the mean difference is negative; however, the plot does not show any trend of height difference.
3.2. Grounding Zone
The second sub-site contains line 8 and 3 at where both profiles cross the grounding line in the western and eastern side and the floating ice tongue in-between (
Figure 5). TDM_CS2 (red) and ATM (black) are well correlated with the mean bias of 2.19 m and 4.05 m and standard deviation of 4.31 m and 4.35 m for line 8 and 3, respectively.
The positive bias of TDM_CS2 may suggest surface lowering during the five months of period. The thinning corresponds with other studies [
35,
36] and sounds plausible; nevertheless, small bias and standard deviation infers that TanDEM-X DEM successfully extract long-wavelength surface elevation near the grounding line where elevation change is the highest.
3.3. Ice Shelf
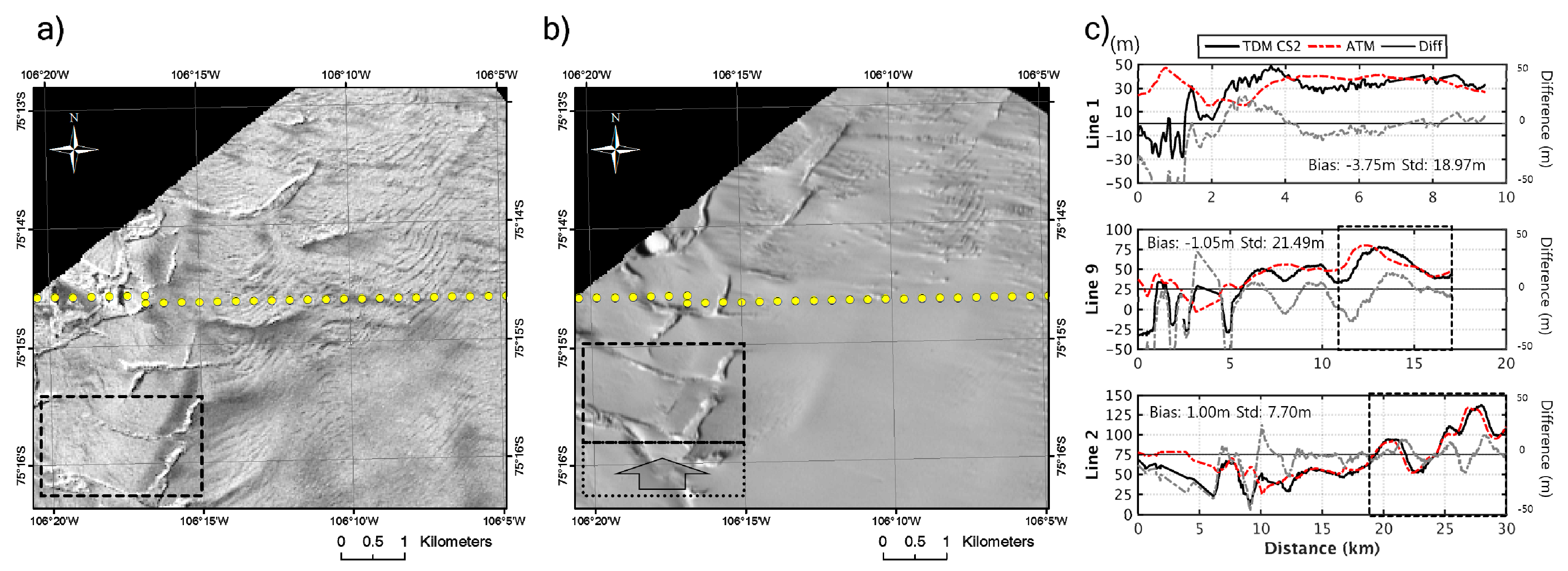
Finally, the third sub-site contains lines 1, 9 and 2, located over the floating ice tongue and the edge of the estimated grounding line of Thwaites Glacier (
Figure 6). Line 1 crosses a region of disintegrating ice tongue at which was reported as the division between the western and eastern ice tongue [
37].
The mean height difference is the largest compared to the other flight lines, mainly due to continuous movement and calving events during the period of five months.
Figure 6 illustrates such surface changes with a similar time span of six months with: (a) an intensity of TanDEM-X; and (b) a Landsat ETM+ image, respectively, acquired on 10 June 2011 and 15 December 2011.
As indicated in a black rectangle box inside the images, the surface feature in the box migrated about 1 km north in six months inferring a flow velocity of around 2 km·a
−1. This flow velocity is roughly close to the velocity of Thwaites Glacier around its grounding line of 3 km·a
−1, estimated using TanDEM-X in 2011 [
13]. The comparison confirms that rapid variation of surface feature is possible during a short period of time and so is the large height difference between ATM and TDM_CS2 at such an area.
Besides, the height differences may be caused by tidal variation. However, when extracting the range of tide in this area using the FES2012 tide model, the range was up to about 1 m. Therefore, the height difference between ATM and TDM_CS2, larger than 1 m, seems to be derived from the time difference between two data.
Lines 9 and 2 show two distinct characteristics along the tracks before and after passing the previously predicted grounding line of [
34] (
Figure 6a). In particular, the profiles of line 2 in a dashed box are almost identical suggesting the fully or partially grounded surface. Surface profiles outside a dashed box in
Figure 6 are located outward from the grounding line, up to 14.25 km from the west in line 9 and up to 19.33 km in line 2, experiencing rapid variation of the ice tongue during the five months.
Line 9 represents a relatively small bias and at the same time shows a very large standard deviation. This phenomenon is due to the horizontal movement of the ice surface for five months and the difference of these surfaces can be displayed in the height difference plot above which changes periodically. Therefore, a mean may become small while its standard deviation becomes high.
4. Grounding Line Estimation
Grounding location at a certain time is found by defining a point at which bottom surface meets bathymetry. Bottom is calculated by subtracting ice thickness from surface where thickness can be computed from ice freeboard assuming hydrostatic equilibrium of a two-layer ice column. Ice freeboard is a distance between surface and sea level which are extractable from satellite data.
A two-layer ice column model consists of layers of ice and firn. The total column thickness:
T is given by
where
is ice freeboard,
is surface height derived from TanDEM-X,
is apparent sea level near-coincident to the acquisition time of TanDEM-X and
is firn layer depth and it is included in the total ice column thickness.
is density of sea water (1028 kg/m
3), ice (917 kg/m
3) and firn. We made an assumption that the firn layer depth is 10 m with a constant surface firn density of 330 kg/m
3 throughout the floating ice tongue.
Apparent sea level is introduced and defined as virtual sea level under ice shelf. In the case of sea-ice, sea level can be extracted from a ridge and a single value might be enough to represent a whole ice floe because sea level does not vary significantly over a small region. However, in the case of ice sheet and ice shelf, the needed extent of sea level is much greater than which might introduce additional errors if a single value is used throughout the region. Besides, it even becomes more challenging to extract sea level at the front of ice shelf if sea ice is present.
In this study, apparent sea level is estimated by compensating EGM08 geoid using CryoSat-2 tide-corrected data acquired in June. After linear least-squares fit between the geoid and radar altimeter in the open water, the mean difference of the compensated sea level is 4.09 cm with RMS of 35 cm. Considering that the sea surface near the coast is covered with sea ice in June, the open water was only available near 73.5°S 113°W. CryoSat-2 data near the polynya in front of the shelf are not used in order to secure enough number of data points for the linear least-square fit.
For comparison with the bottom topography of the ice shelf, the IceBridge Sander AIRGrav L4 Bathymetry data set of the grounding line region of Thwaites Glacier with a spatial resolution of 1 km, constructed from a series of parallel airborne survey lines 10 km apart, is used. Errors are approximated as 70 m for the Thwaites dataset, incorporating errors in gravity measurement, radar ice thickness, ATM surface elevation, 2D model pinning point and some allowance for geological structures [
38]. The bathymetry was interpolated to 25 m spatial resolution using spline interpolation method that is useful for interpolating unevenly distributed dataset [
39]. We expected that spline interpolation could render irregular topographic pattern of the gravity-derived bathymetry which is influenced by non-linear sediment densities.
Figure 2 illustrates the grounding line from this study as well as from MEaSUREs project [
34] and ASAID project [
33]. The grounding line from ASAID project was derived using combined dataset from Landsat 7 and Ice, Cloud, and land Elevation Satellite (ICESat) laser altimetry spanning from 1999 to 2003. The grounding line from MEaSUREs project was measured in 2009 derived using differential satellite synthetic aperture radar interferometry. The ground line has small mismatch of less than 1 km in various places but shows high spatial correlation with the MEaSUREs grounding line. On the other hand, the comparison with the grounding line from ASAID project suggests around 10 km retreat in the central part of the study area.
Figure 5 also shows the previously estimated grounding line in 2009 and newly estimated grounding line from this study, respectively represented in red and black. The surface profile of line 8 and 3 are drawn to the equivalent scale and the locations of intersecting points of each line with ATM are extended. A comparison not only suggests possible grounding line retreat in the east, but also defines grounded region in the west where the previously grounding line might have missed.
5. Discussion
In this study, the absolute height is determined using selected ground control points after the unwrapped phase is converted to the unwrapped height and geocoded. The estimation of zero-phase-offset is proved valid as the coefficient A (Equation (6)) is very close to 1 otherwise the coefficient A must be other than 1 if there were any phase ramp; and this also shows that the phase ramp is negligible in this case.
We decided not to use other available external DEMs in phase unwrapping, estimating the absolute phase offset or minimizing the phase ramp. We had tried to use the available DEMs, such as ASTER and GLAS/ICESat DEMs, over this region; however, the usage of these DEMs over the marginal region of Thwaites Glacier created additional phase ramps due to very poor spatial resolution and relatively extreme surface deformation since the generation of these DEMs. Besides, DEMs are not available over the floating regions.
In spite of high correlation along with small bias and standard deviation between TDM_CS2 and ATM, there is a major factor that needs to be taken into account. The compensated elevation of TanDEM-X represents the scattered surface of Ku-Band radar altimeter instead of X-Band interferometric phase center. Besides, the temporal difference of about five months between the generated DEM and ATM must be taken into consideration and corresponding seasonal variation of surface characteristics may be present.
We strongly believe that the biggest contributors of the uncertainty are the five-month gap between the acquisitions of TanDEM-X and ATM as well as radar penetration. However, it is difficult to distinguish these two effects from a simple height comparison.
Although similar radar penetration was reported by Groh et al. [
13], the comparison of TanDEM-X DEM and ATM data as reported here is insufficient to yield any meaningful penetration as well as temporal variation of the surface because of significant dynamical surface changes during the five-month time difference. Groh et al. [
13] report surface lowering by several meters within one year (2011–2012) on the lower section of Thwaites glacier. Helm et al. [
35] also report thinning of Thwaites Glacier up to 10 m/year based on analysis of CryoSat-2 data. If the thinning rate (10 m/year) is assumed to be linear and spatially homogeneous, the surface decreases about 5 m during five months. This thinning implies that the penetration depth in this area is greater than 9 m.
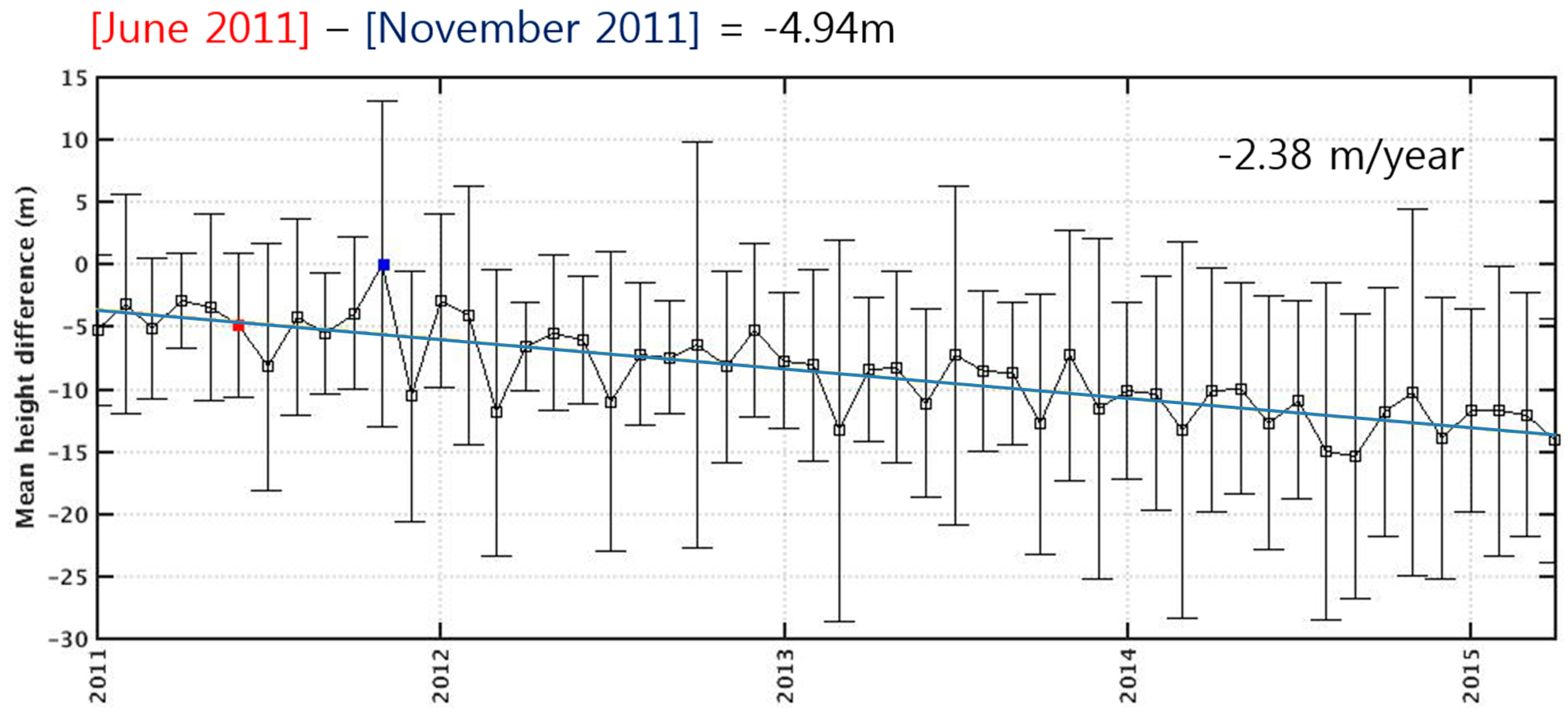
On the other hand, if the penetration is completely neglected, the result infers the surface increase of around 4 m within five months in an area where a surface lowering has been reported as previously mentioned. Although the result sounds contradictory, a monthly basis cross-point analysis between CryoSat-2 and ATM over the grounded ice sheet from 2011 to 2015 suggests that thickening in November 2011 is a possible event (
Figure 7). While indicating surface thinning rate of −4.01 m/year, the relative mean height difference between June (blue) and November (red) in 2011 corresponding to the acquisition dates of TanDEM-X and ATM, respectively is, −4.94 m. What actually caused this thickening at this specific time of year needs additional analyses; however, the comparison between TDM and ATM may be explained without radar penetration. Besides, if seasonal surface variation, known as breathing is taken into consideration, then the penetration depth can vary again. Therefore, in our study, we decided not to interpret the calculated height bias as penetration depth because the actual interferometric penetration and the height variation during five months are indistinguishable.
Meanwhile, the grounding line is also a significant key factor in understanding ice sheet stability and grounding line retreat and its potential danger has been reported from a number of studies [
22,
24,
38]. The line profiles in this study show grounding line migration, especially taking in place in the eastern part of the ice tongue. This gives an insight of the grounding line retreat that had been taking place as described in [
24]. There can be numerous speculations about this, and yet the disappearance of large ice tongue and continuous rapid thinning of the glacier seemed to be the major contributor [
22,
36]. However, it must be reminded that this migration can also be observed mainly due to increase of spatial resolution. It is expected that more sequential TanDEM-X data in this region would be able to validate this result.
The comparison of the estimated grounding line with the ASAID grounding line suggests nearly 10 km retreat from the project to 2011. The same comparison with the MEaSUREs grounding line does not suggest any dramatic retreat since 2009. The existence of a deep trough and its shape around the estimated grounding line may suggest the retreat might have been caused by the basal melting from the intrusion of circumpolar deep water as suggested from many publications (i.e., [
3,
40,
41]). However, the information is not enough to conclude whether the retreat had been progressive or abrupt due to a lack of continuous observation in-between and it is expected that a continuous grounding line observation using the technique in this study would be able to fill the gap in the future to understand the stability of Thwaites Glacier.
In contrast to the increasing resolution of the surface topography, the spatial and vertical uncertainty of the available bathymetry remains much lower than that of other datasets. As a result, the spatial uncertainty of the estimated grounding line caused by the 70 m vertical uncertainty of the bathymetry is around 1 km. It is also expected to increase the accuracy of the grounding line estimation if more accurate bathymetry is available.
The assumption hydrostatic equilibrium might not be satisfied near the grounding line because of the supporting force from the grounded ice. However, we expect that the error from this assumption is relatively minor because the estimated grounding line in 2011 shows high spatial correlation with the previous grounding line in 2009.
The grounding line also can be found using tidal flexure of ice of which can be observed from double- and quadruple-differential InSAR technique. This technique requires the minimum of four independent SAR acquisitions with a short revisit period between each InSAR pair for high interferometric coherence. Rignot et al. [
19] evaluated the grounding line of Thwaites Glacier in 2011 using ERS-2 data that have a three-day repeat cycle and their result agrees with our result, i.e., a small ice rumple in front of the estimated grounding line is shown in both studies.
Besides, we tried to validate the grounding line location and its possible retreat in recent years using 17 Sentinel-1A images. Sentinel-1A has a revisit period of 12 days and the data were acquired from July 2015 to June 2016. We were unable to produce any acceptable interferograms because the interferometric coherence of all pairs was extremely low due to fast flow of Thwaites Glacier near the marginal region.
6. Conclusions
A high resolution digital elevation model in the marginal region of Thwaites Glacier was successfully generated by combined usage of TanDEM-X and TerraSAR-X single-pass interferometry and CryoSat-2 SARIn radar altimetry. Instead of estimating phase offset, the usage of near-coincident radar altimeter as ground control points determined absolute topographic height exploiting linear least-squares algorithm. Reliable GCPs were also carefully selected using normalized cross-correlation and RMS height.
Compared with airborne laser altimeter which was acquired five months after the acquisition of SAR data, a large height bias was observed on the ice tongue region at where intense activities were continuously occurring. Meantime, the result showed different spatial trends; surface lowering was observable near the grounding line (positive bias of 3.19 m), whereas laser altimeter represented higher elevation on the grounded ice sheet suggesting radar penetration (negative bias of −4.31 m). However, the height difference between two epochs was considered not enough to conclude temporal trend of which more time series data will be required.
Besides, it must be stated that the accuracy of the generated elevation model is expected to be different if the laser measurement with less time gap is available. Even without considering the height change due to the time gap, the current result contains errors arising from the radar penetration difference between TanDEM-X interferometry and CryoSat-2 altimetry as well as the difference from the laser measurement. If at least the error of the time gap can be reduced, more precise analysis will be possible.
Grounding line estimation was carried out by exploiting hydrostatic equilibrium of ice shelf. Ice thickness was calculated from freeboard height which required high resolution DEM and apparent sea level at the time of the acquisition. The newly estimated grounding line was compared with the previous grounding lines from different datasets and showed its feasibility of detecting the spatial evolution of grounding line in time series. A continuous observation of grounding line is important because it can directly provide the stability of an ice body. Our result will not only help collect continuous datasets, but also expect to detect small-scaled changes that we have been missing.
In conclusion, the most crucial part of this application was the presence of simultaneous dataset that could be used as ground control points in calculating absolute height. Besides, the importance of the selection process of reliable ground control point must be emphasized as well. After all, this study has shown that TanDEM-X can provide high-resolution elevation information even in the area without any ground truth data by using near coincident CryoSat-2 radar altimeter data.