Energy Mutual Aid Device of Electric Vehicles: Quadratic Boost Converter with Modified Voltage-Mode Controller
Abstract
:1. Introduction
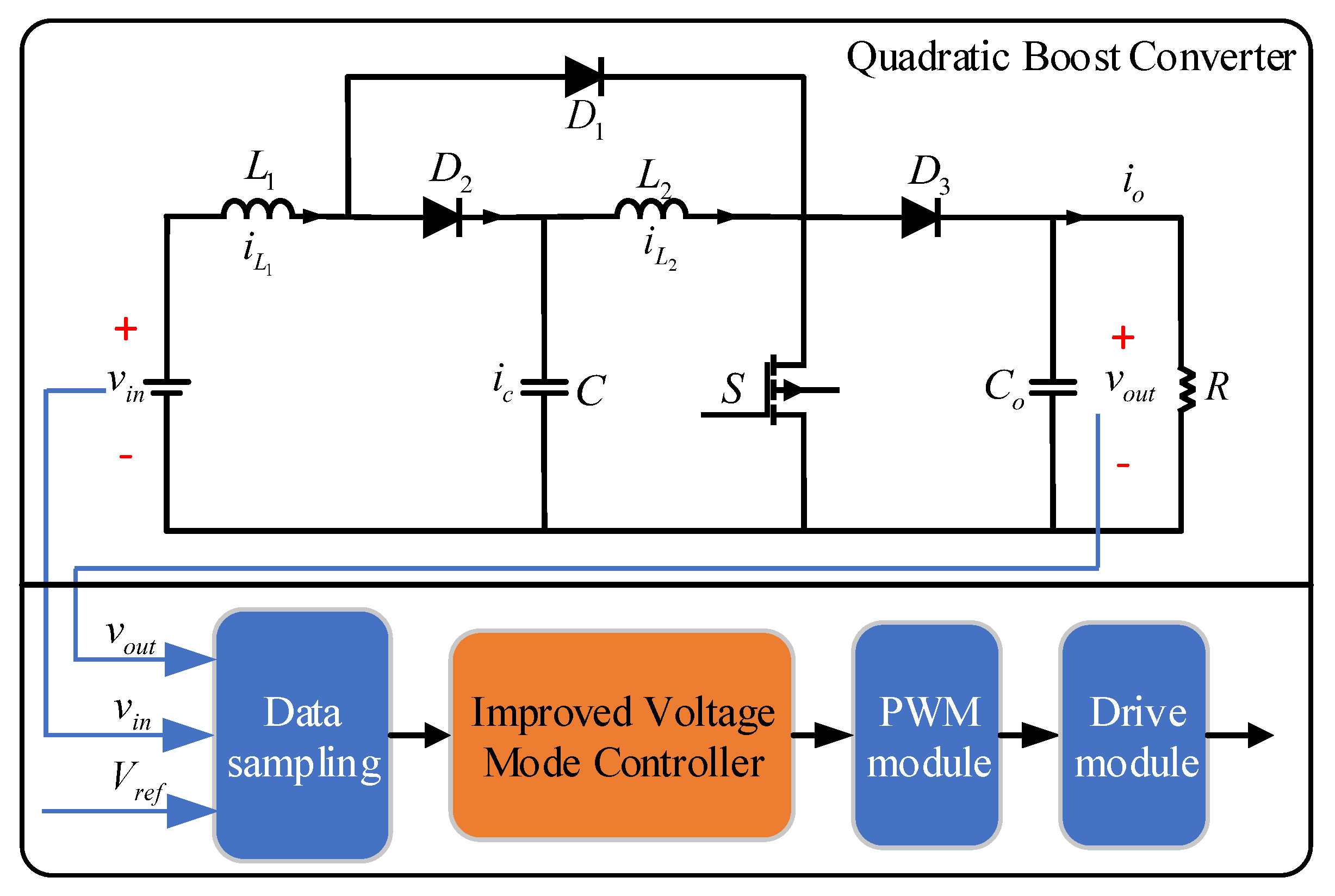
- In this paper, a quadratic boost converter and an improved voltage mode control strategy are adopted for the output voltage, charging voltage, and charging power of the electric vehicle power battery. It can produce both higher and wider voltage gain and higher output power than the conventional boost converter and also avoid the problems of the existing voltage mode control strategy.
- The quadratic boost converter and improved voltage mode control strategy used, which uses only one switching device and fewer sensors to obtain the feedback amount, dramatically reduces the size and weight of the device and makes it more portable.
2. Quadratic Boost Converter
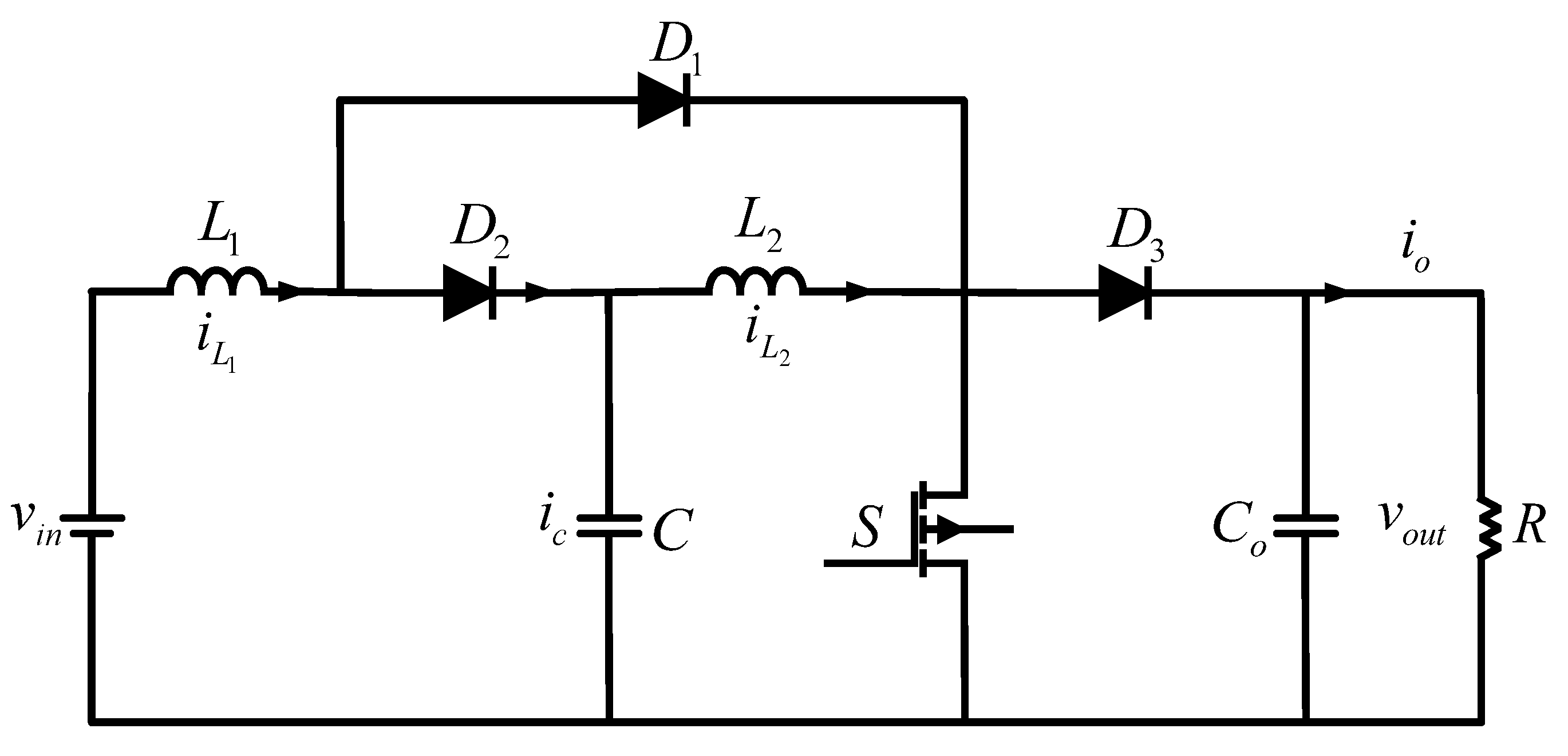
3. Voltage Mode Controller Control Algorithm
3.1. Conventional Voltage Mode Controller
3.2. Improved Voltage Mode Controller
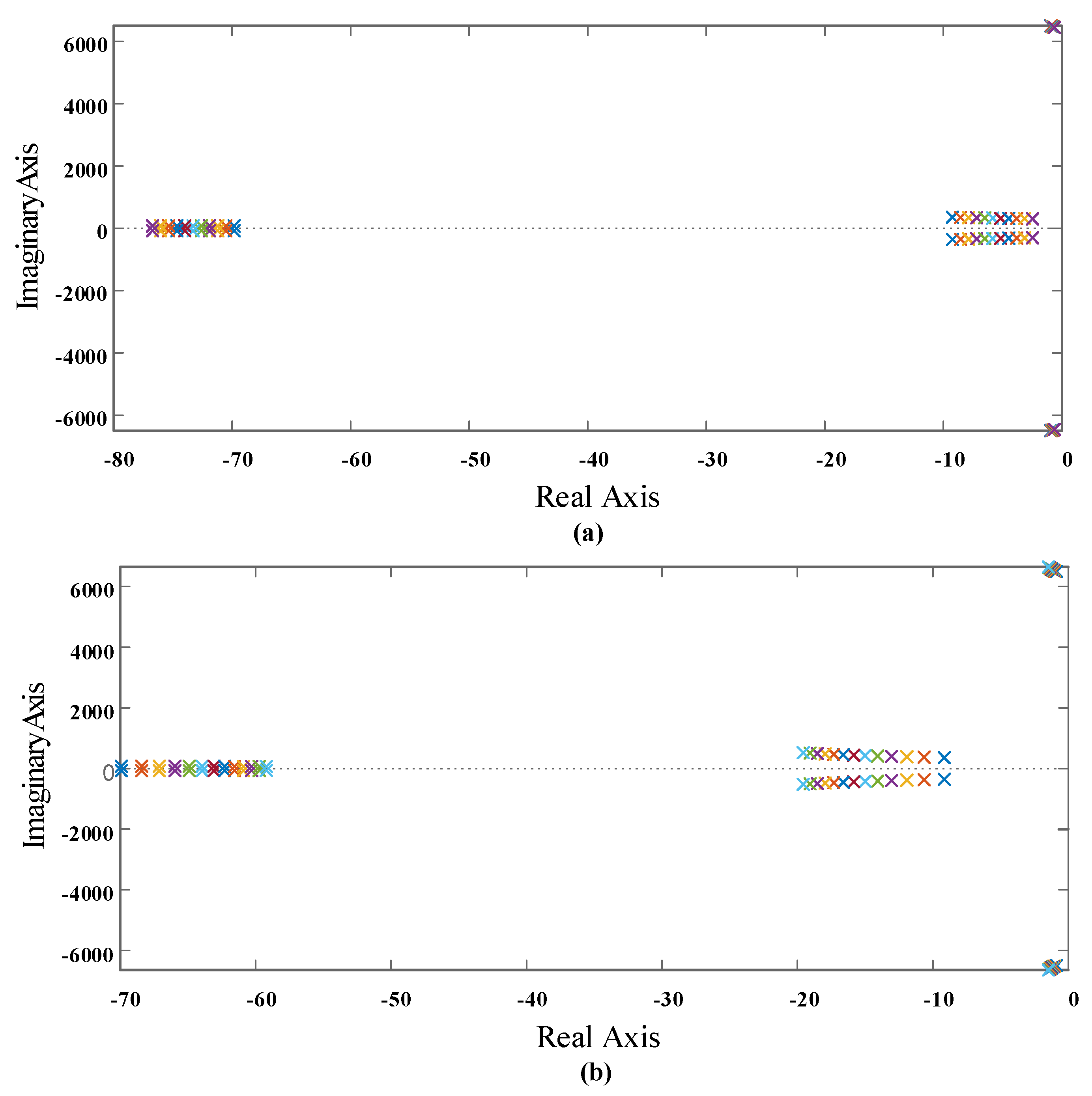
3.3. Stability Analysis
4. Simulation Verification
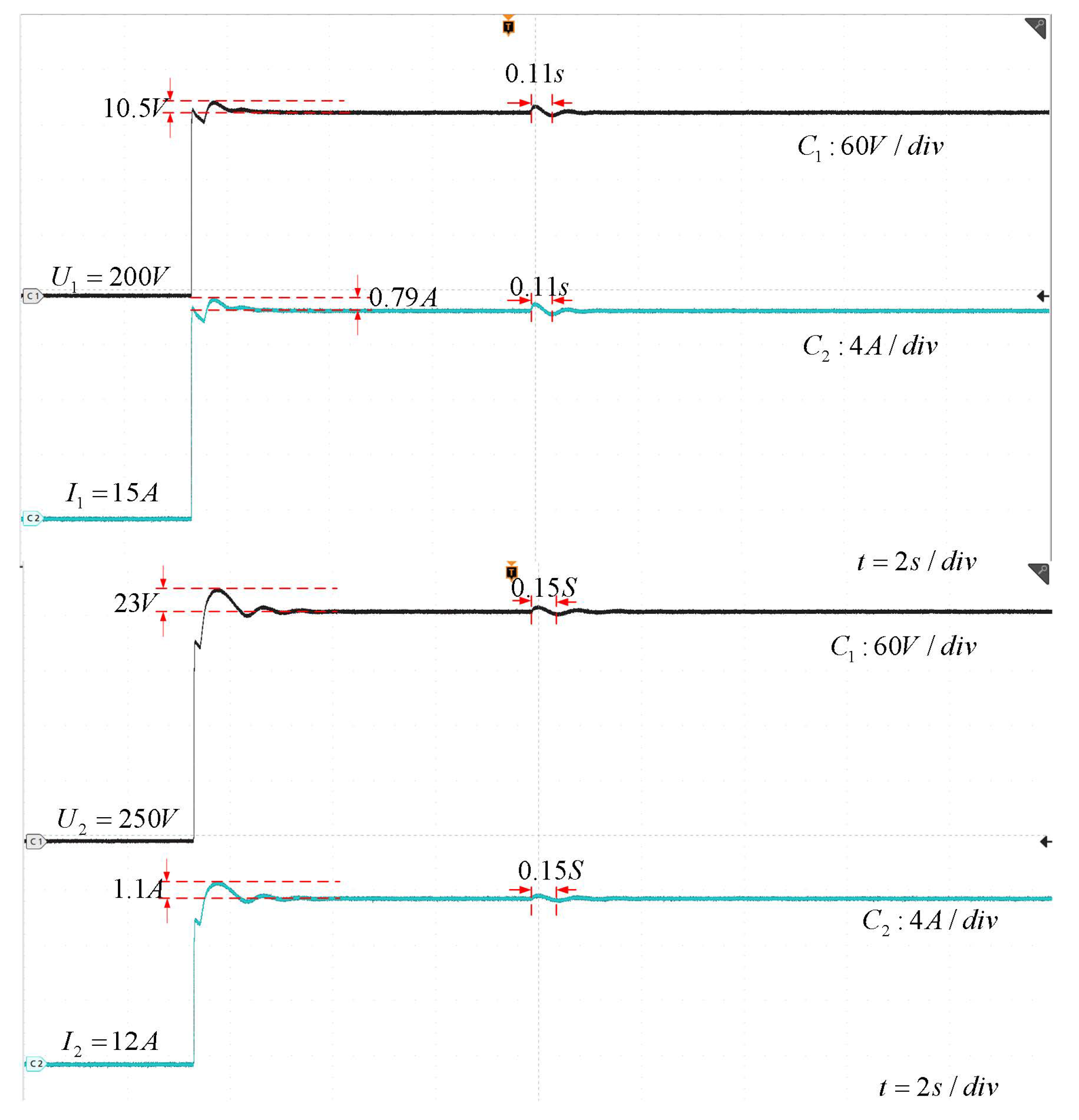
- Case 1:In the first case, the Chery QQ ice-cream is taken as ESV and the BaoJun e100 and Hongguang MINIEV are taken as ECVs. According to the parameters in Table 1, the input voltage of the vehicle–vehicle energy mutual aid device is 90V, i.e., 90 V, and the output voltage is 200 V/250 V. The reference voltage 200 V/250 V.As and show in Figure 5, when the Chery QQ ice-cream charges the BaoJun e100, the output voltage steady-state value 200 V, the maximum overshoot 6.8% (less than 10%), and the regulation time 0.14s. When the simulation proceeds to 2 s when a 20% perturbation occurs in , can still recover 200 V output voltage quickly, and the system has strong robustness. The output voltage 3 kW.As and show in Figure 5, when the Chery QQ ice-cream charges the Hongguang MINIEV, 250 V, maximum overshoot 9.6% (less than 10%), and regulation time 0.23 s. When the simulation proceeds to 2 s when a 20% perturbation occurs in , can still recover the 250 V output voltage quickly, and the system has strong robustness. The output voltage 3 kW.In summary, the Chery QQ ice-cream charges the BaoJun e100, Hongguang MINIEV, and the output response can reach the set value quickly, with the overshoot not exceeding 10% of the set value. When was disturbed, the output voltage of ESV was reduced to 80% of the original voltage, the device was able to regulate quickly to the stable value, and the device was effective.
- Case 2:In this case, the BaoJun e100(A) is taken as ESV and BaoJun e100(B) and the Hongguang MINIEV are taken as ECVs. According to the parameters in Table 1, the input voltage of the vehicle–vehicle energy mutual aid device is 110V, i.e., 110 V, and the output voltage is 200 V/250 V. The reference voltage 200 V/250 V.As and show in Figure 6, when the BaoJun e100(A) charges the BaoJun e100(B), 200 V, the maximum overshoot % = 5.3% (less than 10%), and the regulation time 0.15 s. When the simulation proceeds to 2 s, can recover quickly to 200 V when a 20% perturbation occurs in . The system has strong robustness. The output voltage is still stable at 3 kW.As and show in Figure 6, when the BaoJun e100(A) is charged for the Hongguang MINIEV, 250 V, maximum overshoot 9.2% (less than 10%), and regulation time 0.22 s. When the simulation proceeds to 2s, can recover to 250 V quickly when a 20% perturbation of occurs. The system has strong robustness. The output voltage 3 kW.So, by the same argument, the simulation of choosing the BaoJun e100(A) for the BaoJun e100(B) and the Hongguang MINIEV charging can prove the effectiveness of the device.
- Case 3:In contrast to the two cases above, in this case, the Hongguang MINIEV and the Baojun e200(A) are taken as ESVs and the Hongguang MINIEV and the Baojun e200(A) are taken as ECVs. According to the parameters in Table 1, the input voltage of the vehicle–vehicle energy mutual aid device is 96 V/122 V, i.e., 96 V/122 V, and the output voltage is 220 V. The reference voltage 220 V.As shown in Figure 7, the Hongguang MINIEV powers the Baojun e200(A) (), and the Baojun e200(B) powers the Baojun e200(C) (), corresponding to an overshoot % of 6.8%/6.4% and regulation time 0.17 s/0.16 s, respectively. When the simulation proceeds to 2 s, the output voltage and current can quickly recover to the set value when a 20% disturbance of occurs.This case selects the Hongguang MINIEV and the Baojun e200(A) charging for the Baojun e200(B) for simulation to prove the effectiveness of the device.
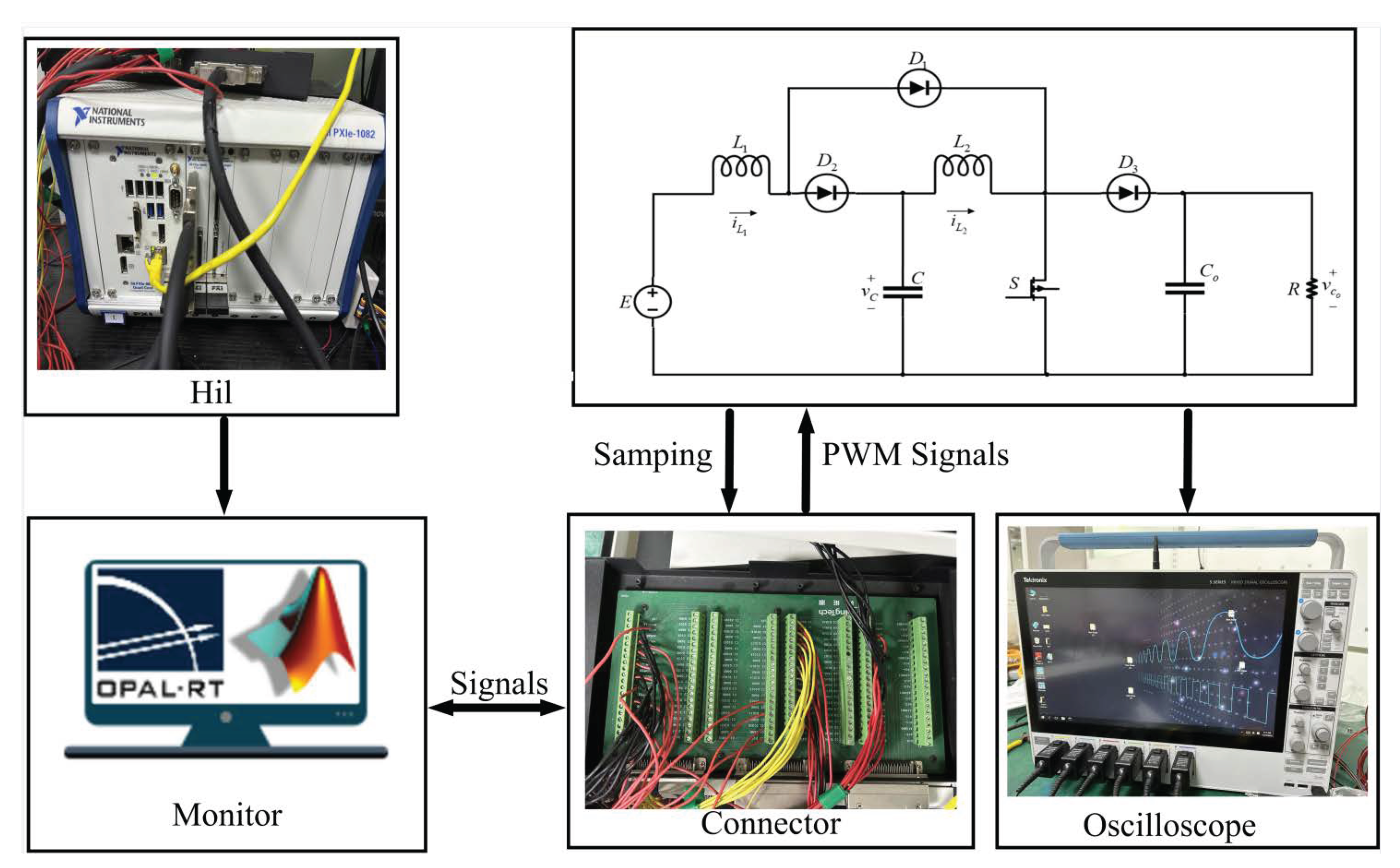
5. Experimental Verification
- Experiment 1:Experiment 1 is based on case 1 in the simulation. ESV is selected from the Chery QQ ice-cream, and ECVs are selected from the BaoJun e100, the Hongguang MINIEV, and the experimental results are shown in Figure 9. When the Chery QQ ice-cream is charged for the BaoJun e100, the input voltage of the vehicle–vehicle energy mutual aid device is 90V, i.e., 90 V, and the output voltage of the device 200 V. When the Chery QQ ice-cream is charged for Hongguang MINIE, the input voltage of the vehicle–vehicle energy mutual aid device is 90 V, i.e., 90 V, and the output voltage of the device 250 V. From the experimental results, the energy mutual aid device can quickly generate the voltage needed for ECVs, the overshoot generated is less than 10%, and the stability can be quickly restored when receives a disturbance. It proves the effectiveness of the device.
- Experiment 2:Experiment 2 is based on case 2. The experimental results are shown in Figure 10. BaoJun e100(A) is selected as ESV, and BaoJun e100(B) and Hongguang MINIEV are selected as ECVs. When BaoJun e100(A) charges BaoJun e100(B), 110 V and 200 V. When BaoJun e100(A) charges Hongguang MINIEV, 110 V and 250 V. From the experimental results, the energy mutual aid device can quickly generate the voltage needed for ECV, and the overshoot is less than 10%. 2 s; when receives a disturbance, the device quickly restores stability. The experimental results prove the effectiveness of the device.
- Experiment 3:Experiment 3 is based on case 3. The experimental results are shown in Figure 11. Hongguang MINIEV and Baojun e200(A) are selected as ESVs, and BaoJun e200(B) is selected as ECV. The output voltage of Hongguang MINIEV and Baojun e200(A) is 96 V/22 V, respectively, and BaoJun e200(B) requires a charging voltage of 220 V. From the experimental results, the energy mutual aid device can quickly generate the voltage needed for ECV, the amount of overshoot generated is less than 10%, and the device quickly returns to stability when receives a perturbation at 2 s. The experimental results prove the effectiveness of the device.
6. Conclusions
- Compared with the hardware topology used in [26,30], the quadratic boost converter is used in this paper. The quadratic boost converter uses fewer electrical components to produce both higher and wider voltage gain and higher output power and can greatly reduce the number of electric components. The size and weight of the device can be greatly reduced. It also reduces the cost of the device.
- Compared with the troditional control algorithm, the modified voltage-mode controller is simpler, and it requires only one feedback amount to achieve the desired output. Meanwhile, the modified voltage-mode controller uses integral action based on the normalized voltage error in (17). This makes the integrand bounded. Therefore, due to this integration process, even if the output voltage deviates from the reference voltage by a large amount, it does not make the integration result too large. This can effectively improve the dynamic response of the output voltage.
- Compared to the existing charging devices, the vehicle–vehicle energy mutual aid device is less costly and does not require the modification of the electric vehicle. The device is smaller in size and weight, making it easy to carry around and use. With these effects, the vehicle–vehicle energy mutual aid device can alleviate the battery charging and range problems. Finally, the simulation and experimental results demonstrate the accuracy and feasibility of the conversion device.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Medvedkina, Y.; Khodochenko, A. Renewable Energy and Their Impact on Environmental Pollution in the Context of Globalization. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Evode, R. Modeling of Electric Grid Behaviors having Electric Vehicle charging stations with G2V and V2G Possibilities. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, 7–8 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Jia, Y.; Jibrin, R.; Görges, D. Energy-optimal adaptive cruise control for electric vehicles based on linear and nonlinear model predictive control. IEEE Trans. Veh. Technol. 2020, 69, 14173–14187. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Y.; Chen, L.; Shi, D.; Wang, S.; Zhu, Z. Research on compound coordinated control for a power-split hybrid electric vehicle based on compensation of non-ideal communication network. IEEE Trans. Veh. Technol. 2020, 69, 14818–14833. [Google Scholar] [CrossRef]
- Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. Coordinated planning strategy for electric vehicle charging stations and coupled traffic-electric networks. IEEE Trans. Power Syst. 2018, 34, 268–279. [Google Scholar] [CrossRef]
- Zhai, C.; Luo, F.; Liu, Y. A novel predictive energy management strategy for electric vehicles based on velocity prediction. IEEE Trans. Veh. Technol. 2020, 69, 12559–12569. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Sun, C.; Zhang, H.; Gui, Y.; Wang, P. Vehicle-vehicle energy interaction converter of electric vehicles: A disturbance observer based sliding mode control algorithm. IEEE Trans. Veh. Technol. 2021, 70, 9910–9921. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, X.; Guo, F.; Chen, J.; Wang, P.; Koh, L.H. Large-signal stability of interleave boost converter system with constant power load using sliding-mode control. IEEE Trans. Ind. Electron. 2019, 67, 9450–9459. [Google Scholar] [CrossRef]
- Jiang, W.; Chincholkar, S.H.; Chan, C.Y. Investigation of a voltage-mode controller for a dc-dc multilevel boost converter. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 908–912. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Pinjia, Z.; Yonghao, G.; Dehao, Q.; Peng, W. Reduced-order transfer function model of the droop-controlled inverter via Jordan continued-fraction expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar] [CrossRef]
- Kumar, N.; Mohamadi, M.; Mazumder, S.K. Passive damping optimization of the integrated-magnetics-based differential-mode ćuk rectifier. IEEE Trans. Power Electron. 2020, 35, 10008–10012. [Google Scholar] [CrossRef]
- Lotfi Nejad, M.; Poorali, B.; Adib, E.; Motie Birjandi, A.A. New cascade boost converter with reduced losses. IET Power Electron. 2016, 9, 1213–1219. [Google Scholar] [CrossRef]
- Maksimovic, D.; Cuk, S. Switching converters with wide DC conversion range. IEEE Trans. Power Electron. 1991, 6, 151–157. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Ramirez, J.M.; Peng, F.Z.; Valderrabano, A. A DC–DC multilevel boost converter. IET Power Electron. 2010, 3, 129–137. [Google Scholar] [CrossRef]
- Luo, F.L.; Ye, H. Super-lift boost converters. IET Power Electron. 2014, 7, 1655–1664. [Google Scholar] [CrossRef]
- Lin, B.R.; Chen, J.J. Analysis and implementation of a soft switching converter with high-voltage conversion ratio. IET Power Electron. 2008, 1, 386–394. [Google Scholar] [CrossRef]
- Yun, J.J.; Choe, H.J.; Hwang, Y.H.; Park, Y.K.; Kang, B. Improvement of power-conversion efficiency of a DC/DC boost converter using a passive snubber circuit. IEEE Trans. Ind. Electron. 2011, 59, 1808–1814. [Google Scholar] [CrossRef]
- Chan, C.Y.; Chincholkar, S.H.; Jiang, W. Adaptive current-mode control of a high step-up DC/DC converter. IEEE Trans. Power Electron. 2016, 32, 7297–7305. [Google Scholar] [CrossRef]
- Chincholkar, S.H.; Chan, C.Y. Design of fixed-frequency pulsewidth-modulation-based sliding-mode controllers for the quadratic boost converter. IEEE Trans. Circuits Syst. II Express Briefs 2016, 64, 51–55. [Google Scholar] [CrossRef]
- Tan, S.C.; Lai, Y.M.; Tse, C.K. A unified approach to the design of PWM-based sliding-mode voltage controllers for basic DC-DC converters in continuous conduction mode. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 1816–1827. [Google Scholar]
- Chincholkar, S.H.; Jiang, W.; Chan, C.Y. An improved PWM-based sliding-mode controller for a DC–DC cascade boost converter. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 1639–1643. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Martinez-Salamero, L.; Garcia, G.; Valderrama-Blavi, H.; Sierra-Polanco, T. Robust sliding-mode control design for a voltage regulated quadratic boost converter. IEEE Trans. Power Electron. 2014, 30, 2313–2327. [Google Scholar] [CrossRef]
- Chan, C.Y. Investigation of voltage-mode controller for cascade boost converter. IET Power Electron. 2014, 7, 2060–2068. [Google Scholar] [CrossRef]
- Jiang, W.; Chincholkar, S.H.; Chan, C.Y. Improved output feedback controller design for the super-lift re-lift Luo converter. IET Power Electron. 2017, 10, 1147–1155. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Xie, Y.; Liu, J.; Fu, C.; Liu, B. Optimized charging of lithium-ion battery for electric vehicles: Adaptive multistage constant current–constant voltage charging strategy. Renew. Energy 2020, 146, 2688–2699. [Google Scholar] [CrossRef]
- Wang, R.; Li, J.; Sun, Q.; Zhang, H.; Wei, Z.; Wang, P. Energy Transfer Converter Between Electric Vehicles: DC-DC Converter Based on Virtual Power Model Predictive Control. IEEE Trans. Consum. Electron. 2023, 69, 556–567. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Qin, D.; Li, Y.; Li, X.; Wang, P. Steady-state Stability Assessment of AC-busbar Plug-in Electric Vehicle Charging Station with Photovoltaic. J. Mod. Power Syst. Clean Energy 2020, 8, 884–894. [Google Scholar] [CrossRef]
- López-Santos, O.; Martínez-Salamero, L.; García, G.; Valderrama-Blavi, H.; Mercuri, D.O. Efficiency analysis of a sliding-mode controlled quadratic boost converter. IET Power Electron. 2013, 6, 364–373. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Dazhong, M.; Dehao, Q.; Yonghao, G.; Peng, W. Line inductance stability operation domain assessment for weak grids with multiple constant power loads. IEEE Trans. Energy Convers. 2020, 36, 1045–1055. [Google Scholar] [CrossRef]
- Wang, R.; Liu, H.; Li, M.J.; Sun, Q.; Li, X.; Wang, P. Fast charging control method for electric vehicle-to-vehicle energy interaction devices. IEEE Trans. Transp. Electrif. 2022, 9, 4941–4950. [Google Scholar] [CrossRef]






| Different Electric Vehicle Brands | Charging Voltage/V | Output Voltage/V |
|---|---|---|
| Hongguang MINIEV | 250 V or More | 96 V or Less |
| BAOJUN e100 | 200 V or More | 110 V or Less |
| BAOJUN e200 | 220 V or More | 122 V or Less |
| CHERY QQ ice-creame | 250 V or More | 90 V or Less |
| BAOJUN e200 | 220 V or More | 125 V or Less |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Zhai, S.; Jia, W.; Wang, W.; Zhang, Z.; Guo, B. Energy Mutual Aid Device of Electric Vehicles: Quadratic Boost Converter with Modified Voltage-Mode Controller. Mathematics 2024, 12, 1531. https://doi.org/10.3390/math12101531
Xiao J, Zhai S, Jia W, Wang W, Zhang Z, Guo B. Energy Mutual Aid Device of Electric Vehicles: Quadratic Boost Converter with Modified Voltage-Mode Controller. Mathematics. 2024; 12(10):1531. https://doi.org/10.3390/math12101531
Chicago/Turabian StyleXiao, Jun, Shuo Zhai, Wei Jia, Weisheng Wang, Zhiyuan Zhang, and Baining Guo. 2024. "Energy Mutual Aid Device of Electric Vehicles: Quadratic Boost Converter with Modified Voltage-Mode Controller" Mathematics 12, no. 10: 1531. https://doi.org/10.3390/math12101531




