Rolling Mechanism of Launch Vehicle during the Prelaunch Phase in Sea Launch
Abstract
:1. Introduction
- Using a dimensionality reduction-driven spatial system projection method, we analyze the rolling mechanism of the prelaunch stage launch vehicle driven by two degrees of freedom in sea launch;
- To establish a multibody dynamics model of the prelaunch stage launch vehicle’s rolling, we utilize a simulation driven by the two degrees of freedom of the transportation vessel’s rolling and pitching. This will be employed to validate the rolling mechanism of the launch vehicle;
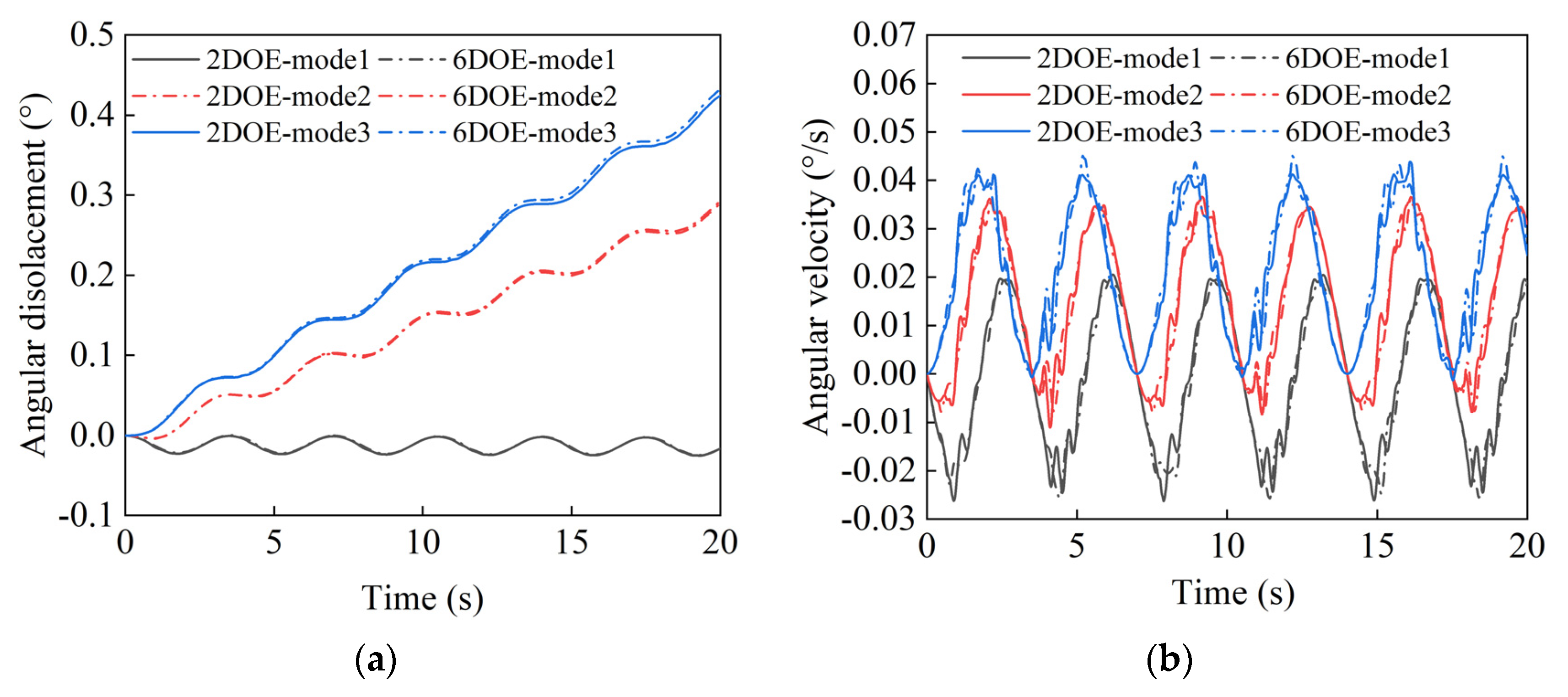
- By comparing the simulation driven by six-degree-of-freedom motion and two-degree-of-freedom motion of the transportation vessel, we analyze the impact of transportation vessel’s motion on launch vehicle’s rolling;
- Through a response surface analysis, we examine the influence of the friction coefficients between the launchpad and launch vehicle and between the adapters and guideways on the launch vehicle’s rolling.
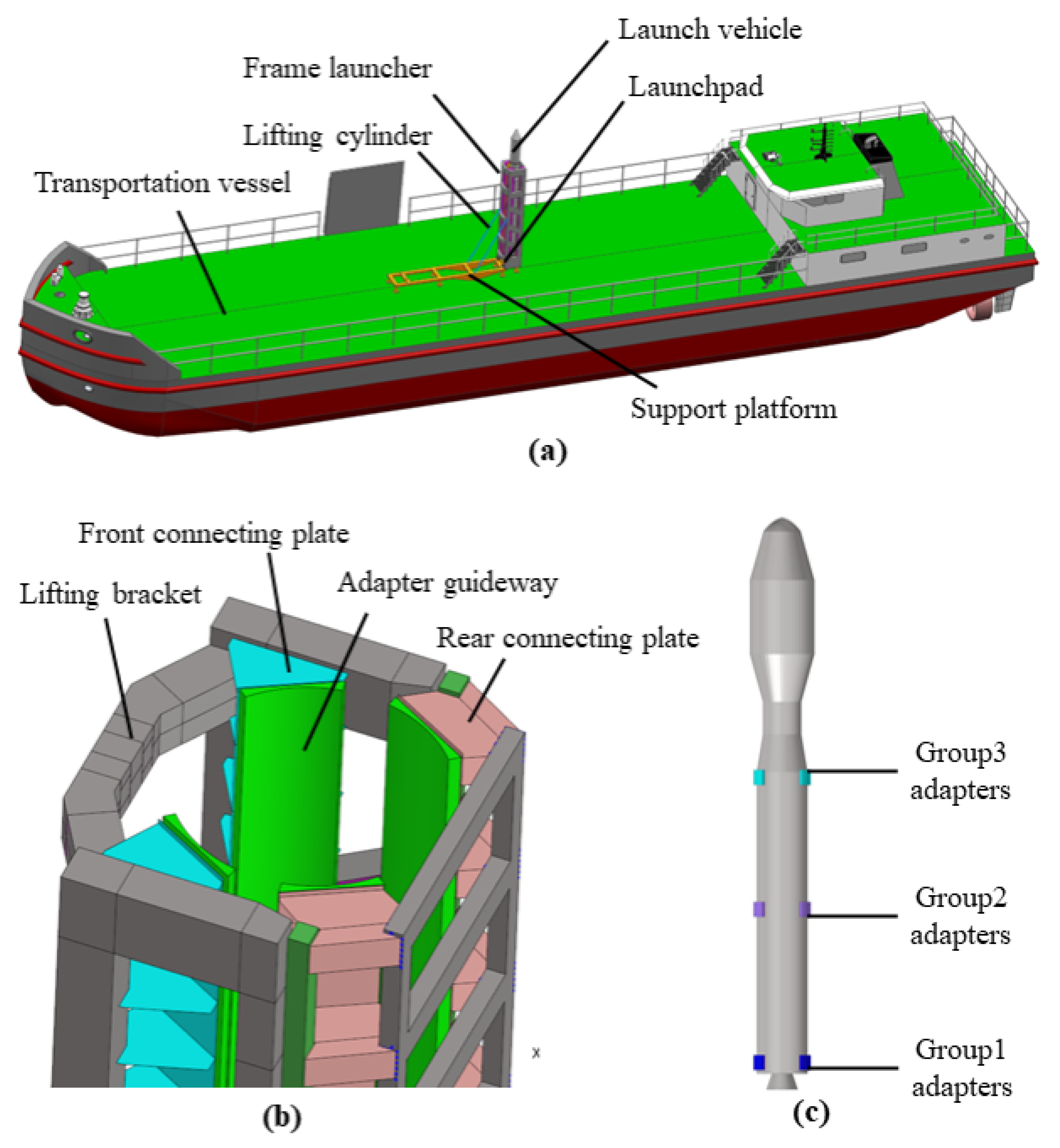
2. Framed Sea Launch System
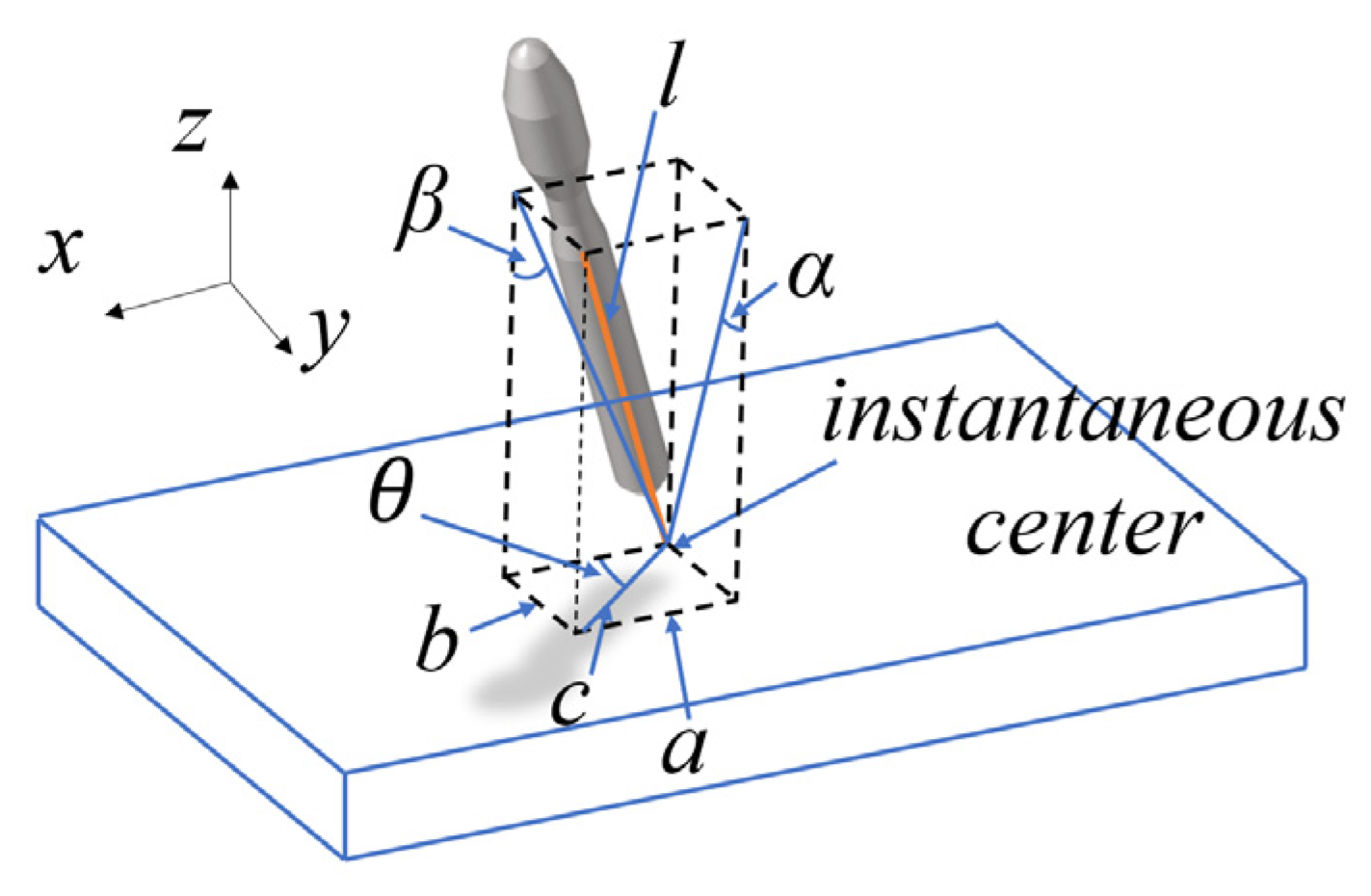
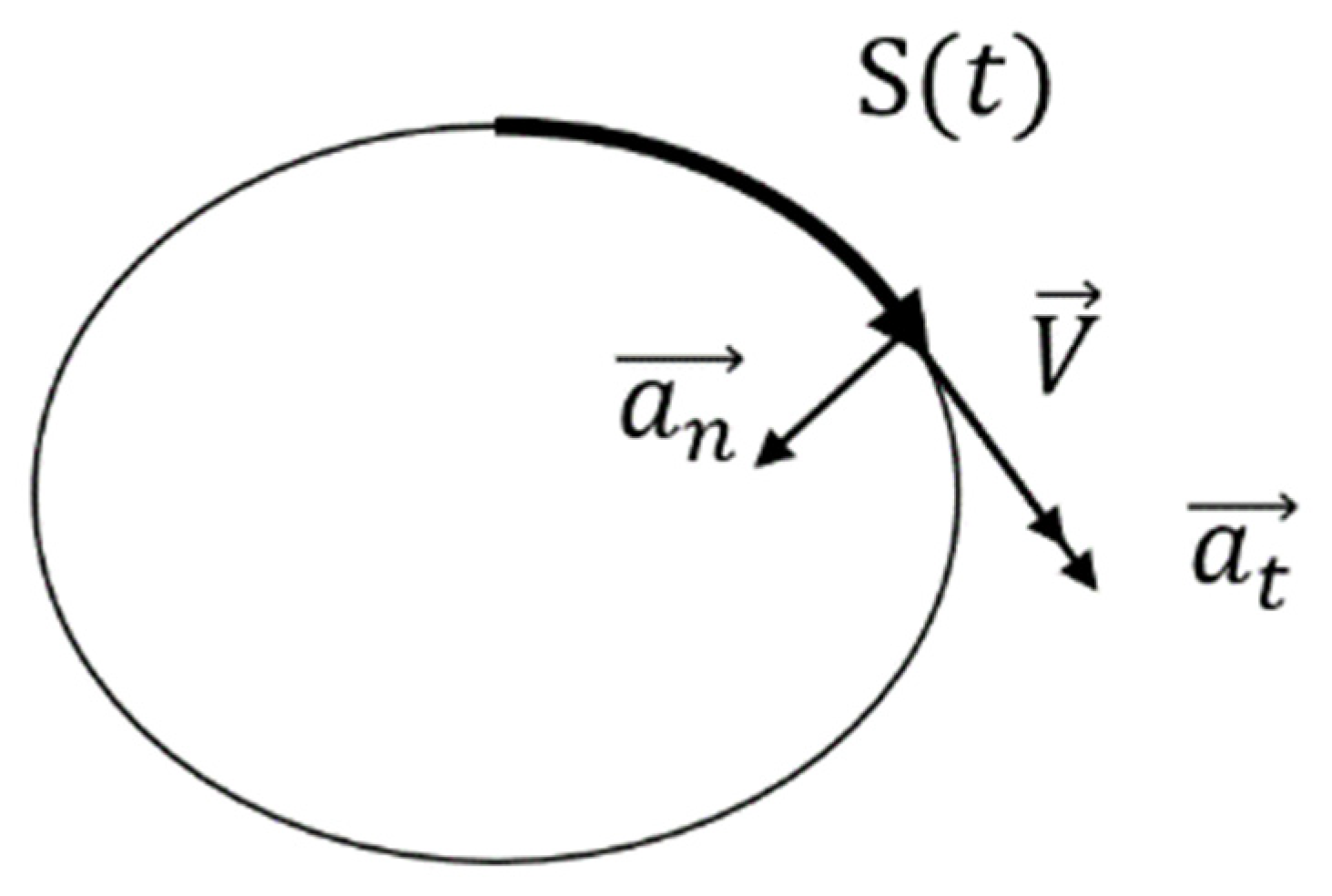
3. Rolling Analysis of 2-D-Driven Sea-Based Launch Vehicle
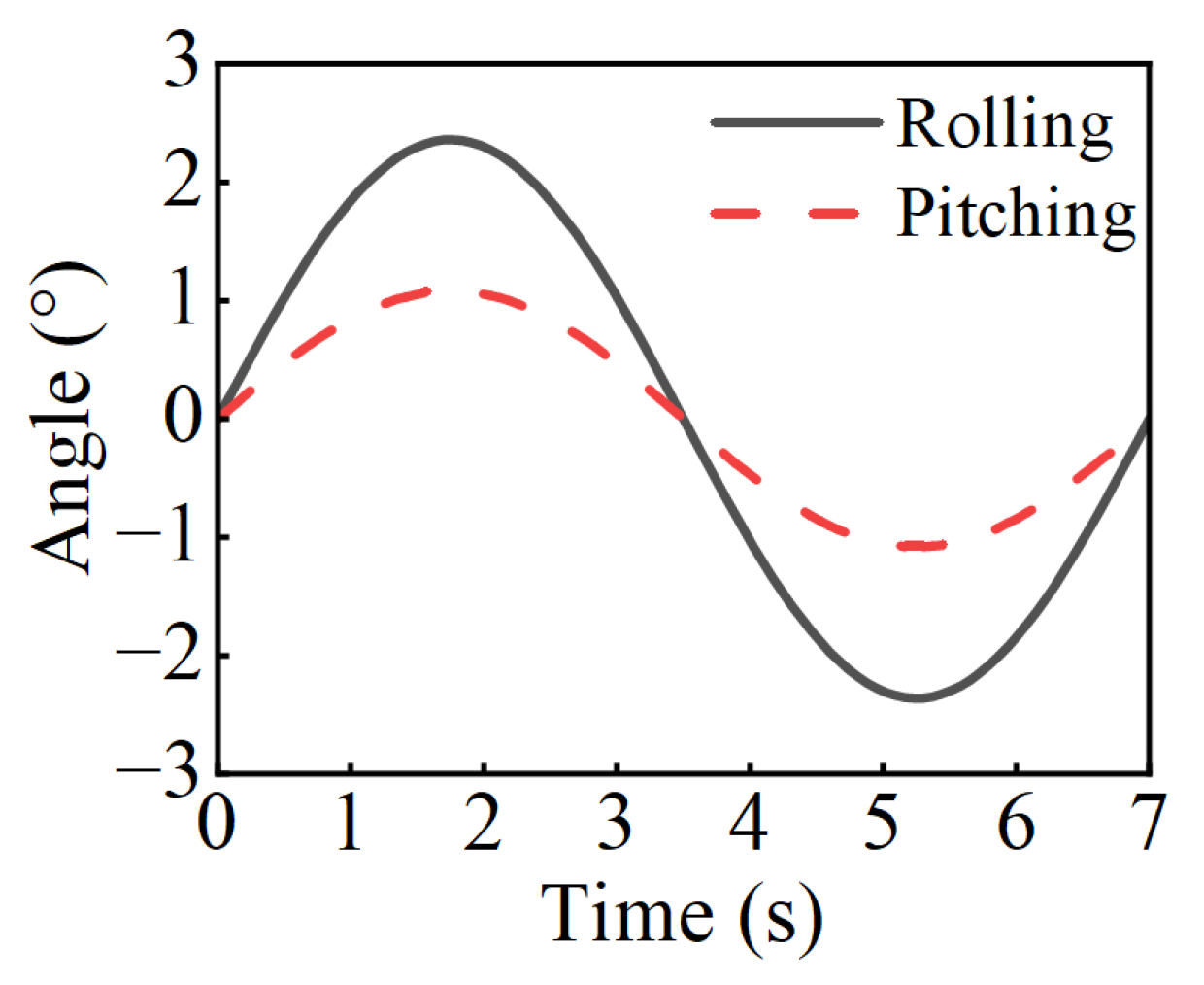
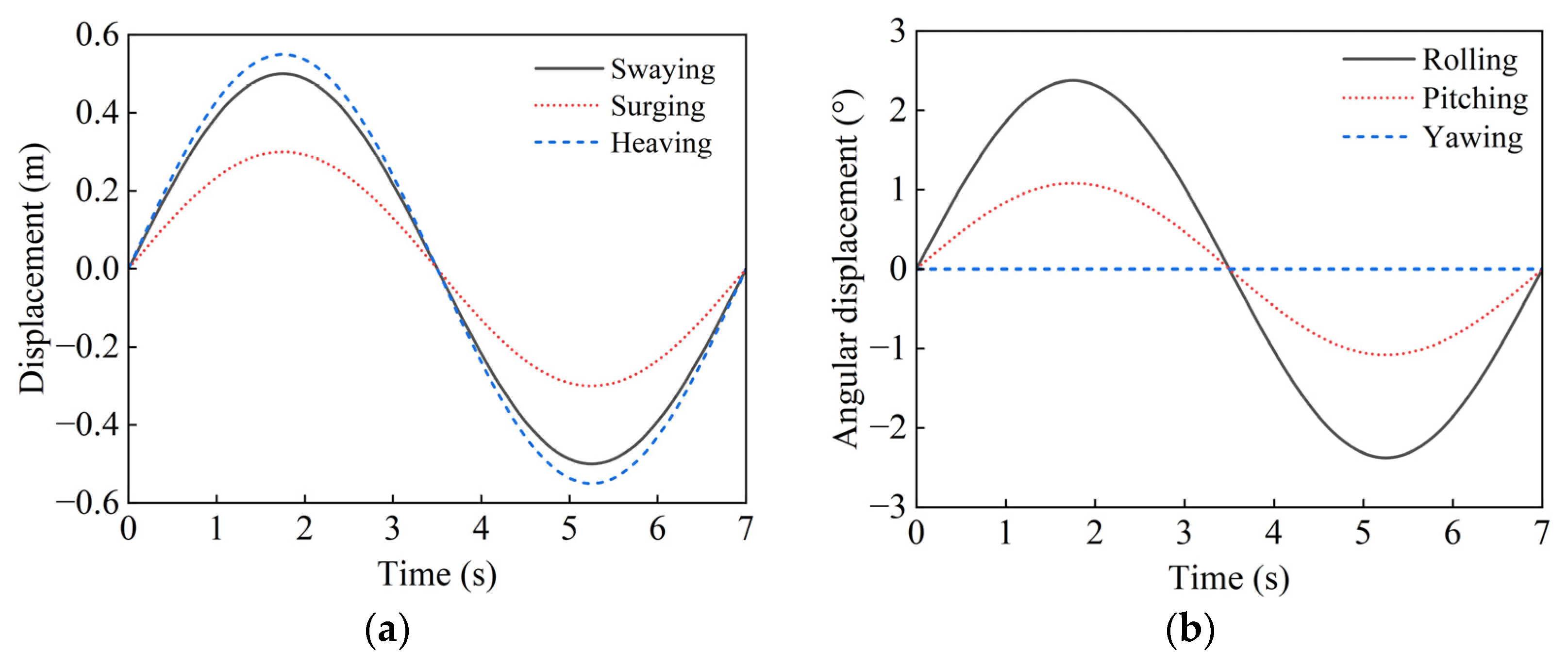
3.1. Transportation Vessel Motion
- The framed sea launch system is a rigid system;
- Only the three types of motion that have a significant impact on the transportation vessel are considered: rolling, pitching, and heaving;
- The rivet constraints between the bottom of the launch vehicle and the launch pad are ignored, and a reliable contact between them without separation is assumed.
3.2. Transportation Vessel Motion Boundary
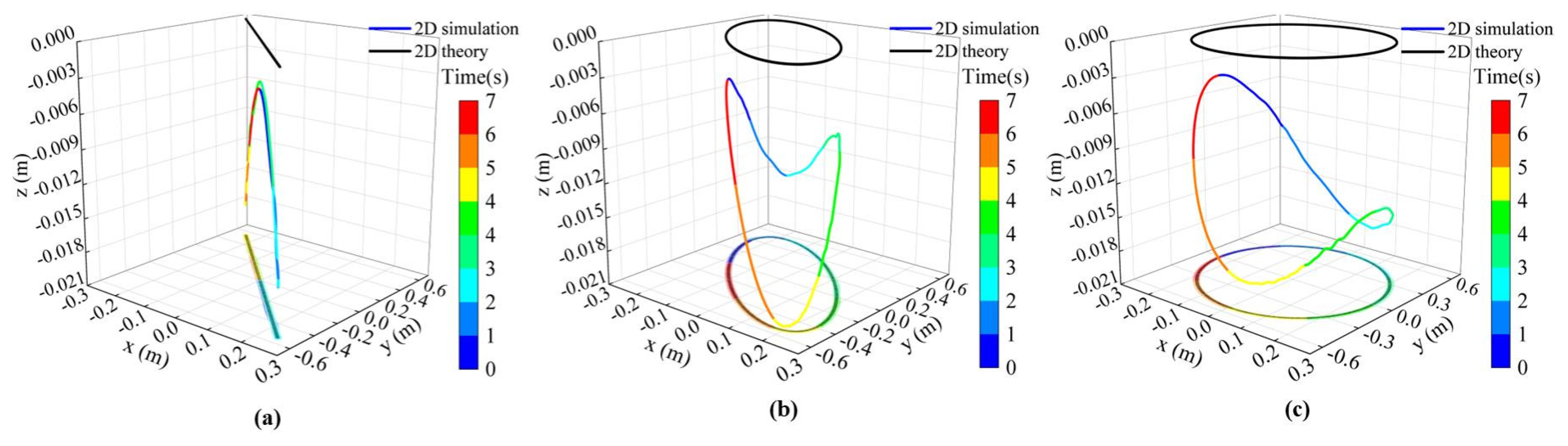
3.3. Dynamics Analysis of 2-D-Driven Sea-Based Launch Vehicle
4. Dynamics Simulation Analysis of Sea-Based Launch Vehicle during Prelaunch
4.1. Multibody Dynamics Calculation Methods
4.2. Framed Sea Launch System during Prelaunch Dynamics Model
- Ignoring the flexible structural deformation of the framed sea launch system, the primary consideration is the system’s motion response under loading conditions.
- The motion of the transportation vessel is considered a simple harmonic motion without considering the mutual coupling effect between the transportation vessel and the waves.
- The lifting cylinder is locked after the lift-off operation. The lifting cylinder is simplified as a single rigid body cylinder, with its upper end connected to the frame launcher via a ball joint, and its lower end connected to the support platform via a ball joint.
- The launchpad and support platform’s legs are fixed on the transportation vessel.
- Without considering adapter deformation, the load transmission of the adapter is represented through penalty functions and contact embedment depth.
- Without considering the separation process of the adapters, adapters are fixed to the launch vehicle.
- The support platform is connected to the launchpad via a rotational joint.
- The main mass characteristics of the launch vehicle are shown in Table 2.
- 2.
- The contact coefficients between each contact are shown in Table 3.
- 3.
- Boundary conditions
- 4.
- Wind load
- 5.
- Gravity
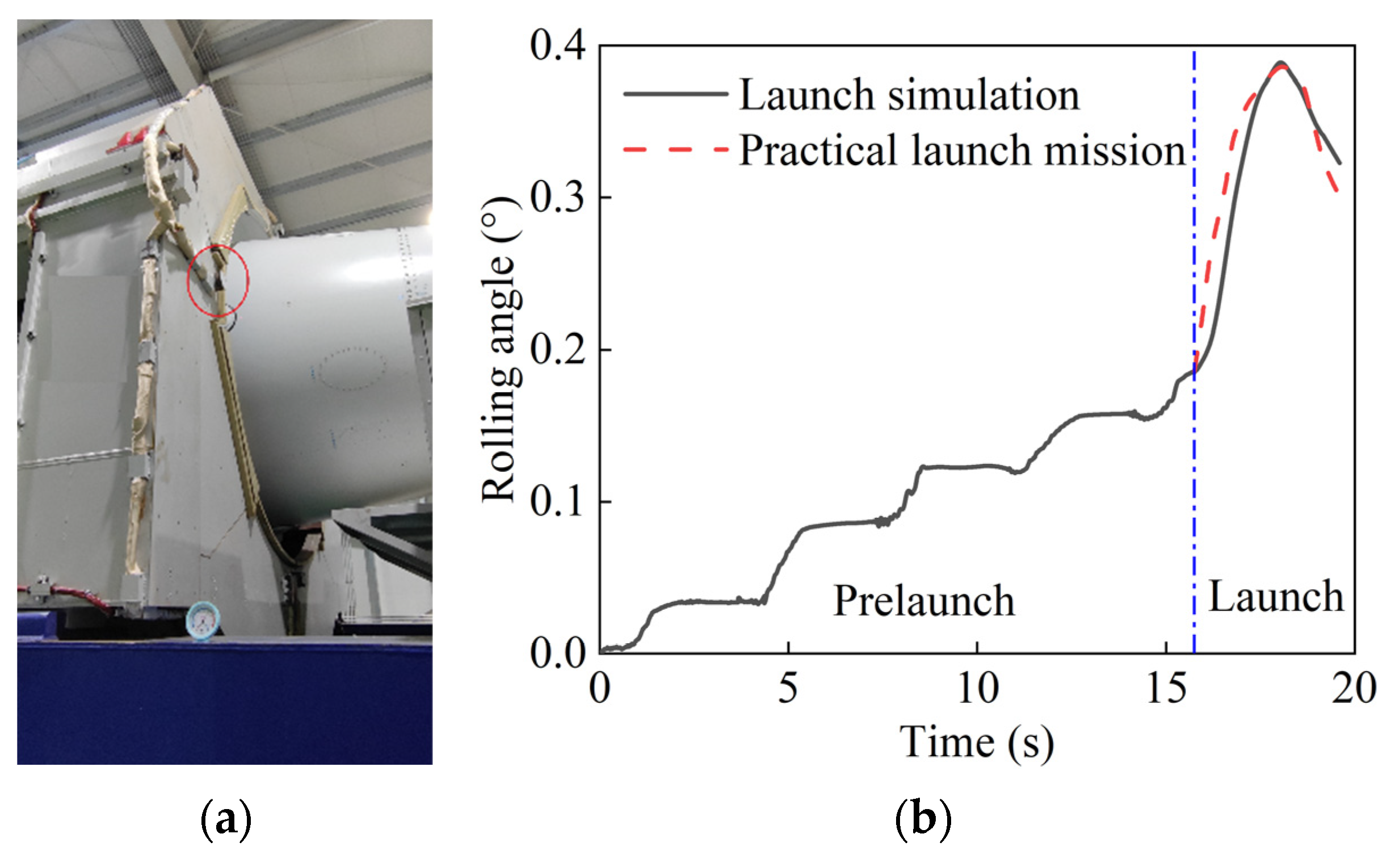
4.3. Dynamics Simulation Results and Analysis
4.3.1. Two-Degree-of-Freedom-Driven Dynamics Simulation
4.3.2. Six-Degree-of-Freedom-Driven Dynamics Simulation
4.3.3. Analysis of the Parameters Influencing Launch Vehicle’s Rolling Loads
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ilcev, S.D. Spacecraft Launching Technique and Systems. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 4514–4517. [Google Scholar]
- Song, Z.; Xie, Z.; Qiu, L.; Xiang, D.; Li, J. Prospects of Sea Launches for Chinese Cryogenic Liquid-Fueled Medium-Lift Launch Vehicles. Chin. J. Aeronaut. 2021, 34, 424–437. [Google Scholar] [CrossRef]
- Xiao, N.; Xiao, L.; Zhang, F.; Zhou, J.; Li, M.; Liu, Y.; Hou, K.; Li, Y. An Architecture of Cross-Domain Support System for Multiple Space Command and Control Platforms. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–10. [Google Scholar]
- Chang, M.R. Sea-Launched TacSats for Responsive Space (STaRS)*. In Proceedings of the 7th Responsive Space Conference, Los Angeles, CA, USA, 27–30 April 2009; Volume 8. [Google Scholar]
- Tuturea, D.; Rajabi, F. Ocean Launch Facility Concept Design. In Proceedings of the Advanced Marine Vehicles Conference; American Institute of Aeronautics and Astronautics: Arlington, VA, USA, 1989. [Google Scholar]
- Jiandong, Y.; Yingliang, M.; Tao, Z.; Dong, J. Design of Maritime Satellite Launch Platform. In Proceedings of the 2020 2nd International Conference on Artificial Intelligence and Advanced Manufacture (AIAM), Manchester, UK, 15–17 October 2020; pp. 416–419. [Google Scholar]
- Lang, D.E.; Choate, D.L.; Nance, M.L. Sea Launch: Commercial Launch Competitiveness. In Engineering, Construction, and Operations in Space V; American Society of Civil Engineers: Albuquerque, NM, USA, 1996; pp. 419–425. [Google Scholar]
- Dong, Y.; Qu, M.; Su, C.; Qi, B.; Yu, C.; Qi, C.; Peng, X. Dynamic Simulation of Shipborne Vertical Launching System Under High Wave Level. In Proceedings of the 2019 International Conference on Advanced Manufacturing, Computation and Optimization, Budapest, Hungary, 20–22 November 2019. [Google Scholar]
- Zeng, W.; Jiang, Y. Launching Dynamics Simulation of Ship-Board Rocket Gun. Adv. Mater. Res. 2012, 625, 140–145. [Google Scholar] [CrossRef]
- Konyukhov, S.N. Applied Mechanics Problems Accompanying Spacecraft Launches from a Floating Platform and Their Resolution by the Sea Launch Project. Int. Appl. Mech. 2004, 40, 115–139. [Google Scholar] [CrossRef]
- Titterton, D.H. The Alignment of Ship Launched Missile IN Systems. In IEE Colloquium on Inertial Navigation Sensor Development; IET: Stevenage, UK, 1990. [Google Scholar]
- Zhao, S.; Meng, X.; Li, H.; Li, D.; Fu, Q. Continuous Multi-Body Dynamic Analysis of Float-over Deck Installation with Rapid Load Transfer Technique in Open Waters. Ocean Eng. 2021, 224, 108729. [Google Scholar] [CrossRef]
- Apeng, D.; Shu, L.; Wenguo, Z. Multi-Body Coupling Dynamic Research of Carrier-Based Aircraft Catapult Launch Based on Natural Coordinate Method. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 195–207. [Google Scholar] [CrossRef]
- Mousaviraad, M.; Conger, M.; Bhushan, S.; Stern, F.; Peterson, A.; Ahmadian, M. Coupled Computational Fluid and Multi-Body Dynamics Suspension Boat Modeling. J. Vib. Control 2018, 24, 4260–4281. [Google Scholar] [CrossRef]
- Sun, L.; Eatock Taylor, R.; Choo, Y.S. Multi-Body Dynamic Analysis of Float-over Installations. Ocean Eng. 2012, 51, 1–15. [Google Scholar] [CrossRef]
- Chang, Z.; Tang, Y.; Li, H.; Yang, J.; Wang, L. Analysis for the Deployment of Single-Point Mooring Buoy System Based on Multi-Body Dynamics Method. China Ocean Eng. 2012, 26, 495–506. [Google Scholar] [CrossRef]
- Cha, J.-H.; Ham, S.-H.; Lee, K.-Y.; Roh, M.-I. Application of a Topological Modelling Approach of Multi-Body System Dynamics to Simulation of Multi-Floating Cranes in Shipyards. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2010, 224, 365–373. [Google Scholar] [CrossRef]
- He, J.; Jin, X.; Xie, S.Y.; Cao, L.; Lin, Y.; Wang, N. Multi-Body Dynamics Modeling and TMD Optimization Based on the Improved AFSA for Floating Wind Turbines. Renew. Energy 2019, 141, 305–321. [Google Scholar] [CrossRef]
- Lei, J.; Jiang, Y.; Zhao, R. Research on the Influence of Launch Time on the Thermal Launch of Solid Rockets at Sea. J. Proj. Rockets Missiles Guid. 2023, 43, 91–97. [Google Scholar]
- Hongyu, C.; Zhiwei, K.; Huifeng, Z.; Mengmeng, Y. Study on Launch Dynamics of Shipborne Missile System. SHIP Sci. Technol. 2021, 43, 10–12. [Google Scholar]
- Wang, D.; Shao, J.; Chen, M.; Zhao, Y.; Jiang, Y. Sea Launch Adapter Response in Rough Sea Conditions Considering Strain Rate Effects. J. Phys. Conf. Ser. 2023, 2508, 012027. [Google Scholar]
- Pang, F.; Qin, Y.; Tang, Y.; Gao, C.; Li, H. Experimental Study on Impact Response of Seaborne Rocket Launch Platform. Ocean Eng. 2023, 280, 114623. [Google Scholar] [CrossRef]
- Su, Y.; Lu, X.; Le, G.; Li, G.; Fu, B. Numerical Simulations of Seawater Spraying on Launch Platform during CZ-8X Offshore Launching. Adv. Space Res. 2023, 72, 3631–3644. [Google Scholar] [CrossRef]
- Mu, R.; Zhang, T.; Li, S. A Rapid Self-Alignment Strategy for a Launch Vehicle on an Offshore Launching Platform. Sensors 2022, 23, 339. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Xu, G.; Niu, G.; Mei, T. The Study of the Motion of the Satellite Launching Platform with Different Shape of Pontoons. In 2023 International Conference on Marine Equipment & Technology and Sustainable Development; Yang, D., Ed.; Springer: Singapore, 2023; Volume 375, pp. 303–315. [Google Scholar]
- Kong, X.; Dong, Y.; Kang, J.; Paik, J.K. Quantitative Risk Assessment and Management of Hydrogen Leaks from Offshore Rocket Launching Platforms. In Proceedings of the 2023 9th International Symposium on System Security, Safety, and Reliability (ISSSR), Hangzhou, China, 10–11 June 2023; pp. 149–155. [Google Scholar]
- Pua, C.; Hu, P.; Ji, C.; Zhu, Z.; Zheng, B.; Zhai, S. Simulation Analysis of Protective Wall against Hydrogen Combustion from Liquified Hydrogen Storage Tank on the Offshore Launching Platform. Int. J. Hydrogen Energy 2023, 48, 12501–12518. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhu, C.; Yang, Y.; Lin, T.; Li, R. XFEM-Based Study of Fatigue Crack Propagation in Rocket Deflector Troughs under Coupled High-Temperature and Impact Conditions. J. Mar. Sci. Eng. 2024, 12, 207. [Google Scholar] [CrossRef]
- Yu, J.; Cheng, X.; Fan, C.; Lu, Z.; Ni, X. Investigation on Hydrodynamic Response of Sea Launch Platform to Impact Load | Compendex. Ship Build. China 2021, 62, 139–148. [Google Scholar]
- Liu, X.; Wang, Y.; Liu, X.; Xu, G. Review of Marine Satellite Launch Platform and Related Study at JUST. In 2023 International Conference on Marine Equipment & Technology and Sustainable Development; Yang, D., Ed.; Springer: Singapore, 2023; Volume 375, pp. 579–590. [Google Scholar]








| Motion | Mode 1 | Mode 2 | Mode 3 |
|---|---|---|---|
| Rolling velocity | |||
| Pitching velocity |
| Parameter | Value | Moment of Inertia | Value |
|---|---|---|---|
| Mass (kg) | 120,000 | Ixx (kg·m2) | 5,010,550 |
| Length (m) | 30.888 | Iyy (kg·m2) | 5,010,550 |
| Distance from barycenter to the tip of rectifier (m) | 21.043 | Izz (kg·m2) | 101,123 |
| Parameter | Adapters and Launcher | Launch Vehicle and Launchpad |
|---|---|---|
| Contact stiffness | 2855 N/mm | 100,000 N/m |
| Damping coefficient | 0.57 N·s/mm | 50 N·s/mm |
| Power contribution index | 1.1 | 1.5 |
| Maximum penetration depth | 0.1 mm | 0.1 mm |
| Static friction coefficient | 0.15 | 0.1 |
| Dynamic friction coefficient | 0.1 | 0.1 |
| Static friction transition speed | 0.3 mm/s | 0.3 mm/s |
| Dynamic friction transition speed | 0.25 mm/s | 0.25 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Xiao, W.; Shao, J.; Li, M.; Zhao, Y.; Jiang, Y. Rolling Mechanism of Launch Vehicle during the Prelaunch Phase in Sea Launch. Aerospace 2024, 11, 399. https://doi.org/10.3390/aerospace11050399
Wang D, Xiao W, Shao J, Li M, Zhao Y, Jiang Y. Rolling Mechanism of Launch Vehicle during the Prelaunch Phase in Sea Launch. Aerospace. 2024; 11(5):399. https://doi.org/10.3390/aerospace11050399
Chicago/Turabian StyleWang, Deng, Wenhao Xiao, Jianshuai Shao, Mingjun Li, Yuanyang Zhao, and Yi Jiang. 2024. "Rolling Mechanism of Launch Vehicle during the Prelaunch Phase in Sea Launch" Aerospace 11, no. 5: 399. https://doi.org/10.3390/aerospace11050399





