Analysis of Kinematics and Dynamics of Rolling Ring Based on Finite Element Method
Abstract
:1. Introduction
2. Motion Stability Theory
- The external stability is characterized by an input–output relationship;
- Internal stability is represented by state motion under zero input conditions.
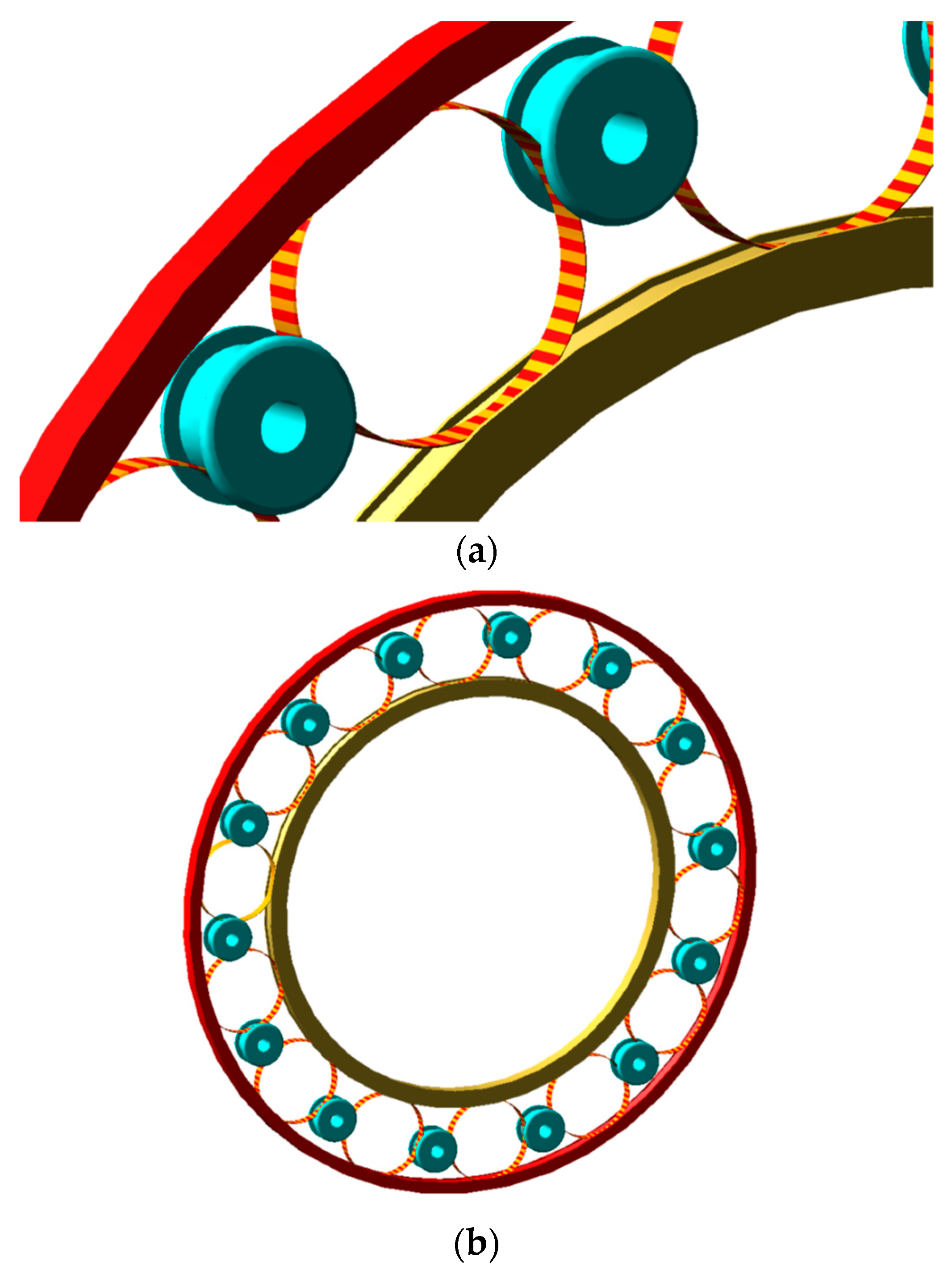
3. Model Building and Meshing
4. Kinematics and Dynamics Simulation
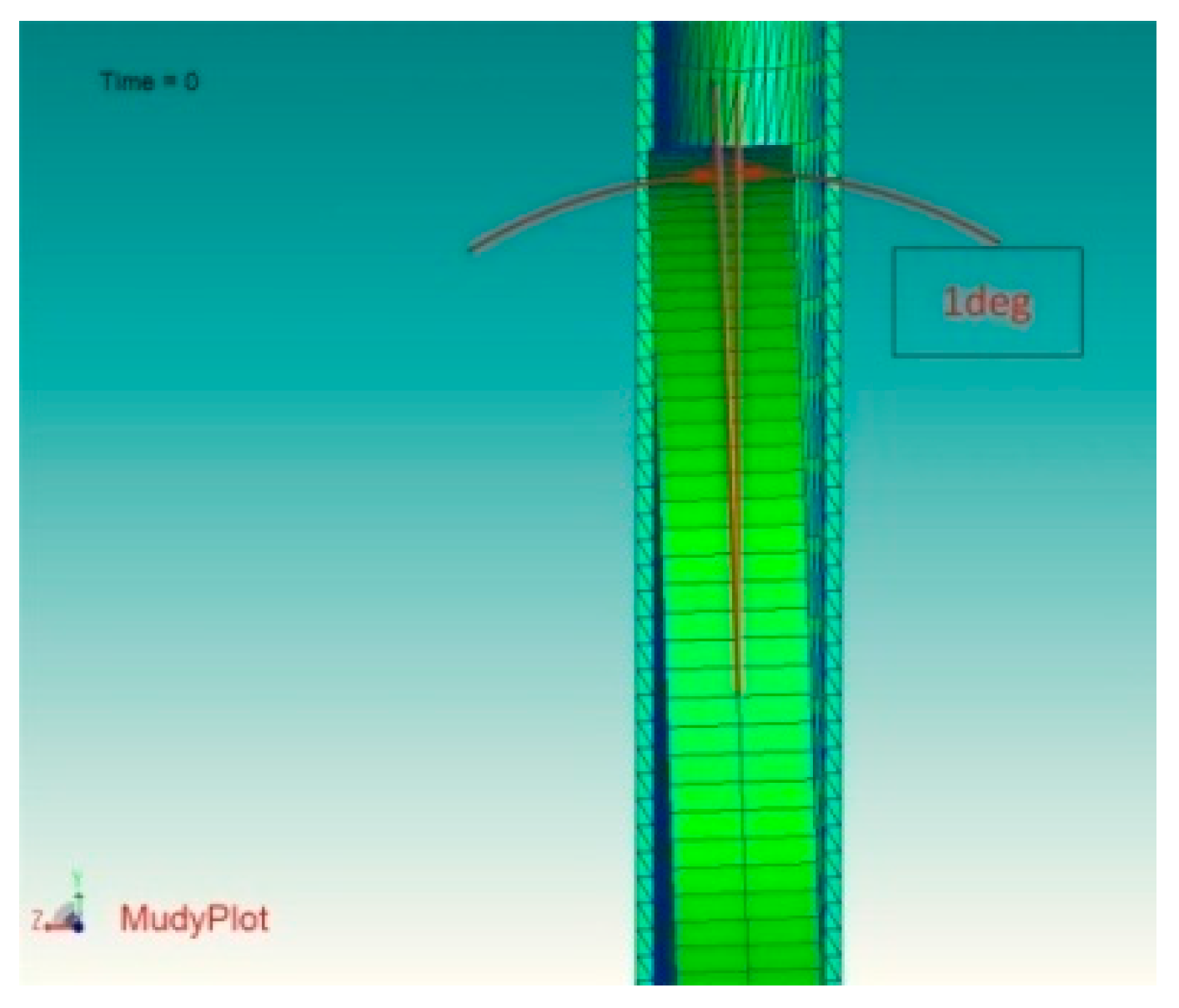
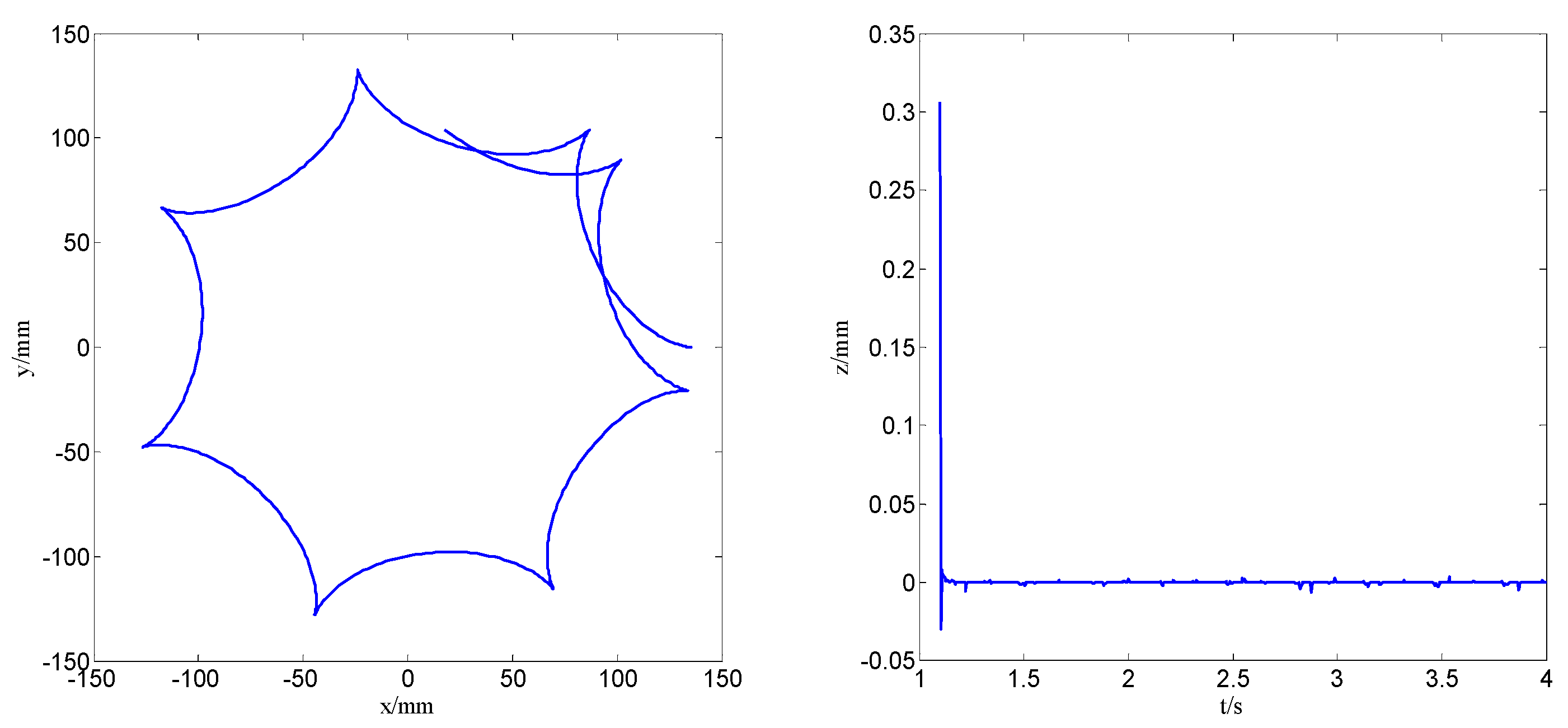
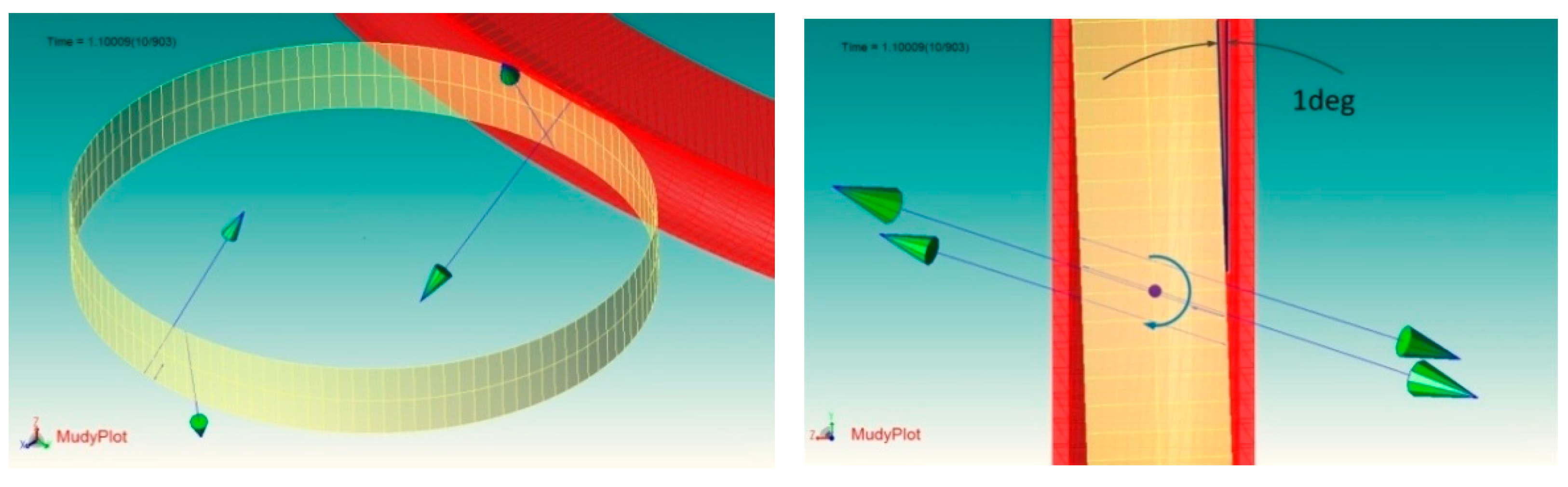
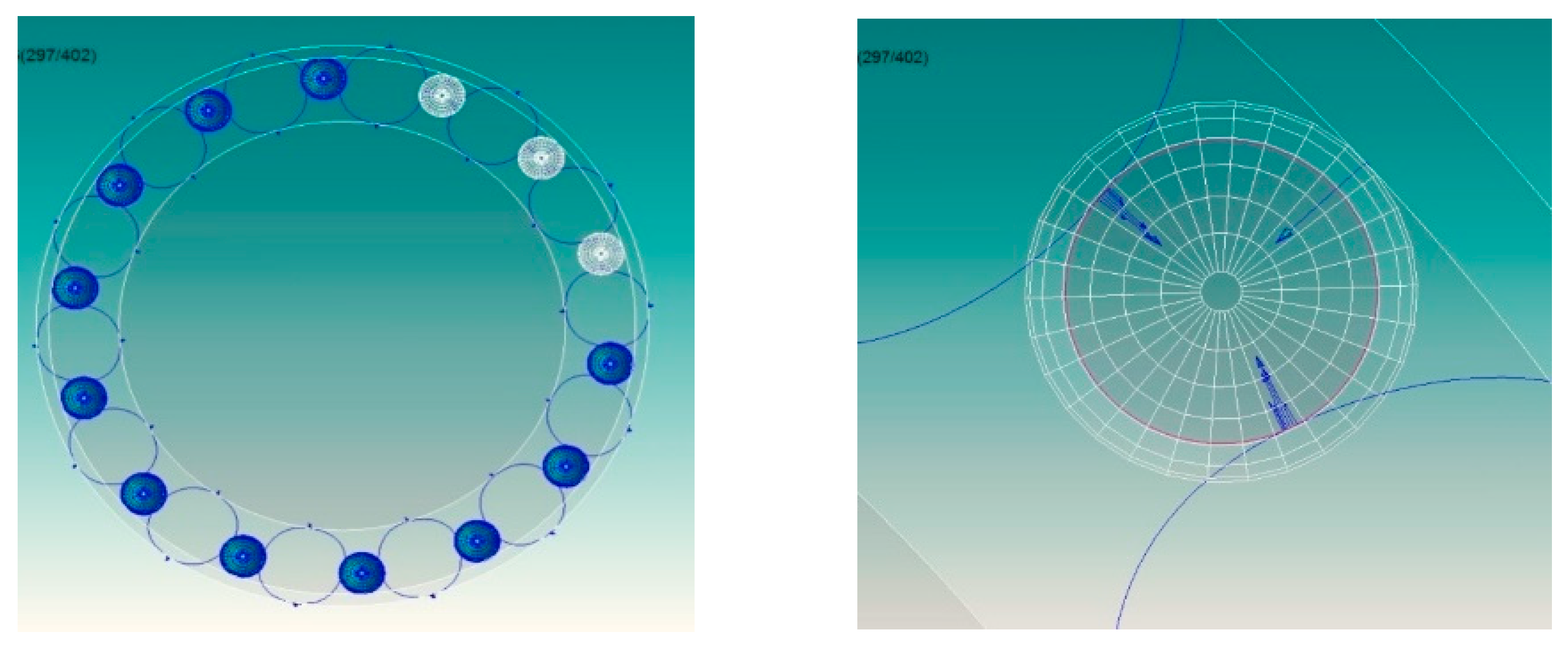
4.1. Motion Stability Analysis
4.2. Dynamic Analysis of Driving Torque and Contact Pressure
4.2.1. Dynamic Analysis of the Relationship between Idler Gear Size and Driving Torque
4.2.2. Dynamic Analysis of the Relationship between the Size of the Idler Gear and the Contact Pressure of the Flexible Ring
5. Discussion
- (1)
- Flexible rotation: The conductive roller ring can realize the free rotation of the rotating part through the auxiliary role of the idler and can realize the function of self-recovery within a certain inclination range while maintaining the transmission of power or signal.
- (2)
- Low-loss transmission: The conductive roller ring can achieve low-loss power or signal transmission through the structural design of the rolling form. Conductive roller rings provide more stable and efficient transmission performance than traditional lead or sliding electrical contacts.
- (3)
- Multi-channel transmission: Some conductive roller rings can also achieve multi-channel transmission, that is, multiple independent power or signal paths are transmitted simultaneously in the same device. This design can meet the needs of multiple signal transmissions in complex systems and improve the overall performance and reliability of the system.
- (1)
- Optimization of the design method: Research the design method of conductive rings with higher reliability and long life to meet the needs of a new generation of long-life satellites;
- (2)
- New material development: Explore new materials to improve the performance of conductive roller rings, reduce friction and wear, and thus improve the service life of satellites;
- (3)
- Tribological performance: Observe the friction and wear behavior of conductive roller rings at different temperatures and speeds to provide a theoretical basis for the design of long-life satellites;
- (4)
- Long-life maintenance: Study the long-term use and maintenance methods of conductive roller rings to ensure high reliability and stability over a long period;
- (5)
- High-precision manufacturing process: Explore high-precision manufacturing processes to improve the processing accuracy of conductive roller rings, reduce installation errors, and improve the stability and reliability of signal transmission;
- (6)
- Noncontact transmission: research the design of noncontact conductive roller rings to reduce friction and wear and improve the stability and reliability of signal transmission.
6. Conclusions
- (1)
- Both numerical simulation and theoretical analysis show that, with the existing camber design of the inner and outer rings, when the initial installation of the rolling ring has a deviation, the deviation angle has a self-recovery function; that is, the lateral motion is stable. The maximum deflection angle of the flexible ring is 1.52°.
- (2)
- The contact force is proportional to the radius of the idler gear, and the two can be approximately linear. The maximum contact force of the idler gear reaches 9.1 N. Therefore, the corresponding selection can be made according to the needs of the design process.
- (3)
- The drive torque and the size of the idler gear have a nonlinear relationship. The larger the size of the idler gear, the greater the required drive torque. The maximum driving torque is 364 N mm.
- (4)
- With the increase in the radius compression of the flexible ring, the driving torque and contact force increase correspondingly. The maximum driving torque reaches 18.9 N mm, the maximum contact pressure of the idler gear reaches 18.9 N, and the maximum contact pressure of the inner and outer rings reaches 19 N.
- (5)
- For the case that the driving torque is small and a certain contact is required to facilitate the transmission of electrical signals, the method of reducing the amount of compression or increasing the size of the idler gear can be adopted.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, J.; Xing, L.; Li, Y.; Ge, F. Key technologies and development trends of precision conductive slip rings. Navig. Control 2015, 14, 20–26. [Google Scholar]
- Tang, F.; Jiang, Y. Design of radar combiner ring on a helicopter. Electron. Mech. Eng. 2010, 26, 30–32. [Google Scholar]
- Sun, Y.; Wang, Y.; Sun, X.; Liu, X.; Yu, J. Research on failure modeling and process optimization of conductive slip rings for aerospace. J. Mech. Eng. 2020, 56, 1–12. [Google Scholar]
- Sun, B.; Feng, J.; Shen, T.; Shen, Z. Contact mechanics analysis of conductive slip ring based on contact. Nav. Electron. Countermeas. 2022, 45, 117–120. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, Y.; Liu, H.; Zhao, L.; Xie, Z. Transmission reliability evaluation of spaceborne long-life conductive slip ring. Opt. Precis. Eng. 2019, 27, 2028–2035. [Google Scholar]
- Yin, N.; Zhang, Z.; Zhang, J. Molecular dynamics simulation of friction and wear behavior of conductive slip ring Au coating. J. Tribol. 2018, 38, 108–114. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Sheng, Y.; Yu, C.; Yang, X.; Xi, J. Vision-Aided Brush Alignment Assembly System for Precision Conductive Slip Rings. Machines 2022, 10, 393. [Google Scholar] [CrossRef]
- Argibay, N.; Bares, J.A.; Sawyer, W.G. Asymmetric wear behavior of self-mated copper fiber brush and slip-ring sliding electrical contacts in a humid carbon dioxide environment. Wear 2010, 268, 455–463. [Google Scholar] [CrossRef]
- Wang, J.; Liu, R.; Xiao, R.; Ping, A.; Liu, J.; Zhang, M.; Li, Q. Optimized Design of Slip Ring Assembly for Aerospace to Reduce Deep Dielectric Charging. IEEE Trans. Nucl. Sci. 2022, 69, 915–924. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Wang, X.; Tian, G.; Fan, J. Machine Vision-Based Method for Measuring and Controlling the Angle of Conductive Slip Ring Brushes. Micromachines 2022, 13, 447. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, X.; Zhu, C.; Song, K.; Zhou, T. Research on Electromagnetic Compatibility of Non-Contact Slip Ring. In Proceedings of the International Conference on Intelligent Computing, Automation and Systems (ICICAS), Chongqing, China, 29 December–31 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 318–321. [Google Scholar]
- Balakrishna, A.; Mishra, P.K. Modelling and analysis of static and modal responses of leaf spring used in automobiles. Int. J. Hydromechatron. 2021, 4, 350–367. [Google Scholar] [CrossRef]
- Rehab, I.; Tian, X.; Gu, F.; Ball, A.D. The influence of rolling bearing clearances on diagnostic signatures based on a numerical simulation and experimental evaluation. Int. J. Hydromechatron. 2018, 1, 16–46. [Google Scholar] [CrossRef]
- Wang, R.; Yu, H.; Wang, G.; Zhang, G.; Wang, W. Study on the dynamic and static characteristics of gas static thrust bearing with micro-hole restrictors. Int. J. Hydromechatron. 2019, 2, 189–202. [Google Scholar] [CrossRef]
- Zhong, W.; Yao, W. Methodology of applied mechanical dual system. Proc. Mech. Hist. Methodol. 2003, 37, 133–141. [Google Scholar]

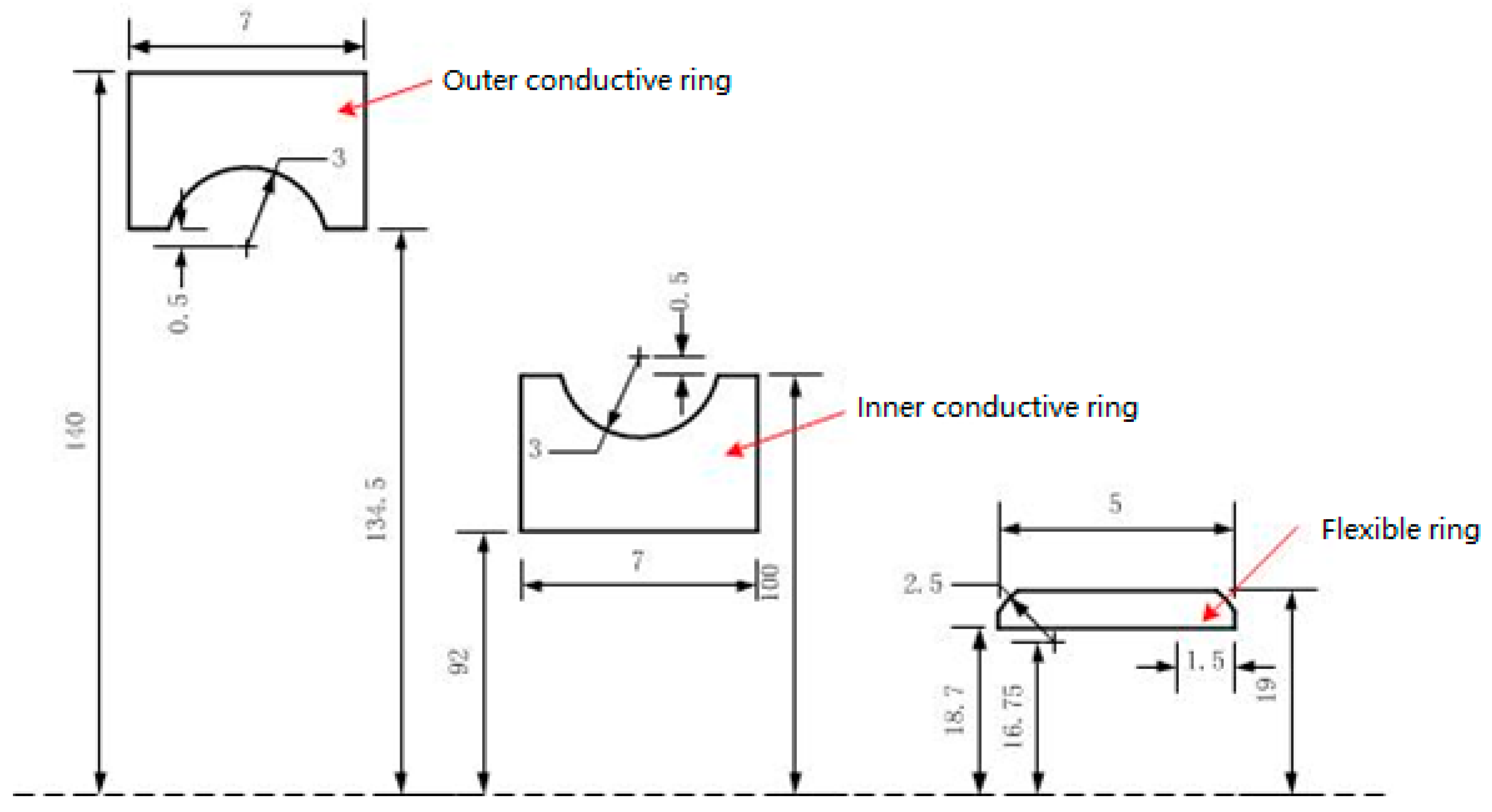







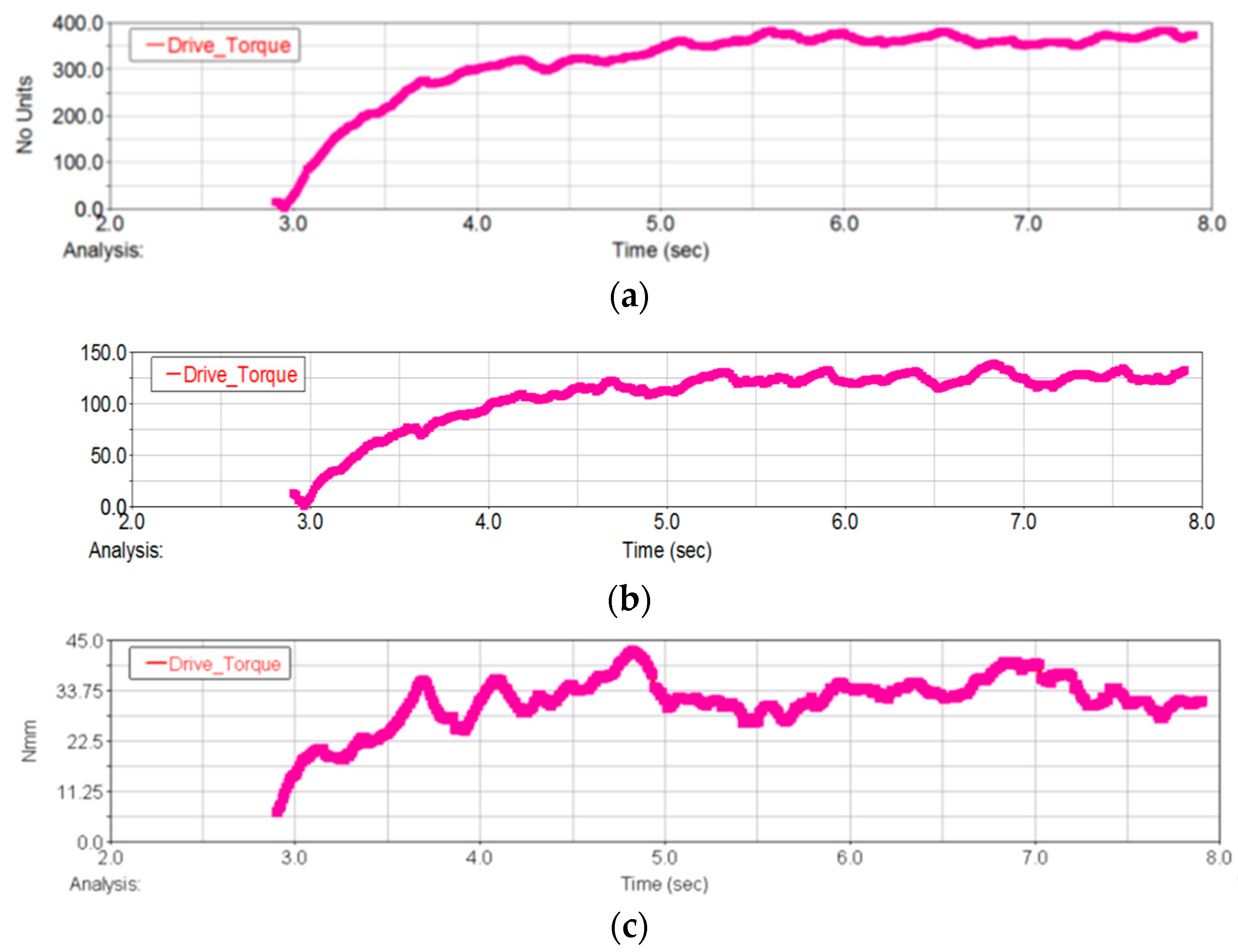
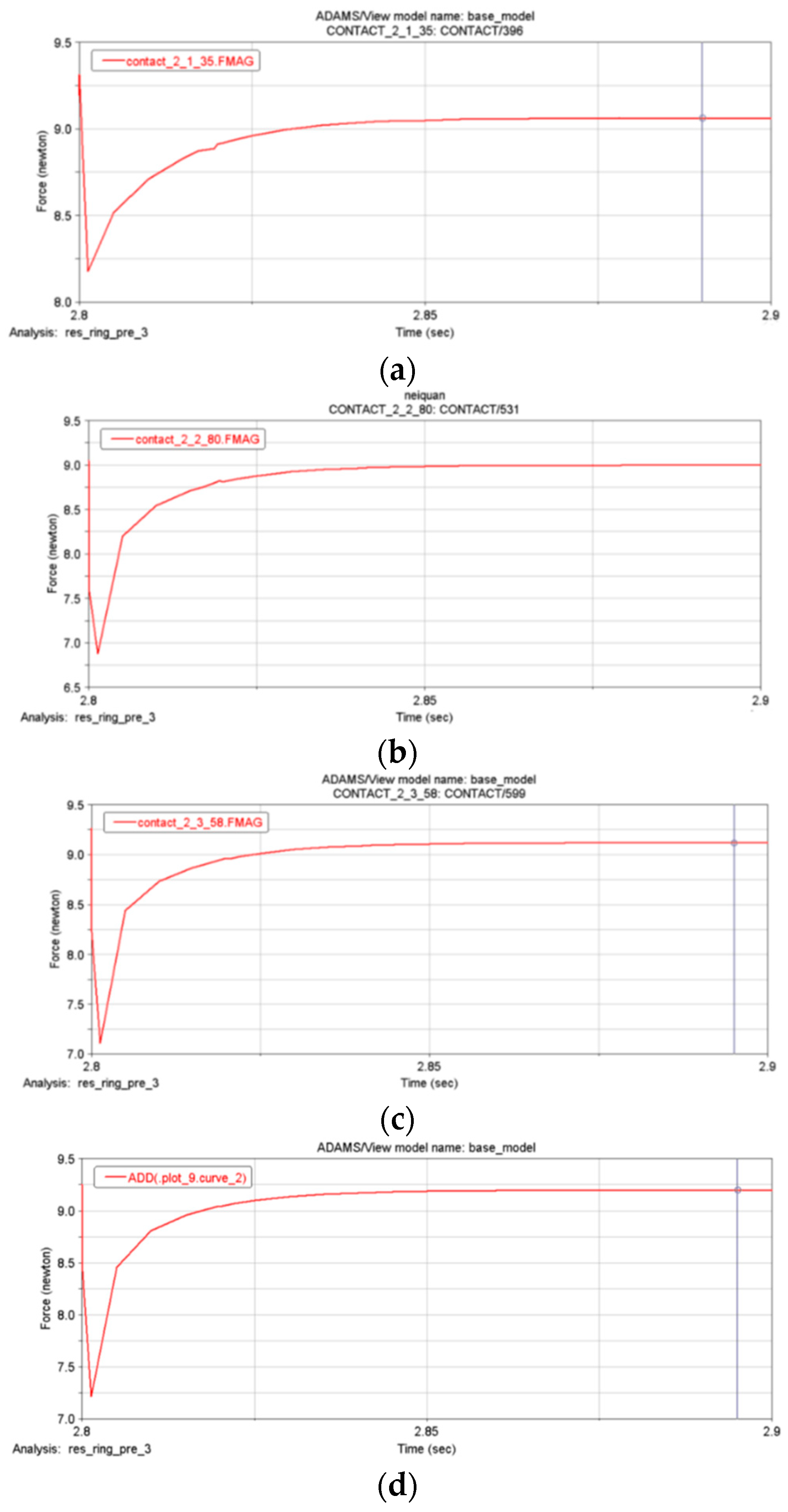

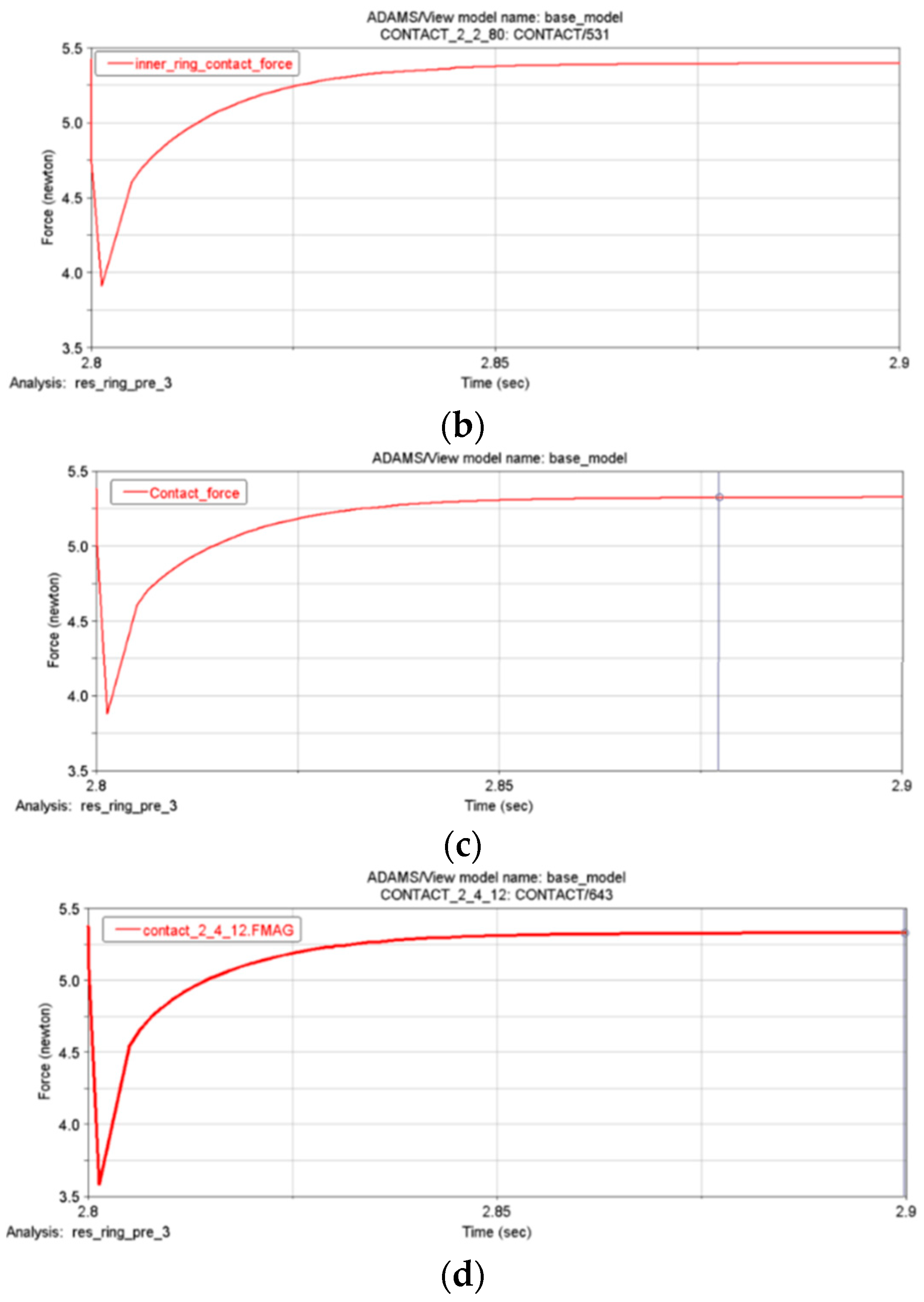
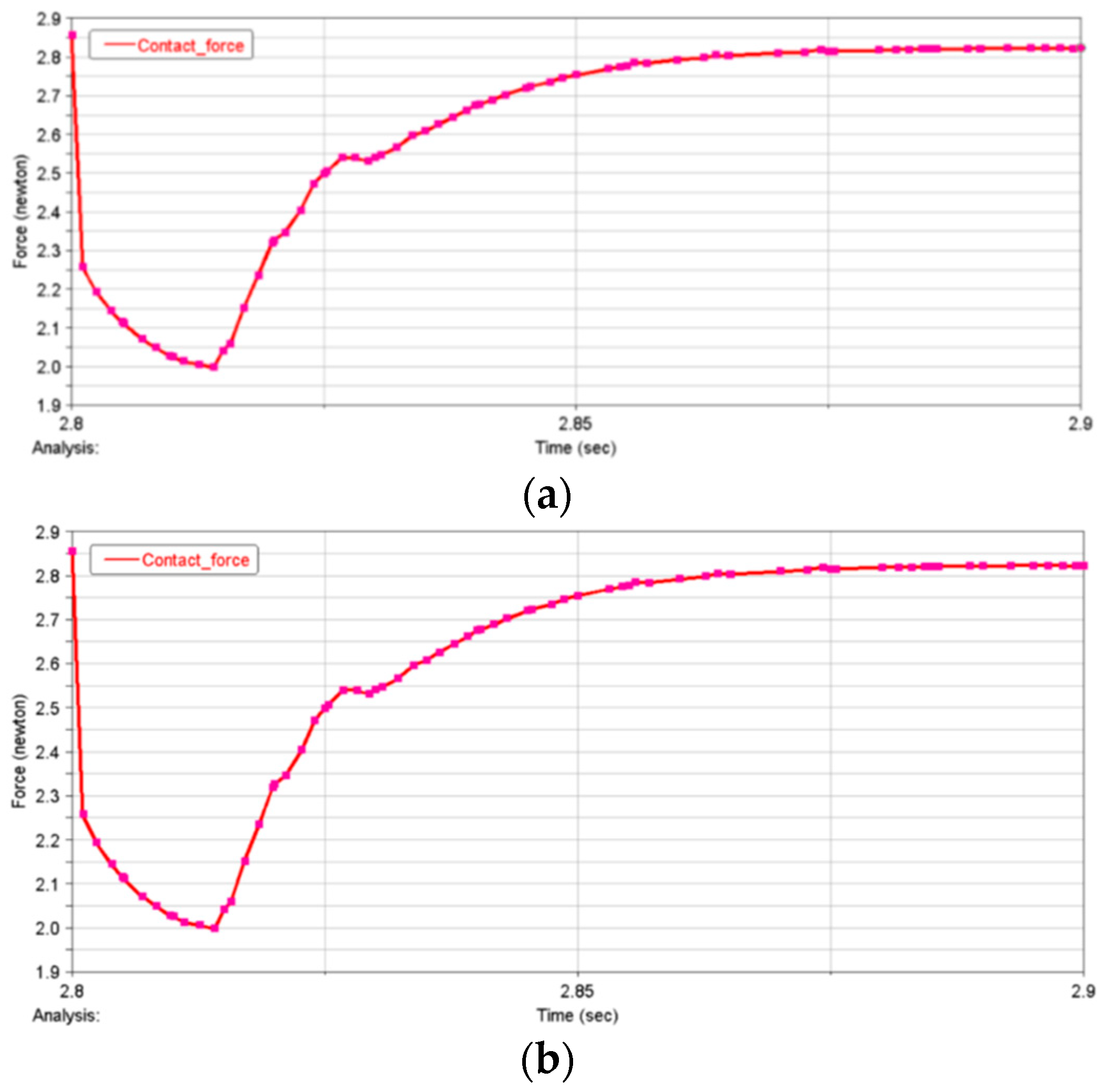
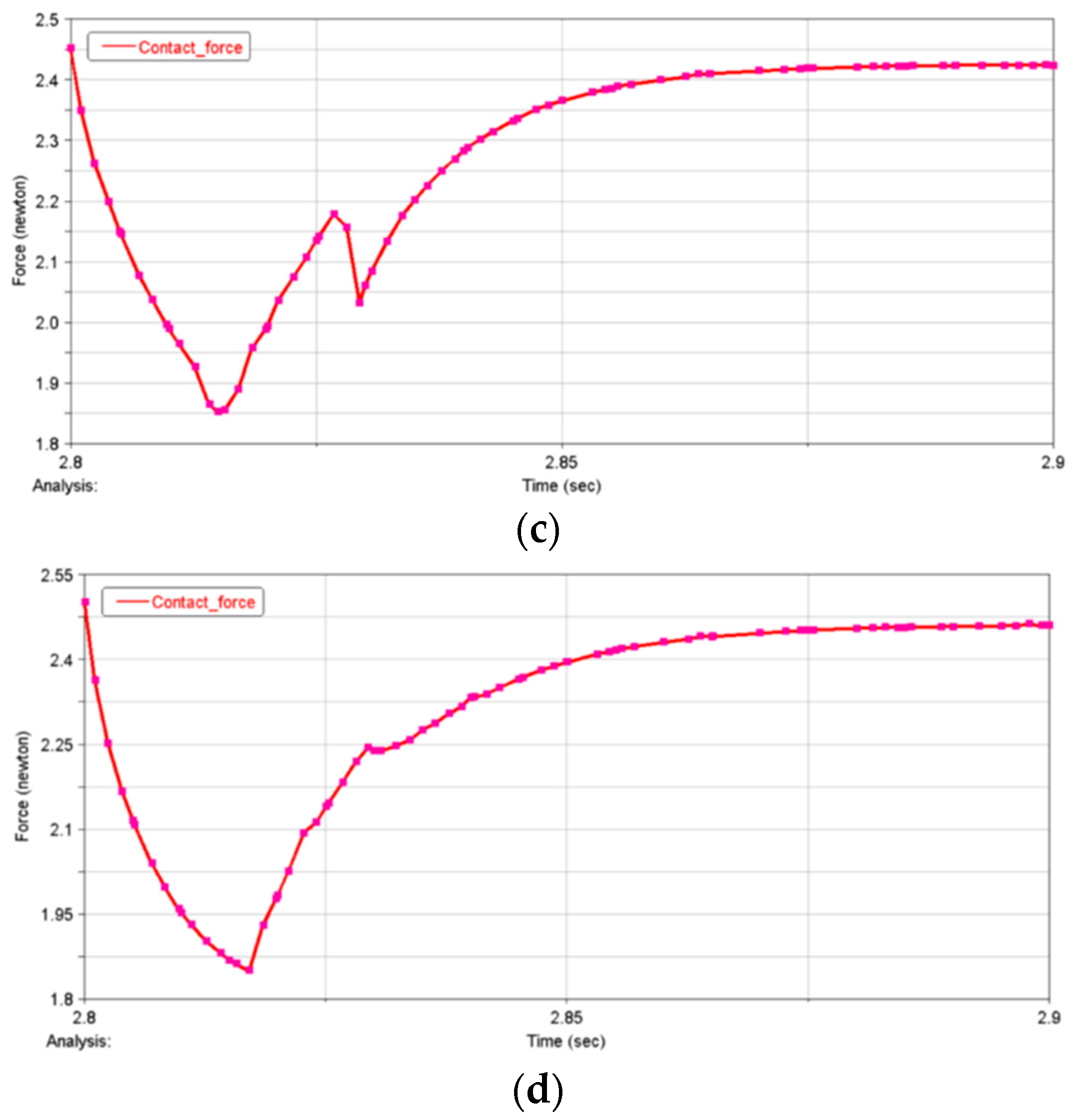
| Serial Number | Idler Gear Radius (mm) | Drive Torque (Nmm) |
|---|---|---|
| 1 | 7 | 33 |
| 2 | 7.2 | 124 |
| 3 | 7.5 | 364 |
| Serial Number | Idler Gear Radius (mm) | Contact Force of Idler Gear (N) |
|---|---|---|
| 1 | 7 | 2.4 |
| 2 | 7.2 | 5.3 |
| 3 | 7.5 | 9.1 |
| Serial Number | Radiusof Flexible Ring (mm) | Shrinkage of Flexible Ring (mm) | Drive Torque (Nmm) | Contact Pressure with Idler Gear (N) | Contact Pressure with Inner and Outer Rings (N) |
|---|---|---|---|---|---|
| 1 | 19.25 | 0.5 | 5.3 | 5.3 | 5.5 |
| 2 | 19.5 | 1 | 11 | 11 | 11 |
| 3 | 19.75 | 1.5 | 15.8 | 15.8 | 16 |
| 4 | 20.0 | 2.0 | 18.9 | 18.9 | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Liu, C.; Qian, Z.; Kang, X.; Liu, H. Analysis of Kinematics and Dynamics of Rolling Ring Based on Finite Element Method. Electronics 2024, 13, 1235. https://doi.org/10.3390/electronics13071235
Wu H, Liu C, Qian Z, Kang X, Liu H. Analysis of Kinematics and Dynamics of Rolling Ring Based on Finite Element Method. Electronics. 2024; 13(7):1235. https://doi.org/10.3390/electronics13071235
Chicago/Turabian StyleWu, Haihong, Chengshan Liu, Zhiyuan Qian, Xiao Kang, and Huiqun Liu. 2024. "Analysis of Kinematics and Dynamics of Rolling Ring Based on Finite Element Method" Electronics 13, no. 7: 1235. https://doi.org/10.3390/electronics13071235




