Wideband Low Phase-Noise Signal Generation Using Coaxial Resonator in Cascaded Phase Locked Loop
Abstract
:1. Introduction
2. Phase-Locked Loop Principle and Phase Noise
2.1. Phase-Locked Loop
2.2. Phase Noise in PLL
2.3. DDS for High-Frequency Generation
3. Proposed Design of Cascaded PLLs
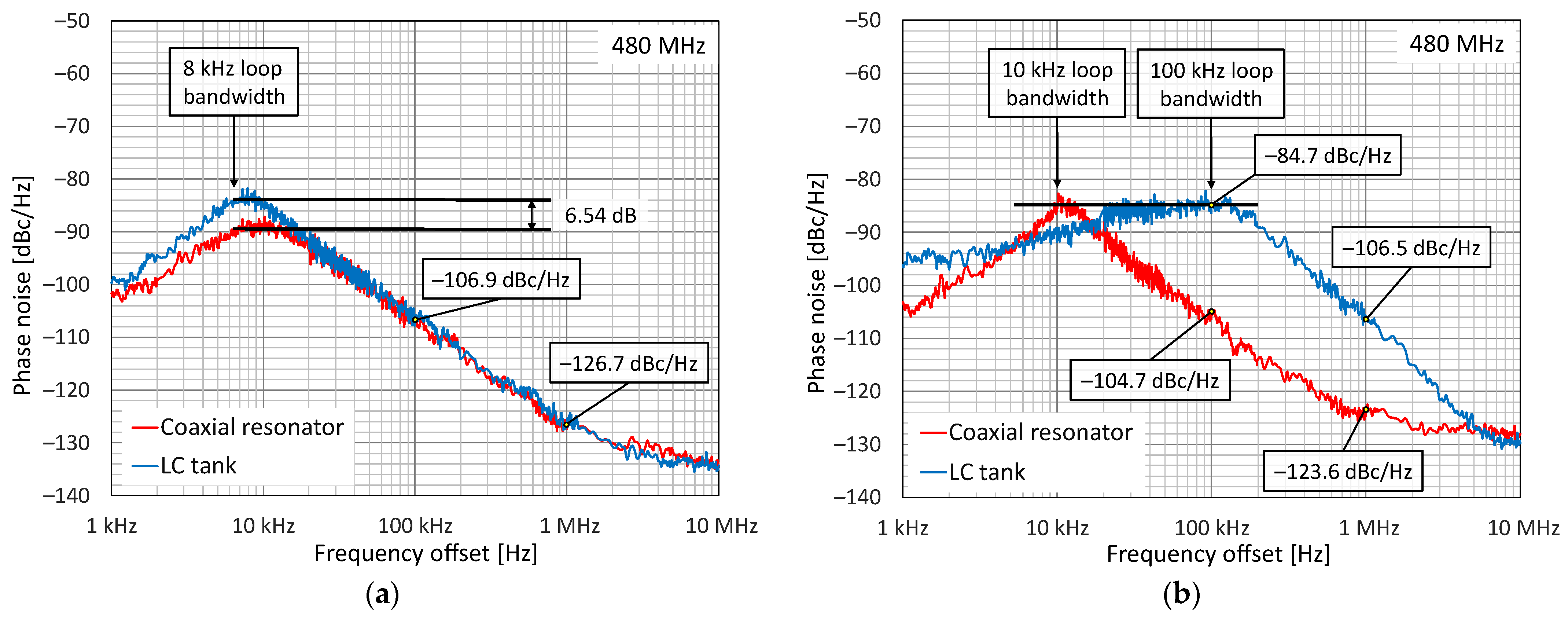
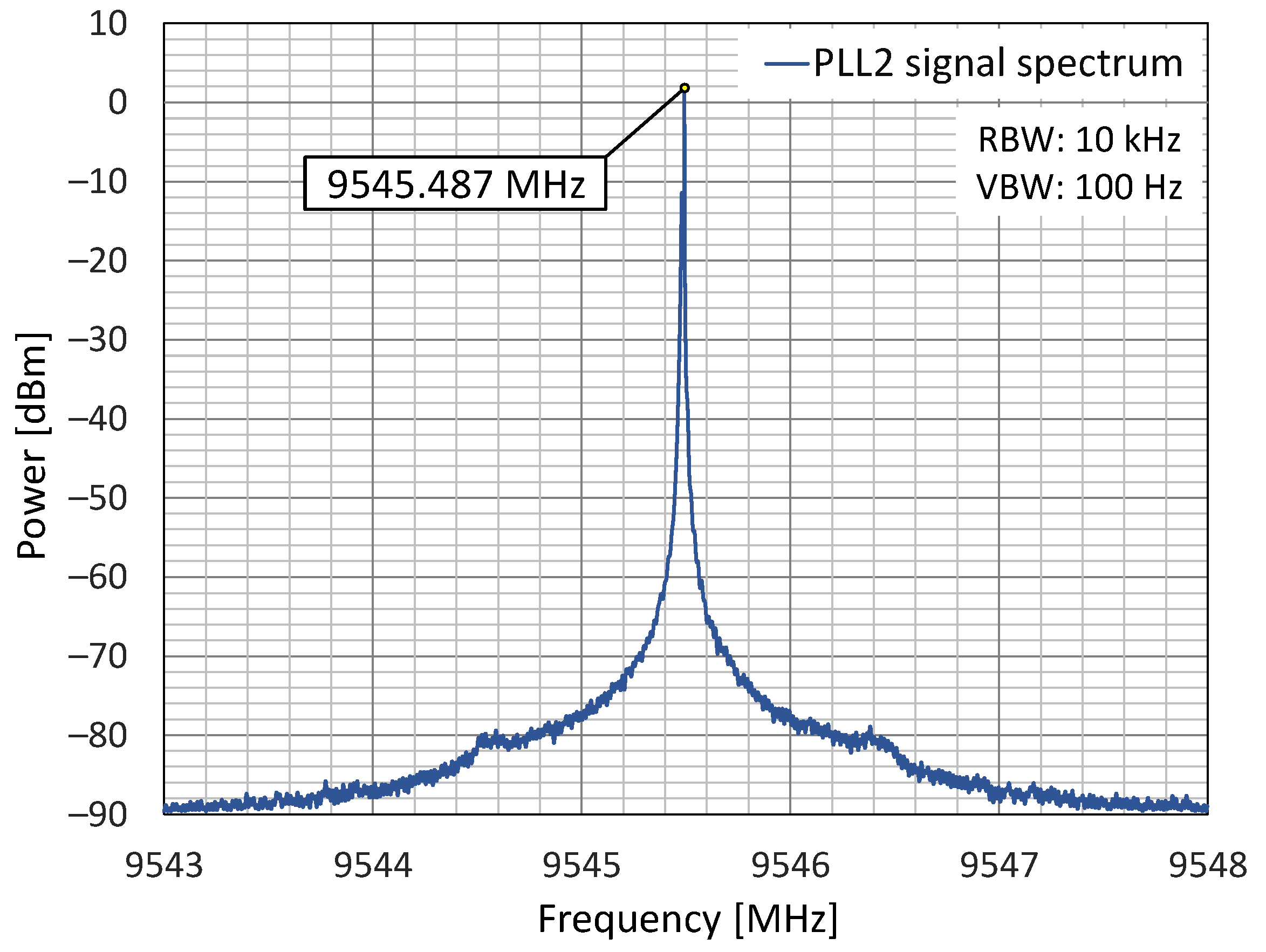
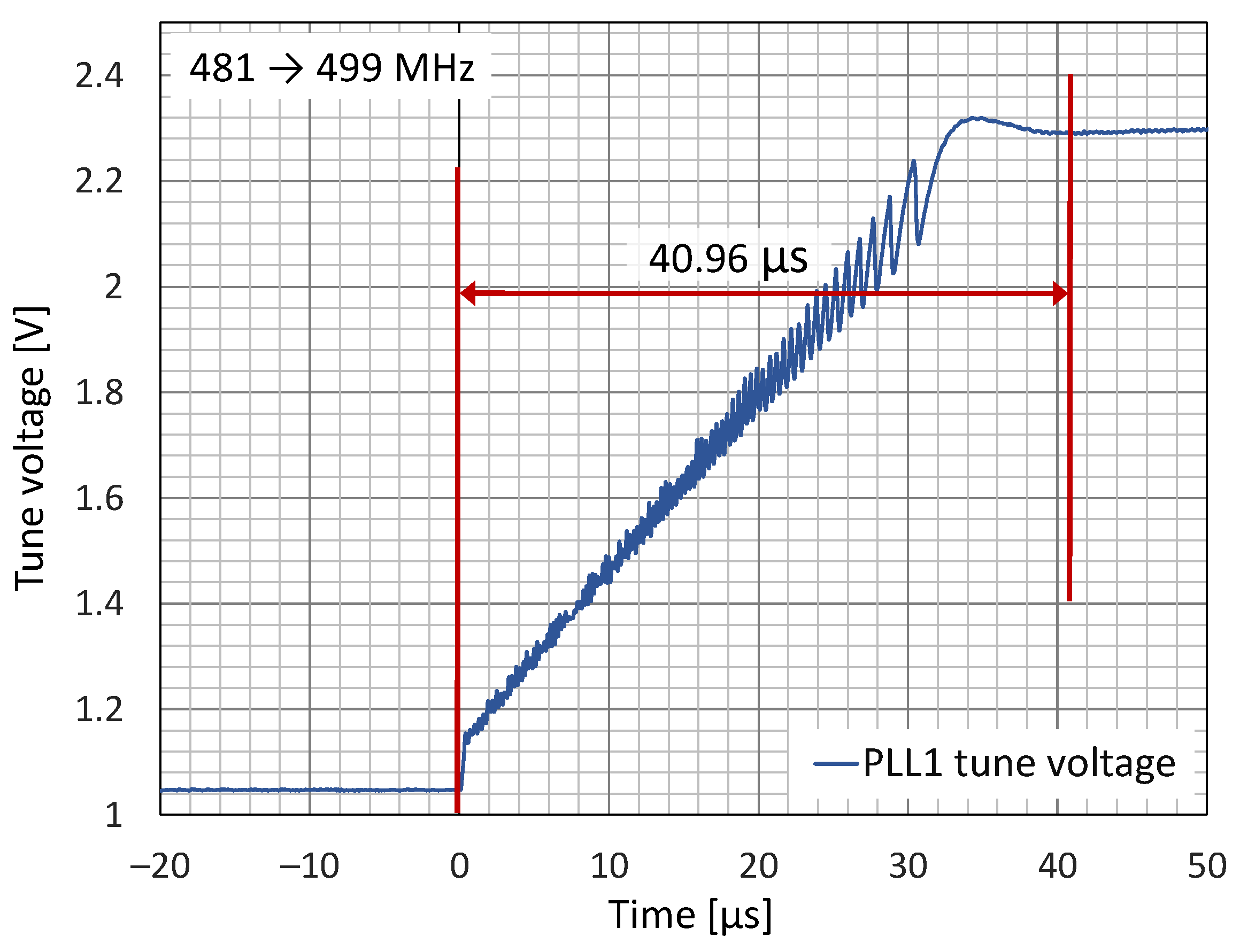
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Yang, S.-M.M. Modern Digital Radio Communication Signals and Systems; Springer Science+Business Media: New York, NY, USA, 2018; ISBN 978-3-319-71567-4. [Google Scholar]
- Alhashimi, H.F.; Hindia, M.N.; Dimyati, K.; Hanafi, E.B.; Safie, N.; Qamar, F.; Azrin, K.; Nguyen, Q.N. A Survey on Resource Management for 6G Heterogeneous Networks: Current Research, Future Trends, and Challenges. Electronics 2023, 12, 647. [Google Scholar] [CrossRef]
- Ho, C.-R.; Chen, M.S.-W. Smoothing the Way for Digital Phase-Locked Loops: Clock Generation in the Future with Digital Signal Processing for Mitigating Spur and Interference. IEEE Microw. 2019, 20, 80–97. [Google Scholar] [CrossRef]
- Jothimani, S.; Narmadha, A.; Santhiya, C.; Priya, S.S. Design of Various Modulation Schemes Using DDS. In Proceedings of the 2023 7th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 23–25 February 2023; pp. 1–6. [Google Scholar]
- Matinmikko-Blue, M.; Yrjola, S.; Ahokangas, P. Spectrum Management in the 6G Era: The Role of Regulation and Spectrum Sharing. In Proceedings of the 2020 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020; pp. 1–5. [Google Scholar]
- Wang, Y.; Liu, Y.; Xu, H.; Li, Z.; Li, Z. A Wideband and Low Reference Spur PLL with Clock Feedthrough Suppressed and Low Current Mismatch Charge Pump and Symmetrical CML Divider. Electronics 2023, 12, 4164. [Google Scholar] [CrossRef]
- Jo, Y.; Kim, J.; Shin, Y.; Park, H.; Hwang, C.; Lim, Y.; Choi, J. A Wideband LO Generator for 5G FR1 Bands Using a Single LC -VCO-Based Subsampling PLL and a Ring-VCO-Based Fractional-Resolution Frequency Multiplier. IEEE J. Solid-State Circuits 2023, 58, 3338–3350. [Google Scholar] [CrossRef]
- Chen, J.; Kuylenstierna, D.; Gunnarsson, S.E.; He, Z.S.; Eriksson, T.; Swahn, T.; Zirath, H. Influence of White LO Noise on Wideband Communication. IEEE Trans. Microw. Theory Tech. 2018, 66, 3349–3359. [Google Scholar] [CrossRef]
- Goldberg, B.-G. Digital Frequency Synthesis Demystified; LLH Technology Publishing: Eagle Rock, VA, USA, 1999; ISBN 978-1-878707-47-5. [Google Scholar]
- Zhang, Y.; Tang, X.; Wei, Z.; Bao, K.; Jiang, N. A Ku-Band Fractional-N Frequency Synthesizer with Adaptive Loop Bandwidth Control. Electronics 2021, 10, 109. [Google Scholar] [CrossRef]
- Bulja, S.; Grebennikov, A. Variable Reflection-Type Attenuators Based on Varactor Diodes. IEEE Trans. Microw. Theory Tech. 2012, 60, 3719–3727. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Huang, H.; Sun, Z.; Liu, B.; Fadila, A.A.; Qiu, J.; Liu, Z.; Wang, W.; Xiong, Y.; et al. A 6.5-to-8 GHz Cascaded Dual-Fractional-N Digital PLL Achieving −63.7 dBc Fractional Spurs with 50 MHz Reference. In Proceedings of the 2023 IEEE Custom Integrated Circuits Conference (CICC), San Antonio, TX, USA, 23–26 April 2023; pp. 1–2. [Google Scholar]
- Shu, Z.; Lee, K.L.; Leung, B.H. A 2.4-GHz Ring-Oscillator-Based CMOS Frequency Synthesizer with a Fractional Divider Dual-PLL Architecture. IEEE J. Solid-State Circuits 2004, 39, 452–462. [Google Scholar] [CrossRef]
- Tsai, T.-H.; Sheen, R.-B.; Hsu, S.-Y.; Chang, Y.-T.; Chang, C.-H.; Staszewski, R.B. A Cascaded PLL (LC-PLL + RO-PLL) with a Programmable Double Realignment Achieving 204fs Integrated Jitter (100 kHz to 100 MHz) and −72 dB Reference Spur. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 16–20 February 2022; pp. 1–3. [Google Scholar]
- Vishnu, R. A DDS-PLL Hybrid Based Fast Settling Wideband Frequency Synthesizer for Frequency Hopping Radios. Procedia Comput. Sci. 2017, 115, 748–755. [Google Scholar] [CrossRef]
- Bonfanti, A.; Amorosa, F.; Samori, C.; Lacaita, A.L. A DDS-Based PLL for 2.4-GHz Frequency Synthesis. IEEE Trans. Circuits Syst. II 2003, 50, 1007–1010. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Ikeda, S.; Ito, H.; Kasamatsu, A.; Obara, T.; Noguchi, N.; Kamisuki, K.; Jiyang, Y.; Hara, S.; Ruibing, D.; et al. Design of High-Frequency Piezoelectric Resonator-Based Cascaded Fractional-N PLL with Sub-Ppb-Order Channel Adjusting Technique. In Proceedings of the 2017 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017; pp. 43–44. [Google Scholar]
- Chary, P.P.; Shaik Peerla, R.; Dutta, A. A Simplified Gm−C Filter Technique for Reference Spur Reduction in Phase-Locked Loop. JLPEA 2024, 14, 17. [Google Scholar] [CrossRef]
- Biswas, D. Dual-Loop Integer PLL for Phase Noise Reduction. Analog Integr. Circuits Signal Process. 2022, 112, 537–544. [Google Scholar] [CrossRef]
- Vidmar, M. Extending Leeson’s Equation. Inf. MIDEM 2021, 51, 135–146. [Google Scholar] [CrossRef]
- Demir, A.; Mehrotra, A.; Roychowdhury, J. Phase Noise in Oscillators: A Unifying Theory and Numerical Methods for Characterization. IEEE Trans. Circuits Syst. I 2000, 47, 655–674. [Google Scholar] [CrossRef]
- Telba, A.A.; Qasim, S.M.; Noras, J.M.; Almashary, B.; El Ela, M.A. Behavioural Modelling and Simulation of Dual Cascaded PLL Based Frequency Synthesizer. In Proceedings of the 2007 14th International Conference on Mixed Design of Integrated Circuits and Systems, Ciechocinek, Poland, 21–23 June 2007; pp. 407–411. [Google Scholar]
- Boroditsky, R.; Gomez, J. Ultra Low Phase Noise 1 GHz OCXO. In Proceedings of the 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, Switzerland, 29 May–1 June 2007; pp. 250–253. [Google Scholar]
- Brannon, A.; Breitbarth, J.; Popovic, Z. A Low-Power, Low Phase Noise Local Oscillator for Chip-Scale Atomic Clocks. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 12–17 June 2005; pp. 1535–1538. [Google Scholar]
- Wersing, W. Microwave Ceramics for Resonators and Filters. Curr. Opin. Solid State Mater. Sci. 1996, 1, 715–731. [Google Scholar] [CrossRef]
- San-Blas, A.A.; Guglielmi, M.; Melgarejo, J.C.; Coves, A.; Boria, V.E. Design Procedure for Bandpass Filters Based on Integrated Coaxial and Rectangular Waveguide Resonators. IEEE Trans. Microw. Theory Tech. 2020, 68, 4390–4404. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, K.-L. Metal-Dielectric Coaxial Dual-Mode Resonator for Compact Inline Bandpass Filters. In Proceedings of the 2023 IEEE/MTT-S International Microwave Symposium—IMS 2023, San Diego, CA, USA, 11–16 June 2023; pp. 403–405. [Google Scholar]
- Das, D.; Biswas, B.; Kumar, G.A.; Mondal, S. A Compact Very Narrow Band Coaxial Cavity Resonator Filter at X-Band with SMA Connector Feed. In Proceedings of the 2020 IEEE Calcutta Conference (CALCON), Kolkata, India, 28–29 February 2020; pp. 93–96. [Google Scholar]
- Fiedziuszko, S.J.; Holmes, S. Dielectric Resonators Raise Your High-Q. IEEE Microw. 2001, 2, 50–60. [Google Scholar] [CrossRef]
- Manjunatha, R.H.V.; Manjunath, R.K. Design and Simulation of Ku-Band Voltage Tuned Dielectric Resonator Oscillator. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 3–5 April 2018; pp. 0299–0304. [Google Scholar]
- Skyworks. Coaxial Resonators for Voltage-Controlled Oscillator (VCO) Applications 2013. Available online: http://www.edatop.com/down/faq/hfss/Coaxial_Resonators_for_VCOs_202664A.pdf (accessed on 23 March 2024).
- Rohde, U.; Poddar, A. Novel Multi-Coupled Line Resonators Replace Traditional Ceramic Resonators in Oscillators/VCOs. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 4–7 June 2006; pp. 432–442. [Google Scholar]
- Hitch, B.; Holden, T. Phase Locked DRO/CRO for Space Use. In Proceedings of the International Frequency Control Symposium, Orlando, FL, USA, 28–30 May 1997; pp. 1015–1023. [Google Scholar]
- Jeon, Y. Study of Ultra-Broadband Synthesizer of Fast Indirect Type in a 0.5–18 GHz Range for SIGINT System. Electronics 2023, 13, 48. [Google Scholar] [CrossRef]
- Mincong, C.; Ruiyu, L.; Tao, H. Study of Optimized Design of DDS Based on FPGA. In Proceedings of the 2019 14th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Changsha, China, 1–3 November 2019; pp. 150–154. [Google Scholar]
- Nilsson, P.; Gerrits, J.F.M.; Yuan, J. A Low Complexity DDS IC for FM-UWB Applications. In Proceedings of the 2007 16th IST Mobile and Wireless Communications Summit, Budapest, Hungary, 1–5 July 2007; pp. 1–5. [Google Scholar]
- Siemens Matsushita. Coaxial Ceramic Resonators. Available online: https://www.rf-microwave.com/resources/products_attachments/5a4386ce05742.pdf (accessed on 4 April 2024).
- Zhang, X.; Du, Q.; Liu, C.; Zhang, H.; Ma, Y.; Li, Y.; Li, J. A Low Phase Noise Frequency Synthesizer with a Fourth-Order RLC Loop Filter. Electronics 2023, 12, 224. [Google Scholar] [CrossRef]
- Hilt, A. Availability and Fade Margin Calculations for 5G Microwave and Millimeter-Wave Anyhaul Links. Appl. Sci. 2019, 9, 5240. [Google Scholar] [CrossRef]
- Ilgaz, M.A.; Lavric, A.; Batagelj, B. Phase-Noise Degradation of an Optically Distributed Local Oscillator in a Radio Access Network. Radioengineering 2021, 30, 10–15. [Google Scholar] [CrossRef]
- Hilt, A.; Zolomy, A.; Berceli, T.; Jaro, G.; Udvary, E. Millimeter Wave Synthesizer Locked to An Optically Transmitted Reference Using Harmonic Mixing. In Proceedings of the International Topical Meeting on Microwave Photonics, Duisburg, Germany, 3–5 September 1997; pp. 91–94. [Google Scholar]
- Krause, B.; Lavric, A.; Tebart, J.; Stohr, A.; Preu, S. Phase Noise of an Electro-Optic Terahertz Comb. Opt. Express 2024. [Google Scholar] [CrossRef]









| Reference | This Work | [15] | [16] | [10] | [38] | [34] |
|---|---|---|---|---|---|---|
| Architecture | PLL-PLL | DDS-PLL | DDS-PLL | Frac PLL | Frac PLL | DDS |
| Frequency Range [GHz] | 1.925–16 | 0.13–1.75 | 2.36–2.44 | 11.37–14.8 | 1.426 | 0.5–18 |
| Phase Noise 1 [dBc/Hz] | −121 @ 1 M −102.5 @ 100 k | −134 @ 1 M −103 @ 100 k | −99 @ 1 M −94 @ 100 k | −112.5 @ 1 M −79 @ 100 k | −138.4 @ 1 M −113.9 @ 100 k | −110.9@ 1 M −112.9 @ 100 k |
| Fractional Spurs 1 [dBc] | −80 | −75 | −53 | N/D | −69 | >−60 |
| Lock Time 1 [µS] | 41 | 51 | 1 | 24 | 94 | N/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blatnik, A.; Batagelj, B. Wideband Low Phase-Noise Signal Generation Using Coaxial Resonator in Cascaded Phase Locked Loop. Electronics 2024, 13, 1934. https://doi.org/10.3390/electronics13101934
Blatnik A, Batagelj B. Wideband Low Phase-Noise Signal Generation Using Coaxial Resonator in Cascaded Phase Locked Loop. Electronics. 2024; 13(10):1934. https://doi.org/10.3390/electronics13101934
Chicago/Turabian StyleBlatnik, Aljaž, and Boštjan Batagelj. 2024. "Wideband Low Phase-Noise Signal Generation Using Coaxial Resonator in Cascaded Phase Locked Loop" Electronics 13, no. 10: 1934. https://doi.org/10.3390/electronics13101934









