Identification and Optimization Study of Cavitation in High Power Torque Converter
Abstract
:1. Introduction
2. Torque Converter Simulation and Analytical Modeling
2.1. Definition of Torque Converter Parameter
2.2. Geometric Modeling of Torque Converter
2.3. Simulation Model of Torque Converter
3. Identification of Cavitation in Torque Converter
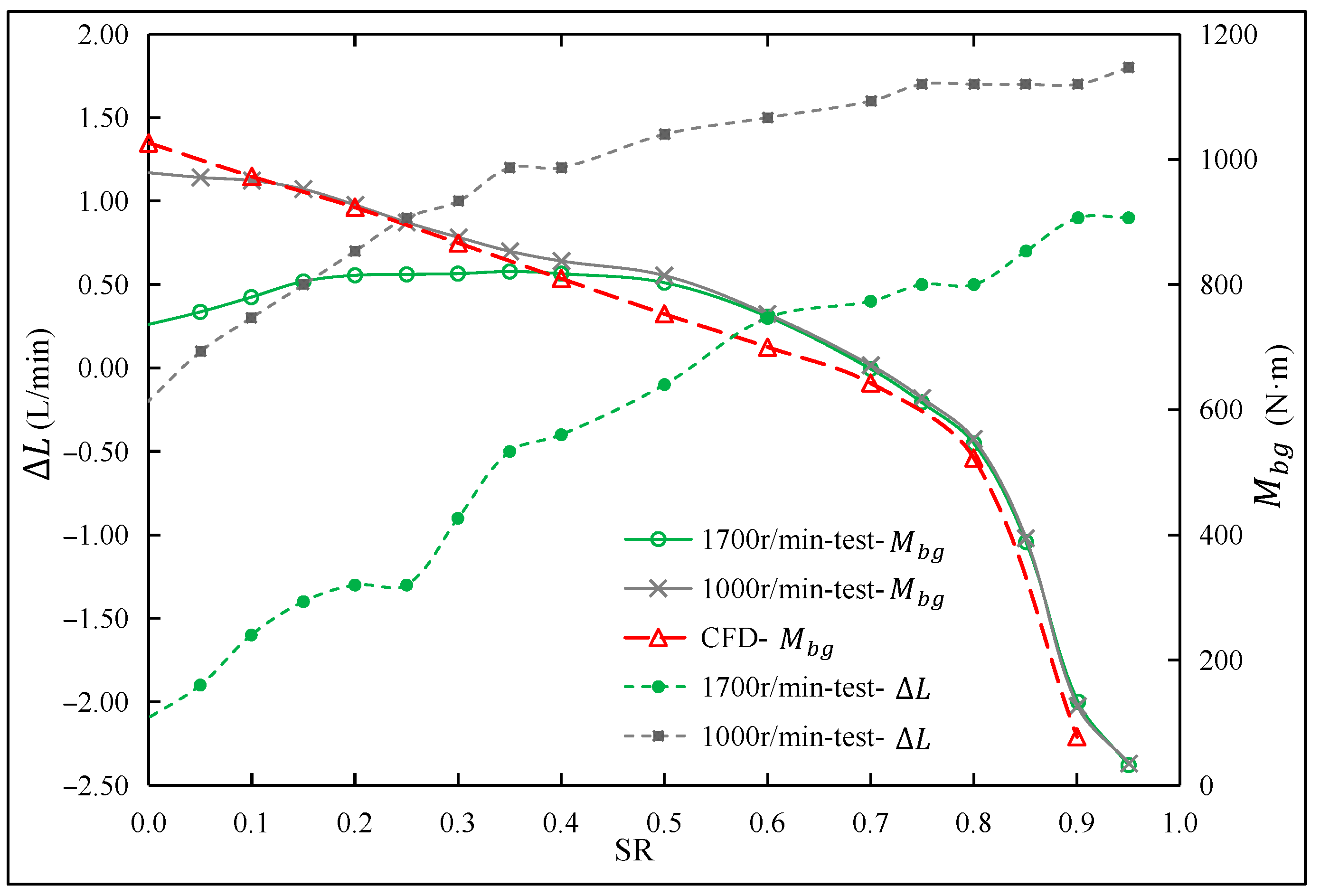
3.1. Cavitation Identification Method Based on Flow Difference
3.2. Test Bench Setup and Test Procedure
3.3. Identification of Cavitation
4. Optimized Design of Cavitation in High Power Torque Converter
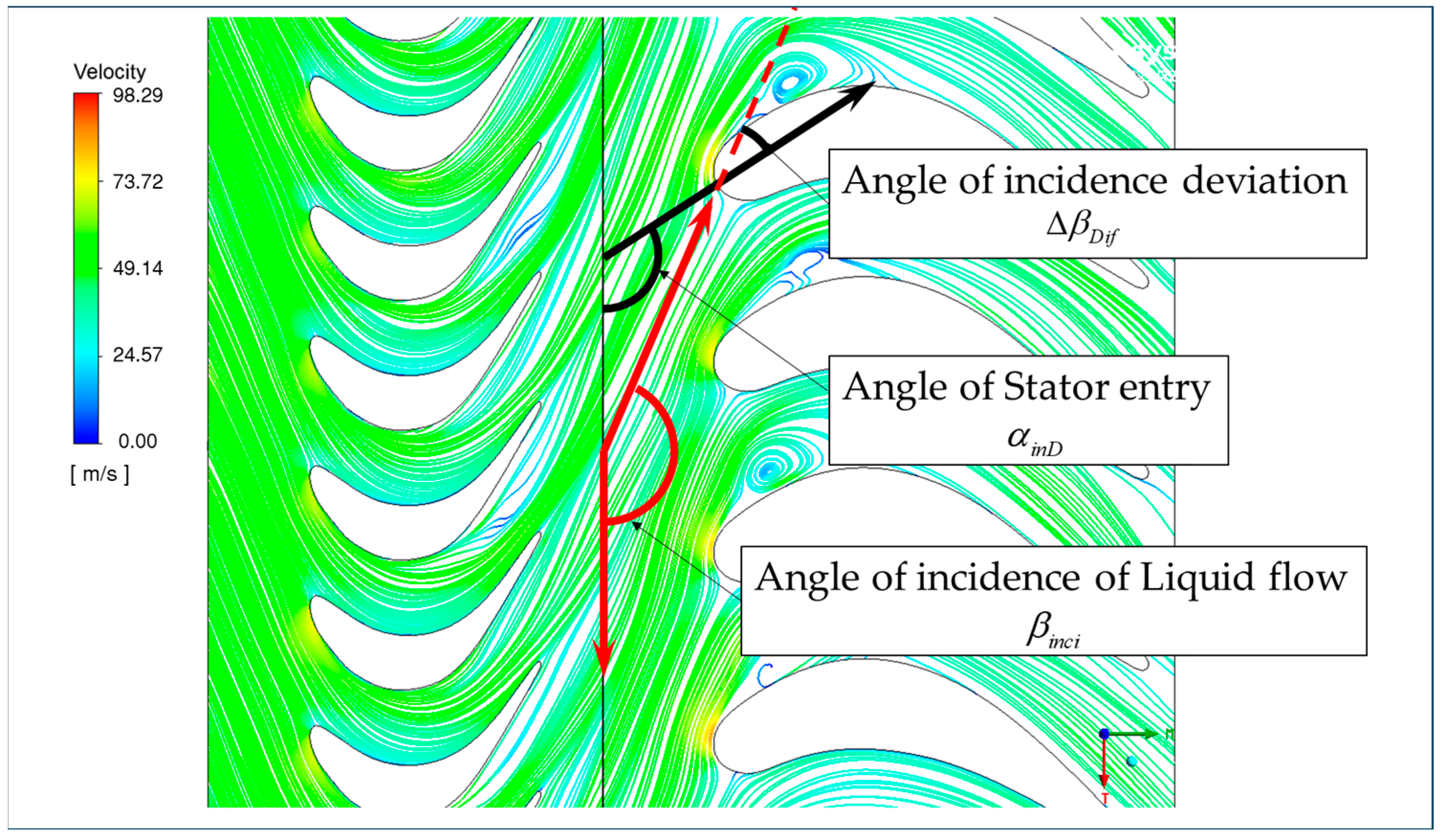
4.1. Analysis of Cavitation Mechanism of Hydraulic Torque Converter
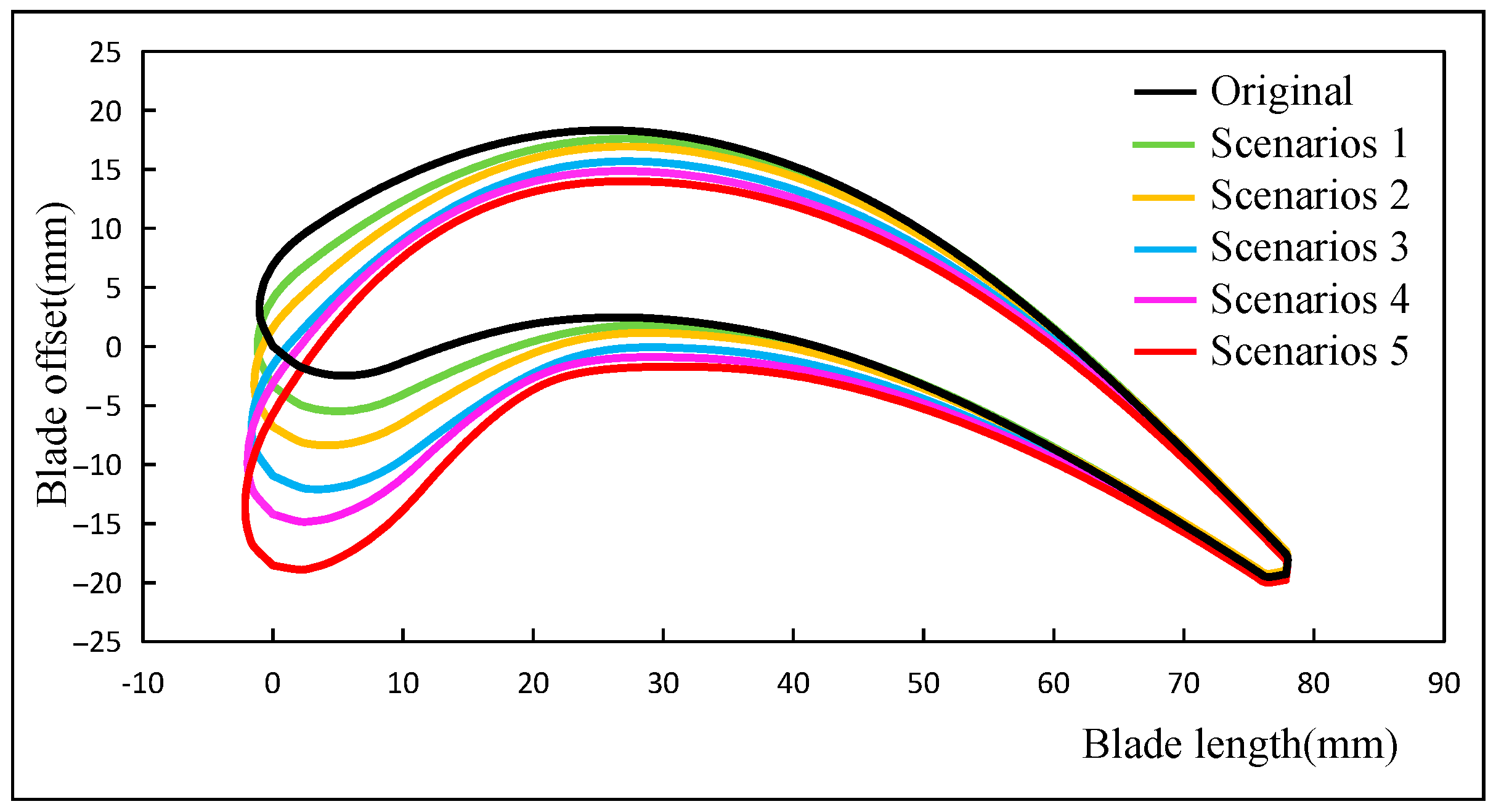
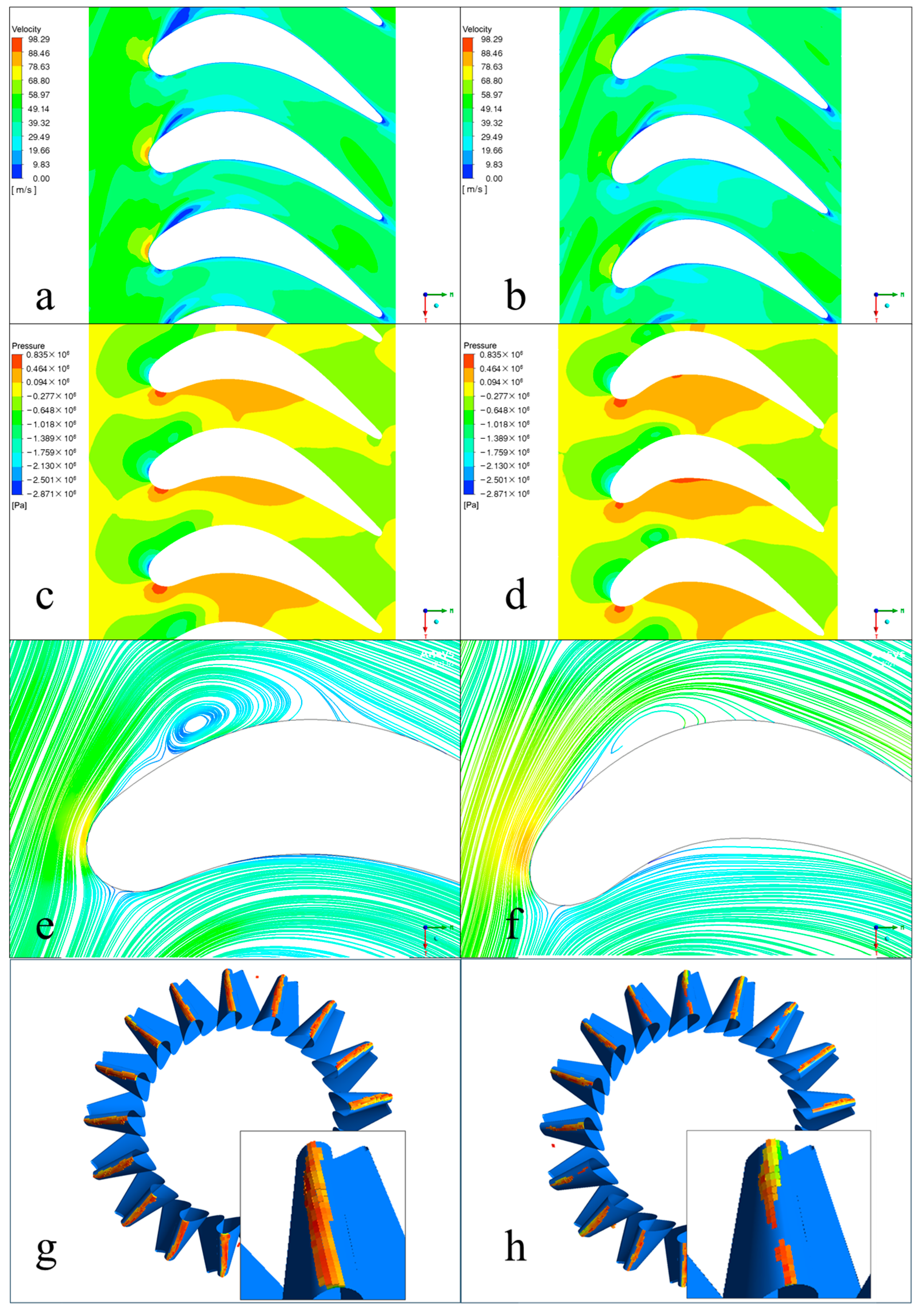
4.2. Optimized Design of Torque Converter Stator
4.3. Simulation Analysis of Torque Converter Stator Optimization Scheme
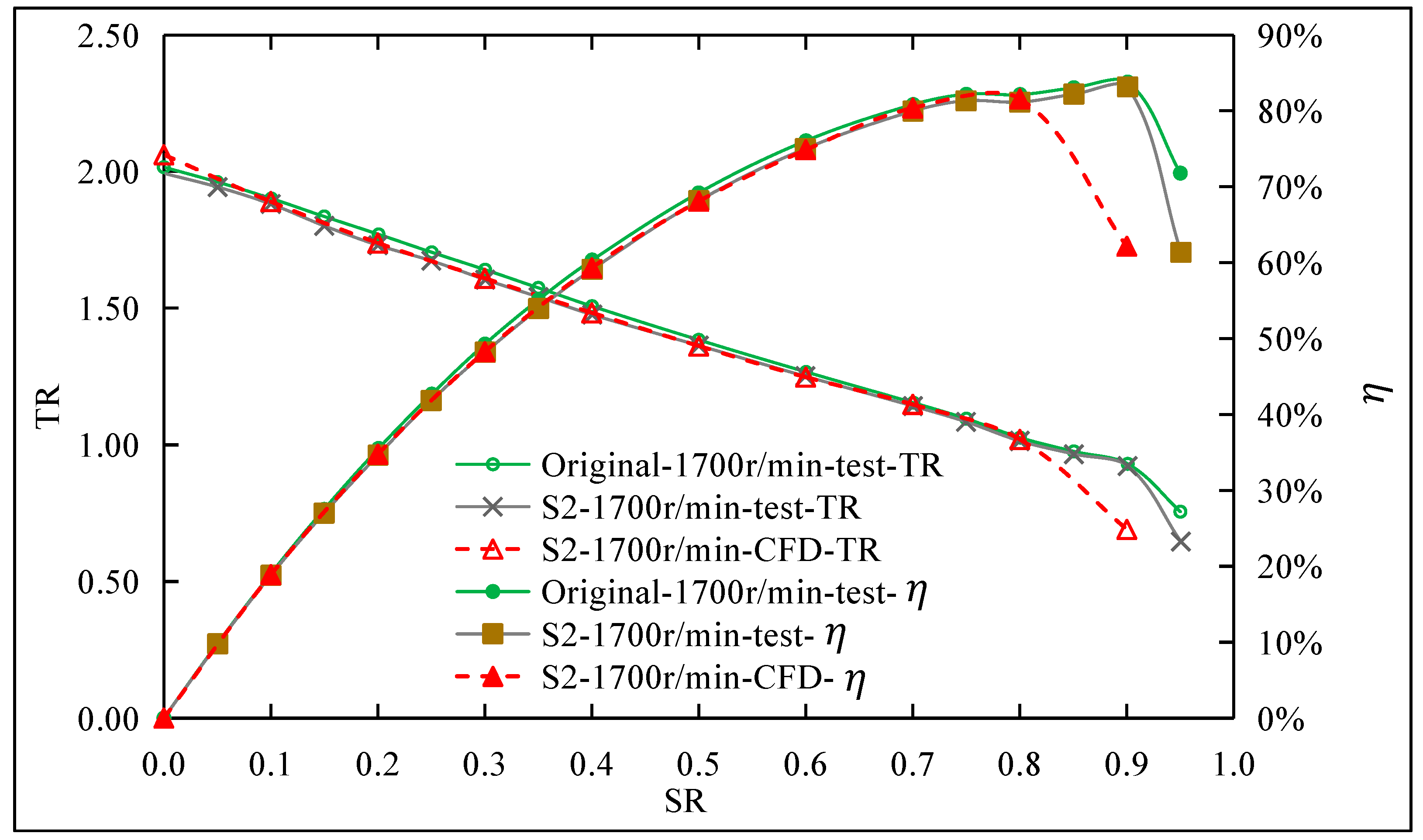
5. Validation of Cavitation Optimization for High Power Torque Converter
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Wu, G. Kriging-assisted design optimization of the impeller geometry for an automotive torque converter. Struct. Multidiscip. Optim. 2018, 57, 2503–2514. [Google Scholar] [CrossRef]
- Yang, Y.; Liou, W.W.; Qureshi, F.; Whitticar, D.J.; Michael, E.H. Transmission fluid properties’ effects on performance characteristics of a torque converter: A computational study. Tribol. Trans. 2021, 64, 1055–1063. [Google Scholar] [CrossRef]
- Xiong, P.; Sun, H.; Zhong, J.; Zhen, C.; Chen, X.; Gao, H. Analysis of the Influence of the Number of Torque Converter Blades on Working Performance Based on the Response Surface Method. J. Phys. Conf. Ser. 2021, 1748, 022028. [Google Scholar] [CrossRef]
- Wang, G. Research on Scale-Resolving Simulation for Flow Field and Cavitation Characteristics of Hydrodynamic Torque Converter. Ph.D. Thesis, Jilin University, Changchun, China, 2022. (In Chinese). [Google Scholar]
- De Jesus Rivera, E. Pressure Measurements Inside Multiple Cavities of a Torque Converter and CFD Correlation. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2018. [Google Scholar]
- Ju, J.; Jang, J.; Choi, M.; Baek, J.H. Effects of cavitation on performance of automotive torque converter. Adv. Mech. Eng. 2016, 8, 1687814016654045. [Google Scholar] [CrossRef]
- Guo, M.; Liu, C.; Liu, S.; Ke, Z.; Wei, W.; Yan, Q.; Khoo, B.C. Detection and evaluation of cavitation in the stator of a torque converter using pressure measurement. Phys. Fluids 2022, 34, 045124. [Google Scholar] [CrossRef]
- Tsutsumi, K.; Watanabe, S.; Tsuda, S.-I.; Yamaguchi, T. Cavitation simulation of automotive torque converter using a homogeneous cavitation model. Eur. J. Mech. B/Fluids 2017, 61, 263–270. [Google Scholar] [CrossRef]
- Zhao, L. The Cavitation Research of the Flow Field in the Hydraulic Torque Converter Based on CFD. Ph.D. Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2016. (In Chinese). [Google Scholar]
- Craig, D.R. Characterization of Torque Converter Cavitation Sound Power Level over Varying Speed Ratio. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2016. [Google Scholar]
- Chad, M.W. Torque Converter Turbine Noise and Cavitation Noise over Varying Speed Ratio. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2012. [Google Scholar]
- Liu, C.; Wei, W.; Yan, Q.; Weaver, B.K.; Wood, H.G. On the application of passive flow control for cavitation suppression in torque converter stator. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 204–222. [Google Scholar] [CrossRef]
- Li, J. Investigation on Scale-Resolving Simulation of Unsteady Cavitation Flow around Blades and Its Bionic Control Mechanism. Ph.D. Thesis, Jilin University, Changchun, China, 2022. (In Chinese). [Google Scholar]
- Xiong, P.; Chen, X.; Sun, H.; Zhong, J.; Wu, L.; Gao, H. Effect of the blade shaped by Joukowsky airfoil transformation on the characteristics of the torque converter. Proc. IMechE Part D J. Automob. Eng. 2021, 235, 3314–3321. [Google Scholar]
- Ran, Z.; Ma, W.; Liu, C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Appl. Sci. 2021, 11, 2798. [Google Scholar] [CrossRef]
- Liu, C.; Yan, Q.; Li, J.; Li, J.; Zou, B. Investigation on the Cavitation Characteristics of High Power-density Torque Converter. J. Mech. Eng. 2020, 56, 147–155. (In Chinese) [Google Scholar]
- Song, J.; Bai, H.; Cheng, B.; Zhang, N.; Zhang, W.; Leng, H.; Zhao, W.; Zhang, Z. A review of large eddy simulation of aviation turbulence. Acta Aerodyn. Sin. 2023, 41, 26–43. (In Chinese) [Google Scholar]
- Wu, T.; Shi, B.; Wang, S.; Zhang, X.; He, G. Wall-Model For Large-Eddy Simulation And Its Applications. Chin. J. Theor. Appl. Mech. 2018, 50, 453–466. (In Chinese) [Google Scholar]
- Ran, Z.; Ma, W.; Liu, C.; Li, J. Multi-objective optimization of the cascade parameters of a torque converter based on CFD and a genetic algorithm. J. Automob. Eng. 2021, 8, 2311–2323. [Google Scholar] [CrossRef]
- Ran, Z.; Ma, W.; Wang, K.; Chai, B. Multi-Objective Optimization Design for a Novel Parametrized Torque Converter Based on an Integrated CFD Cascade Design System. Machines 2022, 10, 482. [Google Scholar] [CrossRef]
- Liu, C.; Xu, Z.; Ma, W.; Wang, S. CFD investigating medium-temperature in fluences on performance prediction and structure stress calculation in a hydrodynamic torque converter. Numer. Heat Transf. Part A Appl. 2017, 72, 563–578. [Google Scholar] [CrossRef]
- Liu, C.; Wei, W.; Yan, Q. Three Dimensional Torque Converter Blade Modelling Based on Bezier Curves. J. Mech. Eng. 2017, 53, 201–208. [Google Scholar] [CrossRef]
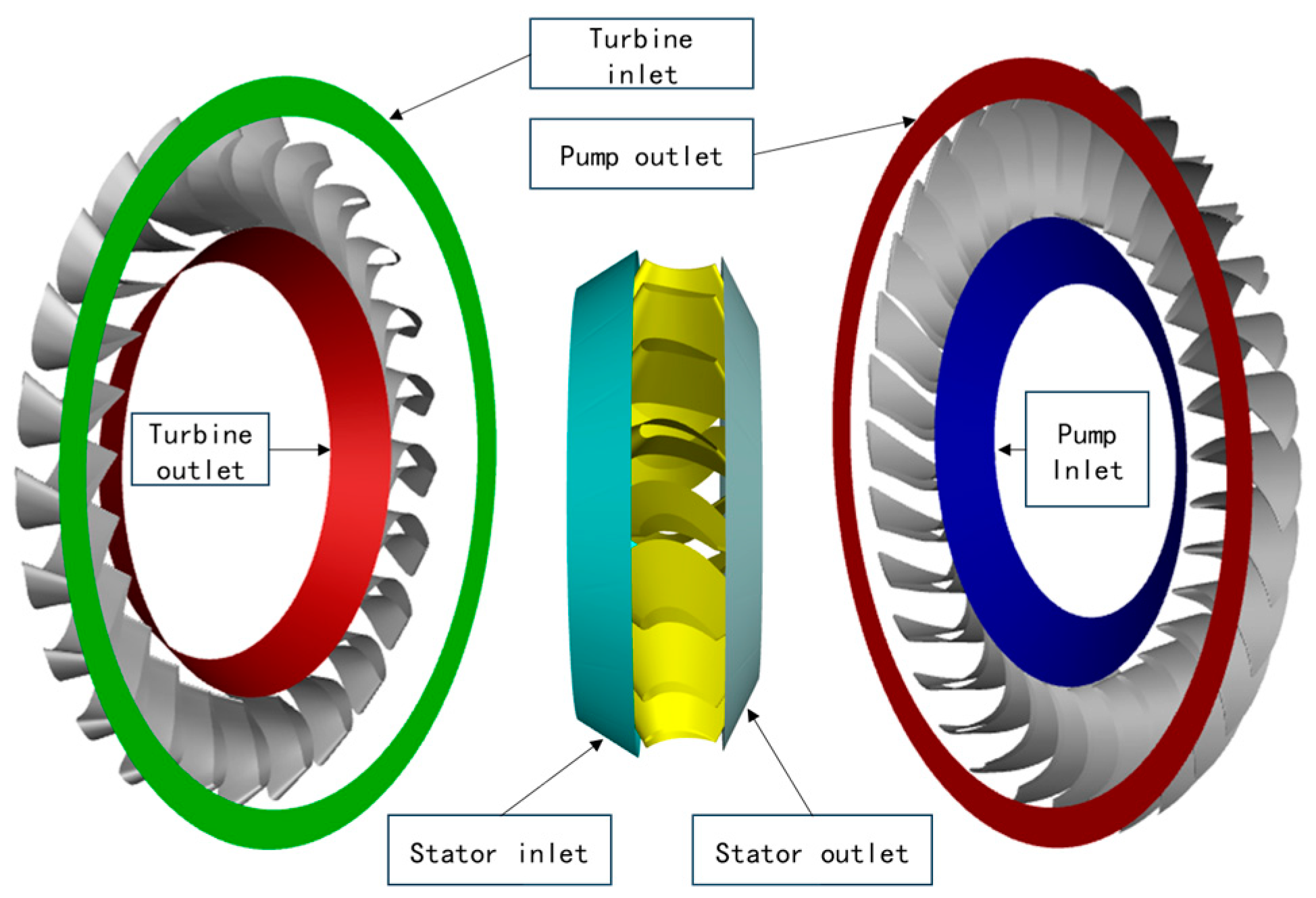










| Rated torque | 3500 N·m | ||
| Torus diameter | 440 mm | ||
| Torus width | 178 mm | ||
| Impeller | Pump | Turbine | Stator |
| Inlet angle | 125.7° | 45.8° | 121.5° |
| Outlet angle | 48.4° | 155.4° | 50.56° |
| Blade number | 31 | 32 | 17 |
| Tot. Elements () | (N·m) | Div./% | Duration (h) |
|---|---|---|---|
| 2.59 | 796.9 | - | 1.8 |
| 3.77 | 876.9 | 10.04% | 2.5 |
| 4.38 | 949.7 | 8.30% | 3.3 |
| 5.31 | 962.5 | 1.35% | 3.9 |
| 7.48 | 966.2 | 0.38% | 6.5 |
| 8.38 | 968.3 | 0.22% | 11.4 |
| Item | Parameter |
|---|---|
| Analysis Type | Transient Calculation |
| Type of fluid domain | Full-flow channel model |
| Turbulence model | RANS/LES |
| Mesh type | Hexahedral structured mesh |
| y+ value | ≤2 |
| Density of hydraulic transmission oil | 860 kg/m3 |
| Fluid oil viscosity | 0.01784 kg/(m·s) |
| Time step | 0.0005 s/step |
| Simulation time step | 400 |
| Pressure-velocity coupling method | SIMPLE |
| Transient spatial discretization method | Bounded second-order implicit |
| Other terms spatial discretization | Second-order upwind |
| Pump rotational speed | 1700 r/min |
| Turbine rotational speed | 0–1700 r/min |
| Stator rotational speed | 0 r/min |
| Part | Model | Range | Accuracy |
|---|---|---|---|
| Drive motor (VEM Gruppe, Dresden, Germany) | EN60034-1 | ±2940 r/min; ±7000 N·m | ±1 r/min; ±0.1% |
| Load Motor (Alibaba, Hangzhou, Chian) | FQDI35.5-4WFI | ±4500 r/min; ±7200 N·m | ±1 r/min; ±0.1% |
| Torque Sensor (S. Himmelstein and Company, Hoffman Estates, IL, USA) | K-T40B-010R-MF-S | ±10,000 N·m | ±0.1% F.S. |
| Encoder (Encoder Products Company (EPC), Sagle, Idaho) | HMCK16 A1 NM02 | 0–3000 r/min | 12 bit |
| Temperature Sensor (Omega Engineering, Norwalk, NJ, USA) | PT100(AA) | −50–200 °C | ±0.5 °C |
| Pressure Sensor (ESI Technology Ltd., Wrexham, Wales) | 1A00QODP5IX | 0–3000 kPa | ±0.5% |
| Item | Parameter | |||
|---|---|---|---|---|
| Angle of incidence deviation of flow injection (°) | original | 34.66 | scenarios 3 | 19.66 |
| scenarios 1 | 25.16 | scenarios 4 | 17.16 | |
| scenarios 2 | 21.16 | scenarios 5 | 14.16 | |
| Outlet angle (°) | 50.56 | |||
| inner ring offset (rad) | 0.097 | |||
| chord length (mm) | 77.82 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Xu, X.; Zhao, W.; Wang, Z.; Lei, Y.; Ma, W. Identification and Optimization Study of Cavitation in High Power Torque Converter. Appl. Sci. 2024, 14, 4240. https://doi.org/10.3390/app14104240
Wang K, Xu X, Zhao W, Wang Z, Lei Y, Ma W. Identification and Optimization Study of Cavitation in High Power Torque Converter. Applied Sciences. 2024; 14(10):4240. https://doi.org/10.3390/app14104240
Chicago/Turabian StyleWang, Kaifeng, Xiangyang Xu, Weiwei Zhao, Zhongshan Wang, Yulong Lei, and Wenxing Ma. 2024. "Identification and Optimization Study of Cavitation in High Power Torque Converter" Applied Sciences 14, no. 10: 4240. https://doi.org/10.3390/app14104240




