Maximum Operational Fluence Limits for Temporally Shaped Nanosecond Long Pulses
Abstract
:Featured Application
Abstract
1. Introduction
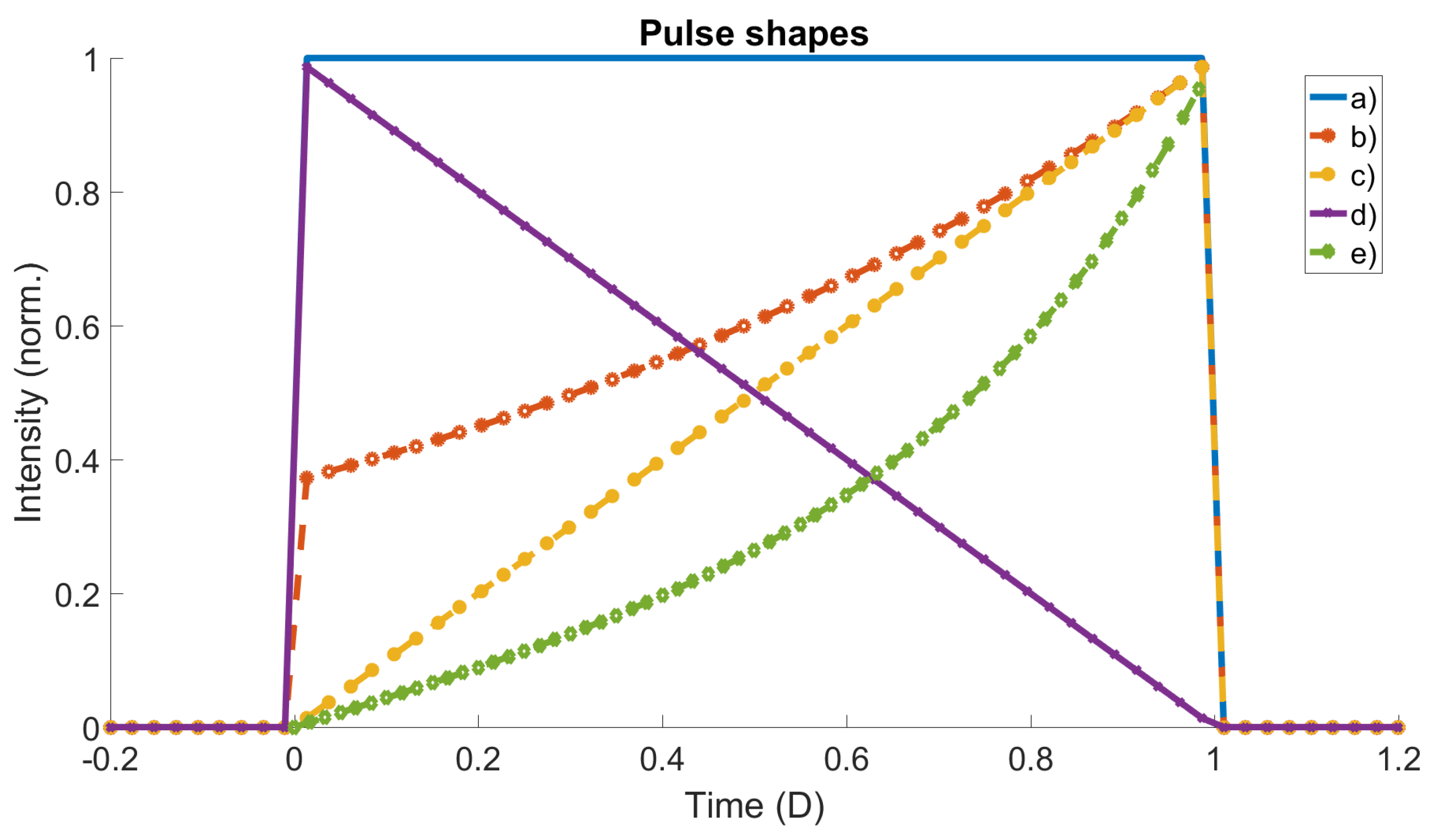
2. Pulse Shape Versus Pulse Length
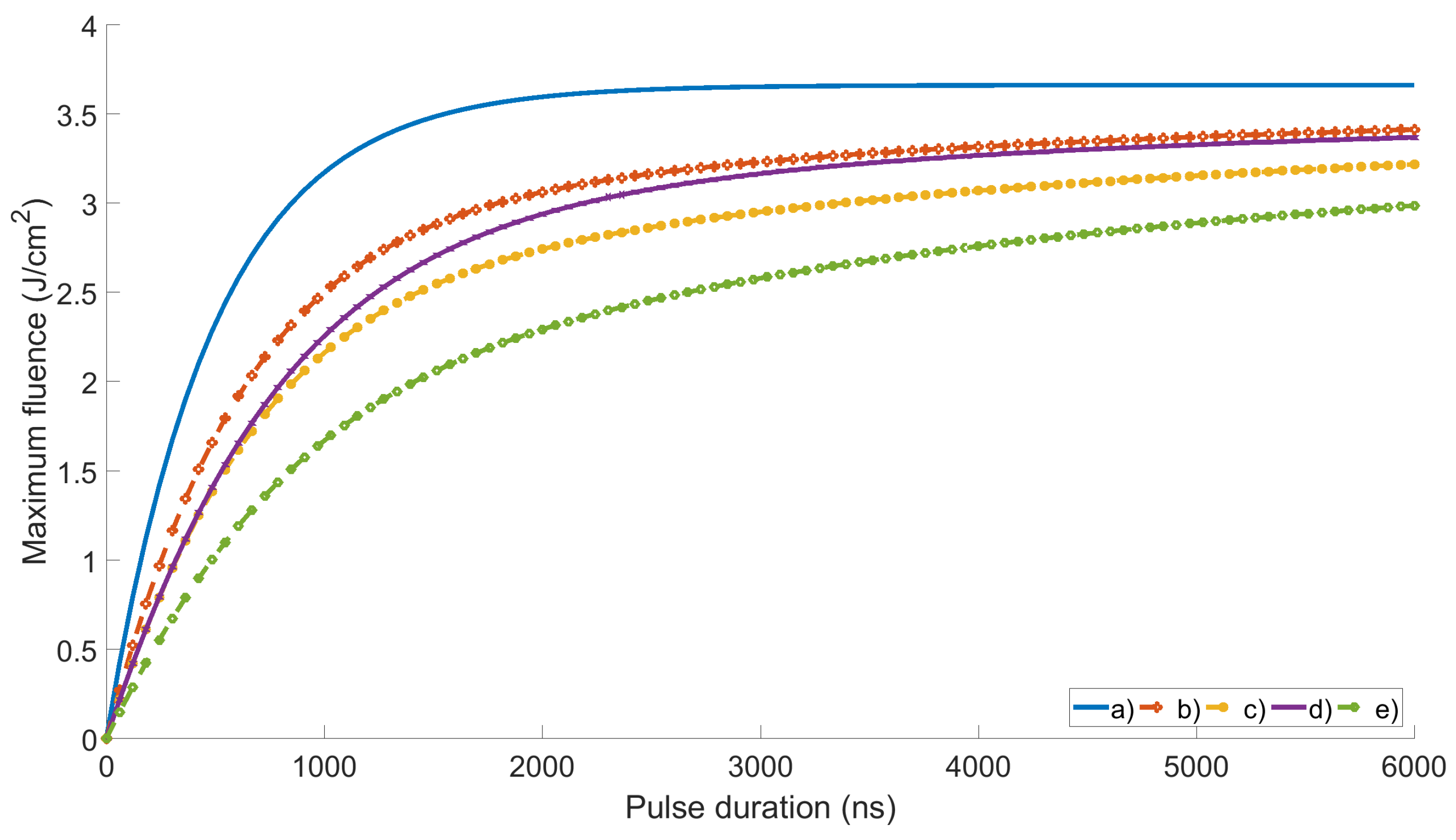
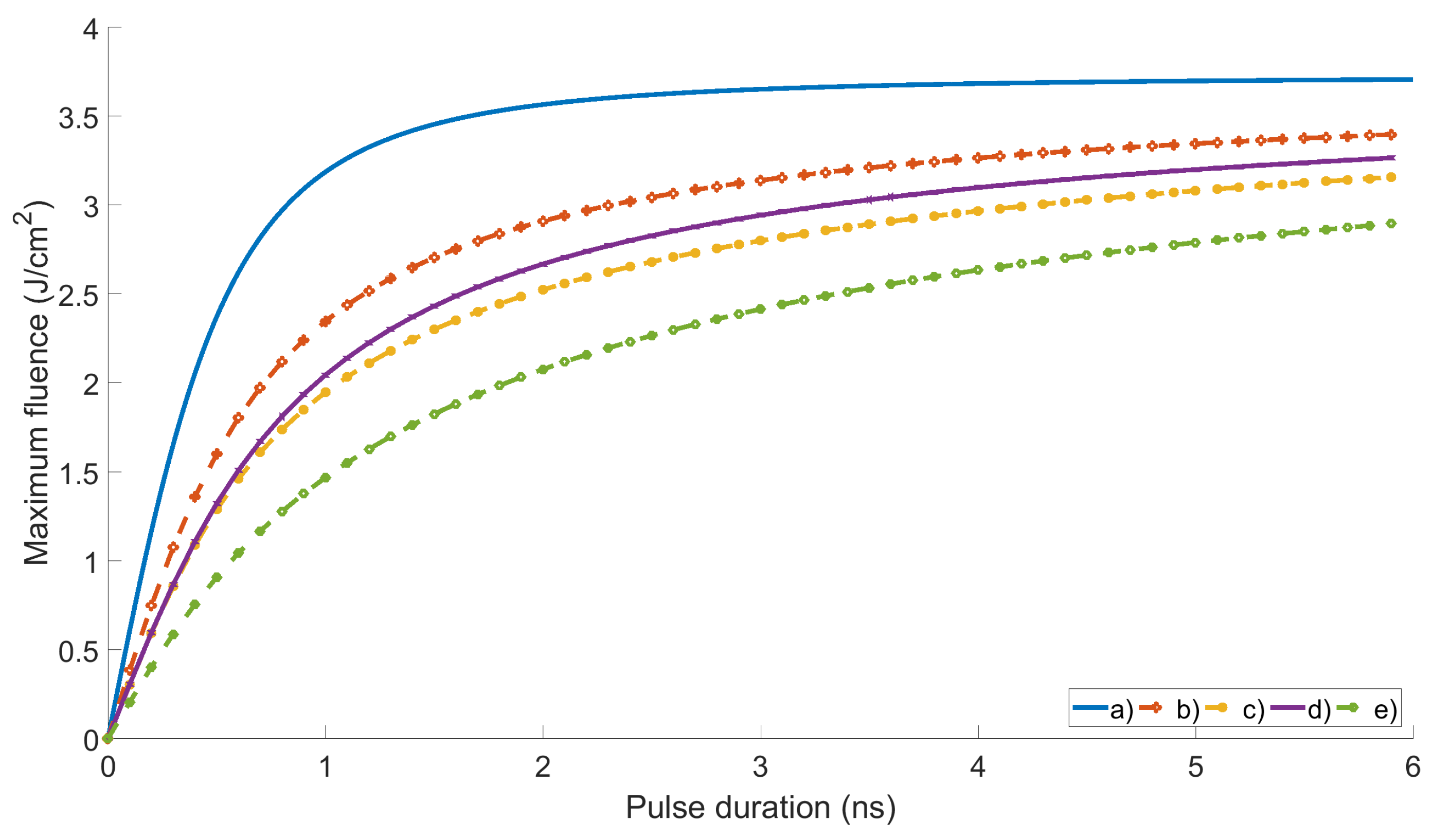
3. Maximum Operational Fluence for Different Pulse Shapes
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patel, R.S.; Stock, M.L.; Sartania, Z.; Bovatsek, J.M.; Arai, A.Y.; Endert, H. Temporal pulse shaping using fiber laser technology: Nano-scaling for flexible industrial laser material processing. In Proceedings of the Third International Symposium on Laser Precision Microfabrication, Osaka, Japan, 27–31 May 2002; Volume 4830, pp. 352–356. [Google Scholar] [CrossRef]
- Özgören, K.; Öktem, B.; Ömer Ilday, F.; Pasin, E.; Eken, K. Micromachining with square-shaped 1 ns-long pulses from an all-fiber Yb-doped laser-amplifier system. In Advances in Optical Materials; Optical Society of America: Washington, DC, USA, 2011; p. AWA15. [Google Scholar] [CrossRef]
- Gill, A.S.; Zhou, Z.; Lienert, U.; Almer, J.; Lahrman, D.F.; Mannava, S.R.; Qian, D.; Vasudevan, V.K. High spatial resolution, high energy synchrotron x-ray diffraction characterization of residual strains and stresses in laser shock peened Inconel 718SPF alloy. J. Appl. Phys. 2012, 111, 084904. [Google Scholar] [CrossRef]
- Koch, C.P.; Shapiro, M. Coherent Control of Ultracold Photoassociation. Chem. Rev. 2012, 112, 4928–4948. [Google Scholar] [CrossRef] [PubMed]
- Pechkis, J.A.; Carini, J.L.; Rogers, C.E.; Gould, P.L.; Kallush, S.; Kosloff, R. Coherent control of ultracold 85Rb trap-loss collisions with nonlinearly frequency-chirped light. Phys. Rev. A 2011, 83, 063403. [Google Scholar] [CrossRef]
- Collins, T.A.; Malinovskaya, S.A. Manipulation of ultracold Rb atoms using a single linearly chirped laser pulse. Opt. Lett. 2012, 37, 2298–2300. [Google Scholar] [CrossRef] [PubMed]
- Parry, B.; Oliveira, P.; Boyle, A.; Shaikh, W.; Musgrave, I. A New ns OPCPA Front End for Vulcan Petawatt. CLF Annu. Rep. 2013, 2014. Available online: https://www.clf.stfc.ac.uk/Pages/62.pdf (accessed on 20 February 2024).
- Rus, B.; Bakule, P.; Kramer, D.; Naylon, J.; Thoma, J.; Green, J.T.; Antipenkov, R.; Fibrich, M.; Novak, J.; Batysta, F.; et al. ELI-Beamlines: Development of next generation short-pulse laser systems. In Research Using Extreme Light: Entering New Frontiers with Petawatt-Class Lasers II; Korn, G., Silva, L.O., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2015; Volume 9515, pp. 33–44. [Google Scholar] [CrossRef]
- Smith, R.G. Optical Power Handling Capacity of Low Loss Optical Fibers as Determined by Stimulated Raman and Brillouin Scattering. Appl. Opt. 1972, 11, 2489–2494. [Google Scholar] [CrossRef] [PubMed]
- Nagao, H.; Nakamura, K.G.; Kondo, K.; Ozaki, N.; Takamatsu, K.; Ono, T.; Shiota, T.; Ichinose, D.; Tanaka, K.A.; Wakabayashi, K.; et al. Hugoniot measurement of diamond under laser shock compression up to 2TPa. Phys. Plasmas 2006, 13, 052705. [Google Scholar] [CrossRef]
- Torchio, R.; Occelli, F.; Mathon, O.; Sollier, A.; Lescoute, E.; Videau, L.; Vinci, T.; Benuzzi-Mounaix, A.; Headspith, J.; Helsby, W.; et al. Probing local and electronic structure in Warm Dense Matter: Single pulse synchrotron X-ray absorption spectroscopy on shocked Fe. Sci. Rep. 2016, 6, 26402. [Google Scholar] [CrossRef] [PubMed]
- Escauriza, E.M.; Olbinado, M.P.; Rutherford, M.E.; Chapman, D.J.; Jonsson, J.C.Z.; Rack, A.; Eakins, D.E. Ultra-high-speed indirect x-ray imaging system with versatile spatiotemporal sampling capabilities. Appl. Opt. 2018, 57, 5004–5010. [Google Scholar] [CrossRef]
- Meinecke, J.; Doyle, H.W.; Miniati, F.; Bell, A.R.; Bingham, R.; Crowston, R.; Drake, R.P.; Fatenejad, M.; Koenig, M.; Kuramitsu, Y.; et al. Turbulent amplification of magnetic fields in laboratory laser-produced shock waves. Nat. Phys. 2014, 10, 520–524. [Google Scholar] [CrossRef]
- Robey, H.F.; MacGowan, B.J.; Landen, O.L.; LaFortune, K.N.; Widmayer, C.; Celliers, P.M.; Moody, J.D.; Ross, J.S.; Ralph, J.; LePape, S.; et al. The effect of laser pulse shape variations on the adiabat of NIF capsule implosions. Phys. Plasmas 2013, 20, 052707. [Google Scholar] [CrossRef]
- Chambonneau, M.; Rullier, J.L.; Grua, P.; Lamaignère, L. Wavelength dependence of the mechanisms governing the formation of nanosecond laser-induced damage in fused silica. Opt. Express 2018, 26, 21819–21830. [Google Scholar] [CrossRef] [PubMed]
- Negres, R.A.; Cross, D.A.; Liao, Z.M.; Matthews, M.J.; Carr, C.W. Growth model for laser-induced damage on the exit surface of fused silica under UV, ns laser irradiation. Opt. Express 2014, 22, 3824–3844. [Google Scholar] [CrossRef] [PubMed]
- Feit, M.D.; Rubenchik, A.M.; Salleo, A.; Eimerl, D. Pulse-shape and pulse-length scaling of ns pulse laser damage threshold due to rate limiting by thermal conduction. In Laser-Induced Damage in Optical Materials: 1997; Exarhos, G.J., Guenther, A.H., Kozlowski, M.R., Soileau, M.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1998; Volume 3244, pp. 5–10. [Google Scholar] [CrossRef]
- Cormont, P.; Gallais, L.; Lamaignère, L.; Rullier, J.L.; Combis, P.; Hebert, D. Impact of two CO2 laser heatings for damage repairing on fused silica surface. Opt. Express 2010, 18, 26068–26076. [Google Scholar] [CrossRef] [PubMed]
- Feit, M.D.; Rubenchik, A.M.; Runkel, M.J. Analysis of bulk DKDP damage distribution, obscuration, and pulse-length dependence. In Laser-Induced Damage in Optical Materials: 2000; Exarhos, G.J., Guenther, A.H., Kozlowski, M.R., Lewis, K.L., Soileau, M.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2001; Volume 4347, pp. 383–388. [Google Scholar] [CrossRef]
- Koldunov, M.F.; Manenkov, A.A.; Pokotilo, I.L. Pulse-width and pulse-shape dependencies of laser-induced damage threshold to transparent optical materials. In 27th Annual Boulder Damage Symposium: Laser-Induced Damage in Optical Materials: 1995; Bennett, H.E., Guenther, A.H., Kozlowski, M.R., Newnam, B.E., Soileau, M.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1996; Volume 2714, pp. 718–730. [Google Scholar] [CrossRef]
- Negres, R.A.; Norton, M.A.; Cross, D.A.; Carr, C.W. Growth behavior of laser-induced damage on fused silica optics under UV, ns laser irradiation. Opt. Express 2010, 18, 19966–19976. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Huang, J.; Wang, F.; Zhou, X.; Ye, X.; Zhou, X.; Sun, L.; Jiang, X.; Sui, Z.; Zheng, W. Subsurface defects of fused silica optics and laser induced damage at 351 nm. Opt. Express 2013, 21, 12204–12217. [Google Scholar] [CrossRef] [PubMed]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-femtosecond laser-induced breakdown in dielectrics. Phys. Rev. B 1996, 53, 1749–1761. [Google Scholar] [CrossRef] [PubMed]
- Bloembergen, N. Laser-induced electric breakdown in solids. IEEE J. Quantum Electron. 1974, 10, 375–386. [Google Scholar] [CrossRef]
- Morice, O. Miro: Complete modeling and software for pulse amplification and propagation in high-power laser systems. Opt. Eng. 2003, 42, 1530–1541. [Google Scholar] [CrossRef]
- Carr, C.; Cross, D.A.; Norton, M.A.; Negres, R.A. The effect of laser pulse shape and duration on the size at which damage sites initiate and the implications to subsequent repair. Opt. Express 2011, 19, A859–A864. [Google Scholar] [CrossRef]
- Kuzuu, N.; Yoshida, K.; Yoshida, H.; Kamimura, T.; Kamisugi, N. Laser-induced bulk damage in various types of vitreous silica at 1064, 532, 355, and 266 nm: Evidence of different damage mechanisms between 266-nm and longer wavelengths. Appl. Opt. 1999, 38, 2510–2515. [Google Scholar] [CrossRef] [PubMed]
- Mehrotra, K.; Taylor, B.N.; Kozlov, A.A.; Papernov, S.; Lambropoulos, J.C. Nano-indentation and laser-induced damage testing in optical multilayer-dielectric gratings. Appl. Opt. 2017, 56, 2494–2503. [Google Scholar] [CrossRef] [PubMed]
- Miller, P.E.; Bude, J.D.; Suratwala, T.I.; Shen, N.; Laurence, T.A.; Steele, W.A.; Menapace, J.; Feit, M.D.; Wong, L.L. Fracture-induced subbandgap absorption as a precursor to optical damage on fused silica surfaces. Opt. Lett. 2010, 35, 2702–2704. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Melnikaitis, A.; Gallais, L.; Kiáčas, S.; Drazdys, R.; Sirutkaitis, V.; Commandré, M. Investigation of the distribution of laser damage precursors at 1064 nm, 12 ns on Niobia-Silica and Zirconia-Silica mixtures. Opt. Express 2012, 20, 26089–26098. [Google Scholar] [CrossRef] [PubMed]
- Mainguy, S.; Garrec, B.L.; Josse, M. Downstream impact of flaws on the LIL/LMJ laser lines. In Laser-Induced Damage in Optical Materials: 2005; Exarhos, G.J., Guenther, A.H., Lewis, K.L., Ristau, D., Soileau, M., Stolz, C.J., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2006; Volume 5991, pp. 63–71. [Google Scholar] [CrossRef]
- Liao, Z.M.; Raymond, B.; Gaylord, J.; Fallejo, R.; Bude, J.; Wegner, P. Damage modeling and statistical analysis of optics damage performance in MJ-class laser systems. Opt. Express 2014, 22, 28845–28856. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.M.; Abdulla, G.M.; Negres, R.A.; Cross, D.A.; Carr, C.W. Predictive modeling techniques for nanosecond-laser damage growth in fused silica optics. Opt. Express 2012, 20, 15569–15579. [Google Scholar] [CrossRef] [PubMed]
- Hooker, C.J.; Reason, C.J.; Toner, W.T.; Gottfeldt, P.; Eason, R.W.; Knight, S.P.; Collins, D.L.; Appleton, S.G. Target Area West Commissioning. In Annual Report to the Laser Facilities Committee; 1985; pp. A6.30–A6.32. Available online: https://www.osti.gov/biblio/6229607 (accessed on 20 February 2024).
- Oliveira, P.; Addis, S.; Gay, J.; Ertel, K.; Galimberti, M.; Musgrave, I. Control of temporal shape of nanosecond long lasers using feedback loops. Opt. Express 2019, 27, 6607–6617. [Google Scholar] [CrossRef] [PubMed]
- Mason, P.D.; Banerjee, S.; Ertel, K.; Phillips, P.J.; Greenhalgh, J.; Collier, J. DiPOLE—An Efficient and Scalable High Pulse Energy and High Average Power Cryogenic Gas Cooled Multi-Slab Amplifier Concept. Plasma Fusion Res. 2013, 8, 3404051. [Google Scholar] [CrossRef]
- Divoky, M.; Smrz, M.; Chyla, M.; Sikocinski, P.; Severova, P.; Novak, O.; Huynh, J.; Nagisetty, S.S.; Miura, T.; Pilař, T. Overview of the HiLASE project: High average power pulsed DPSSL systems for research and industry. High Power Laser Sci. Eng. 2014, 2, e14. [Google Scholar] [CrossRef]
- Carr, C.; Trenholme, J.; Spaeth, M. Effect of temporal pulse shape on optical damage. Appl. Phys. Lett. 2007, 90, 041110. [Google Scholar] [CrossRef]
- Hendrix, J.L.; Schweyen, J.C.; Rowe, J.; Beer, G. Ghost analysis visualization techniques for complex systems: Examples from the NIF final optics assembly. In Proceedings of the Third International Conference on Solid State Lasers for Application to Inertial Confinement Fusion, Monterey, CA, USA, 7–12 June 1999; Lowdermilk, W.H., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1999; Volume 3492, pp. 306–320. [Google Scholar] [CrossRef]
- Duffy, S.T.; Smith, F.R. Ultra-High Pressure Dynamic Compression of Geological Materials. Front. Earth Sci. 2019, 7, 23. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, P.; Galletti, M.; Suciu, C.; Galimberti, M. Maximum Operational Fluence Limits for Temporally Shaped Nanosecond Long Pulses. Appl. Sci. 2024, 14, 4211. https://doi.org/10.3390/app14104211
Oliveira P, Galletti M, Suciu C, Galimberti M. Maximum Operational Fluence Limits for Temporally Shaped Nanosecond Long Pulses. Applied Sciences. 2024; 14(10):4211. https://doi.org/10.3390/app14104211
Chicago/Turabian StyleOliveira, Pedro, Mario Galletti, Cosmin Suciu, and Marco Galimberti. 2024. "Maximum Operational Fluence Limits for Temporally Shaped Nanosecond Long Pulses" Applied Sciences 14, no. 10: 4211. https://doi.org/10.3390/app14104211




