Analytical Solution for Seismic Stability of 3D Rock Slope Reinforced with Prestressed Anchor Cables
Abstract
:1. Introduction
2. Modifications for Hoek–Brown Yield Criterion and the Pseudo-Dynamic Method on Seismicity Analysis
2.1. Nonlinear Hoek–Brown Strength Criterion
2.2. Generalized Tangent Technique
2.3. Modified Pseudo-Dynamic Method
3. Model for 3D Two-Stage Rock Slopes Reinforced with Prestressed Anchor Cables Effected by Seismicity and Its Analytical Solution
3.1. The 3D Horn-Shaped Rotating Failure Mechanism
3.2. Internal Energy Dissipation
3.3. External Force Work
3.3.1. Gravitational Work
3.3.2. Seismic Force Work
3.3.3. Anchoring Force Work
3.4. Analytical Solution for the Factor of Safety
4. Results and Discussions
4.1. Comparisons
4.2. Parametric Effects Discussions
4.2.1. Nonlinear H-B Criterion Parametric Analysis
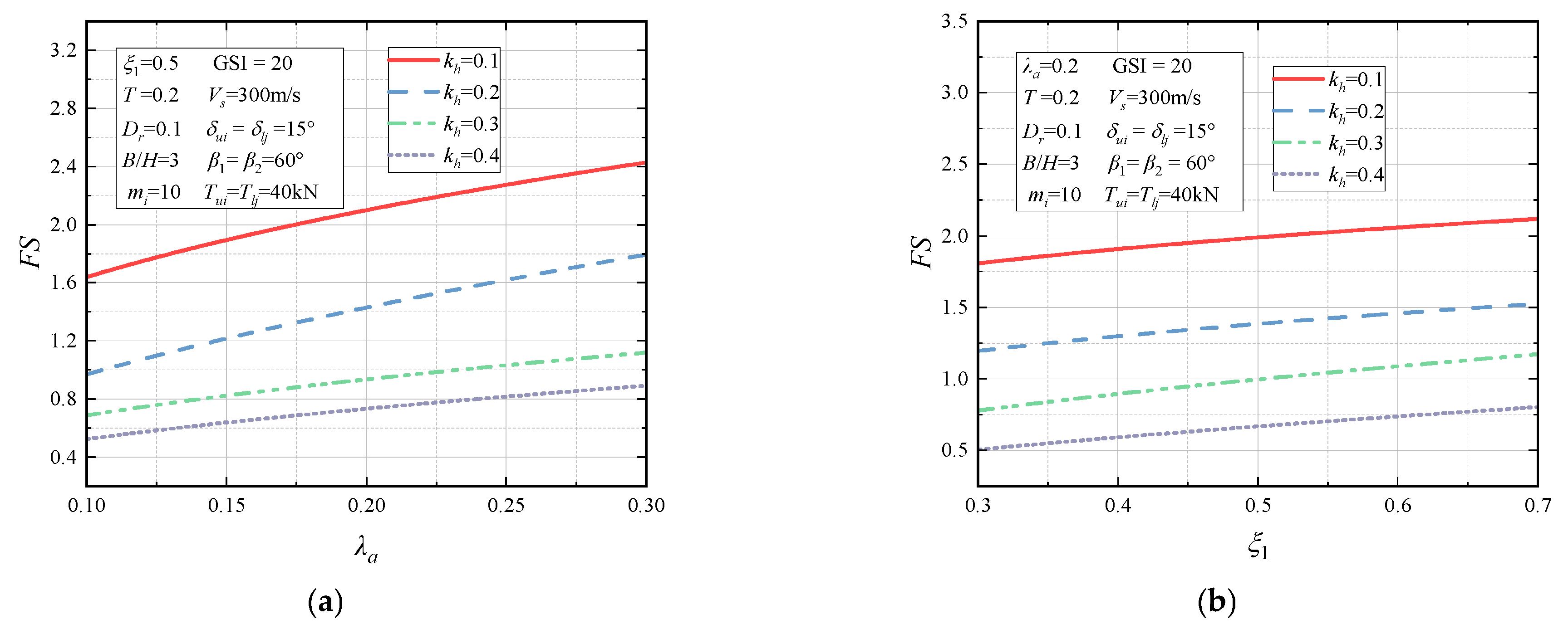
4.2.2. Improved Pseudo-Dynamic Parametric Analysis


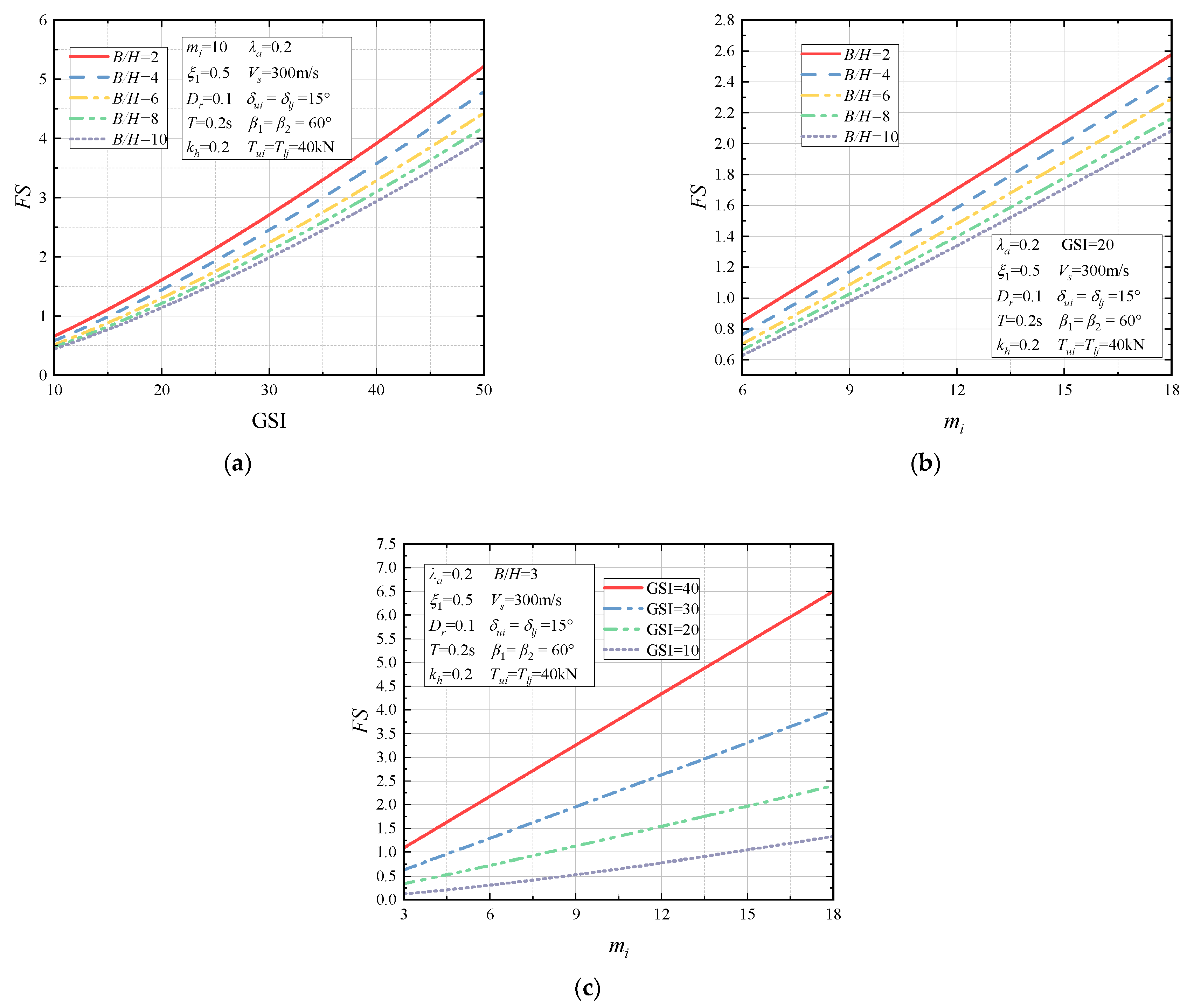
4.2.3. Slope Geometry Parametric Analysis
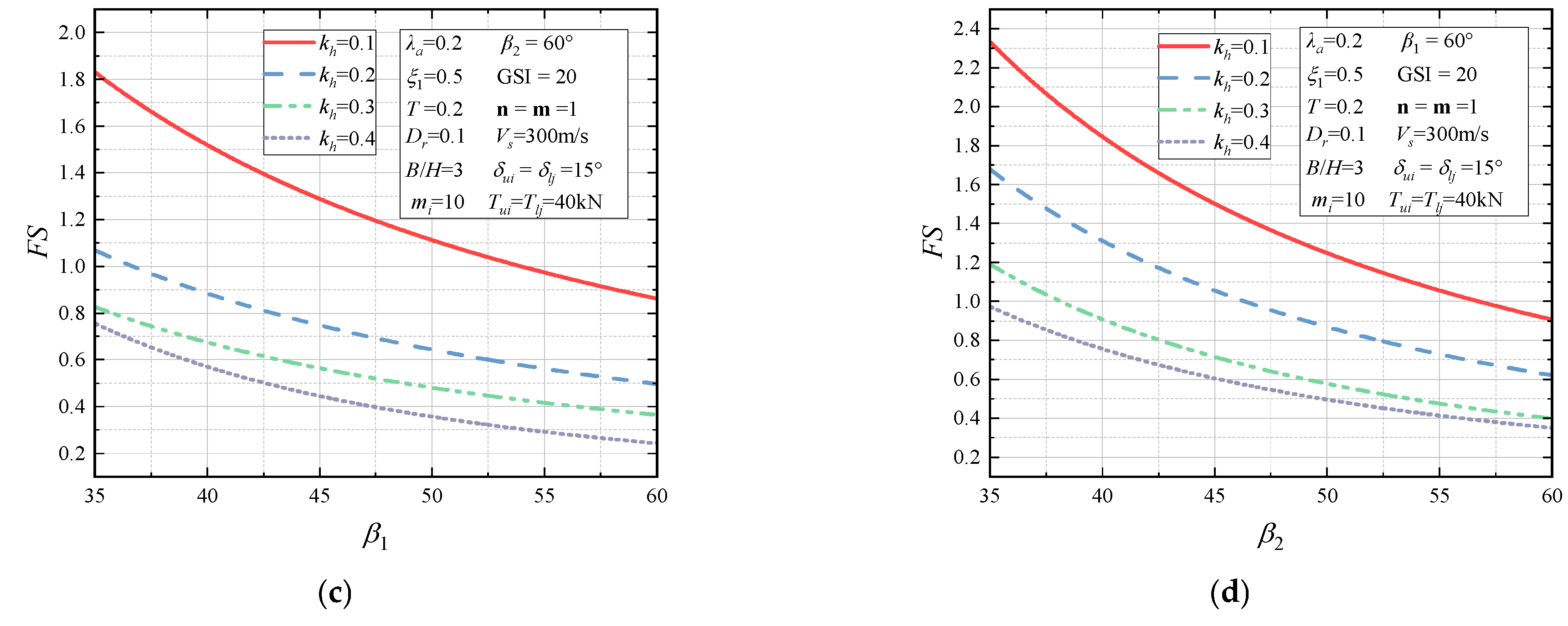
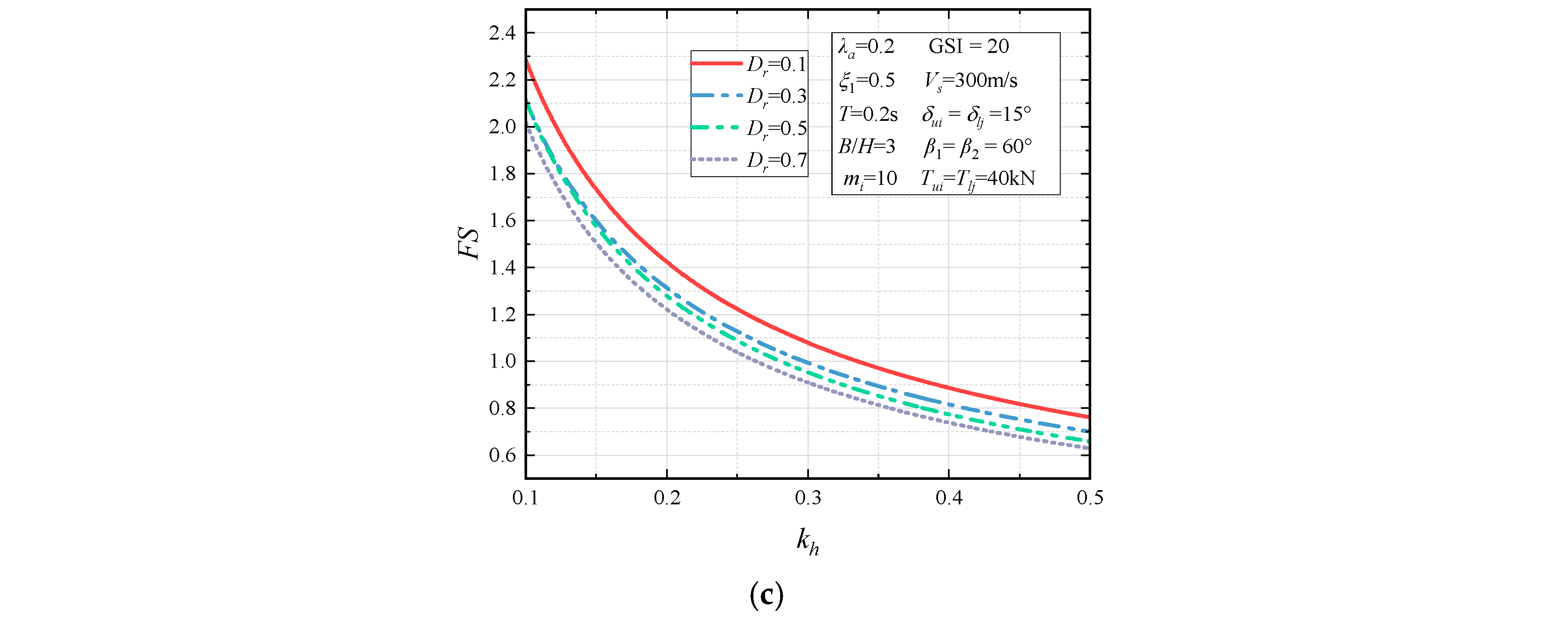
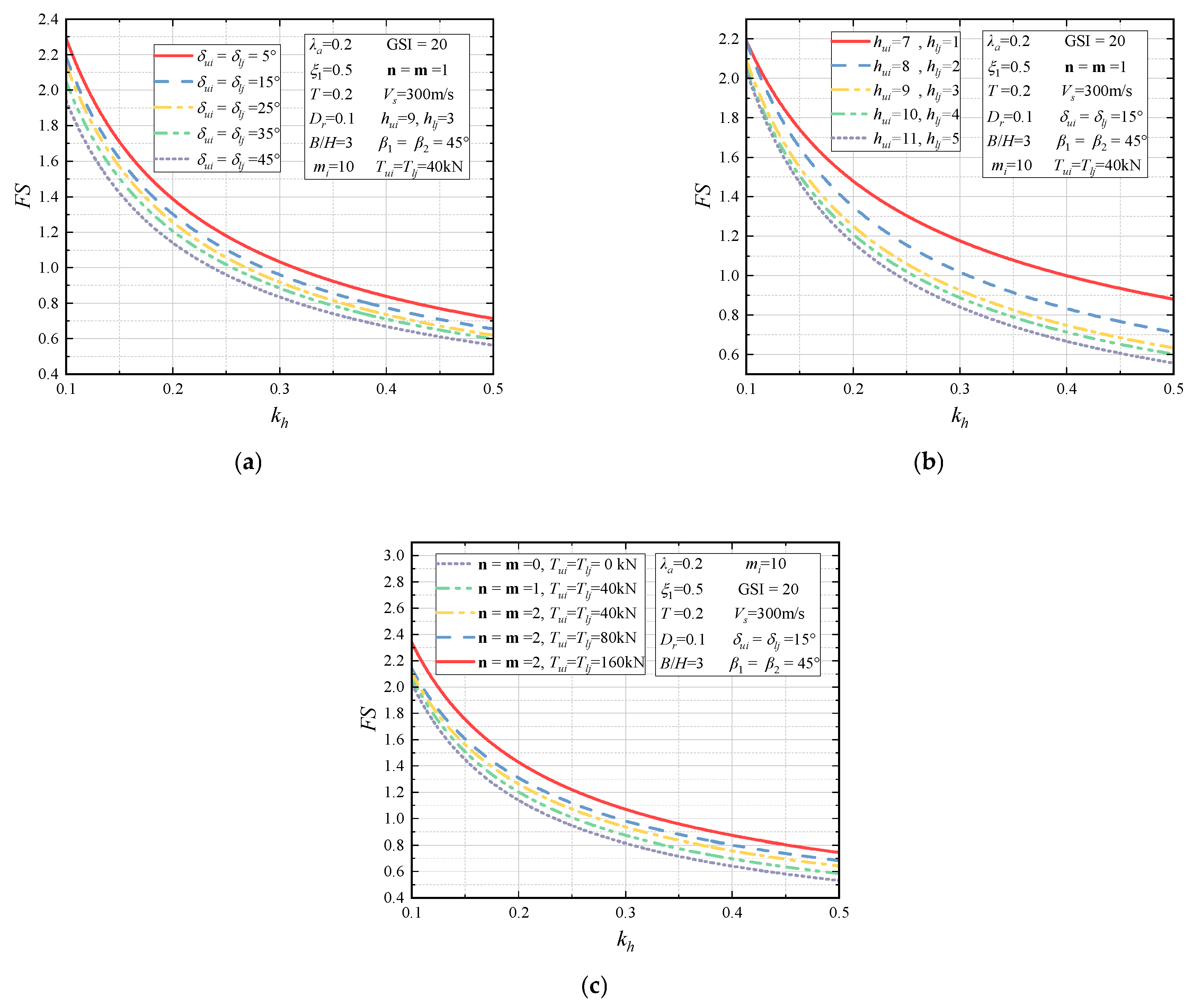
4.2.4. Anchorage Parametric Analysis
5. Conclusions
- (1)
- For the rock mass characteristics, the analyses indicate that the overall quality of the rock mass has more of an impact on the stability of rock slopes than the quality characteristics of the rock in the stability analysis of the rock slopes. And the rock type and quality do not significantly enhance the stability of the rock slopes when the joint fractures in the rock mass are excessively developed.
- (2)
- For the seismicity factors, their variations with FS are not linear. And it is as the value of the seismic pseudo-dynamic parameters change at smaller values that FS decreases more, which demonstrates that the smaller magnitude of seismicity is also additionally significant for the slope reinforcement engineering.
- (3)
- For the slope geometry features, the design pattern for the two-stage slope could significantly withstand the adverse effects of seismicity on slope safety, and its enhancement on FS is more obvious when the seismicity is at a smaller level. Moreover, the location of the additional step on the middle and lower portions of the slope can better improve the stability of the slope.
- (4)
- Equation (87) can provide the reference or verification basis for the anchorage design of rock slopes. For the prestressing anchorage parameters, the slope stability is progressively enhanced with the growth of the anchoring forces and and the number of anchor rows n and m. Additionally, the slippage of the sliding body for the slope can be more effectively controlled with the anchorage angles close to horizontal. These indicate that the anchorage design is essential for the seismic stability of slopes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, S.H.; Li, D.Q.; Zhang, L.M.; Zhou, C.B. Time-dependent system reliability of anchored rock slopes considering rock bolt corrosion effect. Eng. Geol. 2004, 175, 1–8. [Google Scholar] [CrossRef]
- Blanco-Fernandez, E.; Castro-Fresno, D.; Díaz, J.D.C.; Lopez-Quijada, L. Flexible systems anchored to the ground for slope stabilisation: Critical review of existing design methods. Eng. Geol. 2011, 122, 129–145. [Google Scholar] [CrossRef]
- Eskandarinejad, A. Seismic vertical uplift capacity of horizontal strip anchors embedded in sand adjacent to slopes using finite element limit analysis. Arab. J. Geosci. 2022, 15, 16. [Google Scholar] [CrossRef]
- Sun, J.; Yu, T.; Dong, P. Pseudo-dynamic analysis of reinforced slope with anchor cables. Soil Dyn. Earthq. Eng. 2022, 162, 107514. [Google Scholar] [CrossRef]
- Tao, Z.; Zhu, C.; He, M.; Karakus, M. A physical modeling-based study on the control mechanisms of Negative Poisson’s ratio anchor cable on the stratified toppling deformation of anti-inclined slopes. Int. J. Rock Mech. Min. Sci. 2021, 138, 104632. [Google Scholar] [CrossRef]
- Chen, J.F.; Du, C.C.; Peng, M.; Sun, R.; Zhao, F.; Shi, Z.M. System reliability analysis of a slope stabilized with anchor cables and piles under seismic loading. Acta Geotech. 2023, 18, 4493–4514. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Unified solution of safety factors for three-dimensional compound slopes considering local and global instability. Comput. Geotech. 2023, 155, 105227. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Seismic stability of three-dimensional slopes considering the nonlinearity of soils. Soil Dyn. Earthq. Eng. 2021, 140, 106334. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Q.; Peng, D.; Zhu, Z.; Li, W.; Wong, H.; Shen, P. Stability analysis of rock wedge slide subjected to ground water dynamic evolution. Eng. Geol. 2020, 270, 105528. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, D. An Analytical Framework for Assessing the Unsaturated Bearing Capacity of Strip Footings under Transient Infiltration. Mathematics 2023, 11, 3480. [Google Scholar] [CrossRef]
- Kang, X.D.; Zhou, D. Analytical Solution for Bearing Capacity of Reinforced Strip Footings on Unsaturated Soils under Steady Flow. Mathematics 2023, 11, 3746. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Marquez, R.M. Three-dimensional slope stability analysis by elasto-plastic finite elements. Géotechnique 2007, 57, 537–546. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Slope stability analysis with nonlinear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Giger, M.W.; Krizek, R.J. Stability analysis of vertical cut with variable corner angle. Soils Found. 1975, 15, 63–71. [Google Scholar] [CrossRef]
- De Buhan, P.; Garnier, D. Three dimensional bearing capacity analysis of a foundation near a slope. Soils Found. 1998, 38, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Michalowski, R.L.; Drescher, A. Three-dimensional stability of slopes and excavations. Géotechnique 2009, 59, 839–850. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Pseudo-dynamic stability of rock slope considering Hoek-Brown strength criterion. Acta Geotech. 2021, 17, 2481–2494. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Eng. Div. 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Hoek, E.; Wood, D.; Shah, S. A modified Hoek–Brown failure criterion for jointed rock masses. In Rock Characterization: ISRM Symposium, Eurock’92, Chester, UK, 14–17 September 1992; Thomas Telford Publishing: London, UK, 1992; pp. 209–214. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion-2002 edition. Proc. NARMS-Tac 2002, 1, 267–273. [Google Scholar]
- Yang, X.L.; Yin, J.H. Upper bound solution for ultimate bearing capacity with a modified Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2005, 42, 550–560. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. Géotechnique 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Loukidis, D.; Bandini, P.; Salgado, R. Stability of seismically loaded slopes using limit analysis. Géotechnique 2003, 53, 463–479. [Google Scholar] [CrossRef]
- Brink, U.T.; Andrews, B.; Miller, N. Seismicity and sedimentation rate effects on submarine slope stability. Geology 2016, 44, 563–566. [Google Scholar] [CrossRef]
- Macedo, J.; Candia, G.; Lacour, M.; Liu, C. New developments for the performance-based assessment of seismically-induced slope displacements. Eng. Geol. 2020, 277, 105786. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Martel, T. Stability charts for 3D failures of steep slopes subjected to seismic excitation. J. Geotech. Geoenviron. Eng. 2011, 137, 183–189. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Steedman, R.S.; Zeng, X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall. Géotechnique 1990, 40, 103–112. [Google Scholar] [CrossRef]
- Zeng, X.; Steedman, R.S. On the behaviour of quay walls in earthquakes. Géotechnique 1993, 43, 417–431. [Google Scholar] [CrossRef]
- Bellezza, I. A new pseudo-dynamic approach for seismic active soil thrust. Geotech. Geol. Eng. 2014, 32, 561–576. [Google Scholar] [CrossRef]
- Bellezza, I. Seismic active earth pressure on walls using a new pseudo-dynamic approach. Geotech. Geol. Eng. 2015, 33, 795–812. [Google Scholar] [CrossRef]
- Chanda, N.; Ghosh, S.; Pal, M. Analysis of slope using modified pseudo-dynamic method. Int. J. Geotech. Eng. 2018, 12, 337–346. [Google Scholar] [CrossRef]
- Shi, K.; Wu, X.; Liu, Z.; Dai, S. Coupled calculation model for anchoring force loss in a slope reinforced by a frame beam and anchor cables. Eng. Geol. 2019, 260, 105245. [Google Scholar] [CrossRef]
- Li, X.; He, S.; Wu, Y. Limit analysis of the stability of slopes reinforced with anchors. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1898–1908. [Google Scholar] [CrossRef]
- Yan, M.; Xia, Y.; Liu, T.; Bowa, V.M. Limit analysis under seismic conditions of a slope reinforced with prestressed anchor cables. Comput. Geotech. 2019, 108, 226–233. [Google Scholar] [CrossRef]
- Li, A.J.; Lyamin, A.V.; Merifield, R.S. Seismic rock slope stability charts based on limit analysis methods. Comput. Geotech. 2009, 36, 135–148. [Google Scholar] [CrossRef]
- Kokane, A.K.; Sawant, V.A.; Sahoo, J.P. Seismic stability analysis of nailed vertical cut using modified pseudo-dynamic method. Soil Dyn. Earthq. Eng. 2020, 137, 106294. [Google Scholar] [CrossRef]
- Agarwal, E.; Pain, A. Probabilistic stability analysis of geosynthetic-reinforced slopes under pseudo-static and modified pseudo-dynamic conditions. Geotext. Geomembr. 2021, 49, 1565–1584. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, D. Seismic Bearing Capacity Solution for Strip Footings in Unsaturated Soils with Modified Pseudo-Dynamic Approach. Mathematics 2023, 11, 2692. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Seismic stability analysis of slopes with cracks in unsaturated soils using pseudo-dynamic approach. Transp. Geotech. 2021, 19, 100583. [Google Scholar] [CrossRef]
- Qin, C.B.; Chian, S.C. Kinematic analysis of seismic slope stability with a discretisation technique and pseudo-dynamic approach: A new perspective. Géotechnique 2018, 68, 492–503. [Google Scholar] [CrossRef]
- Gazetas, G.; Garini, E.; Anastasopoulos, I.; Georgarakos, T. Effects of near-fault ground shaking on sliding systems. J. Geotech. Geoenviron. Eng. 2009, 135, 1906–1921. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, D. Seismic Stability for 3D Two-Step Slope Governed by Non-Linearity in Soils Using Modified Pseudo-Dynamic Approach. Appl. Sci. 2022, 12, 6482. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, H.; Zhu, J. Stability Analysis of Three-Dimensional Tunnel Face Considering Linear and Nonlinear Strength in Unsaturated Soil. Appl. Sci. 2024, 14, 2080. [Google Scholar] [CrossRef]
- Chen, G.; Chen, T.; Chen, Y.; Huang, R.; Liu, M. A new method of predicting the prestress variations in anchored cables with excavation unloading destruction. Eng. Geol. 2018, 241, 109–120. [Google Scholar] [CrossRef]
- Cheng, Y.; Xu, Y.; Wang, L.; Wang, L. Stability of expansive soil slopes reinforced with anchor cables based on rotational-translational mechanisms. Comput. Geotech. 2022, 146, 104747. [Google Scholar] [CrossRef]
- Qiang, L. Stability Study for Rock Slope and Anchoring Parametric Analysis. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]






| B/H | Solutions | ||||
|---|---|---|---|---|---|
| 1.0 | Ns form Drescher and Michalowski | 54.850 | 23.835 | 14.701 | 11.028 |
| FS using the current approach | 0.9894 | 0.9824 | 0.9992 | 0.9848 | |
| 1.5 | Ns form Drescher and Michalowski | 46.845 | 20.773 | 12.976 | 8.935 |
| FS using the current approach | 0.9921 | 0.9742 | 0.9755 | 0.9927 | |
| 2.0 | Ns form Drescher and Michalowski | 42.732 | 19.103 | 12.109 | 8.604 |
| FS using the current approach | 0.9995 | 0.9918 | 0.9795 | 0.9599 | |
| 3.0 | Ns form Drescher and Michalowski | 39.956 | 17.873 | 11.184 | 7.974 |
| FS using the current approach | 1.0010 | 1.0011 | 0.9956 | 0.9924 | |
| 5.0 | Ns form Drescher and Michalowski | 37.994 | 17.063 | 10.628 | 7.266 |
| FS using the current approach | 1.0062 | 1.0032 | 0.9985 | 0.9938 | |
| 10.0 | Ns form Drescher and Michalowski | 36.703 | 16.527 | 10.265 | 6.944 |
| FS using the current approach | 1.0086 | 1.0025 | 1.0013 | 1.0003 | |
| B/H | Amended Pseudo-Dynamic Results | Original Pseudo-Static Results | ||||
|---|---|---|---|---|---|---|
| kh = 0.2 | kh = 0.5 | kh = 0.8 | kh = 0.2 | kh = 0.5 | kh = 0.8 | |
| 1.5 | 1.981 | 1.215 | 0.926 | 1.932 | 1.135 | 0.920 |
| 3.0 | 1.276 | 0.879 | 0.676 | 1.185 | 0.844 | 0.634 |
| 5.0 | 1.136 | 0.835 | 0.660 | 1.091 | 0.795 | 0.577 |
| 10.0 | 1.031 | 0.771 | 0.598 | 0.992 | 0.755 | 0.545 |
| 2D | 1.016 | 0.735 | 0.579 | 0.962 | 0.718 | 0.503 |
| Methods | ||
|---|---|---|
| 0 | 40 | |
| Finite Element Method/Cai and Ugai [36] | 1.09 | 1.21 |
| Bishop’s Simplified Method/SLOPE/W [36] | 1.095 | 1.207 |
| Finite Difference Method/FLAC [49] | 1.11 | 1.22 |
| Limit Analysis Method (2D)/Li et al. [49] | 1.096 | 1.213 |
| Limit Analysis Method (3D)/This paper | 1.106 | 1.251 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liao, H.; Zhou, D.; Zhu, J. Analytical Solution for Seismic Stability of 3D Rock Slope Reinforced with Prestressed Anchor Cables. Appl. Sci. 2024, 14, 4160. https://doi.org/10.3390/app14104160
Yang Y, Liao H, Zhou D, Zhu J. Analytical Solution for Seismic Stability of 3D Rock Slope Reinforced with Prestressed Anchor Cables. Applied Sciences. 2024; 14(10):4160. https://doi.org/10.3390/app14104160
Chicago/Turabian StyleYang, Yushan, Hong Liao, De Zhou, and Jianqun Zhu. 2024. "Analytical Solution for Seismic Stability of 3D Rock Slope Reinforced with Prestressed Anchor Cables" Applied Sciences 14, no. 10: 4160. https://doi.org/10.3390/app14104160




