Kinematics-Based Design Method and Experimental Validation of Internal Meshing Screw for High-Viscosity Fluid Mixing
Abstract
:1. Introduction
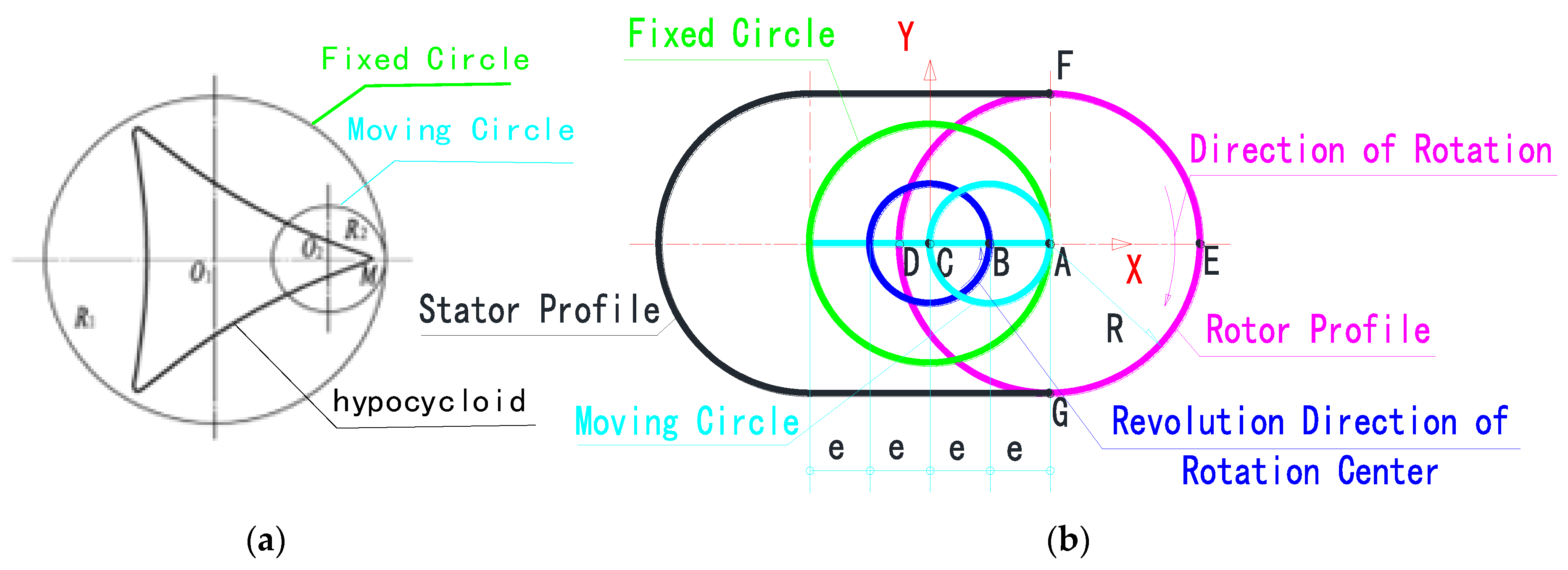
2. Working Principle and Kinematic Modeling of Extension-Dominated Mixer
2.1. Working Principle
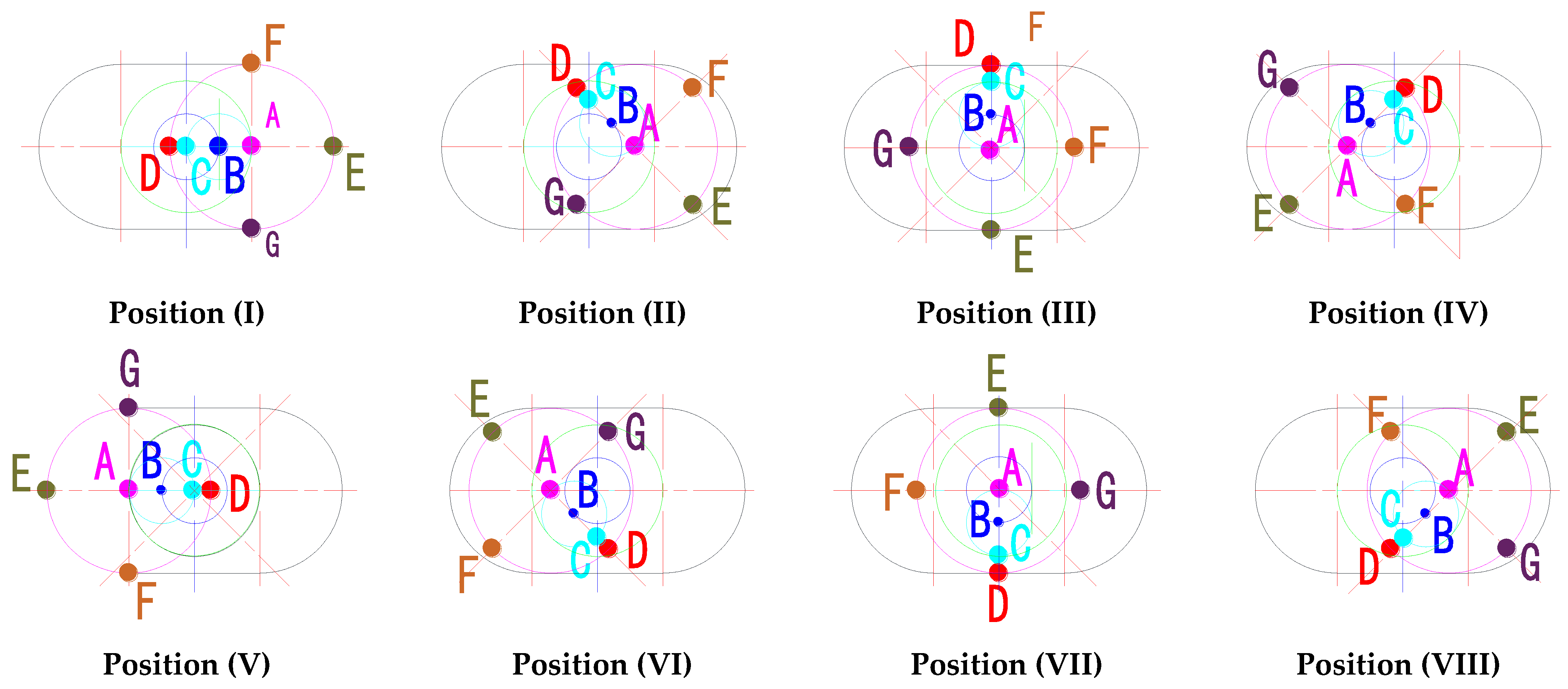
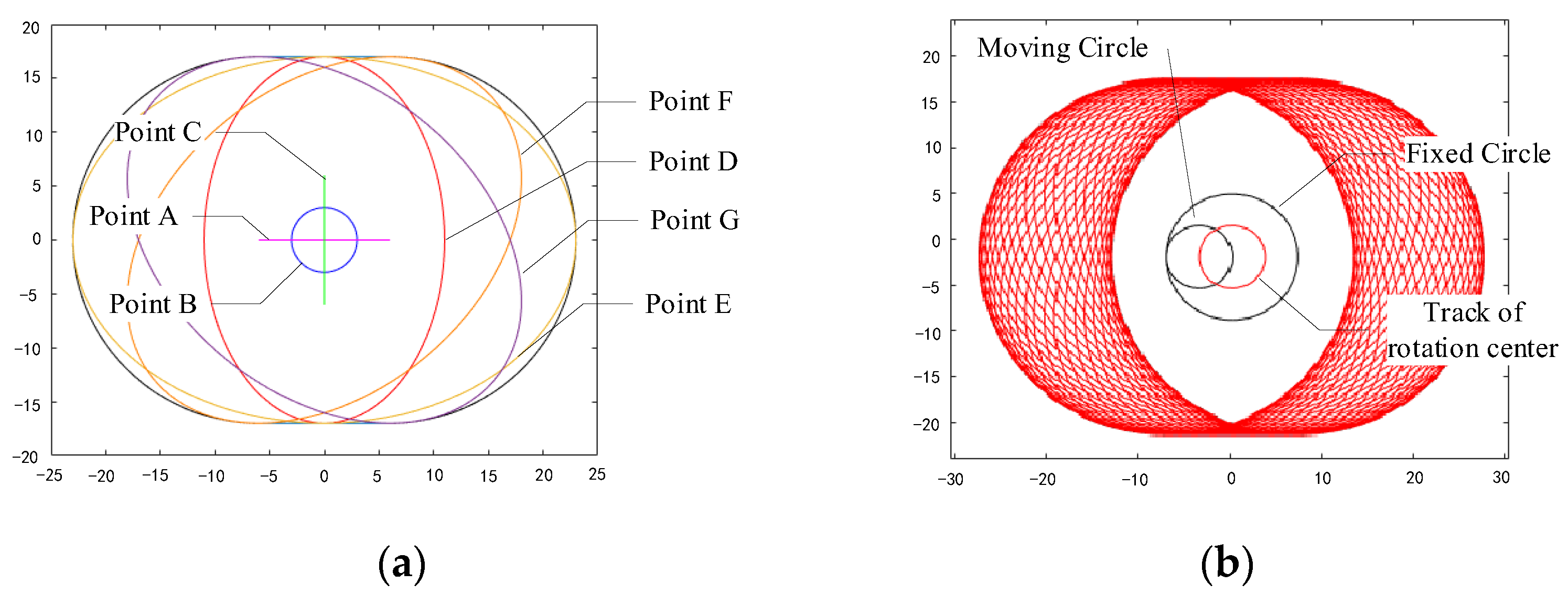
2.2. Kinematic Simulation
2.3. Kinematic Mathematical Analysis
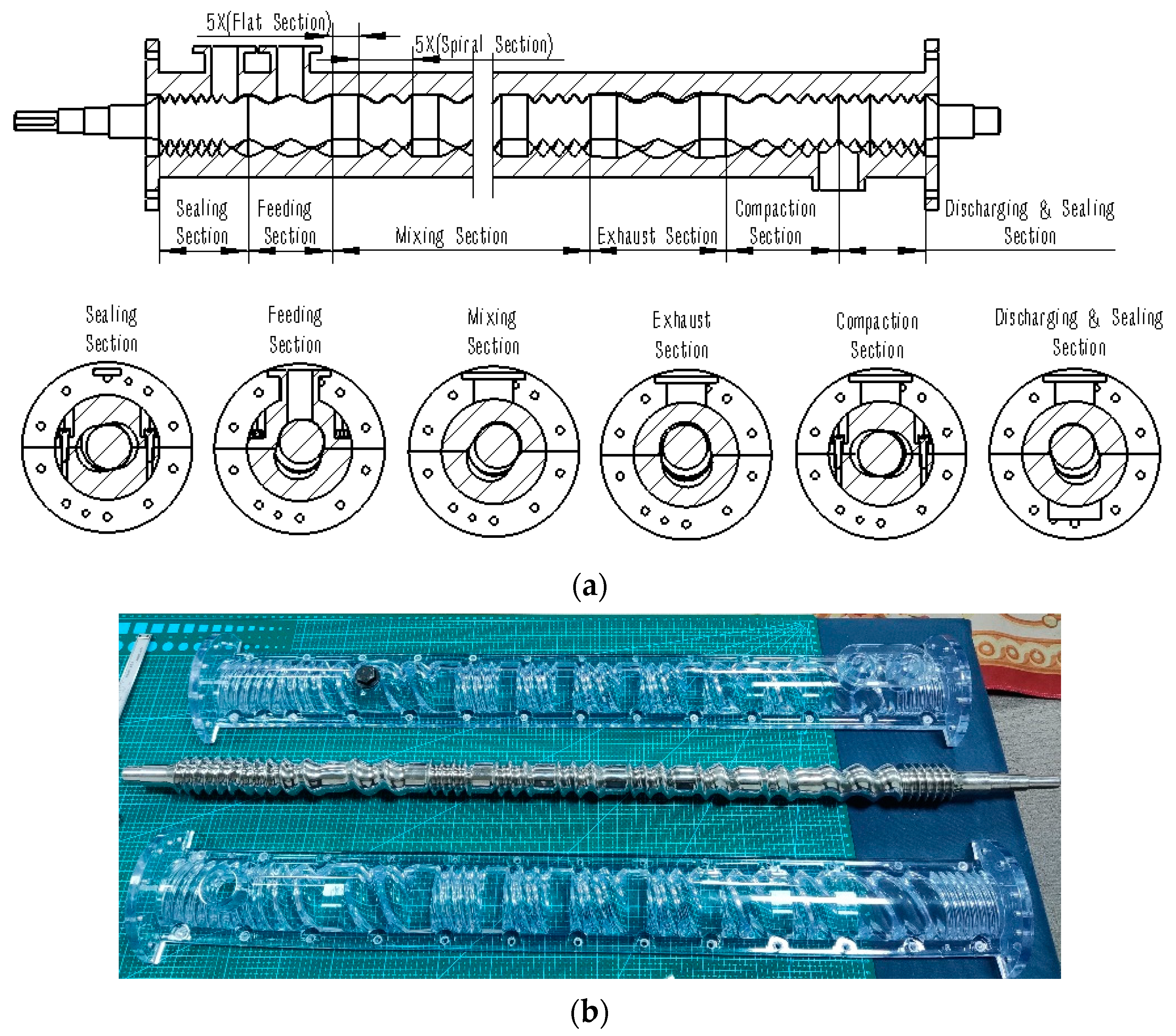
3. Design of Internal Meshing Screw Mixer
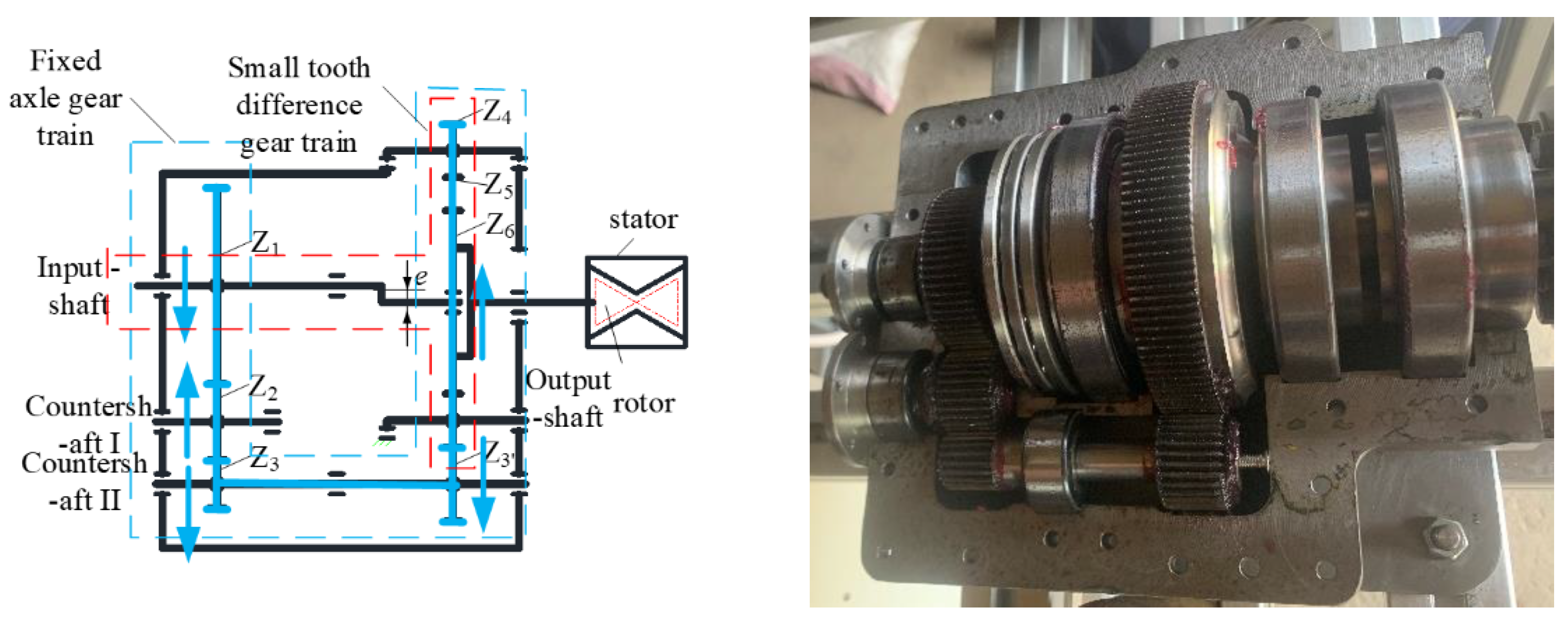
3.1. Transmission Setup
3.2. Internal Meshing Screw Mixer
3.2.1. Stator and Rotor Device of the Internal Meshing Screw Mixer
3.2.2. Sustaining Device for the Rotor of the Internal Meshing Screw Mixer
3.3. Overall Structure of the Internal Meshing Screw Mixer
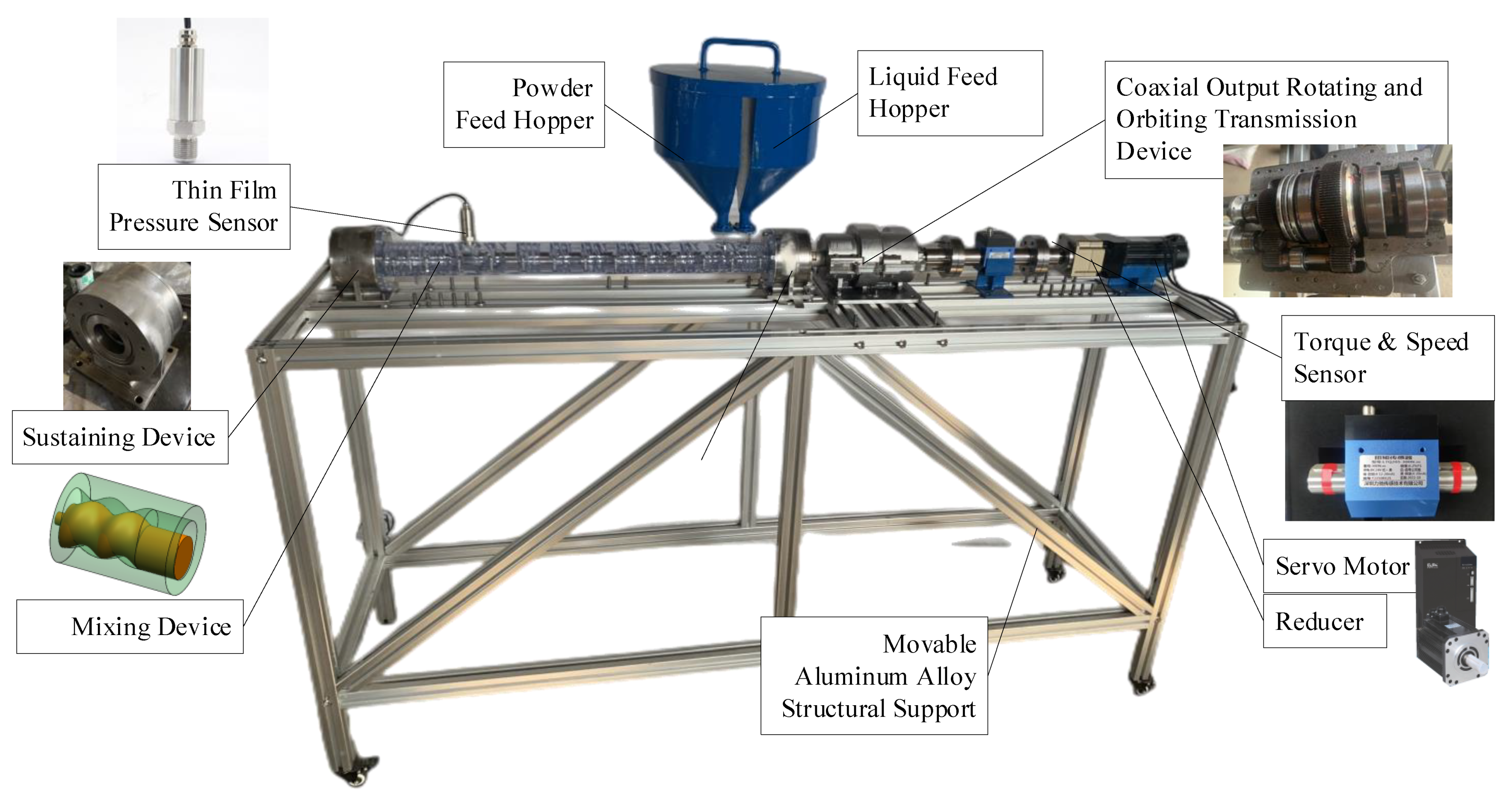
4. Experimental Verification
4.1. Materials and Methods
4.2. Mixing Quality
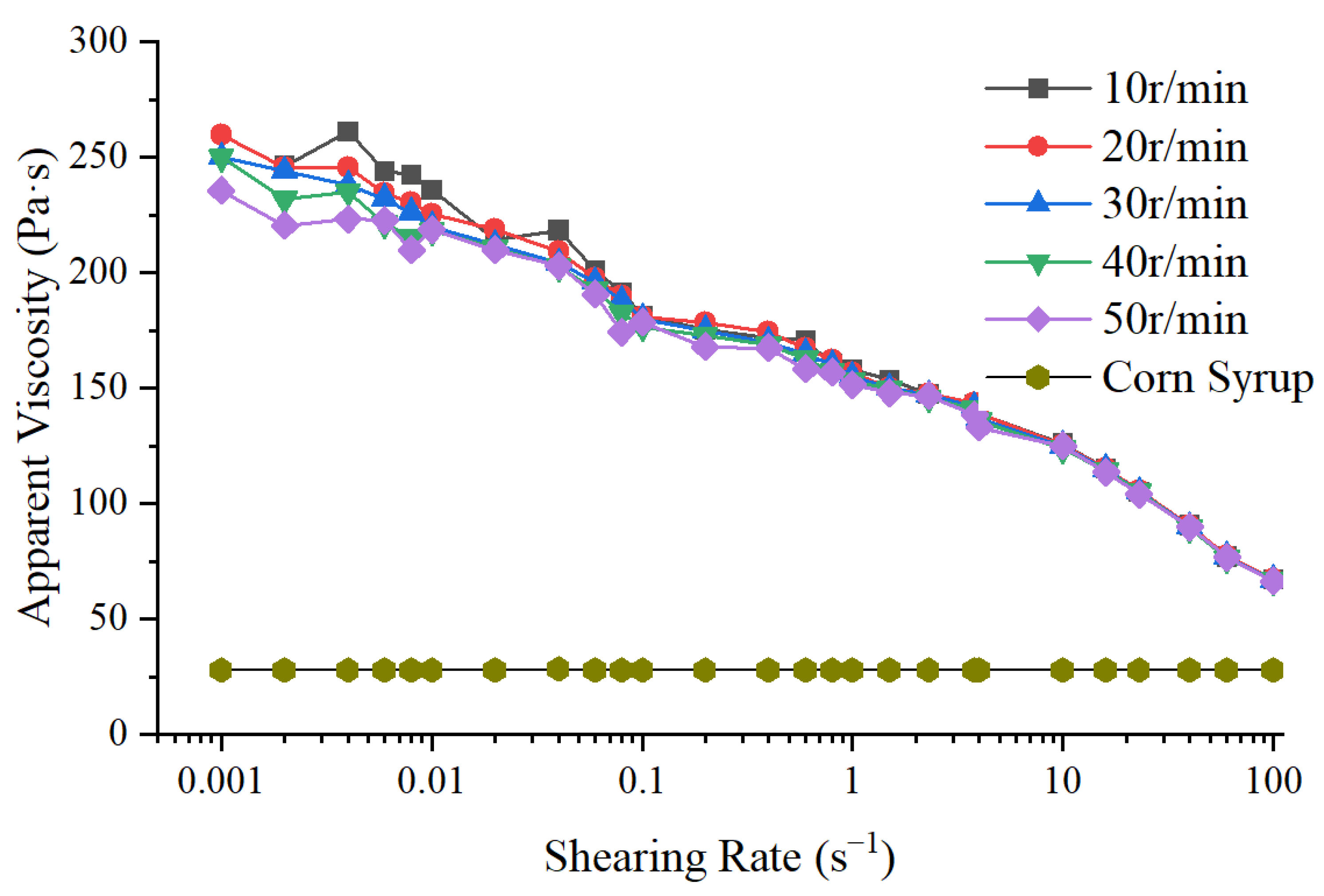
4.3. Rheological Properties of the Slurry
4.4. Mixing Uniformity of the Slurry
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhan, X.; Yu, L.; Jiang, Y.; Jiang, Q.; Shi, T. Mixing Characteristics and Parameter Effects On the Mixing Efficiency of High-Viscosity Solid–Liquid Mixtures Under High-Intensity Acoustic Vibration. Processes 2023, 11, 2367. [Google Scholar] [CrossRef]
- Peddireddy, K.R.; Clairmont, R.; Robertson-Anderson, R.M. Polymer Threadings and Rigidity Dictate the Viscoelasticity of Entangled Ring-Linear Blends and their Composites with Rigid Rod Microtubules. J. Rheol. 2023, 67, 125–138. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Z.; Shangguan, X.; Sun, Y.; Feng, J.; Li, Z.; Chen, L.; Zuo, S.; Zhuo, R.; Yan, P. Preparation of Mono-Dispersed, High Energy Release, Core/Shell Structure Al Nanopowders and their Application in Htpb Propellant as Combustion Enhancers. Sci. Rep. 2017, 7, 5228. [Google Scholar] [CrossRef]
- Li, J.; Lu, B.; Wang, C.-Q.; Bai, X.-X.; Sun, M.-J. Experimental study on mixing properties in ultrasonic wave. Food Mach. 2012, 28, 134–138. [Google Scholar]
- Kim, N.; Lee, J. Optimum Shape and Process Design of Single Equipment for its Mixing Performance Using Finite Volume Method. Korea-Austrilia Rheol. J. 2009, 4, 289–297. [Google Scholar]
- Anderson, P.D.; Galaktionov, O.S.; Peters, G.W.M.; Meijer, H.E.H.; Iii, C.L.T. Material Stretching in Laminar Mixing Flows: Extended Mapping Technique Applied to the Journal Bearing Flow. Int. J. Numer. Methods Fluids 2002, 40, 189–196. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, X.; Yu, D. Recent Advances in Elongational Flow Dominated Polymer Processing Technologies. Polymers 2021, 13, 1792. [Google Scholar] [CrossRef]
- Li, F.Q.; He, L.L. Effects of chain stiffness and shear flow on nanorod distribution and orientation in polymer melts. J. Zhejiang Univ. (Sci. Ed.) 2021, 48, 694–699. [Google Scholar]
- Huang, L.; Ou, X.L.; Wu, S.J. Effect of Elongation Flow Field on Dispersion Mixing of Filled Polymer. China Plast. 2006, 20, 53–58. [Google Scholar]
- Bauer, H.; Khinast, J. Detecting Mixing Barriers in Twin-Screw Extruder Elements Via Lagrangian Coherent Structures. Chem. Eng. Sci. 2022, 263, 118069. [Google Scholar] [CrossRef]
- Pandey, V.; Maia, J.M. Comparative Computational Analysis of Dispersive Mixing in Extension-Dominated Mixers for Single-Screw Extruders. Polym. Eng. Sci. 2020, 60, 2390–2402. [Google Scholar] [CrossRef]
- Netzsch Pump Industry Lanzhou Co., Ltd. Centennial NETZSCH Pioneer in Pump Industry. Gen. Mach. 2008, 10, 44–45. [Google Scholar]
- Ju, J.P.; Zhang, G.Z.; Yin, X.C. An Eccentric Rotor Volume Pulsation Deformation Plasticizing Transportation Method and Device. CN104002447A, 15 May 2014. [Google Scholar]
- Qin, S.; He, H.; Zhang, T.; Huang, Z.; Qu, J. Study on volume-pulsation injection-molding technology for plastics. China Plast. 2023, 37, 96–101. [Google Scholar]
- Qu, J.; Wu, T. Advanced processing technology of polymer materials helps material innovation and development. Sci. Technol. Rev. 2020, 38, 54–62. [Google Scholar]
- Zhu, C.; Hao, Y.; Wu, H.; Chen, M.; Quan, B.; Liu, S.; Hu, X.; Liu, S.; Ji, Q.; Lu, X.; et al. Self-Assembly of Binderless Mxene Aerogel for Multiple-Scenario and Responsive Phase Change Composites with Ultrahigh Thermal Energy Storage Density and Exceptional Electromagnetic Interference Shielding. Nano-Micro Lett. 2024, 16, 57. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Liu, Z.; Li, Y.; Tang, L.; Zhang, W.; Lu, X.; Li, Y.; Niu, R.; Qu, J. High Transparency, Degradable and Uv-Protective Poly(Lactic Acid) Composites Based On Elongational Rheology and Chain Extender Assisted Melt Blending. Int. J. Biol. Macromol. 2024, 256, 128469. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Feng, K.; Zhang, X.; Gong, J.; Qu, J.; Niu, R. Ion-Exchange Enabled Dual-Functional Swarms with Reconfigurability and Magnetic Controllability. Small 2024, 4, 2308318. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, Z.; Li, X.; Ren, J.; Gong, J.; Qu, J.; Niu, R. Mass Production of Biodegradable Porous Foam for Simultaneous Solar Evaporation and Thermoelectricity Generation. J. Mater. Chem. A 2023, 11, 26784–26793. [Google Scholar] [CrossRef]
- Liu, S.; Sheng, M.; Quan, B.; Yang, Y.; Ji, Q.; Hu, X.; Lu, X.; Qu, J. In Situ Mil-101 Growth On Cotton Cloth to Fabricate Multifunctional Phase Change Composites Driven by Solar and Magneto-Thermal for All-Day Desalination. J. Colloid Interface Sci. 2024, 659, 905–913. [Google Scholar] [CrossRef]
- Ji, Q.; Sheng, X.; Li, X.; Liu, S.; Chen, Q.; Guo, P.; Yang, Y.; Huang, Y.; Zhang, G.; Lu, X.; et al. Camel Skin-Fat Structure Inspired Mxene@Pva/Pcc Aerogel Composite for Efficient Medium and Low Temperature Infrared Stealth. Chem. Eng. J. 2023, 476, 146671. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, S.; Jin, L.; Li, G.; Quan, B.; Chen, Q.; Tang, X.; Ji, X.; Wu, H.; Lu, X.; et al. A Novel Multisource Energy Harvester with Enhanced Thermal Conductivity for Efficient Energy Harvesting and Superior Emi Shielding. Compos. Part A—Appl. Sci. Manuf. 2023, 175, 107803. [Google Scholar] [CrossRef]
- Du, Y.; Wu, T.; Zhou, W.; Li, C.; Ding, C.; Chen, P.; Xie, H.; Qu, J. Cicada Wing-Inspired Transparent Polystyrene Film Integrating Self-Cleaning, Antifogging, and Antibacterial Properties. ACS Appl. Mater. Interfaces 2023, 15, 46538–46549. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Shen, W.; Chen, L.; Gong, J.; Palberg, T.; Qu, J.; Niu, R. Weak Ion-Exchange Based Magnetic Swarm for Targeted Drug Delivery and Chemotherapy. Small 2023, 20, e2306798. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Huang, X.; Quan, B.; Zhu, C.; Yang, Y.; Sheng, M.; Ding, C.; Wen, H.; Li, X.; Wei, J.; et al. Tree-Inspired and Scalable High Thermal Conductivity Ethylene-Vinyl Acetate Copolymer/Expanded Graphite/Paraffin Wax Phase Change Composites for Efficient Thermal Management. Chem. Eng. J. 2023, 471, 144720. [Google Scholar] [CrossRef]
- Hu, X.; Quan, B.; Ai, B.; Sheng, M.; Liu, S.; Huang, X.; Wu, H.; Lu, X.; Qu, J. Engineering Asymmetric Multifunctional Phase Change Composites for Improved Electromagnetic Interference Shielding and Wireless Personal Thermal Therapy. J. Mater. Chem. A 2023, 11, 16138–16152. [Google Scholar] [CrossRef]
- Tang, W. The Virtual Prototype Construction and the Dynamics Study Visualization of Screw Pump. Sci. Technol. Vis. 2012, 13, 185–186. [Google Scholar]
- Ni, Y.; Wu, J.; Guo, H. Parameter Modeling and Kinematical Simulation for Rotor and Stator of Screw Pump. J. Donghua Univ. (Eng. Ed.) 2013, 30, 38–43. [Google Scholar]
- Wang, Z. The Virtual Assembly Simulation and Optimization Design On Single Screw Pump of Offshore Petroleum Well Cementing Lads Device. Adv. Mater. Res. 2014, 945–949, 203–208. [Google Scholar] [CrossRef]
- Hu, J. Extrusion Process and Characteristics Study of Polyethylene on Eccentric Rotor Extruder. Master’s Thesis, South China University of Technology, Guangzhou, China, 2016. [Google Scholar]
- Chen, R.Y. Study on Mixing Mechanism and Structural Properties of Nano-Filling Composites via Volume Elongation Deformation. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2016. [Google Scholar]
- Yuan, D. Stuty on Elongational Deformation Effects of the Melt Conveying in an Eccentric Rotor Extruder. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2018. [Google Scholar]
- Wen, J.S.; Yin, C.H.; Fu, Y.; Hu, Z.G. Numerical investigations of energy consumption in the melt conveying section of an eccentric rotor extruder at different rotation rates. China Plast. Ind. 2017, 45, 51–54. [Google Scholar]
- Wu, T.; Yuan, D.; Qiu, F.; Chen, R.; Zhang, G.; Qu, J. Polypropylene/Polystyrene/Clay Blends Prepared by an Innovative Eccentric Rotor Extruder Based on Continuous Elongational Flow: Analysis of Morphology, Rheology Property, and Crystallization Behavior. Polym. Test. 2017, 63, 73–83. [Google Scholar] [CrossRef]
- Luo, S.; Mo, J. Manufacturing and Contact Characteristics Analysis of a Novel 2K-H Internal Meshing Planetary Reducer with Involute-Cycloid Combined Tooth Profiles. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2024, 5, 09544062241228380. [Google Scholar] [CrossRef]
- Hao, Y.; Guo, F.; Wu, G.; Hou, Z.; Li, N.; Liu, G.; Cui, X.; Meng, D.; Li, Y.; Li, X. Numerical Simulation and Experimental Research On Heat Transfer Characteristics Based On Internal Meshing Screw. Appl. Sci. 2024, 14, 220. [Google Scholar] [CrossRef]
- Fan, D.; Yang, M.; Huang, Z.; Wen, J. Numerical Simulation of Mixing Characteristics in the Eccentric Rotor Extruder with Different Process Conditons and Structure Parameters. Adv. Polym. Technol. 2019, 56, 395–408. [Google Scholar]
- Ju, J.P.; Zhang, G.Z. A Transmission Method and Device for Coaxial Output Rotation and Revolution. CN 105065582 A, 13 July 2015. [Google Scholar]
- Li, H.C.; Guo, F. Optimal Design of Parameters of Coaxial Output Rotation and Revolution Transmission System. Chem. Eng. Equip. 2023, 1, 158–160. [Google Scholar]
- Guo, F.; Ma, Y.; Meng, Y.H.; Hao, Y.H.; Liu, X.L.; Wang, Z.; Wu, G.F.; Li, X.W. The Utility Model Relates to a Single-Screw Continuous Mixing Device for High Viscosity Materials. CN 219128925U, 8 December 2022. [Google Scholar]
- Wu, H. Study on Continuous Mixing Technology and Its Mechanism of Solid Propellant Simulation Slurry Dominated by Elongational Deformation. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]










| Number of Turns | Longitudinal Section | Cross-Section Diagram | ||||
|---|---|---|---|---|---|---|
| I | II | III | I | V | ||
| 0 |  |  |  |  |  |  |
| 1/4 |  |  |  |  |  |  |
| 1/2 |  |  |  |  |  |  |
| 3/4 |  |  |  |  |  |  |
| 1 |  |  |  |  |  |  |
| Point | Parameter Value | Trajectory Equation | Velocity Equation |
|---|---|---|---|
| B | -- | ||
| A | |||
| C | |||
| D | |||
| E | |||
| F | |||
| G |
| Material Name | Physical Properties and Parameters |
|---|---|
| Corn syrup | Corn syrup, thick transparent liquid, Deen Food Ingredients Co., LTD., density of 1340 kg·m−3, viscosity (28 ± 0.19) Pa·s (20 °C), transmittal rate of 98.2%. |
| Flour powder | White powder, density 520 kg·m−3, particle size 140 mesh (106 μm). |
| Rotate Speed/(r·min−1) | 15 | 25 | 35 | 45 | 55 |
|---|---|---|---|---|---|
| Corn syrup and water | |||||
| Feed rate of corn syrup/(g min−1) | 73 | 125 | 170 | 220 | 270 |
| Feed rate of water/(g min−1) | 15 | 25 | 34 | 44 | 54 |
| Corn syrup and flour powder | |||||
| Feed rate of corn syrup/(g min−1) | 30 | 48 | 60 | 78 | 96 |
| Feed rate of flour powder/(g min−1) | 5 | 8 | 10 | 13 | 16 |
| Rotational Speed/r·min−1 | Slurry (2:1 Ratio of Corn Syrup to Flour Mixture) | |||||
|---|---|---|---|---|---|---|
| 15 | 25 | 35 | 45 | 55 | Mean Value | |
| Non-newtonian fluid index n | 0.9799 | 0.9803 | 0.9807 | 0.9812 | 0.9817 | 0.98068 |
| Undulate/% | −0.09% | −0.05% | −0.01% | 0.04% | 0.10% | |
| Consistency coefficient k/Pa·sn | 303.88 | 297.17 | 289.67 | 281.84 | 273.09 | 289.1275 |
| Undulate (%) | 5.10% | 2.78% | 0.19% | −2.52% | −5.55% | |
| Degree of fitting R2 | 0.9196 | 0.9184 | 0.9149 | 0.9086 | 0.898 | 0.9119 |
| Rotate Speed/ r·min−1 | Density/ρ (g·cm−3) | Standard Deviation | Average Value/g·cm−3 | |||||
|---|---|---|---|---|---|---|---|---|
| 15 | Group No. | 1 | 2 | 3 | 4 | 5 | 0.0082 | 1.197 |
| Density | 1.196 | 1.193 | 1.201 | 1.205 | 1.186 | |||
| Fluctuation compared to average | 0.002 | 0.005 | 0.003 | 0.007 | 0.012 | |||
| Group No. | 6 | 7 | 8 | 9 | 10 | |||
| Density | 1.203 | 1.211 | 1.196 | 1.191 | 1.183 | |||
| Fluctuation compared to average | 0.005 | 0.013 | 0.002 | 0.007 | 0.015 | |||
| 25 | Group No. | 1 | 2 | 3 | 4 | 5 | 0.0104 | 1.199 |
| Density | 1.195 | 1.199 | 1.198 | 1.215 | 1.191 | |||
| Fluctuation compared to average | 0.011 | 0.007 | 0.008 | 0.009 | 0.015 | |||
| Group No. | 6 | 7 | 8 | 9 | 10 | |||
| Density | 1.201 | 1.219 | 1.217 | 1.220 | 1.212 | |||
| Fluctuation compared to average | 0.005 | 0.013 | 0.011 | 0.013 | 0.006 | |||
| 35 | Group No. | 1 | 2 | 3 | 4 | 5 | 0.0116 | 1.206 |
| Density | 1.192 | 1.193 | 1.195 | 1.221 | 1.218 | |||
| Fluctuation compared to average | 0.013 | 0.012 | 0.010 | 0.017 | 0.013 | |||
| Group No. | 6 | 7 | 8 | 9 | 10 | |||
| Density | 1.195 | 1.205 | 1.208 | 1.216 | 1.187 | |||
| Fluctuation compared to average | 0.010 | 0.000 | 0.003 | 0.011 | 0.018 | |||
| 45 | Group No. | 1 | 2 | 3 | 4 | 5 | 0.0093 | 1.207 |
| Density | 1.210 | 1.179 | 1.181 | 1.183 | 1.187 | |||
| Fluctuation compared to average | 0.022 | 0.009 | 0.007 | 0.005 | 0.001 | |||
| Group No. | 6 | 7 | 8 | 9 | 10 | |||
| Density | 1.186 | 1.197 | 1.192 | 1.178 | 1.184 | |||
| Fluctuation compared to average | 0.002 | 0.009 | 0.003 | 0.010 | 0.004 | |||
| 55 | Group No. | 1 | 2 | 3 | 4 | 5 | 0.0130 | 1.202 |
| Density | 1.200 | 1.209 | 1.229 | 1.177 | 1.222 | |||
| Fluctuation compared to average | 0.010 | 0.001 | 0.020 | 0.033 | 0.012 | |||
| Group No. | 6 | 7 | 8 | 9 | 10 | |||
| Density | 1.233 | 1.181 | 1.218 | 1.217 | 1.196 | |||
| Fluctuation compared to average | 0.023 | 0.028 | 0.008 | 0.008 | 0.013 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Liu, G.; Hao, Y.; Ma, Y.; Wu, G.; Hou, Z.; Li, N.; Li, X. Kinematics-Based Design Method and Experimental Validation of Internal Meshing Screw for High-Viscosity Fluid Mixing. Appl. Sci. 2024, 14, 4119. https://doi.org/10.3390/app14104119
Guo F, Liu G, Hao Y, Ma Y, Wu G, Hou Z, Li N, Li X. Kinematics-Based Design Method and Experimental Validation of Internal Meshing Screw for High-Viscosity Fluid Mixing. Applied Sciences. 2024; 14(10):4119. https://doi.org/10.3390/app14104119
Chicago/Turabian StyleGuo, Fang, Genhao Liu, Yinghai Hao, Yu Ma, Guifang Wu, Zhanfeng Hou, Na Li, and Xiwen Li. 2024. "Kinematics-Based Design Method and Experimental Validation of Internal Meshing Screw for High-Viscosity Fluid Mixing" Applied Sciences 14, no. 10: 4119. https://doi.org/10.3390/app14104119






