Wind-Induced Response Analysis and Fatigue Life Prediction of a Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss
Abstract
:1. Introduction
2. Finite Element Modeling and Modal Analysis of the WindPACT-3MW Wind Turbine Tower
3. Analysis of the Static Mechanical Characteristics of a Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss
3.1. Design Parameters and Finite Element Model for the Hybrid Wind Turbine Tower
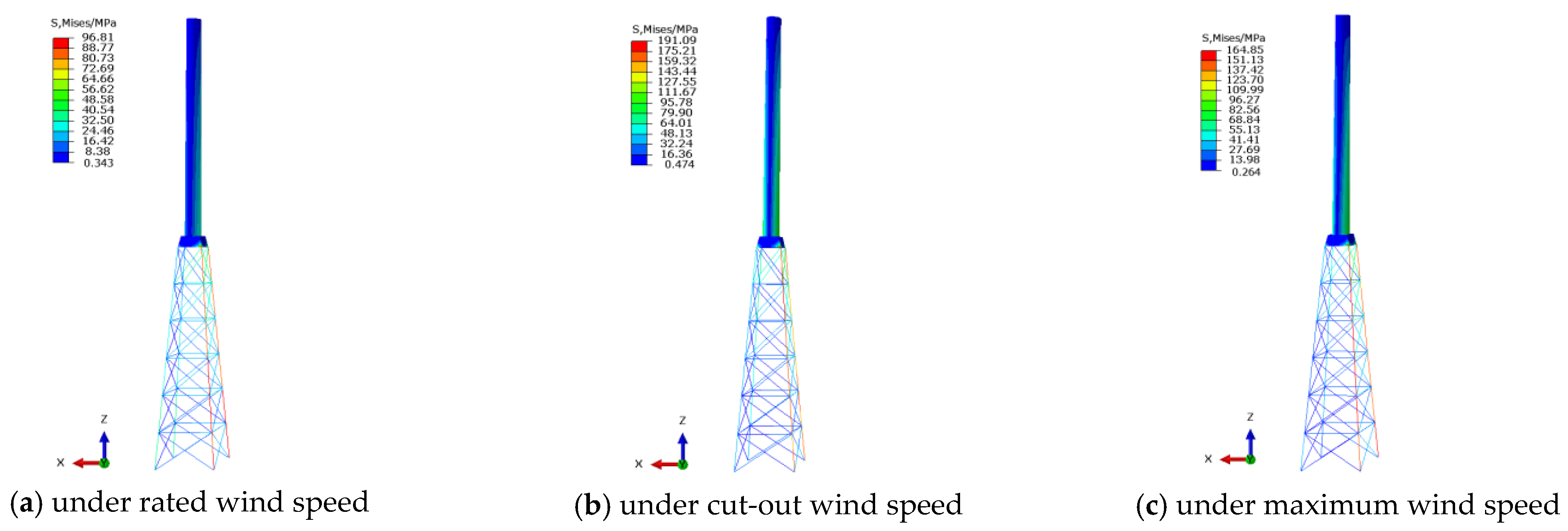
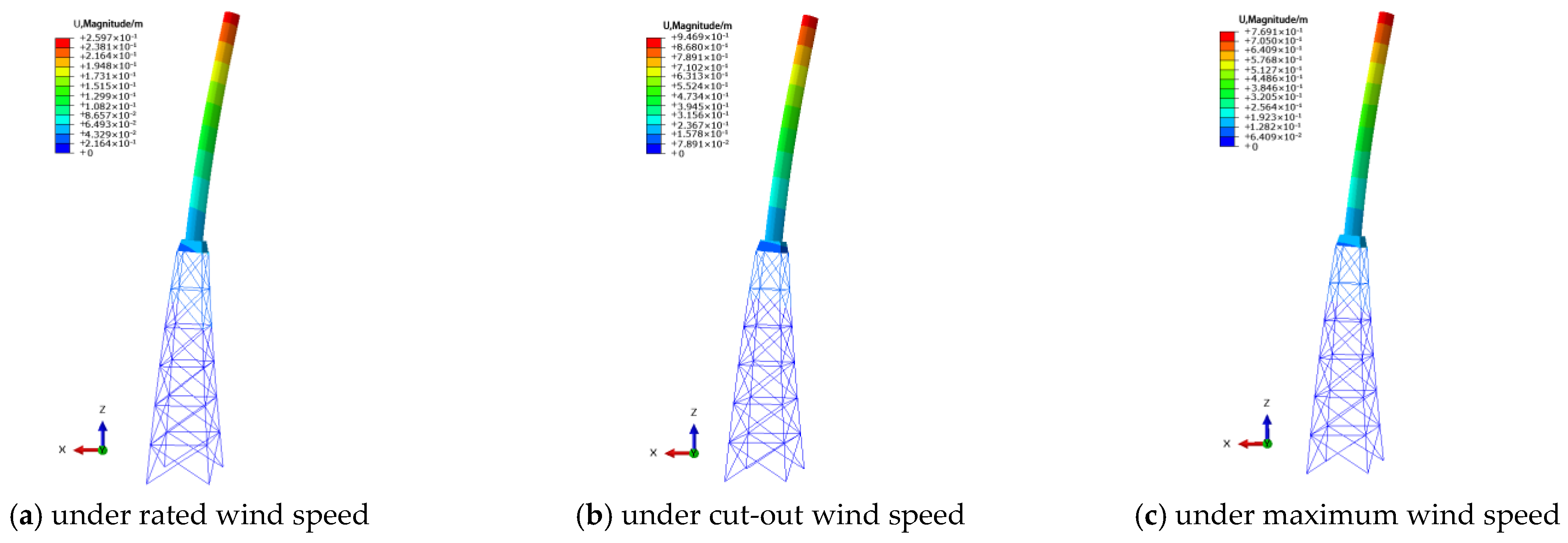
3.2. Analysis of the Static Bearing Capacity of the Hybrid Wind Turbine Tower
4. Static Optimization Analysis of the Hybrid Tower Combining an Upper Steel Tube with a Lower Steel Truss
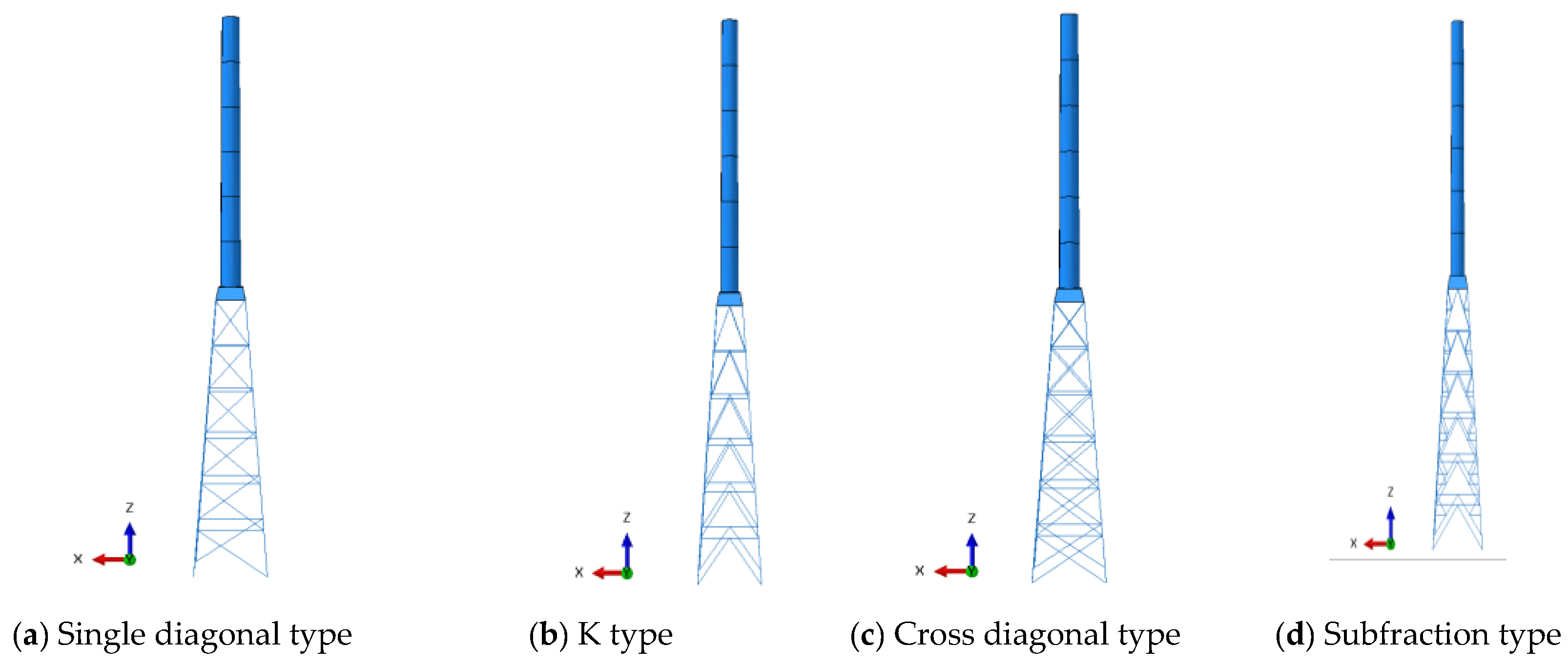
4.1. Influence of the Web Member Type on the Static Bearing Capacity of the Hybrid Tower
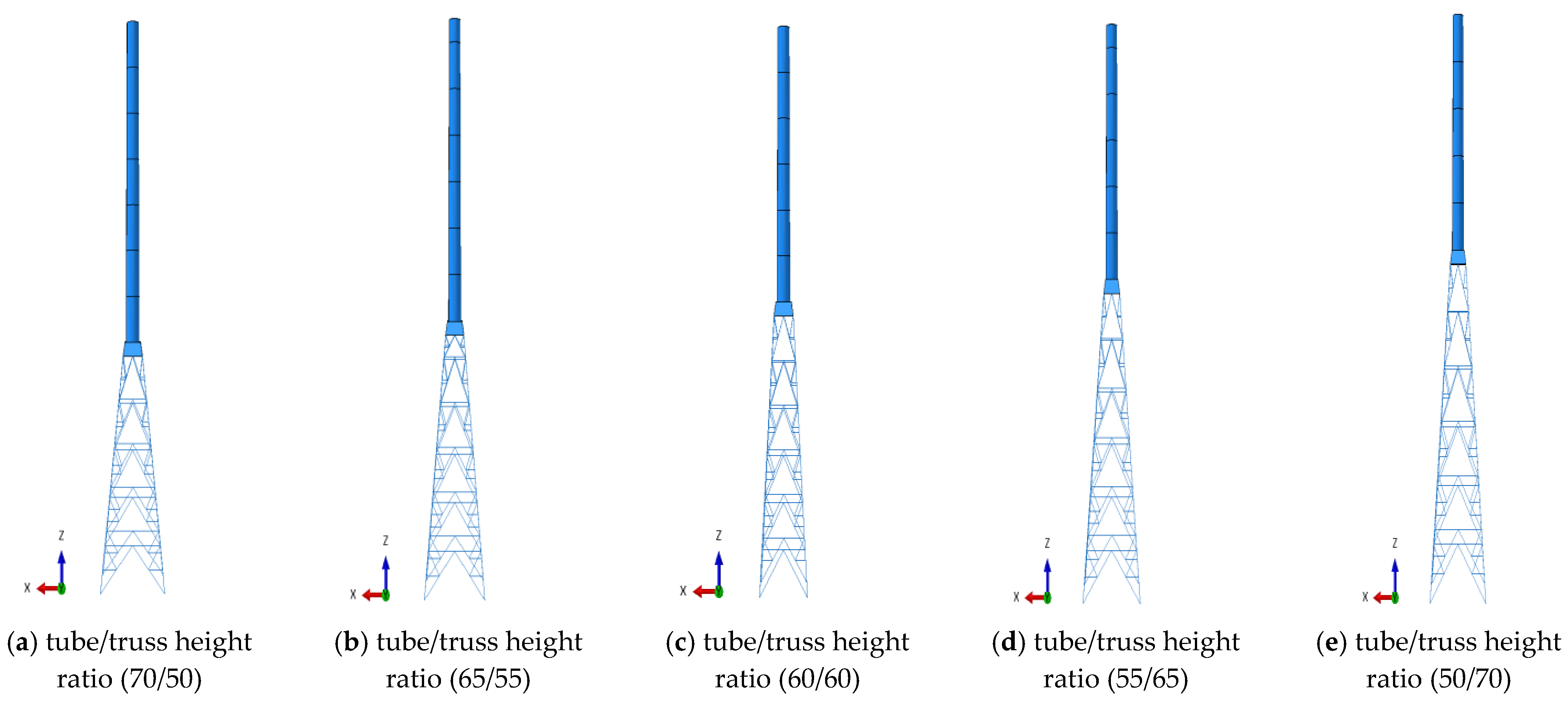
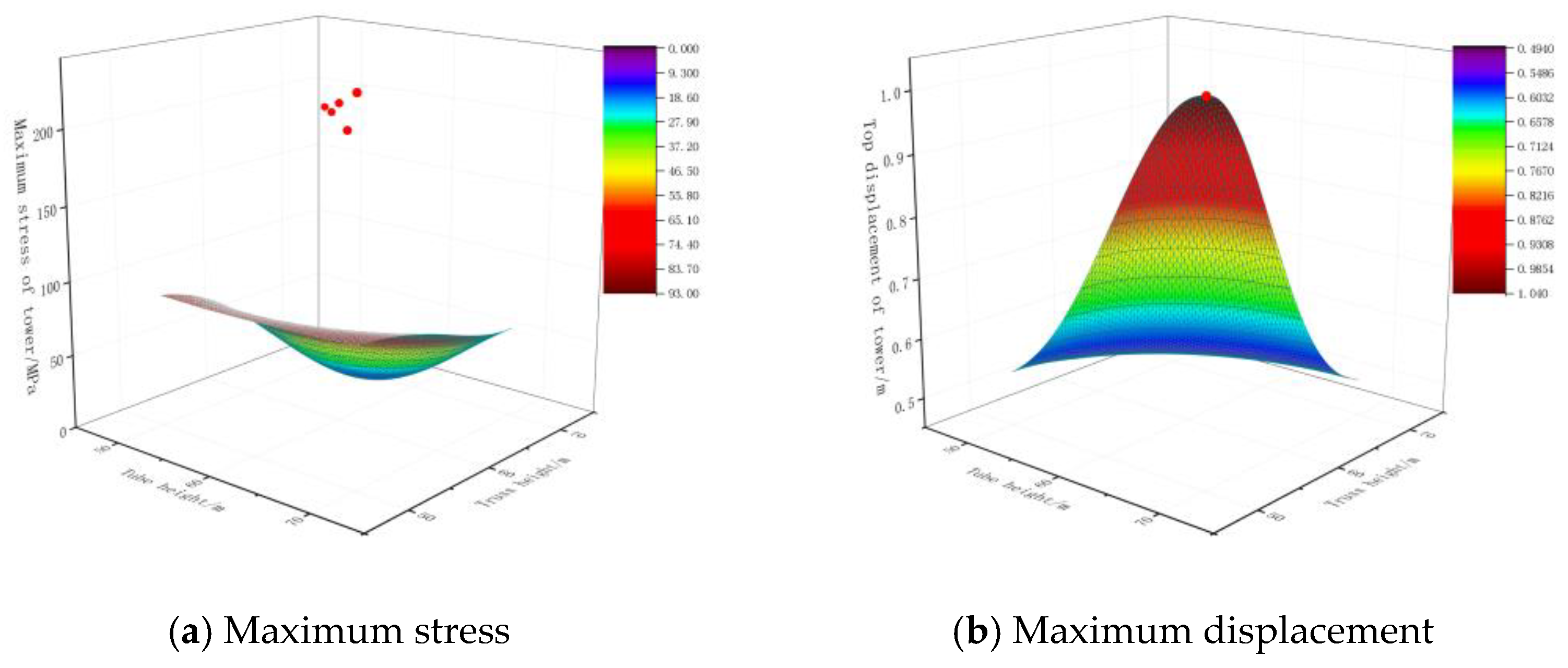
4.2. Influence of the Tube-Height-to-Truss-Height Ratio on the Static Bearing Capacity of the Hybrid Tower
4.3. Influence of the Aspect Ratio on the Static Bearing Capacity of the Hybrid Tower
5. Wind-Induced Dynamic Response of the Hybrid Tower Combining an Upper Steel Tube with a Lower Steel Truss
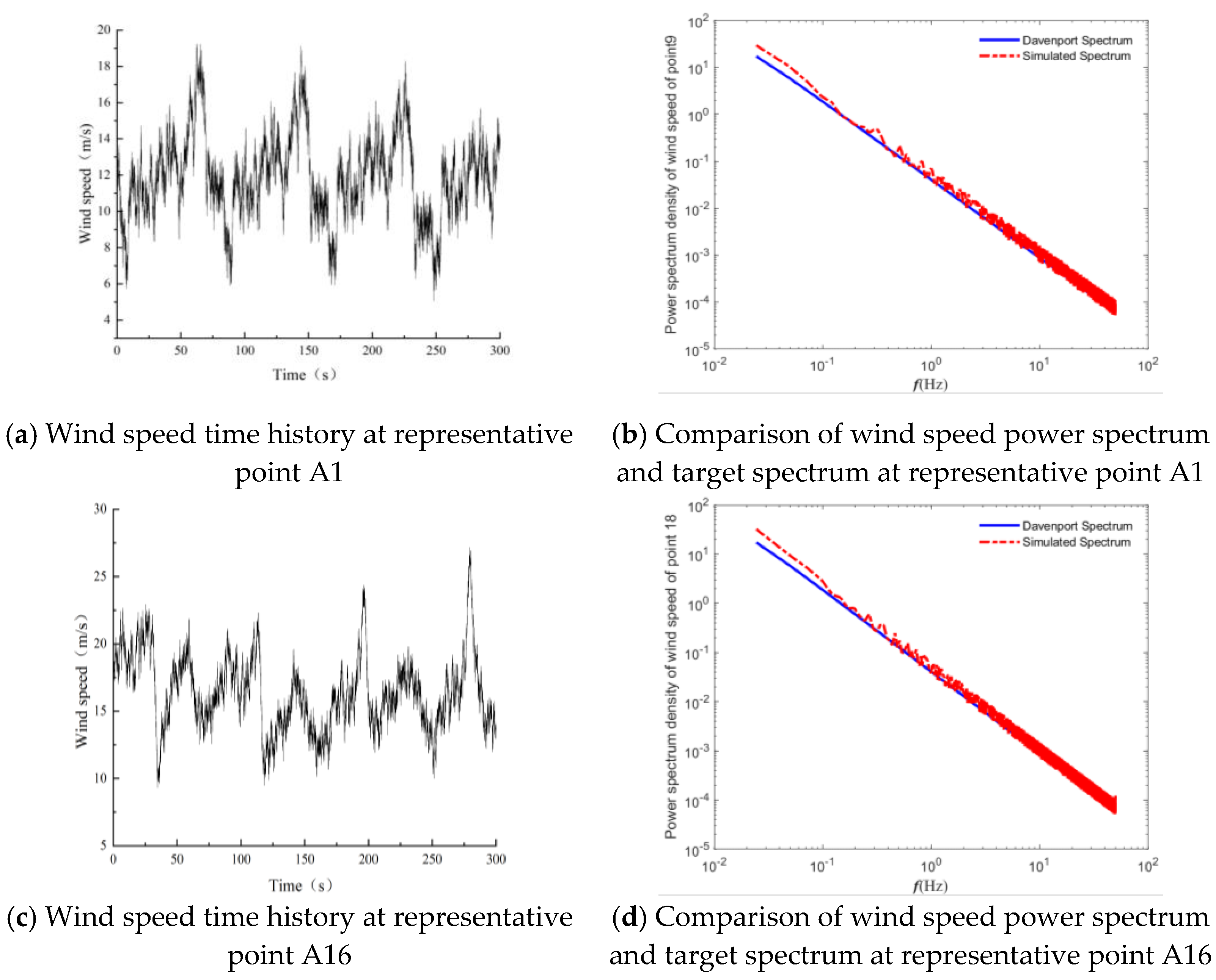
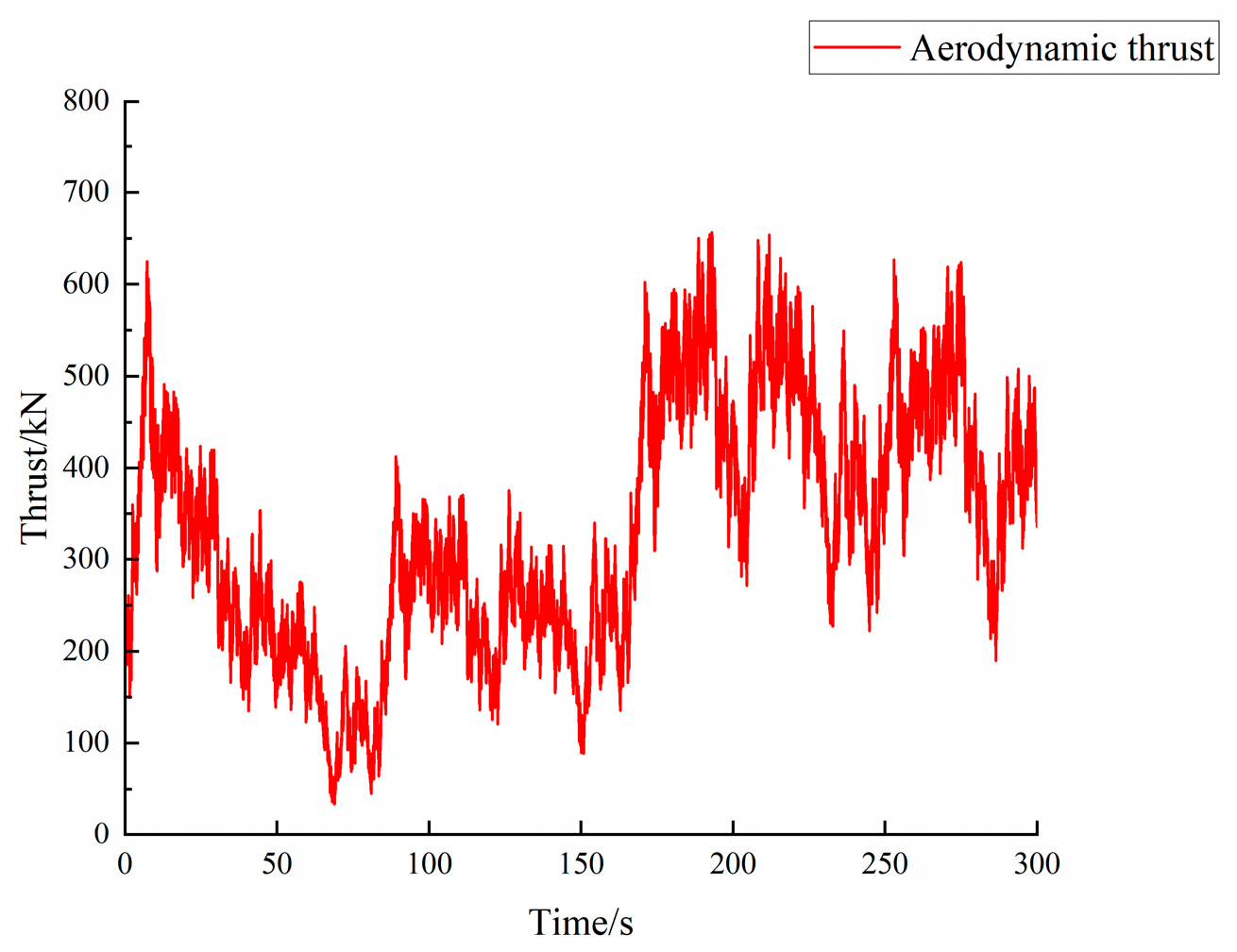
5.1. Wind Load Simulation
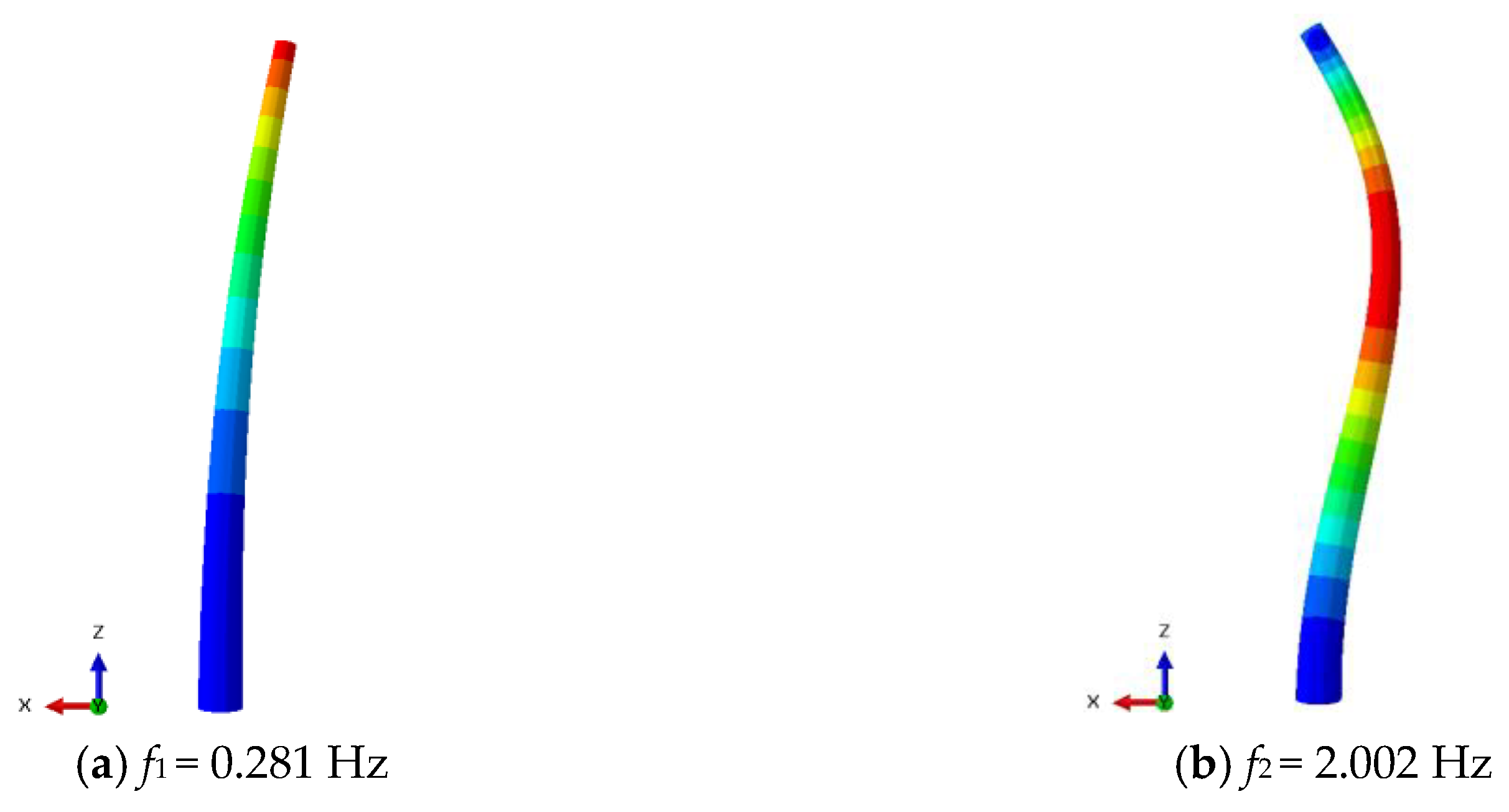
5.2. Modal Analysis of the Hybrid Tower
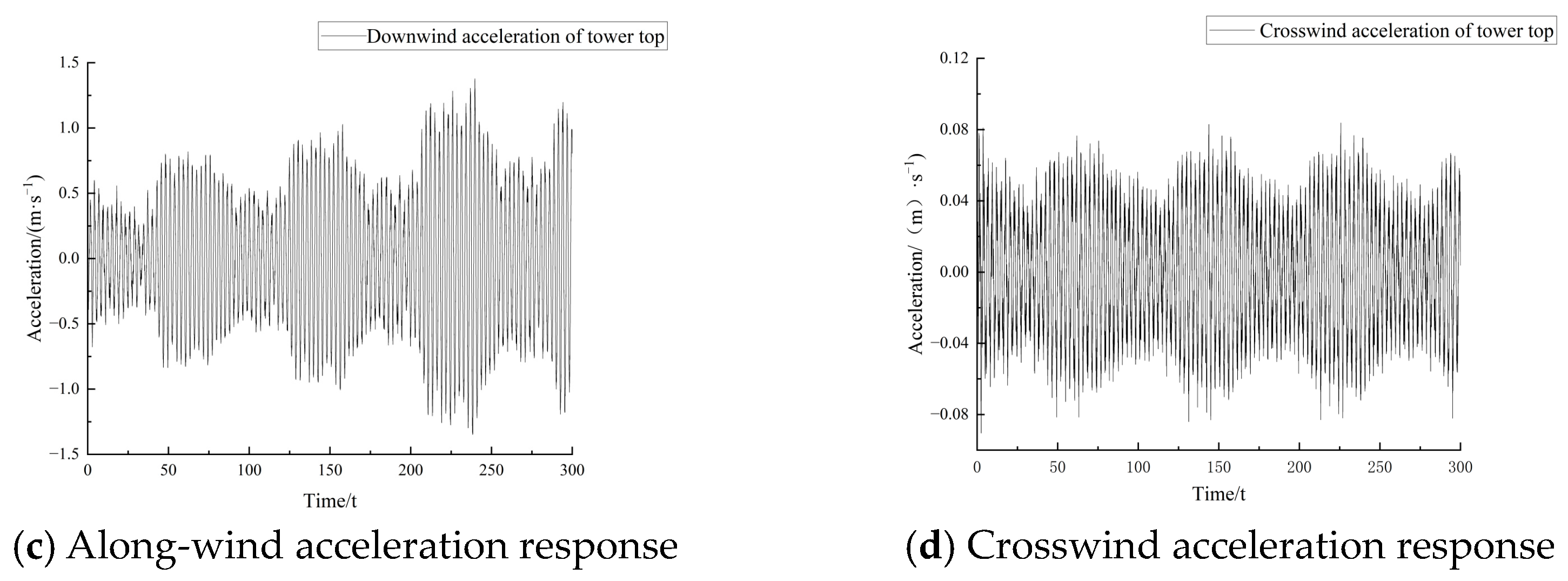
5.3. Wind-Induced Vibration of the Tower
6. Fatigue Life Prediction of the Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss
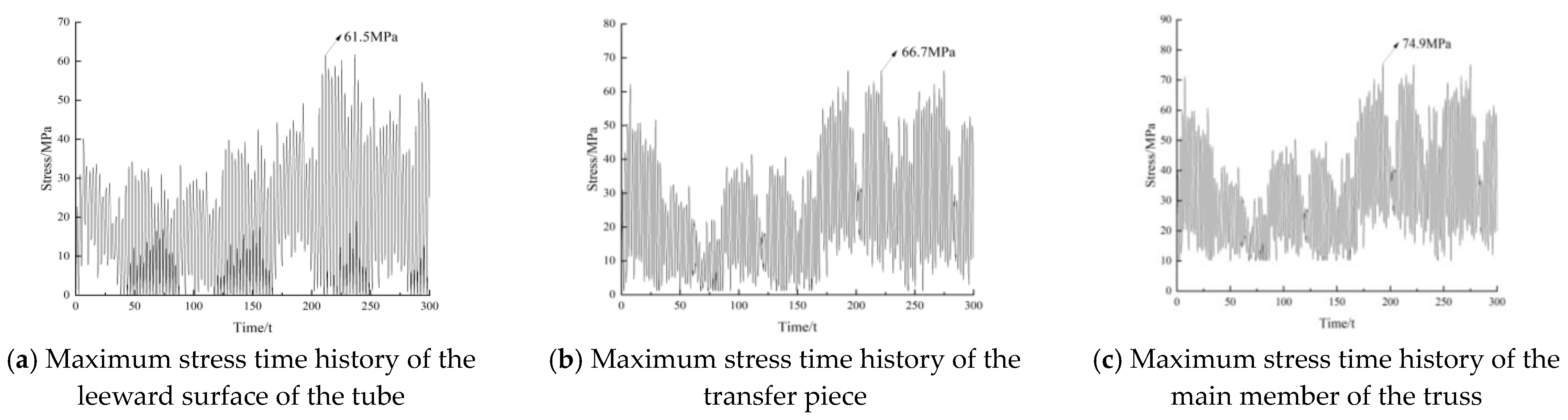
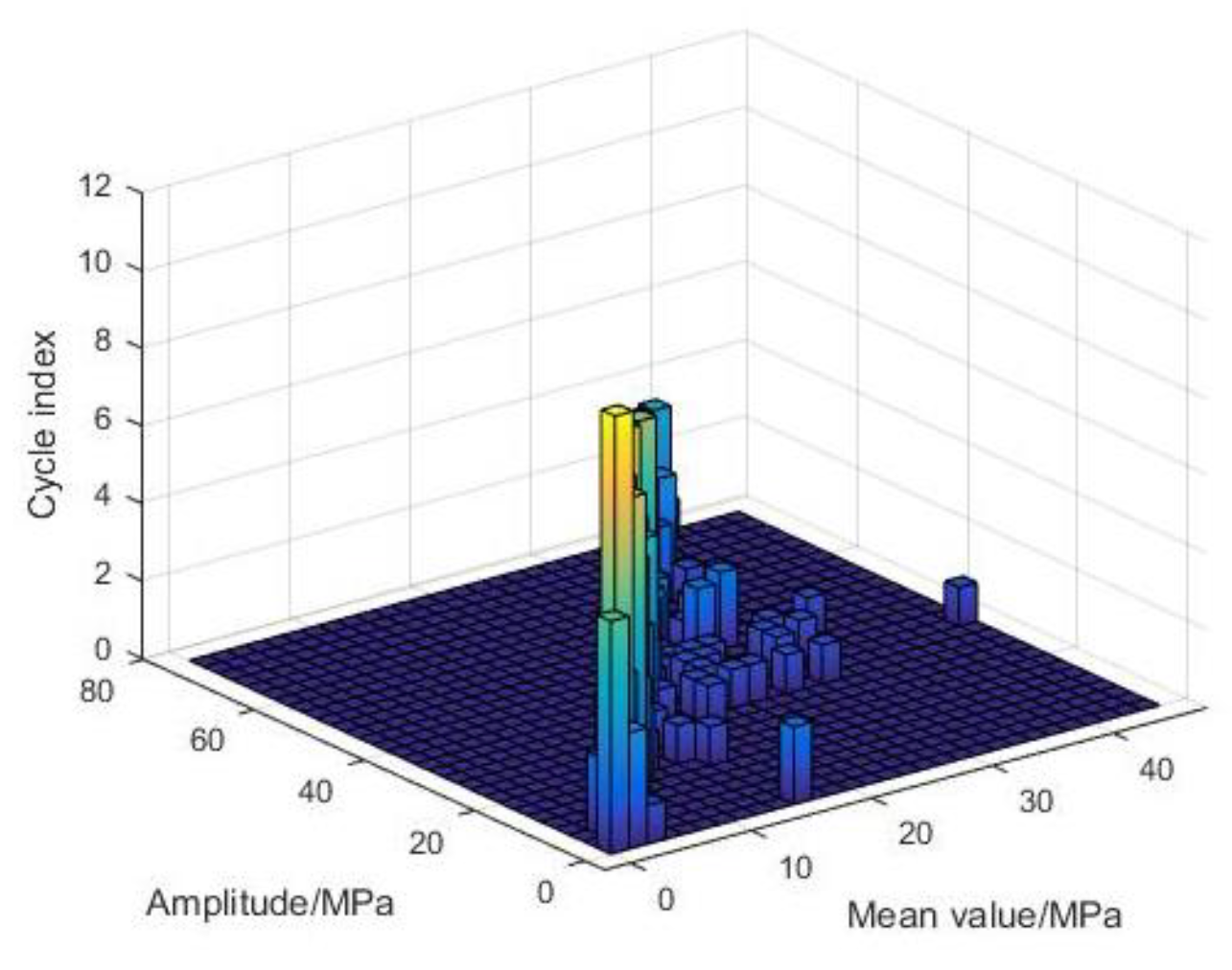
6.1. Fatigue Life of the Hybrid Tower at the Rated Wind Speed
6.2. Fatigue Life of the Hybrid Tower under Various Wind Speeds Ranging from the Cut-In Wind Speed to the Cut-Out Wind Speed
7. Conclusions
- With the same design total height and same material, using a higher truss with subdivided truss webs and larger base dimensions can significantly increase the overall bending stiffness and static bearing capacity of the hybrid wind turbine tower.
- The fundamental natural frequency of the hybrid tower is far from the excitation frequencies caused by the rotor speed (1P) or 3P harmonics from the rotor, indicating that there will be no resonance when blades are running at the rated speed. During normal operation, the along-wind responses of the hybrid tower are significantly greater than the crosswind responses, indicating that the aerodynamic thrust generated by the blades is the main factor causing the wind-induced vibration of the tower.
- For the hybrid tower analyzed in this study, when only the action of the rated wind speed is considered, the annual fatigue cumulative damage factor is 0.021, and the fatigue life is 47.6 (years). When considering the wind load in the entire range from the cut-in wind speed to the cut-out wind speed, the annual fatigue cumulative damage factor is 0.026, and the fatigue life is 38.5 (years). Therefore, when predicting the fatigue life of a hybrid wind turbine tower, the wind loads of the tower should be fully considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Global Wind Energy Council. Global Wind Report 2023; GWEC: Brussels, Belgium, 2024. [Google Scholar]
- Berny-Brandt, E.A.; Ruiz, S.E. Reliability over time of wind turbines steel towers subjected to fatigue. Wind. Struct. 2016, 23, 75–90. [Google Scholar] [CrossRef]
- Jovasevic, S.; Correia, J.; Pavlovic, M.; Dantas, R.; Rebelo, C.; Veljkovic, M.; de Jesus, A.M. Alternative steel lattice structures for wind energy converters Wind energy converters. Int. J. Struct. Integr. 2019, 12, 48–69. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, X.; Fan, Y.; Shi, J.; Luo, C.; Wang, X. A Study on the Ultimate Span of a Concrete-Filled Steel Tube Arch Bridge. Buildings 2024, 14, 896. [Google Scholar] [CrossRef]
- Wei, J.; Ying, H.; Yang, Y.; Zhang, W.; Yuan, H.; Zhou, J. Seismic performance of concrete-filled steel tubular composite columns with ultra high performance concrete plates. Eng. Struct. 2023, 278, 115500. [Google Scholar] [CrossRef]
- Huang, H.; Yao, Y.; Liang, C.; Ye, Y. Experimental study on cyclic performance of steel-hollow core partially encased composite spliced frame beam. Soil Dyn. Earthq. Eng. 2022, 163, 107499. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, T.; Zhang, S.; Sun, C.; Li, J.; Tan, J. Bo-LSTM based cross-sectional profile sequence progressive prediction method for metal tube rotate draw bending. Adv. Eng. Inform. 2023, 58, 102152. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, Z.; Zhang, S.; Jiang, L.; Lin, Y.; Tan, J. Cross-sectional performance prediction of metal tubes bending with tangential variable boosting based on parameters-weight-adaptive CNN. Expert Syst. Appl. 2024, 237, 121465. [Google Scholar] [CrossRef]
- Jovašević, S.; Mohammadi, M.R.S.; Rebelo, C.; Pavlović, M.; Veljković, M. New Lattice-Tubular Tower for Onshore WEC—Part 1: Structural Optimization. Procedia Eng. 2017, 199, 3236–3241. [Google Scholar] [CrossRef]
- Gkantou, M.; Martinez-Vazquez, P.; Baniotopoulos, C. On the structural response of a tall hybrid onshore wind turbine tower. Procedia Eng. 2017, 199, 3200–3205. [Google Scholar] [CrossRef]
- Shah, H.J.; Desai, A.K. Comparison of Monopole and Hybrid Wind Turbine Tower Response for Seismic Loading Under Operational Conditions. J. Vib. Eng. Technol. 2022, 10, 2557–2575. [Google Scholar] [CrossRef]
- Gkantou, M.; Rebelo, C.; Baniotopoulos, C. Life Cycle Assessment of Tall Onshore Hybrid Steel Wind Turbine Towers. Energies 2020, 13, 3950. [Google Scholar] [CrossRef]
- Farhan, M.; Mohammadi, M.R.S.; Correia, J.A.; Rebelo, C. Transition piece design for an onshore hybrid wind turbine with multiaxial fatigue life estimation. Wind. Eng. 2018, 42, 286–303. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Li, Z.; Luo, Y.; Xiao, X.; Liu, Y. Residual stresses effects on fatigue crack growth behavior of rib-to-deck double-sided welded joints in orthotropic steel decks. Adv. Struct. Eng. 2024, 27, 35–50. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, X.; Chen, F.; Zhang, H.; Xiao, X. Numerical Simulation on Crack–Inclusion Interaction for Rib-to-Deck Welded Joints in Orthotropic Steel Deck. Metals 2023, 13, 1402. [Google Scholar] [CrossRef]
- Jia, Y.Z.; Yang, W. Statics finite element analysis of combined wind power tower. Hydroelectr. Energy Sci. 2017, 35, 207–211. [Google Scholar]
- Tenorio, M.; Cavalcante, M. Optimized Structural Design of Lattice Towers for Wind Turbines. In Proceedings of the XLI Ibero-Latin-American Congress on Computational Methods in Engineering, CILAMCE 2020, Foz do Iguaçu, Brazil, 16–19 November 2020. [Google Scholar]
- Rinker, J.M.; Dykes, K. Wind PACT Reference Wind Turbines; National Renewable Energy Laboratory: Golden, CO, USA, 2018.
- GB 50135-2019; Standard for Design of High-Rising Structures. China Planning Press: Beijing, China, 2019.
- Zhang, T. Research on Structural Dynamic Performance of In-Service Megawatt Wind Turbines; Shenyang University of Technology: Shenyang, China, 2022. [Google Scholar]
- Qiu, K.Y.; Ma, R.L.; He, M.J. Research on fatigue resistance of flange joints of 160 m truss-type prestressed steel pipe wind power tower column. Spec. Struct. 2020, 37, 7–12. [Google Scholar]
- Luo, Y.X.; Ma, R.L.; Qiu, K.Y. Anti-fatigue design method of frame-type prestressed anti-fatigue steel pipe wind power tower. Dev. Build. Steel Struct. 2021, 23, 73–81. [Google Scholar]
- GB 50009-2012; Load Code for Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- GB 50017-2017; Standard for Design of Steel Structures. China Building Industry Press: Beijing, China, 2018.
- Davenport, A.G. The spectrum of horizontal gustiness near the ground under high winds. Q. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Hansen, M.O.L. Aerodynamics of Wind Turbines, 3rd ed.; Routledge: London, UK, 2015. [Google Scholar]
- Dowling, N.E. Fatigue at Notches and the Local Strain and Fracture Mechanics Approaches. In Fracture Mechanics: Proceedings of the ASTMSTP, Blacksburg, VA, USA, 12–14 June 1978; ASTM International: West Conshohocken, PA, USA, 1979; pp. 247–273. [Google Scholar]
- ASTM. Standard Practices for Cycle Counting in Fatigue Analysis; ASTM: New York, NY, USA, 2017. [Google Scholar]
- Zhu, L.; Xu, N.; Gao, Y. Guidelines and Explanation of the Tower Structure of Wind Power Generation Equipment; China Building Industry Press: Beijing, China, 2014. [Google Scholar]
- IEC 61400-1:2019; Wind Energy Generation Systems-Part 1: Design Requirements. IEC: Geneva, Switzerland, 2019.
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind. Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]













| Items | Value | Items | Value |
|---|---|---|---|
| Rated power | 3 MW | Mass of tower | 351,798 kg |
| Rotor diameter | 99 m | Nacelle mass | 132,598 kg |
| Number of blades | 3 | Rotor mass | 101,384 kg |
| Hub height | 119 m | Hub diameter | 4.95 m |
| Swept area | 7693.8 m2 | Steel mass density | 7850 kg/m3 |
| Cut-in wind speed | 3 m/s | Steel elastic modulus | 200 GPa |
| Rated speed | 14.469 rpm | Steel shear modulus | 76.0 GPa |
| Rated wind speed | 12.9 m/s | Cut-out wind speed | 25 m/s |
| Mode Order | Simulated Frequency in the Present Study (Hz) f0 | Frequency Results Given by Reference (Rinker J. M. et al.) [18] (Hz) f | Relative Deviation (%) |(f0 − f)/f0| |
|---|---|---|---|
| 1 | 0.281 | 0.283 | 0.7 |
| 2 | 2.002 | 1.996 | 0.3 |
| Items | Value | Items | Value |
|---|---|---|---|
| Rated power | 3 MW | Length of the upper tube | 60 m |
| Diameter of the tube top | 3.9 m | Diameter of the tube bottom | 4.5 m |
| Wall thickness at the top of the tube | 48 mm | Wall thickness at the bottom of the tube | 64 mm |
| Truss height | 60 m | Width of the truss top | 6.5 m |
| Width of the truss base | 15 m | Main material specification of the truss | 680 × 14 mm |
| Diagonal member specifications of the truss | 272 × 6 mm | Web member specification of the truss | 272 × 6 mm |
| Steel mass density | 7850 kg/m3 | Steel elastic modulus | 200 GPa |
| Stress Range (MPa) | Actual Annual Number of Stress Cycles | Theoretical Annual Number of Stress Cycles | Annual Fatigue Damage Coefficient |
|---|---|---|---|
| 4.91 | 33 | 1.07 × 1012 | 3.24 × 10−8 |
| 13.66 | 32 | 6.4 × 109 | 5.42 × 10−4 |
| 24.88 | 33 | 3.19 × 109 | 1.09 × 10−3 |
| 34.37 | 38 | 6.35 × 108 | 6.29 × 10−3 |
| 42.12 | 21 | 2.3 × 108 | 9.6 × 10−3 |
| 50.72 | 12 | 9.07 × 108 | 1.39 × 10−3 |
| 67.74 | 8 | 4.75 × 107 | 1.78 × 10−3 |
| Annual fatigue cumulative damage coefficient: 0.021 | |||
| Wind Speed (m/s) | Annual Lasting Hours (h) | Equivalent Stress Range (MPa) | Actual Annual Number of Stress Cycles | Theoretical Annual Number of Stress Cycles | Annual Fatigue Damage Coefficient |
|---|---|---|---|---|---|
| 3 | 529.3 | 1.023 | 1.3 × 106 | 2.72 × 1015 | 4.78 × 10−10 |
| 5 | 963.9 | 5.041 | 2.0 × 106 | 9.36 × 1012 | 2.14 × 10−7 |
| 7 | 1236.6 | 7.511 | 3.44 × 106 | 1.27 × 1012 | 2.71 × 10−6 |
| 9 | 1324.9 | 31.47 | 2.99 × 106 | 6.68 × 109 | 4.48 × 10−4 |
| 11 | 1250.1 | 55.25 | 2.63 × 106 | 2.97 × 109 | 8.86 × 10−4 |
| 13 | 1063.7 | 60.5 | 2.68 × 106 | 9.57 × 108 | 2.8 × 10−3 |
| 15 | 826.6 | 71.17 | 2.25 × 106 | 2.57 × 108 | 8.75 × 10−3 |
| 17 | 591.2 | 96.41 | 1.54 × 106 | 1.41 × 109 | 1.09 × 10−3 |
| 19 | 390.9 | 139.21 | 1.07 × 106 | 4.48 × 108 | 2.39 × 10−3 |
| 21 | 239.9 | 153.39 | 6.62 × 105 | 1.61 × 108 | 4.11 × 10−3 |
| 23 | 136.9 | 187.47 | 3.78 × 105 | 1.39 × 108 | 2.72 × 10−3 |
| 25 | 72.8 | 208.88 | 2 × 104 | 7.23 × 106 | 2.77 × 10−3 |
| Annual fatigue cumulative damage coefficient: 0.026 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Xie, C.; Li, T.; Hossain, M.N.; Zhao, G. Wind-Induced Response Analysis and Fatigue Life Prediction of a Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss. Buildings 2024, 14, 1441. https://doi.org/10.3390/buildings14051441
Zhang M, Xie C, Li T, Hossain MN, Zhao G. Wind-Induced Response Analysis and Fatigue Life Prediction of a Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss. Buildings. 2024; 14(5):1441. https://doi.org/10.3390/buildings14051441
Chicago/Turabian StyleZhang, Meng, Chenhao Xie, Tianxiang Li, Md Nayim Hossain, and Guifeng Zhao. 2024. "Wind-Induced Response Analysis and Fatigue Life Prediction of a Hybrid Wind Turbine Tower Combining an Upper Steel Tube with a Lower Steel Truss" Buildings 14, no. 5: 1441. https://doi.org/10.3390/buildings14051441





