Correlation Analysis of Tunnel Deformation and Internal Force in the Earthquake Based on Tunnel Inclination
Abstract
:1. Introduction
2. Dynamic Time-History Analysis of the Shield Tunnel
2.1. Model Calculation Range
2.2. Model Calculation Parameters
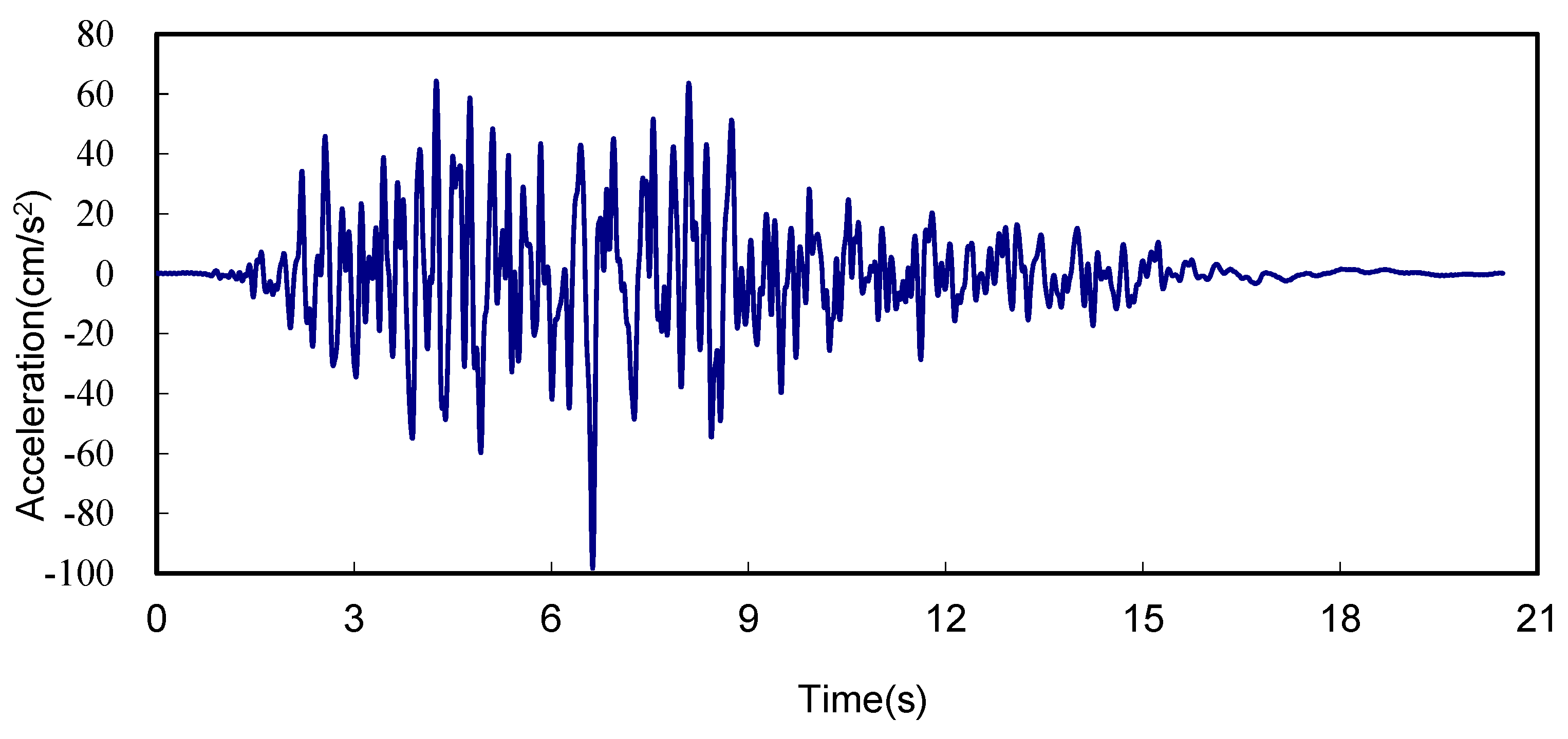
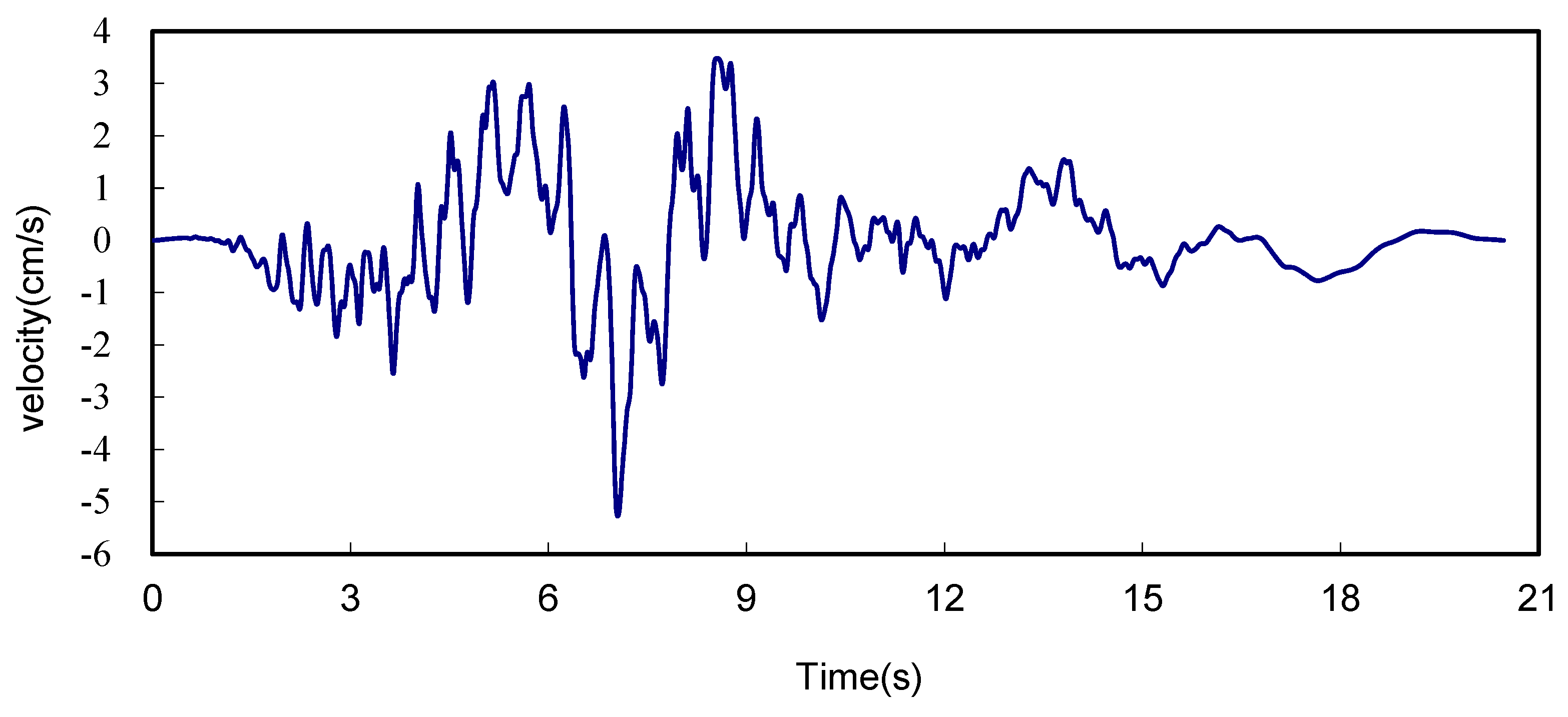
2.3. Treatment of Seismic Waves
2.4. Division of the Grid
2.5. Tunnel Seismic Calculation Process
3. Analysis of the Results of Seismic Response Calculations for Metro Tunnels
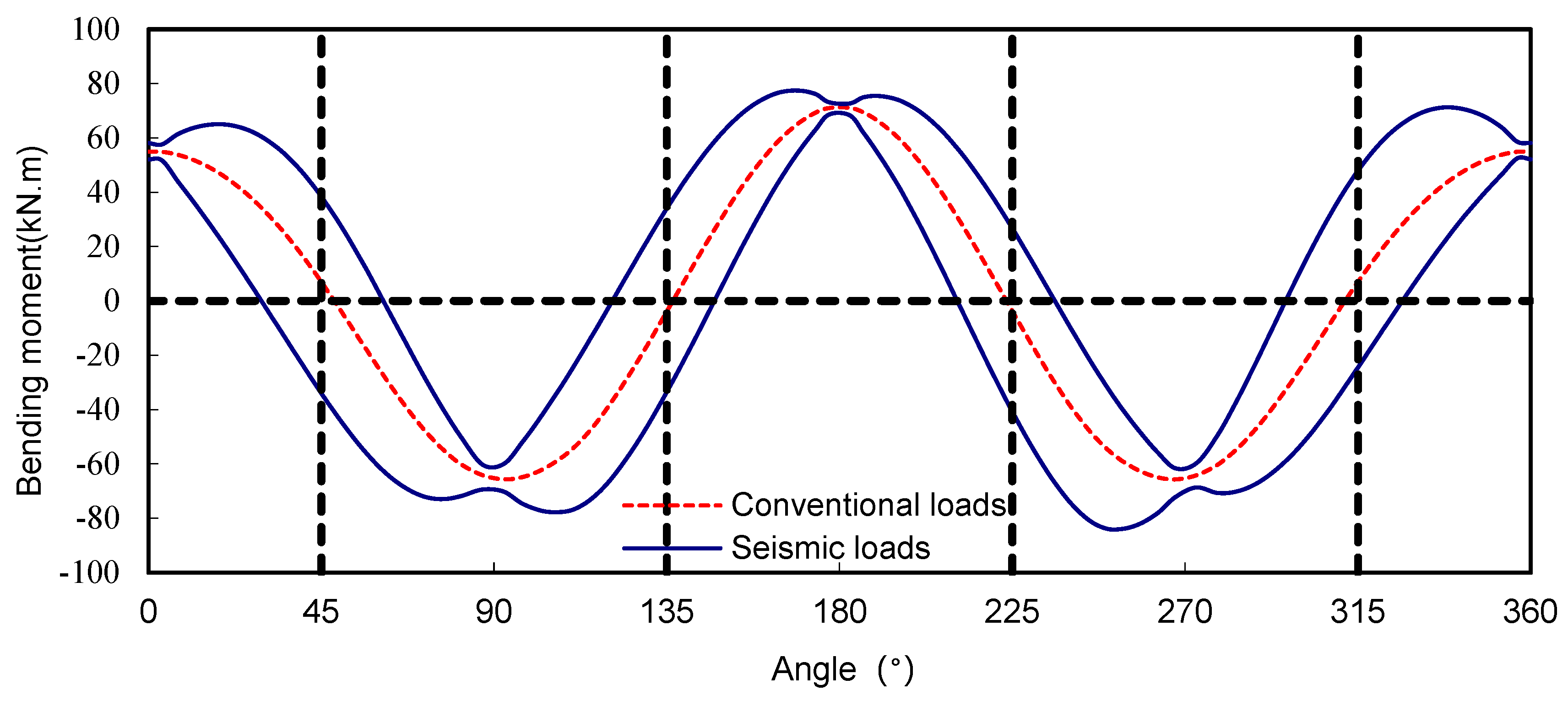
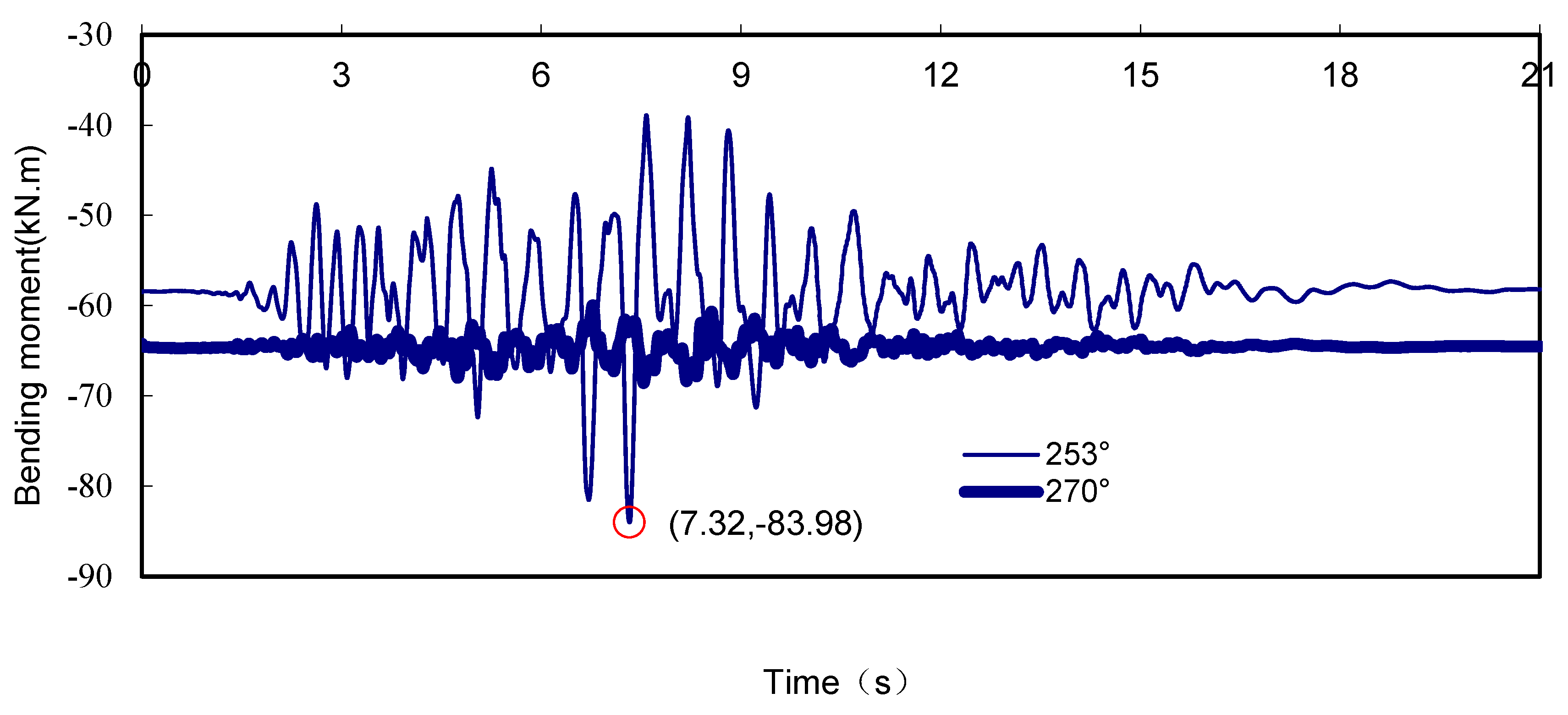
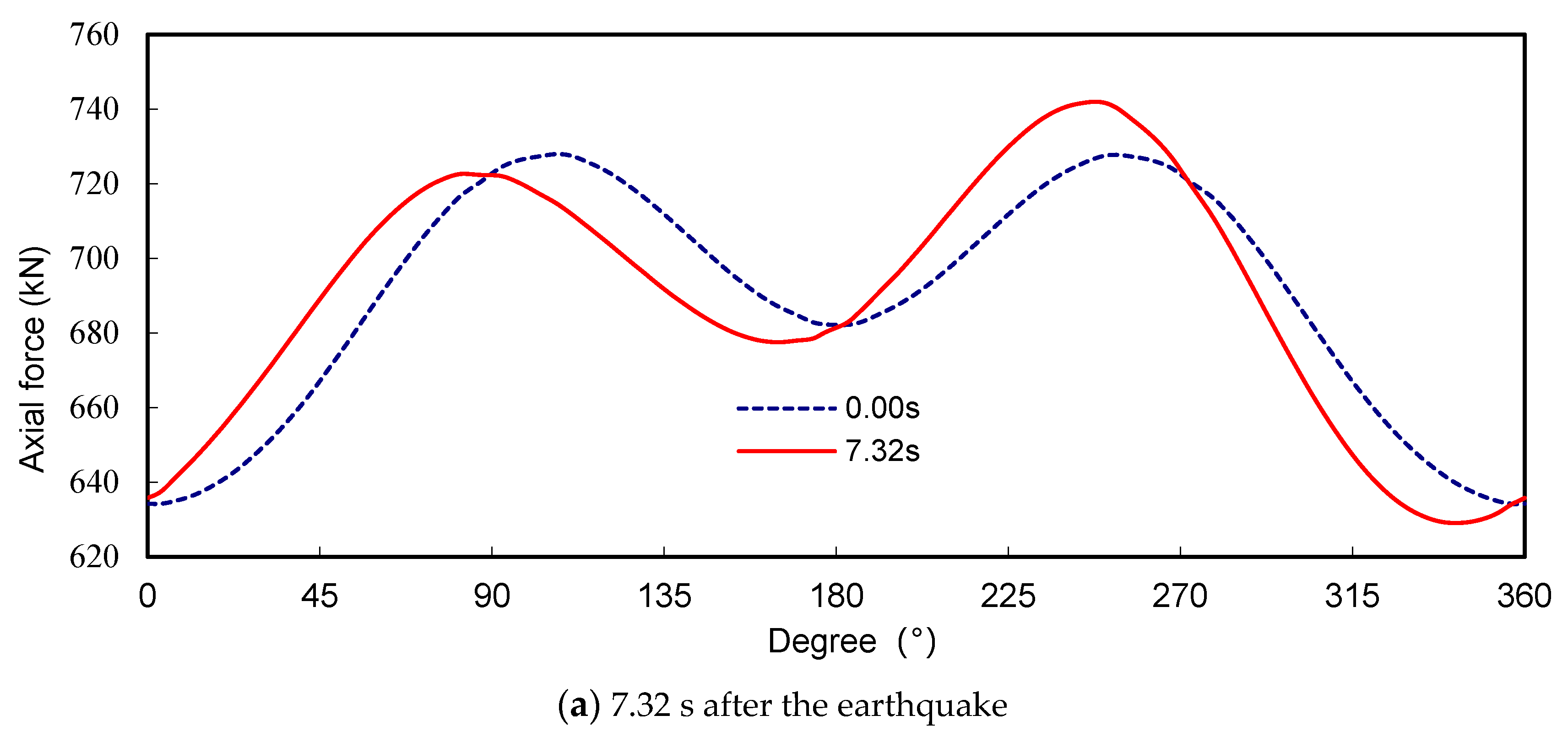
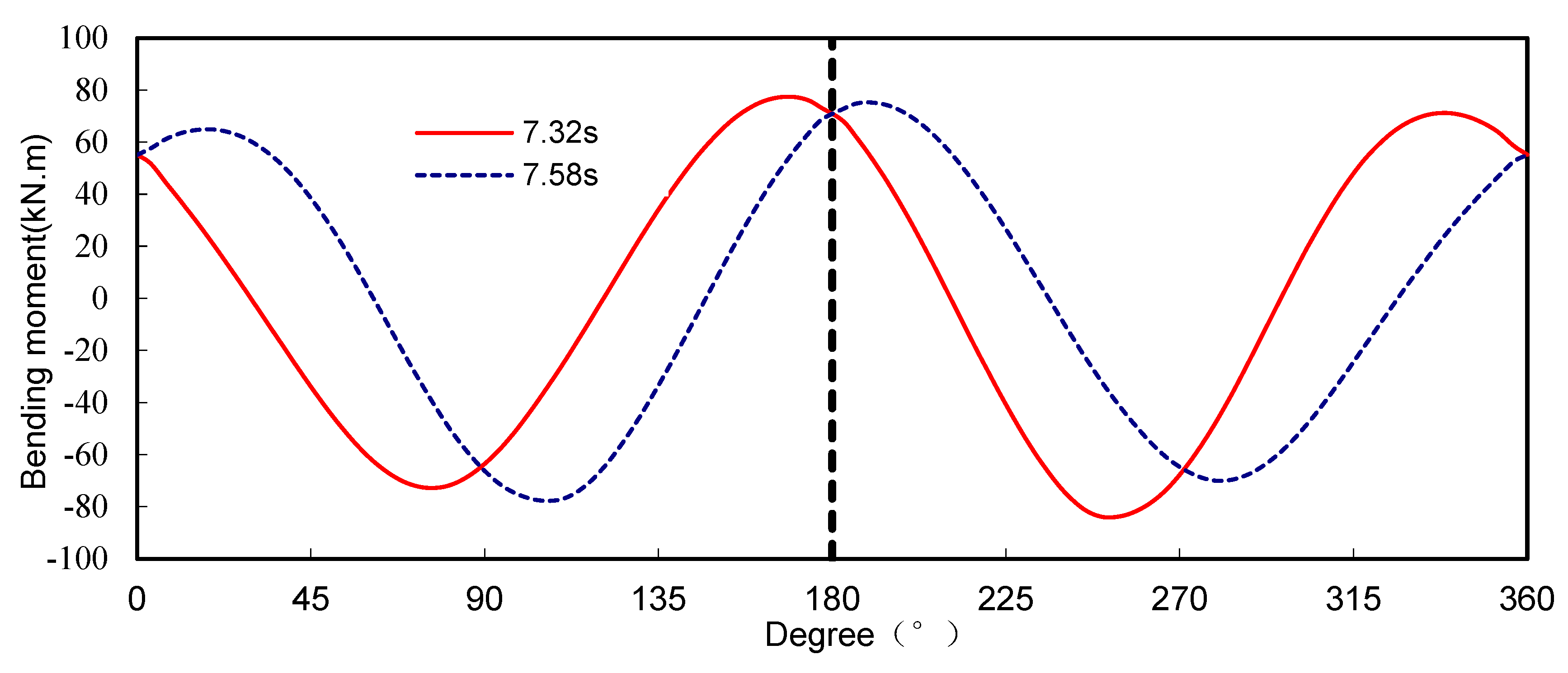
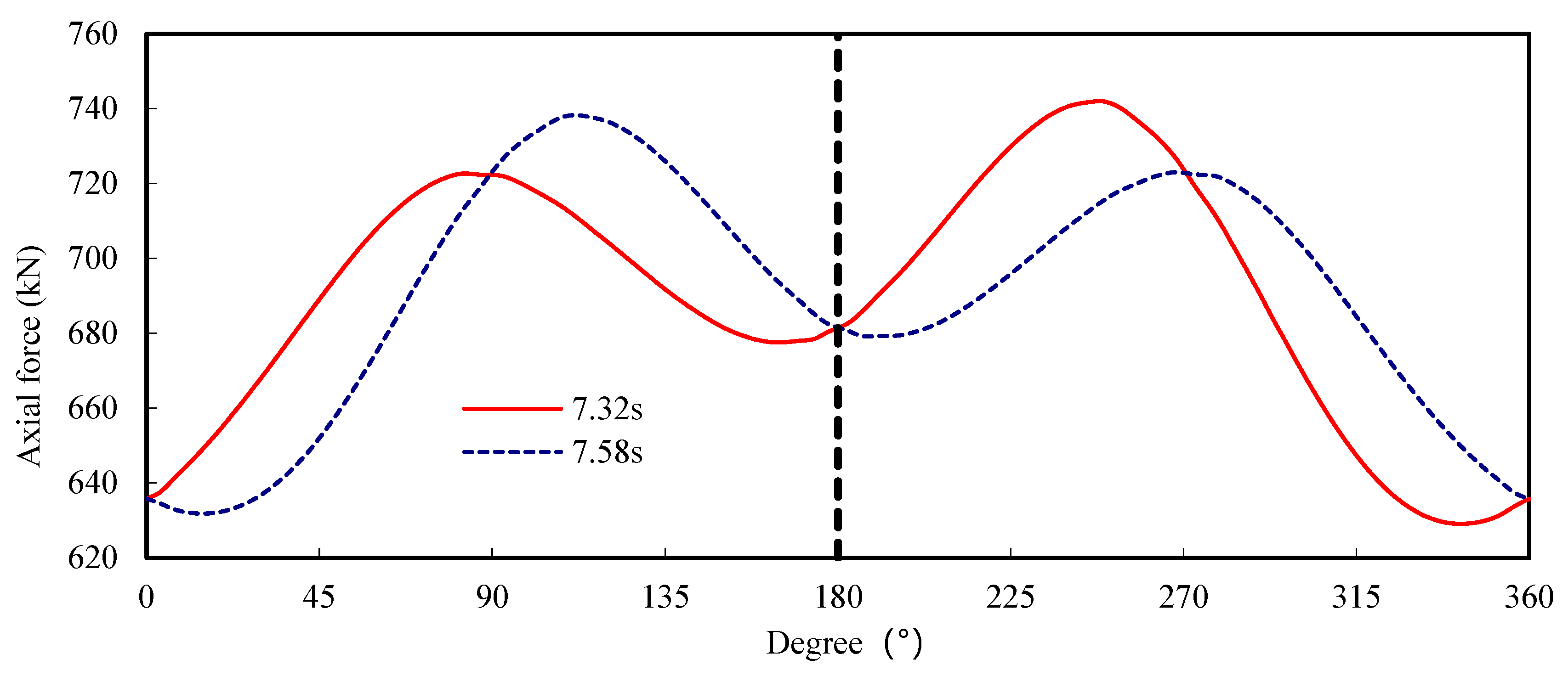
3.1. Internal Force Response Analysis
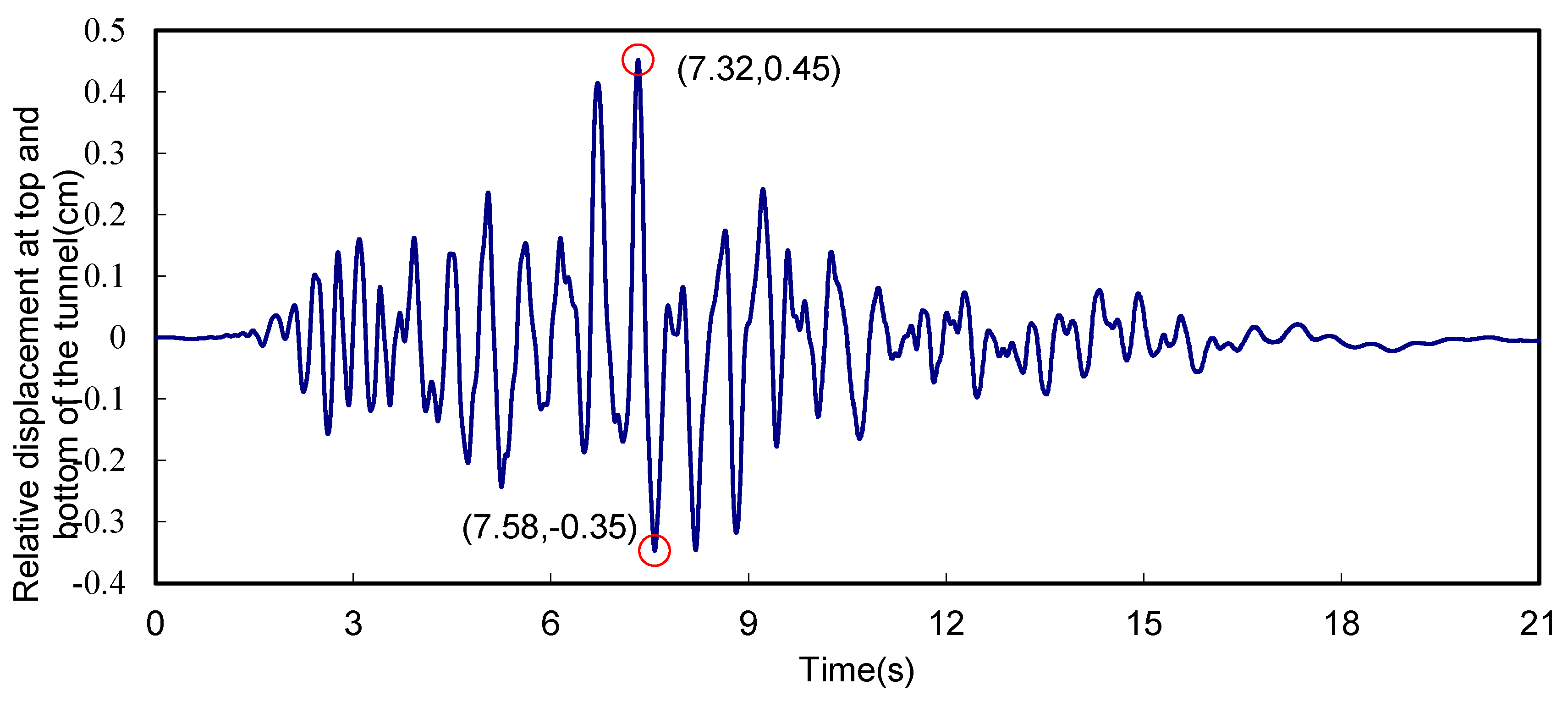
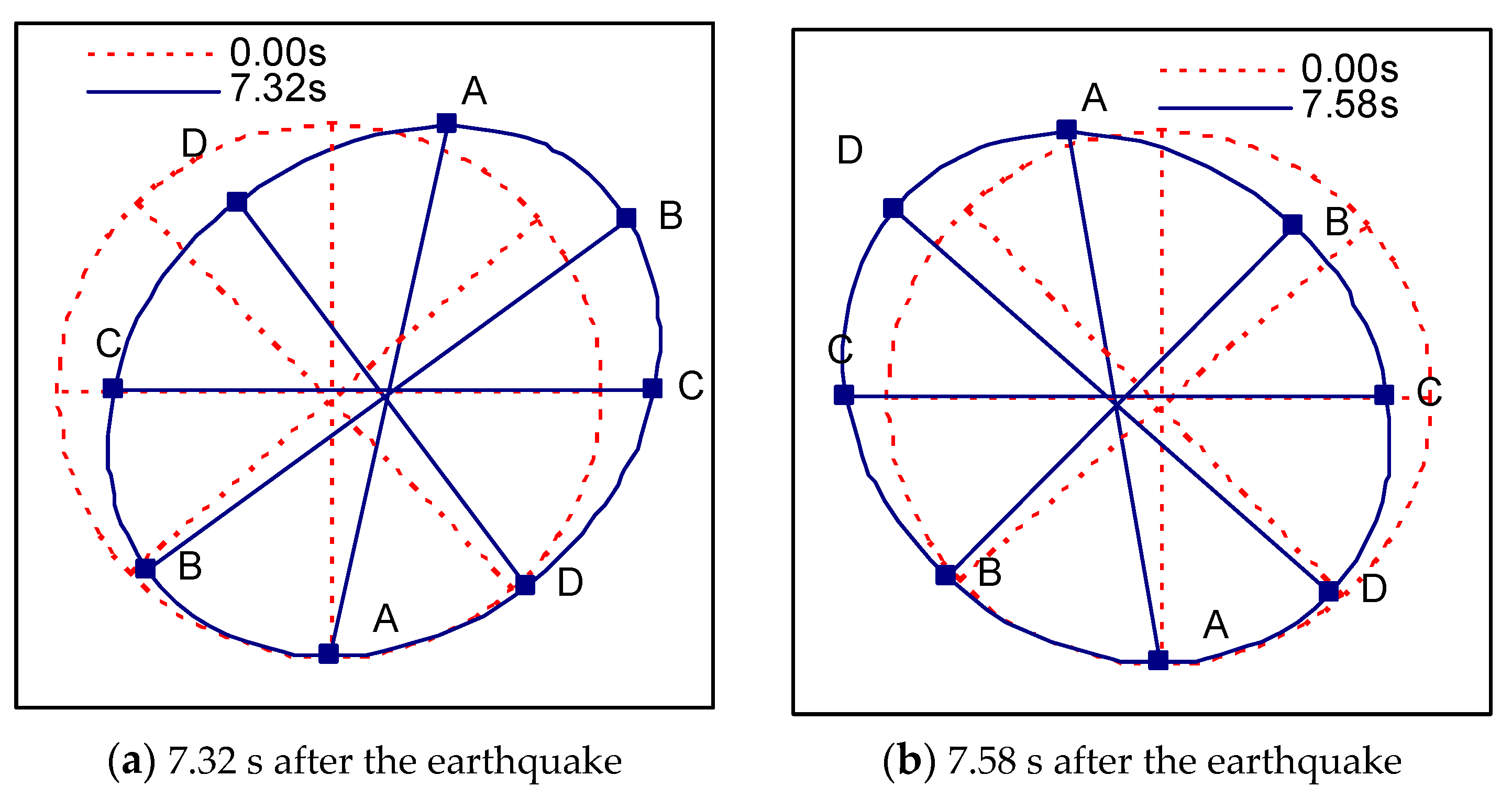
3.2. Deformation Response Analysis
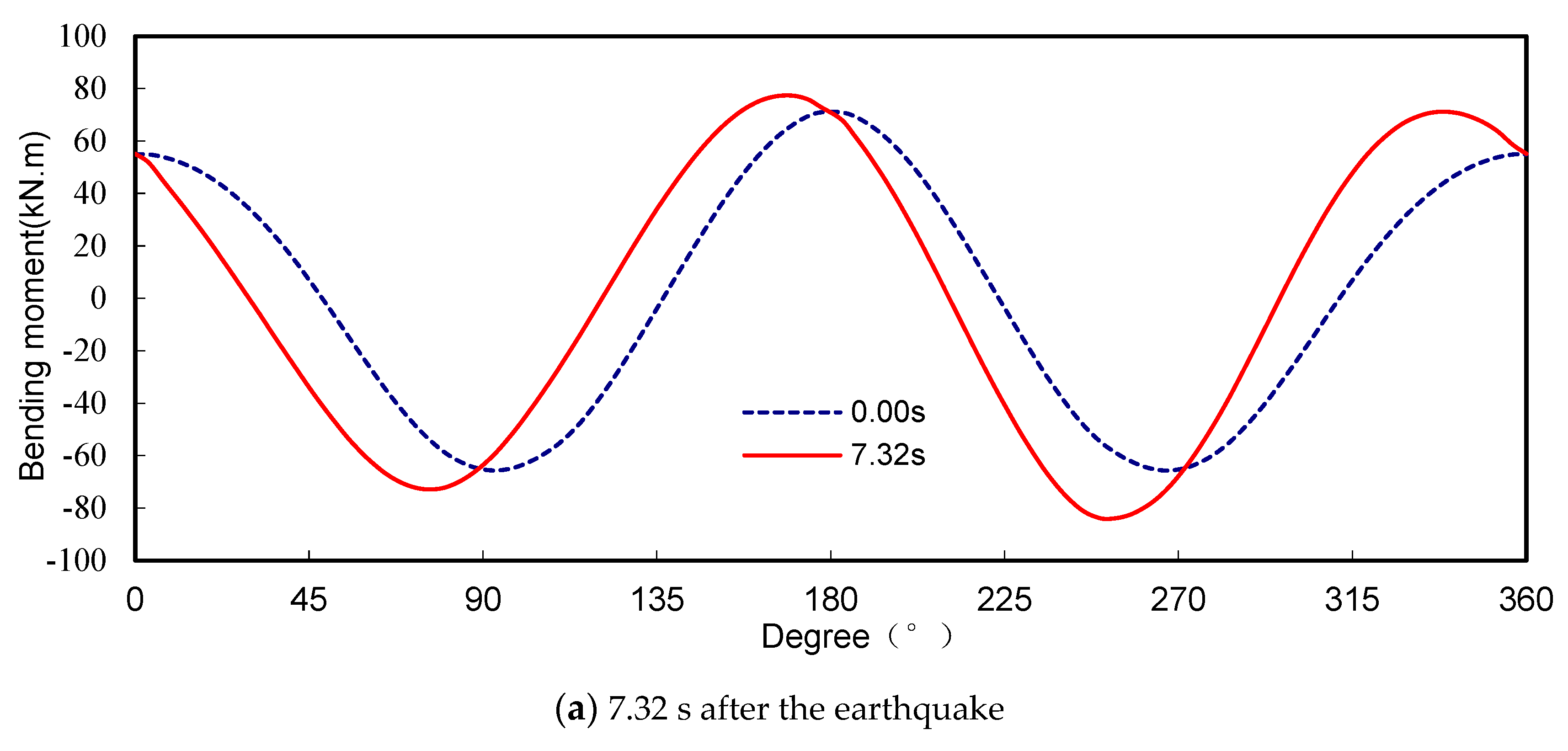
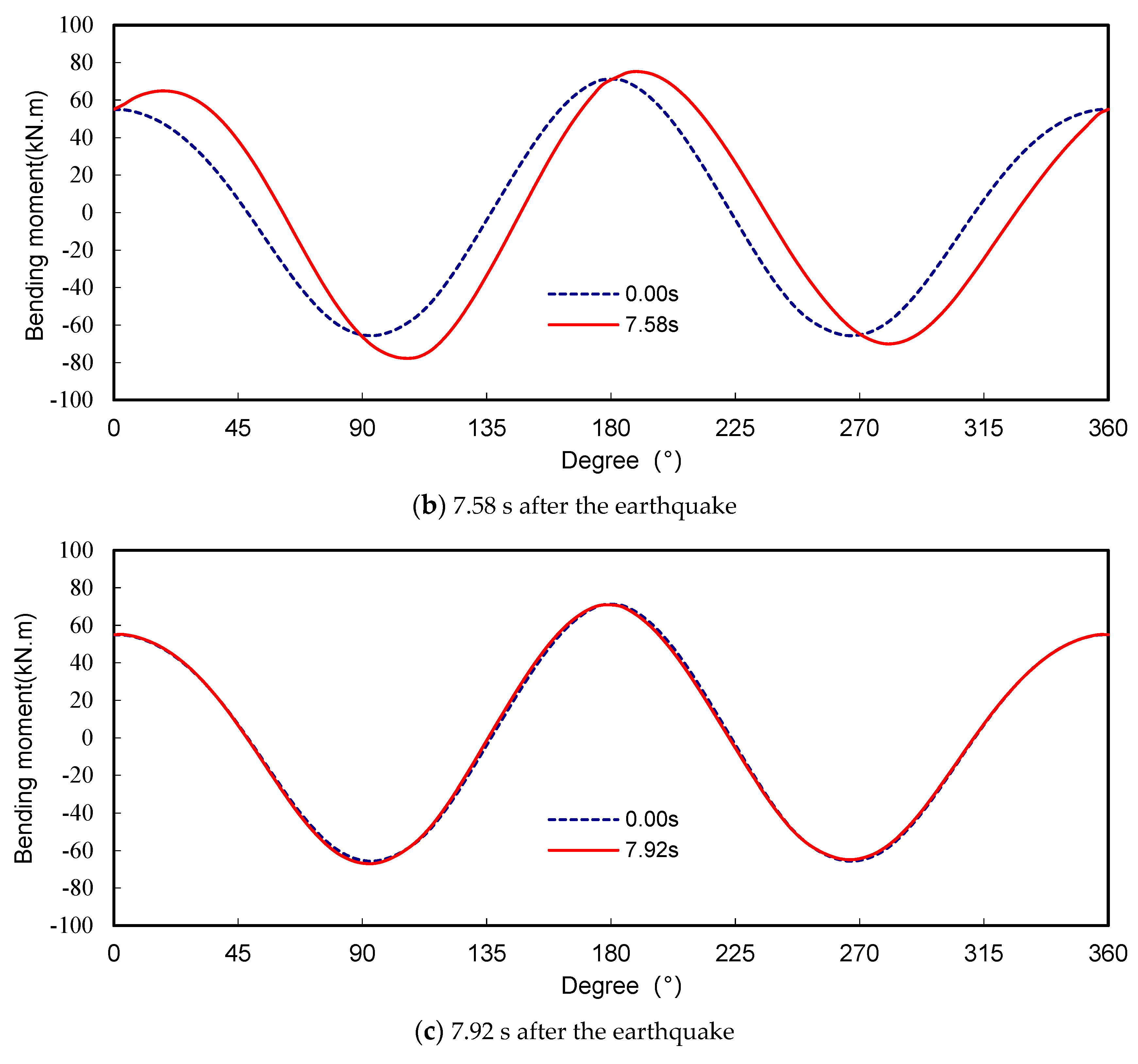
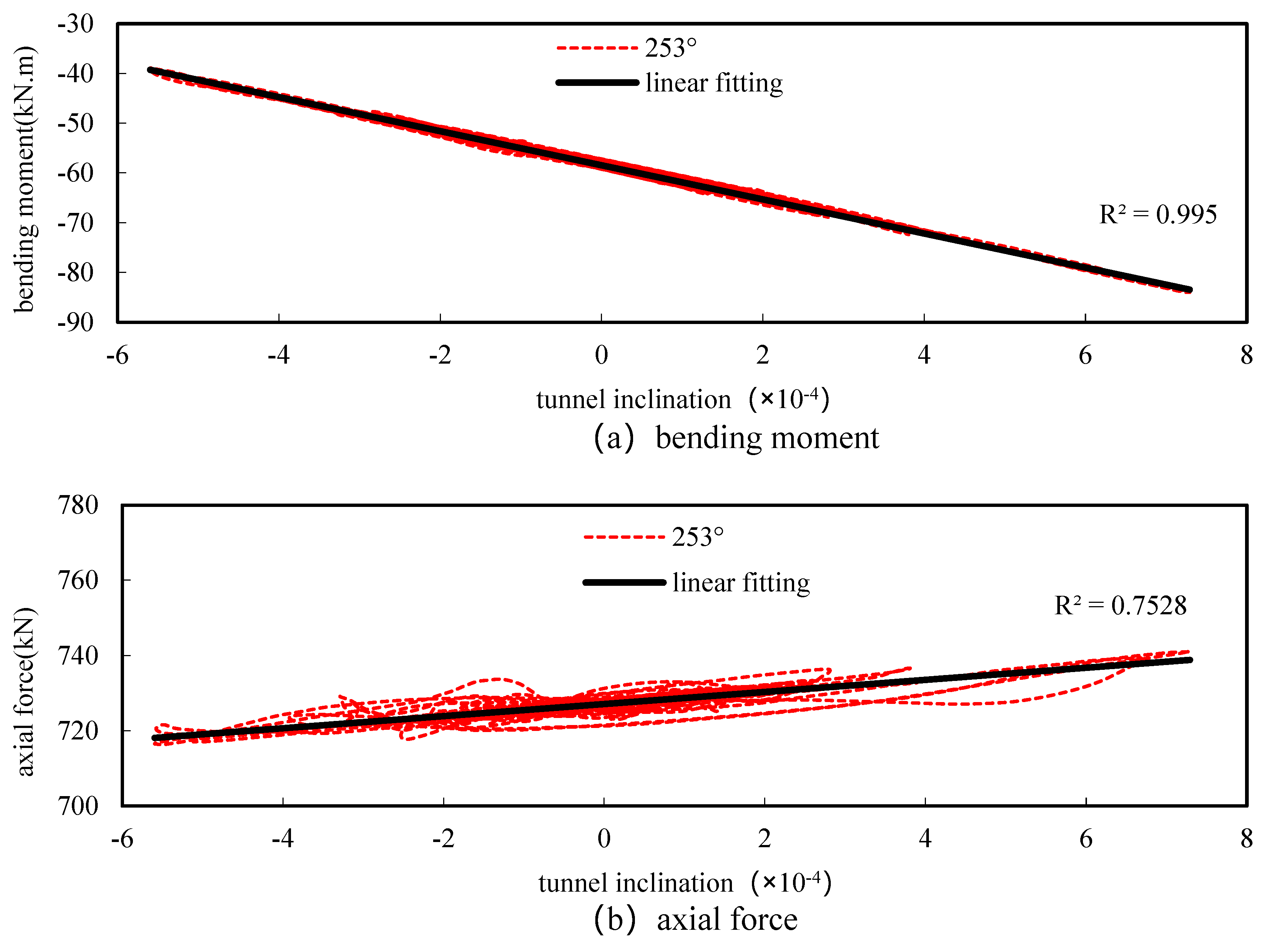
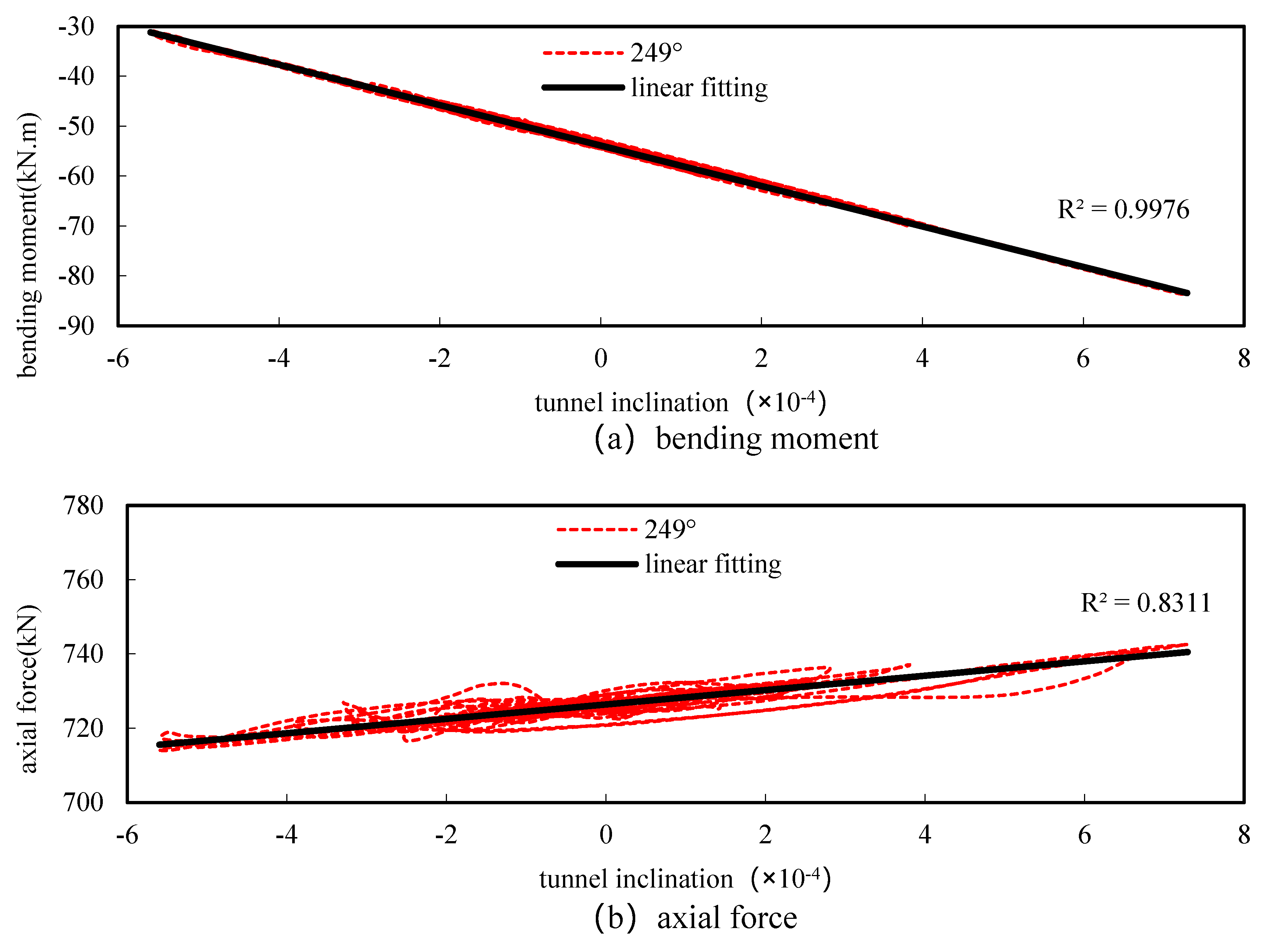
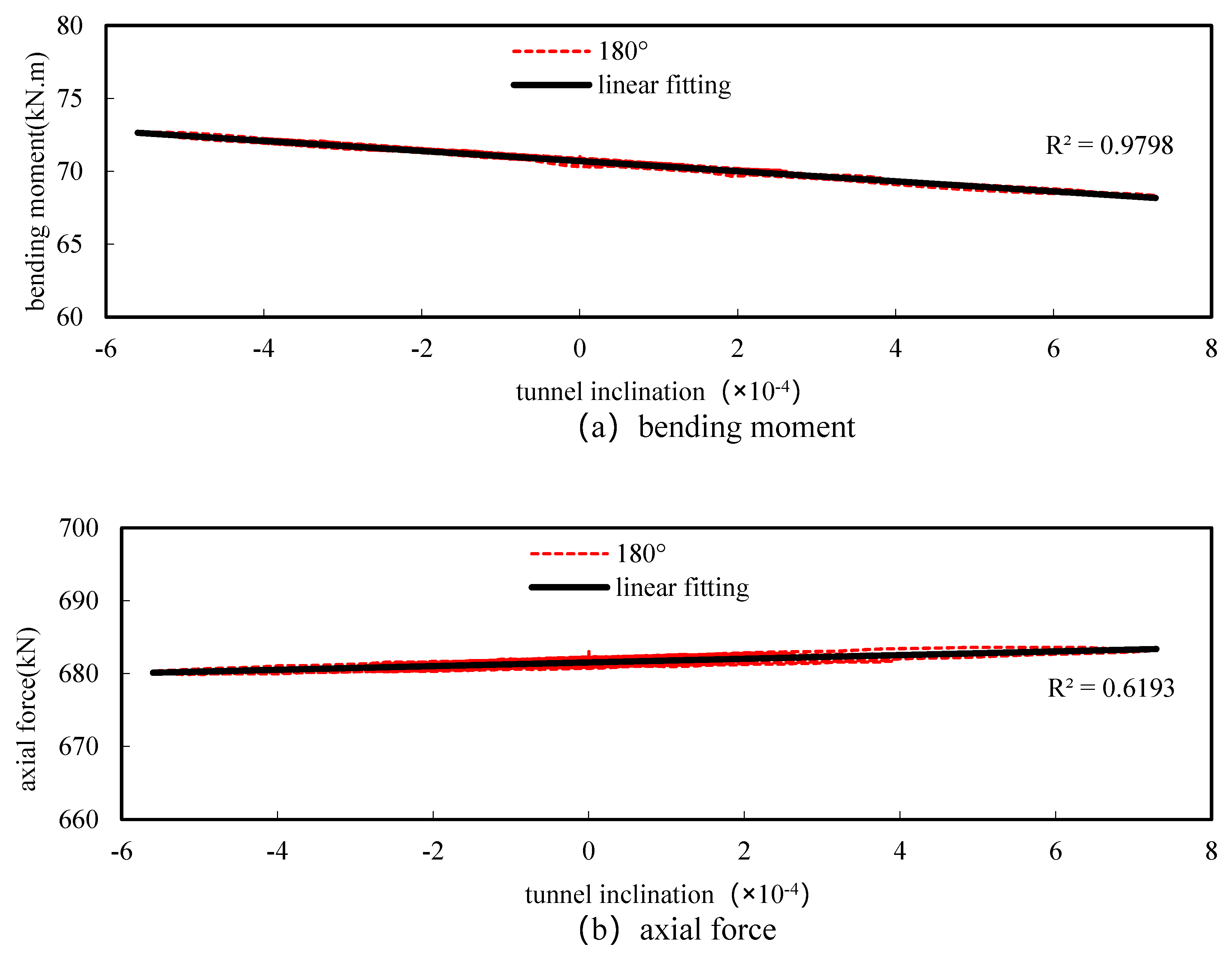
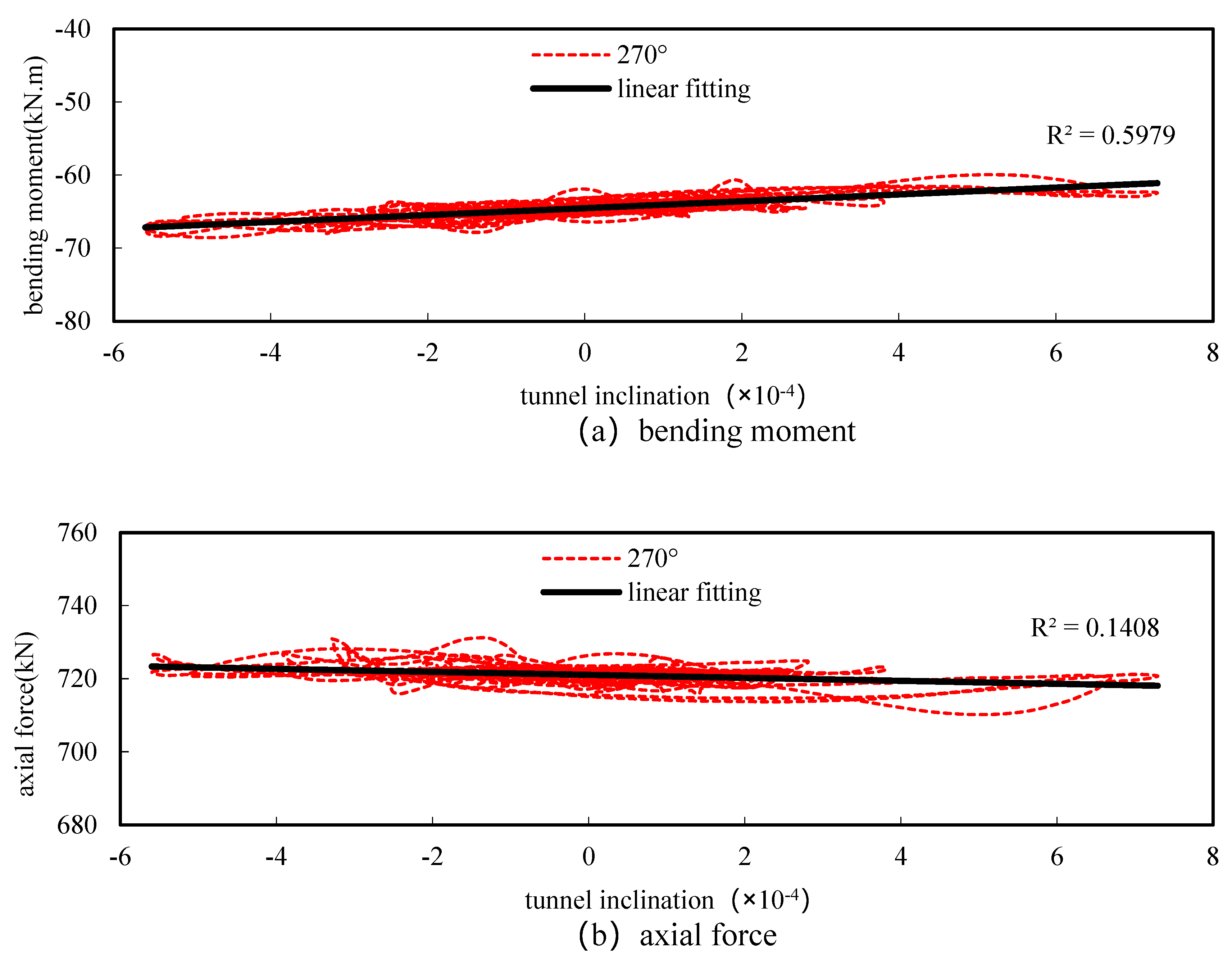
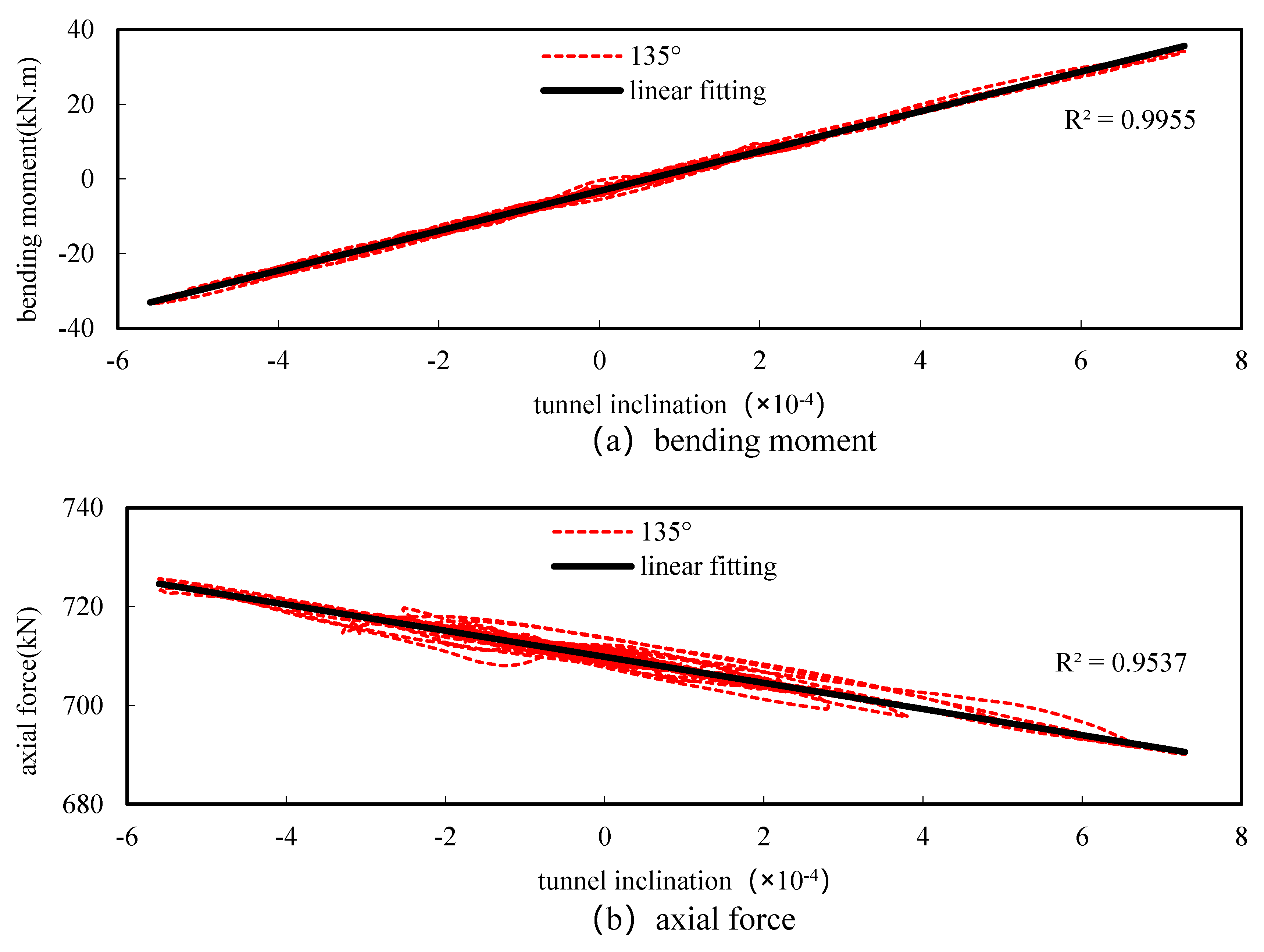
3.3. Analysis of the Relationship between the Internal Forces and the Tunnel Inclination
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Z.; Zhu, H.-H.; Yang, C.; Yang, L.-D. Anti-seismic Calculation for Shield Tunnels. J. Tongji Univ. 2004, 5, 607–611. [Google Scholar]
- Liu, J.; Li, B. Issues on the seismic analysis and design of subway structures. China Civ. Eng. J. 2006, 6, 106–110. [Google Scholar]
- Liu, J.; Li, B.; Liu, X. A static elasto-plastic analysis method in seismic design of underground structures. China Civ. Eng. J. 2007, 40, 68–76. [Google Scholar]
- He, Z.; Man, J.; Song, Y.; Xu, W.; Pang, Y. Longitudinal seismic displacement analysis of Quasi Seismic Isolation Bridge based on Energy-based Multimodal Pushover Method with and without collision. Soil Dyn. Earthq. Eng. 2024, 177, 108365. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, J. Research on the Seismic Isolation Effect of the Ring Spring–Friction Pendulum Bearing in the Dakai Underground Subway Station. Appl. Sci. 2023, 13, 7093. [Google Scholar] [CrossRef]
- Lin, M.-L.; Lin, C.-H.; Li, C.-H.; Liu, C.-Y.; Hung, C.-H. 3D modeling of the ground deformation along the fault rupture and its impact on engineering structures: Insights from the 1999 Chi-Chi earthquake, Shigang District, Taiwan. Eng. Geol. 2021, 281, 105993. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Shayanfar, M. Numerical Study on Seismic Behavior of Flexural Frames with Semi-Rigid Welded Steel Connections Considering Static and Reciprocating Loads: A Performance-Based Earthquake Approach. Appl. Sci. 2022, 12, 7617. [Google Scholar] [CrossRef]
- Cai, X.; Yang, C.; Yuan, Y. Hybrid Simulation of Seismic Responses of a Typical Station with a Reinforced Concrete Column. Appl. Sci. 2020, 10, 1331. [Google Scholar] [CrossRef]
- Amorosi, A.; Boldini, D.; Elia, G. Parametric study on seismic ground response by finite element modelling. Comput. Geotech. 2010, 37, 515–528. [Google Scholar] [CrossRef]
- Ming, S.; Tao, L.; Wang, Z. Shaking Table Tests on the Seismic Response of Symmetrically Integrated Underground Stations. Symmetry 2024, 16, 232. [Google Scholar] [CrossRef]
- Wen, H.; Zhou, Z.; Li, X.; Song, D.; He, Z.; Xin, C. Evaluation of the Damping Layer between the Tunnel Lining and Surrounding Rock via a Shaking Table Test. Sustainability 2023, 15, 13244. [Google Scholar] [CrossRef]
- Chen, C.; Zou, W.; Geng, P.; Gu, W.; Yuan, F.; He, C. Study on Seismic Damage Risk Assessment of Mountain Tunnel Based on the Extension Theory. Sustainability 2023, 15, 5294. [Google Scholar] [CrossRef]
- Shen, J.; Bao, X.; Chen, X.; Wu, X.; Cui, H. Prediction of Tunnel Earthquake Damage Based on a Combination Weighting Analysis Method. Symmetry 2022, 14, 1922. [Google Scholar] [CrossRef]
- Wang, T.-T.; Kwok, O.-L.A.; Jeng, F.-S. Seismic response of tunnels revealed in two decades following the 1999 Chi-Chi earthquake (Mw 7.6) in Taiwan: A review. Eng. Geol. 2021, 287, 106090. [Google Scholar] [CrossRef]
- Lu, C.; Hwang, J.-H. Damage analysis of the new Sanyi railway tunnel in the 1999 Chi-Chi earthquake: Necessity of second lining reinforcement. Tunn. Undergr. Space Technol. 2018, 73, 48–59. [Google Scholar] [CrossRef]
- Jiang, J.; Tao, R.; El Naggar, M.H.; Liu, H.; Du, X. Seismic performance and vulnerability analysis for bifurcated tunnels in soft soil. Comput. Geotech. 2024, 167, 106065. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, Y.; Yang, Y.; Li, C.; Yu, H. Experimental investigation of seismic performance of segmental tunnel with secondary lining under strong earthquake. Structures 2024, 60, 105833. [Google Scholar] [CrossRef]
- Sun, Q.; Hou, M.; Dias, D. Numerical study on the use of soft material walls to enhance seismic performance of an existing tunnel. Undergr. Space 2024, 15, 90–112. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, Y.; Liu, H.; Liu, H.; Miao, Y. Performance-based seismic assessment of shield tunnels by incorporating a nonlinear pseudostatic analysis approach for the soil-tunnel interaction. Tunn. Undergr. Space Technol. 2021, 114, 103981. [Google Scholar] [CrossRef]
- Liu, L.; Xu, C.; Du, X.; Iqbal, K. Longitudinal seismic response of shield tunnel: A multi-scale numerical analysis. Tunn. Undergr. Space Technol. 2023, 138, 105163. [Google Scholar] [CrossRef]
- Shekari, M.R.; Amiri, S.M.; Zareifard, M.R. A numerical approach for coupled analysis of the seismic response of a cable-moored submerged floating tunnel. Mar. Struct. 2022, 83, 103156. [Google Scholar] [CrossRef]
- Li, P.; Song, E.-X. Three-dimensional numerical analysis for the longitudinal seismic response of tunnels under an asynchronous wave input. Comput. Geotech. 2015, 63, 229–243. [Google Scholar] [CrossRef]
- Andreotti, G.; Lai, C.G. Use of fragility curves to assess the seismic vulnerability in the risk analysis of mountain tunnels. Tunn. Undergr. Space Technol. 2019, 91, 103008. [Google Scholar] [CrossRef]
- Fabozzi, S.; Bilotta, E.; Lanzano, G. A numerical study on seismic vulnerability of tunnel linings. In Proceedings of the 3rd Performance Based Design in Earthquake Geotechnical Engineering, Vancouver, BC, Canada, 16–19 July 2017; pp. 16–19. [Google Scholar]
- Moayedifar, A.; Nejati, H.R.; Goshtasbi, K.; Khosrotash, M. Seismic fragility and risk assessment of an unsupported tunnel using incremental dynamic analysis (IDA). Earthq. Struct. 2019, 16, 705. [Google Scholar]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Jan, T.S.; Liu, M.W.; Kao, Y.C. An upper-bound pushover analysis procedure for estimating the seismic demands of high-rise buildings. Eng. Struct. 2004, 26, 117–128. [Google Scholar] [CrossRef]
- Ye, L.; Pan, W. The Principle of Nonlinear Static Analysis (Push-over) and Numerical Examples. J. Build. Struct. 2000, 21, 37–43. [Google Scholar]
- Liu, J.; Li, B.; Liu, X. A pushover analysis method for seismic analysis of underground subway structures. J. Disaster Prev. Mitig. Eng. 2007, 27, 303–307. [Google Scholar]
- Fujiki, I.; Nakajima, M.; Otsuka, T.; Kosaka, A. Observation of earthquake response of subway tunnel. JSCE 1994, 11, 245–250. [Google Scholar]
- Koichiro, M.; Atsushi, K. A basic study on the earthquake resistant design method of shield tunnel in transverse direction. JSCE 2001, 9, 107–123. [Google Scholar]
- Lou, M.; Wu, J. Seimic response analysis of pile foundation structure system. China Civ. Eng. J. 1999, 5, 56–61. [Google Scholar]
- Chen, Y.; Lv, X.; Li, P. Shaking table testing for layered soil-foundation-structure interaction system. Earthq. Eng. Eng. Vib. 2001, 21, 104–112. [Google Scholar] [CrossRef]
- Demir, A.; Kayhan, A.H.; Palanci, M. Response- and probability-based evaluation of spectrally matched ground motion selection strategies for bi-directional dynamic analysis of low- to mid-rise RC buildings. Structures 2023, 58, 105533. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite Dynamic Model for Infinite Media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar] [CrossRef]
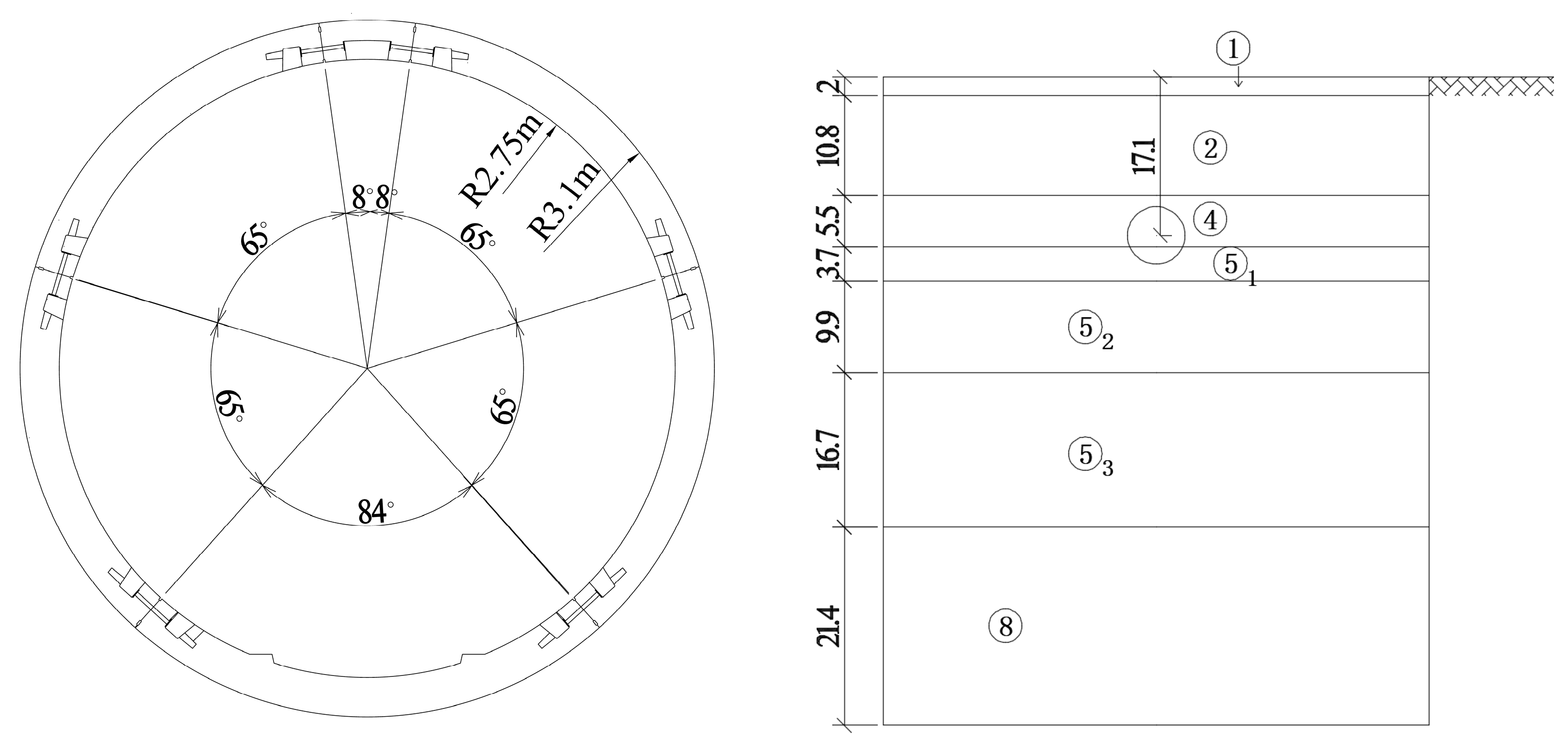










| Layer No. | Thickness (m) | Unit Weight γ (kN/m3) | c (kPa) | φ (°) | Coefficient of Static Lateral Pressure K0 | Shear Wave Velocity Vs (m/s) |
|---|---|---|---|---|---|---|
| ① | 2 | 18.4 | ||||
| ② | 10.8 | 18.5 | 4 | 29 | 0.4 | 220.4 |
| ④ | 5.5 | 17 | 13 | 10.5 | 0.55 | 161.2 |
| ⑤1 | 3.7 | 17.8 | 14 | 12 | 0.5 | 191.1 |
| ⑤2 | 9.9 | 18.2 | 4 | 28.5 | 0.4 | 194 |
| ⑤3 | 16.7 | 18.2 | 14 | 15.5 | 0.47 | 195.1 |
| ⑧ | 21.4 | 18.4 | 20 | 17.5 | 0.47 | 320 |
| Material | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| C50 Concrete | 3.45 × 104 | 0.18 |
| Material | Maximum Frequency of Seismic Waves (Hz) | Shear Wave Velocity (m/s) | Maximum Grid Size (m) |
|---|---|---|---|
| ② | 15 | 220.4 | 1.84 |
| ④ | 161.2 | 1.34 | |
| ⑤1 | 191.1 | 1.59 | |
| ⑤2 | 195.1 | 1.62 | |
| ⑤3 | 195.1 | 1.63 | |
| ⑧ | 320 | 2.67 |
| 169° (Maximum Positive Moment) | 253° (Maximum Negative Moment) | 249° (Maximum Axial Force) | 343° (Minimum Axial Force) | |
|---|---|---|---|---|
| Maximum bending moment (kNm) | 77.43 | −83.98 | −83.69 | 70.61 |
| Minimum Bending Moment (kNm) | 55.07 | −38.94 | −30.81 | 30.89 |
| Conventional bending moment (kNm) | 65.49 | −58.48 | −53.98 | 47.80 |
| Maximum rate of change of bending moment | 18.2% | 43.6% | 55.0% | 47.7% |
| Maximum axial force (kN) | 693.50 | 740.40 | 741.90 | 651.10 |
| Minimum axial force (kN) | 677.85 | 717.55 | 715.35 | 629.00 |
| Conventional axial force (kN) | 690.60 | 722.30 | 722.25 | 643.90 |
| Maximum rate of change of axial force | 1.8% | 2.5% | 2.7% | 2.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Liu, Y.; Chen, C. Correlation Analysis of Tunnel Deformation and Internal Force in the Earthquake Based on Tunnel Inclination. Buildings 2024, 14, 1395. https://doi.org/10.3390/buildings14051395
Yang Z, Liu Y, Chen C. Correlation Analysis of Tunnel Deformation and Internal Force in the Earthquake Based on Tunnel Inclination. Buildings. 2024; 14(5):1395. https://doi.org/10.3390/buildings14051395
Chicago/Turabian StyleYang, Zhiyong, Yin Liu, and Can Chen. 2024. "Correlation Analysis of Tunnel Deformation and Internal Force in the Earthquake Based on Tunnel Inclination" Buildings 14, no. 5: 1395. https://doi.org/10.3390/buildings14051395






