Delay Effects on Plant Stability and Symmetry-Breaking Pattern Formation in a Klausmeier-Gray-Scott Model of Semiarid Vegetation
Abstract
1. Introduction
2. Models and Results
2.1. Models without Delay
2.1.1. Non-Spatial Model
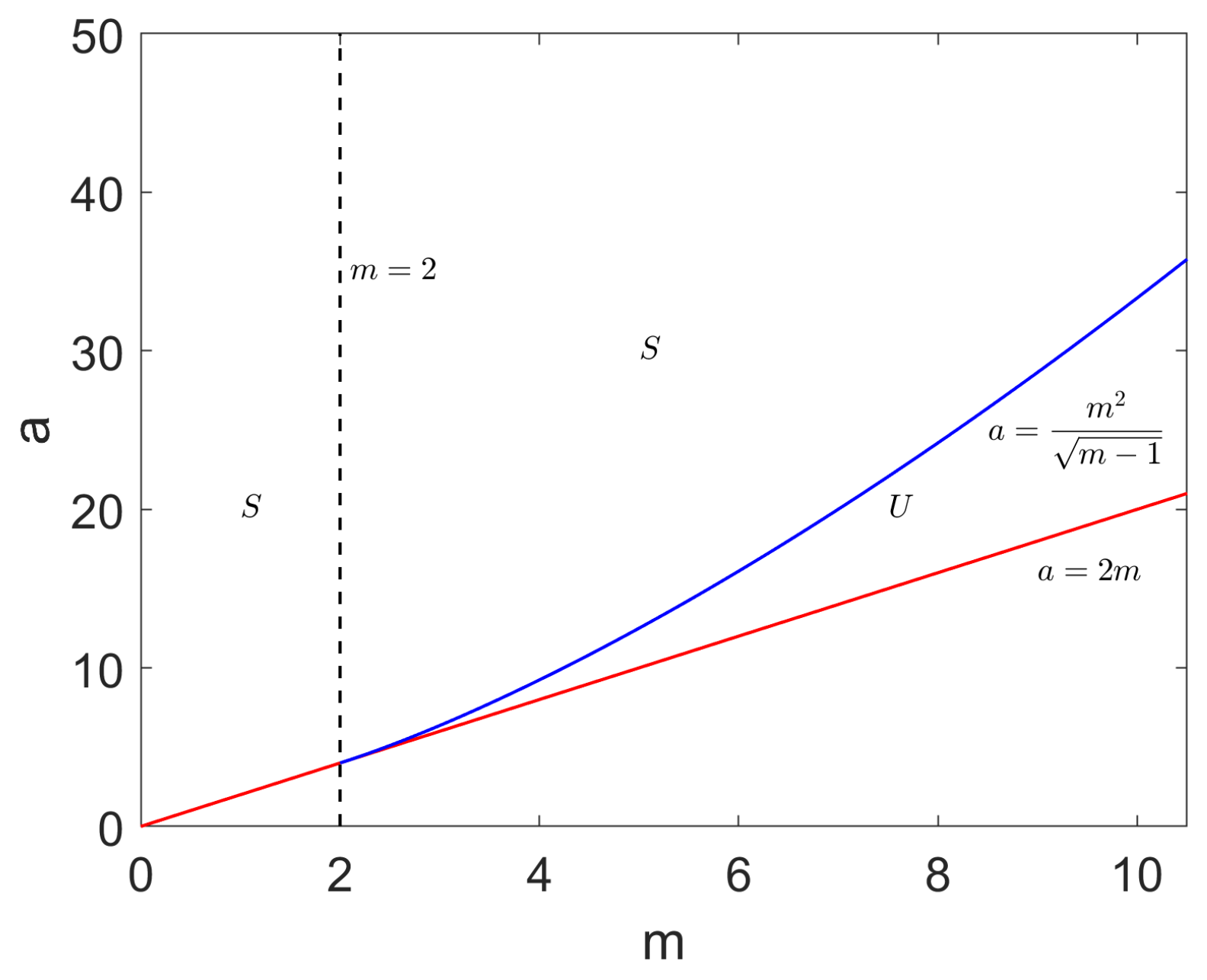
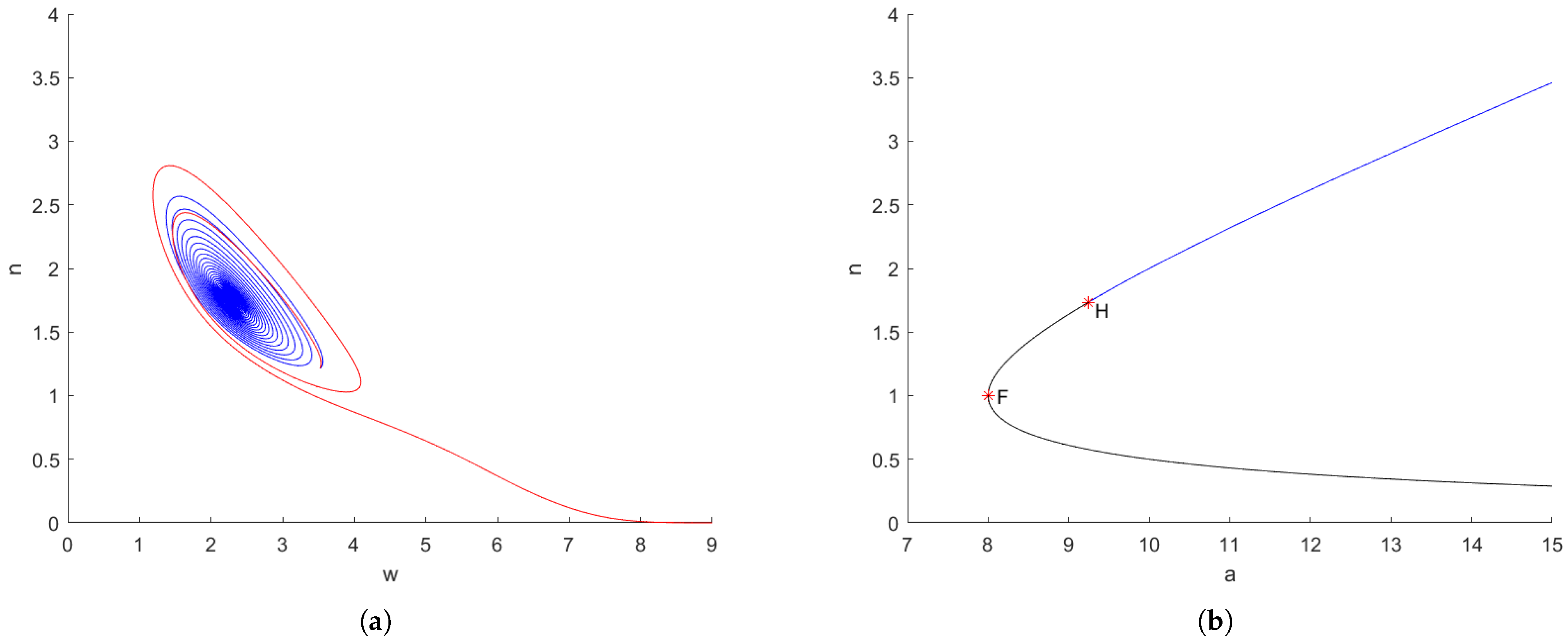
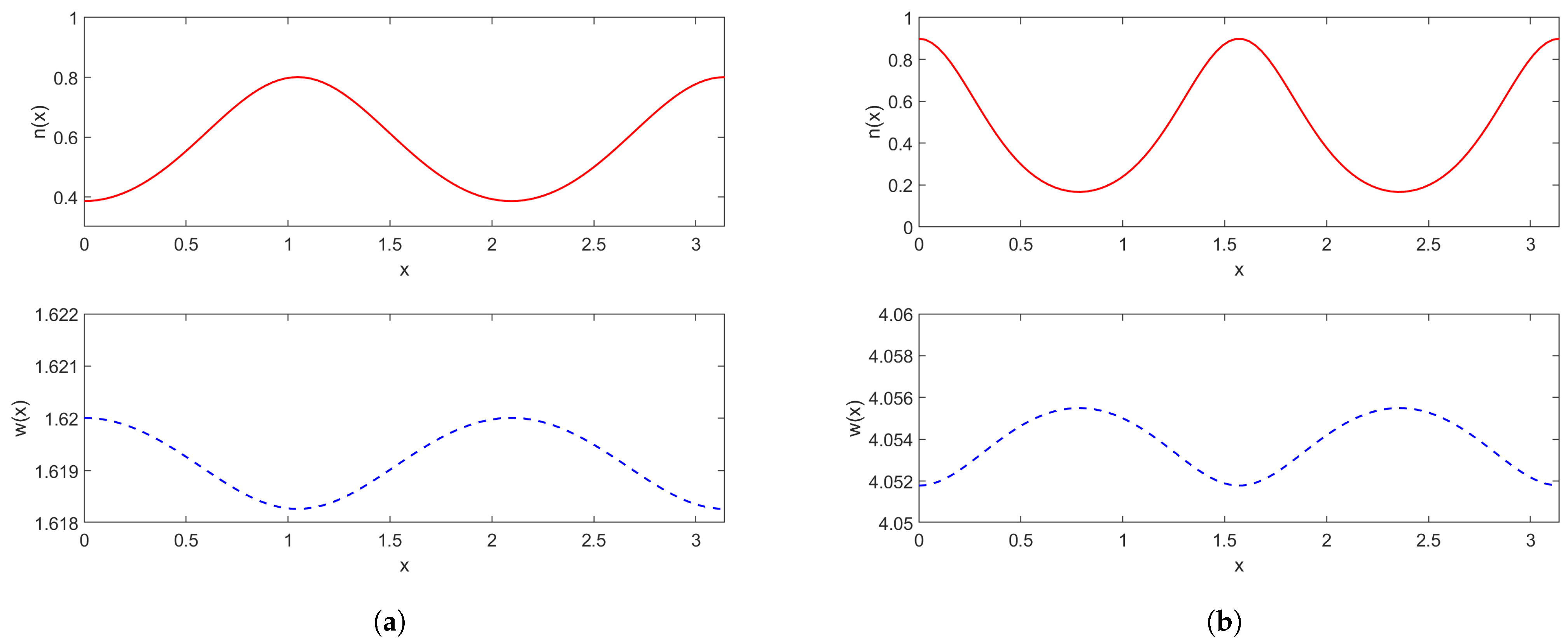
2.1.2. Spatial Model
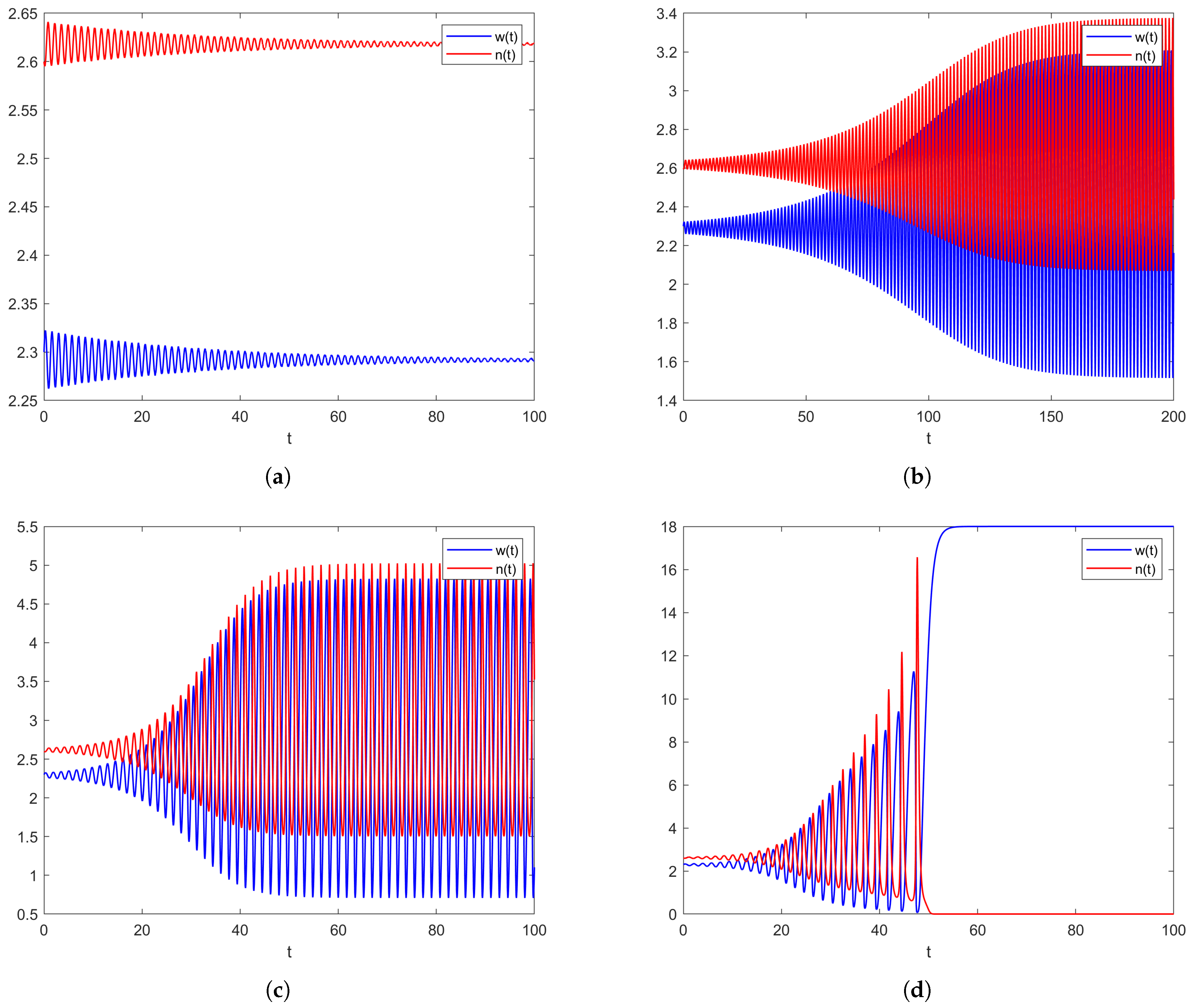
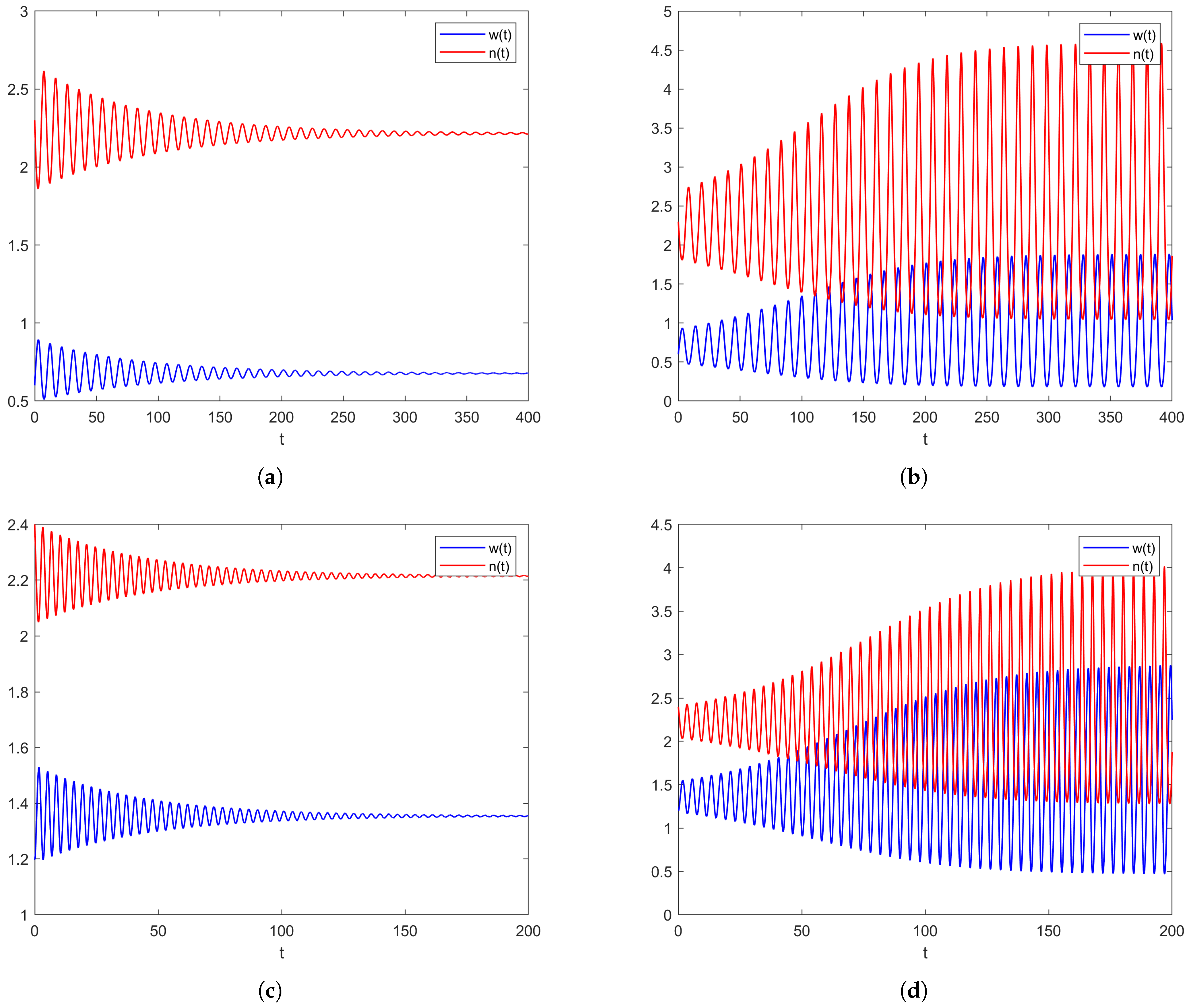
2.2. Models with Distributed Delay
2.2.1. Non-Spatial Model with a Weak Kernel
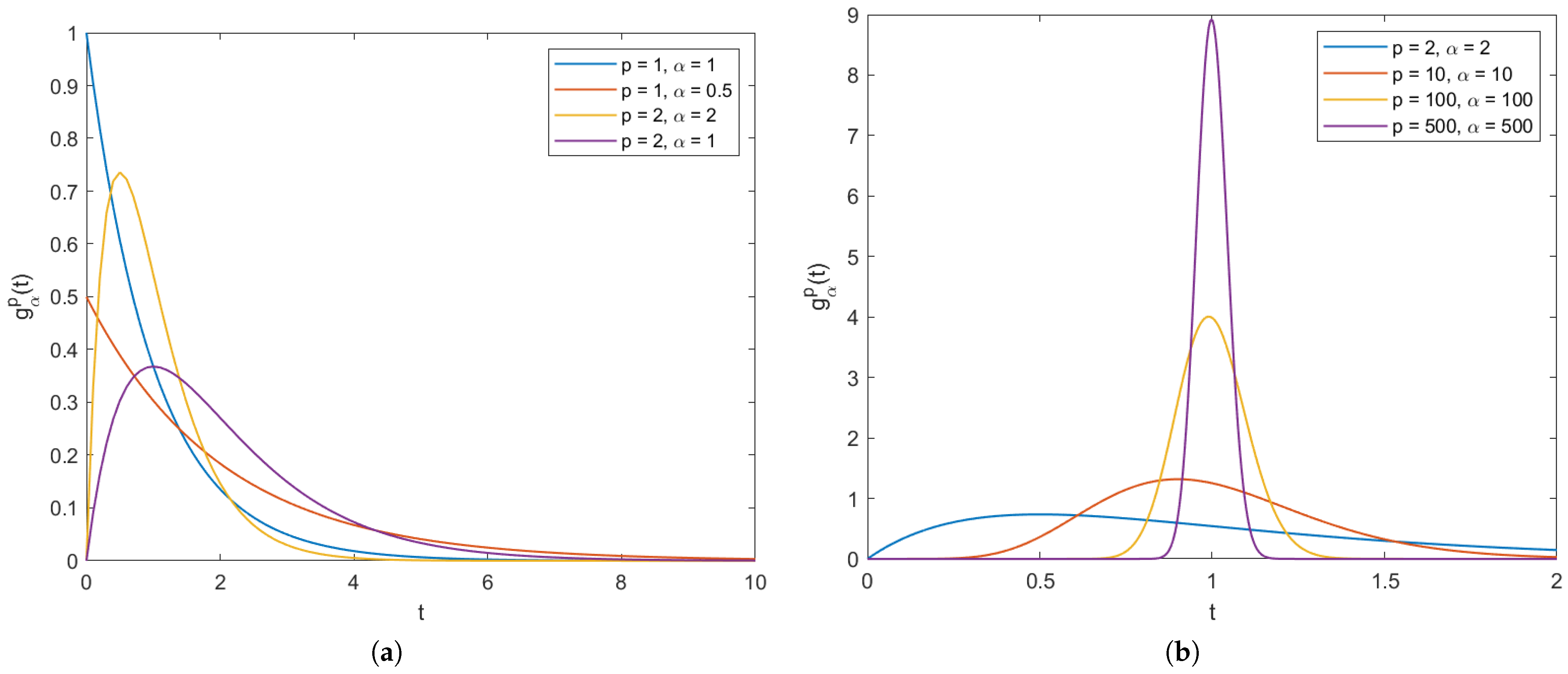
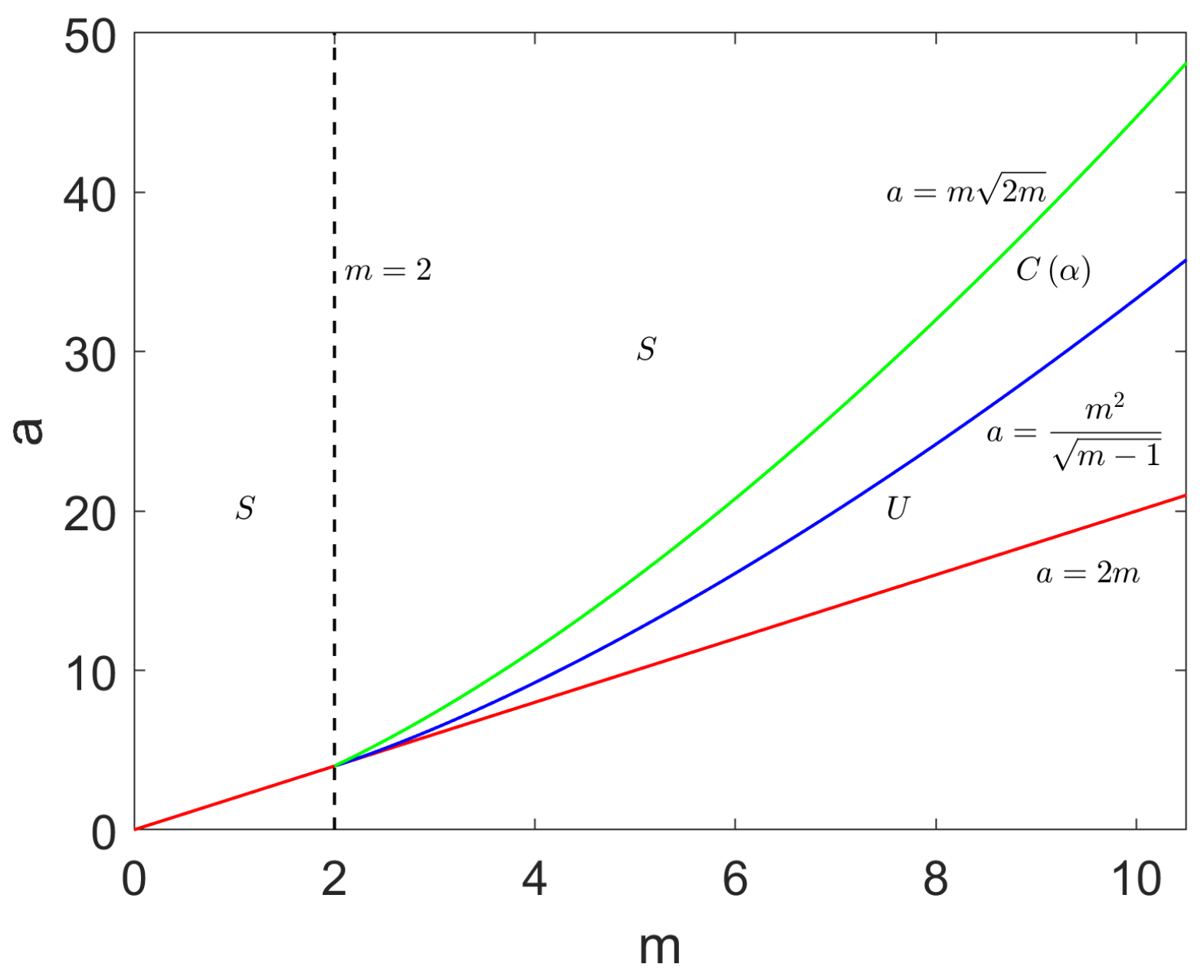
2.2.2. Spatial Model with a Weak Kernel
2.2.3. Models with Strong Kernels
3. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rietkerk, M.; van de Koppel, J. Alternate stable states and threshold effects in semi-arid grazing. Oikos 1997, 79, 69–76. [Google Scholar] [CrossRef]
- Aguiar, M.R.; Sala, O.E. Patch structure, dynamics and implications for the functioning of arid ecosystems. Trends Ecol. Evol. 1999, 14, 273–277. [Google Scholar] [CrossRef]
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar] [CrossRef]
- Deblauwe, V.; Barbier, N.; Couteron, P.; Lejeune, O.; Bogaert, J. The global biogeography of semi-arid periodic vegetation patterns. Glob. Ecol. Biogeogr. 2008, 17, 715–723. [Google Scholar] [CrossRef]
- Bastiaansen, R.; Jaïbia, O.; Deblauwe, V.; Eppinga, M.B.; Siteur, K.; Siero, E.; Mermoz, S.; Bouvet, A.; Doelman, A.; Rietkerk, M. Multistability of model and real dryland ecosystems through spatial self-organization. Proc. Natl. Acad. Sci. USA 2018, 115, 11256–11261. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; Alados, C.; Pueyo, Y.; Papanastasis, V.P.; ElAich, A.; de Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Guttal, V.; Jayaprakash, C. Spatial variance and spatial skewness: Leading indicators of regime shifts in spatial ecological systems. Theor. Ecol. 2009, 2, 3–12. [Google Scholar] [CrossRef]
- Dakos, V.; van Nes, E.H.; Donangelo, R.; Fort, H.; Scheffer, M. Spatial correlation as leading indicator of catastrophic shifts. Theor. Ecol. 2010, 3, 163–174. [Google Scholar] [CrossRef]
- Dakos, V.; Kéfi, S.; Rietkerk, M.; van Nes, E.H.; Scheffer, M. Slowing down in spatially patterned ecosystems at the brink of collapse. Am. Nat. 2011, 177, E153–E166. [Google Scholar] [CrossRef]
- Kéfi, S.; Guttal, V.; Brock, W.A.; Carpenter, S.R.; Ellison, A.M.; Livina, V.N.; Seekell, D.A.; Scheffer, M.; van Nes, E.H.; Dakos, V. Early warning signals of ecological transitions: Methods for spatial patterns. PLoS ONE 2014, 9, e92097. [Google Scholar] [CrossRef] [PubMed]
- Rietkerk, M.; Bastiaansen, R.; Banerjee, S.; van de Koppel, J.; Baudena, M.; Doelman, A. Evasion of tipping in complex systems through spatial pattern formation. Science 2021, 374, eabj0359. [Google Scholar] [CrossRef] [PubMed]
- Kéfi, S.; Génin, A.; García-Mayor, A.; Guirado, E.; Cabral, J.S.; Berdugo, M.; Guerber, J.; Solé, R.; Maestre, F.T. Self-organization as a mechanism of resilience in dryland ecosystems. Proc. Natl. Acad. Sci. USA 2024, 121, e2305153121. [Google Scholar] [CrossRef] [PubMed]
- Kéfi, S.; Rietkerk, M.; van Baalen, M.; Loreau, M. Local facilitation, bistability and transitions in arid ecosystems. Theor. Popul. Biol. 2007, 71, 367–379. [Google Scholar] [CrossRef]
- Mayor, Á.G.; Kéfi, S.; Bautista, S.; Rodríguez, F.; Cartení, F.; Rietkerk, M. Feedbacks between vegetation pattern and resource loss dramatically decrease ecosystem resilience and restoration potential in a simple dryland model. Landsc. Ecol. 2013, 28, 931–942. [Google Scholar] [CrossRef]
- Mayor, A.G.; Bautista, S.; Rodríguez, F.; Kéfi, S. Connectivity-mediated ecohydrological feedbacks and regime shifts in drylands. Ecosystems 2019, 22, 1497–1511. [Google Scholar] [CrossRef]
- Couteron, P.; Lejeune, O. Periodic spotted patterns in semi-arid vegetation explained by a propagation- inhibition model. J. Ecol. 2001, 89, 616–628. [Google Scholar] [CrossRef]
- von Hardenberg, J.; Meron, E.; Shachak, M.; Zarmi, Y. Diversity of vegetation patterns and desertification. Phys. Rev. Lett. 2001, 87, 198101. [Google Scholar] [CrossRef]
- Rietkerk, M.; Boerlijst, M.C.; van Langevelde, F.; HilleRisLambers, R.; van de Koppel, J.; Kumar, L.; Prins, H.H.T.; de Roos, A.M. Self-organization of vegetation in arid ecosystems. Am. Nat. 2002, 160, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Kéfi, S.; Eppinga, M.B.; de Ruiter, P.C.; Rietkerk, M. Bistability and regular spatial patterns in arid ecosystems. Theor. Ecol. 2010, 3, 257–269. [Google Scholar] [CrossRef]
- von Hardenberg, J.; Kletter, A.Y.; Yizhaq, H.; Nathan, J.; Meron, E. Periodic versus scale-free patterns in dryland vegetation. Proc. R. Soc. B Biol. Sci. 2010, 277, 1771–1776. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Prigogine, I.; Lefever, R. Symmetry breaking instabilities in dissipative systems. II. J. Chem. Phys. 1968, 48, 1695–1700. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology. I. An Introduction, 3rd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Murray, J.D. Mathematical Biology. II. Spatial Models and Biomedical Applications, 3rd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Rietkerk, M.; van de Koppel, J. Regular pattern formation in real ecosystems. Trends Ecol. Evol. 2008, 23, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Rev. Geophys. 2009, 47, RG1005. [Google Scholar] [CrossRef]
- Sherratt, J.A. An analysis of vegetation stripe formation in semi-arid landscapes. J. Math. Biol. 2005, 51, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Sherratt, J.A. Pattern solutions of the Klausmeier model for banded vegetation in semi-arid environments I. Nonlinearity 2010, 23, 2657–2675. [Google Scholar] [CrossRef]
- Sherratt, J.A. Pattern solutions of the Klausmeier model for banded vegetation in semi-arid environments II: Patterns with the largest possible propagation speeds. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2011, 467, 3272–3294. [Google Scholar] [CrossRef]
- van der Stelt, S.; Doelman, A.; Hek, G.; Rademacher, J.D.M. Rise and fall of periodic patterns for a generalized Klausmeier–Gray–Scott Model. J. Nonlinear Sci. 2013, 23, 39–95. [Google Scholar] [CrossRef]
- Sherratt, J.A. Pattern solutions of the Klausmeiermodel for banded vegetation in semi-arid environments III: The transition between homoclinic solutions. Physica D 2013, 242, 30–41. [Google Scholar] [CrossRef]
- Sherratt, J.A. Pattern solutions of the Klausmeier model for banded vegetation in semiarid environments IV: Slowly moving patterns and their stability. SIAM J. Appl. Math. 2013, 73, 330–350. [Google Scholar] [CrossRef]
- Sherratt, J.A. Pattern solutions of the Klausmeier model for banded vegetation in semiarid environments V: The transition from patterns to desert. SIAM J. Appl. Math. 2013, 73, 1347–1367. [Google Scholar] [CrossRef]
- Siteur, K.; Siero, E.; Eppinga, M.B.; Rademacher, J.D.M.; Doelman, A.; Rietkerk, M. Beyond Turing: The response of patterned ecosystems to environmental change. Ecol. Complex. 2014, 20, 81–96. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J.; Zhang, G. Bifurcation and pattern formation in diffusive Klausmeier-Gray-Scott model of water-plant interaction. J. Math. Anal. Appl. 2021, 497, 124860. [Google Scholar] [CrossRef]
- Sun, G.-Q.; Zhang, H.-T.; Song, Y.-L.; Li, L.; Jin, Z. Dynamic analysis of a plant-water model with spatial diffusion. J. Differ. Equ. 2022, 329, 395–430. [Google Scholar] [CrossRef]
- Gray, P.; Scott, S.K. Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Isolas and other forms of multistability. Chem. Eng. Sci. 1983, 38, 29–43. [Google Scholar] [CrossRef]
- Gray, P.; Scott, S.K. Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Oscillations and instabilities in the system A +2B→3B; B→C. Chem. Eng. Sci. 1984, 39, 1087–1097. [Google Scholar] [CrossRef]
- Gray, P.; Scott, S.K. Sustained oscillations and other exotic patterns of behavior in isothermal reactions. J. Phys. Chem. 1985, 89, 22–32. [Google Scholar] [CrossRef]
- Li, J.; Sun, G.-Q.; Guo, Z.-G. Bifurcation analysis of an extended Klausmeier–Gray–Scott model with infiltration delay. Stud. Appl. Math. 2022, 148, 1519–1542. [Google Scholar] [CrossRef]
- Cushing, J.M. Integrodifferential Equations and Delay Models in Population Dynamics; Springer: Heidelberg, Germany, 1977. [Google Scholar]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- Verwijmeren, M.; Smit, C.; Bautista, S.; Wassen, M.J.; Rietkerk, M. Combined grazing and drought stress alter the outcome of nurse: Beneficiary interactions in a semi-arid ecosystem. Ecosystems 2019, 22, 1295–1307. [Google Scholar] [CrossRef]
- Gong, X.; Wang, Y.; Zhan, T.; Wang, C.; Li, C.; Liu, Y. Advances in meta-analysis of the effects of grazing on grassland ecosystems in China. Agriculture 2023, 13, 1084. [Google Scholar] [CrossRef]
- Siero, E. Nonlocal grazing in patterned ecosystems. J. Theor. Biol. 2018, 436, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Kéfi, S.; Rietkerk, M.; Katul, G.G. Vegetation pattern shift as a result of rising atmospheric CO2 in arid ecosystems. Theor. Popul. Biol. 2008, 74, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wu, Y.P.; Feng, G.L.; Qian, Z.H.; Sun, G.Q. Effects of global warming on pattern dynamics of vegetation: Wuwei in China as a case. Appl. Math. Comput. 2021, 390, 125666. [Google Scholar] [CrossRef]
- Sun, G.-Q.; Li, L.; Li, J.; Liu, C.; Wu, Y.-P.; Gao, S.; Wang, W.; Feng, G.-L. Impacts of climate change on vegetation pattern: Mathematical modeling and data analysis. Phys. Life Rev. 2022, 43, 239–270. [Google Scholar] [CrossRef] [PubMed]
- HilleRisLambers, R.; Rietkerk, M.; van den Bosch, F.; Prins, H.H.T.; de Kroon, H. Vegetation pattern formation in semi-arid grazing systems. Ecology 2001, 82, 50–61. [Google Scholar] [CrossRef]
- Gilad, E.; Shachak, M.; Meron, E. Dynamics and spatial organization of plant communities in water limited systems. Theor. Popul. Biol. 2007, 72, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Consolo, G.; Currò, C.; Valenti, G. Pattern formation and modulation in a hyperbolic vegetation model for semiarid environments. Appl. Math. Model. 2017, 43, 372–392. [Google Scholar] [CrossRef]
- Consolo, G.; Currò, C.; Valenti, G. Supercritical and subcritical Turing pattern formation in a hyperbolic vegetation model for flat arid environments. Physica D 2023, 398, 141–163. [Google Scholar] [CrossRef]
- Grifó, G.; Consolo, G.; Currò, C.; Valenti, G. Rhombic and hexagonal pattern formation in 2D hyperbolic reaction–transport systems in the context of dryland ecology. Physica D 2023, 449, 133745. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medjahdi, I.; Lachachi, F.Z.; Castro, M.Á.; Rodríguez, F. Delay Effects on Plant Stability and Symmetry-Breaking Pattern Formation in a Klausmeier-Gray-Scott Model of Semiarid Vegetation. Symmetry 2024, 16, 609. https://doi.org/10.3390/sym16050609
Medjahdi I, Lachachi FZ, Castro MÁ, Rodríguez F. Delay Effects on Plant Stability and Symmetry-Breaking Pattern Formation in a Klausmeier-Gray-Scott Model of Semiarid Vegetation. Symmetry. 2024; 16(5):609. https://doi.org/10.3390/sym16050609
Chicago/Turabian StyleMedjahdi, Ikram, Fatima Zohra Lachachi, María Ángeles Castro, and Francisco Rodríguez. 2024. "Delay Effects on Plant Stability and Symmetry-Breaking Pattern Formation in a Klausmeier-Gray-Scott Model of Semiarid Vegetation" Symmetry 16, no. 5: 609. https://doi.org/10.3390/sym16050609
APA StyleMedjahdi, I., Lachachi, F. Z., Castro, M. Á., & Rodríguez, F. (2024). Delay Effects on Plant Stability and Symmetry-Breaking Pattern Formation in a Klausmeier-Gray-Scott Model of Semiarid Vegetation. Symmetry, 16(5), 609. https://doi.org/10.3390/sym16050609






