Investigation of Macroscopic Mechanical Behavior of Magnetorheological Elastomers under Shear Deformation Using Microscale Representative Volume Element Approach
Abstract
:1. Introduction
2. Materials and Methods
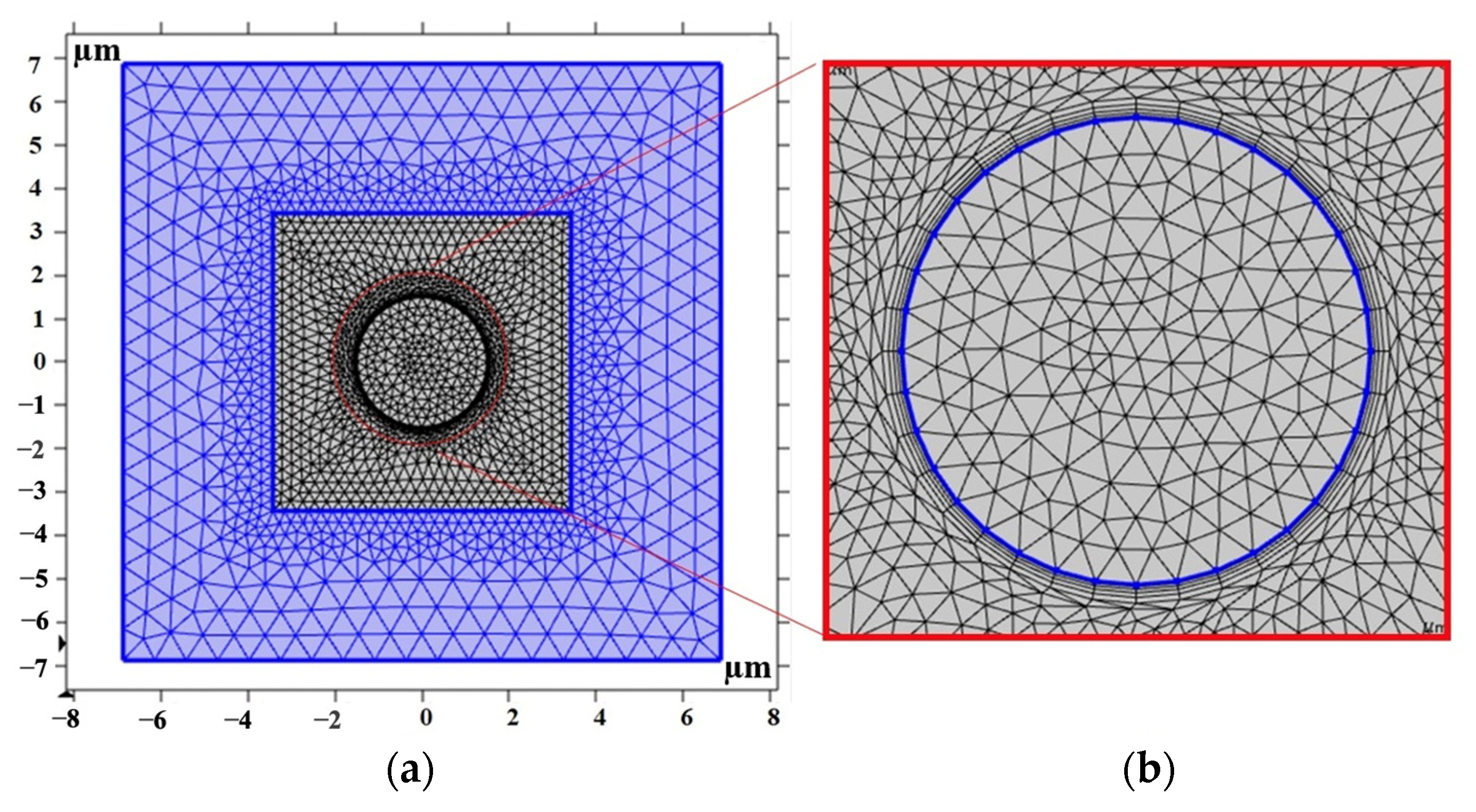
2.1. Representative Volume Element (RVE)
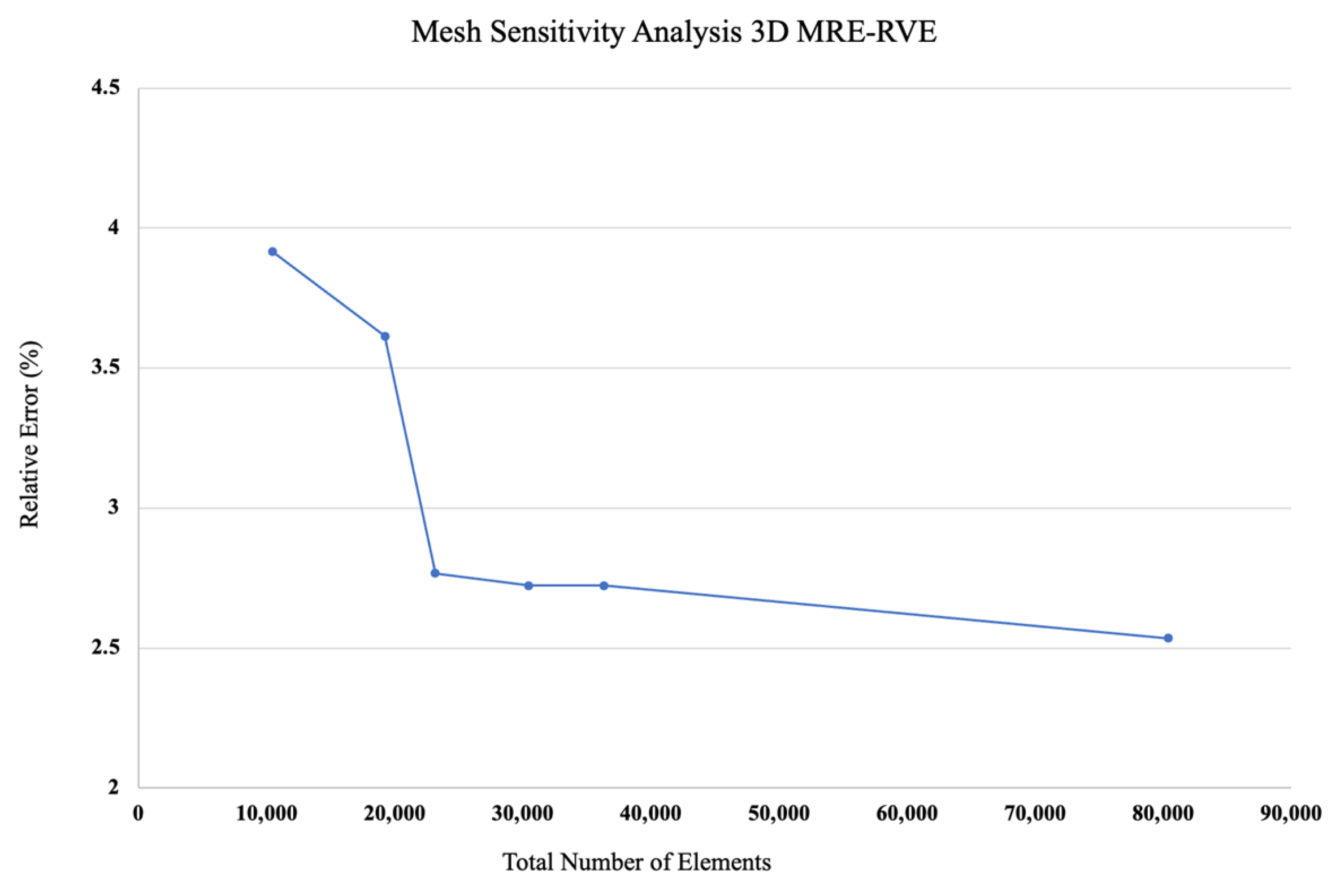
2.2. The RVE Size for Models Containing Hard Particles
2.3. Periodic Boundary Conditions
2.3.1. Periodic Boundary Conditions in 2D
2.3.2. Periodic Boundary Conditions in 3D
2.4. Maxwell’s Stress Tensor
2.5. Governing Equations
2.6. Characterization of Elastomeric Matrix and Magnetic Inclusion in MREs
2.6.1. Characterization of the MRE’s Elastomeric Matrix Using the Uniaxial Tensile Test
2.6.2. Magnetic Properties of Carbonyl Iron Particles
3. Results
3.1. Modeling the 2D Isotropic MRE-RVE in COMSOL
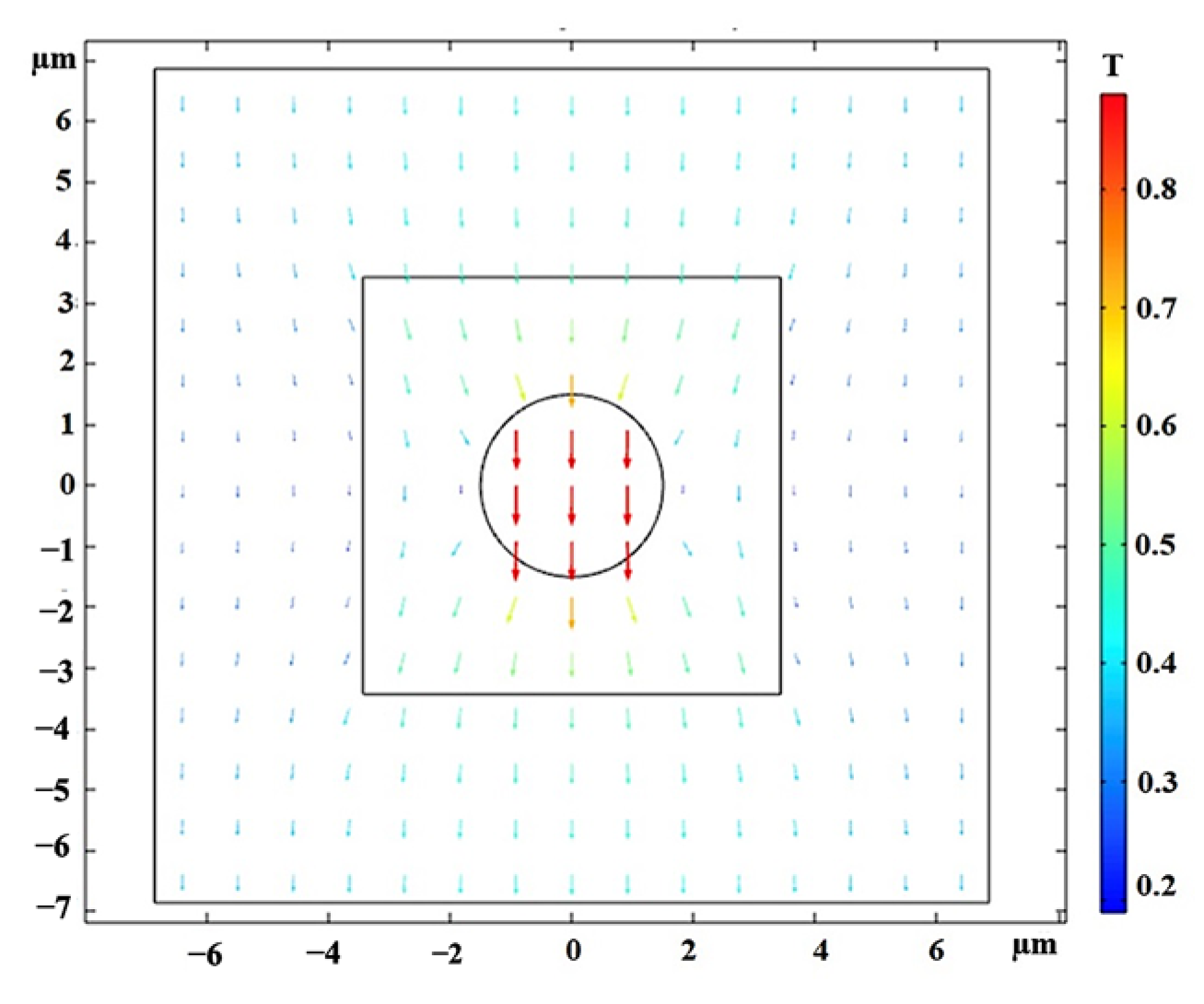
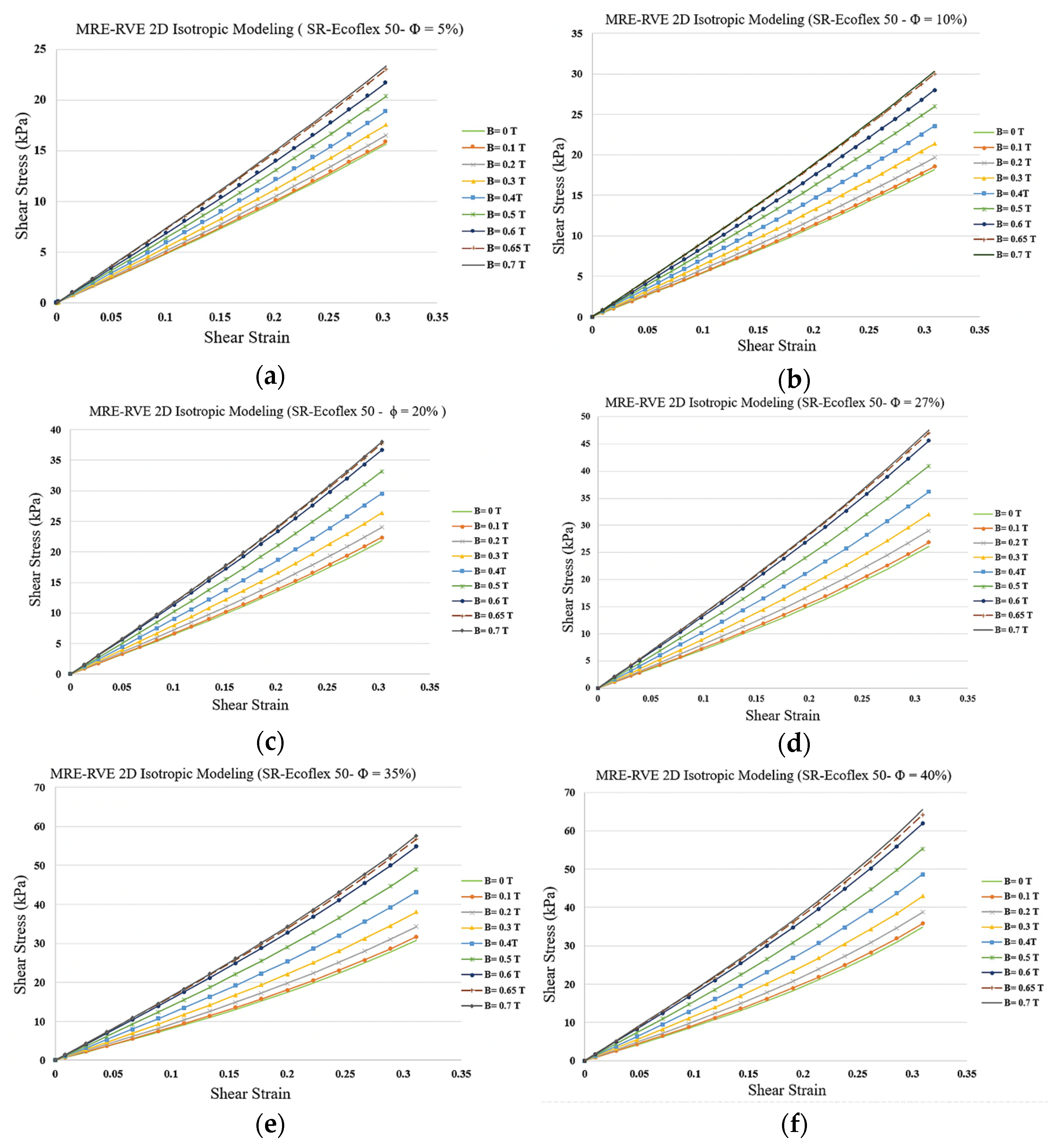
Shear Deformation of Isotropic MRE-RVE
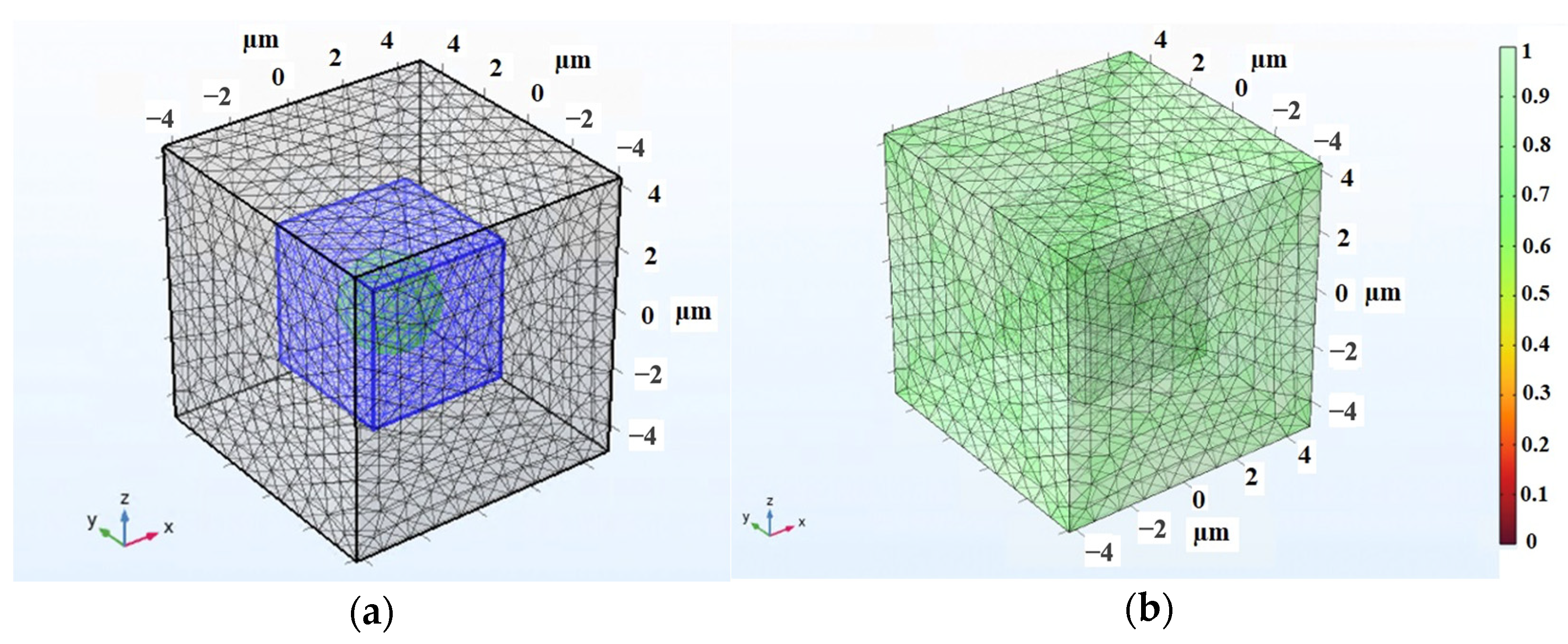
3.2. Modeling the 3D Isotropic MRE-RVE in COMSOL
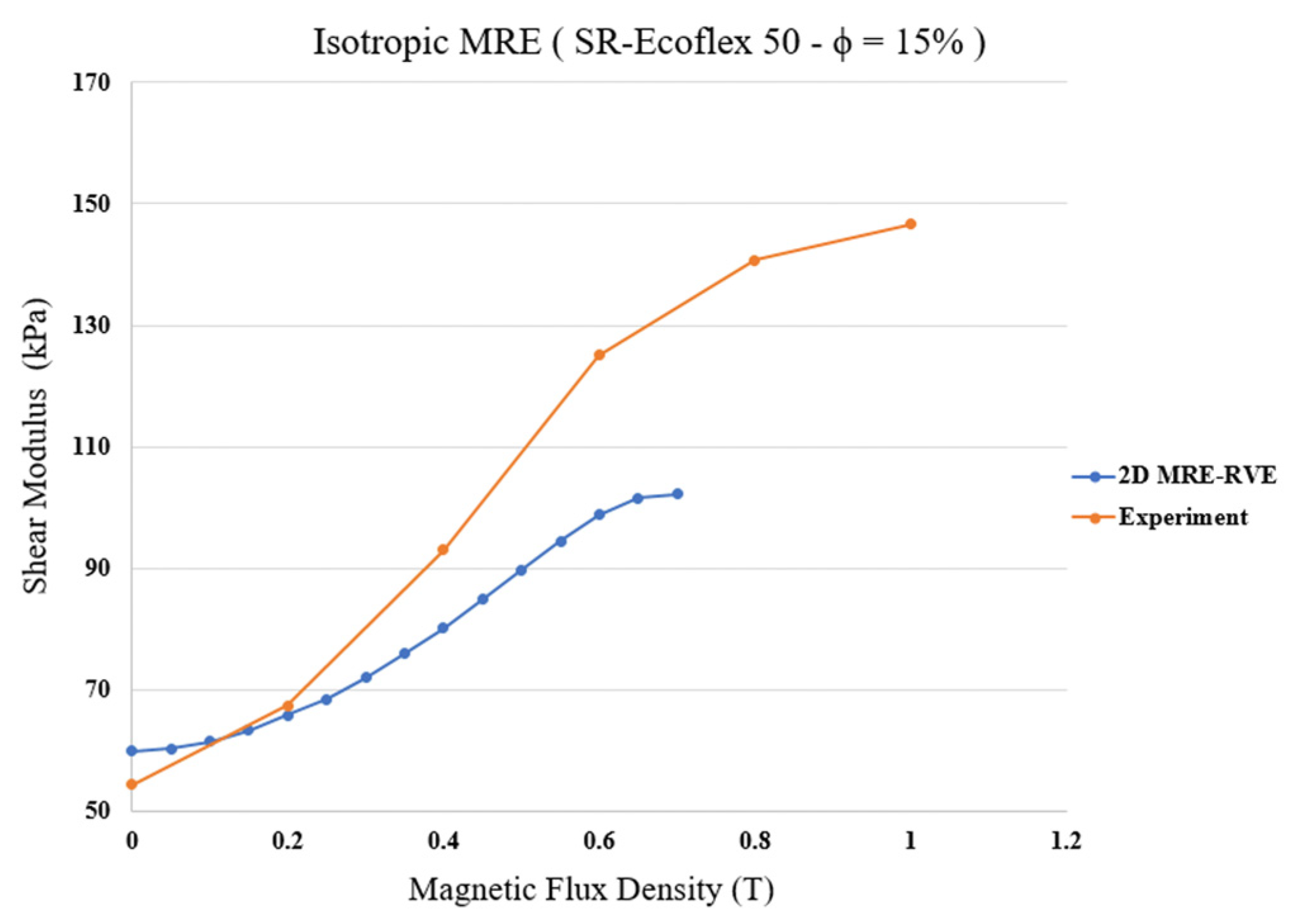
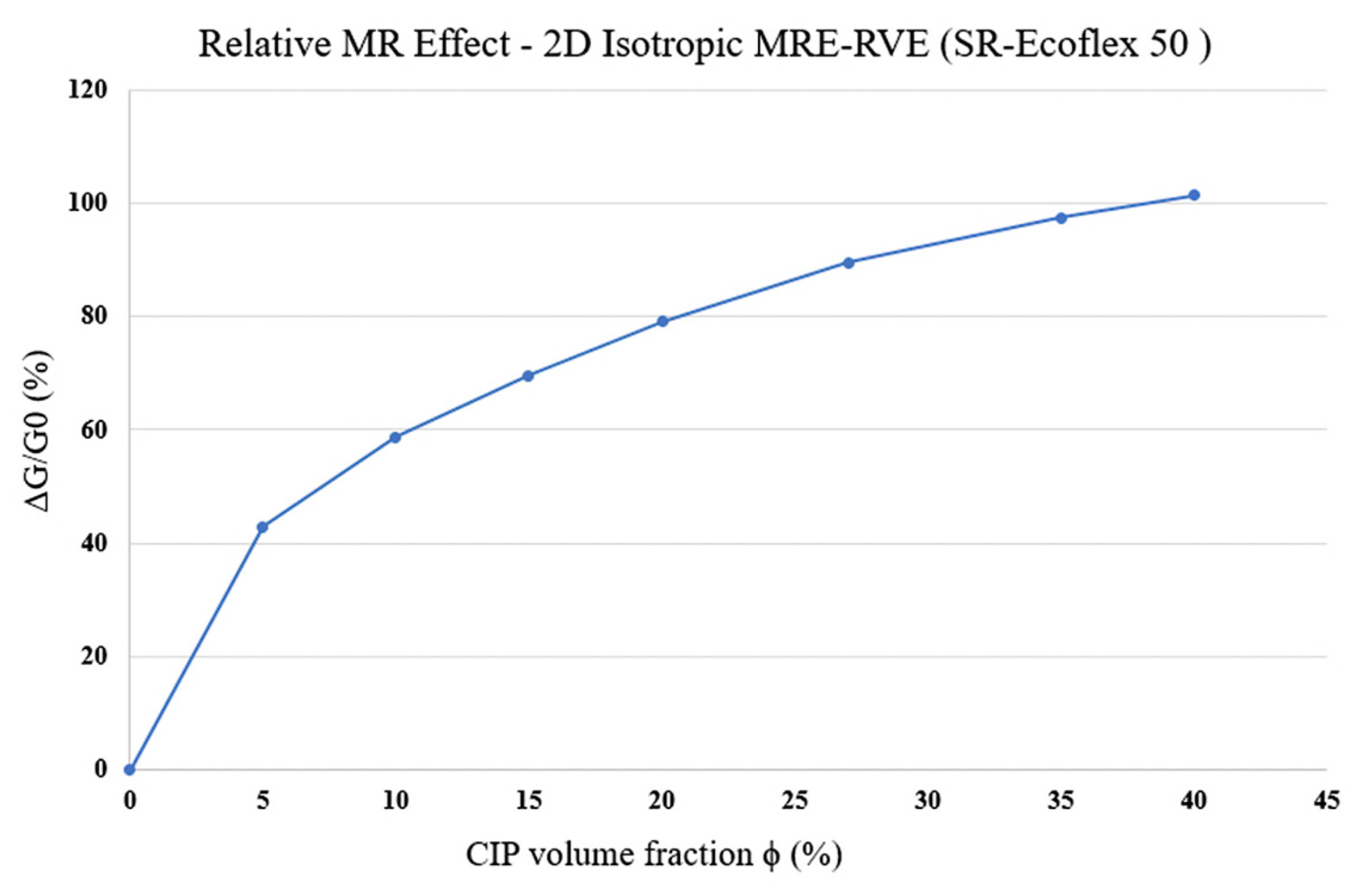
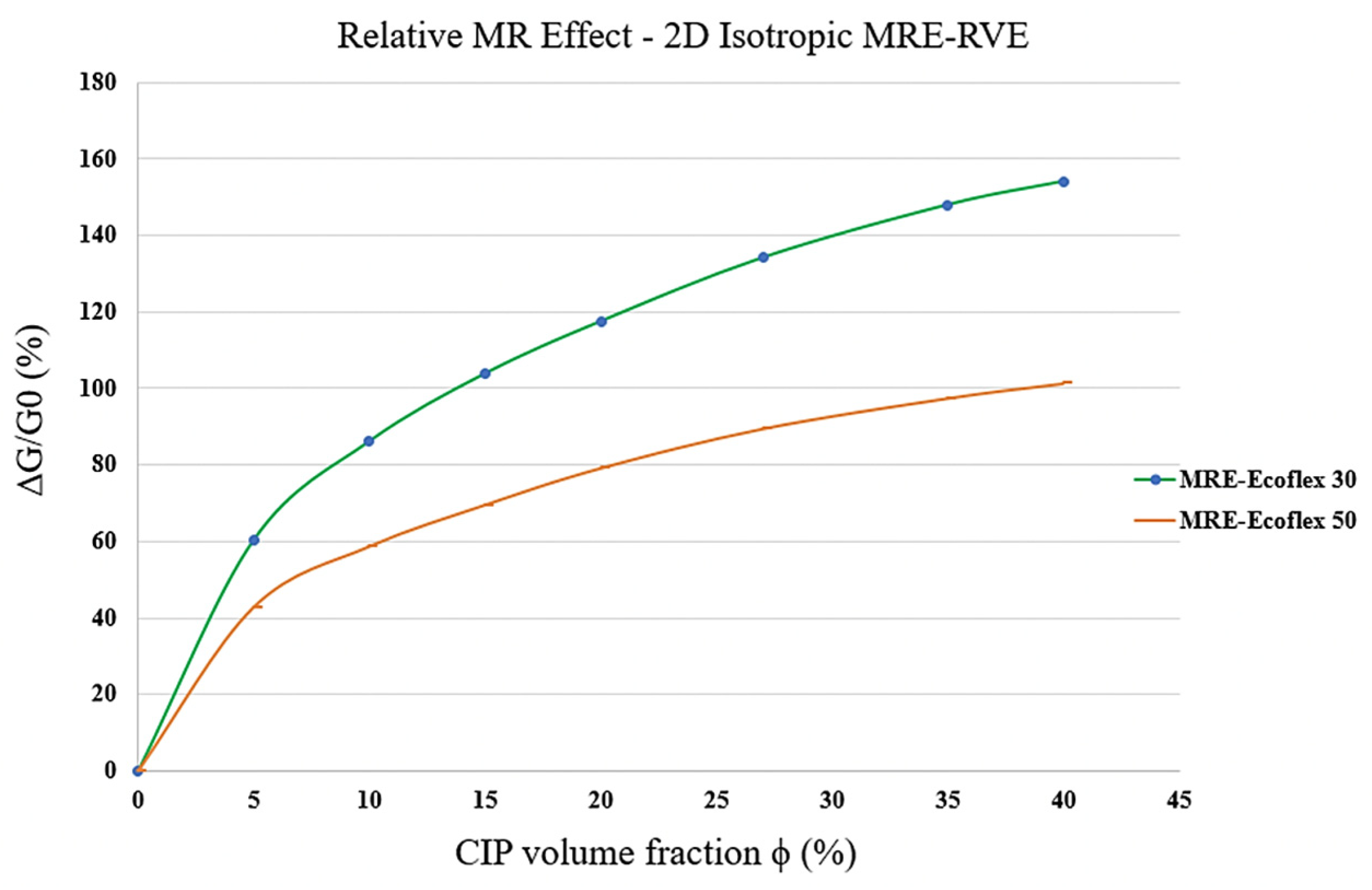
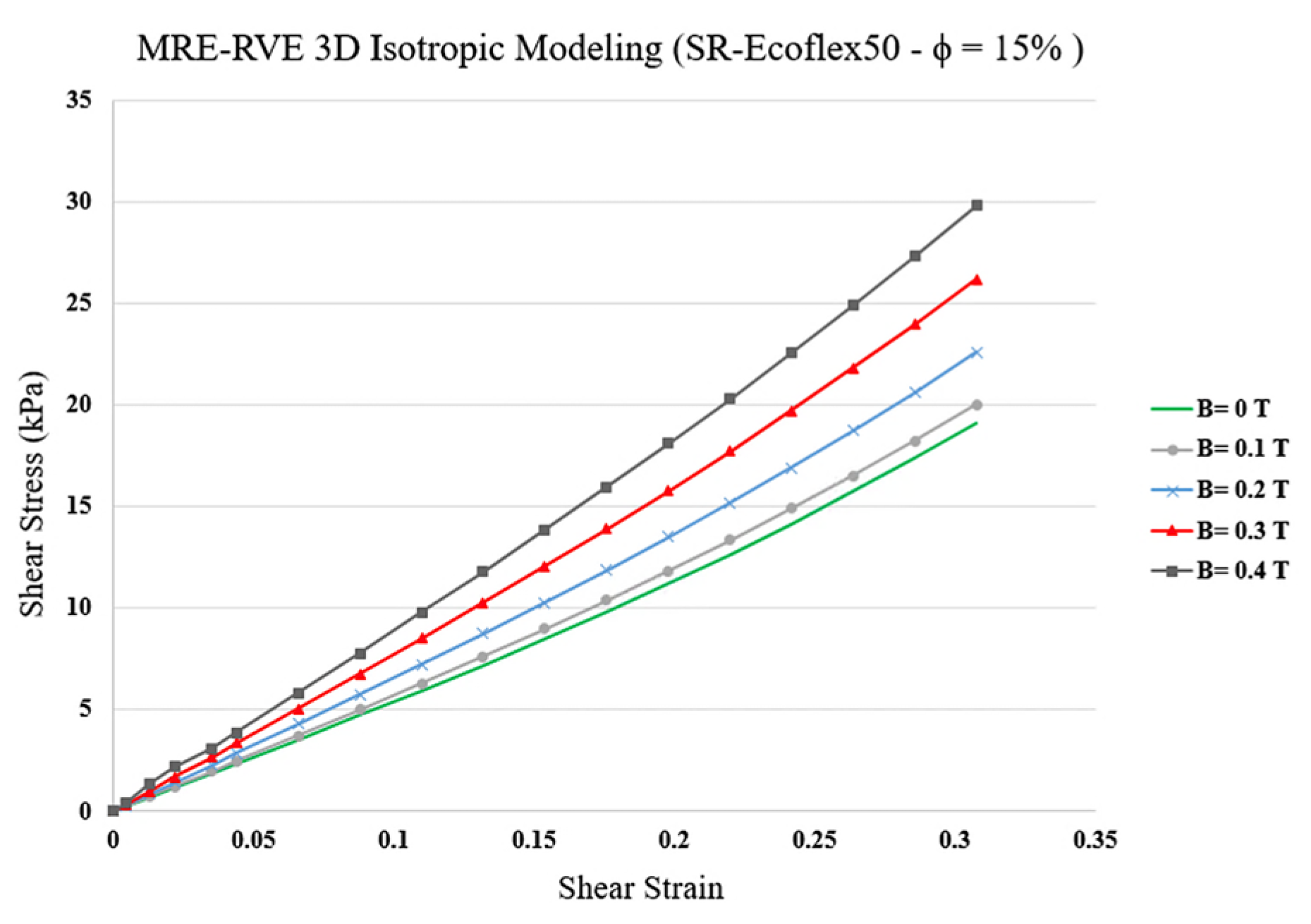
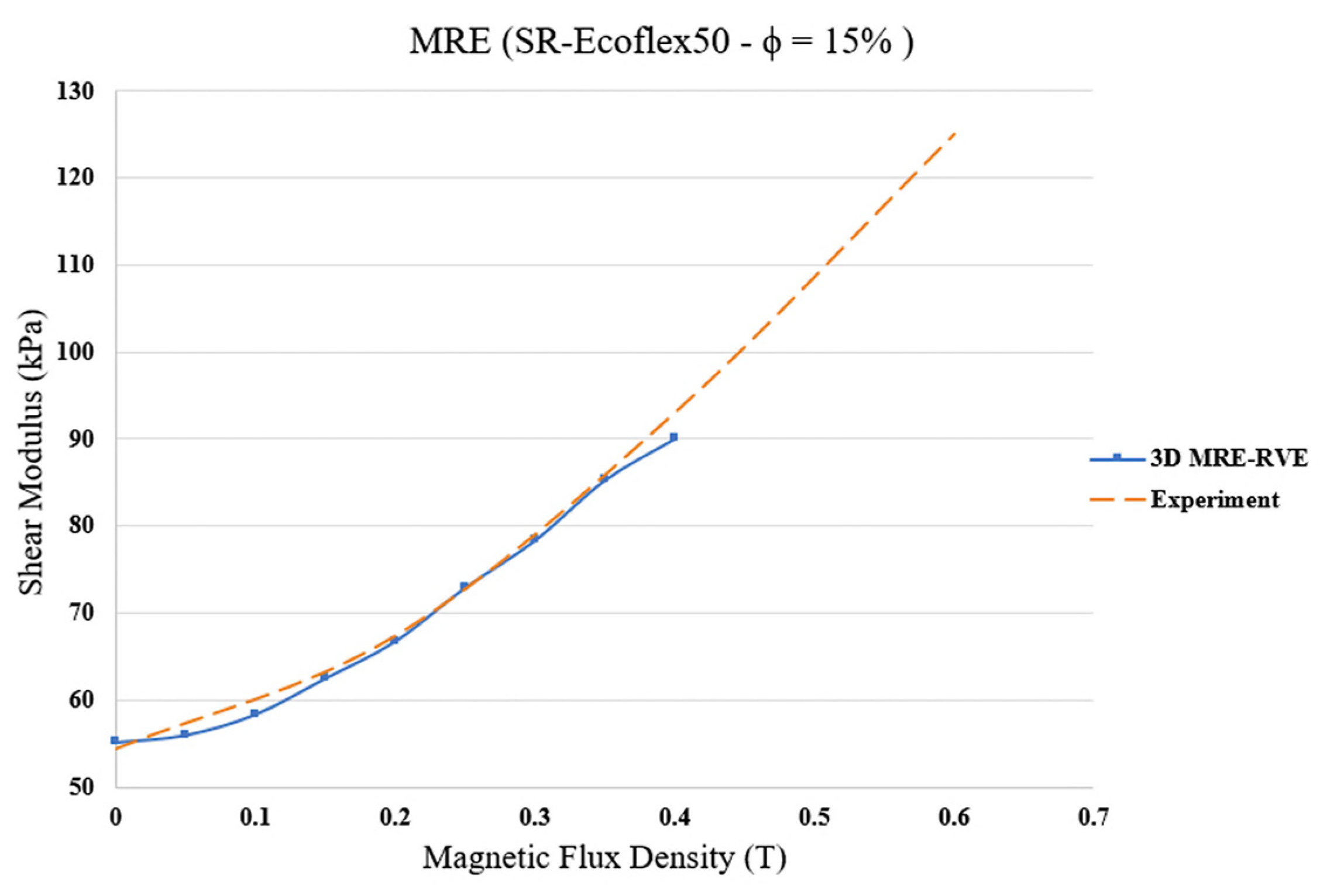
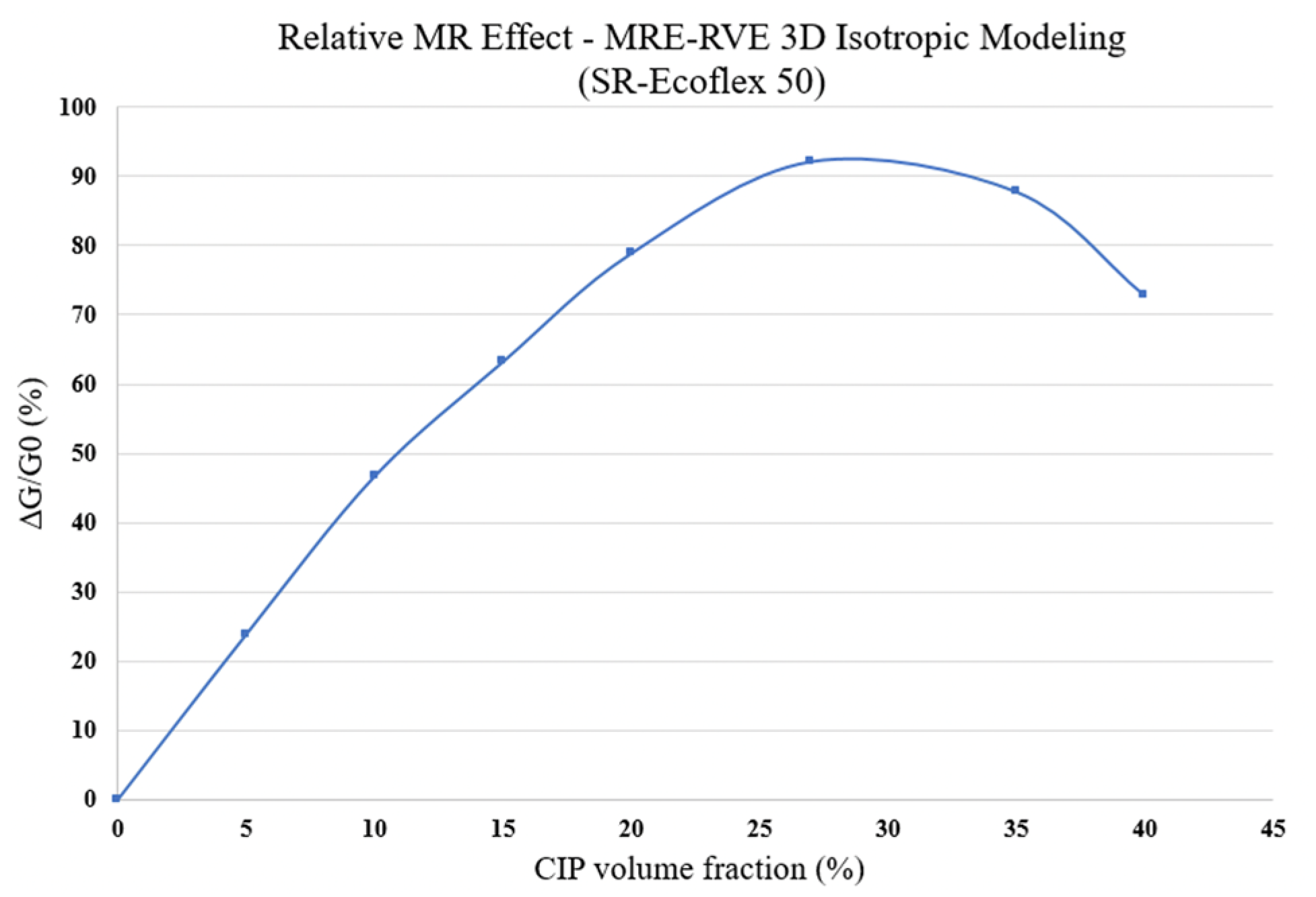
3.2.1. MRE-RVE-Silicone Rubber Ecoflex 50
3.2.2. Silicone Rubber Ecoflex 30 MRE-RVE
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carlson, J.D.; Jolly, M. MR Fluid, foam and elastomer devices. Mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W. Recent progress of magnetorheological elastomers: A review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Saber, A.; Sedaghati, R. The Modeling of Magnetorheological Elastomers: A State-of-the-Art Review. Adv. Eng. Mater. 2023, 25, 2300182. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Li, W.; Du, H. A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Liu, Y. A review on magnetorheological elastomers. Adv. Eng. Technol. Res. 2023, 4, 503–514. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part B Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Jaafar, M.F.; Mustapha, F.; Mustapha, M. Review of current research progress related to magnetorheological elastomer material. J. Mater. Res. Technol. 2021, 15, 5010–5045. [Google Scholar] [CrossRef]
- Cantera, M.A.; Behrooz, M.; Gibson, R.F.; Gordaninejad, F. Modeling of magneto-mechanical response of magnetorheological elastomers (MRE) and MRE-based systems: A review. Smart Mater. Struct. 2017, 26, 023001. [Google Scholar] [CrossRef]
- Díez, A.G.; Tubio, C.R.; Etxebarria, J.G.; Lanceros-Mendez, S. Magnetorheological Elastomer-Based Materials and Devices: State of the Art and Future Perspectives. Adv. Eng. Mater. 2021, 23, 2100240. [Google Scholar] [CrossRef]
- Li, W.H.; Zhang, X.Z.; Du, H. Magnetorheological Elastomers and Their Applications. Adv. Elastomers I 2013, 11, 357–374. [Google Scholar]
- Li, W.; Zhang, X. Research and Applications of MR Elastomers. Recent Pat. Mech. Eng. 2010, 1, 161–166. [Google Scholar] [CrossRef]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent progress on magnetorheological solids: Materials, fabrication, testing, and applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Sharif, U.; Sun, B.; Hussain, S.; Ibrahim, D.S.; Adewale, O.O.; Ashraf, S.; Bashir, F. Dynamic behavior of sandwich structures with magnetorheological elastomer: A review. Materials 2021, 14, 7025. [Google Scholar] [CrossRef]
- Faizal Johari, M.A.; Mazlan, S.A.; Ubaidillah Harjana Abdul Aziz, S.A.; Nordin, N.A.; Johari, N.; Nazmi, N. An Overview of Durability Evaluations of Elastomer-Based Magnetorheological Materials. IEEE Access 2020, 8, 134536–134552. [Google Scholar] [CrossRef]
- Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Tardiff, J.L. Magnetorheological elastomers: Properties and applications. In Smart Structures and Materials 1999: Smart Materials Technologies; SPIE: Newport Beach, CA, USA, 1999; pp. 131–138. [Google Scholar]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C.; Todd, A. The magnetoviscoelastic response of elastomer composites consisting of ferrus particles embedded in a polymer matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–622. [Google Scholar] [CrossRef]
- Davis, L.C. Model of magnetorheological elastomers. J. Appl. Phys. 1999, 85, 3348–3351. [Google Scholar] [CrossRef]
- Berasategi, J.; Salazar, D.; Gomez, A.; Gutierrez, J.; Sebastián, M.S.; Bou-Ali, M.; Barandiaran, J.M. Anisotropic behaviour analysis of silicone/carbonyl iron particles magnetorheological elastomers. Rheol. Acta 2020, 59, 469–476. [Google Scholar] [CrossRef]
- Vatandoost, H.; Sedaghati, R.; Rakheja, S.; Hemmatian, M. Effect of pre-strain on compression mode properties of magnetorheological elastomers. Polym. Test. 2021, 93, 106888. [Google Scholar] [CrossRef]
- Syam, T.M.I.; Muthalif, A.G.A.; Salem, A.M.H.; Hejazi, A.A.A. 3D numerical modelling and analysis of a magnetorheological elastomer (MRE). J. Vibroeng. 2020, 22, 1251–1265. [Google Scholar] [CrossRef]
- Asadi Khanouki, M.; Sedaghati, R.; Hemmatian, M. Experimental characterization and microscale modeling of isotropic and anisotropic magnetorheological elastomers. Compos. Part B Eng. 2019, 176, 107311. [Google Scholar] [CrossRef]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the properties of magnetorheological elastomers in shear mode: Design, fabrication and characterization. Compos. Part B Eng. 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Sun, S.; Peng, X.; Guo, Z. Study on macroscopic and microscopic mechanical behavior of magnetorheological elastomers by representative volume element approach. Adv. Condens. Matter Phys. 2014, 2014, 232510. [Google Scholar] [CrossRef]
- Xu, H.; Ye, L. Characterization and Simulation of Magnetorheological Elastomer Filled with Carbonyl Iron and NdFeB Particles under Uniaxial Tension, Compression, and Pure Shear Modes. Master’s Thesis, The University of Sydney, Sydney, Australia, 2019. [Google Scholar]
- Kiarie, W.M.; Jiles, D.C. Modeling of Effect of Particle Size on Macroscopic Behavior of Magnetorheological Elastomers. In Proceedings of the COMSOL Conference 2020, Virtual, 7–8 October 2020. [Google Scholar]
- Li, R.; Ma, S.; Jin, F.; Yin, S.; Nian, C.; Xin, N.; Yu, Q. Coupled multi-physics field simulation research of magneto-rheological elastomeric magneto-shear mechanical properties based on COMSOL. In Proceeding of the International Conference on Optical Technology, Semiconductor materials, and Devicesc (OTSMD 2022), Longyan, China, 14 February 2023. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of Composite Materials. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Evesque, P. Fluctuations, Correlation and Representative Elementary Volume (REV) in Granular Materials. Poudres Grains 2005, 11, 6–17. [Google Scholar]
- El Moumen, A.; Kanit, T.; Imad, A. Numerical evaluation of the representative volume element for random composites. Eur. J. Mech. A/Solids 2021, 86, 104181. [Google Scholar] [CrossRef]
- Madi, K.; Forest, S.; Jeulin, D.; Boussuge, M. Estimating RVE sizes for 2D/3D viscoplastic composite materials. In Matériaux 2006; HAL Open Science: Dijon, France, 2006; Volume 12, p. hal-00144481. [Google Scholar]
- El Moumen, A.; Imad, A.; Kanit, T.; Hilali, E.; El Minor, H. A multiscale approach and microstructure design of the elastic composite behavior reinforced with natural particles. Compos. Part B Eng. 2014, 66, 247–254. [Google Scholar] [CrossRef]
- Moumen AEl Kanit, T.; Imad, A.; Minor, H.E.L. Effect of overlapping inclusions on effective elastic properties of composites. Mech. Res. Commun. 2013, 53, 24–30. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Jeulin, D. Morphology and effective properties of multi-scale random sets: A review. Comptes Rendus Mec. 2012, 340, 219–229. [Google Scholar] [CrossRef]
- Willot, F.; Jeulin, D. Elastic behavior of composites containing Boolean random sets of inhomogeneities. Int. J. Eng. Sci. 2009, 47, 313–324. [Google Scholar] [CrossRef]
- Suquet, P. Elements of homogenization for inelastic solid mechanics. Lect. Notes Phys. 1987, 272, 193–278. [Google Scholar]
- Anthoine, A. Derivation of the in-plane elastic characteristics of masonry through homogenization theory. Int. J. Solids Struct. 1995, 32, 137–163. [Google Scholar] [CrossRef]
- Terada, K.; Hori, M.; Kyoya, T.; Kikuchi, N. Simulation of the multi-scale convergence in computational homogenization approaches. Int. J. Solids Struct. 2000, 37, 2285–2311. [Google Scholar] [CrossRef]
- Van Der Sluis, O.; Schreurs, P.J.G.; Brekelmans, W.A.M.; Meijer, H.E.H. Overall behaviour of heterogeneous elastoviscoplastic materials: Effect of microstructural modelling. Mech. Mater. 2000, 32, 449–462. [Google Scholar] [CrossRef]
- Smit, R.J.M.; Brekelmans, W.A.M.; Meijer, H.E.H. Prediction of the large-strain mechanical response of heterogeneous polymer systems: Local and global deformation behaviour of a representative volume element of voided polycarbonate. J. Mech. Phys. Solids 1999, 47, 201–221. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. A virtual framework for prediction of full-field elastic response of unidirectional composites. Comput Mater. Sci. 2013, 70, 82–99. [Google Scholar] [CrossRef]
- Davis, A.; Onoochin, V. The Maxwell Stress Tensor and Electromagnetic Momentum. Prog. Electromagn. Res. Lett. 2020, 94, 151–156. [Google Scholar] [CrossRef]
- Pao, Y.-H. Electromagnetic forces in deformable continua. Mech. Today 1978, 4, 209–305. [Google Scholar]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for Chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- Ogden, R.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef]
- Bergström, J. Elasticity/Hyperelasticity. In Mechanics of Solid Polymers; Elsevier: Amsterdam, The Netherlands, 2015; pp. 209–307. [Google Scholar] [CrossRef]
- Rackl, M. Curve Fitting for Ogden, Yeoh and Polynomial Models. In Proceeding of the Scilab TEC, 7th International Scilab Users Conference, Paris, France, 21–22 May 2015. [Google Scholar]
- Rao, D.K.; Kuptsov, V. Effective Use of Magnetization Data in the Design of Electric Machines with Overfluxed Regions. IEEE Trans. Magn. 2015, 51, 6100709. [Google Scholar] [CrossRef]




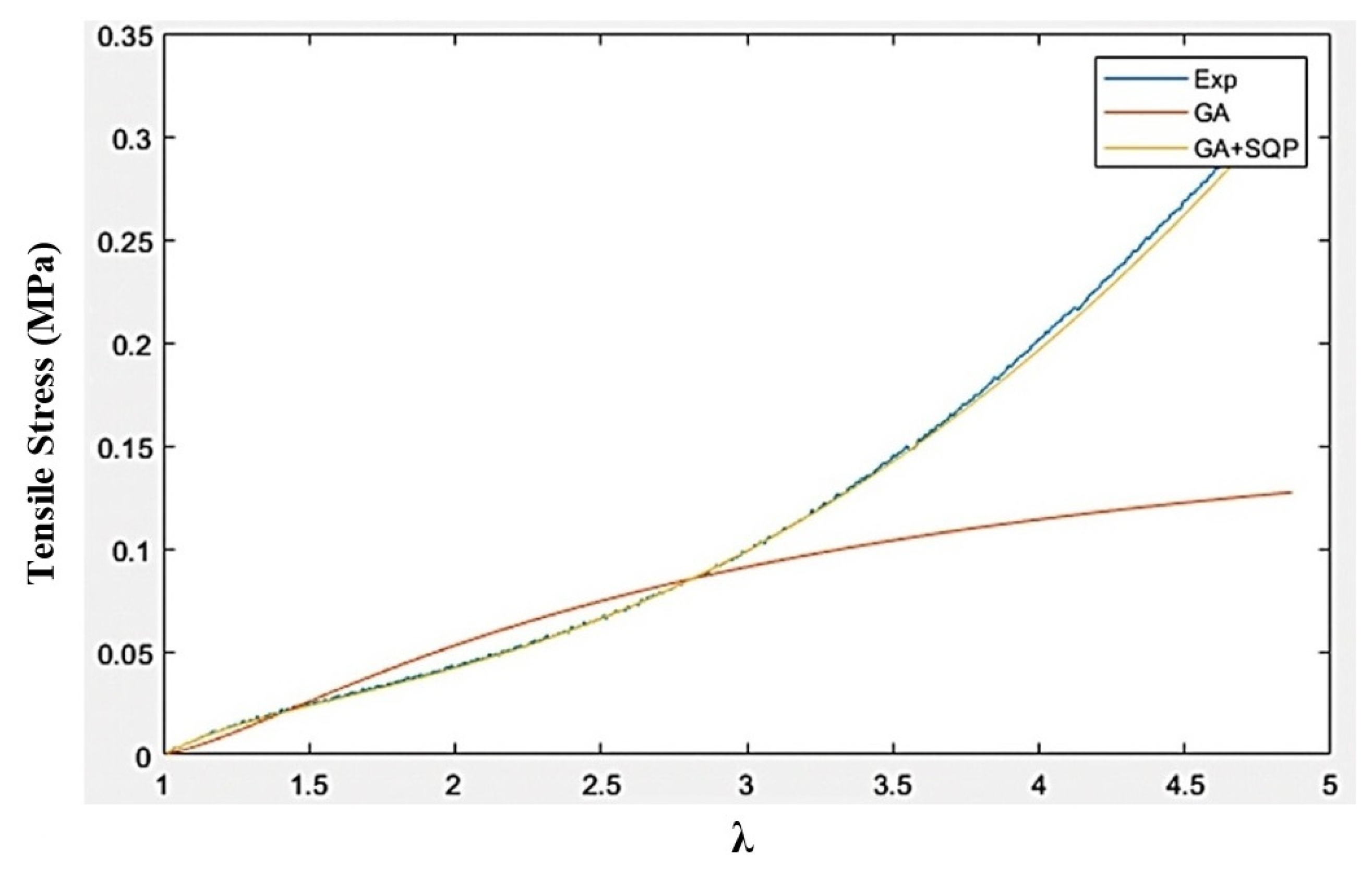














| Material | Optimization Method | (Pa) | (Pa) | (Pa) | G (kPa) | |||
|---|---|---|---|---|---|---|---|---|
| Silicone Rubber Ecoflex 50 | GA | 0.0849 × | 1.0000 | 0.0005 × | 5.5354 | −0.0001 × | −1.000 | 43.884 |
| GA + SQP | 0.0001 × | 1.0000 | 0.0088 × | 3.4927 | −0.0076 × | −5.3724 | 35.833 | |
| Silicone Rubber Ecoflex 30 | GA | −6.9874 × | 1.6760 | 5.2412 × | 1.5601 | 1.8713 × | 1.9162 | 25.850 |
| GA + SQP | 4.3891 × | 1.4354 | −4.3380 × | 1.4529 | 0.0163 × | 3.1195 | 24.141 |
| Material | Material Properties | Value |
|---|---|---|
| Silicone Rubber | ) | |
| 0.5 (incompressible material) | ||
| 2 |
| Material | Material Properties | Value |
|---|---|---|
| Air | 1 | |
| CIP | Young’s Modulus E | 210 GPa |
| 0.33 | ||
| Optimized Extrapolation Parameters for CIP B-H Curve | a | 6.1746 |
| b | 6.1943 m/A | |
| 1.38 T |
| Zero-Field Shear Modulus (kPa) | Maximum Shear Modulus (kPa) | Saturation Magnetic Flux Density (T) | ||
|---|---|---|---|---|
| MRE-RVE | 59.9 | 102.27 | 0.65 | 70.73% |
| Experiments [21] | 54.43 | 146.59 | 0.8 | 169% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahi, I.; Sedaghati, R. Investigation of Macroscopic Mechanical Behavior of Magnetorheological Elastomers under Shear Deformation Using Microscale Representative Volume Element Approach. Polymers 2024, 16, 1374. https://doi.org/10.3390/polym16101374
Abdollahi I, Sedaghati R. Investigation of Macroscopic Mechanical Behavior of Magnetorheological Elastomers under Shear Deformation Using Microscale Representative Volume Element Approach. Polymers. 2024; 16(10):1374. https://doi.org/10.3390/polym16101374
Chicago/Turabian StyleAbdollahi, Ilda, and Ramin Sedaghati. 2024. "Investigation of Macroscopic Mechanical Behavior of Magnetorheological Elastomers under Shear Deformation Using Microscale Representative Volume Element Approach" Polymers 16, no. 10: 1374. https://doi.org/10.3390/polym16101374





