Numerical Simulation of Compressive Mechanical Properties of 3D Printed Lattice-Reinforced Cement-Based Composites Based on ABAQUS
Abstract
:1. Introduction
2. Finite Element Model Modeling
2.1. Material Parameters
2.2. Structural Design
2.3. Finite Element Simulation
3. Results and Discussion
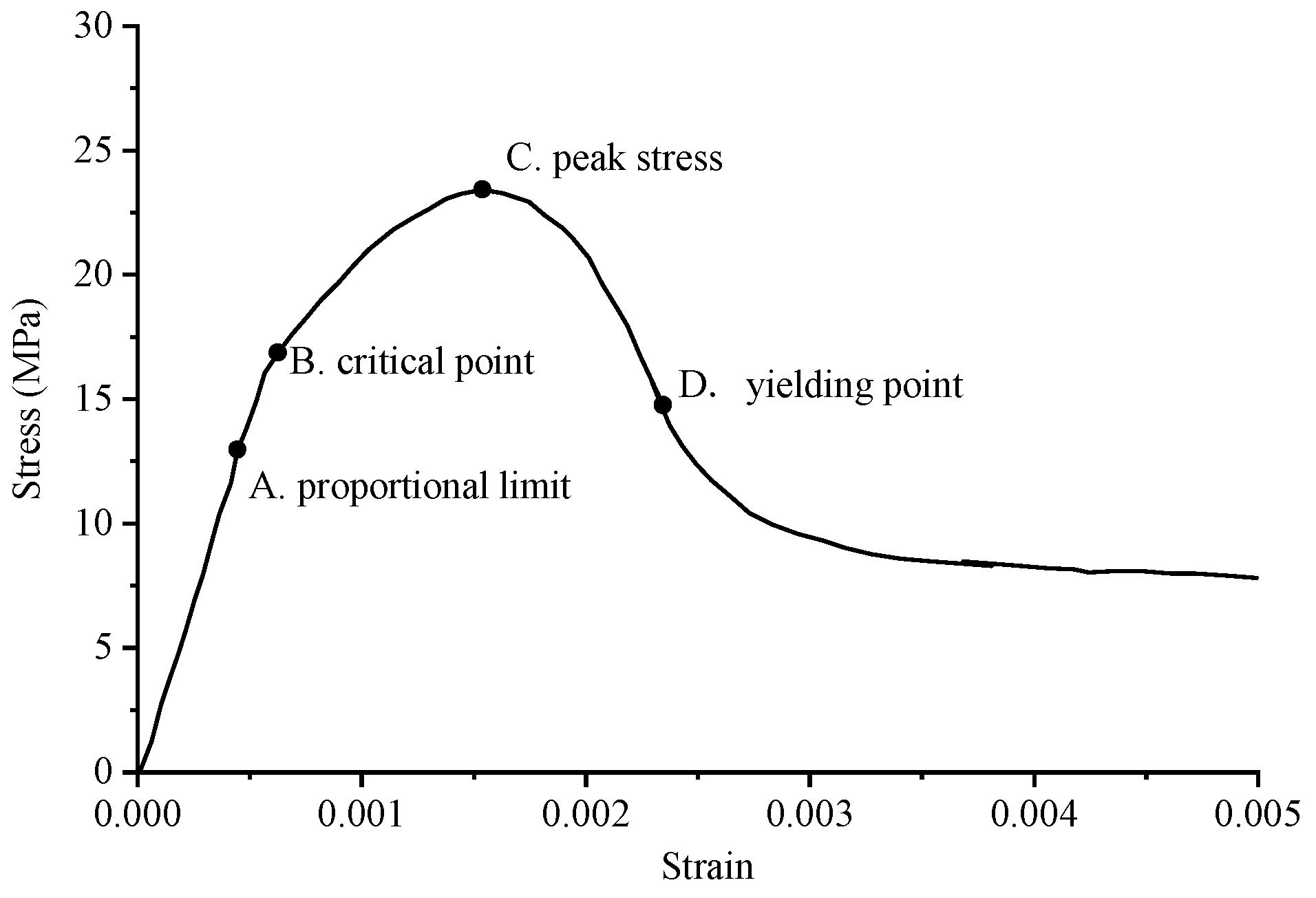
3.1. Stress–Strain Curve Analysis
- (1)
- Initial Stage (O-A): During this phase, the stress level reaches approximately 70% to 85% of the peak stress. At this point, the deformation observed in the specimen is predominantly elastic, resulting from the interaction between the cement matrix and the polymer lattice. This behavior is interpreted as linear elastic deformation, evident from the near-linear relationship depicted in the stress–strain curve. Concurrently, material displacement changes are minimal, despite the significant alterations in the load.
- (2)
- Second Stage (A-B): At this stage, stress levels range from approximately 85% to 93% of the peak stress. The deformation behavior of the specimen is marked by the gradual emergence and expansion of small cracks within the sample, commensurate with the loading process.
- (3)
- Second Stage (A-B): In this stage, the stress reaches roughly 85% to 93% of the peak load. The stage is characterized by the gradual appearance and steady expansion of small cracks within the specimen.
- (4)
- Third Stage (B-C): Stress levels during this stage approximate 93% to 100% of peak stress. This phase is marked by a deceleration in the material’s compressive capacity enhancement. Concurrently, the stress–strain curves exhibit an increasing curvature, transitioning towards a more gradual trend. The predominant deformation observed in the specimen is of an irreversible plastic nature, with a minor component of elastic deformation also present at this stage.
- (5)
- Fourth Stage (C-): Upon exceeding the peak stress, the sample’s compressive properties begin to diminish correspondingly. As the external force applied to the material escalates with continued loading, the damage to the specimen progressively worsens.
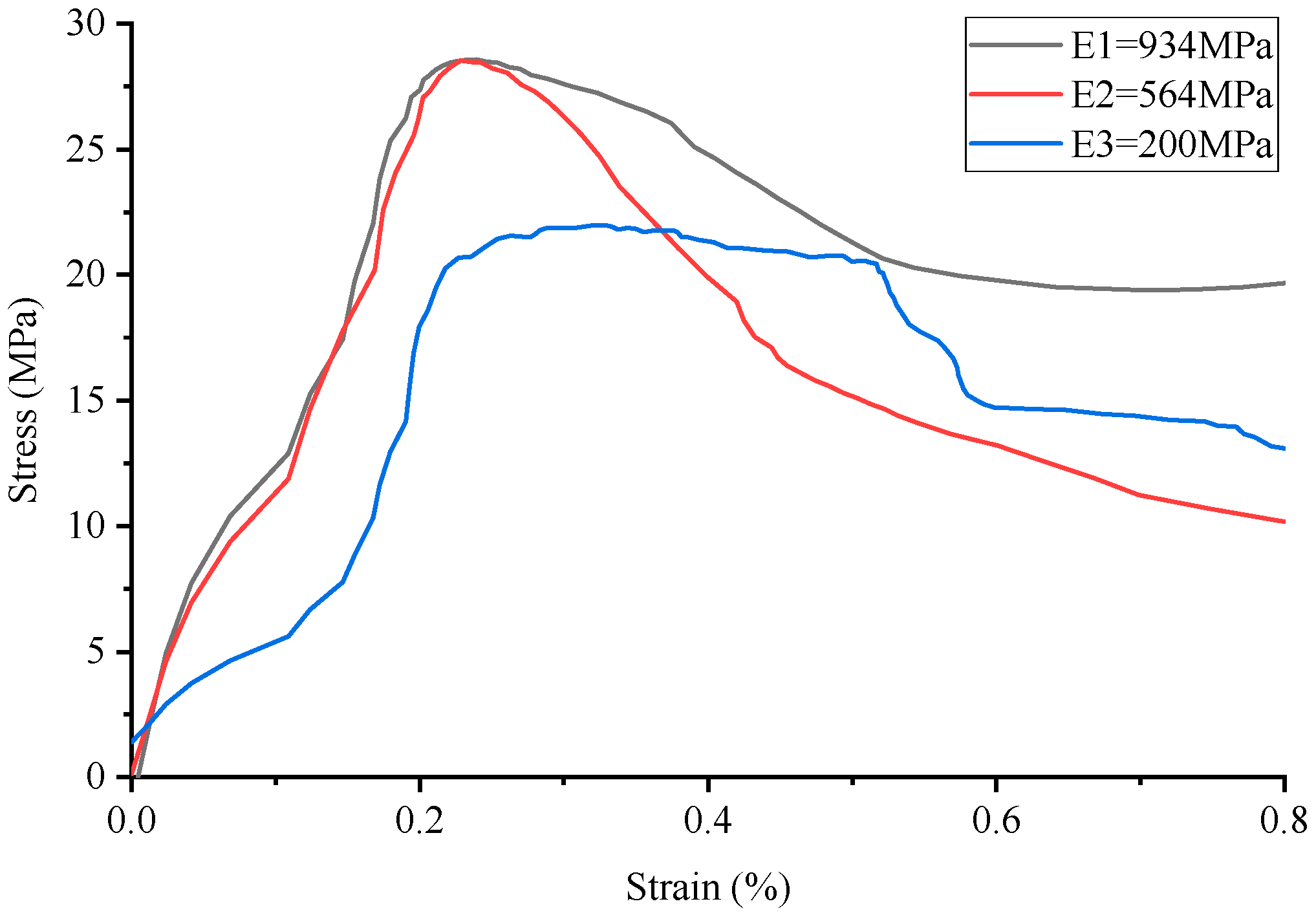
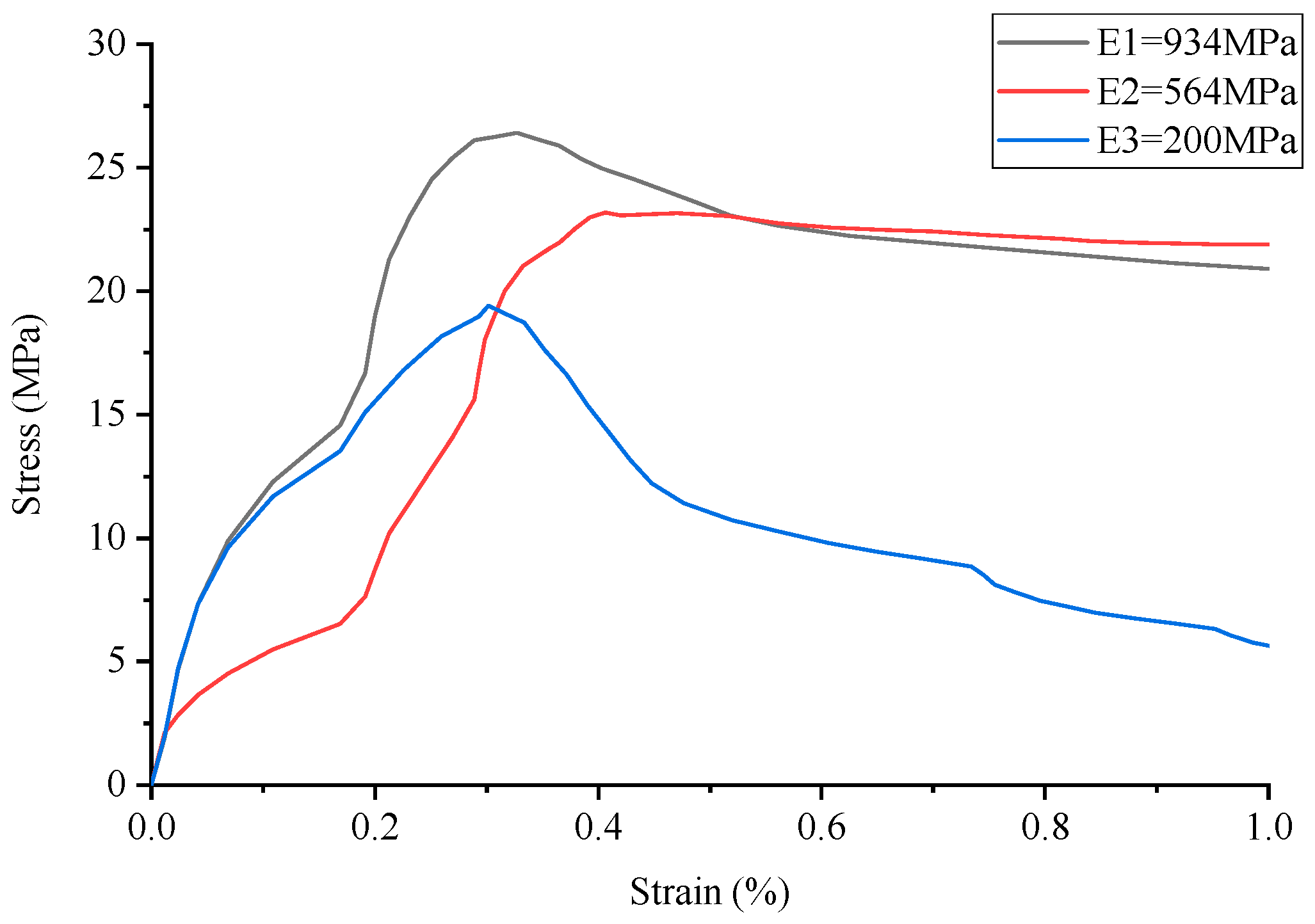
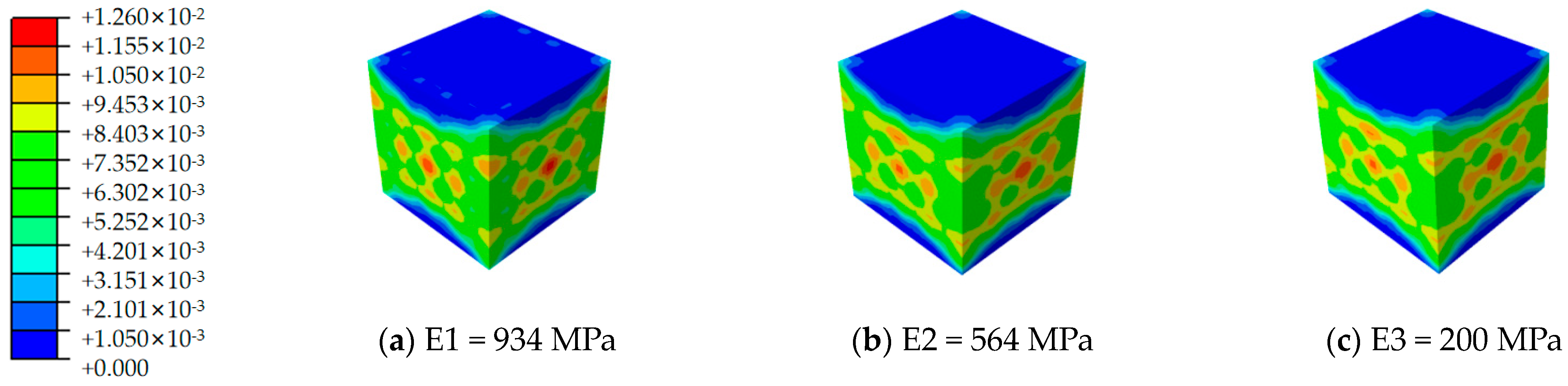
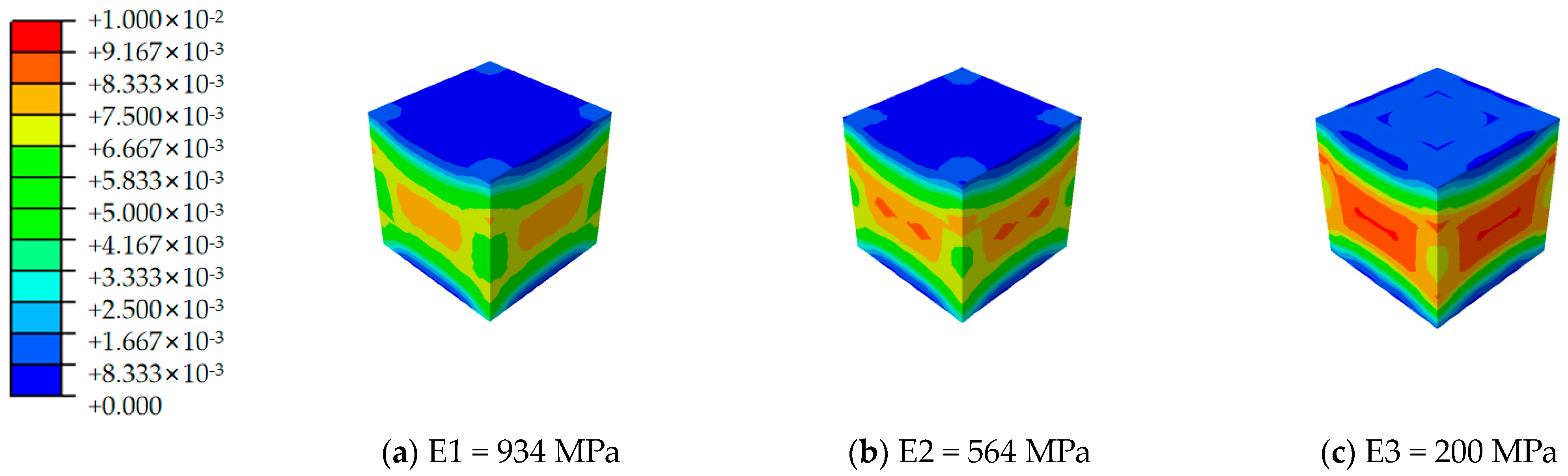
3.2. Strain Analysis
4. Conclusions
- (1)
- Through the creation of a precise finite element model and the simulation of laboratory uniaxial compression tests, this study has successfully validated the accuracy of its numerical analysis model. This achievement not only furnishes a dependable simulation methodology for subsequent research endeavors but also lays a robust groundwork for the enhanced analysis and application of experimental data. Moreover, the process of developing and validating the model serves as a valuable benchmark for the numerical simulation of analogous materials and structures.
- (2)
- The study reveals that variations in ambient temperature markedly influence the elastic modulus of 3D-printed polymer materials, subsequently altering the compressive mechanical properties of cement-based composites. This finding underscores the necessity of accounting for material performance shifts under diverse temperature conditions in practical engineering applications to ensure the reliability and safety of structures.
- (3)
- This study demonstrates that the compressive strength of composite materials tends to decrease as the elastic modulus of polymer materials is reduced. This observation holds significant implications for the optimization of composite material design and the enhancement of their structural characteristics.
- (4)
- The findings indicate that as Young’s modulus of the polymer decreases, the strain region widens while the maximum strain diminishes, suggesting an impact on both the ductility and load-bearing capacity of the structure. Furthermore, when the elastic modulus falls to a specific critical threshold, specimen cracking occurs at the onset of the compression test. This highlights the necessity for meticulous attention to the lower limits of material properties during the design process to prevent premature failure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carpinteri, A. Mechanical Damage and Crack Growth in Concrete: Plastic Collapse to Brittle Fracture; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hrițuc, A.; Mihalache, M.A.; Dodun, O.; Nagîț, G.; Beșliu-Băncescu, I.; Rădulescu, B.; Slătineanu, L. Propagation of Sounds through Small Panels Made of Polymer Materials by 3D Printing. Polymers 2023, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, M.R.; Ayatollahi, M.R.; Reinicke, T. Effects of post-processing techniques on the mechanical characterization of additively manufactured parts. J. Manuf. Process. 2023, 107, 98–114. [Google Scholar] [CrossRef]
- Johnson, L.K.; Richburg, C.; Lew, M.; Ledoux, W.R.; Aubin, P.M.; Rombokas, E. 3D Printed lattice microstructures to mimic soft biological materials. Bioinspir. Biomim. 2018, 14, 016001. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.D.; Kim, S. Development of a 3D printing method for the textile hybrid structure. Int. J. Cloth. Sci. Technol. 2021, 34, 262–272. [Google Scholar] [CrossRef]
- Park, S.; Shou, W.; Makatura, L.; Matusik, W.; Fu, K. 3D printing of polymer composites: Materials, processes, and applications. Matter 2022, 5, 43–76. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Šavija, B.; Figueiredo, S.C.; Schlangen, E. Deformation and fracture of 3D printed disordered lattice materials: Experiments and modeling. Mater. Des. 2019, 162, 143–153. [Google Scholar] [CrossRef]
- Qin, S.; Cao, S.; Yilmaz, E. Employing U-shaped 3D printed polymer to improve flexural properties of cementitious tailings backfills. Constr. Build. Mater. 2022, 320, 126296. [Google Scholar] [CrossRef]
- Balla, V.K.; Kate, K.H.; Satyavolu, J.; Singh, P.; Tadimeti, J.G.D. Additive manufacturing of natural fiber reinforced polymer composites: Processing and prospects. Compos. Part B Eng. 2019, 174, 106956. [Google Scholar] [CrossRef]
- Nam, Y.J.; Hwang, Y.K.; Park, J.W.; Lim, Y.M. Feasibility study to control fiber distribution for enhancement of composite properties via three-dimensional printing. Mech. Adv. Mater. Struct. 2019, 26, 465–469. [Google Scholar] [CrossRef]
- Farina, I.; Fabbrocino, F.; Carpentieri, G.; Modano, M.; Amendola, A.; Goodall, R.; Feo, L.; Fraternali, F. On the reinforcement of cement mortars through 3D printed polymeric and metallic fibers. Compos. Part B Eng. 2016, 90, 76–85. [Google Scholar] [CrossRef]
- Tian, H.; Zhou, Z.; Zhang, Y.; Wei, Y. Axial behavior of reinforced concrete column with ultra-high performance concrete stay-in-place formwork. Eng. Struct. 2020, 210, 110403. [Google Scholar] [CrossRef]
- Rosewitz, J.A.; Choshali, H.A.; Rahbar, N. Bioinspired design of architected cement-polymer composites. Cem. Concr. Compos. 2019, 96, 252–265. [Google Scholar] [CrossRef]
- Xu, Y.; Šavija, B. Development of strain hardening cementitious composite (SHCC) reinforced with 3D printed polymeric reinforcement: Mechanical properties. Compos. Part B Eng. 2019, 174, 107011. [Google Scholar] [CrossRef]
- Salazar, B.; Aghdasi, P.; Williams, I.D.; Ostertag, C.P.; Taylor, H.K. Polymer lattice-reinforcement for enhancing ductility of concrete. Mater. Des. 2020, 196, 109184. [Google Scholar] [CrossRef]
- Ding, S.; Xiang, Y.; Ni, Y.Q.; Thakur, V.K.; Wang, X.; Han, B.; Ou, J. In-situ synthesizing carbon nanotubes on cement to develop self-sensing cementitious composites for smart high-speed rail infrastructures. Nano Today 2022, 43, 101438. [Google Scholar] [CrossRef]
- Han, B.; Sun, S.; Ding, S.; Zhang, L.; Yu, X.; Ou, J. Review of nanocarbon-engineered multifunctional cementitious composites. Compos. Part A Appl. Sci. Manuf. 2015, 70, 69–81. [Google Scholar] [CrossRef]
- Ráž, K.; Chval, Z.; Thomann, S. Minimizing Deformations during HP MJF 3D Printing. Materials 2023, 16, 7389. [Google Scholar] [CrossRef]
- Robar, J.L.; Kammerzell, B.; Hulick, K.; Kaiser, P.; Young, C.; Verzwyvelt, V.; Cheng, X.; Shepherd, M.; Orbovic, R.; Fedullo, S.; et al. Novel multi jet fusion 3D-printed patient immobilization for radiation therapy. J. Appl. Clin. Med. Phys. 2022, 23, e13773. [Google Scholar] [CrossRef]
- Shalchy, F. An Investigation on Interfacial Adhesion Energy between Polymeric and Cellulose-Based Additives Embedded in CSH Gel. Master’s Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2016. [Google Scholar]
- Kakavand, M.R.; Taciroglu, E.; Hofstetter, G. Evaluation of the Performance of an Enhanced Damage Plasticity Model for Predicting the Cyclic Response of Plain Concrete under Multiaxial Loading Conditions. Int. J. Struct. Civ. Eng. Res. 2020, 9, 273–277. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Taqieddin, Z.N. Elastic plastic and damage model for concrete materials: Part I-theoretical formulation. Int. J. Struct. Chang. Solids 2009, 1, 31–59. [Google Scholar]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, C.; Zhang, J. Calculation and Analysis of Sluice Bottom Seepage with Two Methods. IOP Conf. Ser. Earth Environ. Sci. 2021, 643, 012103. [Google Scholar] [CrossRef]
- Merzuki, M.N.M.; Ma, Q.; Rejab, M.R.M.; Sani, M.; Zhang, B. Experimental and numerical investigation of fibre-metal-laminates (FMLs) under free vibration analysis. Mater. Today Proc. 2022, 48, 854–860. [Google Scholar] [CrossRef]
- Rizwan, M.; Liang, Q.Q.; Hadi, M.N.S. Fiber-based computational modeling of rectangular double-skin concrete-filled steel tubular short columns including local buckling. Eng. Struct. 2021, 248, 113268. [Google Scholar] [CrossRef]











| Density (kg/m3) | 2.4 × 10−9 |
| Young’s modulus (GPa) | 30 |
| Poisson’s ratio | 0.2 |
| expansion angle (°) | 30 |
| eccentricity ratio | 0.1 |
| fb0/fco | 1.16 |
| k | 0.6667 |
| Viscous parameter | 0.0005 |
| Density (kg/m3) | Indoor Temperature Young’s Modulus (MPa) | Poisson’s Ratio |
|---|---|---|
| 1.1 × 10−9 | 934 | 0.38 |
| Environment Temperature | Indoor Temperature | 50 °C | 100 °C |
|---|---|---|---|
| elasticity modulus | 934 MPa | 564 MPa | 200 MPa |
| Structure Serial Number | Lattice Unit Cell Type | Unit Cell Design | Cell Design Parameters (mm) | CAD Southwest View |
|---|---|---|---|---|
| 1 | circle | 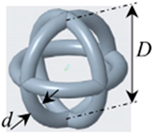 | D = 10, d = 1.246 |  |
| 2 | cubic | 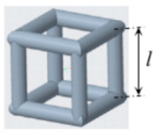 | l = 10, d = 1.659 |  |
| 3 | kelvin | 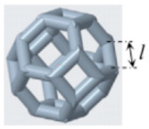 | l = 3.54, d = 1.183 |  |
| 4 | octagonal (Oct), | 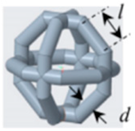 | l = 4.14, d = 0.979 |  |
| 5 | rhombicubactahedron (RO) | 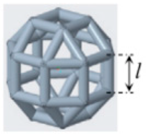 | l = 1.414, d = 0.916 |  |
| 6 | strengthened octagon octagonal (SO) |  | l = 3.54, d = 0.979 |  |
| Elasticity Modulus | E1 = 934 MPa | E2 = 564 MPa | E3 = 200 MPa | |
|---|---|---|---|---|
| Crystal Structure | ||||
| Circular | 26.23 | 26.04 | 22.74 | |
| Cubic | 25.23 | 25.17 | 23.16 | |
| Kelvin | 28.49 | 28.45 | 21.79 | |
| Oct. | 28.57 | 23.48 | 20.21 | |
| RO | 26.02 | 23.27 | 19.46 | |
| SO | 26.26 | 23.18 | 19.41 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Qiao, J.; Wei, Y.; Hao, W.; Tang, C. Numerical Simulation of Compressive Mechanical Properties of 3D Printed Lattice-Reinforced Cement-Based Composites Based on ABAQUS. Materials 2024, 17, 2370. https://doi.org/10.3390/ma17102370
Wu W, Qiao J, Wei Y, Hao W, Tang C. Numerical Simulation of Compressive Mechanical Properties of 3D Printed Lattice-Reinforced Cement-Based Composites Based on ABAQUS. Materials. 2024; 17(10):2370. https://doi.org/10.3390/ma17102370
Chicago/Turabian StyleWu, Weiguo, Jing Qiao, Yuanyuan Wei, Wenfeng Hao, and Can Tang. 2024. "Numerical Simulation of Compressive Mechanical Properties of 3D Printed Lattice-Reinforced Cement-Based Composites Based on ABAQUS" Materials 17, no. 10: 2370. https://doi.org/10.3390/ma17102370






