Early-Age Cracking of Fly Ash and GGBFS Concrete Due to Shrinkage, Creep, and Thermal Effects: A Review
Abstract
1. Introduction
2. Supplementary Cementitious Materials (SCMs)
2.1. Fly Ash
2.2. Slag
3. Time-Dependent Behaviors
3.1. Autogenous Shrinkage
3.2. Drying Shrinkage
3.3. Creep
3.4. Thermal Effects
3.5. Mechanical Properties
4. Factors Influencing Cracking in Concrete
4.1. Degree of Restraint
4.2. Effect of Concrete Constituents
5. Analytical Models That Predict Factors Affecting Early-Age Concrete Cracking
5.1. Analytical Models for Predicting Shrinkage
5.2. Analytical Models for Predicting Creep
5.3. Analytical Models for Predicting Evolution of Tensile Stress during the Restrained Ring Test
5.4. Analytical Models That Predict the Risk of Cracking at Early Ages
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- von Greve-Dierfeld, S.; Lothenbach, B.; Vollpracht, A.; Wu, B.; Huet, B.; Andrade, C.; Medina, C.; Thiel, C.; Gruyaert, E.; Vanoutrive, H.; et al. Understanding the carbonation of concrete with supplementary cementitious materials: A critical review by RILEM TC 281-CCC. Mater. Struct. 2020, 53, 136. [Google Scholar] [CrossRef]
- Elahi, M.; Shearer, C.; Reza, A.; Saha, A.; Khan, M.; Hossain, M.; Sarker, P. Improving the sulfate attack resistance of concrete by using supplementary cementitious materials (SCMs): A review. Constr. Build. Mater. 2021, 281, 1226280. [Google Scholar] [CrossRef]
- Beglarigale, A.; Yazici, H. Mitigation of detrimental effects of alkali-silica reaction in cement-based composites by combina-tion of steel microfibers and ground-granulated blast-furnace slag. J. Mater. Civ. Eng. 2014, 26, 04014091. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, H.; Tang, S.; Liu, H. Study on early autogenous shrinkage and crack resistance of fly ash high-strength lightweight aggregate concrete. Mag. Concr. Res. 2013, 65, 906–913. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Yang, W. Influence of fly ash on crack resistance of mass concrete. Adv. Mater. Res. 2011, 194–196, 825–828. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, D. The research of GGBS’ influence on the cracking resistance of concrete. Adv. Mater. Res. 2014, 919–921, 1864–1867. [Google Scholar] [CrossRef]
- Qu, Z.; Si, R.; Jia, P.; Zhang, Y. Creep and relaxation responses of fly ash concrete: Linear and nonlinear cases. Case Stud. Constr. Mater. 2022, 17, e01562. [Google Scholar] [CrossRef]
- Bentz, D. A review of early-age properties of cement-based materials. Cem. Concr. Res. 2008, 38, 196–204. [Google Scholar] [CrossRef]
- Maruyama, I.; Lura, P. Properties of early-age concrete relevant to cracking in massive concrete. Cem. Concr. Res. 2019, 123, 105770. [Google Scholar] [CrossRef]
- Safiuddin, M.; Kaish, A.; Woon, C.; Raman, S. Early-age cracking in concrete: Causes, consequences, remedial measures, and recommendations. Appl. Sci. 2018, 8, 1730. [Google Scholar] [CrossRef]
- Yu, Z.; Ye, G. New perspective of service life prediction of fly ash concrete. Constr. Build. Mater. 2013, 48, 764–771. [Google Scholar] [CrossRef]
- Khaliq, W.; Kodur, V. Behavior of high strength fly ash concrete columns under fire conditions. Mater. Struct. 2013, 46, 857–867. [Google Scholar] [CrossRef]
- Wang, S.; Baxter, L.E.; Fonseca, F. Durability of biomass fly ash concrete: Freezing and thawing and rapid chloride permeability tests. Fuel 2008, 87, 359–364. [Google Scholar] [CrossRef]
- Termkhajornkit, P.; Nawa, T.; Nakai, M.; Saito, T. Effect of fly ash on autogenous shrinkage. Cem. Concr. Res. 2005, 35, 473–482. [Google Scholar] [CrossRef]
- Afroz, S.; Zhang, Y.; Nguyen, Q.; Kim, T.; Castel, A. Shrinkage of blended cement concrete with fly ash or limestone calcined clay. Mater. Struct. 2023, 56, 15. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Liu, B. Degradation technologies and mechanisms of dioxins in municipal solid waste incineration fly ash: A review. J. Clean. Prod. 2020, 250, 119507. [Google Scholar] [CrossRef]
- De la Varga, I.; Castro, J.; Bentz, D.; Zunino, F.; Weiss, J. Evaluating the hydration of high volume fly ash mixtures using chemically inert fillers. Constr. Build. Mater. 2018, 161, 221–228. [Google Scholar] [CrossRef]
- Wongkeo, W.; Thongsanitgarn, P.; Poon, C.; Chaipanich, A. Heat of hydration of cement pastes containing high-volume fly ash and silica fume. J. Therm. Anal. Calorim. 2019, 138, 2065–2075. [Google Scholar] [CrossRef]
- Dockter, B. Using class C fly ash to mitigate alkali-silica reactions in concrete. In Proceedings of the 3rd World of Coal Ash, WOCA Conference Proceedings, Lexington, KY, USA, 4–7 May 2009. [Google Scholar]
- Hay, R.; Ostertag, C. New insights into the role of fly ash in mitigating alkali-silica reaction (ASR) in concrete. Cem. Concr. Res. 2021, 144, 106440. [Google Scholar] [CrossRef]
- Ling, X.; Setunge, S.; Patnaikuni, I. Effect of different concentrations of lime water on mechanical properties of high volume fly ash concrete. In From Materials to Structures: Advancement Through Innovation, Proceedings of the 22nd Australasian Conference on the Mechanics of Structures and Materials, ACMSM 2012, Sydney, Australia, 11–14 December 2012; CRC Press: Leiden, The Netherlands, 2013. [Google Scholar]
- Naik, T.; Singh, S.; Hossain, M. Permeability of concrete containing large amounts of fly ash. Cem. Concr. Res. 1994, 24, 913–922. [Google Scholar] [CrossRef]
- Fládr, J.; Bílý, P.; Chylík, R.; Prošek, Z. Macroscopic and microscopic properties of high performance concrete with partial replacement of cement by fly ash. Solid State Phenom. 2019, 292, 108–113. [Google Scholar] [CrossRef]
- Liu, J.; Ou, G.; Qiu, Q.; Chen, X.; Hong, J.; Xing, F. Chloride transport and microstructure of concrete with/without fly ash under atmospheric chloride condition. Constr. Build. Mater. 2017, 146, 493–501. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, Z.; Li, J.; Li, Z.; Wang, Z.; Cao, L.; Rong, G.; Wu, M.; Zhao, D.; Zhao, Z. Experimental investigation on the high-volume fly ash ecological self-compacting concrete. J. Build. Eng. 2022, 60, 105163. [Google Scholar] [CrossRef]
- Niu, Q.; Feng, N.; Yang, J.; Zheng, X. Effect of superfine slag powder on cement properties. Cem. Concr. Res. 2002, 32, 615–621. [Google Scholar] [CrossRef]
- Liu, S.; Li, L. Influence of fineness on the cementitious properties of steel slag. J. Therm. Anal. Calorim. 2014, 117, 629–634. [Google Scholar] [CrossRef]
- Tavasoli, S.; Nili, M.; Serpoosh, B. Effect of GGBS on the frost resistance of self-consolidating concrete. Constr. Build. Mater. 2018, 165, 717–722. [Google Scholar] [CrossRef]
- Gao, J.; Qian, C.; Liu, H.; Wang, B.; Li, L. ITZ microstructure of concrete containing GGBS. Cem. Concr. Res. 2005, 35, 1299–1304. [Google Scholar] [CrossRef]
- Zhang, S.; Niu, D.; Wang, Y.; Tian, W.; Luo, D.; Zhang, L. Insight into mechanical properties and microstructure of concrete containing steel slag and ground-granulated blast-furnace slag. J. Sustain. Cem.-Based Mater. 2023, 12, 1169–1180. [Google Scholar] [CrossRef]
- Yalçınkaya, Ç.; Çopuroğlu, O. Elephant skin formation on UHPC surface: Effects of climatic condition and blast furnace slag content. Constr. Build. Mater. 2021, 268, 121126. [Google Scholar] [CrossRef]
- Li, Z.; Ding, Z. Property improvement of Portland cement by incorporating with metakaolin and slag. Cem. Concr. Res. 2003, 33, 579–584. [Google Scholar] [CrossRef]
- Kovler, K.; Zhutovsky, S. Overview and future trends of shrinkage research. Mater. Struct. 2006, 39, 827–847. [Google Scholar] [CrossRef]
- Zhang, Y.; Afroz, S.; Nguyen, Q.; Kim, T.; Nguyen, D.; Castel, A.; Nairn, J.; Gilbert, R. Autogenous Shrinkage of Fly Ash and Ground Granulated Blast Furnace Slag Concrete. Mag. Concr. Res. 2023, 75, 283–295. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K.; Kim, B. Autogenous shrinkage of high-performance concrete containing fly ash. Mag. Concr. Res. 2003, 55, 507–515. [Google Scholar] [CrossRef]
- Yan, P.; Chen, Z. Autogenous Shrinkage of Fly Ash Concrete with Different Water Binder Ratio. In Proceedings of the 8th International Symposium on Cement & Concrete, Nanjing, China, 20–23 September 2013. [Google Scholar]
- Afroz, S.; Zhang, Y.; Nguyen, Q.; Kim, T.; Castel, A. Effect of limestone in General Purpose cement on autogenous shrinkage of high strength GGBFS concrete and pastes. Constr. Build. Mater. 2022, 327, 126949. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, J.; Zhao, S. Experimental study on shrinkage of HPC containing fly ash and ground granulated blast-furnace slag. Constr. Build. Mater. 2017, 155, 145–153. [Google Scholar] [CrossRef]
- Lim, S.; Wee, T. Autogenous shrinkage of ground-granulated B last-furnace slag concrete. ACI Struct. J. 2000, 97, 587–593. [Google Scholar]
- Wei, Y.; Hansen, W.; Biernacki, J.; Schlangen, E. Unified Shrinkage Model for Concrete from Autogenous Shrinkage Test on Paste with and without Ground-Granulated Blast-Furnace Slag. ACI Mater. J. 2011, 108, 13–20. [Google Scholar]
- Nath, P.; Sarker, P. Effect of Mixture Proportions on the Drying Shrinkage and Permeation Properties of High Strength Concrete Containing Class F Fly Ash. KSCE J. Civ. Eng. 2013, 17, 1437–1445. [Google Scholar] [CrossRef]
- Seo, T.; Lee, M.; Choi, C.; Ohno, Y. Properties of drying shrinkage cracking of concrete containing fly ash as partial replacement of fine aggregate. Mag. Concr. Res. 2010, 62, 427–433. [Google Scholar] [CrossRef]
- Yuan, J.; Lindquist, W.; Darwin, D.; Browning, J. Effect of slag cement on drying shrinkage of concrete. ACI Mater. J. 2015, 112, 267–276. [Google Scholar] [CrossRef]
- Saluja, S.; Kaur, K.; Goyal, S.; Bhattacharjee, B. Long-Term Drying Shrinkage of GGBFS-Incorporated RCC under Various Temperature Exposures. J. Mater. Civ. Eng. 2021, 33, 04021122. [Google Scholar] [CrossRef]
- Liu, J.; Yu, J.; Hu, S.; Hu, C.; Wang, J.; Yu, Z.; Huang, K. Analysis of crack evolution of expansive soil embankment under extreme arid climate. Case Stud. Constr. Mater. 2024, 20, e02902. [Google Scholar] [CrossRef]
- Wei, J.; Farzadnia, N.; Khayat, K. Synergistic effect of macro synthetic fiber and shrinkage-reducing admixture on engineering properties of fiber-reinforced super-workable concrete. Constr. Build. Mater. 2024, 414, 134566. [Google Scholar] [CrossRef]
- Zhou, F.; Huang, J.; Jian, S.; Tan, H.; Lv, Y.; Hu, H.; Wang, W.; Yang, R.; Manuka, M.; Yin, Y.; et al. Photocurable resin as rapid in-situ protective coating for slag concrete against dry shrinkage. Constr. Build. Mater. 2023, 396, 132171. [Google Scholar] [CrossRef]
- Dong, D.; Huang, Y.; Pei, Y.; Zhang, X.; Cui, N.; Zhao, P.; Hou, P.; Lu, L. Effect of spherical silica fume and fly ash on the rheological property, fluidity, setting time, compressive strength, water resistance and drying shrinkage of magnesium ammonium phosphate cement. J. Build. Eng. 2023, 63, 105484. [Google Scholar] [CrossRef]
- Neville, A.; Dilger, W.; Brooks, J. Creep of Plain and Structural Concrete; Construction Press: London, UK; New York, NY, USA, 1983. [Google Scholar]
- Han, B.; Xie, H.; Zhu, L.; Jiang, P. Nonlinear model for early age creep of concrete under compression strains. Constr. Build. Mater. 2017, 147, 203–211. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, X.; Jiang, J. Effect of curing temperature on creep behavior of fly ash concrete. Constr. Build. Mater. 2015, 96, 326–333. [Google Scholar] [CrossRef]
- Wei, Y.; Hansen, W. Tensile Creep Behavior of Concrete Subject to Constant Restraint at Very Early Ages. J. Mater. Civ. Eng. 2013, 25, 1277–1284. [Google Scholar] [CrossRef]
- Khan, I.; Xu, T.; Khan, M.; Castel, A.; Gilbert, R. Effect of Various Supplementary Cementitious Materials on Early-Age Concrete Cracking. J. Mater. Civ. Eng. 2020, 32, 04020049. [Google Scholar] [CrossRef]
- Shariq, M.; Prasad, J.; Abbas, H. Creep and drying shrinkage of concrete containing GGBFS. Cem. Concr. Compos. 2016, 68, 35–45. [Google Scholar] [CrossRef]
- Zhu, B. Thermal Stresses & Temperature Control of Mass Concrete; Tsinghua University Press: Beijing, China, 2014. [Google Scholar]
- ACI Committee 207. ACI207.1R-05: Guide to Mass Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2012. [Google Scholar]
- Ha, J.; Jung, Y.; Cho, Y. Thermal crack control in mass concrete structure using an automated curing system. Autom. Constr. 2014, 45, 16–24. [Google Scholar] [CrossRef]
- Bamforth, P.; Oenton, S. Early-age Thermal Crack Control in Concrete—Changes in UK design resulting from the introduction of EN1992. In Proceedings of the 11th Annual International Fib Symposium—Concrete: 21st Century Superhero: Building a Sustainable Future, London, UK, 22–24 June 2009. [Google Scholar]
- Kada, H.; Lachemi, M.; Petrov, N.; Bonneau, O.; Aitcin, P.-C. Determination of the coefficient of thermal expansion of high performance concrete from initial setting. Mater. Struct. 2002, 35, 35–41. [Google Scholar] [CrossRef]
- Tang, P.; Wen, J.; Fu, Y.; Liu, X.; Chen, W. Improving the early-age properties of eco-binder with high volume waste gypsum: Hydration process and ettringite formation. J. Build. Eng. 2024, 86, 108988. [Google Scholar] [CrossRef]
- Springenschmid, R.; Breitenbücher, R. Influence of Constituents, Mix Proportions and Temperature on Cracking Sensitivity of Concrete. In Prevention of Thermal Cracking in Concrete; RILEM Report 15; CRC Press: London, UK, 1998. [Google Scholar]
- De Schutter, G.; Taerwe, L. Degree of Hydration-Based Description of Mechanical Properties of Early Age Concrete. Mater. Struct. 1996, 29, 335–344. [Google Scholar] [CrossRef]
- Gutsch, A. Properties of early age concrete—Experiments and modelling. Mater. Struct. 2002, 34, 76–79. [Google Scholar]
- Igarashi, S.; Bentur, A.; Kovler, K. Autogenous shrinkage and induced restraining stresses in high-strength concretes. Cem. Concr. Res. 2000, 30, 1701–1707. [Google Scholar] [CrossRef]
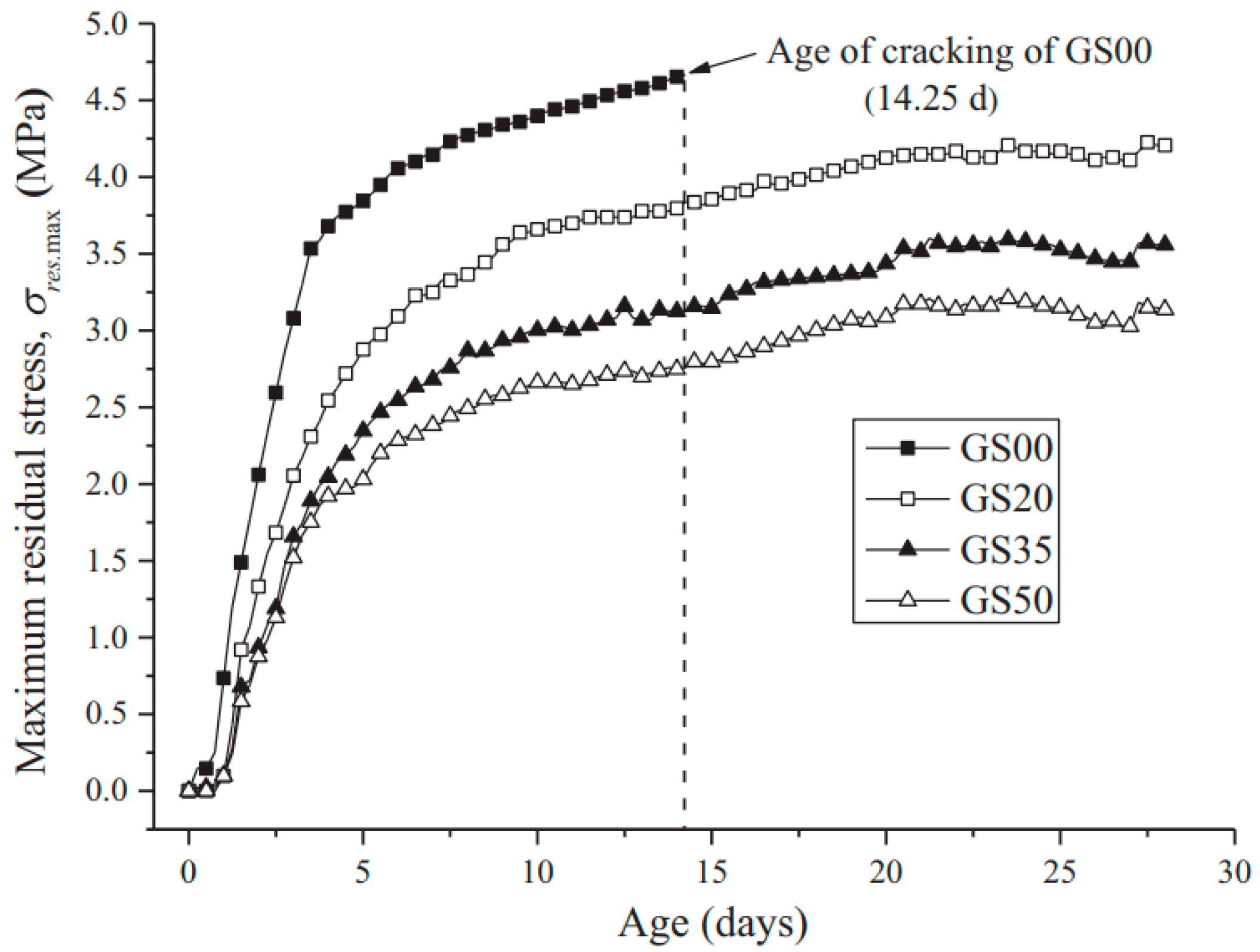
- Shen, D.; Liu, K.; Wen, C.; Shen, Y.; Jiang, G. Early-age cracking resistance of ground granulated blast furnace slag concrete. Constr. Build. Mater. 2019, 222, 278–287. [Google Scholar] [CrossRef]
- Khan, I.; Castel, A.; Gilbert, R. Tensile creep and early-age concrete cracking due to restrained shrinkage. Constr. Build. Mater. 2017, 149, 705–715. [Google Scholar] [CrossRef]
- Zhang, Y.; Afroz, S.; Nguyen, Q.; Kim, T.; Eisentrager, J.; Castel, A.; Xu, T. Analytical model predicting the concrete tensile stress development in the restrained shrinkage ring test. Constr. Build. Mater. 2021, 307, 124930. [Google Scholar] [CrossRef]
- Kawabata, Y.; Ueda, N.; Miura, T.; Multon, S. The influence of restraint on the expansion of concrete due to delayed ettringite formation. Cem. Concr. Compos. 2021, 121, 104062. [Google Scholar] [CrossRef]
- Zych, M. Degree of external restraint of wall segments in semi-massive reinforced concrete tanks: Part I rectangular segments. Struct. Concr. 2018, 19, 820–828. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, Z.; Si, R.; Zhang, Y. Effect of Various Fly Ash and Ground Granulated Blast Furnace Slag Content on Concrete Properties: Experiments and Modelling. Materials 2022, 15, 3016. [Google Scholar] [CrossRef] [PubMed]
- Altoubat, S.; Junaid, M.; Leblouba, M.; Badran, D. Effectiveness of fly ash on the restrained shrinkage cracking resistance of self-compacting concrete. Cem. Concr. Compos. 2017, 79, 9–20. [Google Scholar] [CrossRef]
- Shen, D.; Jiao, Y.; Kang, J.; Feng, Z.; Shen, Y. Influence of ground granulated blast furnace slag on early-age cracking potential of internally cured high performance concrete. Constr. Build. Mater. 2020, 233, 117083. [Google Scholar] [CrossRef]
- Mehta, P.; Monteiro, J. Concrete: Microstructure, Properties and Materials; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
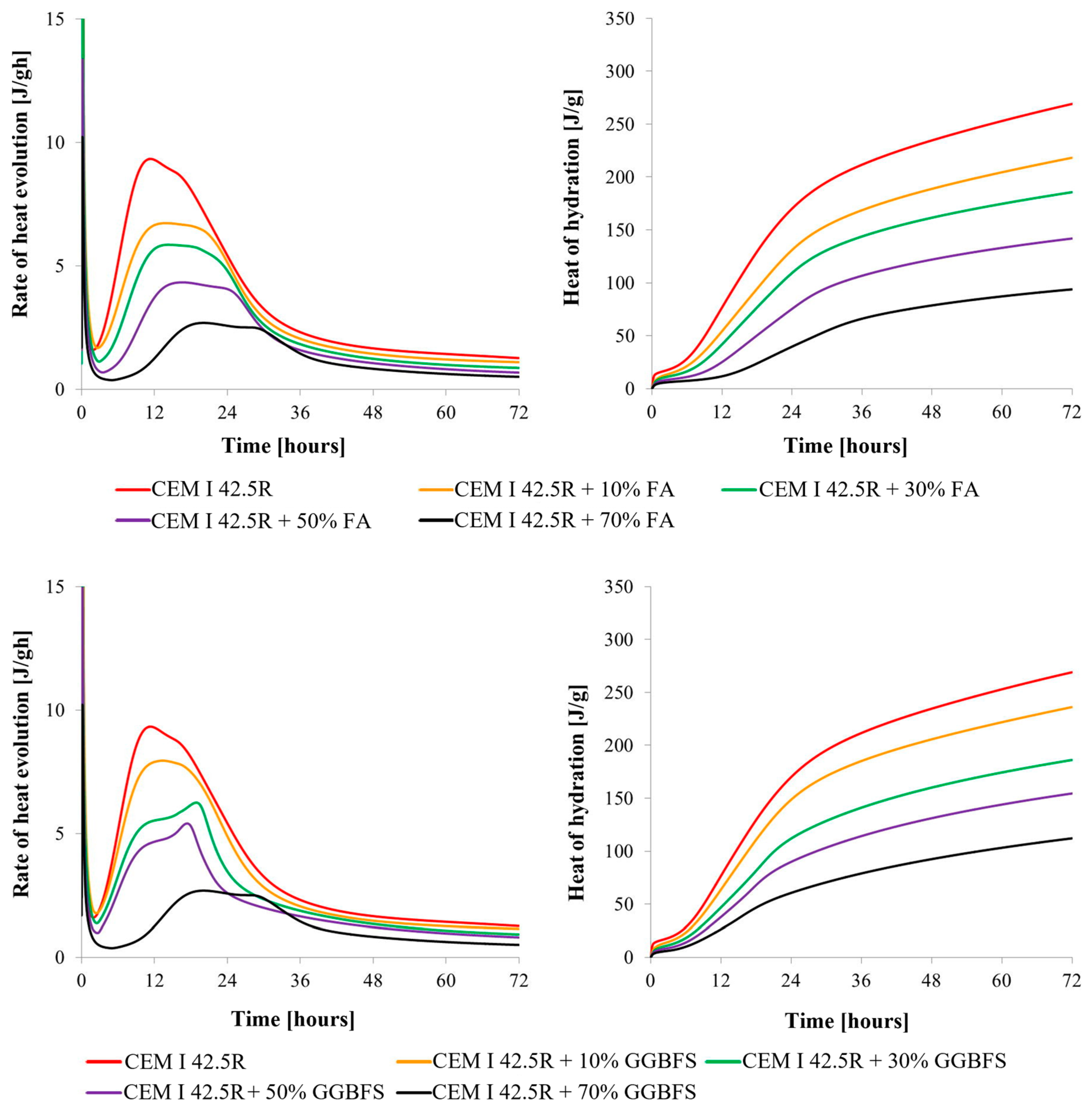
- Ballim, Y.; Graham, P. The effects of supplementary cementing materials in modifying the heat of hydration of concrete. Mater. Struct. 2009, 42, 803–811. [Google Scholar] [CrossRef]
- Kim, G.; Lee, E.; Nam, J.; Koo, K. Analysis of hydration heat and autogenous shrinkage of high-strength mass concrete. Mag. Concr. Res. 2011, 63, 377–389. [Google Scholar] [CrossRef]
- Batog, M.; Giergiczny, Z. Influence of mass concrete constituents on its properties. Constr. Build. Mater. 2017, 146, 221–230. [Google Scholar] [CrossRef]
- Markandeya, A.; Shanahan, N.; Gunatilake, D.; Riding, K.; Zayed, A. Influence of slag composition on cracking potential of slag-portland cement concrete. Constr. Build. Mater. 2018, 164, 820–829. [Google Scholar] [CrossRef]
- ACI Committee 209. ACI209R: Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures; American Concrete Institute Committee 209: Farmington Hills, MI, USA, 2008. [Google Scholar]
- FIB. fib Model Code for Concrete Structures; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010. [Google Scholar]
- Bazant, Z. RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: Material model and structural analysis* Model B4 for creep, drying shrinkage and autogenous shrinkage of normal and high-strength concretes with multi-decade applicability. Mater. Struct. 2015, 48, 753–770. [Google Scholar]
- Gardner, N.; Lockman, M. Design provisions for drying shrinkage and creep of normal strength concrete. ACI Mater. J. 2001, 98, 159–167. [Google Scholar]
- AS3600-2018; Australian Standard for Concrete Structures. Standards Australia: Sydney, Australia, 2018.
- Eurocode 2 and EN 19920101; Design of Concrete Structures. General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Goel, R.; Kumar, R.; Paul, D. Comparative study of various creep and shrinkage prediction models for concrete. J. Mater. Civ. Eng. 2007, 19, 249–260. [Google Scholar] [CrossRef]
- Al-Manaseer, A.; Prado, A. Statistical comparisons of creep and shrinkage prediction models using RILEM and NU-ITI databases. ACI Mater. J. 2015, 112, 125–136. [Google Scholar] [CrossRef]
- Kataoka, L.; MacHado, M.; Bittencourt, T. Short-term experimental data of drying shrinkage of ground granulated blast-furnace slag cement concrete. Mater. Struct. 2011, 44, 671–679. [Google Scholar] [CrossRef]
- Bazant, Z.; Murphy, W. Creep and shrinkage prediction model for analysis and design of concrete structures—Model B3. Mater. Struct. 1995, 28, 357–365. [Google Scholar]
- Østergaard, L.; Lange, D.; Altoubat, S.; Stang, H. Tensile basic creep of early-age concrete under constant load. Cem. Concr. Res. 2001, 31, 1895–1899. [Google Scholar] [CrossRef]
- D’Ambrosia, M.; Lange, D.A.; Grasley, Z.C. Measurement and Modeling of Concrete Tensile Creep and Shrinkage at Early Age; ACI Special Publication; American Concrete Institute: Farmington Hills, MI, USA, 2004; Volume SP-220, pp. 99–112. [Google Scholar]
- Dabarera, A.; Li, L.; Dao, V. Experimental evaluation and modelling of early-age basic tensile creep in high-performance concrete. Mater. Struct. 2021, 54, 130. [Google Scholar] [CrossRef]
- Ji, G.; Kanstad, T.; Bjøntegaard, O.; Sellevold, E. Tensile and compressive creep deformations of hardening concrete containing mineral additives. Mater. Struct. 2013, 46, 1167–1182. [Google Scholar] [CrossRef]
- Atrushi, D. Tensile and Compressive Creep of Early Age Concrete: Testing and Modelling. Ph.D. Thesis, The Norwegian University of Science and Technology, Trondheim, Norway, 2003. [Google Scholar]
- Zhang, Y.; Afroz, S.; Nguyen, Q.; Kim, T.; Castel, A.; Xu, T. Modeling blended cement concrete tensile creep for standard ring test application. Struct. Concr. 2022, 24, 2170–2188. [Google Scholar] [CrossRef]
- Carlson, R.; Reading, T. Model of studying shrinkage cracking in concrete building walls. ACI Struct. J. 1988, 85, 395–404. [Google Scholar]
- Swamy, R.; Stavrides, H. Influence of fiber reinforcement on restraint shrinkage and cracking. ACI Mater. J. 1979, 76, 443–460. [Google Scholar]
- Bloom, R.; Bentur, A. Free and restrained shrinkage of normal and high-strength concretes. ACI Mater. J. 1995, 92, 211–217. [Google Scholar]
- Altoubat, S.; Lange, D. A New Look at Tensile Creep of Fiber Reinforced Concrete. In ACI Special Publication on Fiber Reinforced Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2003. [Google Scholar]
- Banthia, N.; Yan, C.; Mindess, S. Restrained shrinkage cracking in fiber reinforced concrete—A novel test technique. Cem. Concr. Res. 1996, 26, 9–14. [Google Scholar] [CrossRef]
- Weiss, J.; Yang, W.; Shah, S. Shrinkage cracking of restrained concrete slabs. J. Eng. Mech. 1998, 124, 765–774. [Google Scholar] [CrossRef]
- Hossain, A.; Weiss, J. Assessing residual stress development and stress relaxation in restrained concrete ring specimens. Cem. Concr. Compos. 2004, 26, 531–540. [Google Scholar] [CrossRef]
- Shen, D.; Shi, H.; Tang, X.; Ji, Y.; Jiang, G. Effect of internal curing with super absorbent polymers on residual stress development and stress relaxation in restrained concrete ring specimens. Constr. Build. Mater. 2016, 120, 309–320. [Google Scholar] [CrossRef]
- See, H.; Attiogbe, E.; Miltenberger, M. Shrinkage cracking characteristics of concrete using ring specimens. ACI Mater. J. 2003, 100, 239–245. [Google Scholar]




| Parameters | ACI209-R92 | fib 2010 | GL 2000 | B4 | AS3600-2018 | Eurocode 2 |
|---|---|---|---|---|---|---|
| Compressive strength at 28 days | Yes | Yes | Yes | Yes | ||
| Elastic modulus of concrete at loading | Yes | |||||
| Type of cement | Yes | Yes | Yes | Yes | ||
| Curing method | Yes | Yes | Yes | |||
| Age of concrete at loading | Yes | Yes | Yes | Yes | Yes | Yes |
| Relative humidity | Yes | Yes | Yes | Yes | Yes | |
| Volume to surface ratio | Yes | Yes | Yes | Yes | ||
| Slump | Yes | |||||
| Fine aggregate content | Yes | |||||
| Air content | Yes | |||||
| Shape of section | Yes | |||||
| w/c ratio | Yes | |||||
| a/c ratio | Yes | |||||
| Admixtures | Yes | |||||
| Hypothetical thickness | Yes | Yes | ||||
| Location | Yes |
| Parameters | ACI209-R92 | fib 2010 | GL 2000 | B4 | AS3600-2018 | Eurocode 2 |
|---|---|---|---|---|---|---|
| Compressive strength at 28 days | Yes | Yes | Yes | Yes | Yes | |
| Elastic modulus of concrete at loading | Yes | Yes | Yes | Yes | Yes | Yes |
| Type of cement | Yes | Yes | Yes | Yes | ||
| Curing method | Yes | Yes | Yes | |||
| Age of concrete at loading | Yes | Yes | Yes | Yes | Yes | Yes |
| Relative humidity | Yes | Yes | Yes | Yes | Yes | |
| Volume to surface ratio | Yes | Yes | Yes | Yes | ||
| Slump | Yes | |||||
| Fine aggregate content | Yes | |||||
| Air content | Yes | |||||
| Shape of section | Yes | |||||
| w/c ratio | Yes | |||||
| a/c ratio | Yes | |||||
| Admixtures | Yes | |||||
| Hypothetical thickness | Yes | Yes | ||||
| Location | Yes | |||||
| Nonlinear creep | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, X.; Xu, Z.; Yuan, W.; Xu, Y.; Yao, Z.; Liu, Z.; Si, R. Early-Age Cracking of Fly Ash and GGBFS Concrete Due to Shrinkage, Creep, and Thermal Effects: A Review. Materials 2024, 17, 2288. https://doi.org/10.3390/ma17102288
Zhang Y, Liu X, Xu Z, Yuan W, Xu Y, Yao Z, Liu Z, Si R. Early-Age Cracking of Fly Ash and GGBFS Concrete Due to Shrinkage, Creep, and Thermal Effects: A Review. Materials. 2024; 17(10):2288. https://doi.org/10.3390/ma17102288
Chicago/Turabian StyleZhang, Yingda, Xinyue Liu, Ziyi Xu, Weiguang Yuan, Yong Xu, Zuobang Yao, Zihao Liu, and Ruizhe Si. 2024. "Early-Age Cracking of Fly Ash and GGBFS Concrete Due to Shrinkage, Creep, and Thermal Effects: A Review" Materials 17, no. 10: 2288. https://doi.org/10.3390/ma17102288
APA StyleZhang, Y., Liu, X., Xu, Z., Yuan, W., Xu, Y., Yao, Z., Liu, Z., & Si, R. (2024). Early-Age Cracking of Fly Ash and GGBFS Concrete Due to Shrinkage, Creep, and Thermal Effects: A Review. Materials, 17(10), 2288. https://doi.org/10.3390/ma17102288







