An Adaptive Virtual Inertial Control Strategy for DC Distribution Networks
Abstract
:1. Introduction
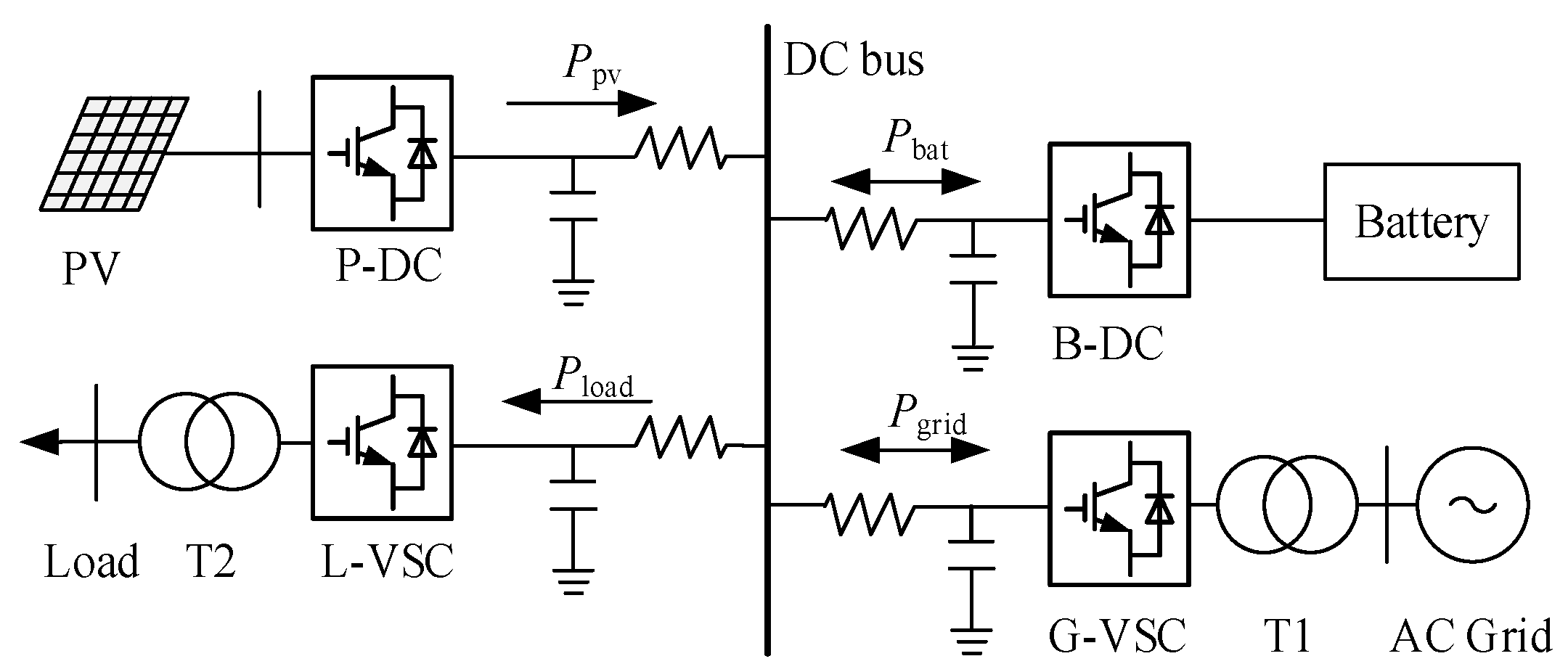
2. DC Distribution Network Topology
- (a)
- Grid-connected converter: The AC grid is connected to the AC grid through the converter G-VSC, which adopts droop control and controls the DC bus voltage together with B-DC.
- (b)
- Distributed power: The PV array is connected to the DC grid by converter P-DC, which adopts maximum power tracking (MPPT).
- (c)
- Energy storage system: The battery is connected to the DC grid through the converter B-DC, which adopts droop control to control the DC bus voltage.
- (d)
- Load system: The AC loads in the grid are connected to the DC grid through the AC/DC converter L-VSC, which adopts constant voltage to control AC loads.
3. Virtual Inertia of the Power Grid
3.1. Inherent Inertia of the AC Grid
3.2. Inherent Inertia of the DC Grid
3.3. Virtual Inertia of the DC Grid
3.4. Calculation of Virtual Capacitance Size
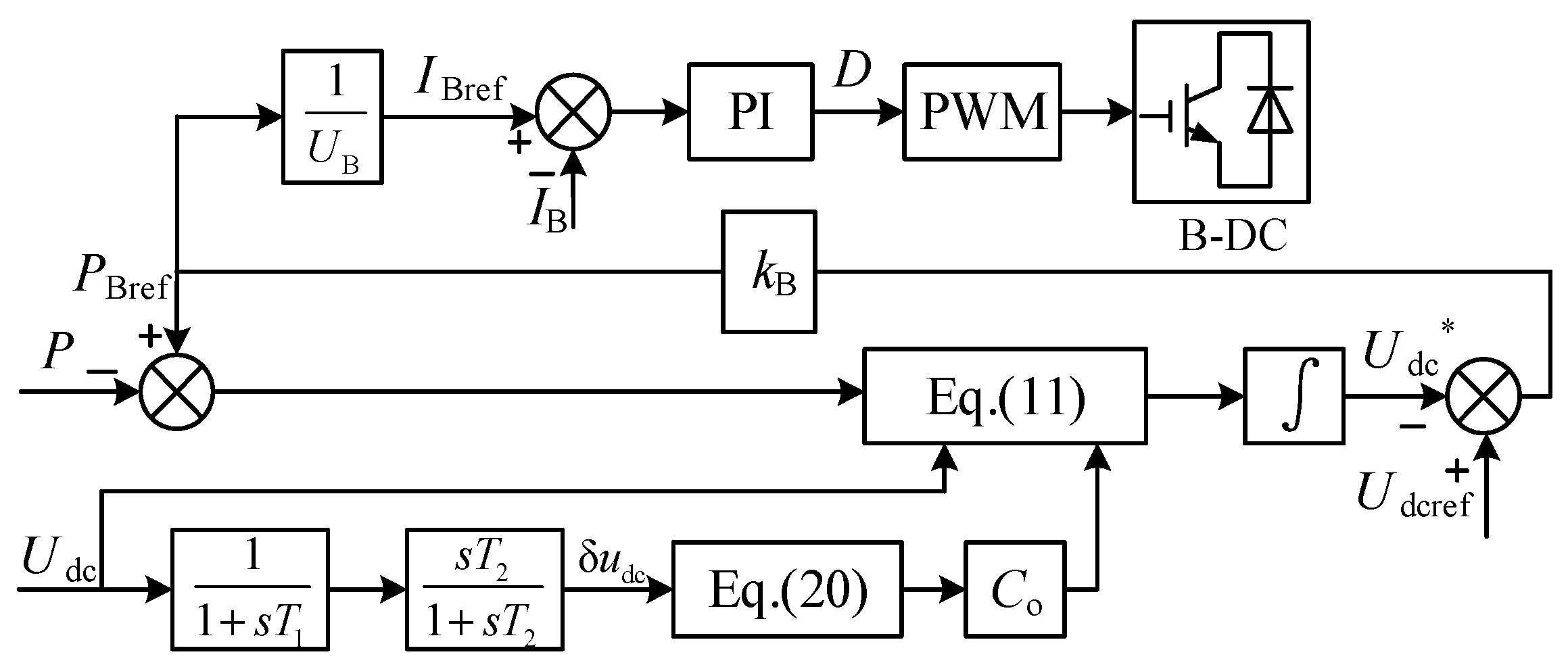
4. Adaptive Virtual Capacitance Control Strategy
4.1. Flexible Virtual Capacitance Control Strategy
4.2. An Improved Flexible Virtual Capacitance Strategy
4.3. An Adaptive Virtual Inertial Control Strategy for the DC Distribution Network
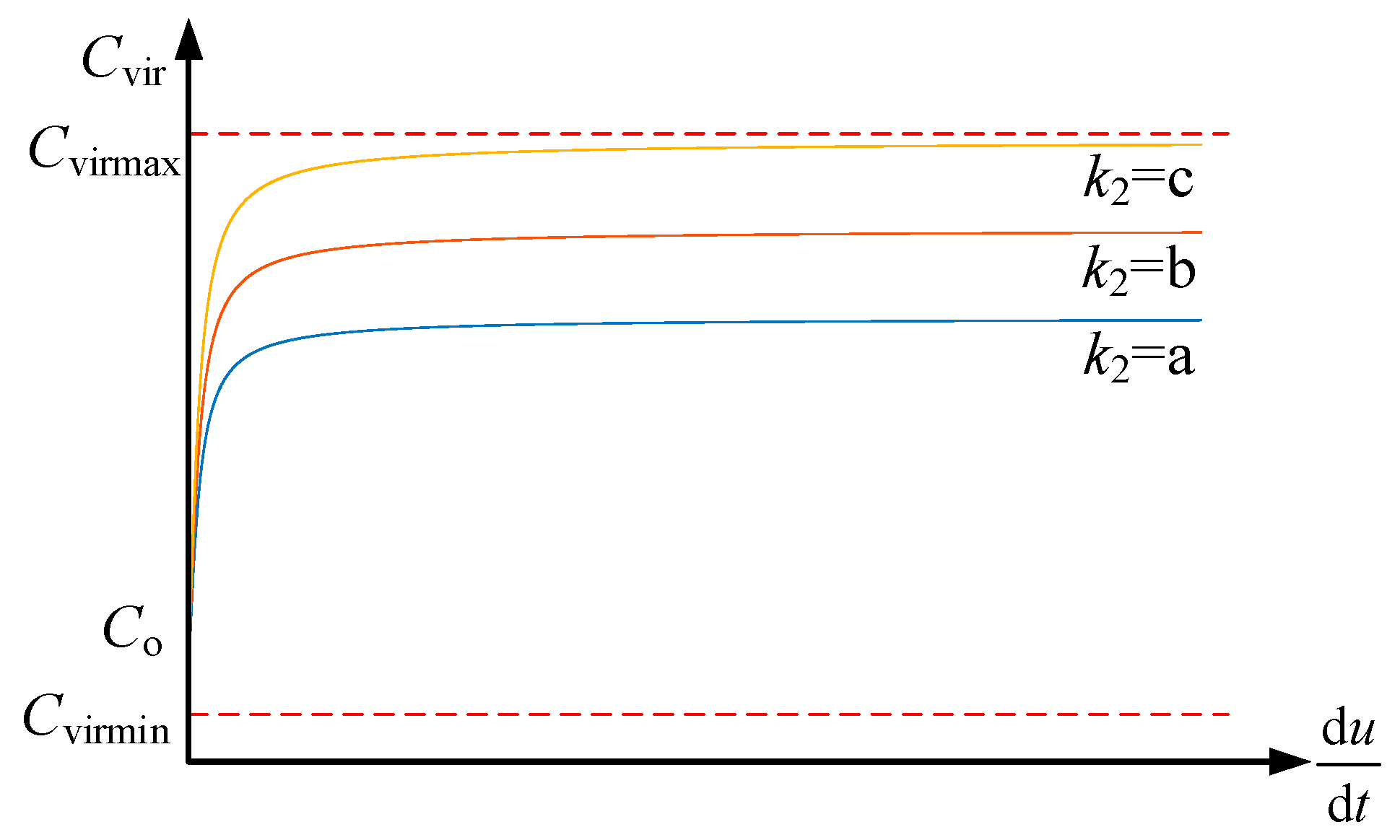
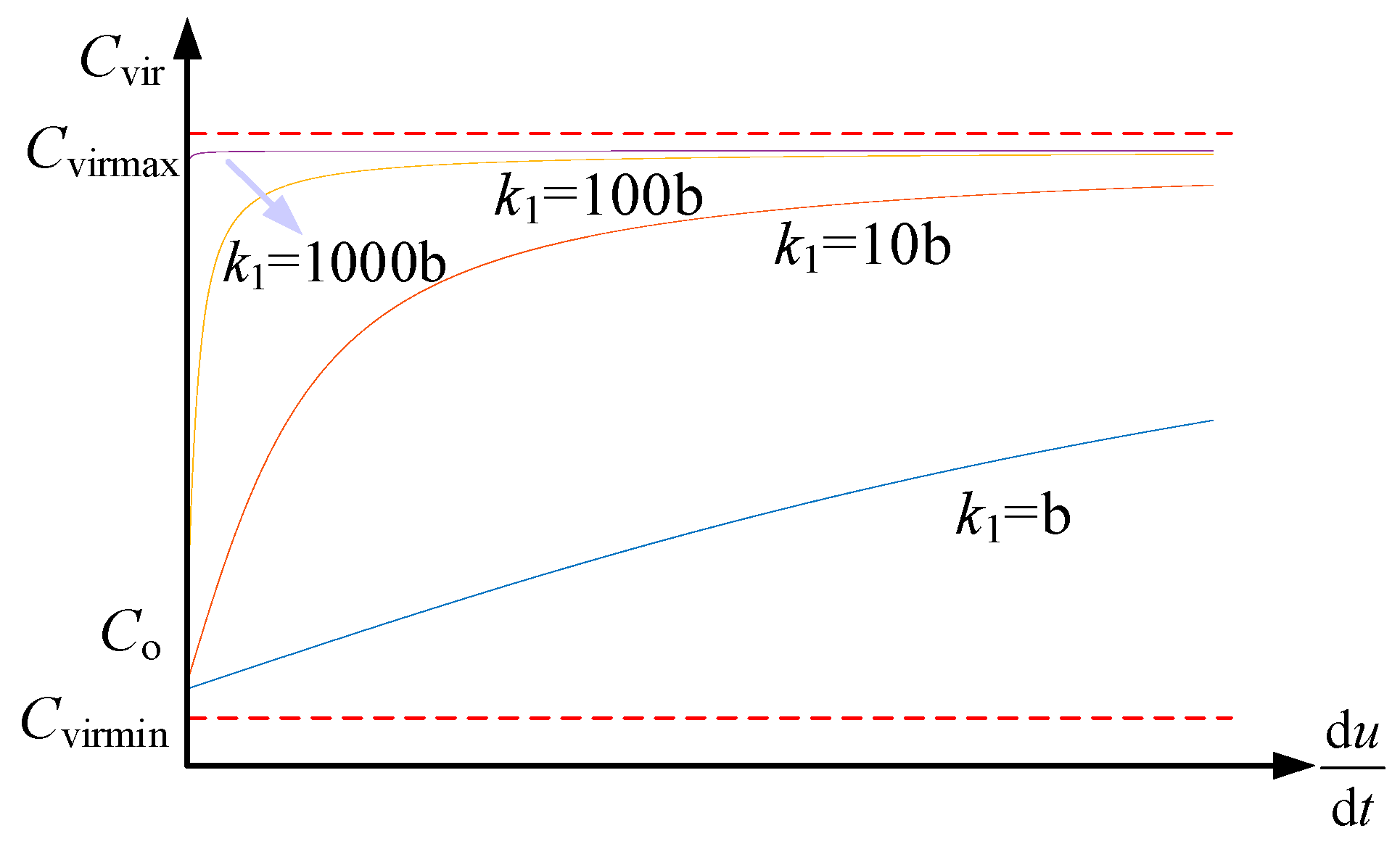
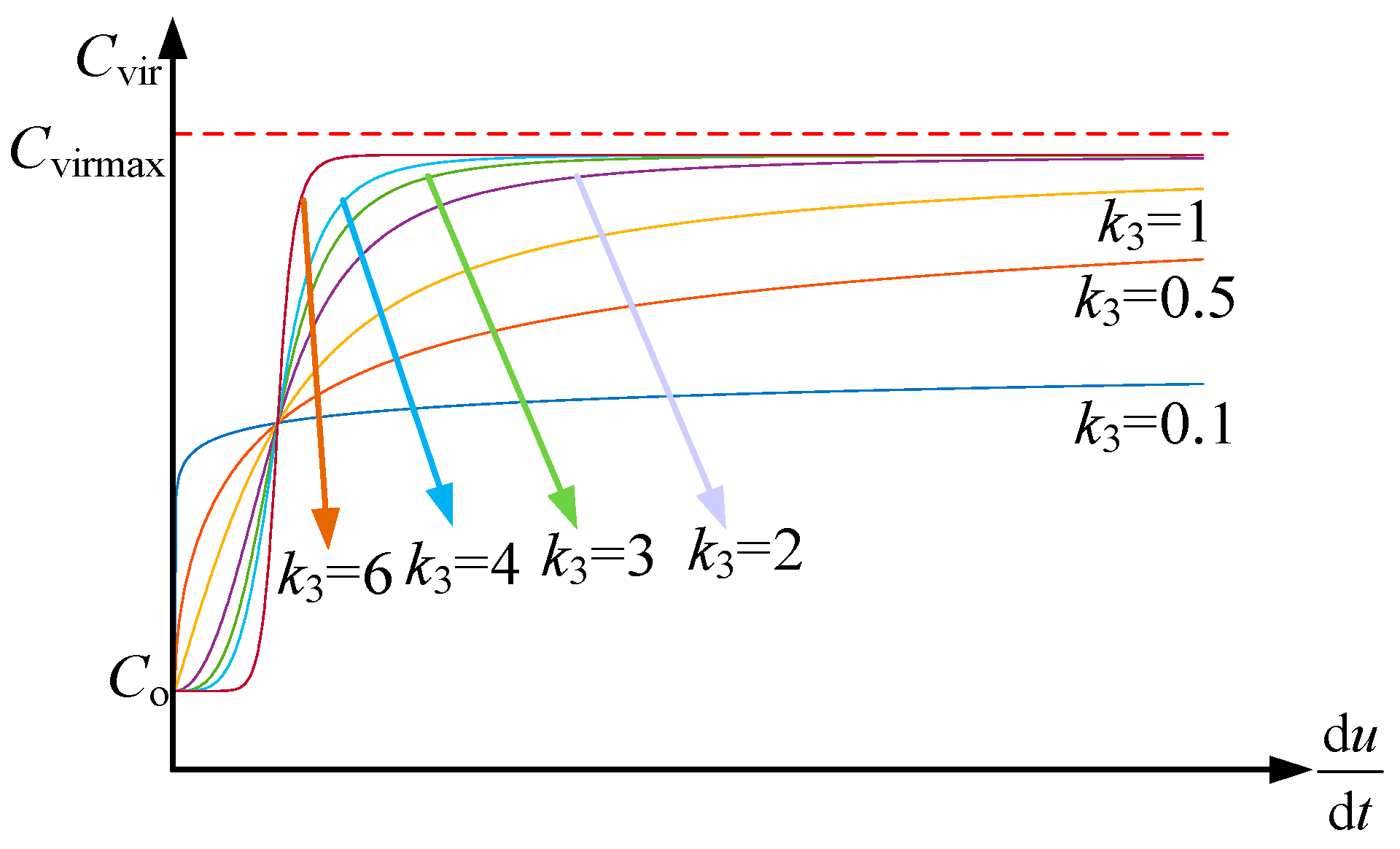
4.4. Parametric Analyses
- (1)
- Analysis of the k2 parameter.
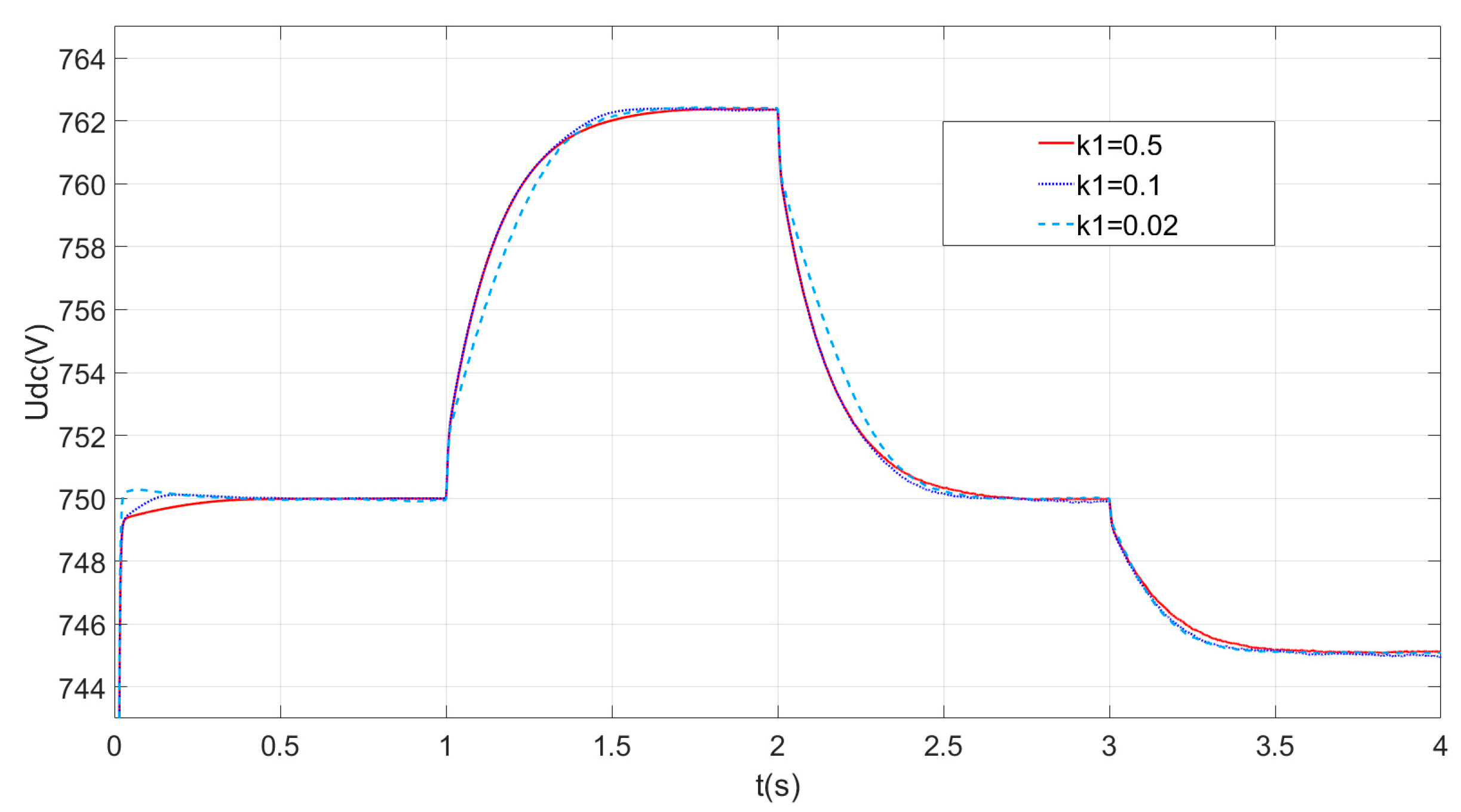
- (2)
- Analysis of the k1 parameter.
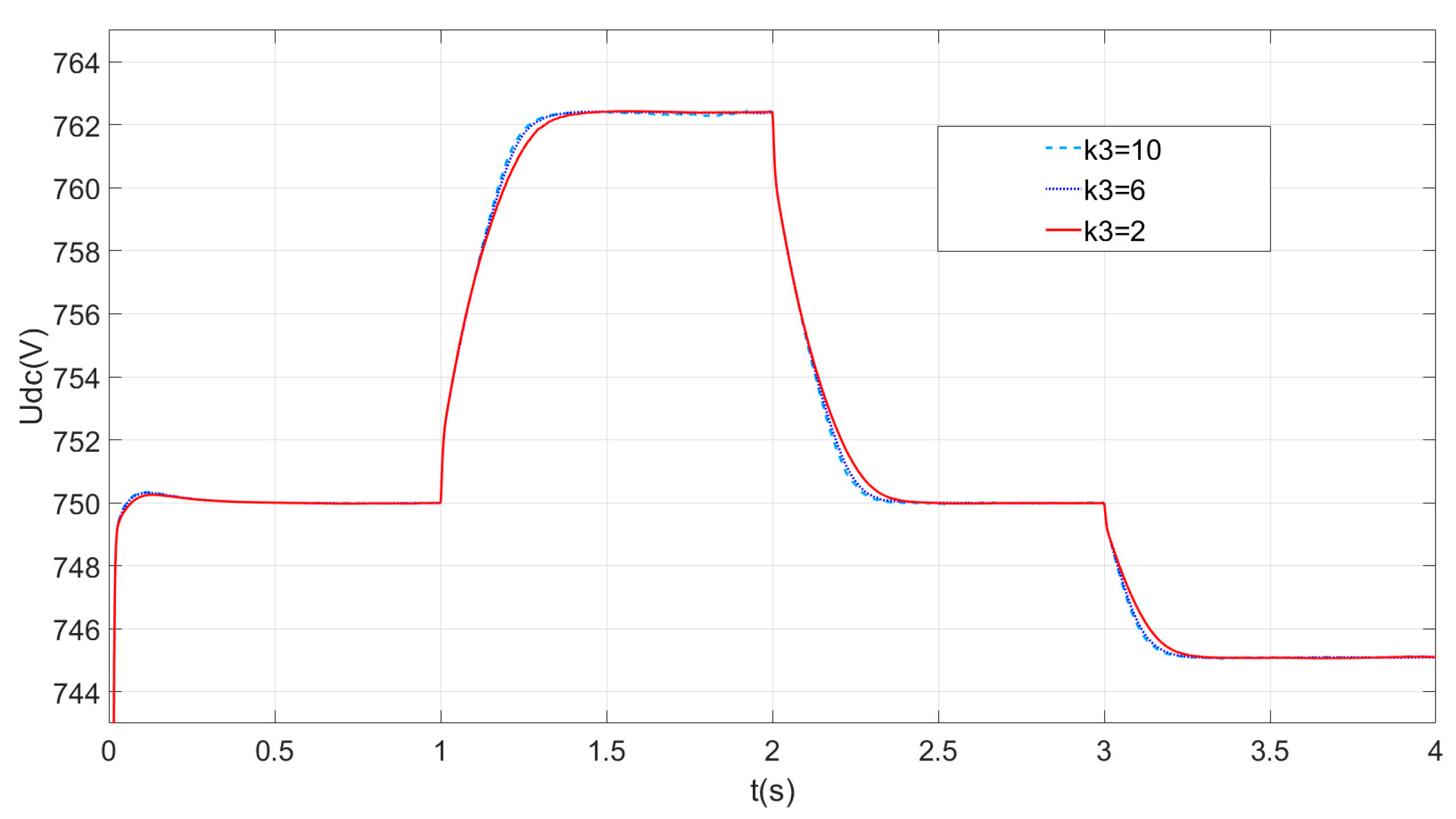
- (3)
- Analysis of the k3 parameter.
5. Simulation and Analysis
5.1. Simulation Analysis of Power Mutation
5.2. Simulation Analysis of Different Parameters
6. Conclusions
- (1)
- A virtual capacitance adaptive control strategy is proposed, which can adaptively change the virtual capacitance size during load fluctuation and provide flexible inertia support for the DC side by utilizing the converter of the energy storage system to quickly release and absorb energy, which improves the dynamic performance of the system.
- (2)
- A direct calculation of the virtual capacitance of this control strategy is proposed, and the effect of the virtual capacitance size on the system is qualitatively analyzed and simulated experimentally.
- (3)
- The strategy can effectively improve the dynamic performance of the DC distribution network when the parameters are within the appropriate range. Through the combination of the inverse tangent function and power function, it can effectively eliminate small disturbances and quickly respond to large disturbances, while maximizing the virtual inertia support.
- (4)
- By adopting this strategy on the battery side and combining it with the widespread application of droop control in the DC grid, it can effectively reduce the impact of the DC system on the AC grid, which has certain practical advantages.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, R.; Zhao, Y.M.; Zhao, B.; Zhong, Q.; Tong, Y.; Yuan, Z.; Yu, Z.; Zhao, Z.; Li, Y.; Chen, J. Aprospective look on research and application of DC powerdistribution technology. Proc. CSEE 2018, 38, 6791–6801. [Google Scholar]
- Wang, S.X.; Liu, Q.; Xue, S.M.; Yuan, D.; Wang, C.; Yang, J. Key technologies and prospect for coordinated control and protection in DC distribution system. Autom. Electr. Power Syst. 2019, 43, 23–30. [Google Scholar]
- Jiang, S.H.; Peng, K.; Xu, B.Y.; Zhang, X.; Liu, Y. Current situation and prospect of demonstration projects of DC distribution system. Electr. Power Autom. Equip. 2021, 41, 219–231. [Google Scholar]
- Liu, L.; Lin, G.; Jiao, S.Q.; An, B.; Li, Y.; Wang, Z.; Wang, S. Virtual DC generator control strategy and its dynamic analysis of DC charging station microgrid. Power Syst. Prot. Control 2020, 48, 28–35. [Google Scholar]
- Jami, M.; Shafiee, Q.; Gholami, M.; Bevrani, H. Control of a super-capacitor energy storage system to mimic inertia and transient response improvement of a direct current micro-grid. J. Energy Storage 2020, 32, 101788. [Google Scholar] [CrossRef]
- Sun, D.; Liu, H.; Gao, S.; Wu, L.; Song, P.; Wang, X. Comparison of Different Virtual Inertia Control Methods for Inverter-based Generators. J. Mod. Power Syst. Clean Energy 2020, 8, 768–777. [Google Scholar] [CrossRef]
- Wang, Q.G.; Zhou, Y.Y.; Liao, J.Q.; Zhou, N.C.; Zhang, X.F.; Zhang, Y. Review on Power Quality in DC Distribution Network. Autom. Electr. Power Syst. 2023, 47, 193–207. [Google Scholar]
- dos Santos Neto, P.J.; dos Santos Barros, T.A.; Silveira, J.P.C.; Ruppert Filho, E.; Vasquez, J.C.; Guerrero, J.M. Power management strategy based on virtual inertia for DC microgrids. IEEE Trans. Power Electron. 2020, 35, 12472–12485. [Google Scholar] [CrossRef]
- Cao, X.H.; Liu, Y.L.; Miao, S.H.; Li, L.; Liu, Z.; Li, Z. Research on virtual inertial control strategy of DC/DC converter in DC microgrid considering self-adaptive parameters. High Volt. Eng. 2020, 46, 1281–1290. [Google Scholar]
- Jiang, Z.H.; Liu, L.G.; Liu, Z.F. Research on Power Flow Control and the Voltage Fluctuation Characteristics of DC Distribution Networks Based on Different Control Strategies. Proc. CSEE 2016, 36, 919–926. [Google Scholar]
- Li, Y.; He, L.; Liu, F. Flexible voltage control strategy considering distributed energy storages for DC distribution network. IEEE Trans. Smart Grid 2019, 10, 163–172. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.L.; Li, S.; Shao, Z.; Chen, X. Power distribution and virtual inertia control of photovoltaic and hybrid energy storage system based on VSG. Electr. Power Autom. Equip. 2023, 43, 27–34. [Google Scholar]
- Wang, Y.; Hei, Y.; Fu, Y.; Shi, K. Adaptive Virtual Inertia Control of DC Distribution Network Based on Variable Droop Coefficient. Autom. Electr. Power Syst. 2017, 41, 116–124. [Google Scholar]
- Wang, H.; Zhao, S.Q.; Meng, J.H.; Wang, C.; Tian, Y. Adaptive Virtual Inertia Control for DC Microgrid Based on Droop Curve Intercept Adjustment. Autom. Electr. Power Syst. 2021, 45, 97–105. [Google Scholar]
- Li, C.; Zhang, X.; He, P.; Zhen, Z.; Zhao, K. Adaptive Droop Control of VSC-MTDC System Based on Virtual Inertia. Electronics 2023, 12, 2324. [Google Scholar] [CrossRef]
- Meng, J.H.; Zou, P.G.; Wang, Y.; Wang, C. Small-signalmodeling and parameter analysis of the DC microgrid based on flexible virtual inertia control. Trans. China Electrotech. Soc. 2019, 32, 2615–2626. [Google Scholar]
- Wu, W.H.; Chen, Y.D.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L. A Virtual Inertia Control Strategy for Bidirectional Grid-connected Converters in DC Micro-grids. Proc. CSEE 2017, 37, 360–371. [Google Scholar]
- Chen, W.Q.; Xin, X.N.; Cheng, Z.P. Control of Grid-Connected of Photovoltaic System with Storage Based on Virtual Synchronous Generator. Trans. China Electrotech. Soc. 2018, 33, 538–545. [Google Scholar]
- Fu, Y.; Du, F.X.; Zhang, X.Y. Voltage hierarchical transient stability control of DC microgrid. Renew. Energy Resour. 2022, 40, 1105–1114. [Google Scholar]
- Chen, Y.Z.; Zhao, Q. Segmented Virtual Inertia Control Strategy for DC Distribution Networks. Electr. Autom. 2021, 43, 66–68. [Google Scholar]
- Zhu, X.R.; Cai, J.; Wang, Y.; Feng, Y.; Hu, X. Virtual Inertia Control of Wind-battery-based DC Micro-grid. Proc. CSEE 2016, 36, 49–58. [Google Scholar]
- Ma, W.Z.; Wang, L.B.; Wang, Y.S.; Wan, R.R.; Wang, X.R.; Wang, J.X. Hybrid energy storage power distribution and adaptive virtual inertia control considering SOC Power System Protection and Control. Power Syst. Prot. Control 2024, 52, 83–93. [Google Scholar]
- Zhang, X.Y.; Chen, L.W.; Fu, Y. Research on transient adaptive virtual inertia control strategy of DC microgrid and its parameter feasibility region. Electr. Power Autom. Equip. 2023, 43, 1–14. [Google Scholar]
- Fu, Y.; Huang, X.Y.; Xu, Y.; Bai, C.C. Controllable inertial control strategy of rotating motor in DC distribution network. Electr. Power Autom. Equip. 2018, 38, 32–38. [Google Scholar]
- Fu, Y.; Shao, X.Y.; Li, H. Transient Voltage Stability Control Strategy of DC Distribution Network. High Volt. Eng. 2021, 47, 1354–1362. [Google Scholar]
- Meng, J.H.; Song, M.Q.; Wang, Y. Multi-constraint Stable Operation Boundary of Grid-connected Voltage Source Converter of DC Microgrid with Virtual Capacitance Control. Autom. Electr. Power Syst. 2019, 43, 172–179. [Google Scholar]




| Parameters | Unit | Value |
|---|---|---|
| UN | V | 380 |
| PN | kW | 30 |
| J | kg·m2 | 28.7 |
| ω | r/min | 1500 |
| HS | s | 7.9 |
| Parameters | Unit | Value |
|---|---|---|
| Udc | V | 750 |
| SNDC | kW | 30 |
| C | mF | 2 |
| Hdc | s | 0.012 |
| Parameters | Value |
|---|---|
| UDC | 750 V |
| DC side capacitance | 2000 μF |
| G-VSC | Rated capacity of 30 kW |
| Energy storage | Battery voltage of 120 V, rated capacity of 100 A·h, rated capacity of 30 kW, SOC: 20~80% |
| Droop coefficient kB | −1/30,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Liu, W.; He, G. An Adaptive Virtual Inertial Control Strategy for DC Distribution Networks. Energies 2024, 17, 2401. https://doi.org/10.3390/en17102401
Xu J, Liu W, He G. An Adaptive Virtual Inertial Control Strategy for DC Distribution Networks. Energies. 2024; 17(10):2401. https://doi.org/10.3390/en17102401
Chicago/Turabian StyleXu, Junhua, Weixun Liu, and Guopeng He. 2024. "An Adaptive Virtual Inertial Control Strategy for DC Distribution Networks" Energies 17, no. 10: 2401. https://doi.org/10.3390/en17102401






