Abstract
This paper presents an experimental investigation conducted to determine the influence of parameters such as the ambient temperature, pollution level, and substrate material on the formation of dry bands on polluted layers. To investigate these parameters, we applied a simplified insulator geometry, developed in our previous work, to experimentally control the complex process of dry band formation on a polluted surface. The simple geometry of the experimental model enabled the use of Plexiglas, RTV, and glass as construction substrate materials. RTV and glass were used to simulate a composite and ceramic insulator surface, respectively. Moreover, an electrooptic (EO) probe enabled the measurement of the axial E-field evolution at the surface of the dry band during dry band formation. The results indicated that the substrate material, ambient temperature, and pollution level substantially influence dry band formation. The effects of the first two parameters are directly associated with heat transfer phenomena in the substrate material and at the ambient air/substrate interface. The effect of the third parameter is associated with absorption and evaporation of the pollution layer. In addition, the appearance of the dry band can be clearly identified by a rapid increase in both the pollution layer resistance and the axial E-field in the dry band area. The value of the axial E-field is influenced primarily by the width of the dry band and by the pollution layer resistance, which is directly dependent on the humidification duration. Finally, because most of the results obtained herein were in accordance with those in the literature, we conclude that the proposed experimental model may provide an effective and inexpensive testing method for developing new materials and solutions for improving the dielectric performance of insulators used in polluted environments. Similarly, the simple geometry of the experimental model and the ability to easily control the experimental parameters may enable this tool to validate the results of various numerical models in studies of the thermoelectrical behavior of polluted insulators.
1. Introduction
Dry band formation is a major parameter influencing the development of flashover phenomena on high-voltage polluted surfaces [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], as well as the distribution of the potential and electric field along these surfaces [17,18,19,20,21,22,23,24,25,26]. Flashover of polluted insulators is a complex phenomenon induced by partial arcs initially established along dry bands and propagating along the insulator surface, owing to local heating of the pollution layer induced by a local increase in leakage current density [1,2,3].
As dry bands are primarily responsible for polluted insulator flashover, many studies have been conducted on this phenomenon in recent decades [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].
Experimental investigations have identified several parameters significantly influencing polluted insulator flashover, including the pollution level, characterized by the equivalent salt deposit density (ESDD) and the non-soluble deposit density (NSDD) [7,10,13,15,21,22]; ambient temperature and humidity [6,11]; and the position, number, and width of the dry bands [5,9,11]. In general, the flashover voltage of a polluted insulator increases with increasing ESDD/NSDD, ambient temperature, and humidity. Moreover, the number of dry bands has a greater influence on flashover voltage than the positions of the dry bands.
Efforts to identify the parameters significantly influencing polluted insulator flashovers have been aimed at identifying the parameters influencing the initiation and growth of dry bands on polluted insulators [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. ESDD and fog concentration have been found to affect the formation and location of dry bands [6,14]. Moreover, measurement of the surface resistance or conductivity of the pollution layer has been found to provide a significant indication of the pollution state of the insulator. In particular, surface conductivity increases with ESDD and significantly decreases in the presence of dry bands [5,11]. Other studies conducted on real insulators have also highlighted that surface resistance is affected by the insulator material [20,21]. For example, the inert materials glass and EPDM have surface resistances 10 and 3.5 times lower than that of silicone, respectively. Silicone rubber, such as RTV, can be considered an active material because of its ability to retain and recover surface hydrophobicity [20]. Similarly, the shape of the insulator and the presence of a textured surface (rather than a smooth surface) also affect the surface resistance of polluted surfaces [10,14].
Another aspect of dry band formation at the surface of a polluted insulator is the influence on the potential and E-field distribution along the polluted surface. Many studies have examined this topic, but most have used numerical approaches on real insulators or rectangular plates [17,18,19,20,21,22,23,24,25,26]. The results have generally suggested that the presence of dry bands leads to redistribution of the potential along the polluted surface, where voltage drops can be observed along the different dry bands. These voltage drops are responsible for the rapid increase in the E-field value along different dry bands [17,18,19,20,21,22,23,24,25,26].
Despite the interesting results obtained from both experimental and numerical investigations, the literature has indicated the difficulties in investigating the influence of combinations of several parameters with the same experimental model used as a polluted insulator. In particular, studying the parameters influencing pollution severity, such as the material substrate, can be highly challenging. Indeed, among the few relevant studies conducted, only the surface conductivity of the pollution layer in real polymeric and glass insulators has been compared [20,21]. These studies do not appear to have considered the effects of insulator geometry on the evolution of surface conductivity, including the formation and location of dry bands. A major difficulty lies in studying real insulators with identical geometries but made from different materials. A similar concept has been used with a textured insulator surface condition [14,27]. Instead of using real insulators, several studies have used rectangular or triangular models to study the behavior of polluted insulators on which dry bands were artificially created [4,5,6,7,11]. These models have aided in the investigation of classical parameters, such as the ESDD, ambient temperature, and humidity level, on flashover voltage; however, they have not considered dry band formation in the dynamic evolution of pollution layer resistance.
We recently proposed a new experimental model of simple insulator geometry that enables experimental simulation of the complex phenomenon of dry band formation in a controlled and repetitive manner [28]. Due to its simple and small geometry, the proposed model can be easily made with different materials. Because all other known influencing parameters can be easily controlled, this model facilitates studies of the effects of various parameters on dry band formation along polluted insulators. This article presents experimental results obtained with the proposed experimental model, wherein the influence of Plexiglas, glass, and RTV as materials, with different ESDDs and ambient temperatures, was investigated. By using an electrooptic (EO) sensor for E-field measurement together with the proposed experimental model, we recorded the evolution of the axial E-field during dry band formation. These measurements were also correlated with the evolution of pollution layer resistance as well as the average temperature in the dry band area.
2. Materials and Methods
2.1. Characteristics of the Experimental Models
As described in detail in our previous article [28], the experimental model used in this study has a simple geometry (Figure 1). Developed from a numerical investigation, the model enables the experimental simulation of dry band formation by locally increasing the leakage current in the middle of the model.
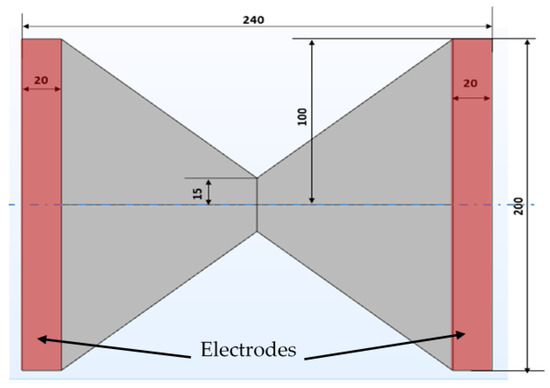
Figure 1.
Geometry and dimensions (in mm) of the experimental model.
The main advantage of the model lies in its simple and symmetrical geometry, thus allowing for the study of various material substrates, which can be easily cut to obtain the desired shape. Moreover, because of the small dimensions of the experimental model, the experimental setup is not complicated, and only a small climatic chamber for the humidification process and an electrical source are required. The voltage is applied using aluminum tape electrodes, as illustrated in Figure 1.
To study the influence of the material substrate on dry band formation, we fabricated several experimental models with Plexiglas, glass, and RTV. Because Plexiglas was principally used in our initial study [28], it served as a reference for comparison of the behaviors of the experimental models made of glass and RTV. Glass material with a thickness of 6 mm was used to simulate a glass and ceramic type insulator, whereas RTV was used to simulate a composite insulator type.
To simulate the surface of a composite insulator, we formed an RTV layer on 3–4 mm thick PVC samples (Figure 2). The RTV layer was obtained by mixing two liquid components followed by curing at room temperature for 24 h. Figure 3 presents the measurement of the contact angles for the three RTV experimental models. The contact angle varied from 104.5° to 107.6°, representing a relative difference of approximately 3%, and also demonstrated that the RTV coating was a hydrophobic surface. These values are of the same order as those obtained for silicone rubber surfaces used for simulating polymer insulator surfaces in different studies [29,30].

Figure 2.
Production of RTV substrate to simulate the composite insulator surface.
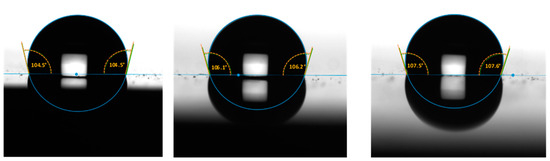
Figure 3.
Contact angles obtained for the three RTV experimental models.
To mask the hydrophobicity of the RTV coating, we used kaolin powder according to the instructions in CIGRE, WG C4.303 [31]. With this recommended method, the hydrophobicity of the RTV experimental model was substantially reduced (Figure 4). After treatment, the contact angle obtained varied from 28.61° to 32.11°, corresponding to a relative difference of approximately 12% among the three RTV experimental models. These results also confirm that the method used to mask the hydrophobicity of the RTV coating is repeatable.

Figure 4.
Contact angles obtained for the three RTV experimental models after kaolin treatment.
2.2. Pollution Procedure in Experimental Models
The application of pollution on the experimental models made of Plexiglas-, glass-, and kaolin-treated RTV coatings followed the same procedure as extensively described in our initial work [28]. The pollution suspension was produced from various formulations based on 500 mL of demineralized water, 20 g of kaolin, and various quantities of salt, to simulate high, moderate, and light pollution [28,31]. These quantities were weighed with a PS 1000 R1 scale from Radwag Canada, Ontario, with a readability of 0.001 g. The pollution solution was applied on the surfaces of the experimental models with a spraying system, model SEMI-PRO2 from Fuji Spray Canada, Ontarioconsisting of a low-pressure compressed-air gun and a compressor. The gun was placed vertically 15–20 cm from the surfaces of the samples. This method of application resulted in the formation of relatively uniform pollution layers on the surfaces of the tested samples. Once applied, the pollution layer was allowed to dry at room temperature for at least 24 h, as recommended by IEC 60507 [32].
2.3. Experimental Test Setup
Figure 5 presents the setup used to study the different parameters influencing dry band formation. This setup comprised a climatic chamber measuring 1 m × 1 m × 1.2 m with controlled humidity and temperature, a 100 kV transformer, and a data acquisition system to record the applied voltage and the leakage current. The measurement of the E-field above the middle of the dry band was performed with an EO sensor from Kapteos (Figure 2), which has successfully been used for various HV applications in several studies [33,34,35]. This sensor is composed of an optoelectronic converter (Figure 6a), which converts the optical information generated by the EO E-field probe (Figure 6b) into an analog electrical signal. This signal is directly proportional to the single component of the E-field measured by the 5 mm diameter EO probe and can be directly read by a data acquisition system. Being composed of only dielectric material, the EO probe is non-invasive and offers natural galvanic isolation for use in high-voltage environments [35]. Moreover, the EO probe is highly selective, as it only allows the measurement of the component of the E-field orthogonal to it [33].
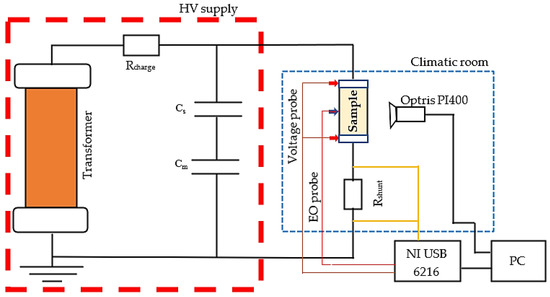
Figure 5.
High-voltage test diagram.

Figure 6.
Electric field measurement system with (a) the optoelectronic converter and (b) the EO probe positioned above the dry band zone of formation.
2.4. Test Procedure
The procedure for studying dry band formation in dedicated experimental models, as previously described in detail [28], is summarized as follows:
- ▪
- Each polluted and weighed sample was placed into the climate chamber set at the desired temperature, controlled at ±1 °C, for a minimum of 3 h, to allow the experimental model to reach the same temperature as that of the climate chamber.
- ▪
- The humidity of the chamber was set at 95 ± 5% and was generated by steam for a duration of 810 s, the time previously demonstrated to be required to reach the maximum surface conductivity [1].
- ▪
- A high voltage of 2 kVrms was then applied, and the leakage current was recorded, to automatically compute the pollution layer resistance until the dry band had completely formed.
- ▪
- At the end of each test, the ESDD on the surface of the samples was measured and determined as previously described [28].
For each experimental condition, three experimental models of the same substrate material were polluted with the same kaolin and salt solution and tested under the same conditions. From the three tested samples, the evolution of the average pollution layer resistance was determined for each experimental condition.
For the measurement of evolution of the E-field during dry band formation, two different test series were performed. In the first series, the E-field above the dry band was measured as a control. A dry band of controlled width was created during the pollution process with a mask (Figure 7). The EO probe was positioned 5 mm above the surface, at the center of the dry band, and oriented to measure the axial component of the E-field parallel to the surface. Three dry band widths were used: 6.4 mm, 12.8 mm, and 18 mm. These values represented the average width obtained in the previously reported preliminary results [28]. For this series, high voltage was applied at the same time as the humidification of the climatic chamber to measure the evolution of the E-field above the artificial dry band during the humidification of the dry pollution layer.

Figure 7.
EO probe centered on an artificial dry band.
The second series of E-field measurements was performed during dry band formation (Figure 6b), as previously described [28]. The EO probe was also positioned 5 mm above the sample surface in the region of dry band formation. The evolution of the axial E-field was recorded after the application of high voltage, when the surface conductivity peaked, i.e., after 810 s of humidification, as previously demonstrated [28].
3. Parameters Influencing the Dry Band Formation Process
As demonstrated in our prior work [28], the main advantage of the proposed experimental model lies in its ability to experimentally reproduce the complex process of dry band formation on composite insulators in a repetitive and controlled manner. However, owing to its simple geometry, the proposed experimental model also enables the assessment of the influence of various parameters, such as the pollution level, environmental temperature, and substrate material, on dry band formation. Such studies are generally difficult to perform with real insulators with different geometries and materials.
3.1. Influence of Pollution Level
The influence of the pollution level on dry band formation was studied with the experimental model made with glass. All tests were conducted at 20 °C with ESDDs of 0.14 mg/cm2, 0.22 mg/cm2, 0.31 g/cm2, and 0.83 g/cm2. These values correspond toto mean, heavy, and very heavy pollution level according to [31,32]. Figure 8 presents the evolution of the average pollution layer resistance recorded after a humidification period of 810 s with an applied voltage of 2 kVrms.
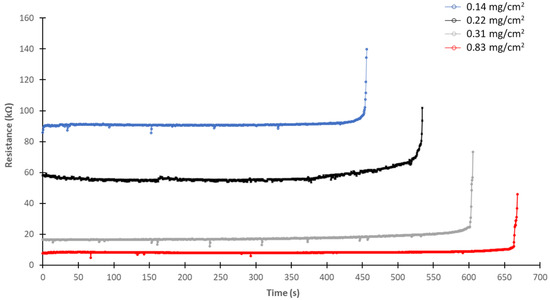
Figure 8.
Evolution of the average polluted layer resistance obtained for different ESDDs with the glass experimental model at an ambient temperature of 20 °C.
The evolution of the polluted layer resistance clearly indicated the appearance of the dry band, which corresponded to a rapid increase in the resistance value. As expected, the resistance of the pollution layer was inversely proportional to the ESDD. When the ESDD and, consequently, the quantity of salt is high, the pollution layer absorbs more water, thus resulting in greater layer thickness. Furthermore, with more salt dissolution, thus resulting in a greater salt concentration, the conductivity of the pollution layer increases and its electrical resistance consequently decreases [9]. Moreover, as demonstrated in Figure 8, dry band formation was delayed as the ESDD increased, despite a lower pollution layer resistance resulting in a greater leakage current. This finding is attributable to the pollution layer absorbing more water with increasing ESDD, thus requiring more thermal energy and time to evaporate. Hence, these results suggest that the dry band formation time is longer with higher levels of pollution under the same environmental conditions.
Figure 9 presents the correlation of the ESDD and the average surface conductivity of the pollution layer, as previously determined [28], corresponding to the results in Figure 8. The average surface conductivity was determined with the average pollution layer resistance values obtained immediately before the appearance of the dry band. The average surface conductivity of the glass experimental model increased linearly with increasing ESDD, as demonstrated by the linear fitted curve obtained. The correlation obtained between surface conductivity and ESDD was in accordance with results previously obtained for real EPDM, porcelain, and RTV insulators [20].
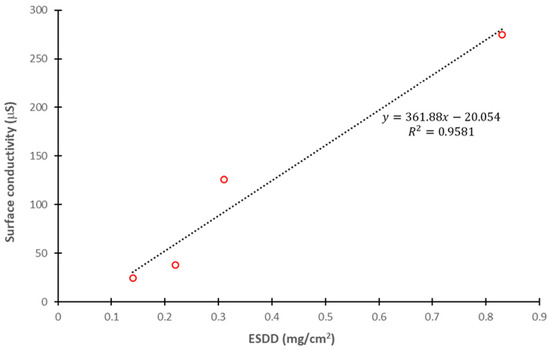
Figure 9.
Correlation of ESDD with average pollution layer surface conductivity in the glass experimental model at an ambient temperature of 20 °C.
3.2. Influence of Substrate Material
Three experimental models made of Plexiglas, solidified liquid RTV (to simulate a composite insulator surface), and glass were polluted at the same average ESDD of 0.3 mg/cm2 and tested under the same ambient temperature of 20 °C. The results (Figure 10) indicated that the evolution of pollution layer resistance was strongly dependent on the substrate material. The average resistance value of the RTV substrate before dry band appearance was approximately five times greater than the average resistance of glass and approximately two times greater than that of Plexiglas. Moreover, the dry band on the Plexiglas model appeared more quickly than that on the RTV model and much more quickly than that on the glass model. Figure 11 presents the corresponding average surface layer conductivity and average surface temperature measured at the middle of the zone of dry band appearance with an IR camera. A strong correlation was observed between the maximum surface temperature and the appearance of the dry band. For the Plexiglas sample, the maximum average temperature reached 99.5 °C, as compared with 81.7 °C for the RTV substrate, and 33.7 °C for the glass substrate.
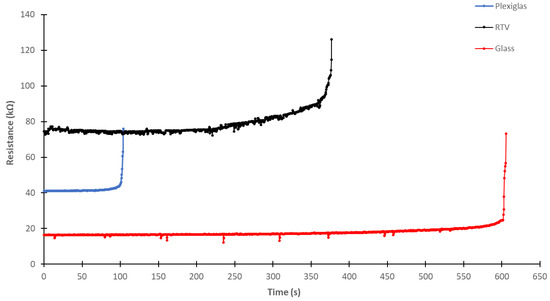
Figure 10.
Evolution of polluted layer resistance on different substrate materials, with an ambient temperature of 20 °C and average ESDD of 0.3 mg/cm2.
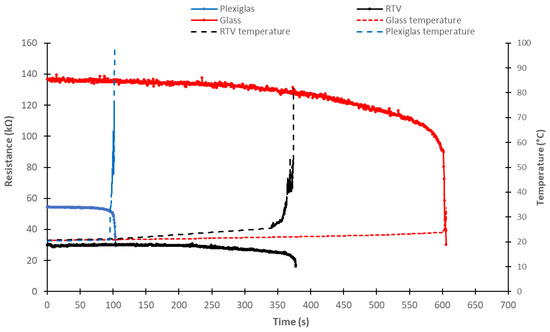
Figure 11.
Evolution of average pollution layer surface conductivity and average surface temperature in the middle of the dry band zone for different substrate materials, with an ambient temperature of 20 °C and average ESDD of 0.3 mg/cm2.
3.3. Influence of Ambient Temperature
This section presents the influence of the ambient temperature on the dry band appearance time. Several test series were performed for the three material substrates under four temperatures: 3 °C, 10 °C, 20 °C, and 30 °C. These temperatures simulated dry band formation under environmental conditions ranging from cold humid weather to warm humid weather. The results are presented in Figure 12, Figure 13 and Figure 14 for the Plexiglas, RTV, and glass substrates, respectively.
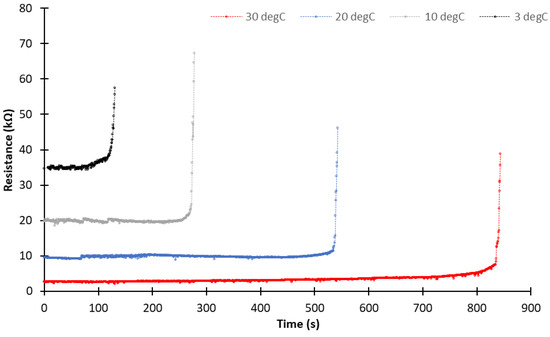
Figure 12.
Evolution of average polluted layer resistance as a function of the ambient temperature for Plexiglas substrate with an average ESDD of 0.96 mg/cm2.
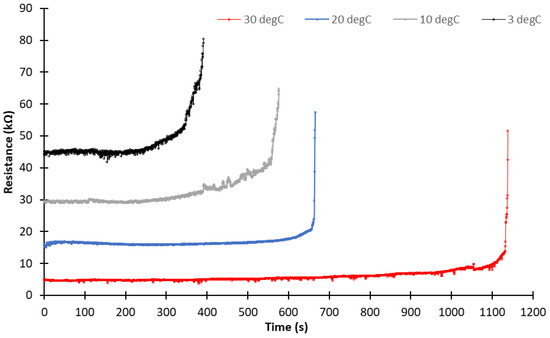
Figure 13.
Evolution of average polluted layer resistance as a function of the ambient temperature for glass substrate with an average ESDD of 0.81 mg/cm2.
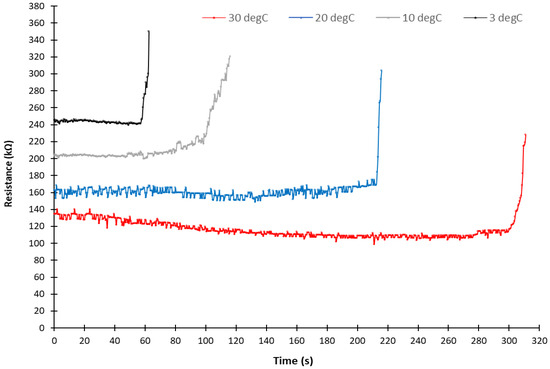
Figure 14.
Evolution of average polluted layer resistance as a function of the ambient temperature for RTV substrate with an average ESDD of 0.21 mg/cm2.
According to the evolution of the average pollution layer resistance (Figure 12, Figure 13 and Figure 14), the dry band appearance time significantly increased with decreasing ambient temperature. This observation was valid for the three substrate materials and for different ESDDs. The influence of temperature on the dry band appearance time was explained by two phenomena. First, the amount of water absorbed during the humidification phase decreased with decreasing ambient temperature. To demonstrate this phenomenon, we measured the water mass absorbed during the HV test with different ambient temperatures and pollution layer masses. The results (Figure 15) demonstrated that the mass of absorbed water for the same pollution layer mass (or ESDD) significantly increased with increasing ambient temperature. In addition, for the same ambient temperature, the absorbed water mass increased with increasing pollution layer mass. These results are in accordance with the results obtained from a mathematical model of pollution layer humidification proposed in [36].
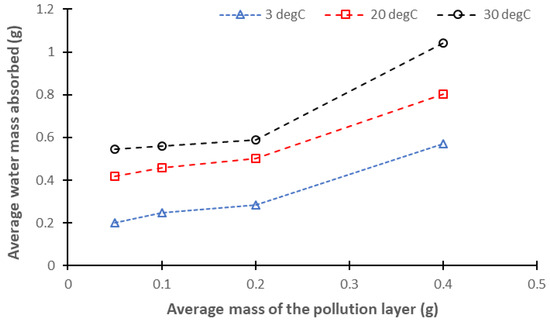
Figure 15.
Evolution of the average water mass absorbed by the pollution layer during the HV test as a function of the average mass of the pollution layer, under different ambient temperatures.
The second phenomenon was the rate of water evaporation of the pollution layer, which is directly associated with the temperature gradient between the surface and the ambient air via the Clausius–Clapeyron equation, as described in [19] and in the experimental investigation presented in [37]. As reported in [37], the initiation of dry band formation occurred when the power dissipated in the pollution layer became sufficient to raise the surface temperature by less than 1 °C above the ambient temperature. Hence, this condition can be more rapidly reached when the ambient temperature decreases, thereby promoting faster evaporation.
Figure 16 presents the evolution of the average surface resistance of the pollution layer before dry band appearance as a function of the ambient temperature, as well as the corresponding fitted curves obtained for the three substrates. As expected, the surface conductivity increased with increasing temperature for all substrates. However, this increase was more pronounced with the Plexiglas and glass substrates than with the RTV substrate. For the Plexiglas and glass substrates, an exponential fitted curve was obtained, in contrast to the linear fitted curve for the RTV.
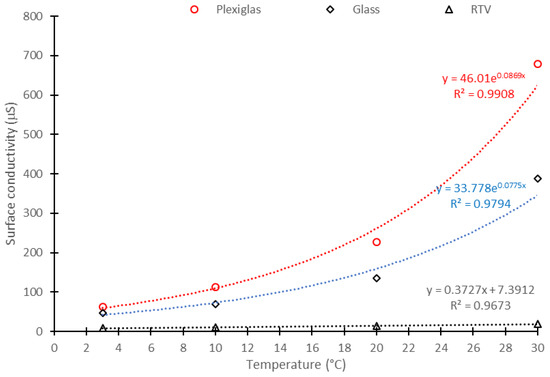
Figure 16.
Evolution of the average polluted layer surface conductivity as a function of the ambient temperature for Plexiglas, glass, and RTV substrates with ESDDs of 0.96, 0.81, and 0.21 mg/cm2, respectively.
4. Axial E-Field Evolution above the Dry Band during Dry Band Formation
4.1. Experimental E-Field Evolution above an Artificial Dry Band
We first measured the evolution of the axial component of the E-field above a dry band, which was artificially created on the experimental model, as explained previously and illustrated in Figure 7. A 2 kVrms voltage was applied after the pollution layer had initially dried, and the axial E-field evolution was recorded during the humidification process. The axial E-field evolution was measured for three dry band widths of 6.4 mm, 12.8 mm, and 18 mm, corresponding to the average widths of dry bands during the formation process obtained in our previous work [28]. The EO probe was positioned 5 mm above the surface. With a diameter of 5 mm, the axial E-field was assumed to have been measured at 7.5 mm above the experimental model surface. The results obtained for the three dry band widths artificially created on the Plexiglas model are presented in Figure 17. The axial E-field evolution for each dry band was determined by the average obtained from three different tests with the same dry band width.
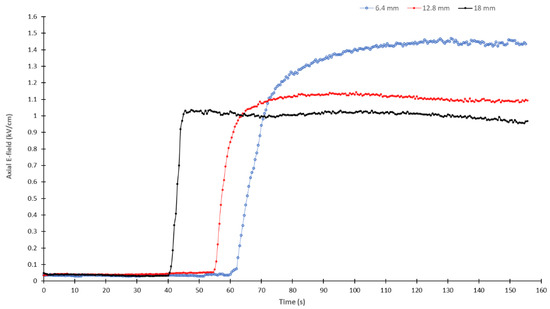
Figure 17.
Evolution of the average axial E-field in the center of the dry band at 7.5 mm from the surface, obtained at an ambient temperature of 20 °C for Plexiglas substrate with an average ESDD of 0.52 mg/cm2.
The results (Figure 17) indicated that the evolution of the axial E-field during the humidification process followed the same pattern for the three dry band widths. In particular, the E-field value was initially constant and ostensibly of the same order (between 0.032 and 0.053 kV/cm) for the three dry bands when the humidification persisted until a certain level of conductivity was reached in the pollution layer. At that time, between 40 and 60 s, the axial E-field value started to increase rapidly until saturation was reached. The maximum or saturation value reached by the axial E-field was obtained when the voltage drop along the dry band was near the 2 kVrms applied voltage. This finding also explains why the maximum axial E-field value decreased as the dry band width increased.
Table 1 presents the experimental value of the axial E-field and the average value obtained at saturation when the voltage drop along the dry band was equal to the applied voltage. The experimental results presented in Table 1 also include the maximum and minimum values of the axial E-field obtained during dry band formation.

Table 1.
Experimental values of the axial E-field obtained for the EO sensor positioned at the center of the dry band at 5 mm from the surface.
4.2. E-Field Simulations with an Artificial Dry Band
Using controlled dry band widths as well as controlled experimental conditions also enabled numerical simulation of the experimental models to determine the value of the axial E-field along the dry band. The simulations were performed in three dimensions to correctly simulate the experimental model inside the climatic chamber (Figure 18a), which features a grounded metallic envelope (0 V potential). Figure 18b presents a closed view of the Plexiglas experimental model with a dry band with an 18 mm width. All the simulations were performed using the general commercial software Comsol Multiphysics®, version 6.0, based on the finite element method, which is well adapted to simulation of the E-field around a polluted insulator [17,18,19,26]. The simulation parameters used are presented in Table 2.
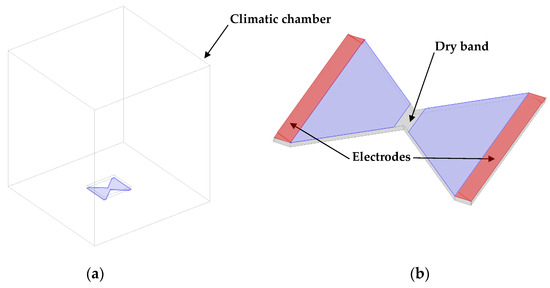
Figure 18.
Numerical model with (a) the entire model with the climatic chamber and (b) a closed view of the experimental model with an artificial dry band with an 18 mm width.

Table 2.
Simulation parameters.
The value of the relative permittivity of the pollution layer was fixed at 80 as it can be regarded as a perfect electrolyte solution when fully saturated with water [38,39].
To compare the simulation with the experimental results, we computed the axial E-field distribution along three reference lines: one vertical line situated in the middle of the dry band and extending from the surface of the model to a distance of 10 mm; one horizontal line 18 mm in length situated at 7.5 mm from the surface and extending across the middle of the dry band; and one horizontal line 30 mm length situated at 7.5 mm from the model surface and extending along the middle of the dry band. The results obtained for the three dry band widths (6.4, 12.8, and 18 mm) are presented in Figure 19, Figure 20 and Figure 21, respectively.
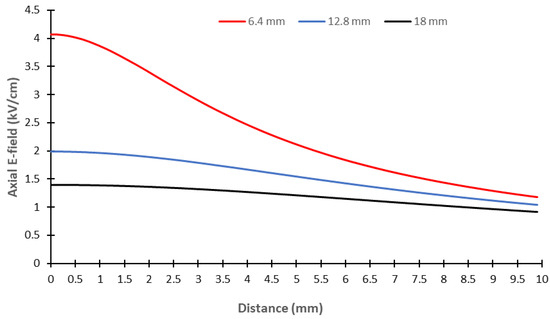
Figure 19.
Vertical distribution of the axial E-field in the middle of the artificial dry band as a function of dry band width.
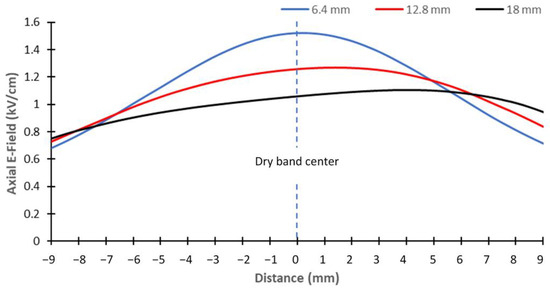
Figure 20.
Horizontal distribution of the axial E-field across the middle of the artificial dry band at a distance of 7.5 mm from the surface as a function of dry band width.
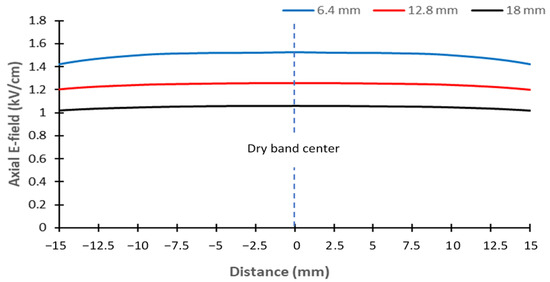
Figure 21.
Horizontal distribution of the axial E-field along the middle of the artificial dry band at a distance of 7.5 mm from the surface as a function of dry band width.
As shown in Figure 19, the axial E-field value decreased rapidly as the distance from the model surface increased and the width of the dry band decreased. In addition, as shown in Figure 20, the axial E-field had a higher value on the side of the HV value than on the side of the ground. However, along the middle of the dry band, the evolution of the axial E-field value in Figure 21 did not appear to significantly vary.
Table 3 presents the numerical results including the vertical and horizontal axial E-field values obtained numerically. The values were computed at the center of the dry band at 7.5 mm and also at ±1 mm from the center of the dry band in the vertical and horizontal directions across the dry band.

Table 3.
Values of the axial E-field at ±1 mm around the center of the dry band at 7.5 mm from the surface.
The results in Table 3 demonstrate that the axial E-field value varied more significantly in the vertical direction with a small dry band width. However, the axial E-field variation appeared to be more important in the horizontal direction with increasing dry band width.
Comparison of the results in Table 1 and Table 3 indicates good agreement, given that the position of the EO probe above the surface was not exact and varied by approximately ±1 mm. Hence, the discrepancies between the numerical axial E-field values at the centers of the dry bands (0 mm) and the experimental average values were 5.6%, 12.5%, and 5.0% for 6.4 mm, 12.8 mm, and 18 mm, respectively. To better visualize the results, Figure 22 presents a comparison between the experimental and numerical axial E-field values, with the error bars corresponding to the maximum discrepancy obtained, which was 12.5%. Moreover, Figure 22 presents the linear regressions obtained for both experimental and numerical results. As can be observed, the axial E-field value decreased linearly with the increase in the dry band width.
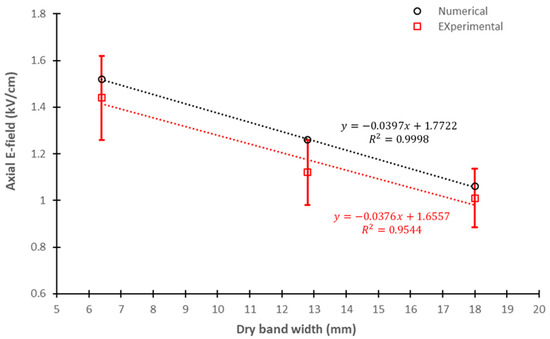
Figure 22.
Comparison of the numerical and experimental axial E-field values obtained in the middle of the artificial dry band at a distance of 7.5 mm from the surface.
We conducted a final simulation of the axial E-field evolution at the center of the dry band, 7.5 mm from the experimental model surface, as a function of the surface conductivity of the pollution layer. The results obtained for the three dry band widths are presented in Figure 23. The numerical results in Figure 23 show that the evolution of the axial E-field followed the same behavior as that in the experimental results in Figure 17. Because the surface conductivity of the pollution was very low, the axial E-field values for the three dry band widths had similar values of approximately 0.052 kV/cm. This value is similar to the experimental values of approximately 0.04 kV/cm. As the humidification of the pollution layer increased, its conductivity and the voltage drop along the dry band increased. However, the numerical results demonstrated that the surface conductivity of the pollution layer did not need to be high (approximately 1 × 10−21 S) to obtain the maximum axial E-field value. This result explains why the maximum value of the axial E-field was obtained rapidly in the experiments during the humidification process of the pollution layer.
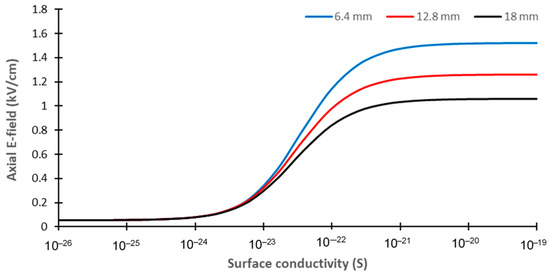
Figure 23.
Evolution of the axial E-field along the middle of the artificial dry band at a distance of 7.5 mm from the surface, as a function of dry band surface conductivity.
4.3. Experimental E-Field Evolution during Dry Band Formation
The E-field evolution was experimentally measured during dry band formation, according to the experimental procedure in Section 2.4. The 2 kVrms voltage was applied after 810 s of humidification, and the EO probe was positioned at the center of the experimental model in the zone of dry band formation, as illustrated in Figure 6b, and at 5 mm above the surface. As described previously, this position is equivalent to measuring the axial E-field at 7.5 mm from the surface of the experimental model. The EO probe was positioned 5 mm from the surface to avoid pollution deposition on the probe during dry band formation, as was observed during preliminary measurements. In addition, in contrast to the experimental tests conducted with an artificial dry band, in this experiment, the primary challenge was exactly positioning the EO probe near the middle of the dry band, even if the area of dry band formation was known. As demonstrated in our previous work [28], the proposed experimental model enabled repeated correct simulations of dry band formation in a very small zone. However, the width and exact geometry of the dry band exhibited a random behavior that was difficult to control. Therefore, the measurement of the axial E-field during dry band formation was difficult to reproduce under the same conditions with significant repeatability. Despite this constraint, we were able to record the evolution of the axial E-field. The results are presented in Figure 24 for the RTV substrate with an ESDD of 0.36 g/cm2 at an ambient temperature of 20 °C. Figure 25 presents another axial E-field evolution during the dry band formation obtained for the glass substrate with an ESDD of 0.16 g/cm2 at an ambient temperature of 20 °C.
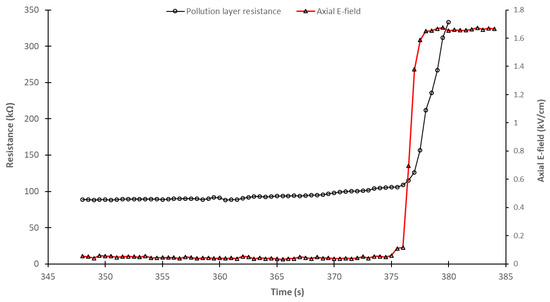
Figure 24.
Evolution of the axial E-field and pollution layer resistance during the formation of a dry band with the RTV experimental model at an ambient temperature of 20 °C and an ESDD of 0.36 mg/cm2.
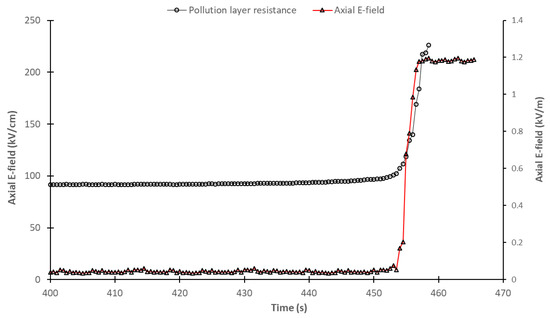
Figure 25.
Evolution of the axial E-field and pollution layer resistance during the formation of a dry band on glass substrate with an ambient temperature of 20 °C and ESDD of 0.16 mg/cm2.
As shown in Figure 24 and Figure 25, the evolution of the axial E-field is similar to that obtained for the artificial dry band tests in Figure 17. Indeed, even with high humidification of the pollution layer, the axial E-field value remained very low, at approximately 0.05 kV/cm. However, as the dry band began to appear, a rapid increase in the axial E-field was observed as a maximum or saturation value was reached. As explained for the artificial dry band tests, this maximum value was obtained when the voltage drop along the dry band was equal to the applied voltage. Moreover, the rapid increase in the axial E-field correlated with the rapid increase in pollution resistance, thus confirming that this was due to the appearance of the dry band.
5. Discussion
5.1. Influence of Parameters on Dry Band Formation
In general, the evolution of the pollution layer resistance obtained for the different experimental tests demonstrated that dry band formation occurs rapidly, within approximately 10 s. This observation is in agreement with previous studies, both experimental and numerical, on polluted insulators, in which the appearance time of the dry band was 1.6–19 s [19,25]. The rapid increase in the pollution layer resistance observed in Figure 8, Figure 10, Figure 12, Figure 13 and Figure 14 is directly correlated with a rapid increase in temperature (see Figure 11) in the middle of the sample where the dry band is formed. This rapid increase occurs at the moment the dry band formation is completed, along the narrow part of the sample where the leakage current density is the highest, as explained in detail in [28]. When the formation of the dry band is completed, the equivalent resistive circuit is interrupted and almost becomes capacitive, with a drastic reduction in the current intensity flowing in the pollution layer, leading to a significant increase in the pollution layer resistance.
The ESDD (Figure 8) significantly influenced the appearance time of the dry band, which increased with increasing ESDD. Simultaneously, the pollution layer resistance decreased with an increase in the ESDD. However, in all experimental tests, the humidity level, ambient temperature, and applied voltage were consistent. The rapid dry band formation with low ESDD was defined not only by the leakage current intensity but also by the humidification process of the pollution layer, as explained previously. This aspect was confirmed by the results in Figure 15, in which the average water mass absorbed by the pollution layer increased with the increasing average mass of the pollution layer, and consequently increasing ESDD. These observations may also explain the increase in flashover voltage of polluted insulators with decreasing ESDD reported in several studies [1]. The flashover process of polluted insulators is dynamic and complex, and it is governed principally by the surface conductivity, leakage current, and arc propagation [19]. Generally, experimental and numerical investigations have not considered the influence of dry band formation, which can be significant in the complex process of flashover.
Another notable result was the influence of the substrate material. A comparison of the results in Figure 10 indicated that, for the same ESDD and humidity level, the pollution layer resistance was significantly higher for the RTV substrate than for the Plexiglas and glass substrates. As previously explained [20,21], Plexiglas and glass are considered inert materials, whereas RTV is considered an active material because of its hydrophobicity recovery capability. This capability explains the average pollution layer resistance value obtained for the RTV, which was approximately 4.4 times and 1.9 times higher than that of glass and Plexiglas, respectively (Figure 10). These results were of the same order as those previously obtained for RTV, EPDM, and porcelain insulators [20,21].
Another notable finding was the influence of the substrate material on the appearance time of the dry band (Figure 10 and Figure 11). The differences observed among substrates are attributable to the differences in the thermal conductivity K of each material [40,41]. For glass, K is approximately 1.4 W/m.K, a value much higher than those of RTV (approximately 0.29 W/m.K) and Plexiglas (approximately 0.19 W/m.K). This conclusion appears to be justified by the results in Figure 11, in which the maximum average temperature reached at the middle of the dry band was highest for Plexiglas (99 °C), followed by RTV (82 °C) and glass (34 °C). The value obtained for the glass substrate seems to be in accordance with experimental measurements performed on a real wet contaminated ceramic insulator [42]. These observations suggested that the higher thermal conductivity of the glass substrate decreased the temperature at the surface of the pollution layer by allowing for better thermal conduction through the sample thickness. Consequently, a lower surface temperature resulted, as confirmed by the results in Figure 11, thus delaying dry band formation. The findings also confirmed that the appearance time of the dry band was higher for RTV than for Plexiglas, which has a lower thermal conductivity. Therefore, we concluded that a material with higher thermal conductivity can delay the appearance of the dry band by more efficiently dissipating the increased temperature inside the dry band zone. Thus, the time delay may be sufficient to decrease the surface conductivity of the pollution layer under rain conditions, for example, to avoid the flashover of the insulator.
Regarding the effects of ambient temperature, our results suggested that the appearance time decreased significantly with decreasing ambient temperature, as demonstrated in [36,37]. However, the results also demonstrated that the resistance of the pollution layer markedly increased as the temperature decreased. The flashover of polluted insulators is a complex phenomenon involving the presence of dry bands and an equilibrium between the applied voltage and the pollution layer resistance, thus inducing partial arc propagation. As demonstrated by several studies, the flashover voltage decreases with decreasing temperature. In general, this decrease is primarily attributed to the decrease in pollution layer conductivity with temperature [1,4,7]. Hence, from the results obtained in Figure 13, Figure 14 and Figure 15, we propose that the early dry band formation may also contribute to a decrease in the flashover of polluted insulators under low-temperature ambient temperatures. The results in Figure 15 and Figure 16 also demonstrate that dry band formation is governed by dependent parameters including the ambient temperature, humidification process, leakage current, and heat exchange between interfaces.
As proposed in [19], the thermal energy balance in the pollution layer in the absence of partial arcs at the insulator surface can be expressed as follows [19]:
where
- ▪
- is the thermal convection energy at the pollution surface, which is the same for the three material substrates with the same geometry;
- ▪
- is the energy needed to evaporate the water of the polluted layer, governed by the Clausius–Clapeyron equation and dependent on the pollution layer temperature;
- ▪
- is the thermal conduction energy, dependent on the thermal conductivity K of each material;
- ▪
- is the leakage current injection energy, directly dependent on the pollution layer resistance.
is the thermal energy responsible for dry band formation dependent on the pollution layer temperature. Under the same experimental conditions, can be considered to be the same for the three substrates. In that particular situation and from Equation (1), it can be posited that depends on the difference , where is the only thermal energy directly affected by the substrate material via its thermal conductivity K.
From the results presented in Figure 10 and Figure 11, is higher for the glass substrate compared to Plexiglas and RTV as the pollution layer resistance of glass is lower. However, as the results in Figure 10 indicate, dry band formation for the glass is delayed compared to that for RTV and Plexiglas. Consequently, the glass substrate must present a higher value of in order to maintain low compared to RTV and Plexiglas. To achieve this, the glass must have a higher thermal conductivity K.
5.2. Study of Axial E-Field Evolution during Dry Band Formation
The use of a special EO sensor enabled, to our knowledge, the first study of the evolution of the E-field during dry band formation. The first series of E-field measurements performed on artificial dry bands allowed us to study the evolution of the axial E-field during the humidification period of the pollution layer under applied voltage. As shown in Figure 17, the axial E-field at the center of the dry band increased with decreasing dry band width, in agreement with the results presented in several numerical studies [17,18,19,20,21,22,23]. These results are also in good agreement with the numerical results in Table 1 and Table 3, given that the exact position of the EO probe can vary by ±1 mm with respect to the evaluation point of the axial E-field in the numerical model. This good agreement is confirmed by the results outlined in Figure 22, proving that the axial E-field values decreases linearly with the increase in dry band width. The significant discrepancy between numerical and experimental results also confirmed that the EO probe can serve as an adequate and useful tool for studying the influence of dry bands on the dielectric behavior of real polluted insulators. The results also demonstrated that the increase in the voltage drop along the dry band is a very fast process that rapidly increases the axial E-field until a maximum or saturation value is reached. This value corresponds to the situation in which the voltage drop along the dry band equals the applied voltage. The rapid increase in the axial E-field occurs quite rapidly in the humidification period with respect to the 810 s required to obtain the maximum surface resistance of the pollution layer, as demonstrated in our previous work [28]. Therefore, the pollution layer need not be very humid to obtain the maximum voltage drop along the dry band. This observation is confirmed by the experimental results in Figure 17 and numerical results in Figure 23. These results allow the conclusion to be drawn that the surface conductivity of the pollution layer does not need to be very high, only approximately 10−21 S, to permit the maximum value of the axial E-field to be obtained at the center of the dry band.
Finally, during dry band formation, we observed that the axial E-field evolution was similar to that obtained with the artificial dry band. The similarity was observed both in the evolution of the axial E-field and in the maximum value obtained once the dry band was created. The rapid increase in the axial E-field correlated with the rapid increase in pollution layer resistance as well as the surface temperature. Consequently, in terms of E-field behavior, experimental models with artificial dry bands can serve as a simple way to study E-field behavior inside dry bands. Such studies can be used to determine the minimum E-field value for initiation of a partial arc along the dry band. These results may be useful in validating numerical models.
6. Conclusions
The simple geometry of the proposed experimental model enabled the parameters influencing dry band formation on polluted insulators to be examined. We studied the influence of Plexiglas, RTV, and glass materials with the same experimental model geometry on pollution layer parameters, such as the resistance and appearance time, which characterized dry band formation as well as the evolution of the axial E-field. A major advantage of the proposed experimental model is that such studies would be difficult to perform with real insulators. Moreover, the proposed experimental tests do not require costly test equipment, thus providing a substantial advantage for companies wishing to develop and test new materials and surface designs for improving insulator performance under polluted environments. Moreover, the proposed model enabled direct measurement and the first reported examination of the evolution of the axial E-field above the dry band during dry band formation with the use of an EO sensor.
The different experimental results obtained demonstrated that our simple geometric model provides a simple and efficient method to evaluate the effects of substrate material and environmental parameters (ambient temperature and ESDD) on polluted insulators. All of our results were in accordance with findings in the literature obtained on real insulators. In particular, for the same experimental conditions, the material substrate significantly influenced the surface resistivity of the pollution layer as well as the appearance time of the dry band. As the thermal conductivity of the material increased, the appearance time of the dry band also increased. We further demonstrated that the dry band’s appearance was delayed as the ambient temperature and ESDD increased.
This study of the evolution of pollution layer resistance and axial E-fields highlights that dry band formation is a rapid process, as also described in the literature. The dry band’s appearance is characterized by a rapid and correlated increase in the pollution resistance and the axial E-field. The axial E-field reaches a maximum value when the voltage drop along the dry band equals the applied voltage, and it consequently directly influences the dry band width.
Finally, the results presented herein provide a new understanding of the influence of several parameters on dry band formation along polluted ceramic and non-ceramic insulators. In future work, the proposed experimental model may be used to study the parameters influencing partial arc formation along dry bands and subsequent propagation until the occurrence of flashover. The proposed experimental model also provides a tool for validating numerical models of dry band formation and arc propagation to flashover. It offers a simpler geometry than that of real insulators, allowing for easy material substrate modification without requiring sophisticated research infrastructure. Some of the proposed applications of the proposed experimental model will be presented in our future paper involving the validation of a numerical model of dry band formation.
Author Contributions
Numerical simulations were performed by M.-A.A., who was also responsible for the experimental investigation and the original draft preparation. Validation, review and editing, visualization, and supervision were the responsibility of C.V., who was also responsible for funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the Natural Sciences and Engineering Research Council of Canada for financial support (Discovery grant RGPIN-2019-06700).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Salem, A.A.; Lau, K.Y.; Rahiman, W.; Abdul-Malek, Z.; Al-Gailani, S.A.; Mohammed, N.; Rahman, R.A.; Al-Ameri, S.M. Pollution flashover voltage of transmission line insulators: Systematic review of experimental works. IEEE Access 2022, 10, 10416–10444. [Google Scholar] [CrossRef]
- Terrab, H.; Bayadi, A. Experimental study using design of experiment of pollution layer effect on insulator performance taking into account the presence of dry bands. IEEE Trans. Electr. Insul. 2014, 21, 2486–2495. [Google Scholar] [CrossRef]
- Loberg, J.O.; Salthouse, E.C. Dry-Band Growth on Polluted Insulation. IEEE Trans. Electr. Insul. 1971, 6, 136–141. [Google Scholar] [CrossRef]
- Arshad; Nekahi, A.; McMeekin, S.G.; Farzaneh, M. Influence of dry band width and location on flashover characteristics of silicone rubber insulators. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Montréal, QC, Canada, 19–22 June 2016. [Google Scholar]
- Dhofir, M.; Andaru, D.D.; Hasanah, R.N. The influence of conduction band location on the leakage current level of a glass insulator. In Proceedings of the 5th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 6–8 October 2017. [Google Scholar]
- Liang, F.; Macalpine, M.; Guan, Z.; Zhang, R. Factors Affecting Dry- band Formation on the Surface of Polluted Insulator. Gaodianya Jishu High Volt. Eng. 2012, 38, 2604–2610. [Google Scholar]
- Arshad; Mughal, M.A.; Nekahi, A.; Khan, M.; Umer, F. Influence of single and multiple dry bands on critical flashover voltage of silicone rubber outdoor insulators: Simulation and experimental study. Energies 2018, 11, 1335. [Google Scholar] [CrossRef]
- Williams, D.L.; Haddad, A.; Rowlands, A.; Young, H.; Waters, R.T. Formation and characterization of dry bands in clean fog on polluted insulators. IEEE Trans. Electr. Insul. 1999, 6, 724–731. [Google Scholar] [CrossRef]
- Dhahbi-Megriche, N.; Slama, M.E.; Beroual, A. Influence of dry bands on polluted insulator performance. In Proceedings of the International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017. [Google Scholar]
- Albano, M.; Haddad, A.; Bungay, N. Is the dry-band characteristic a function of pollution and insulator design? Energies 2019, 12, 3607. [Google Scholar] [CrossRef]
- Arshad; Nekahi, A.; McMeekin, S.G.; Farzaneh, M. Measurement of surface resistance of silicone rubber sheets under polluted and dry band conditions. Electr. Eng. 2018, 100, 1729–1738. [Google Scholar] [CrossRef]
- Yang, H.; Cao, W.; Wen, R.; Wang, Y.; Shen, W.; Zhang, L. Study on surface conductivity distribution of pollution layer during the propagation of local arc on the wet polluted insulation surface. AIP Adv. 2022, 12, 015311. [Google Scholar] [CrossRef]
- Chakraborty, R.; Reddy, B. Investigation on the pollution performance of silicone rubber insulator samples. In Proceedings of the 10th Conference of the French Society of Electrostatics (SFE), Poitiers, France, 29–31 August 2016. [Google Scholar]
- Albano, M.; Charalampidis, P.; Waters, R.; Griffiths, H.; Haddad, A. Silicone rubber insulators for polluted environments part 2: Textured insulators. IEEE Trans. Electr. Insul. 2014, 21, 749–757. [Google Scholar] [CrossRef]
- Hussain, M.; Farokhi, S.; McMeekin, S.G.; Farzaneh, M. Dry Band Formation on HV Insulators polluted with Different Salt Mixtures. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015. [Google Scholar]
- Chrzan, K.L.; Moro, F. Concentrated discharges and dry bands on polluted outdoor insulators. IEEE Trans. Power Deliv. 2006, 22, 466–471. [Google Scholar] [CrossRef]
- Volat, C. Comparison between the use of surface and volume conductivity to compute potential distribution along an insulator in presence of a thin conductive layer. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 2–5 June 2013. [Google Scholar]
- Jabbari, M.; Volat, C.; Fofana, I. Application of a new dynamic numerical model to predict polluted insulator flashover voltage. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Philadelphia, PA, USA, 8–11 June 2014. [Google Scholar]
- He, J.H.; Kang, H.E.; Bingtuan, G. Modeling of dry band formation and arcing processes on the polluted composite insulator surface. Energies 2019, 12, 3905. [Google Scholar] [CrossRef]
- Bo, L.; Gorur, R.S. Modeling flashover of AC outdoor insulators under contaminated conditions with dry band formation and arcing. IEEE Trans. Electr. Insul. 2012, 19, 1037–1043. [Google Scholar] [CrossRef]
- Gorur, R.; Schneider, H.; Cartwright, J.; Beausajour, Y.; Kondo, K.; Gubanski, S.; Hartings, R.; Shah, M.; McBride, J.; de Tourreil, C.; et al. Surface resistance measurements on nonceramic insulators. IEEE Trans. Power Deliv. 2001, 16, 801–805. [Google Scholar] [CrossRef]
- Slama, M.E.A.; Krzma, A.; Albano, M.; Haddad, A.M. Experimental Study and Modeling of the Effect of ESDD/NSDD on AC Flashover of SiR Outdoor Insulators. Energies 2022, 15, 3782. [Google Scholar] [CrossRef]
- Texier, C.; Kouadri, B. Model of the formation of a dry band on an NaCl-polluted insulation. IEE Proc. A (Phys. Sci. Meas. Instrum. Manag. Educ. Rev.) 1986, 133, 285–290. [Google Scholar] [CrossRef]
- Zhou, J.-B.; Gao, B.; Zhang, Q.-G. Dry band formation and its influence on electric field distribution along polluted insulator. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010. [Google Scholar]
- Bi, J.; Hao, Y.; Zheng, Y.; Wu, X.; Wu, H.; Yang, L. Thermal Characteristics of the Polluted Silicone Rubber During the Formation Process of Dry Band and Arc Discharge. In Proceedings of the International Conference on Electrical Materials and Power Equipment (ICEMPE), Shanghai, China, 7–10 May 2023. [Google Scholar]
- Das, A.; Ghosh, D.K.; Bose, R.; Chatterjee, S. Electric stress analysis of a contaminated polymeric insulating surface in presence of dry bands. In Proceedings of the International Conference on Intelligent Control Power and Instrumentation (ICICPI), Kolkata, India, 21–23 October 2016. [Google Scholar]
- Montoya, G.; Ramirez, I.; Montoya, J. Correlation among ESDD, NSDD and leakage current in distribution insulators. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 334–340. [Google Scholar] [CrossRef]
- Andoh, M.-A.; Gbah, K.; Volat, C. Development of a Simple Experimental Setup for the Study of the Formation of Dry Bands on Composite Insulators. Energies 2022, 15, 5108. [Google Scholar] [CrossRef]
- Tokoro, T.; Kojima, S.; Nagao, M. Effect of surface condition on the evaluation of hydrophobicity of polymer insulator. In Proceedings of the International Symposium on Electrical Insulating Materials (ISEIM), Kyoto, Japan, 6–10 September 2011. [Google Scholar]
- Miyoshi, M.; Homma, H.; Goshima, H. Effect of Local Arc Discharge on Hydrophobicity Decrease of Silicone Rubber Surface. IEEJ Trans. Fundam. Mater. 2020, 140, 451–456. [Google Scholar] [CrossRef]
- Engelbrecht, C.S.; Gutman, I.; Garcia, R.W.; Kondo, K.; Lumb, C.; Matsuoka, R.; Rowland, S.; Sklenicka, V. Artificial Pollution Test for Polymer Insulators—Results of Round Robin Tests; CIGRE Working Group C4.303: Paris, France, 2003. [Google Scholar]
- IEC 60507; Articifial Pollution Tests on High-Voltage Ceramic and Glass Insulators to be Used on A.C. Systems. IEC: Geneva, Switzerland, 2013.
- Gaborit, G.; Jarrige, P.; Lecoche, F.; Dahdah, J.; Duraz, E.; Volat, C.; Duvillaret, L. Single shot and vectorial characterization of intense electric field in various environments with pigtailed electrooptic probe. IEEE Trans. Plasma Sci. 2014, 42, 1265–1273. [Google Scholar] [CrossRef]
- Gaborit, G.; Dahdah, J.; Lecoche, F.; Jarrige, P.; Gaeremynck, Y.; Duraz, E.; Duvillaret, L. A nonperturbative electrooptic sensor for in situ electric discharge characterization. IEEE Trans. Plasma Sci. 2013, 41, 2851–2857. [Google Scholar] [CrossRef]
- Kone, G.; Volat, C.; Ezzaidi, H. Numerical investigation of electric field distortion induced by internal defects in composite insulators. High Volt. 2017, 2, 253–260. [Google Scholar] [CrossRef]
- Saison, J.Y. Étude du Phénomène D’humidification de Dépôts Naturels et Artificiels de Pollution sur des Isolateurs Électriques. Ph.D. Thesis, Université Louis Pasteur, Strasbourg, France, 1994. [Google Scholar]
- Salthouse, E.C. Initiation of dry bands on polluted insulation. Proc. Inst. Electr. Eng. 1968, 15, 1707–1712. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, W.; Li, J.; Sun, J.W.; Sun, Y.; Sun, C. Simulation of Radial Electric Field and Voltage Distribution of 500 kV MOA Under Different Conditions of Pollution. In Proceedings of the 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020. [Google Scholar]
- Nouir-Masmoudi, H.; Dhahbi-Megriche, N. Effect of pollution layer discontinuity due to the dry bands presence on potential and electric field along insulator. In Proceedings of the 5th International Conference on Advanced Systems and Emergent Technologies (ICASET), Hammamet, Tunisia, 22–25 March 2022. [Google Scholar]
- Baudit, A.; Mazuer, J.; Odin, J. Thermal conductivity of a RTV silicone elastomer between 1.2 and 300 K. Cryogenics 1998, 38, 227–230. [Google Scholar] [CrossRef]
- Hartiwig, G. Polymer Properties at Room and Cryogenic Temperatures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Zhang, D.; Meng, F. Research on the interrelation between temperature distribution and dry band on wet contaminated insulators. Energies 2019, 12, 4289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).