Simultaneous Reconstruction of Gas Concentration and Temperature Using Acoustic Tomography
Abstract
:1. Introduction
- The proposed method, based solely on the measurement of the speed of sound, can simultaneously reconstruct both the gas concentration and temperature fields.
- The feasibility and effectiveness of this method have been verified through numerical simulation and experimental research.
2. Theoretical Background
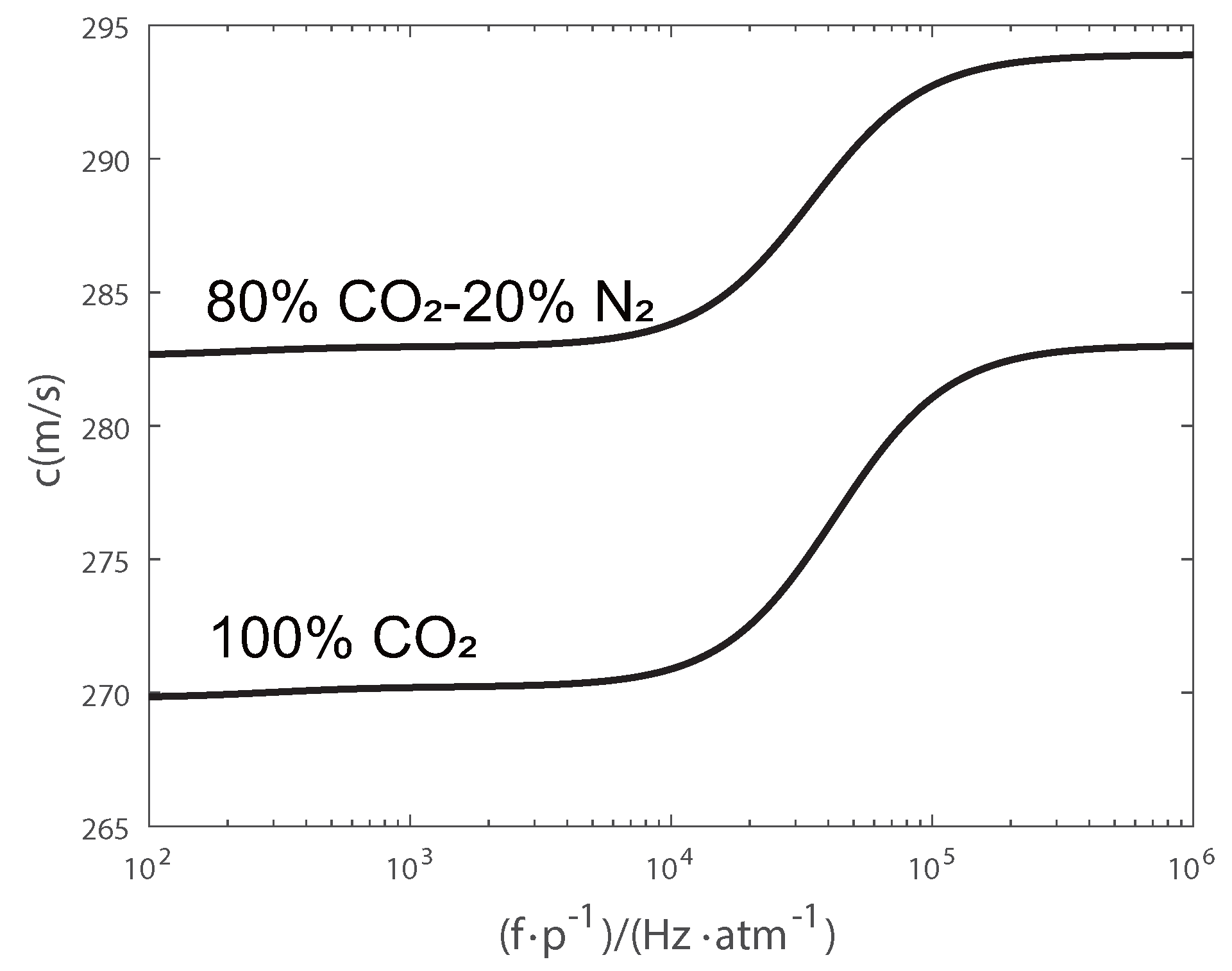
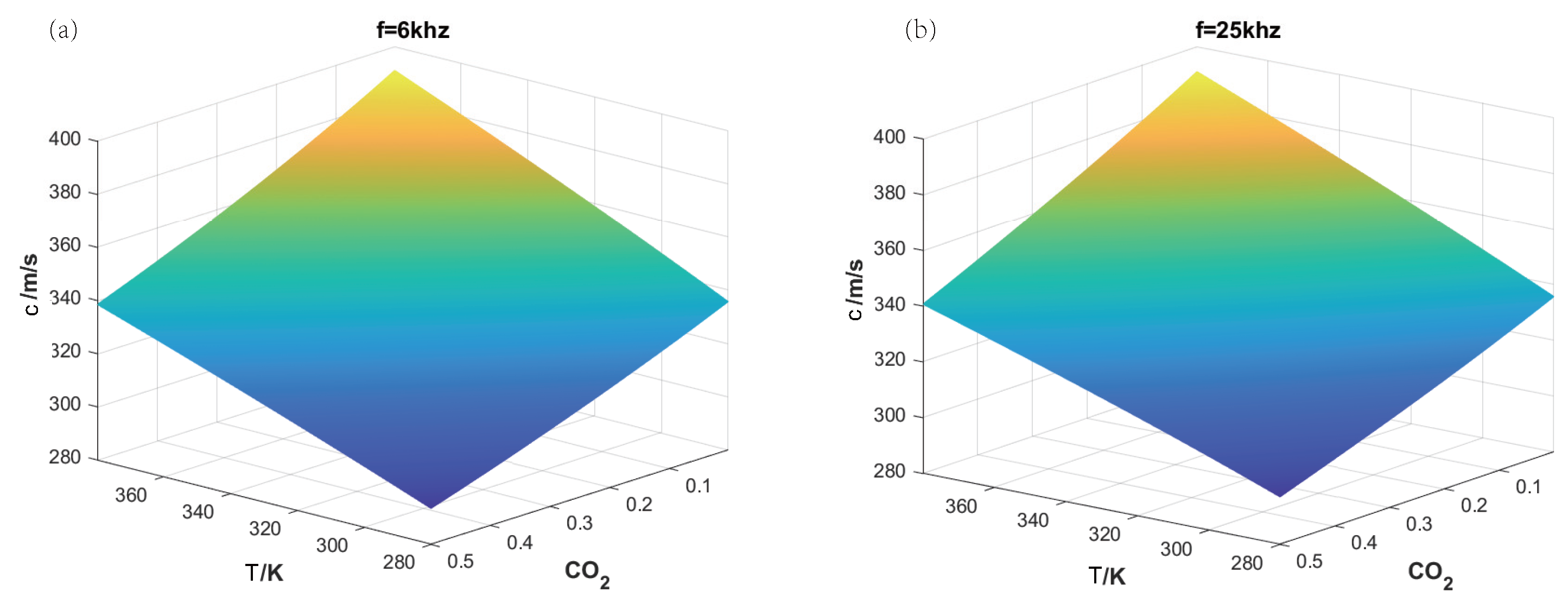
2.1. Acoustic Relaxation Property
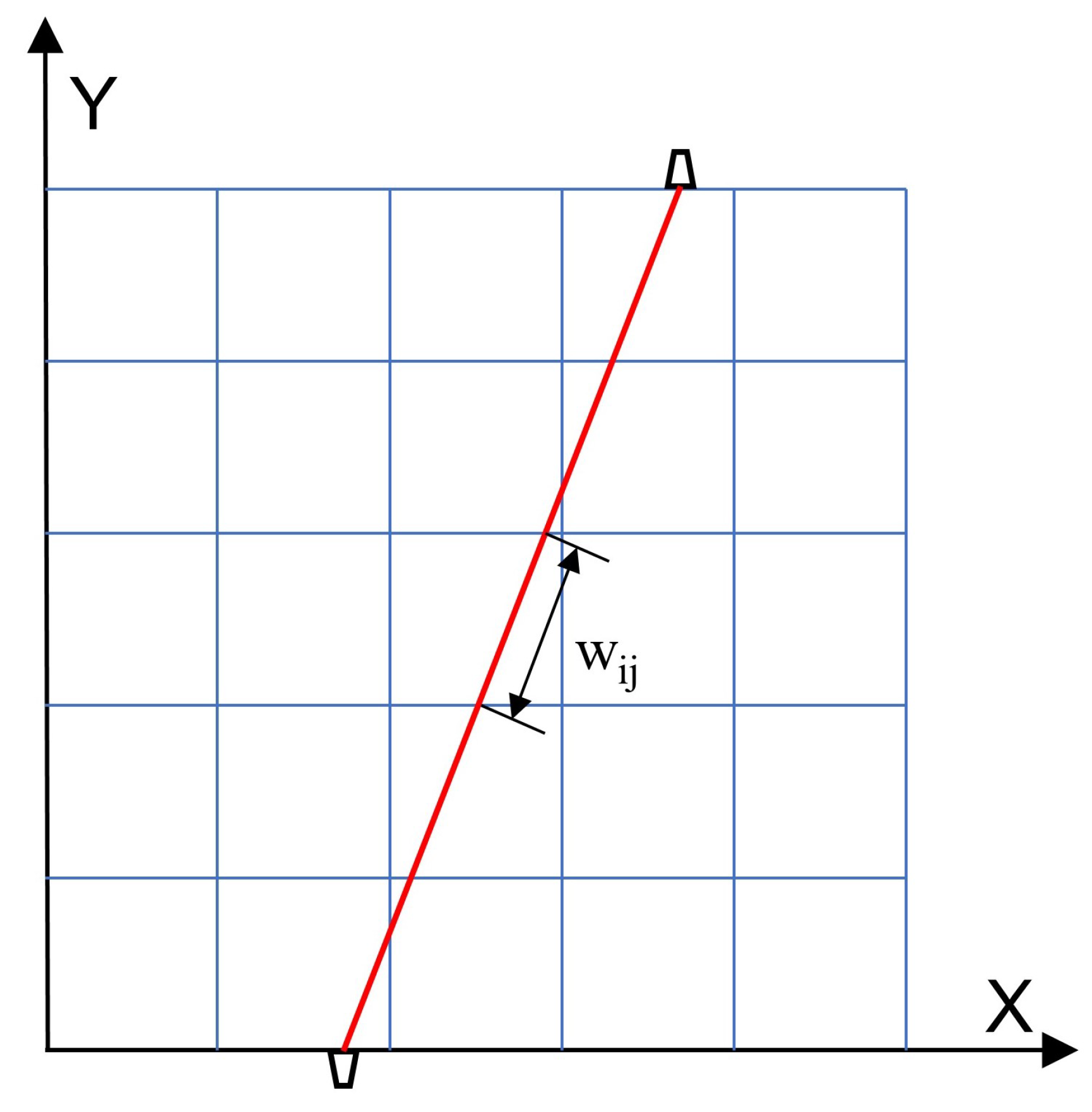
2.2. Acoustic Tomography Model
3. Simultaneous Reconstruction Method
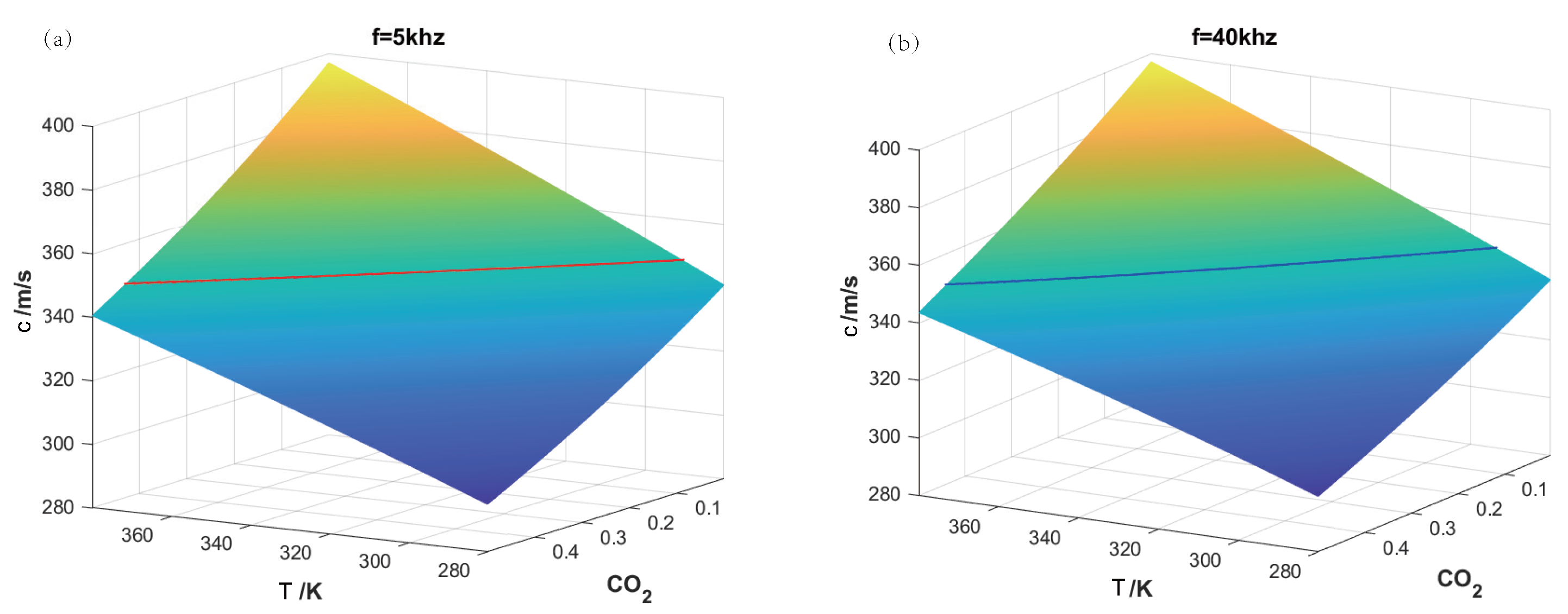
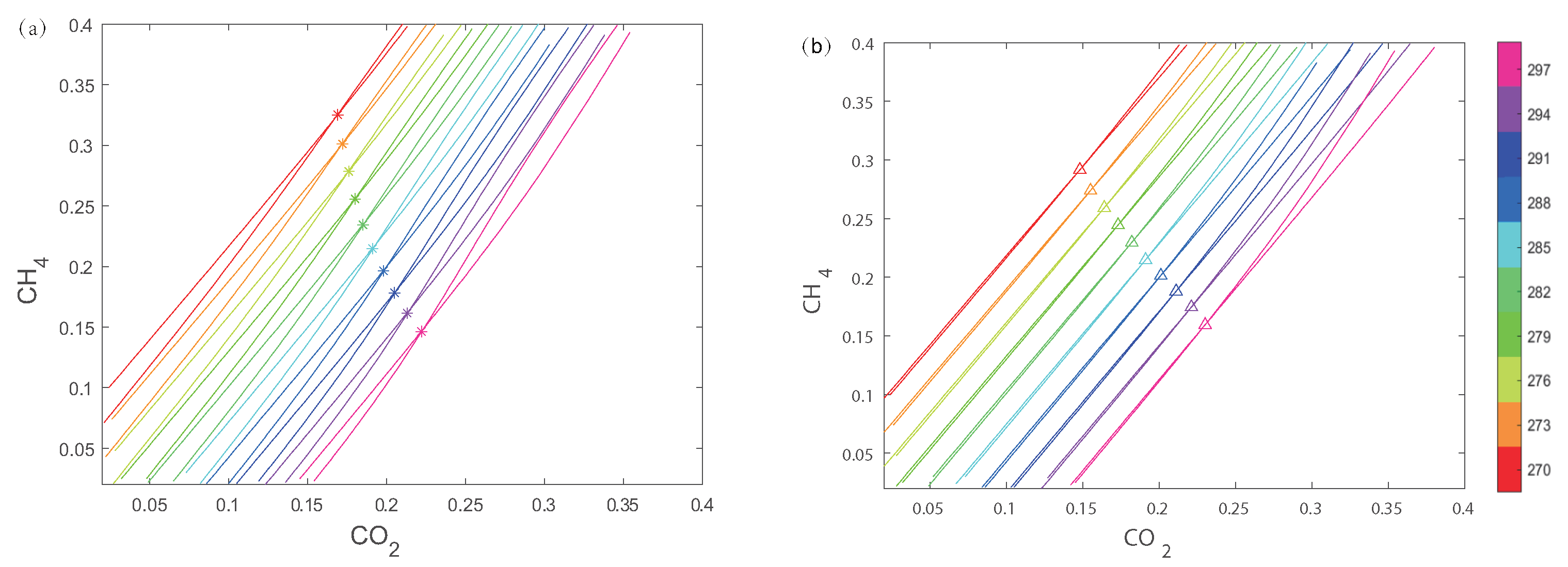
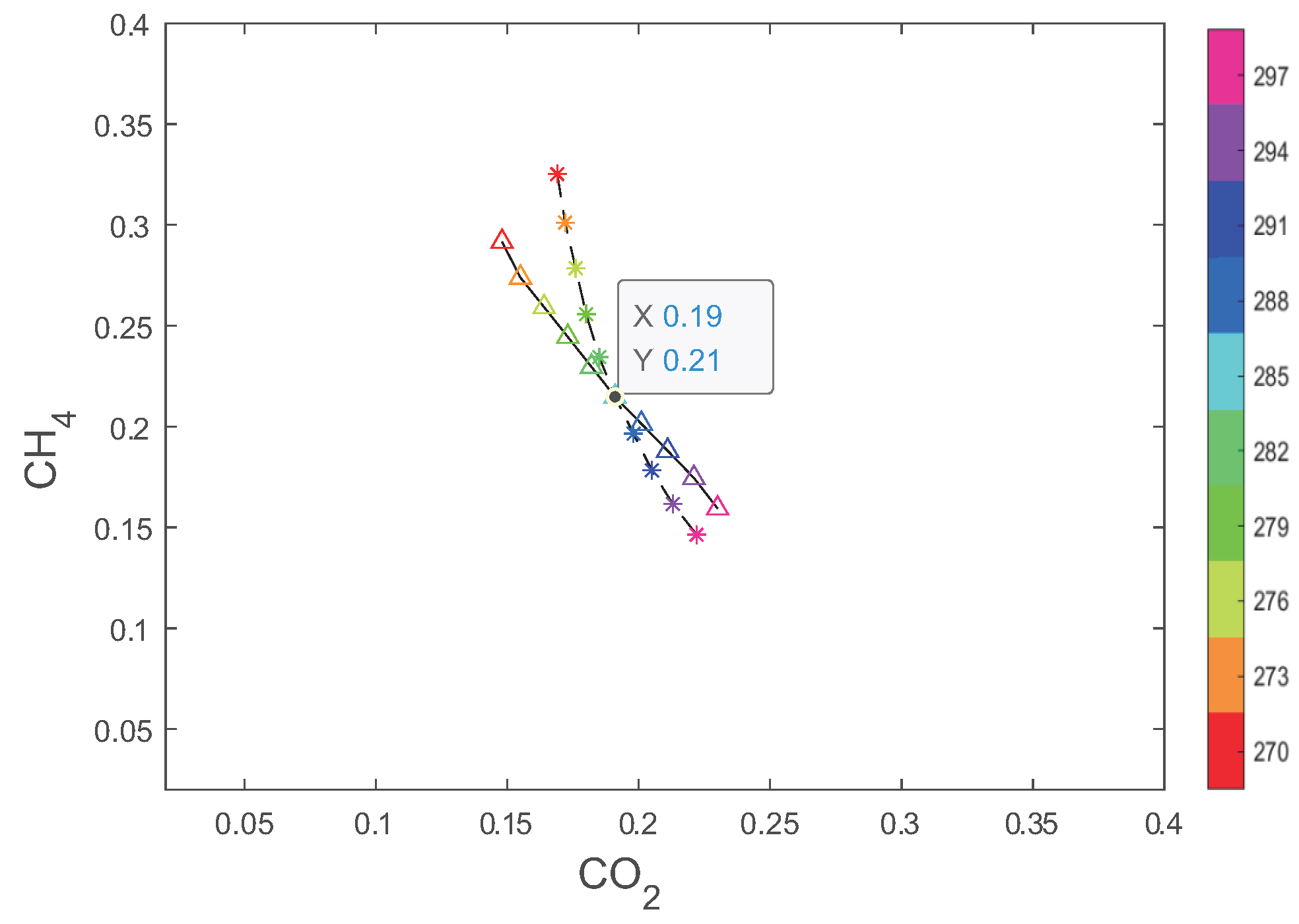
3.1. Reconstruction for Binary Gas Mixture
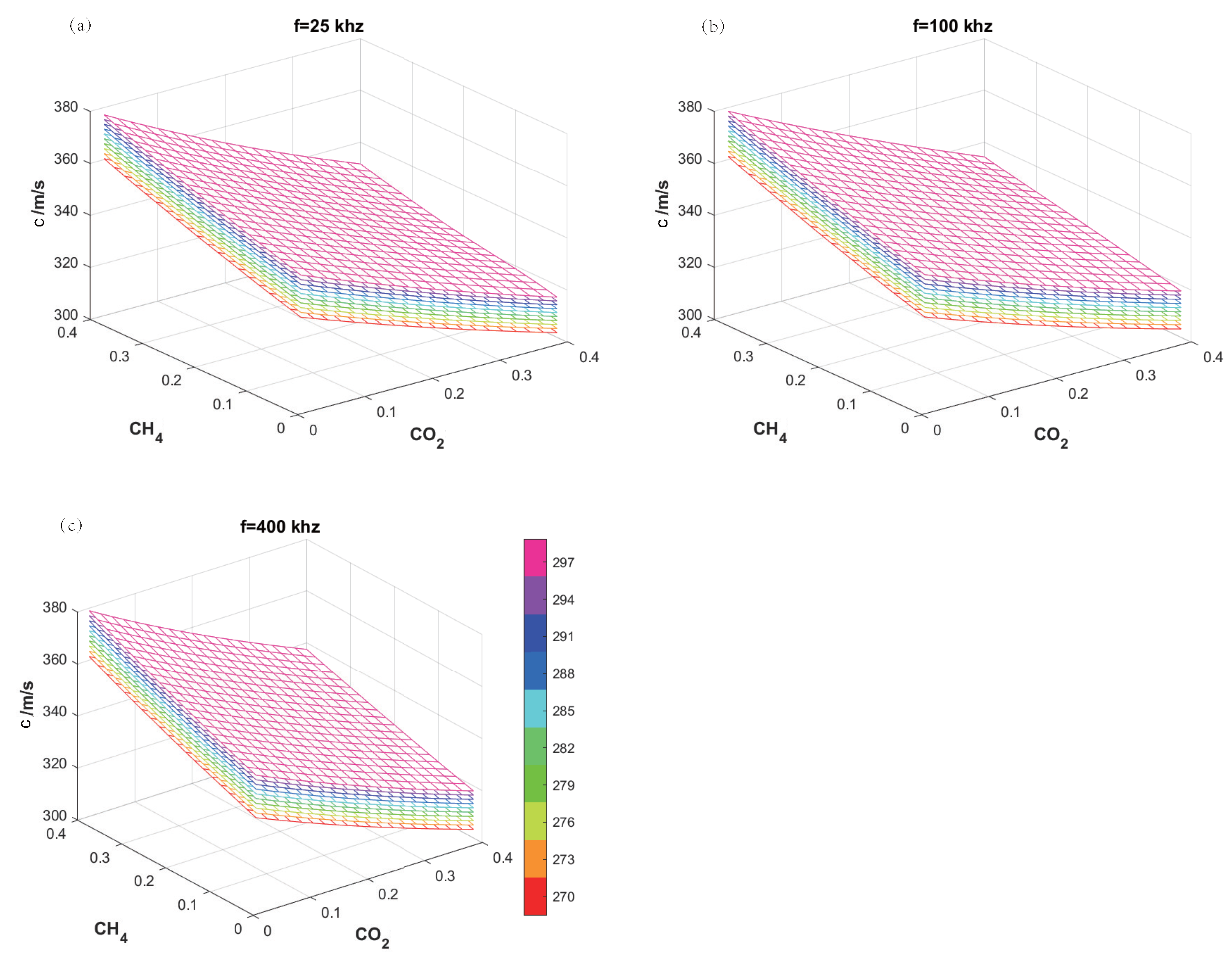
3.2. Reconstruction for Ternary Gas Mixture
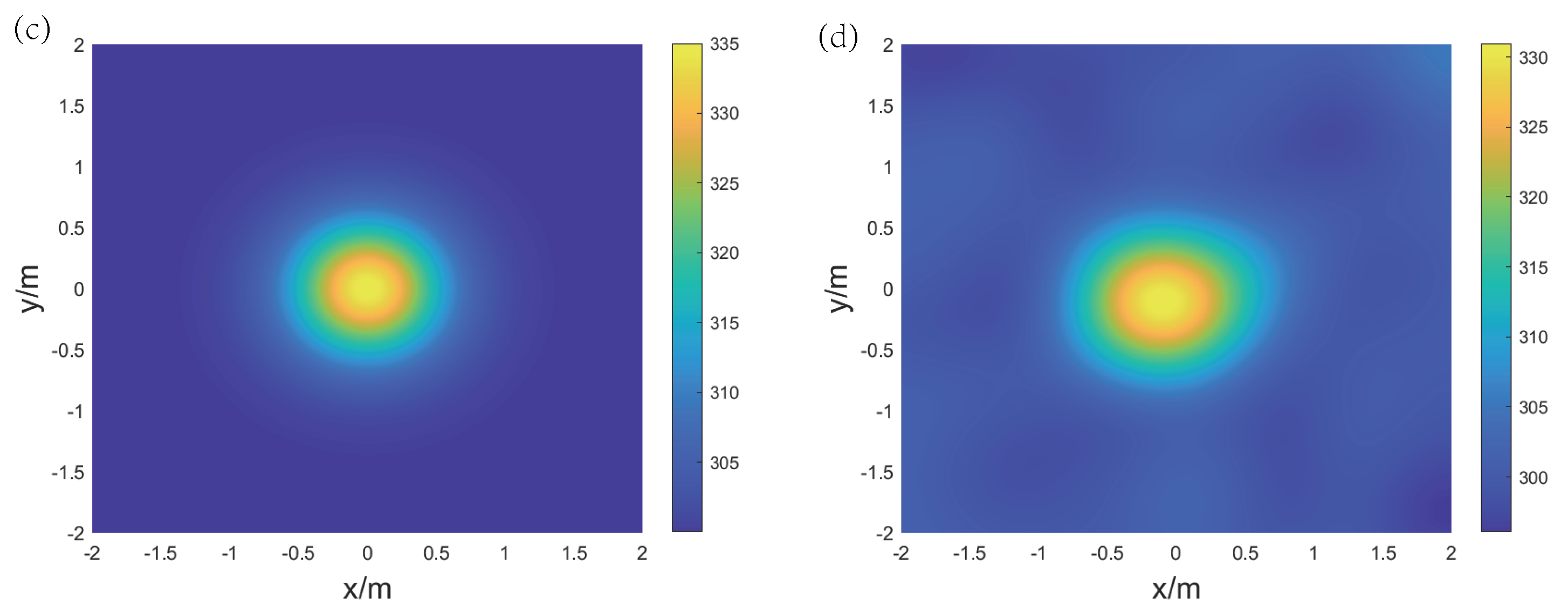
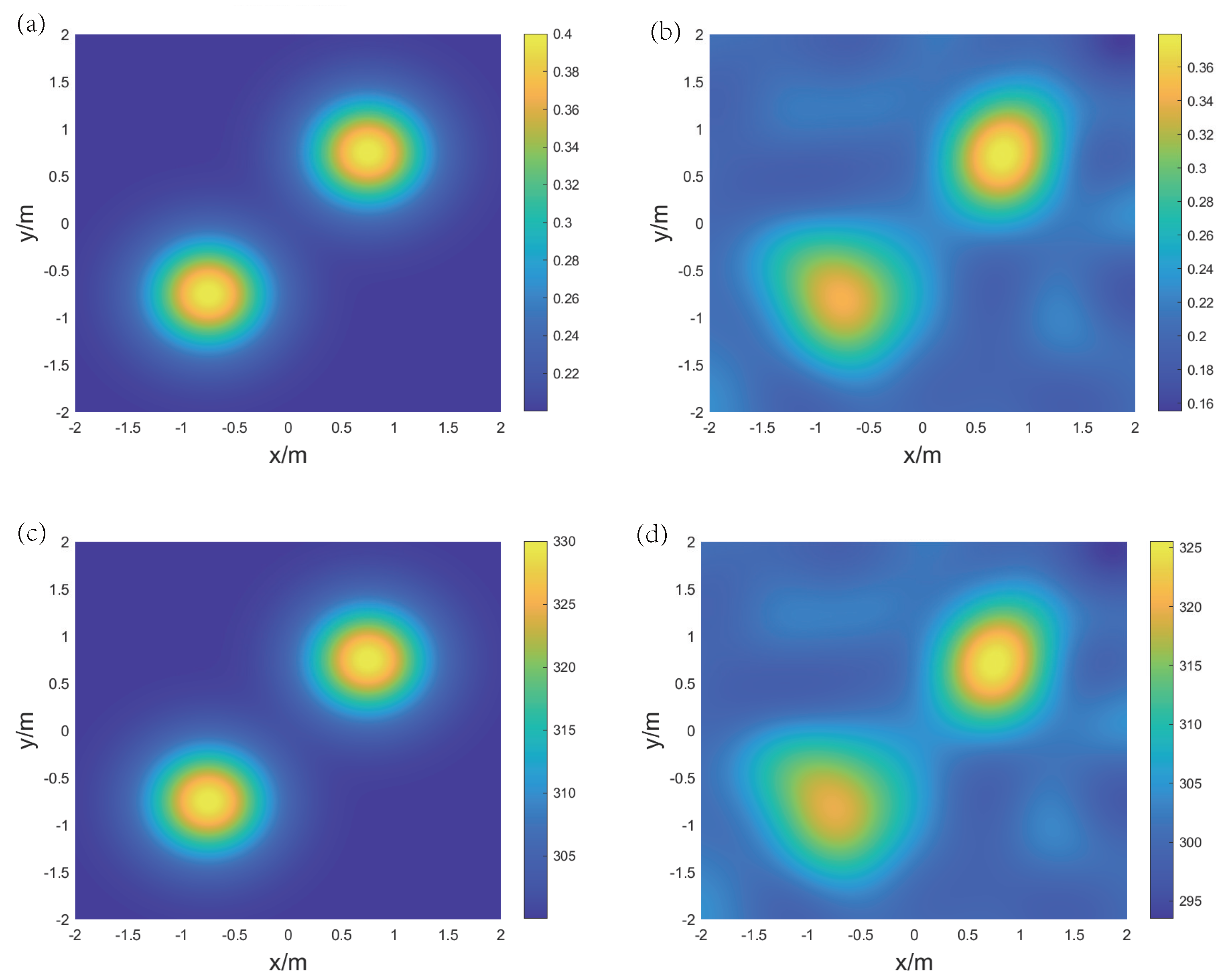
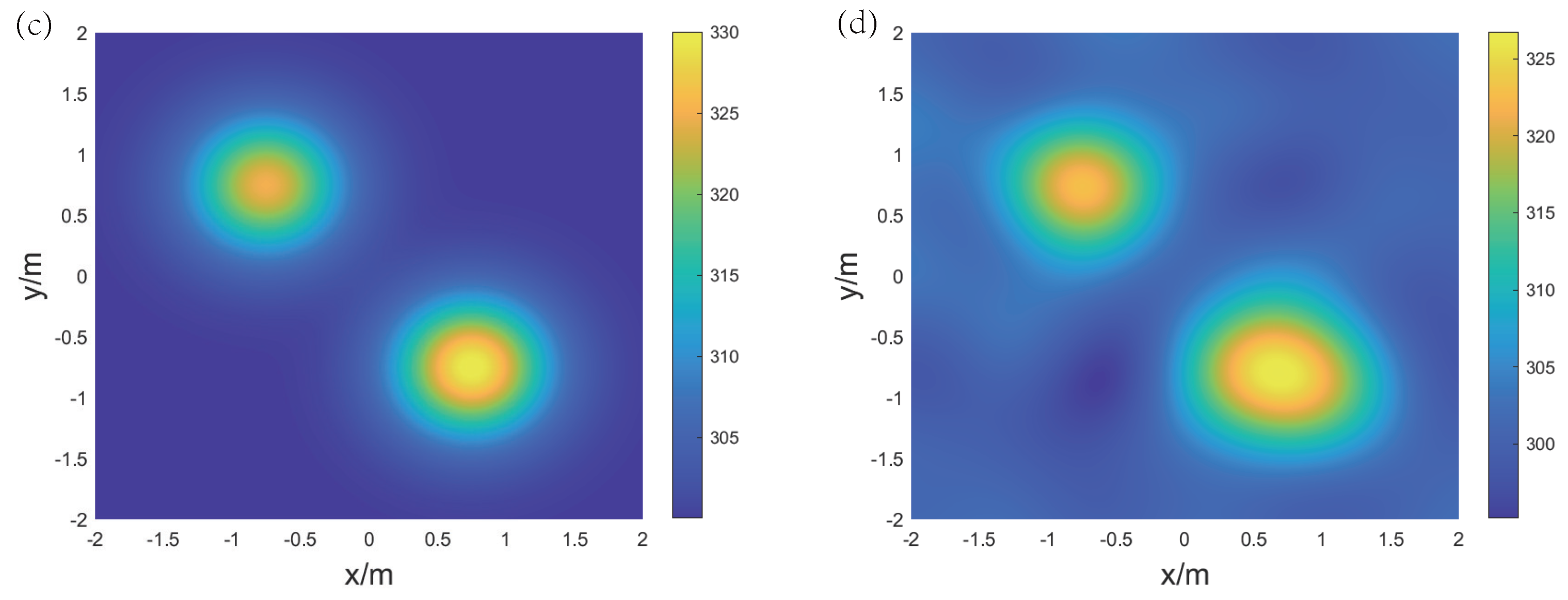
4. Numerical Simulations and Discussion
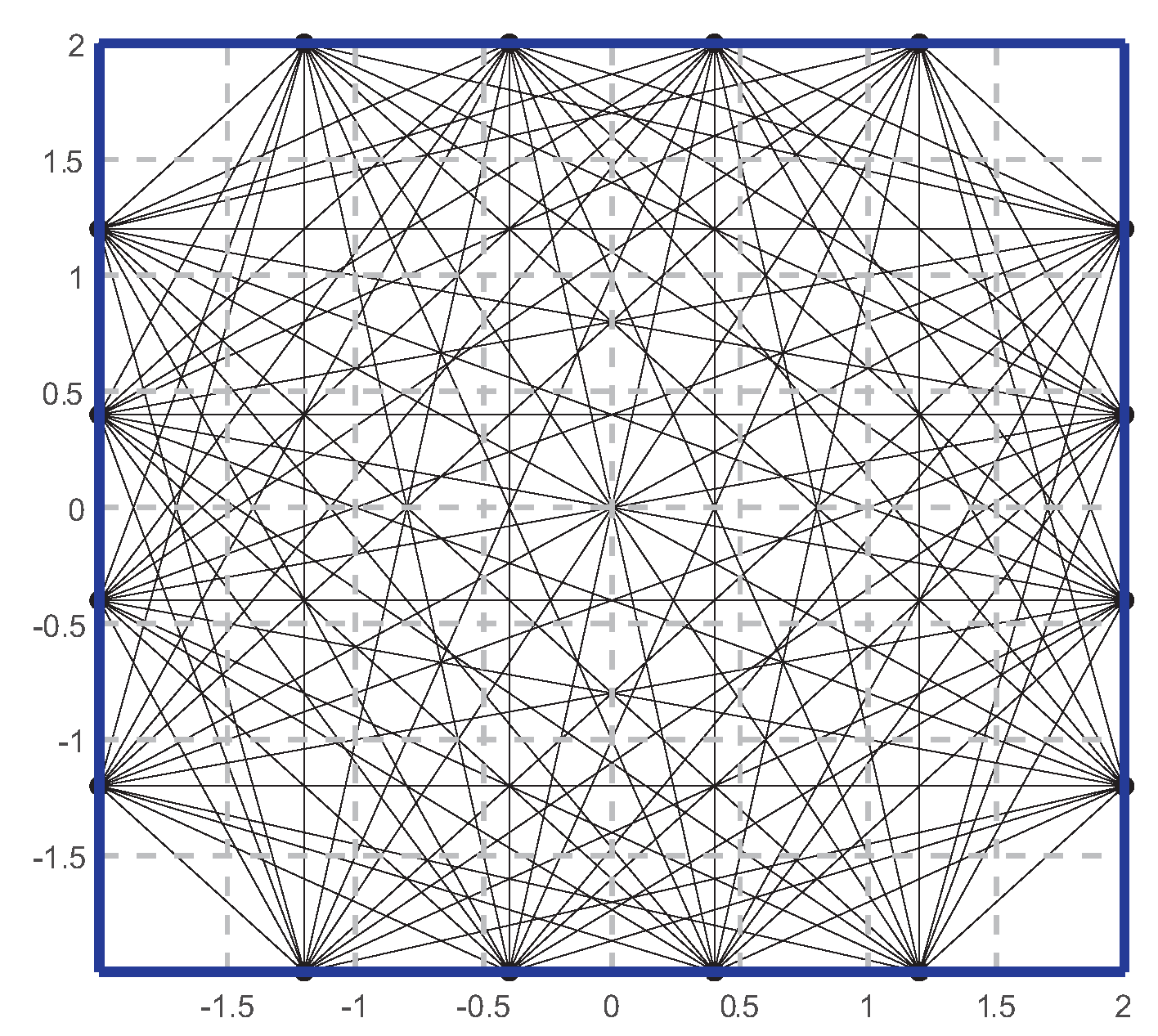
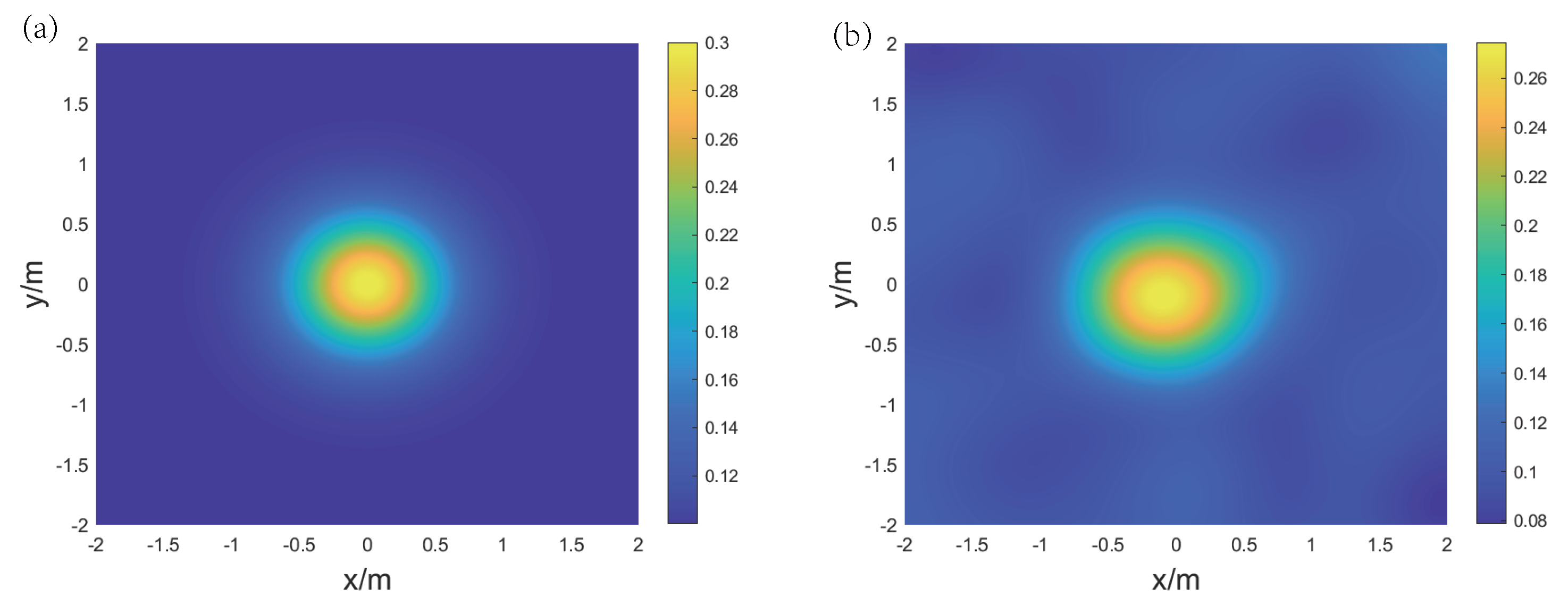
4.1. Reconstruction Procedure and Details
- Divide the test area into n discrete small regions;
- Arrange an array of acoustic sensors with multiple frequencies within the area of interest, forming m acoustic paths for each frequency;
- Measure the propagation time of each path to obtain a vector of sound propagation times for each frequency;
- Calculate the coefficient matrix W;
- Use the LSM to solve Equation (5), obtaining a vector of the reciprocal of the speed of sound for each frequency, thus obtaining the multi-frequency speeds of sound in each grid;
- Employ the GPR interpolation method to obtain the reconstructed speed of sound field with a refined grid;
- Utilize the projection intersection method to determine the physical parameters in the refined grids, thereby obtaining the results for the concentration and temperature fields.
4.2. AT for Binary Gas Mixture
4.3. AT for Ternary Gas Mixture
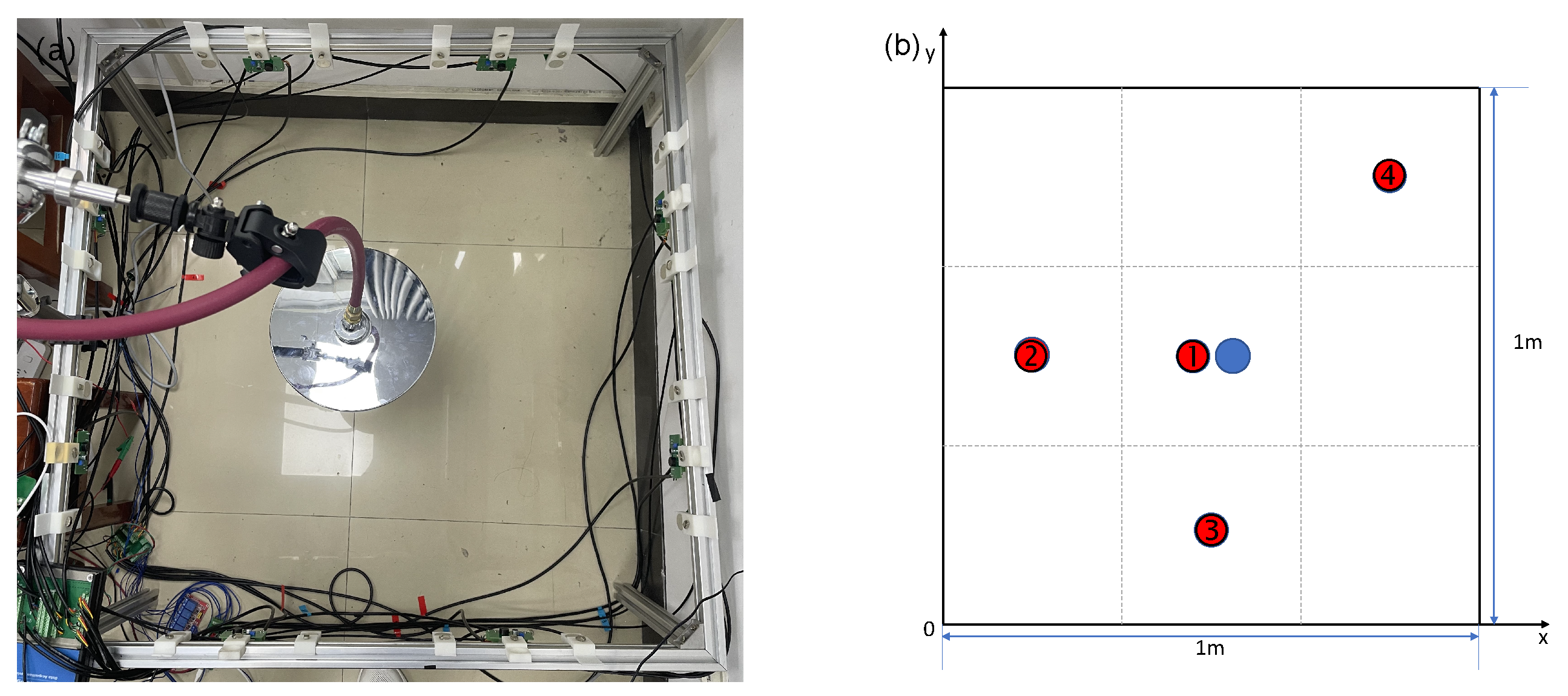
5. Experimental Study
5.1. Apparatus
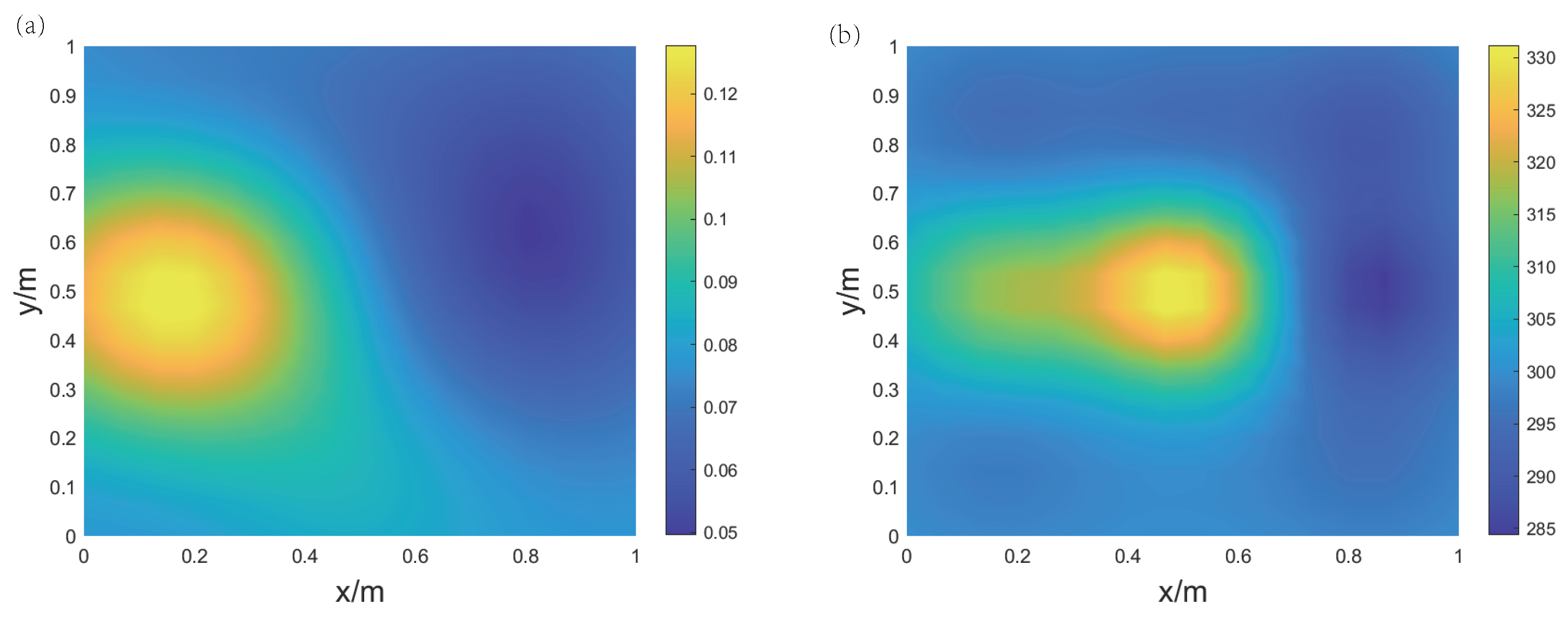
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.; Manh, T.D.; Nam, N.D.; Barzegar Gerdroodbary, M.; Moradi, R.; Tlili, I. Optimization of micro Knudsen gas sensor for high precision detection of SO2 in natural gas. Results Phys. 2020, 16, 102933. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, J.; Zhang, X.; Fang, J.; Zhao, Y. Open-path sensor based on QCL for atmospheric N2O measurement. Results Phys. 2021, 31, 104909. [Google Scholar] [CrossRef]
- Iwaszenko, S.; Kalisz, P.; Sota, M.; Rudzki, A. Detection of Natural Gas Leakages Using a Laser-Based Methane Sensor and UAV. Remote Sens. 2021, 13, 510. [Google Scholar] [CrossRef]
- Rahiman, M.F.; Rahim, R.A.; Zakaria, Z. Design and modelling of ultrasonic tomography for two-component high-acoustic impedance mixture. Sensors Actuators Phys. 2008, 147, 409–414. [Google Scholar] [CrossRef]
- Zhu, B.; Zhong, Q.; Chen, Y.; Liao, S.; Li, Z.; Shi, K.; Sotelo, M.A. A Novel Reconstruction Method for Temperature Distribution Measurement Based on Ultrasonic Tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2352–2370. [Google Scholar] [CrossRef] [PubMed]
- Terzija, N.; Davidson, J.L.; Garcia-Stewart, C.A.; Wright, P.; Ozanyan, K.B.; Pegrum, S.; Litt, T.J.; McCann, H. Image optimization for chemical species tomography with an irregular and sparse beam array. Meas. Sci. Technol. 2008, 19, 094007. [Google Scholar] [CrossRef]
- Fisher, E.M.D.; Tsekenis, S.A.; Yang, Y.; Chighine, A.; Liu, C.; Polydorides, N.; Wright, P.; Kliment, J.; Ozanyan, K.; Benoy, T.; et al. A Custom, High-Channel Count Data Acquisition System for Chemical Species Tomography of Aero-Jet Engine Exhaust Plumes. IEEE Trans. Instrum. Meas. 2020, 69, 549–558. [Google Scholar] [CrossRef]
- Ma, L.; Cai, W. Numerical investigation of hyperspectral tomography for simultaneous temperature and concentration imaging. Appl. Opt. 2008, 47, 3751–3759. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Cao, Z.; Zhao, W.; Zhang, H.; Xu, L. Frequency-Division Multiplexing and Main Peak Scanning WMS Method for TDLAS Tomography in Flame Monitoring. IEEE Trans. Instrum. Meas. 2020, 69, 9087–9096. [Google Scholar] [CrossRef]
- Si, J.; Fu, G.; Zhang, R.; Liu, C. A quality-hierarchical temperature imaging network for TDLAS tomography. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference(I2MTC 2021), Glasgow, UK, 17–20 May 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Liang, G.; Ren, S.; Dong, F. A Shape-Based Statistical Inversion Method for EIT/URT Dual-Modality Imaging. IEEE Trans. Image Process. 2020, 29, 4099–4113. [Google Scholar] [CrossRef]
- Yan, H.; Chen, G.; Zhou, Y.; Liu, L. Primary study of temperature distribution measurement in stored grain based on acoustic tomography. Exp. Therm. Fluid Sci. 2012, 42, 55–63. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, Y.; Zhu, B.; Liao, S.; Shi, K. A temperature field reconstruction method based on acoustic thermometry. Measurement 2022, 200, 111642. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J. Acoustic Tomography Temperature Reconstruction Based on Virtual Observation and Residual Network. IEEE Sens. J. 2022, 22, 17054–17064. [Google Scholar] [CrossRef]
- Pereira dos Santos, D.; Guilherme Haach, V. Generation of ultrasonic tomography from time-domain propagation spectrum. Ultrasonics 2022, 120, 106666. [Google Scholar] [CrossRef] [PubMed]
- Dain, Y.; Lueptow, R.M. Acoustic attenuation in three-component gas mixtures–theory. J. Acoust. Soc. Am. 2001, 109, 1955–1964. [Google Scholar] [CrossRef] [PubMed]
- Petculescu, A.G.; Lueptow, R.M. Fine-tuning molecular acoustic models: Sensitivity of the predicted attenuation to the Lennard-Jones parameters. J. Acoust. Soc. Am. 2005, 117, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Cai, W. Simultaneous reconstruction of temperature and velocity fields using nonlinear acoustic tomography. Appl. Phys. Lett. 2019, 115, 104104. [Google Scholar] [CrossRef]
- Othmani, C.; Dokhanchi, N.S.; Merchel, S.; Vogel, A.; Ercan Altinsoy, M.; Voelker, C.; Takali, F. Acoustic tomographic reconstruction of temperature and flow fields with focus on atmosphere and enclosed spaces: A review. Appl. Therm. Eng. 2023, 223, 119953. [Google Scholar] [CrossRef]
- Liu, S.; Liu, S.; Tong, G. Reconstruction method for inversion problems in an acoustic tomography based temperature distribution measurement. Meas. Sci. Technol. 2017, 28, 115005. [Google Scholar] [CrossRef]
- Wang, C.; Luo, X.; Yu, W.; Guo, Y.; Zhang, L. A variational proximal alternating linearized minimization in a given metric for limited-angle CT image reconstruction. Appl. Math. Model. 2019, 67, 315–336. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Lei, J.; Liu, J.; Schlaberg, H.I.; Yan, Y. A method for simultaneous reconstruction of temperature and concentration distribution in gas mixtures based on acoustic tomography. Acoust. Phys. 2015, 61, 597–605. [Google Scholar] [CrossRef]
- Choi, D.W.; Hutchins, D.A. Ultrasonic propagation in various gases at elevated pressures. Meas. Sci. Technol. 2003, 14, 822–830. [Google Scholar] [CrossRef]
- Lueptow, R.M.; Phillips, S. Acoustic sensor for determining combustion properties of natural gas. Meas. Sci. Technol. 1994, 5, 1375–1381. [Google Scholar] [CrossRef]
- Petculescu, A.G.; Lueptow, R.M. Future trends in acoustic gas sensing. J. Optoelectron. Adv. Mater. 2005, 8, 1959. [Google Scholar] [CrossRef]
- Petculescu, A.; Hall, B.; Fraenzle, R.; Phillips, S.; Lueptow, R.M. A prototype acoustic gas sensor based on attenuation. J. Acoust. Soc. Am. 2006, 120, 1779–1782. [Google Scholar] [CrossRef]
- Ke-Sheng, Z.; Shu, W.; Ming, Z.; Yi, D.; Yi, H. Decoupling multimode vibrational relaxations in multi-component gas mixtures: Analysis of sound relaxational absorption spectra. Chin. Phys. 2013, 22, 014305. [Google Scholar] [CrossRef]
- Zhang, K.S.; Zhu, M.; Tang, W.Y.; Ou, W.H.; Jiang, X.Q. Algorithm for reconstructing vibrational relaxation times in excitable gases by two-frequency acoustic measurements. Acta Phys. Sin. 2016, 65, 134302. [Google Scholar] [CrossRef]










| Distribution | ||||||
|---|---|---|---|---|---|---|
| Single-peak symmetric | 26.77% | 6.99% | 11.58% | 3.23% | 0.53% | 0.84% |
| Double-peak symmetric | 16.31% | 3.25% | 5.31% | 2.89% | 0.43% | 0.67% |
| Double-peak skewed | 14.54% | 3.70% | 4.98% | 2.59% | 0.60% | 0.78% |
| Distribution | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Single-peak symmetric | 20.25% | 10.08% | 10.52% | 15.98% | 5.61% | 5.77% | 5.63% | 1.56% | 1.68% |
| Double-peak symmetric | 11.02% | 4.43% | 5.18% | 13.80% | 8.39% | 8.92% | 3.10% | 1.20% | 1.29% |
| Temperature Point 1 | Temperature Point 2 | Temperature Point 3 | Temperature Point 4 | Concentration Point | |
|---|---|---|---|---|---|
| Reconstructed results | 300.1 K | 291.6 K | 297.3 K | 291.6 K | 8.0% |
| Measured values | 293.5 K | 292.7 K | 293.6 K | 294.8 K | 6.3% |
| Temperature Point 1 | Temperature Point 2 | Temperature Point 3 | Temperature Point 4 | Concentration Point | |
|---|---|---|---|---|---|
| Reconstructed results | 331.2 K | 316.4 K | 301.2 K | 290.3 K | 12.7% |
| Measured values | 342.4 K | 324.6 K | 307.4 K | 294.8 K | 9.3% |
| Temperature Point 1 | Temperature Point 2 | Temperature Point 3 | Temperature Point 4 | Concentration Point | |
|---|---|---|---|---|---|
| Reconstructed results | 332.8 K | 293.0 K | 305.3 K | 297.7 K | 6.3% |
| Measured values | 337.8K | 300.4 K | 298.3 K | 296.7K | 7.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhu, M.; Deng, M.; Hu, Z.; Cheng, Z.; He, X. Simultaneous Reconstruction of Gas Concentration and Temperature Using Acoustic Tomography. Sensors 2024, 24, 3128. https://doi.org/10.3390/s24103128
Liu S, Zhu M, Deng M, Hu Z, Cheng Z, He X. Simultaneous Reconstruction of Gas Concentration and Temperature Using Acoustic Tomography. Sensors. 2024; 24(10):3128. https://doi.org/10.3390/s24103128
Chicago/Turabian StyleLiu, Shuangling, Ming Zhu, Meng Deng, Zesheng Hu, Zhuo Cheng, and Xingshun He. 2024. "Simultaneous Reconstruction of Gas Concentration and Temperature Using Acoustic Tomography" Sensors 24, no. 10: 3128. https://doi.org/10.3390/s24103128





