A Procedure for Precise Determination and Compensation of Lead-Wire Resistance of a Two-Wire Resistance Temperature Detector
Abstract
:1. Introduction
2. Principle of the Proposed Procedure
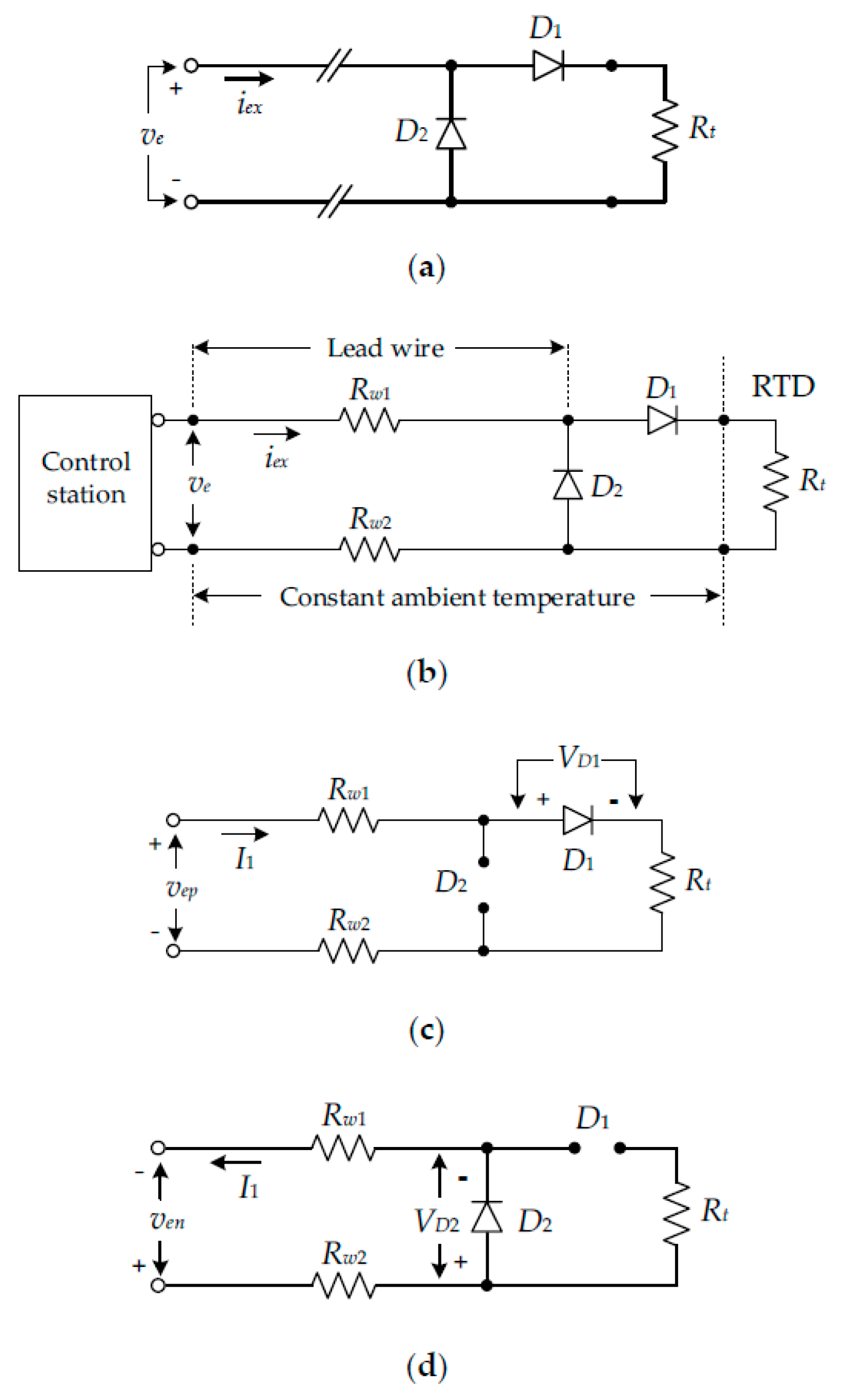
2.1. Conventional Procedure
2.2. Proposed Procedure
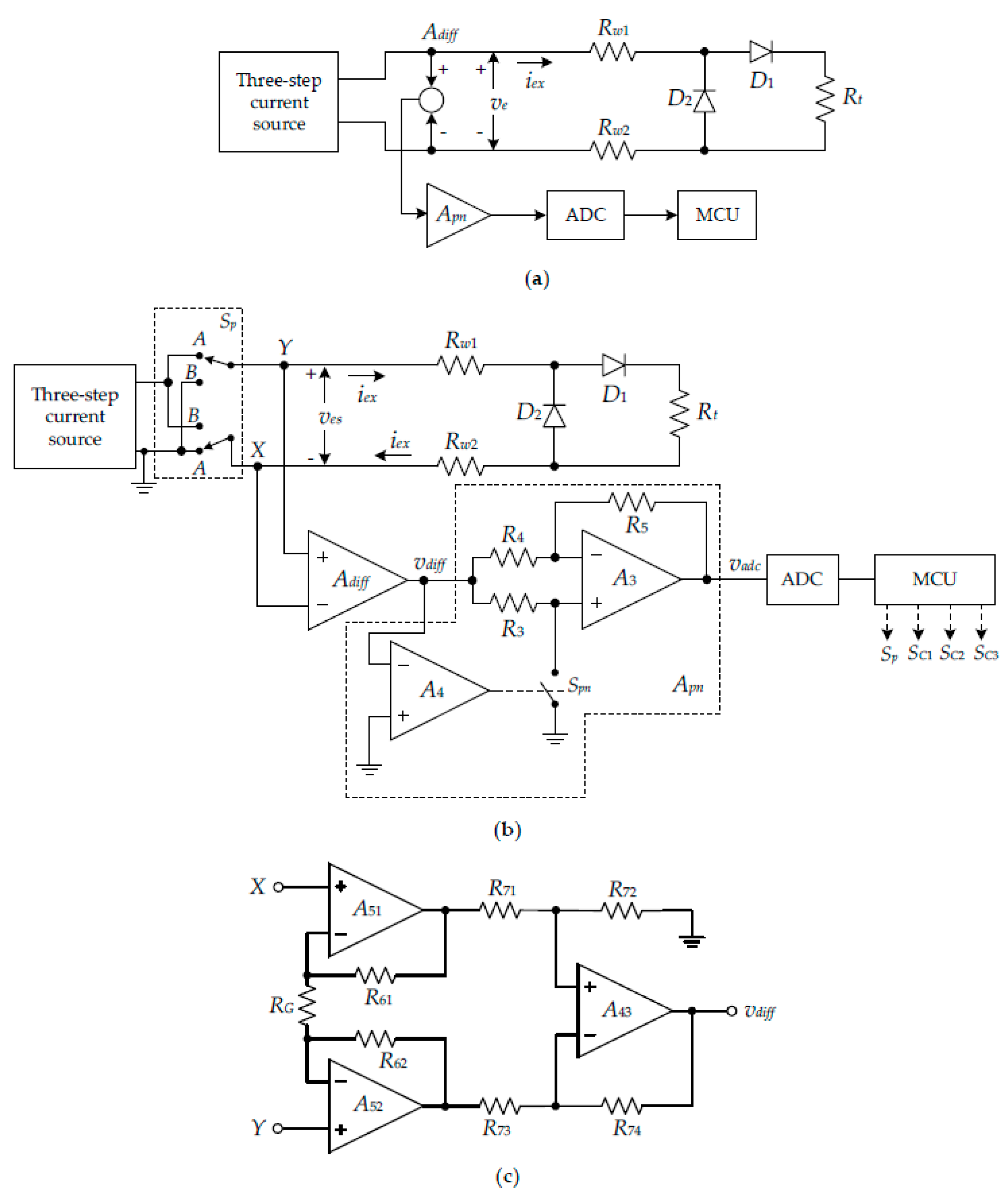
2.3. Implementation of the Proposed Procedure
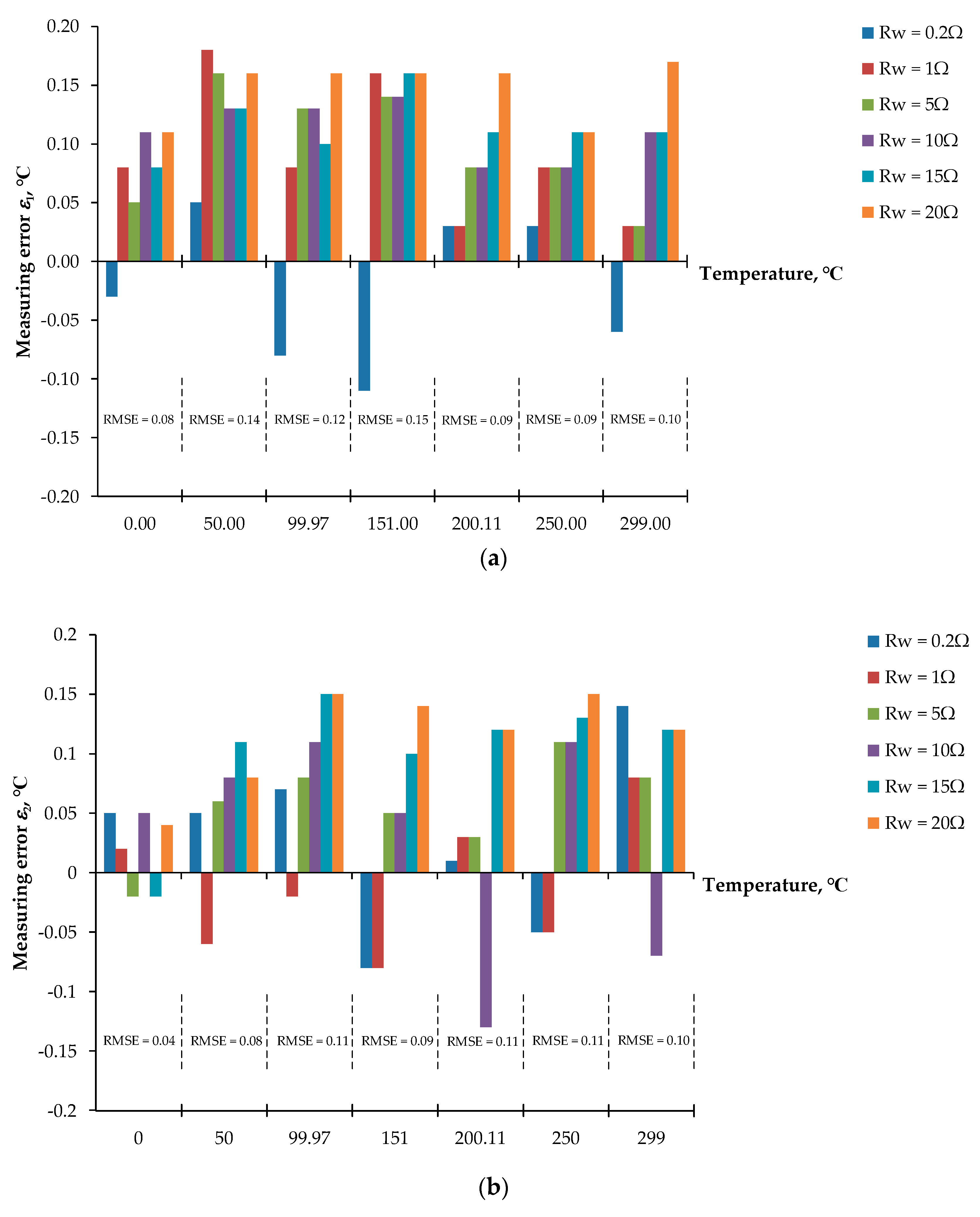
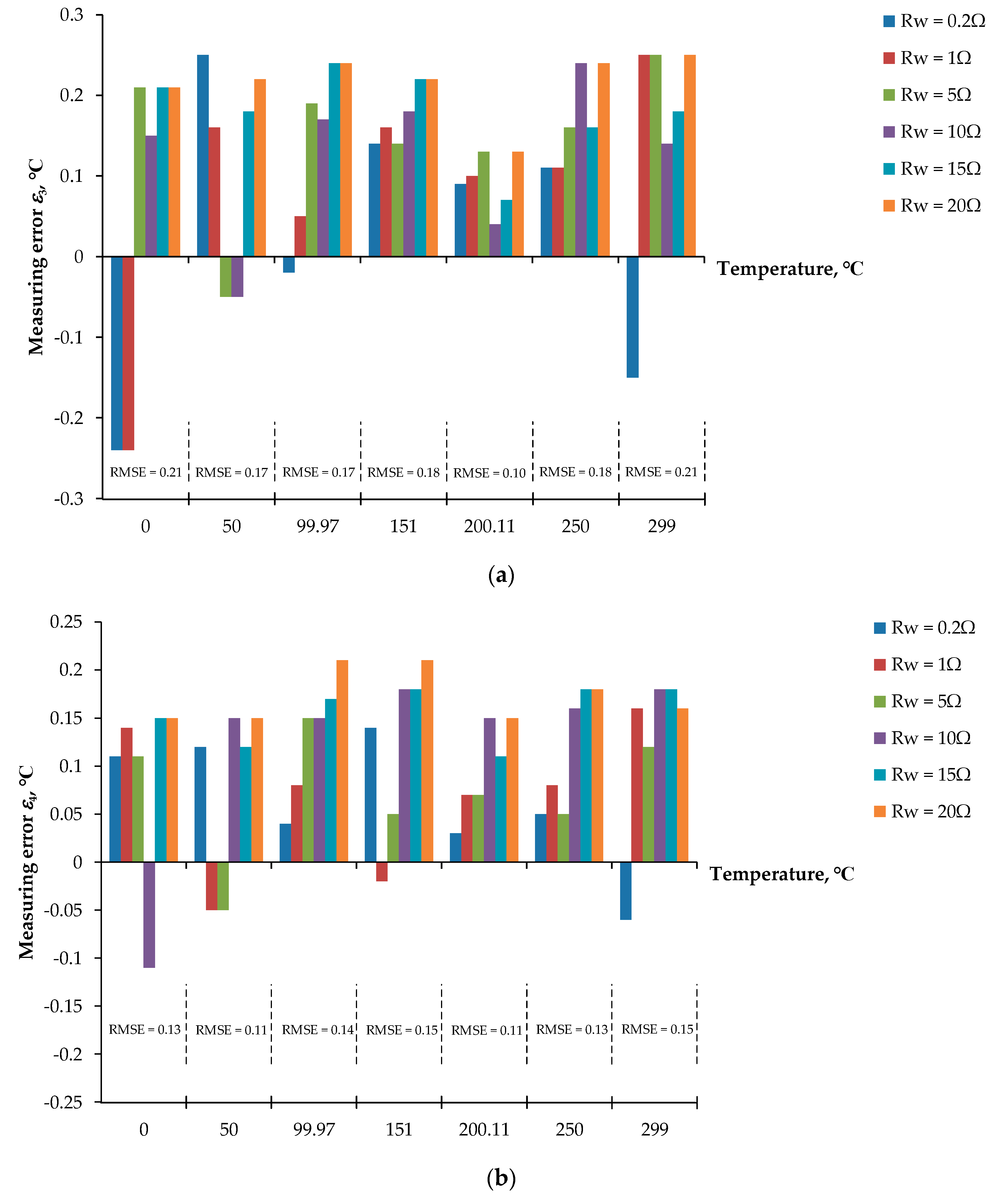
3. Performance Analysis
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cetinkunt, S. Mechatronics; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 978-0-471-47987-1. [Google Scholar]
- Pallás-Areny, R.; Webster, J.G. Sensors and Signal Conditioning, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001; ISBN 0-471-33232-1. [Google Scholar]
- Neubert, H.K.P. Instrument Transducers: An Introduction to Their Performance and Design; Clarendon: Oxford, UK, 1975; ISBN 0-19-856320-5. [Google Scholar]
- Baker, B.C. Precision Temperature Sensing with Three-Wire RTD Circuits. AN687 (Microchip Technology, Inc.). 2008. Available online: http://ww1.microchip.com/downloads/en/appnotes/00687c.pdf (accessed on 9 April 2022).
- Wu, J. A Basic Guide to RTD Measurements. Application Report SBAA275 (Texas Instruments, Inc.). 2018. Available online: https://www.ti.com/lit/an/sbaa275/sbaa275.pdf (accessed on 9 April 2022).
- Ibrahim, D. Microcontroller-Based Temperature Monitoring and Control; Elsevier: Oxford, UK, 2002; ISBN 0-7506-5556-9. [Google Scholar]
- Maiti, T.K. A Novel Lead-Wire-Resistance Compensation Technique Using Two-Wire Resistance Temperature Detector. IEEE Sens. J. 2006, 6, 1454–1458. [Google Scholar] [CrossRef]
- Maiti, T.K.; Kar, A. Novel Remote Measurement Technique Using Resistive Sensor as Grounded Load in an Opamp Based V-to-I Converter. IEEE Sens. J. 2009, 9, 244–245. [Google Scholar] [CrossRef]
- Nagarajan, P.R.; George, B.; Kumar, V.J. Improved Single-Element Resistive Sensor-to-Microcontroller Interface. IEEE Trans. Instrum. Meas. 2017, 66, 2736–2743. [Google Scholar] [CrossRef]
- Anandanatarajan, R.; Mangalanathan, U.; Gandhi, U. Enhanced Microcontroller Interface of Resistive Sensors Through Resistance-to-Time Converter. IEEE Trans. Instrum. Meas. 2020, 69, 2698–2706. [Google Scholar] [CrossRef]
- Moaveni, S. Engineering Fundamentals: An Introduction to Engineering; Cengage: Boston, MA, USA, 2019; ISBN 9780357112151. [Google Scholar]
- Pradhan, S.; Sen, S. An improved lead compensation technique for three-wire resistance temperature detectors. IEEE Trans. Instrum. Meas. 1999, 48, 903–905. [Google Scholar] [CrossRef]
- Neji, B.; Ferko, N.; Ghandour, R.; Karar, A.S.; Arbess, H. Micro-Fabricated RTD Based Sensor for Breathing Analysis and Monitoring. Sensors 2021, 21, 318. [Google Scholar] [CrossRef]
- Nagarajan, P.R.; George, B.; Kumar, V.J. A Linearizing Digitizer for Wheatstone Bridge Based Signal Conditioning of Resistive Sensors. IEEE Sens. J. 2017, 17, 1696–1705. [Google Scholar] [CrossRef]
- Kester, W. Practical Design Techniques for Sensor Signal Conditioning; Analog Devices Inc.: New York, NY, USA, 1999; ISBN 0-916550-20-6. [Google Scholar]
- Sen, S.K.; Pan, T.K.; Ghosal, P. An improved lead wire compensation technique for conventional four wire resistance temperature detectors (RTDs). Measurement 2011, 44, 842–846. [Google Scholar] [CrossRef]
- Maiti, T.K.; Kar, A. A new and low cost lead resistance compensation technique for resistive sensors. Measurement 2010, 43, 735–738. [Google Scholar] [CrossRef]
- Li, W.; Xiong, S.; Zhou, X. Lead-Wire-Resistance Compensation Technique Using a Single Zener Diode for Two-Wire Resistance Temperature Detectors (RTDs). Sensors 2020, 20, 2742. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Li, Y.; Hao, Q. Development and Application of Resistance Strain Force Sensors. Sensors 2020, 20, 5826. [Google Scholar] [CrossRef] [PubMed]
- Mobaraki, B.; Lozano-Galant, F.; Soriano, R.P.; Castilla Pascual, F.J. Application of Low-Cost Sensors for Building Monitoring: A Systematic Literature Review. Buildings 2021, 11, 336. [Google Scholar] [CrossRef]
- Aygun, L.E.; Kumar, V.; Weaver, C.; Gerber, M.; Wagner, S.; Verma, N.; Glisic, B.; Sturm, J.C. Large-Area Resistive Strain Sensing Sheet for Structural Health Monitoring. Sensors 2020, 20, 1386. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; La, H.M.; Gucunski, N. Review of Non-Destructive Civil Infrastructure Evaluation for Bridges: State-of-the-Art Robotic Platforms, Sensors and Algorithms. Sensors 2020, 20, 3954. [Google Scholar] [CrossRef] [PubMed]
- D’Alessandro, A.; Birgin, H.B.; Cerni, G.; Ubertini, F. Smart Infrastructure Monitoring through Self-Sensing Composite Sensors and Systems: A Study on Smart Concrete Sensors with Varying Carbon-Based Filler. Infrastructures 2022, 7, 48. [Google Scholar] [CrossRef]
- Glisic, B. Concise Historic Overview of Strain Sensors Used in the Monitoring of Civil Structures: The First One Hundred Years. Sensors 2022, 22, 2397. [Google Scholar] [CrossRef]
- Kosec, T.; Kuhar, V.; Kranjc, A.; Malnarič, V.; Belingar, B.; Legat, A. Development of an Electrical Resistance Sensor from High Strength Steel for Automotive Applications. Sensors 2019, 19, 1956. [Google Scholar] [CrossRef] [Green Version]
- Hamdani, S.T.A.; Fernando, A. The Application of a Piezo-Resistive Cardiorespiratory Sensor System in an Automobile Safety Belt. Sensors 2015, 15, 7742–7753. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.; Fang, X.; Chen, N.; Xue, X.; Wu, G. A Sensing Mechanism and the Application of a Surface-Bonded FBG Dynamometry Bolt. Appl. Sci. 2022, 12, 3225. [Google Scholar] [CrossRef]
- Jung, W. Op Amp Applications Handbook; Elsevier: Oxford, UK, 2005; ISBN 0-7506-7844-5. [Google Scholar]
- Volodchenko, A.A.; Lesovik, V.S.; Cherepanova, I.A.; Volodchenko, A.N.; Zagorodnjuk, L.H.; Elistratkin, M.Y. Peculiarities of non-autoclaved lime wall materials production using clays. IOP Conf. Ser. Mater. Sci. Eng. 2018, 327, 022021. [Google Scholar] [CrossRef]
- Amran, M.; Fediuk, R.; Murali, G.; Avudaiappan, S.; Ozbakkaloglu, T.; Vatin, N.; Karelina, M.; Klyuev, S.; Gholampour, A. Fly Ash-Based Eco-Efficient Concretes: A Comprehensive Review of the Short-Term Properties. Materials 2021, 14, 4264. [Google Scholar] [CrossRef] [PubMed]
- Boylestad, R.L.; Nashelsky, L. Electronic Devices and Circuit Theory, 11th ed.; Pearson Education Ltd.: London, UK, 2014; ISBN 13: 978-1-292-02563-6. [Google Scholar]
- Petchmaneelumka, W.; Mano, P.; Songsuwankit, K.; Riewruja, V. High-accuracy resolver-to-linear signal converter. Int. J. Electron. 2018, 105, 1520–1534. [Google Scholar] [CrossRef]
- Analog Devices. Low Cost Low Power Instrumentation Amplifier. Datasheet AD620. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD620.pdf (accessed on 9 April 2022).
- Ali, S.; Badar, J.; Akhter, F.; Bukhari, S.S.H.; Ro, J.-S. Real-Time Controller Design Test Bench for High-Voltage Direct Current Modular Multilevel Converters. Appl. Sci. 2020, 10, 6004. [Google Scholar] [CrossRef]
- Swain, K.; Cherukuri, M.; Mishra, S.K.; Appasani, B.; Patnaik, S.; Bizon, N. LI-Care: A LabVIEW and IoT Based eHealth Monitoring System. Electronics 2021, 10, 3137. [Google Scholar] [CrossRef]
- Letizia, P.S.; Signorino, D.; Crotti, G. Impact of DC Transient Disturbances on Harmonic Performance of Voltage Transformers for AC Railway Applications. Sensors 2022, 22, 2270. [Google Scholar] [CrossRef]
- STMicroelectronics. NUCLEO-L476RG. Data brief STM32 Nucleo-64. Available online: https://www.st.com/en/evaluation-tools/nucleo-l476rg.html (accessed on 9 April 2022).
- Dellinger, J.H. The Temperature Coefficient of Resistance of Copper. Available online: https://nvlpubs.nist.gov/nistpubs/bulletin/07/nbsbulletinv7n1p71_A2b.pdf (accessed on 9 April 2022).







| Lead-Wire Resistance (Ω) at 30 °C | Temperature (°C) pt100 RTD (Ω) | Diode Voltage (mV) at 30 °C and ID = 1 mA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VD1 | VD2 | ||||||||
| 0.00 | 0.00 100.00 | 50.00 119.40 | 99.97 138.50 | 151.00 157.70 | 200.11 175.90 | 250.00 194.10 | 299.00 211.70 | 600.68 | 598.21 |
| 0.20 | −0.03 99.99 | 50.05 119.42 | 99.89 138.47 | 150.89 157.74 | 200.14 175.91 | 250.03 194.11 | 298.94 211.68 | 600.68 | 598.71 |
| 1.00 | 0.08 100.03 | 50.18 119.47 | 100.05 138.53 | 151.16 157.76 | 200.14 175.91 | 250.08 194.03 | 299.03 211.71 | 600.71 | 599.28 |
| 5.00 | 0.05 100.02 | 50.16 119.46 | 100.10 138.55 | 151.14 157.75 | 200.19 175.93 | 250.08 194.03 | 299.03 211.71 | 600.78 | 599.64 |
| 10.00 | 0.11 100.04 | 50.13 119.45 | 100.10 138.55 | 151.14 157.75 | 200.19 175.93 | 250.08 194.03 | 299.11 211.74 | 601.04 | 599.77 |
| 15.00 | 0.08 100.03 | 50.13 119.45 | 100.07 138.54 | 151.16 157.76 | 200.22 175.94 | 250.11 194.14 | 299.11 211.74 | 600.75 | 598.25 |
| 20.00 | 0.11 100.04 | 50.16 119.46 | 100.13 138.56 | 151.16 157.76 | 200.27 175.96 | 250.11 194.14 | 299.17 211.76 | 601.07 | 599.86 |
| Lead-Wire Resistance (Ω) at 30 °C | Temperature (°C) pt1000 RTD (Ω) | Diode Voltage (mV) at 30 °C and ID = 1 mA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VD1 | VD2 | ||||||||
| 0.00 | 0.00 | 50.00 | 99.97 | 151.00 | 200.11 | 250.00 | 299.00 | 600.67 | 598.19 |
| 1000.00 | 1194.00 | 1385.00 | 1577.00 | 1759.00 | 1941.00 | 2117.00 | |||
| 0.20 | 0.05 | 50.05 | 100.04 | 150.92 | 200.12 | 249.95 | 299.14 | 600.67 | 598.21 |
| 1000.19 | 1194.19 | 1385.27 | 1576.70 | 1759.04 | 1940.82 | 2117.50 | |||
| 1.00 | 0.02 | 49.94 | 99.95 | 150.92 | 200.14 | 249.95 | 299.08 | 601.44 | 599.51 |
| 1000.08 | 1193.77 | 1384.92 | 1576.70 | 1759.07 | 1940.82 | 2117.29 | |||
| 5.00 | −0.02 | 50.06 | 100.05 | 151.05 | 200.14 | 250.11 | 299.08 | 601.41 | 599.49 |
| 999.92 | 1194.23 | 1385.30 | 1577.19 | 1759.07 | 1941.40 | 2117.29 | |||
| 10.00 | 0.05 | 50.08 | 100.08 | 151.05 | 199.98 | 250.11 | 298.93 | 601.41 | 599.48 |
| 1000.19 | 1194.3 | 1385.42 | 1577.19 | 1758.52 | 1941.4 | 2116.75 | |||
| 15.00 | −0.02 | 50.11 | 100.12 | 151.10 | 200.23 | 250.13 | 299.12 | 602.15 | 600.26 |
| 999.92 | 1194.42 | 1385.57 | 1577.37 | 1759.44 | 1941.47 | 2117.43 | |||
| 20.00 | 0.04 | 50.08 | 100.12 | 151.14 | 200.23 | 250.15 | 299.12 | 601.93 | 600.11 |
| 1000.02 | 1194.30 | 1385.57 | 1577.52 | 1759.44 | 1941.54 | 2117.43 | |||
| Lead-Wire Resistance (Ω) at 30 °C | Temperature (°C) pt100 RTD (Ω) | Diode Voltage (mV) at 30 °C and ID = 1 mA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VD1 | VD2 | ||||||||
| 0.00 | 0.00 | 50.00 | 99.97 | 151.00 | 200.11 | 250.00 | 299.00 | 600.65 | 598.20 |
| 100.00 | 119.40 | 138.50 | 157.70 | 175.90 | 194.10 | 211.70 | |||
| 0.20 | −0.24 | 50.25 | 99.95 | 151.14 | 200.20 | 250.11 | 298.85 | 600.65 | 598.19 |
| 99.91 | 119.50 | 138.48 | 157.75 | 175.93 | 194.57 | 211.65 | |||
| 1.00 | −0.24 | 50.16 | 100.02 | 151.16 | 200.21 | 250.11 | 299.25 | 600.67 | 598.45 |
| 99.91 | 119.46 | 138.52 | 157.76 | 175.94 | 194.57 | 211.79 | |||
| 5.00 | 0.21 | 49.95 | 100.16 | 151.14 | 200.24 | 250.16 | 299.25 | 599.87 | 598.45 |
| 100.08 | 119.38 | 138.57 | 157.75 | 175.99 | 194.16 | 211.79 | |||
| 10.00 | 0.15 | 49.95 | 100.14 | 151.18 | 200.15 | 250.24 | 299.14 | 599.94 | 598.86 |
| 100.06 | 119.38 | 138.56 | 157.77 | 175.95 | 194.17 | 211.75 | |||
| 15.00 | 0.21 | 50.18 | 100.21 | 151.22 | 200.18 | 250.16 | 299.18 | 601.12 | 599.23 |
| 100.08 | 119.47 | 138.59 | 157.78 | 175.97 | 194.16 | 211.76 | |||
| 20.00 | 0.21 | 50.22 | 100.21 | 151.22 | 200.24 | 250.24 | 299.25 | 601.12 | 599.24 |
| 100.08 | 119.48 | 138.59 | 157.78 | 175.99 | 194.17 | 211.79 | |||
| Lead-Wire Resistance (Ω) at 30 °C | Temperature (°C) pt1000 RTD (Ω) | Diode Voltage (mV) at 30 °C and ID = 1 mA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VD1 | VD2 | ||||||||
| 0.00 | 0.00 1000.00 | 50.00 1194.00 | 99.97 1385.00 | 151.00 1577.00 | 200.11 1759.00 | 250.00 1941.00 | 299.00 2117.00 | 600.68 | 598.19 |
| 0.20 | 0.11 1000.42 | 50.12 1194.46 | 100.01 1385.15 | 151.14 1577.52 | 200.14 1759.11 | 250.05 1941.18 | 298.94 2116.78 | 600.68 | 598.20 |
| 1.00 | 0.14 1000.53 | 49.95 1193.81 | 100.05 1385.3 | 150.98 1576.93 | 200.18 1759.26 | 250.08 1941.29 | 299.16 2117.58 | 601.1 | 598.58 |
| 5.00 | 0.11 1000.42 | 49.95 1193.81 | 100.12 1385.57 | 151.05 1577.19 | 200.18 1759.26 | 250.05 1941.18 | 299.12 2117.43 | 600.9 | 599.11 |
| 10.00 | −0.11 999.58 | 50.15 1194.57 | 100.12 1385.57 | 151.18 1577.67 | 200.26 1759.56 | 250.16 1941.58 | 299.18 2117.65 | 601.14 | 599.30 |
| 15.00 | 0.15 1000.57 | 50.12 1194.46 | 100.14 1385.65 | 151.18 1577.67 | 200.22 1759.41 | 250.18 1941.65 | 299.18 2117.65 | 600.86 | 599.31 |
| 20.00 | 0.15 1000.57 | 50.15 1194.57 | 100.18 1385.8 | 151.21 1577.78 | 200.26 1759.56 | 250.18 1941.65 | 299.16 2117.58 | 600.87 | 599.26 |
| Ambient Temperature (°C) | Temperature (°C) pt1000 RTD (Ω) | Diode Voltage (mV) at ID = 1 mA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| VD1 | VD2 | ||||||||
| 0.00 | 0.00 100.00 | 50.00 119.40 | 99.97 138.50 | 151.00 157.70 | 200.11 175.90 | 250.00 194.10 | 299.00 211.70 | - | - |
| 30.00 | 0.05 100.20 | 50.08 119.43 | 100.10 138.55 | 151.11 157.74 | 200.18 175.93 | 250.15 194.15 | 299.22 211.78 | 600.68 | 598.19 |
| 40.00 | 0.08 100.03 | 50.08 119.43 | 100.15 138.57 | 151.11 157.74 | 200.17 175.92 | 250.14 194.15 | 299.22 211.78 | 573.72 | 572.24 |
| 50.00 | 0.15 100.06 | 50.16 119.46 | 100.18 138.58 | 151.16 157.76 | 200.18 175.93 | 250.17 194.16 | 299.24 211.79 | 544.71 | 543.55 |
| 60.00 | 0.15 100.06 | 50.18 119.47 | 100.24 138.60 | 151.21 157.78 | 200.24 175.95 | 250.20 194.17 | 299.15 211.75 | 522.26 | 521.88 |
| 70.00 | 0.24 100.09 | 50.25 119.50 | 100.24 138.60 | 151.24 157.79 | 200.26 175.96 | 250.27 194.20 | 299.26 211.79 | 500.37 | 499.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rerkratn, A.; Prombut, S.; Kamsri, T.; Riewruja, V.; Petchmaneelumka, W. A Procedure for Precise Determination and Compensation of Lead-Wire Resistance of a Two-Wire Resistance Temperature Detector. Sensors 2022, 22, 4176. https://doi.org/10.3390/s22114176
Rerkratn A, Prombut S, Kamsri T, Riewruja V, Petchmaneelumka W. A Procedure for Precise Determination and Compensation of Lead-Wire Resistance of a Two-Wire Resistance Temperature Detector. Sensors. 2022; 22(11):4176. https://doi.org/10.3390/s22114176
Chicago/Turabian StyleRerkratn, Apinai, Supatsorn Prombut, Thawatchai Kamsri, Vanchai Riewruja, and Wandee Petchmaneelumka. 2022. "A Procedure for Precise Determination and Compensation of Lead-Wire Resistance of a Two-Wire Resistance Temperature Detector" Sensors 22, no. 11: 4176. https://doi.org/10.3390/s22114176






