Classical Dynamics of Rydberg States of Muonic-Electronic Helium and Helium-Like Ions in a Weak Electric Field: Counter-Intuitive Linear Stark Effect

Abstract

According to the existing paradigm, helium atoms and helium-like ions (hereafter, heliumic systems) in a relatively weak external static electric field do not exhibit the linear Stark effect—in distinction to hydrogen atoms and hydrogen-like ions. In the present paper we consider the classical dynamics of a muonic-electronic heliumic system in Rydberg states–starting from the concept from our previous paper. We show that there are two states of the system where the averaged electric dipole moment is non-zero. Consequently, in these states the heliumic system should exhibit the linear Stark effect even in a vanishingly small electric field, which is a counter-intuitive result. We also demonstrate the possibility of controlling the overall precession of the electronic orbit by an external electric field. In particular, we show the existence of a critical value of the external electric field that would “kill” the precession and make the electronic orbit stationary. This is another counter-intuitive result. We calculate analytically the value of the critical field and show that it is typically smaller or even much smaller than 1 V/cm.

1. Introduction

According to the existing paradigm, helium atoms and helium-like ions in a relatively weak external electric field do not exhibit the linear Stark effect—in distinction to hydrogen atoms and hydrogen-like ions (see, e.g., the textbooks [1,2]). It is well-known that the linear Stark effect in hydrogenic systems (atoms and ions) is due to the fact that the overwhelming majority of states of these systems are characterized by a non-zero value of the averaged electric dipole moment. “Averaged” here refers to the averaging over the unperturbed wave functions in the quantum formalism or over the unperturbed orbit in the classical formalism (the latter being appropriate for Rydberg states).

As for heliumic systems (helium atoms and helium-like ions), according to the existing paradigm, the electric dipole moment vanishes under such averaging. If so, there should be no linear Stark effect for heliumic systems—even for Rydberg states, where one of the electrons is highly-excited while the other electron is not. In the latter case, in classical formalism the elliptical (in the first approximation) orbit of the Rydberg electron undergoes a precession—because at relatively small distances the effective potential for the Rydberg electron differs from the Coulomb potential of the effective nuclear charge (Z − 1), where Z is the actual nuclear charge. While the elliptical orbit is characterized by a non-zero electric dipole moment, it vanishes after averaging over the precession.

In the present paper we consider the classical dynamics of muonic-electronic heliumic system in Rydberg states—starting from the concept from our previous paper [3]. We show that there are two states of the system where the averaged electric dipole moment is non-zero. Consequently, in these states the heliumic system should exhibit the linear Stark effect even in a vanishingly small electric field.

We also demonstrate the possibility of controlling the overall precession of the electronic orbit by an external electric field. In particular, we calculate the critical value of the external electric field that would “kill” the precession and make the electronic orbit stationary.

We present the classical description of the considered phenomena: in terms of various kinds of precessions of the elliptical orbit of the electron (though we also give quasiclassical counterparts of the corresponding formulas). Of course, precessions of the orbit are purely classical phenomena. The linear Stark effect also has classical roots, as it is well-known since at least 1923—see, e.g., Born book [4] of 1923, as well as book [5] (problem 2.32) and book [6].

2. Setup and New Results

Since the present paper is the further development of the results from our previous paper [3], we have to start from the setup from paper [3]. We consider classically the following three-body atomic system: a nucleus of the charge Z and of the mass M_nucl, a muon in a circular Rydberg state (i.e., revolving in a circular orbit of the radius R_μ), and an electron in an elliptical Rydberg state (i.e., revolving an elliptical orbit of the major semiaxis R_e). Here:

$${\mathrm{R}}_{\mathrm{e}}\gg {\mathrm{R}}_{\mathsf{\mu }}$$

(1)

It is well-known that for atomic systems in Rydberg states, the classical (or quasiclassical) description is appropriate. Quasiclassical counterparts of the orbital sizes R_e and R_μ are the corresponding principal quantum numbers:

$${\mathrm{n}}_{\mathrm{e}}={\left[\frac{\left(\mathrm{Z}-1\right){\mathrm{R}}_{\mathrm{e}}}{{\mathrm{a}}_0}\right]}^{1/2}{, \mathrm{n}}_{\mathsf{\mu }}={\left[\frac{{\mathrm{ZR}}_{\mathsf{\mu }}{\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}}{{\mathrm{a}}_0{\mathrm{m}}_{\mathrm{er}}}\right]}^{1/2}$$

(2)

where a₀ is the Bohr radius. Here:

$${\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}=\frac{{\mathrm{m}}_{\mathsf{\mu }}\left({\mathrm{m}}_{\mathrm{e}}{+\mathrm{M}}_{\mathrm{nucl}}\right)}{\left({\mathrm{m}}_{\mathrm{e}}{+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{M}}_{\mathrm{nucl}}\right)}$$

(3)

and:

$${\mathrm{m}}_{\mathrm{er}}=\frac{{\mathrm{m}}_{\mathrm{e}}\left({\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{M}}_{\mathrm{nucl}}\right)}{\left({\mathrm{m}}_{\mathrm{e}}{+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{M}}_{\mathrm{nucl}}\right)}$$

(4)

are the reduced masses of the muon and of the electron, respectively; m_e and m_μ are the electron and muon masses, respectively (m_μ/m_e = 206.8).

The electronic motion can be considered as the slow subsystem, while the motion of the muon and of the nucleus can be considered as the rapid subsystem under the condition:

$$\frac{{\mathrm{R}}_{\mathsf{\mu }}}{{\mathrm{R}}_{\mathrm{e}}}\ll {\left(\frac{{\mathrm{m}}_{\mathrm{e}}}{{\mathrm{m}}_{\mathsf{\mu }}}\right)}^{1/3}{\left[\frac{\mathrm{Z}}{\left(\mathrm{Z}-1\right)}\right]}^{1/3}$$

(5)

Under this condition, the electron revolves over its elliptical (in the first approximation) orbit with a frequency that is much higher than the frequency of the rotation of the muon and the nucleus (about their center of mass). The quasiclassical counterpart of the condition (5) is:

$$\frac{{\mathrm{n}}_{\mathsf{\mu }}}{{\mathrm{n}}_{\mathrm{e}}}\ll \frac{{\left({\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}{\mathrm{Z}}^2\right)}^{1/3}}{{\left[{\mathrm{m}}_{\mathrm{er}}{\left(\mathrm{Z}-1\right)}^2\right]}^{1/3}}$$

(6)

The averaging over the rapid subsystem (required by the analytical method of separating rapid and slow subsystems) brings up the following situation. The electron “sees” two concentric “rings”: the ring of the radius R_μ, having the muon charge uniformly distributed over it, and the ring of the radius R_n, having the nuclear charge uniformly distributed over it (here R_n is the radius of the circular orbit of the nucleus; of course, R_n ≪ R_μ).

In [3] it was shown that the effective potential energy of the Rydberg electron is mathematically equivalent to the potential energy of a satellite around the oblate Earth. The latter problem has a well-known solution—see, e.g., Beletsky’s book [7], Sec. 1.7. According to this analogy with the celestial mechanics, the “unperturbed” elliptical orbit of the Rydberg electron is involved in two types of the precession: (1) the precession of the orbit in its plane; (2) the precession of the orbital plane about the axis of the rotation of the muon and the nucleus. The frequencies of these two precessions can be expressed as follows (see publications [3,7,8]—in units of the Kepler frequency of the Rydberg electron):

$${\mathsf{\omega }}_{\mathrm{precession} \mathrm{in} \mathrm{plane}}=\left[\frac{3\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{er}}^2{\mathrm{e}}^4{\mathrm{R}}_{\mathsf{\mu }}^2}{\left({8\mathrm{M}}_{\mathrm{e}}^4\right)}\right]\left(1-{5\cos }^2\mathrm{i}\right)$$

(7)

$${\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}=-\left[\frac{3\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{er}}^2{\mathrm{e}}^4{\mathrm{R}}_{\mathsf{\mu }}^2}{\left({4\mathrm{M}}_{\mathrm{e}}^4\right)}\right]\cos \mathrm{i}$$

(8)

where M_e is the angular momentum of the Rydberg electron. The quantity i in Equations (7) and (8) is the angle between the classical orbital plane of the electron and the classical plane of the muonic and nuclear rings. In the celestial mechanics this angle is called inclination. Also in Equations (7) and (8), the value of radius R_n of the nuclear ring, which could have entered these equations as (R_μ² − R_n²) was disregarded because of the strong inequality given by Equation (1). The minus sign in Equation (8) indicates that the orbital plane of the Rydberg electron rotates clockwise if viewed from the positive side of the z-axis.

The quasiclassical counterparts of the classical Formulas (7) and (8) are as follows:

$${\mathsf{\omega }}_{\mathrm{precession} \mathrm{in} \mathrm{plane}}\left(\mathrm{i}\right)=\left(\frac{3}{8}\right)\left[\frac{\left(\mathrm{Z}-1\right)}{{\mathrm{Z}}^2}\right]\left(1-{5\cos }^2\mathrm{i}\right){\left[\frac{{\mathrm{n}}_{\mathsf{\mu }}}{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}\right]}^4{\left(\frac{{\mathrm{m}}_{\mathrm{er}}}{{\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}}\right)}^2$$

(9)

$${\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}\left(\mathrm{i}\right)=-\left(\frac{3}{4}\right)\left[\frac{\left(\mathrm{Z}-1\right)}{{\mathrm{Z}}^2}\right]\left(\cos \mathrm{i}\right){\left[\frac{{\mathrm{n}}_{\mathsf{\mu }}}{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}\right]}^4{\left(\frac{{\mathrm{m}}_{\mathrm{er}}}{{\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}}\right)}^2$$

(10)

where l_e is the angular momentum quantum number of the electron.

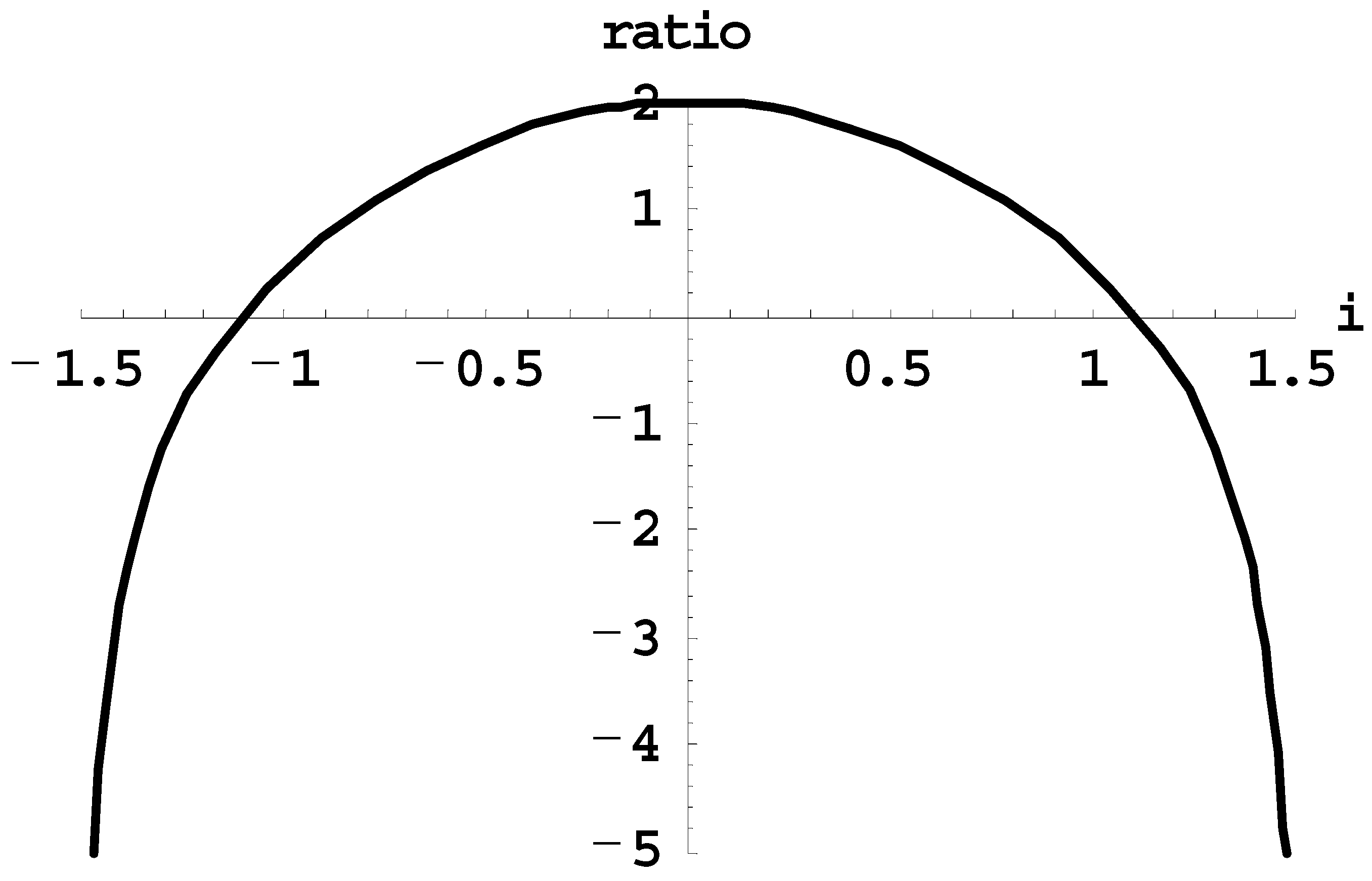
Figure 1 shows the ratio of the frequency of the precession in plane (from Equation (7)) to the frequency of the precession of the plane (from Equation (8)) versus the inclination i of the orbital plane of the electron. It is seen that for the range of |i| < 1.4 rad = 80°, the absolute values of both frequencies are of the same order of magnitude, except for the vicinity of |i| = arcos(1/5^1/2) = 1.107 rad = 63.43°, resulting from the solution of the equation 1 − 5 cos²i = 0. Below we call it the critical angle and denote arcos(1/5^1/2) as i_c.

At this point it is worth emphasizing the following. In the previous part of Section 2, while conveying the concepts from our previous paper [3] (necessary for understanding the primary new results of the present paper given below), we also provided some news results. For example, Equations (2), (5), (7), and (8) express new results; also Figure 1 is new.

Now we proceed to present the primary new results. From Equation (7) it is clear that the frequency of the precession of the electron orbit in its plane vanishes for the following two values of the inclination angle:

$$\mathrm{i}=\pm {\mathrm{i}}_{\mathrm{c}}\approx \pm 1.107 \mathrm{rad}=\pm {63.43}^{\circ }$$

(11)

Since at this inclination there is no precession in the orbital plane, then the dipole moment does not vanish.

At i = ±i_c, Equation (8) for the frequency of the precession of the classical orbital plane of the electron becomes:

$${\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}=-\left[\frac{3\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{er}}^2{\mathrm{e}}^4{\mathrm{R}}_{\mathsf{\mu }}^2}{\left(5^{1/2}{4\mathrm{M}}_{\mathrm{e}}^4\right)}\right]$$

(12)

This precession does not eliminate the dipole moment: in the course of this precession, the dipole moment precesses with the frequency ω_{precession of plane}. Therefore, the projection of the dipole moment on the axis of the precession remains constant. Thus, at the two values of the inclination given by Equation (11), the system should exhibit the linear Stark effect even in a vanishingly small electric field.

We emphasize that a sufficiently high electric field would intermix energy levels of a heliumic system and thus cause the linear Stark effect. However, the new result presented above is the linear Stark effect in a heliumic system even in an arbitrarily small electric field. This is a counter-intuitive result.

The linear Stark effect has classical roots, as noted in the Introduction. In the classical description, the linear Stark effect manifests as the precession of the elliptical orbit of a Rydberg electron in a hydrogenic atom/ion about the direction of the electric field. The frequency of the precession is proportional to the electric field. Let us calculate the frequency of the precession in our situation of the heliumic system.

From the separation of the center-of-mass motion and the relative motion, it follows that the projection of the dipole moment on the axis of the precession (chosen as the z-axis) is equal to (see Appendix A):

$${\mathrm{d}}_{\mathrm{z}}{=\mathrm{e}‹\mathrm{z}}_{\mathrm{e}}›\frac{\left[{\mathrm{M}}_{\mathrm{n}}{+\mathrm{m}}_{\mathsf{\mu }}+\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{e}}\right]}{\left({\mathrm{M}}_{\mathrm{n}}{+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{m}}_{\mathrm{e}}\right)}$$

(13)

$$‹{\mathrm{z}}_{\mathrm{e}}›‹‹{\mathrm{r}}_{\mathrm{e}}›cos\mathsf{\theta }=‹{\mathrm{r}}_{\mathrm{e}}›sin\mathrm{i}=\frac{\pm 2‹{\mathrm{r}}_{\mathrm{e}}›}{5^{1/2}}$$

(14)

where <z_e> is the average value of the z-coordinate of the electron:

Here <r_e> is the absolute value of the radius-vector of the electron after averaging over the unperturbed elliptical orbit within its plane. It can be expresses as follows (see, e.g., [5,8,9,10]):

$${‹\mathrm{r}}_{\mathrm{e}}›=\left[\frac{{3\mathrm{e}}^2\left(\mathrm{Z}-1\right)}{\left({4|\mathrm{E}}_{\mathrm{e}}|\right)}\right]{\left\{1-\frac{2\left|{\mathrm{E}}_{\mathrm{e}}\right|{\mathrm{M}}_{\mathrm{e}}^2}{\left[{\left(\mathrm{Z}-1\right)}^2{\mathrm{m}}_{\mathrm{er}}{\mathrm{e}}^4\right]}\right\}}^{1/2}$$

(15)

where E_e is the unperturbed energy of the Rydberg electron. The quasiclassical counterpart of the classical result (15) is the following:

$${‹\mathrm{r}}_{\mathrm{e}}›=\frac{3{\mathsf{ћ}}^2{\mathrm{n}}_{\mathrm{e}}{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}}{\left[2\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{er}}{\mathrm{e}}^2\right]}$$

(16)

On substituting Equations (14) and (15) in Equation (13), we obtain:

$${\mathrm{d}}_{\mathrm{z}}=\pm \left\{\frac{\left[{\mathrm{M}}_{\mathrm{n}}{+\mathrm{m}}_{\mathsf{\mu }}+\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{e}}\right]}{\left({\mathrm{M}+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{m}}_{\mathrm{e}}\right)}\right\}\left[\frac{{3\mathrm{e}}^3\left(\mathrm{Z}-1\right)}{\left(5^{1/2}2\left|{\mathrm{E}}_{\mathrm{e}}\right|\right)}\right]{\left\{1-\frac{2\left|{\mathrm{E}}_{\mathrm{e}}\right|{\mathrm{M}}_{\mathrm{e}}^2}{\left[{\left(\mathrm{Z}-1\right)}^2{\mathrm{m}}_{\mathrm{er}}{\mathrm{e}}^4\right]}\right\}}^{1/2}$$

(17)

The quasiclassical counterpart of the classical result (17) is as follows:

$${\mathrm{d}}_{\mathrm{z}}=\pm \left\{\frac{\left[{\mathrm{M}}_{\mathrm{n}}{+\mathrm{m}}_{\mathsf{\mu }}+\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{e}}\right]}{\left({\mathrm{M}+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{m}}_{\mathrm{e}}\right)}\right\}3{\mathsf{ћ}}^2{\mathrm{n}}_{\mathrm{e}}\frac{{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}}{\left[5^{1/2}\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{er}}{\mathrm{e}}^2\right]}$$

(18)

A uniform electric field F along the z-axis (i.e., along the axis of the rotation of the muon and the nucleus) causes another precession of the orbital plane of the electron. By using the relation between the precession frequency from the book [5] and the corresponding value of d_z from [5], we obtain the following classical expression for the precession frequency ω_F in our case:

$${\mathsf{\omega }}_{\mathrm{F}}=\pm \left(\frac{3\mathrm{eF}}{2}\right){\left\{\frac{{[\mathrm{M}}_{\mathrm{n}}{+\mathrm{m}}_{\mathsf{\mu }}+\left(\mathrm{Z}-1\right){\mathrm{m}}_{\mathrm{e}}]}{[\left({\mathrm{M}+\mathrm{m}}_{\mathsf{\mu }}{+\mathrm{m}}_{\mathrm{e}}\right)5^{1/2}{\mathrm{m}}_{\mathrm{er}}\left|{\mathrm{E}}_{\mathrm{e}}\right|]}\right\}}^{1/2}$$

(19)

The corresponding quasiclassical expression is as follows:

$${\mathsf{\omega }}_{\mathrm{F}}=\pm \left[\frac{1}{{\mathrm{m}}_{\mathrm{e}}}+\frac{\left(\mathrm{Z}-1\right)}{\left({\mathrm{M}+\mathrm{m}}_{\mathsf{\mu }}\right)}\right]{3\mathrm{n}}_{\mathrm{e}}{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}\mathsf{ћ}\frac{\mathrm{F}}{\left[5^{1/2}\left(\mathrm{Z}-1\right)\mathrm{e}\right]}$$

(20)

The two possible signs of the precession frequency correspond to two possible directions of the precession/rotation of the orbital plane of the electron caused by the electric field. In particular, the positive sign in Equations (19) and (20) corresponds to the critical value of the angle of the inclination i_c ≈ +1.107 rad = +63.43°.

The total frequency of the precession of the orbital plane is:

$$\mathsf{\omega }{=\mathsf{\omega }}_{\mathrm{F}}{+\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}$$

(21)

Thus, we encounter a possibility of the electrically-controlled precession of the orbital plane of the electron.

In particular, for the critical value of the angle of the inclination i_c ≈ +1.107 rad = +63.43°, there exists a critical value of the electric field F_crit, such that there would be no precession: ω = 0. In other words, the electric field F_crit would “kill” the precession and make the elliptical orbit stationary. This is another counter-intuitive result.

For finding the critical value F_crit, first we calculate the following ratio (using the corresponding quasiclassical expressions):

$$\frac{\left|{\mathsf{\omega }}_{\mathrm{F}}\right|}{{\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}}=\left[\frac{1}{{\mathrm{m}}_{\mathrm{e}}}+\frac{\left(\mathrm{Z}-1\right)}{\left({\mathrm{M}+\mathrm{m}}_{\mathsf{\mu }}\right)}\right]{4\mathrm{Z}}^2{\mathrm{m}}_{\mathsf{\mu }\mathrm{r}}^2{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^4{\mathrm{n}}_{\mathrm{e}}^4{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}\frac{{\mathsf{ћ}}^4\mathrm{F}}{\left[{\left(\mathrm{Z}-1\right)}^4{\mathrm{n}}_{\mathsf{\mu }}^4{\mathrm{m}}_{\mathrm{er}}^3{\mathrm{e}}^5\right]}$$

(22)

By using the fact that 1/m_e ≫ (Z − 1)/(M + m_μ) and by approximating m_μr ≈ m_μ and m_er ≈ m_e, we simplify Equation (22) to:

$$\frac{\left|{\mathsf{\omega }}_{\mathrm{F}}\right|}{{\mathsf{\omega }}_{\mathrm{precession} \mathrm{of} \mathrm{plane}}}\approx \left[\frac{{4\mathrm{Z}}^2}{{\left(\mathrm{Z}-1\right)}^4}\right]{\left(\frac{{\mathrm{m}}_{\mathsf{\mu }}}{{\mathrm{m}}_{\mathrm{e}}}\right)}^2{\left(\frac{{\mathrm{n}}_{\mathrm{e}}}{{\mathrm{n}}_{\mathsf{\mu }}}\right)}^4{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^4{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}\frac{\mathrm{F}}{{\mathrm{F}}_{\mathrm{at}}}$$

(23)

where:

$${\mathrm{F}}_{\mathrm{at}}=\frac{{\mathrm{m}}_{\mathrm{e}}^2{\mathrm{e}}^5}{{\mathsf{ћ}}^4}$$

(24)

is the atomic unit of the electric field.

Then by equating the right side of Equation (23) to unity, we get:

$$\frac{{\mathrm{F}}_{\mathrm{crit}}}{{\mathrm{F}}_{\mathrm{at}}}\approx \frac{{\left(\mathrm{Z}-1\right)}^4{\left(\frac{{\mathrm{m}}_{\mathrm{e}}}{{\mathrm{m}}_{\mathsf{\mu }}}\right)}^2{\left(\frac{{\mathrm{n}}_{\mathsf{\mu }}}{{\mathrm{n}}_{\mathrm{e}}}\right)}^4}{\left\{4{\mathrm{Z}}^2{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^4{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}\right\}}$$

(25)

By using the validity condition (6), we obtain the following inequality from Equation (25):

$$\frac{{\mathrm{F}}_{\mathrm{crit}}}{{\mathrm{F}}_{\mathrm{at}}}\ll \frac{{\mathrm{Z}}^{2/3}{\left(\mathrm{Z}-1\right)}^{1/3}{\left(\frac{{\mathrm{m}}_{\mathrm{e}}}{{\mathrm{m}}_{\mathsf{\mu }}}\right)}^{2/3}}{\left\{4{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^4{\left[{\mathrm{n}}_{\mathrm{e}}^2-{\left({\mathrm{l}}_{\mathrm{e}}+\frac{1}{2}\right)}^2\right]}^{1/2}\right\}}~\frac{{\mathrm{Z}}^{2/3}{\left(\mathrm{Z}-1\right)}^{1/3}}{\left({4\mathrm{n}}_{\mathrm{e}}^5\right)}{{\displaystyle (}\frac{{\mathrm{m}}_{\mathrm{e}}}{{\mathrm{m}}_{\mathsf{\mu }}}{\displaystyle )}}^{2/3}\ll 1$$

(26)

It is seen that for eliminating the precession and making the elliptical orbit of the electron stationary, it would suffice an electric field really much smaller than the atomic unit. For example, for muonic-electronic Rydberg atoms of helium at n_e ~ n_μ ≪ 1 and l_e = n_e − k, where the integer k ≪ n_e, we obtain from Equation (25) the following:

$$\frac{{\mathrm{F}}_{\mathrm{crit}}}{{\mathrm{F}}_{\mathrm{at}}}\sim \frac{1.5\times {10}^{-6}}{\left[{\mathrm{n}}_{\mathrm{e}}^{9/2}{\left(2\mathrm{k}-1\right)}^{1/2}\right]}$$

(27)

For n_e ~ 10 and k = 2, from Equation (23) we find F_crit ~ 10⁻¹ V/cm. This is a really much smaller electric field compared, e.g., to the maximum electric field used in the experimental study [11] of the Stark effect in helium atoms. For the case of n_e ≪ n_μ ≪ 1, one would have even much smaller values of the critical field F_crit:

$$\frac{{\mathrm{F}}_{\mathrm{crit}}}{{\mathrm{F}}_{\mathrm{at}}}\ll \frac{1.5\times {10}^{-6}}{\left[{\mathrm{n}}_{\mathrm{e}}^{9/2}{\left(2\mathrm{k}-1\right)}^{1/2}\right]}$$

(28)

3. Conclusions

We have considered the classical dynamics of Rydberg states of muonic-electronic helium or helium-like ions. In our previous paper [3] we showed that the elliptical orbit of the electron, generally speaking, undergoes two kinds of the precession: the precession of the orbital plane and the precession of the orbit within its plane. Proceeding from the setup from our previous paper [3], we obtained the following primary new results:

(1)

We pointed out that there are two values of the inclination angle i of the elliptical orbit of the electron, for which there is no precession of the orbit within its plane, but only the precession of the orbital plane.

(2)

We emphasized that at these values of i, the projection of the precessing electric dipole moment of the electron on the axis of the precession would conserve, so the system would exhibit a linear Stark effect even in a vanishingly small electric field. This is a counterintuitive result—since according to the existing paradigm, helium atoms and helium-like ions in a vanishingly small external electric field do not exhibit the linear Stark effect—in distinction to the hydrogen atom and hydrogenlike ions. We underscored that the linear Stark effect has classical roots, manifesting as the precession of the elliptical orbit of a Rydberg electron about the direction of the electric field.

(3)

We calculated the overall precession frequency of the system in the external electric field. This result demonstrated a possibility of the electrically-controlled precession of the orbital plane of the electron.

(4)

We showed that there exists a critical value of the electric field F_crit, such that there would be no precession: the electric field F_crit would “kill” the precession and make the classical elliptical orbit of the electron stationary. This is another counter-intuitive result. We calculated analytically the value of the critical field and showed that it is typically smaller or even much smaller than 1 V/cm.

In addition to the above primary new results, we also provided some other classical new results, represented by Equations (2), (5), (7), and (8), as well as by Figure 1. Finally, we note that for the usual helium atom or helium-like ion, where both light particles are electrons, the linear Stark effect in a vanishingly small electric field could be still possible, provided that the size of the major semiaxis of the elliptical orbit of the outer electron is much greater than the radius of the circular orbit of the inner electron.