Next Article in Journal
Gender Differences in E-Learning Tool Usage Among University Faculty Members in Saudi Arabia Post-COVID-19
Previous Article in Journal
COVID-19 Influenced the Epidemiology of Facial Trauma: A Narrative Review, 2020–2024
Previous Article in Special Issue
Adherence to Pelvic Floor Physical Therapy During COVID-19: A Retrospective Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
COVID
Volume 5
Issue 5
10.3390/covid5050070
covid-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Delay in COVID-19 Vaccinations: The Role of Travel Time to Vaccine Sites

by
Yuxia Huang
1,* and
Jim Lee
2
1
College of Engineering and Computer Science, Texas A&M University-Corpus Christi, Corpus Christi, TX 78412, USA
2
College of Business, Texas A&M University-Corpus Christi, Corpus Christi, TX 78412, USA
*
Author to whom correspondence should be addressed.
COVID 2025, 5(5), 70; https://doi.org/10.3390/covid5050070
Submission received: 28 March 2025 / Revised: 2 May 2025 / Accepted: 6 May 2025 / Published: 12 May 2025
(This article belongs to the Special Issue COVID and Public Health)
Browse Figures
Versions Notes

Abstract

:
Introduction: A growing body of literature has identified a variety of factors affecting vaccine uptake, but the role of geographic accessibility remains unclear. This study fills this knowledge gap by empirically investigating the extent to which the time driving to vaccine sites as a measure of geographic friction affected COVID-19 vaccine uptake. Methods: A logistic model and a hazard-based duration model were applied to the official data of more than 142,000 adults who took at least one COVID-19 vaccine in Nueces County, Texas, between December 2020 and August 2022. Using the street network, travel time was calculated from individuals’ home addresses to the addresses of the sites where they received their vaccinations. Results: The logistic model indicated that individuals living farther from vaccine sites were less likely to receive full vaccination, controlling for their sociodemographic characteristics that affected vaccine hesitancy. The duration model further showed that fully vaccinated persons would delay a booster shot longer if they had to travel longer for a vaccine. Conclusions: To the extent that the health protection of a COVID-19 vaccine declines over time, the integration of spatial and temporal dimensions in the duration model allowed us to shed light on the relationship between travel time and delay in booster vaccination. A vaccination campaign should make vaccination services physically convenient for vaccine recipients from different communities.

1. Introduction

Vaccination is regarded as highly effective for protecting people from COVID-19 infection [1]. Since the COVID-19 pandemic hit in 2020, a growing body of literature has identified a wide range of factors affecting vaccine uptake. Research has found, among other things, higher reluctance to vaccinate in the United States among socially and medically vulnerable populations, including racial/ethnic minorities and senior adults [2,3,4,5,6,7,8,9]. Studies have also identified disparities in vaccination uptake between urban and rural areas, with urban residents demonstrating higher vaccination rates than those in rural communities [5,10].
Vaccine hesitancy refers to the delay in acceptance or refusal of vaccination [11]. The World Health Organization (WHO) has conceptualized a “3 Cs” framework for vaccine hesitancy to recognize the importance of complacency, confidence, and convenience [12]. Most research in the literature addresses vaccination complacency (low perceived risk of vaccine-preventable diseases) and confidence (trust in vaccines) [12,13]. Vaccine convenience refers to the ease of receiving vaccination services. However, full acceptance of COVID-19 vaccines does not guarantee a high vaccination rate if vaccination is not readily accessible [14]. In particular, long travel distances to vaccine facilities make their services inaccessible geographically. Today, it remains unclear the extent to which the ease of traveling to vaccine sites, or convenience in general, has affected COVID-19 vaccine uptake [15]. This paper aims to fill this knowledge gap.
Existing studies have evaluated the role of geographic or spatial accessibility to COVID-19 vaccination services. Travel impedance as a barrier to vaccination services aligns with the widespread evidence of lower vaccine uptake in rural versus urban areas [5,16]. By calculating the Euclidean distance from individuals’ home ZIP code centroids to clinic addresses, Cochran et al. [15] reported that males and White individuals traveled significantly farther for vaccination appointments.
However, most studies on spatial accessibility rely on the overall availability, or capacity, of vaccination services in a region or community, such as the average distance to vaccine locations or their distribution density within an area, such as a ZIP code in the United States [15,17,18,19,20,21]. Those measures of “potential” or “theoretical” accessibility consider where people may go for vaccination, assuming that all residents in a given area have equal access to their nearest vaccine locations and, therefore, overlook the impacts of individuals’ actual vaccination behavior [22]. Gligoric et al. [23] showed that actual travel distances to healthcare facilities tended to be longer than potential travel distances in many countries and regions during the pandemic. In addition to the theoretical availability of vaccine services, however, demand for vaccines varies widely across and within regions [6,24].
In this study, we address the above drawback using a direct measure of geographic barriers, calculated based on the travel impedance from individual COVID-19 vaccine recipients to the actual locations where they received their vaccines. The actual utilization of services by individuals, rather than their theoretical or potential access to those services, measures “revealed” or realized accessibility [22,23]. Realized accessibility is critical as it reflects individuals’ actual vaccination behavior rather than their availability of services.
Because our dataset covers multiple doses over the study period for each vaccine recipient, the travel distance data also allow us to investigate whether the distance traveled for a vaccine affected the time intervals between vaccinations. We calculated the travel distance for each individual from their home address to the actual vaccination site through the street network. In addition, we converted these travel distances to the amounts of driving time, which accounts for average road and traffic conditions during a typical day. Although travel distance and travel time are highly correlated, travel time, as opposed to travel distance, provides a more accurate representation of travel impedance, especially in urban areas, by accounting for road and traffic conditions [25,26].
A vaccine’s protection declines over time. Medical experts have recommended a supplemental dose, or booster, after two to six months of primary COVID-19 vaccination [27]. In addition to the discrete choice of receiving a vaccine, another novel approach of this study is to evaluate if travel impedance is associated with a longer delay in taking a booster after receiving the primary doses. The influence of individuals’ sociodemographic backgrounds on the willingness to take a booster is in line with their influence on the willingness to take the primary doses [5,28,29]. However, it is less clear whether travel time hinders the desire of fully vaccinated individuals to receive their next vaccine.
In this study, we applied a hazard-based duration model to the official data of vaccine recipients in one county of the state of Texas, USA. Hazard-based nonparametric regression has been utilized to identify factors associated with the time interval between vaccinations [30,31], but our study is the first to apply a parametric duration model to estimate the relationship between the delay in taking a booster vaccine and the time spent traveling to the vaccine site.

2. Materials and Methods

2.1. Sample Data

Our sample draws from COVID-19 vaccination records collected by the Nueces County Public Health District in Texas, USA. According to the U.S. Census Bureau’s American Community Survey, Nueces County covers 1166 square miles of land area, and its population in 2021 was approximately 350,000. Approximately 72% of the county population was adult (aged 18 years and older), and 62% identified as Hispanic or Latino. Huang et al. [5] described disparities in COVID-19 vaccine uptake among various socioeconomic and demographic groups in this area.
The full sample comprises 142,712 adults who received at least one dose of one of the three alternative COVID-19 vaccines available, namely, Pfizer, Moderna, and Johnson & Johnson (Janssen), during a 21-month study period from 15 December 2020 to 30 August 2022. The number of vaccination sites grew over time, reaching 104 by the end of the sample period. For the Pfizer and Moderna vaccines, two primary doses were required for an individual to become fully vaccinated. Only one primary dose of the Johnson & Johnson vaccine was required. For the first booster, our sample began on 1 October 2021, when the Nueces County Public Health District began offering free COVID-19 booster vaccination services with Pfizer and Moderna. The data collection period ends on 30 August 2022, meaning that the sample of the first booster contains only those fully vaccinated recipients who took an additional COVID-19 vaccine by that date.
The Health District records include the name, home address, age, gender, and race/ethnicity of each vaccine recipient, along with the dates, vaccination locations, and names of the vaccines administered. The dataset also includes information on whether vaccine recipients had been previously infected with COVID-19. Because reinfection is uncommon shortly after infection, the CDC recommends a three-month delay for infected persons [1]. For this reason, we include such data as an individual health factor that might have affected the time interval between vaccinations. Because the dataset involves personal information, the data compilation process in this study was reviewed and subsequently approved by the researchers’ affiliated Institutional Review Board.
In addition to the demographic data of vaccine recipients, we considered their socioeconomic backgrounds, which have been found to affect vaccine uptake [5,6,7,32]. To this end, we supplemented vaccination records with the median household income level and the population share of bachelor’s degree holders by census tracts based on the home addresses of vaccine recipients. Nueces County consists of 82 census tracts. Median household income represents socioeconomic status. The share of college degree holders represents a neighborhood’s overall educational attainment level. Another census tract-level variable is the classification of an urban versus rural area by the Census Bureau [33]. This is motivated by the widespread evidence supporting higher vaccine uptake among urban residents compared to rural residents [5,10,15,34].
Our focus in this study is the impact of individuals’ travel time to vaccine sites on their vaccination recipients. In contrast to the Euclidean (straight-line) geographical length as for other studies of geographic accessibility [19,21,22], we measure distance through the local street network. Drawing from Open Street Map’s OSMnx geospatial package [35], travel time was measured by the number of driving minutes from each vaccine recipient’s home address to the clinic where they received their vaccines. Although not all vaccine recipients might have driven from home, driving time with a private vehicle from home addresses is a reasonable proxy measure of geographic accessibility in the absence of actual observations. In Nueces County, the average household owns approximately two cars, and public transportation options in the county are limited, suggesting that most residents likely had access to private transportation to vaccination sites.

2.2. Regression Models

Our empirical work began with modeling vaccination outcomes as a discrete or binary variable. The dependent variable equals one if an individual received a COVID-19 vaccine and zero otherwise. Following the conventional approach, we applied logistic regression (logit) to estimate the relationships between vaccination outcomes and covariates or predictor variables. The predictor of our primary interest is the driving time between a vaccine recipient’s home address and the location of the vaccination service. Logit regression results enable us to compare the odds of vaccination among individuals traveling to vaccination sites. The regression model controls for the effects of a variety of sociodemographic factors that might independently affect individuals’ willingness to take a vaccine at any location [30,31].
In addition to vaccination outcomes as a binary variable, we are interested in modeling the time intervals, or durations, between vaccinations. Because duration data are non-negative by construction, the conventional least-squares regression, which assumes normally distributed errors, yields biased inferences [36]. Following the conventional time-to-event analysis, we applied a hazard-based approach to estimate the expected duration for a fully vaccinated person to receive a booster shot based on the hazard function. In our case, the hazard function describes the rate at which the duration of receiving booster vaccination ends immediately after a given duration. A popular parametric duration model takes the form of the Weibull distribution, which allows for the hazard function to increase or decrease monotonically over different durations [37]. Appendix A.1 provides details of the hazard-based duration modeling framework.
To account for potential nonlinearity in quantitative data, a logarithmic transformation was applied to travel time, age, income, and the population share of bachelor’s degree holders. For those variables with log data values, the coefficients capture the effects of percentage changes. All regression models were estimated using the maximum likelihood method in Regression Analysis of Time Series (RATS) software version 10.0 developed by Estima.

3. Results

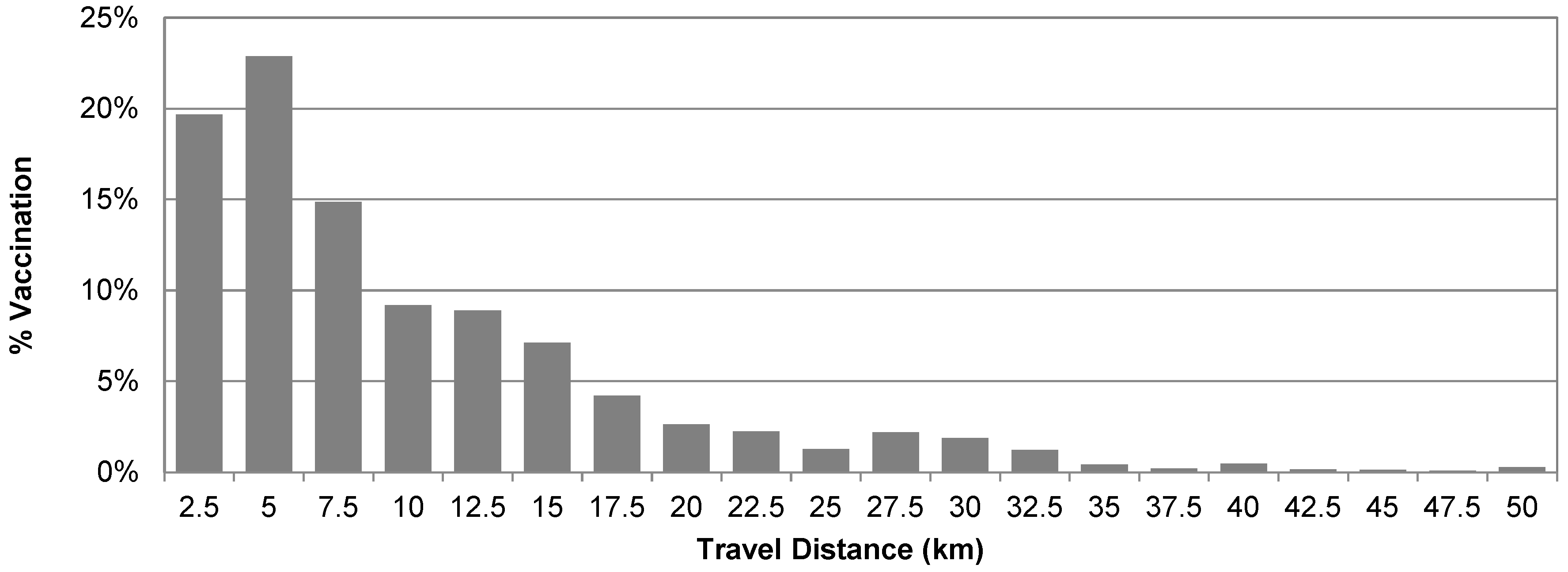
3.1. Descriptive Analysis

Table 1 displays the descriptive statistics of the variables included in our empirical work. Medians and their interquartile ranges (IQRs) that measure data dispersion are reported for continuous variables, such as age and household income, because those data are not normally distributed. Except for quantitative measures, such as travel time, age, income, and the population share with a college degree, most variables contain binary data (i.e., dummy variables). For instance, the “male” variable equals one if vaccine recipients are male and zero if they are female. The first panel shows the sociodemographic data. The typical person in the sample was 54 years old. Males made up 45% of the sample as opposed to their 50% county population share. This means that disproportionately fewer males than females in Nueces County took COVID-19 vaccines.
For each race/ethnicity variable, the mean in the table represents the sample share of the corresponding race/ethnicity group: 51% Hispanic (or Latino), 29% White, 3% Black (African American), 3% Asian, and 0.2% Pacific Islander. Notably, the share of Hispanics in the sample was smaller than their 62% county population share, highlighting disproportionately low vaccine uptake among Hispanics, especially in comparison with non-Hispanic Whites [5].
The median annual household income of USD 61,485, according to the 2021 American Community Survey’s census tract-level data, was below the national and state levels. In Nueces County, household income varied considerably between the census tract with the lowest level of USD 7500 and the census tract with the highest level of more than USD 200,000. Similarly, disparities in educational attainment across communities are striking. The percentage of college graduates ranged between less than one percent (0.36%) to 100%. The table indicates that 95% of vaccine recipients lived in an urban area of Nueces County. Based on the Health District data, 9% of the sample confirmed COVID-19 infection before receiving a vaccine.
The bottom three panels of Table 1 present data for the primary COVID-19 doses and the first booster vaccine received through the end of August 2022. The mean and median driving times shortened from one vaccine dose to the next, implying that some vaccine recipients might have visited a new vaccine site closer to home. On average, vaccine recipients drove 2 min closer to their chosen vaccine facilities between the first vaccine and the booster. However, statistical tests (based on means and standard deviations) indicate no meaningful differences in the average travel time for the three subsequent vaccine doses. Appendix B displays plots of the percentages of booster recipients by travel time and travel distance, respectively, assuming the use of private vehicles.
For the Pfizer and Moderna vaccines, a typical vaccine recipient took 28 days (median) between their two primary doses. A typical fully vaccinated person waited an additional 240 days (approximately 8 months) before receiving their first booster. The median time intervals are longer than the recommended intervals, which range from two to six months [27].
The means for the three specific vaccines represent their shares among all vaccine recipients in the sample. More than half of vaccine recipients took Moderna for the primary doses, followed by Pfizer. Less than 10% of individuals in Nueces County took the Johnson & Johnson vaccine. Among 142,712 recipients of the first dose, 94% became fully vaccinated within our sample period. Only 52% of the sample received a booster shot by the end of August 2022.
Figure 1 shows the frequency distribution of time intervals, or delays, for fully vaccinated individuals to receive the first booster. The time interval data, expressed in months following full vaccination, were calculated from the individuals’ vaccination dates, as summarized in Table 1. Out of 135,548 fully vaccinated individuals, 782 (0.6%) took a booster within one month. Booster uptake picked up in the fifth month, reaching a peak in the eighth month (the median).
Another way to visualize booster uptake over time is the cumulative incidence function [31], which displays the percentage of the sample population that has taken a booster over time. Figure 2 illustrates the cumulative incidence of booster vaccination, corresponding to the frequency distribution data in Figure 1. This plot is analogous to the Kaplan–Meier curve that provides estimates of the hazard function in time-to-event analysis (see below). The cumulative incidence function increases rapidly after four months and then remains relatively flat after nine months. Among those who received primary vaccinations, 48% did not receive a booster within 12 months.

3.2. Model Estimation Results

This section presents the estimation results for vaccination outcomes in Nueces County, Texas, with a particular focus on the impact of travel time for a vaccine as a measure of geographic friction, or inconvenience in general. Table 2 shows the results of the logit models for estimating the odds of receiving the second primary COVID-19 vaccine and the first booster shot. Recipients of the Johnson & Johnson vaccine, which required only one dose for full vaccination, were excluded from the model for the second primary vaccine. For the covariates, the exponents of their coefficient estimates equal the odds ratios, which compare the odds of taking a vaccine for one sample group over the odds of taking a vaccine for its reference group. Most coefficient estimates are statistically significant, according to their point estimates and their corresponding 95% confidence levels (CIs). The exceptions are the “Asian” variable (0.056: 95% CI −0.058–0.170) in the model for full vaccination and the “Pacific Islander” variable (0.138: 95% CI −0.098–0.374) in the model for booster vaccination. The coefficient estimates for travel time (−0.023: 95% CI −0.049–−0.003), male (−0.182: 95% CI −0.222–−0.142), Hispanic (−0.115: 95% CI −0.157–−0.073), Pacific Islander (−0.351: 95% CI −0.709–−0.007), and the Johnson & Johnson vaccine (−0.539: 95% CI −0.587–−0.491) are negative. A negative coefficient estimate is translated into an odds ratio below one, meaning relatively lower odds. For instance, the estimate for the travel time variable means, other things equal, a 1% longer travel time was associated with 2.3% (1–0.977) lower odds for recipients of the first dose to follow up with the second dose. The odds of fully vaccinated persons taking a booster reduced drastically by 26% (1–0.740).
For the race/ethnicity variables, the estimation results suggest that the odds of taking a vaccine among Hispanics as Nueces County’s dominant demographic group were lower than the odds among non-Hispanic Whites (the reference group). More specifically, Hispanics’ overall odds were 10.9% lower of taking the second dose and 6.3% of taking the first booster. Conversely, the odds of taking a booster were relatively higher among Blacks and Asians.
The other sociodemographic variables indicate that the odds of COVID-19 vaccination were higher for adults who were older and female. Vaccine uptake also tended to be higher among individuals living in more educated and higher-income neighborhoods, as well as in urban areas. Interestingly, having a COVID-19 infection raised the odds of taking the second vaccine dose but lowered the odds of taking a booster. In comparison with Pfizer, the odds were higher if the first dose was Moderna. If the primary dose was Johnson & Johnson instead of Pfizer, the odds of taking a booster were considerably lower.
Next, we evaluated factors that affected vaccination outcomes using individual data for the time intervals between vaccinations. A hazard-based Weibull duration model was applied to estimate the time interval between full vaccination and the first booster. The duration model is considered an extension of the logit model with the consideration of the time dimension in vaccinations. The Pfizer and Moderna vaccines require two doses for full vaccination. For those 131,866 vaccine recipients, the duration equals the days between the second dose and the booster vaccine. For 10,846 persons who took the Johnson & Johnson vaccine who did not require a second dose, the duration equals the days between the first (primary) dose and the booster vaccine.
Table 3 presents Weibull regression results for the duration data. The sample of the baseline model consists of 74,352 persons who received a booster in Nueces County. In the Weibull model, the shape parameter (α) reveals whether the hazard function is monotonically increasing or decreasing over time. The positive estimate suggests that the likelihood that the duration ended (i.e., booster receipt) at a given time, conditional on duration up to that time, was increasing as time passed. This corresponds to the steep curvature of the Kaplan–Meier cumulative incidence curve in Figure 2. In other words, the longer fully vaccinated people stayed “unboosted” against COVID-19, the more likely they would take a booster.
Our primary variable of interest in modeling the duration data is the driving time between a vaccine recipient’s home address and the vaccine site. In the hazard-based duration model, coefficients reflect changes in the log hazard. The corresponding hazard ratio, which is the exponentiated value of the coefficient estimate, reveals the effect on the “risk” of an event (i.e., booster receipt) occurring over time. The negative coefficient estimate signifies a lower “risk” with a longer travel time. A hazard ratio of less than one indicates a negative effect of booster vaccination on an increase in travel time, holding other covariates constant. In other words, a longer travel time was associated with a longer delay for fully vaccinated individuals to take a booster shot.
Among the demographic variables, the model estimation results suggest that older people (−0.785: 95% CI −0.797–−0.773), Hispanics (−0.251: 95% CI −0.267–−0.235), and Blacks (−1.017: 95% CI −1.063–−0.971) tended to experience longer delays in booster vaccination. While a delay was negatively related to higher educational attainment (0.162: 95% CI 0.154–0.170) and urban (0.174: 95% CI 0.132–0.216) versus rural residence, people with a higher household income (−0.911: 95% CI −0.917–−0.905) and COVID-19 infection (−0.020: 95% CI −0.050–−0.012) tended to take a booster later. Compared with Pfizer recipients, people who took Moderna (−0.078: 95% CI −0.092–−0.064) as the primary dose tended to experience a longer delay. Conversely, those who took Johnson & Johnson (0.229: 95% CI 0.195–0.263) as the primary dose tended to receive a booster vaccine sooner, perhaps due to the lack of a second dose.

3.3. Sensitivity Analysis

As for most duration-based data, two features of our sample might have potentially generated biased model estimation results. For this reason, it is instructive to evaluate whether the duration modeling results are robust to such bias. First, the sample of the estimated model was right censored on 30 August 2022, in the sense that fully vaccinated individuals were not included in our model if they did not receive a booster by the end of the sample period, including those who died or moved out of Nueces County. Our full sample includes 61,196 individuals who took primary vaccinations only and no booster. As a result, we cannot observe the exact time to receive a booster for those individuals, even if they did so after August 2022. Right-censored data potentially lead to an underestimation of the true average duration since the modeling sample excludes individuals who might have taken longer to take a booster. Bias might be more severe if disproportionately more individuals of certain demographic groups (e.g., Hispanic) in our sample were censored.
To deal with right-censored data, we modified the likelihood function in duration model estimation to account for the portion of the data sample that had been omitted from the model [37]. For individuals who never received a booster, we substituted the travel time to a booster site with the travel time to the site of their previous vaccination (i.e., the second vaccine for Pfizer and Moderna and the first vaccine for Johnson & Johnson). Those data observations reflect the travel time perceived by individuals in the censored sample. Table 4 displays the Weibull regression results with censored data. Overall, most coefficient estimates are qualitatively similar to their counterparts in the baseline regression shown in Table 3. Notably, the estimates for travel time differ minimally between the two models. However, the new estimates of some sociodemographic variables change signs. In contrast to previous results, a longer delay is associated with the Asian demographic (−0.071, 95% CI: −0.107–−0.035) and a bachelor’s degree (−0.012, 95% CI: −0.022–−0.002).
The second potential source of estimation bias stems from the fact that the time duration under investigation and the sample selection process are not independent. The duration data for booster vaccinations were observed only for those individuals who completed the primary doses. The results of logit regression for modeling the full vaccination process are presented above in Table 2. As a result of the non-random sample selection, the model regression errors of the two processes are correlated, resulting in potential bias in the duration modeling results.
To deal with potential estimation bias due to non-random sample selection, we followed Boehmke et al.’s [38] two-stage full information maximum likelihood (FIML) estimator, which binds the sample selection (logit) and duration models together. As detailed in Appendix A.2, the sample selection and duration processes are assumed to follow a bivariate exponential distribution along with an error correlation term (φ) that captures the association between the two processes. Table 5 displays the FIML estimation results. Overall, the signs of most estimates for the covariates are the same as their counterparts in the regression with censored data, although their absolute sizes tend to be larger when the logit model for full vaccination outcomes is included in the estimation. In particular, a one percentage increase in driving time reduced the conditional incidence rate by approximately 5%, and, therefore, vaccination receipt would happen later in time. The estimated parameter for error correlation is 0.215 (95% CI: 0.177–0.243), which suggests a positive association between the selection and duration processes.

4. Discussion

Despite the overall widespread availability of COVID-19 vaccines across the United States, we have evaluated the relevance of “convenience” highlighted by the WHO as a major factor behind vaccine uptake. One aspect of “convenience” in vaccination services is accessibility to vaccine sites. Much of the existing literature confirms the impact of spatial accessibility on broad healthcare outcomes [26,39] and, more recently, COVID-19 vaccine uptake [19,20,21]. Travel distance or time is also regarded as a driver of disparities between rural and urban areas in accessing healthcare services [26] and vaccinations [5,16,34]. In those studies, however, accessibility to vaccination services is measured by the density of distribution sites in a given area rather than the realized accessibility of the actual utilization of vaccination services that affect the behavior of vaccine recipients. Cochran [15] measured the realized accessibility of vaccination services. However, travel distances to appointments were calculated using the Euclidean distance from individuals’ home ZIP code centroids to clinic addresses. We contribute to this literature using the driving time from individuals’ home addresses to vaccine sites as a proxy measure of geographic friction.
We have explored the role of individuals’ travel time for COVID-19 vaccination services using alternatively a logit model and a hazard-based duration model. The empirical results unequivocally confirm the role of travel time as a hindrance to COVID-19 vaccine uptake. A U.S. nationwide survey conducted by Rader et al. [20] revealed that people were less willing to travel to a more distant vaccine site. Only about 10% of respondents were willing to spend more than 60 min traveling for a COVID-19 vaccine. Our empirical results show that people who had to travel longer to a vaccine site were not only less likely to take a COVID-19 vaccine, but they also tended to wait longer before taking a booster. The individual-level travel impedance metric as a measure of “revealed” or realized accessibility [22,23] allows us to quantitatively estimate how the odds of an individual taking a vaccine will change if the travel distance or time for vaccination is longer or shorter, controlling for vaccine recipients’ own sociodemographic backgrounds that might affect their attitudes towards vaccination.
In addition to travel impedance to vaccine sites, our models include a host of covariates to control for vaccine recipients’ sociodemographic backgrounds that have been found to affect vaccine hesitancy. While the estimation results for travel time are robust, the results for some of those controlling variables seem sensitive to potential bias due to right-censored data and sample selection. Models that account for such bias yield overall results more consistent with previous findings for individual or demographic characteristics [2,3,4,5,6,8,9,28,29,32,40]. For instance, COVID-19 vaccine acceptance or uptake was lower for younger adults and socially vulnerable demographics, including race/ethnic minorities, like Hispanics and Blacks. The findings on the relationships between demographic characteristics and COVID-19 vaccine uptake also reinforce the nonparametric hazard regression results of Ioannou et al. [30] and Bajema et al. [31]. However, while the odds of taking a vaccine were relatively higher among people living in neighborhoods of higher income and educational attainment, they tended to wait a longer time before taking a booster. This finding is attributable to the higher “opportunity cost” among those who earned more, and thus gave up more, for spending the same amount of time traveling and taking a vaccine. Even though our finding of higher vaccine uptake for urban versus rural residents is widely documented in the literature [5,16,34], we have found that travel time within an urban area also matters.
Despite our findings supporting the role of travel time in vaccination uptake, this study is subject to limitations. For instance, the dataset consists of individuals in a relatively small geographical area as opposed to a broad region. Extensions of our research work to other areas or broader regions are warranted. This is particularly true for other cities or communities with more extensive public transportation or walking/biking infrastructure, which makes measuring geographic friction using driving time by private vehicles less relevant to certain vaccine recipients.

5. Conclusions

Travel time or distance is a form of physical barrier or friction. In this study, we have evaluated whether the time traveling to a vaccine site interfered with people’s decision to take a vaccine during the COVID-19 pandemic. Based on the vaccination records of Nueces County, Texas, USA, the logistic regression results confirm that the odds of residents taking a COVID-19 vaccine, either a primary dose or booster, were negatively associated with the time traveling to vaccine sites. A longer travel time not only made it less likely for a person to take a booster shot on any given day but it also caused a longer delay in booster vaccination. The empirical evidence on the role of travel time in vaccine uptake is robust to potential sampling bias. The estimation results also account for a myriad of sociodemographic factors that independently affect people’s willingness to receive a vaccine.
Our modeling results on the role of spatial accessibility in COVID-19 vaccine uptake align with recent findings based on geographic-level data. Yet, the individual-level travel metric better captures “revealed” accessibility from the perspective of vaccine recipients [41]. The integration of spatial and temporal dimensions in our duration model has also allowed us to shed light on delays in booster vaccination. The health protection of a COVID-19 vaccine declines over time, but the majority of individuals in our sample took a booster later than the official recommendations [1]. To the extent that individuals’ accessibility to vaccination services is a factor behind vaccine uptake, despite their sociodemographic backgrounds, a vaccination campaign should make vaccination services physically convenient for vaccine recipients from diverse communities. Given limited resources, public health policymakers should also pay particular attention to the spatial efficiency of vaccination facilities [42].

Author Contributions

Conceptualization, Y.H. and J.L.; methodology, Y.H. and J.L.; software, Y.H. and J.L.; validation, Y.H. and J.L.; formal analysis, Y.H. and J.L.; investigation, Y.H. and J.L.; resources, Y.H. and J.L.; data curation, Y.H. and J.L.; writing—original draft preparation, Y.H. and J.L.; writing—review and editing, Y.H. and J.L.; visualization, Y.H. and J.L.; funding acquisition, Y.H. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This study was partially supported by the Department of Commerce, Economic Development Administration, Grant/Award Number 087905589, and the National Science Foundation, Grant/Award Number 2112631.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and was approved by the Institutional Review Board of Texas A&M University-Corpus Christi on 05/04/2022 (TAMU-CC-IRB-2022-0448).

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are unavailable due to privacy or ethical restrictions.

Acknowledgments

We thank Hossein Naderi for his invaluable assistance with compiling and measuring driving time data for this study.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Appendix A.1. Hazard-Based Duration Model

In this study, we are particularly interested in factors that affected the time interval, or duration, before fully vaccinated individuals received their first COVID-19 booster shot. This section outlines our methodology for modeling those durations. Conceptually, the term “time” in time-to-event analysis refers to the duration until a particular event occurs. Let t * be a duration between one state and a new state for individual i (i = 1, 2, …, N), such as being “boosted” with another COVID-19 vaccine. The model for estimating the duration with a set of K covariates, X i = [ x 1 i , x 2 i , … , x K i ] , can be written as follows:
t i * = X i β + v i
where β is a set of free parameters and t i * = X i β + v i is an error term. Because duration data are non-negative by construction, the ordinary least-squares (OLS) assumption of normal distribution is violated. More specifically, estimating Equation (A.1) by the traditional least-squares method may result in negative predicted values that are impossible for time intervals.
Following the conventional approach in duration analysis, we model the duration between receiving two COVID-19 vaccines in the context of the “hazard” function [36]. The concept of “hazard” is commonly applied to survival analysis in biometrics and health sciences. In our case, by contrast, the hazard function describes the rate at which the delay in receiving a vaccine ends immediately after the duration t, given that it has lasted at least through t. Let t be a particular value or realization of t * , and then the cumulative probability distribution for t * is F t = Pr ⁡ t * ≤ t . The probability that a vaccination delay will end in the next short interval of time, say ∆t, given that the duration has lasted at least through t, is Pr ⁡ t ≤ t * < t + ∆ t   t * ≥ t ) .   The hazard function conditional on the same set of covariates in X i as above can be expressed as follows:
h t ; X i = lim ∆ t → 0 ⁡ Pr ⁡ t ≤ t * < t + ∆ t   t * ≥ t ; X i ) ∆ t
A popular parametric duration model takes the form of the Weibull distribution, conditional on the observed covariates in X i and unobserved heterogeneity v i as follows [36]:
h ( t i ,   X i , β , v i ) = h 0 ( t ) exp   ( X i β ) v i
where h 0 t = α t α − 1 . The parameters in β represent the elasticities of the hazard with respect to the exponential of the variables in X i , and exp ⁡ β i   is called the hazard ratio. The Weibull distribution of the hazard allows for possible duration dependence. The term α is called the shape parameter, which determines whether the hazard function is monotonically increasing or decreasing with t. If α > 1, the hazard rate is monotonically increasing over time (i.e., ∂ h t ∂ t > 0 ), and vice versa. Given the Weibull distribution of the hazard rate, the duration model can be expressed in regression form as follows [37]:
  α ln ⁡ t i * = z i t = − X i β + ε i
where the error term ε i   is distributed independently of X i . The mean of ε i is not zero. Following [36,37], we estimate the Weibull model using maximum likelihood (ML).
However, two features of our sample might potentially generate estimation bias. First, our sample is non-random (or biased) because individuals were left out of our sample if they never took a COVID-19 vaccine. In other words, individual i is observed only if ti > 0. If X i β is small, then individual i enters the sample only if vi is sufficiently large so that ti is positive. In this case, X i is negatively correlated with vi, and thus the least-squares estimation of β will be biased toward zero. This also results in the inference of a shorter duration if X i is large and a longer duration if vi is small. Another source of biased coefficient estimates arises from the fact that the duration under investigation and the sample selection process are not independent. As a result, the model regression errors of the two processes are correlated.
Second, part of our full sample is right censored as some fully vaccinated individuals never took a booster shot, including those who died or moved out of the study area before the end of the sampling period. Right censoring occurs when we cannot observe the exact time to receive a booster for an individual. Right-censored data potentially lead to an underestimation of the true average duration, or the probability of taking a booster sooner, since the modeling sample excludes individuals who might have taken longer to take a booster.

Appendix A.2. Sample Selection Bias

One popular approach to dealing with non-random sample selection bias is to estimate both the duration and selection processes simultaneously. More specifically, this model yields estimates for the potential factors affecting the time length before taking a booster while accounting for the full vaccination outcome. Let d i * be the full vaccination outcome of an individual i. This outcome can be expressed as follows:
d i * = Z i θ + u i
where Z i is a set of covariates with their corresponding free parameters in θ and u i is an error term. The asterisk superscript on the dependent variable indicates that it is a latent or unobserved variable, which can be measured as a binary outcome (i.e., 1 for vaccination receipt and 0 otherwise) as follows:
d i = 0   if   d i * ≤ 0 1   if   d i * > 0
A logistic (logit) model assumes the logistic distribution, i. P r ( d i = 1 | Z i ) = e x p ( Z i θ ) / ( 1 + e x p ( Z i θ ) . The probability of observations for the time intervals before taking a booster conditional on the full vaccination process is Pr ⁡ t i * = t i d i = 1 . As such, the likelihood function for all individuals becomes the following:
Pr ⁡ t * , d = ∏ i = 1 N [ Pr ⁡ ( d i = 0 ) ] d i = 0 × Pr ⁡ t i * = t i d i = 1 × f t i d i = 1
The next step is to calculate each of the probabilities based on the specific distributions of the two processes. Following [38], we assume a bivariate exponential distribution along with the error correlation given by φ/4, where −1 ≤ φ ≤ 1 is a measure of the association between the two processes.
The duration and sample selection processes are estimated using the two-stage full information maximum likelihood (FIML) estimator [38]. Denote Ψ1i = exp( Z i θ ) and Ψ2i = exp(Xi β ); the log-likelihood function for the Weibull duration model with sample selection can be written as follows:
ln   L ( β , θ ,   φ ,   α   | X ,   Z ,   t ,   d ) = ∑ i = 1 N d i   ×   { Ψ 1 i + ln [ 1 + φ ( 2 exp ( − ( Ψ 2 i t i ) α ) − 1 ) × ( exp ( Ψ 1 i ) − 1 ) ] + ln ( α ) + ln ( Ψ 2 i ) + ( α − 1 )   ln ( Ψ 2 i t i ) − ( Ψ 2 i t i ) α } + ( 1 − d i ) × ln [ 1 − exp ( Ψ 1 i ) ] .

Appendix B

Covid 05 00070 g0a1
Figure A1. Distribution of Booster Vaccination by Travel Time in 5-Minute Intervals.
Figure A1. Distribution of Booster Vaccination by Travel Time in 5-Minute Intervals.
Covid 05 00070 g0a1
Covid 05 00070 g0a2
Figure A2. Distribution of Booster Vaccination by Travel Distance in 2.5-Km Intervals.
Figure A2. Distribution of Booster Vaccination by Travel Distance in 2.5-Km Intervals.
Covid 05 00070 g0a2

References

  1. Centers for Disease Control and Prevention (CDC). Stay Up to Date with COVID-19 Vaccines. Available online: https://www.cdc.gov/covid/vaccines/stay-up-to-date.html (accessed on 25 April 2025).
  2. Brownstein, N.C.; Reddy, H.; Whiting, J.; Kasting, M.L.; Head, K.J.; Vadaparampil, S.T.; Giuliano, A.R.; Gwede, C.K.; Meade, C.D.; Christy, S.M. COVID-19 vaccine behaviors and intentions among a national sample of United States adults ages 18-45. Prev. Med. 2022, 160, 107038. [Google Scholar] [CrossRef] [PubMed]
  3. Caspi, G.; Dayan, A.; Eshal, Y.; Liverant-Taub, S.; Twig, G.; Shalit, U.; Lewis, Y.; Shina, A.; Caspi, O. Socioeconomic disparities and COVID-19 vaccination acceptance: A nationwide ecologic study. Clin. Microbiol. Infect. 2021, 27, 1502–1506. [Google Scholar] [CrossRef]
  4. Frisco, M.L.; van Hook, J.; Thomas, K.J.A. Racial/ethnic and nativity disparities in U.S. COVID-19 vaccination hesitancy during vaccine rollout and factors that explain them. Soc. Sci. Med. 2022, 307, 115183. [Google Scholar] [CrossRef] [PubMed]
  5. Huang, Y.; Lee, J.; Jin, L.; Rahman, M.M.; Guerrero, A.; Zhao, M.; Lee, K. Sociodemographic and geographic disparities in COVID-19 booster vaccination in Nueces County, Texas, USA. Heliyon 2024, 10, e27763. [Google Scholar] [CrossRef] [PubMed]
  6. Lee, J.; Huang, Y. COVID-19 vaccine hesitancy: The role of socioeconomic factors and spatial effects. Vaccines 2022, 10, 352. [Google Scholar] [CrossRef]
  7. Mondal, P.; Sinharoy, A.; Su, L. Sociodemographic predictors of COVID-19 vaccine acceptance: A nationwide US-based survey study. Public Health 2021, 198, 252–259. [Google Scholar] [CrossRef]
  8. Nino, M.; Hearne, B.; Cai, T. Trajectories of COVID-19 vaccine intentions among US adults: The role of race and ethnicity. SSM-Popul. Health 2021, 15, 100824. [Google Scholar] [CrossRef]
  9. Prickett, K.C.; Habibi, H.; Carr, P.A. COVID-19 vaccine hesitancy and acceptance in a cohort of diverse New Zealanders. Lancet Reg. Health West. Pac. 2021, 14, 100241. [Google Scholar]
  10. Chen, H.; Cao, Y.; Feng, L.; Chen, K.; Bei, H.; Murcio, R. Addressing the spatial disparity of COVID-19 vaccination services: A spatial optimization approach. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103881. [Google Scholar] [CrossRef]
  11. MacDonald, N.E.; SAGE Working Group on Vaccine Hesitancy. Vaccine hesitancy: Definition, scope and determinants. Vaccine 2015, 33, 4161–4164. [Google Scholar] [CrossRef]
  12. Hardin, B.; Graboyes, M.; Kosty, D.; Cioffi, C. Vaccine decision making among people who inject drugs: Improving on the WHO’s 3C model of vaccine hesitancy. Preventive Med. Rep. 2023, 35, 102341. [Google Scholar] [CrossRef] [PubMed]
  13. Parisi, A.; Regazzi, L.; Spanaus, E.; Gris, A.; Cadeddu, C.; Moore, M.; Ricciardi, W.; Lomazzi, M. Impact of COVID-19 pandemic on vaccine hesitancy and sentiment changes: A survey of healthcare workers in 12 counties. Public Health 2025, 238, 188–196. [Google Scholar] [CrossRef] [PubMed]
  14. Naderi, H.; Abbasian, Z.; Huang, Y. Measuring spatial accessibility of COVID-19 vaccination sites. Int. J. Manag. Appl. Sci. (IJMAS) 2023, 9, 111–114. [Google Scholar]
  15. Cochran, A.L.; Wang, J.; Wolfe, M.; Iacobucci, E.; Vinella-Brusher, E.; McDonald, N.C. Spatial and temporal trends in travel for COVID-19 vaccinations. AJPM Focus 2023, 2, 100122. [Google Scholar] [CrossRef]
  16. Cuadros, D.; Branscum, A.; Mukandavire, Z.; Miller, F.; MacKinnon, N. Dynamics of the COVID-19 epidemic in urban and rural areas in the United States. Ann. Epidemiol. 2021, 59, 16–20. [Google Scholar] [CrossRef]
  17. Bemanian, A.; Mosser, J.F. Investigating the spatial accessibility and coverage of the pediatric COVID-19 vaccine: An ecologic study of regional health data. Vaccines 2024, 12, 545. [Google Scholar] [CrossRef]
  18. Cao, Y.; Li, T.; Chen, H.; Zhao, Q.; Sun, J.; Grépin, K.A.; Kang, J. Evaluating geographic accessibility to COVID-19 vaccination across 54 countries/regions. BMJ Glob. Health 2025, 10, e017761. [Google Scholar] [CrossRef]
  19. Mazar, A.; Jaro, D.; Tomaino, G.; Carmon, Z.; Wood, W. Distance to vaccine sites is tied to decreased COVID-19 vaccine uptake. Proc. Natl. Acad. Sci. USA 2023, 2, pgad411. [Google Scholar] [CrossRef]
  20. Rader, B.; Astley, C.M.; Sewalk, K.; Delamater, P.L.; Cordiano, K.; Wronski, L.; Rivera, J.M.; Hallberg, K.; Pera, M.F.; Cantor, J.; et al. Spatial modeling of vaccine deserts as barriers to controlling SARS-CoV-2. Commun. Med. 2022, 2, 141. [Google Scholar] [CrossRef]
  21. Xu, Z.; Jiang, B. Effects of social vulnerability and spatial accessibility on COVID-19 vaccination coverage: A census-tract level study in Milwaukee County, USA. Int. J. Environ. Res. Public Health 2022, 19, 12304. [Google Scholar] [CrossRef]
  22. Chen, H.; Cao, Y.; Feng, L.; Zhao, Q. Measuring and Validating Spatial Accessibility to COVID-19 Vaccination Sites: A Case Study in England. 2022. Available online: https://osf.io/preprints/socarxiv/xvnps_v1 (accessed on 25 April 2025).
  23. Gligoric, K.; Kamath, C.; Weiss, D.J.; Bavadekar, S.; Liu, Y.; Shekel, T.; Schulman, K.; Gabrilovich, E. Revealed versus potential spatial accessibility of healthcare and changing patterns during the COVID-19 pandemic. Commun. Med. 2023, 3, 157. [Google Scholar] [CrossRef] [PubMed]
  24. Masters, N.B.; Zhou, T.; Meng, L.; Lu, P.J.; Kriss, J.L.; Black, C.; Omari, A.; Boone, K.; Weiss, D.; Carter, R.J.; et al. Geographic heterogeneity in behavioral and social drivers of COVID-19 vaccination. Am. J. Prev. Med. 2022, 63, 883–893. [Google Scholar] [CrossRef] [PubMed]
  25. Huang, Y.; Meyer, P.; Jin, L. Spatial access to health care and elderly ambulatory care sensitive hospitalizations. Public Health 2019, 169, 76–83. [Google Scholar] [CrossRef] [PubMed]
  26. Mseke, E.P.; Jessup, B.; Barnett, T. Impact of distance and/or travel time on healthcare service access in rural and remote areas: A scoping review. J. Transp. Health 2024, 37, 101819. [Google Scholar] [CrossRef]
  27. Waller, A. Wondering Who Can Get a COVID-19 Vaccine Booster Shot and When? Here’s What Texans Need to Know. Texas Tribune. 2021. Available online: https://www.texastribune.org/2021/10/29/covid-19-vaccine-booster-shots/ (accessed on 25 April 2025).
  28. Neely, S.R.; Scacco, J.M. Receptiveness of American adults to COVID-19 vaccine boosters: A survey analysis. PEC Innov. 2022, 1, 100019. [Google Scholar] [CrossRef]
  29. Raman, S.; Kriner, D.; Ziebarth, N.; Simon, K.; Kreps, S. COVID-19 booster uptake among US adults: Assessing the impact of vaccine attributes, incentives, and context in a choice-based experiment. Soc. Sci. Med. 2022, 310, 115277. [Google Scholar] [CrossRef]
  30. Ioannou, G.N.; Green, P.; Locke, E.R.; Berry, K. Factors associated with early receipt of COVID-19 vaccination and adherence to second dose in the Veterans Affairs healthcare system. PLoS ONE 2021, 16, e0259696. [Google Scholar] [CrossRef]
  31. Bajema, K.L.; Rowneki, M.; Berry, K.; Bohnert, A.; Bowling, C.B.; Boyko, E.J.; Iwashyna, T.J.; Maciejewski, M.L.; O’Hare, A.M.; Osborne, T.F.; et al. Rates of and factors associated with primary and booster COVID-19 vaccine receipt by US veterans, December 2020 to June 2022. JAMA Netw. Open 2023, 6, e2254387. [Google Scholar] [CrossRef]
  32. Valckx, S.; Crevecoeur, J.; Verelst, F.; Vranckx, M.; Hendrickx, G.; Hens, N.; Van Damme, P.; Pepermans, K.; Beutels, P.; Neyens, T. Individual factors influencing COVID-19 vaccine acceptance in between and during pandemic waves (July–December 2020). Vaccine 2022, 40, 151–161. [Google Scholar] [CrossRef]
  33. Census Bureau. Urban and Rural. 2024. Available online: https://www.census.gov/programs-surveys/geography/guidance/geo-areas/urban-rural.html (accessed on 25 April 2025).
  34. Bennet, K.; Pumkam, C.; Probst, J. Rural-urban differences in the location of influenza vaccine administration. Vaccine 2011, 29, 5970–5977. [Google Scholar] [CrossRef]
  35. Boeing, G. Modeling and Analyzing Urban Networks and Amenities with OSMnx. 2024. Available online: https://geoffboeing.com/publications/osmnx-paper/ (accessed on 25 April 2025).
  36. Greene, W.H. Econometric Analysis, 8th ed.; Pearson: New York, NY, USA, 2018. [Google Scholar]
  37. Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
  38. Boehmke, F.J.; Morey, D.S.; Shannon, M. Selection bias and continuous-time duration models: Consequences and a proposed solution. Am. J. Political Sci. 2006, 50, 192–207. [Google Scholar] [CrossRef]
  39. Kelly, C.; Hulme, C.; Farragher, T.; Clarke, G. Are differences in travel time or distance to healthcare for adults in global north countries associated with an impact on health outcomes? A systematic review. BMJ Open 2016, 6, e013059. [Google Scholar] [CrossRef] [PubMed]
  40. Paul, E.; Fancourt, D. Predictors of uncertainty and unwillingness to receive the COVID-19 booster vaccine: An observational study of 22,139 fully vaccinated adults in the UK. Lancet Reg. Health Eur. 2022, 14, 100317. [Google Scholar] [CrossRef] [PubMed]
  41. Naderi, H.; Abbasian, Z.; Huang, Y. Disparity between expected spatial accessibility and actual travel time to vaccination sites: Implications for COVID-19 immunization delays. SSM-Population Health 2025, 30, 101804. [Google Scholar] [CrossRef]
  42. Chen, H.; Cao, Y.; Feng, L.; Zhao, Q.; Torres, J. Understanding the spatial heterogeneity of COVID-19 vaccine uptake in England. BMC Public Health 2023, 23, 895. [Google Scholar]
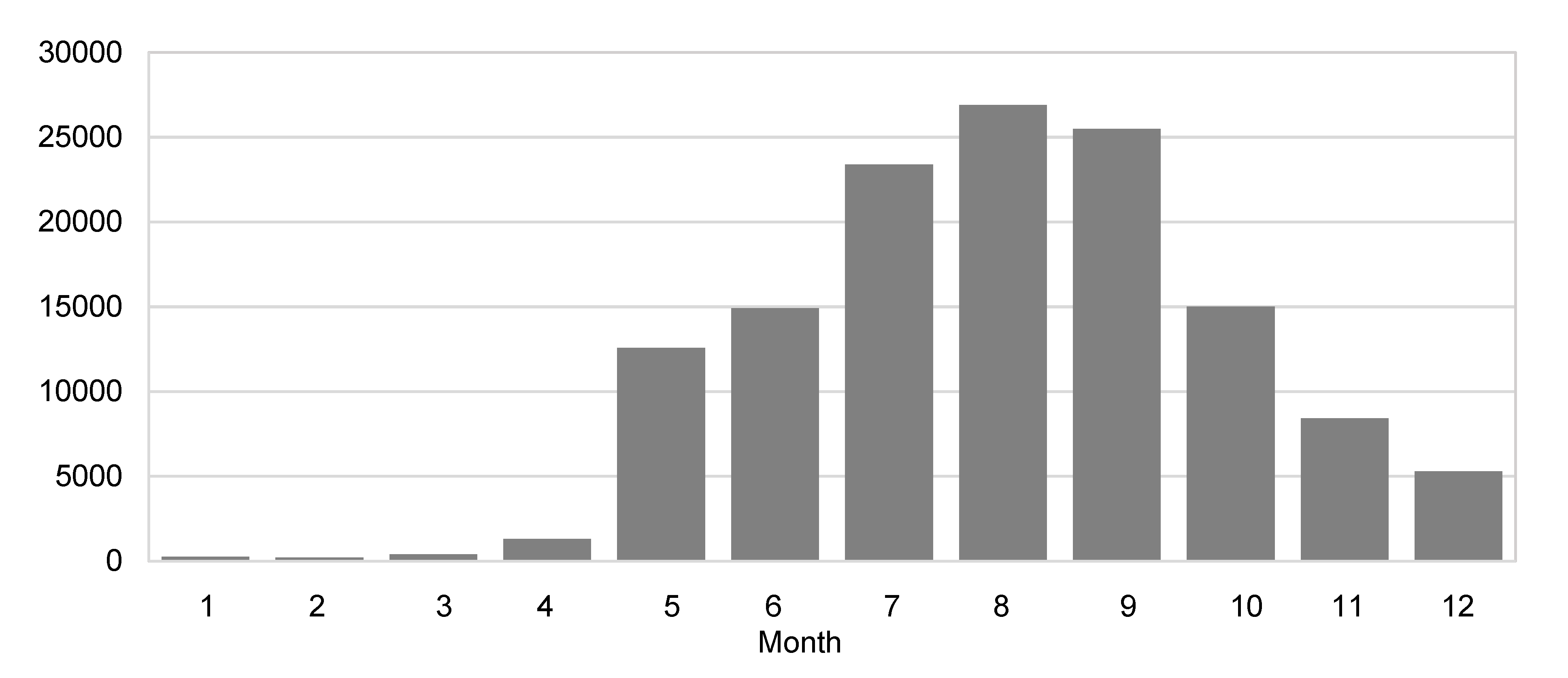
Covid 05 00070 g001
Figure 1. Frequency distribution of time intervals for booster vaccination by month.
Figure 1. Frequency distribution of time intervals for booster vaccination by month.
Covid 05 00070 g001
Covid 05 00070 g002
Figure 2. Cumulative incidence of COVID-19 booster vaccination by month.
Figure 2. Cumulative incidence of COVID-19 booster vaccination by month.
Covid 05 00070 g002
Table 1. Descriptive statistics.
Table 1. Descriptive statistics.
Demographics (n = 142,712):
Age [years], Median (IQR)54 (41–66)
Male, n (%)64,363 (45)
Non-Hispanic White, n (%)41,243 (29)
Hispanic, n (%)73,211 (51)
Black, n (%)4852 (3)
Asian, n (%)4709 (3)
Pacific Islander, n (%)285 (0)
Household income [USD], Median (IQR)61,485 (40,819–82,150)
Bachelor’s Degree, n (%)22,808 (16)
Urban Area, n (%)135,576 (95)
COVID-19 Infection, n (%)12,273 (9)
First Dose (n = 142,712):
Travel Time [minutes], Median (IQR)7.648 (3.206–12.090)
Vaccine: Pfizer, n (%)50,234 (35)
Vaccine: Moderna, n (%)81,631 (57)
Vaccine: Johnson & Johnson, n (%)10,846 (8)
Second Dose (n = 135,548):
Days between Vaccines, Median (IQR)28 (5–57)
Travel Time [minutes], Median (IQR)7.345 (2.934–11.756)
Vaccine: Pfizer, n (%)45,273 (33)
Vaccine: Moderna, n (%)74,144 (54)
First Booster (n = 74,352):
Days between Vaccines, Median (IQR)240 (206–273)
Travel Time [minutes], Median (IQR)5.402 (1.456–9.348)
Vaccine: Pfizer, n (%)13,978 (18)
Vaccine: Moderna, n (%)23,495 (31)
Notes: IQR = interquartile range between the 25th percentile and 75th percentile of data.
Table 2. Estimation results of the logit model for vaccinations.
Table 2. Estimation results of the logit model for vaccinations.
Coeff.95% CIOdds Ratio
(A) Second Primary Dose
Constant−2.053(−2.623, −1.483) *0.128
Travel Time (log)−0.023(−0.049, −0.003)0.977
Age (log)0.719(0.671, 0.767) *2.053
Male−0.182(−0.222, −0.142) *0.834
Hispanic−0.115(−0.157, −0.073) *0.891
Black0.234(0.114, 0.354) *1.263
Asian0.056(−0.058, 0.170)1.058
Pacific Islander−0.351(−0.709, −0.007) *0.704
Income (log)0.116(0.064, 0.168) *1.123
Bachelor’s Degree (log)0.162(0.132, 0.192) *1.175
Urban Area0.360(0.274, 0.446) *1.434
COVID-19 Infection0.200(0.126, 0.274) *1.221
Moderna0.208(0.16, 0.256) *1.231
Pseudo R20.184(0.184, 0.184) *
Log Likelihood−35,592
Observations (n)135,548
(B) First Booster
Constant−8.028(−8.364, −7.692) *0.000
Travel Time (log)−0.301(−0.315, −0.287) *0.740
Age (log)1.198(1.168, 1.228) *3.314
Male−0.096(−0.12, −0.072) *0.908
Hispanic−0.065(−0.089, −0.041) *0.937
Black0.221(0.155, 0.287) *1.248
Asian0.433(0.367, 0.499) *1.542
Pacific Islander0.138(−0.098, 0.374)1.148
Income (log)0.324(0.294, 0.354) *1.382
Bachelor’s Degree (log)0.094(0.076, 0.112) *1.098
Urban Area0.035(−0.001, 0.071)1.036
COVID-19 Infection−0.142(−0.184, −0.101) *0.868
Moderna (dose 2)0.308(0.282, 0.334) *1.360
Johnson & Johnson (primary dose)−0.539(−0.587, −0.491) *0.583
Pseudo R20.101
Log Likelihood−85,919
Observations (n)142,712
Notes: * p < 0.05. CI = Confidence Interval.
Table 3. Estimation results of the Weibull duration model for a booster.
Table 3. Estimation results of the Weibull duration model for a booster.
Coeff.95% CIHazard Ratio
Constant−12.899(−12.989, −12.809) *0.000
Travel Time (log)−0.014(−0.020, −0.008) *0.986
Age (log)−0.785(−0.797, −0.773) *0.456
Male0.096(0.082, 0.110) *1.100
Hispanic−0.251(−0.267, −0.235) *0.778
Black−1.017(−1.063, −0.971) *0.362
Asian0.080(0.044, 0.116) *1.083
Pacific Islander0.082(−0.06, 0.224)1.085
Household Income (log)−0.911(−0.917, −0.905) *0.402
Bachelor’s Degree (log)0.162(0.154, 0.170) *1.175
Urban Area0.174(0.132, 0.216) *1.190
COVID-19 Infection−0.020(−0.050, −0.012) *0.980
Moderna (dose 2)−0.078(−0.092, −0.064) *0.925
Johnson & Johnson (primary dose)0.229(0.195, 0.263) *1.257
Shape Parameter (α)4.612(4.586, 4.638) *
Log Likelihood−369,309
Observations (n)74,352
Notes: * p < 0.05. CI = Confidence Interval.
Table 4. Estimation results of the Weibull duration model for a booster with censored data.
Table 4. Estimation results of the Weibull duration model for a booster with censored data.
Coeff.95% CIHazard Ratio
Constant−31.944(−32.23, −31.658) *0.000
Travel Time (log)−0.015(−0.023, −0.007) *0.985
Age (log)0.174(0.154, 0.194) *1.190
Male0.112(0.098, 0.126) *1.118
Hispanic−0.067(−0.081, −0.053) *0.935
Black−0.121(−0.163, −0.079) *0.886
Asian−0.071(−0.107, −0.035) *0.931
Pacific Islander0.247(0.111, 0.383) *1.280
Household Income (log)−0.016(−0.034, 0.002) *0.984
Bachelor’s Degree (log)−0.012(−0.022, −0.002) *0.988
Urban Area0.087(0.055, 0.119) *1.091
COVID-19 Infection−0.060(−0.082, −0.038) *0.942
Moderna (dose 2)−0.107(−0.121, −0.093) *0.899
Johnson & Johnson (primary dose)0.073(0.041, 0.105) *1.076
Shape Parameter (α)5.671(5.639, 5.703) *
Log Likelihood−352,672
Observations (n)135,548
Notes: * p < 0.05. CI = Confidence Interval.
Table 5. Estimation results of the model for a booster with sample selection.
Table 5. Estimation results of the model for a booster with sample selection.
Coeff.95% CIHazard Ratio
Constant−9.351(−9.413, −9.289) *0.000
Travel Time (log)−0.055(−0.065, −0.045) *0.946
Age (log)−1.776(−1.790, −1.762) *0.169
Male0.474(0.458, 0.490) *1.606
Hispanic−0.179(−0.193, −0.165) *0.836
Black−0.452(−0.492, −0.412) *0.636
Asian−0.323(−0.371, −0.275) *0.724
Pacific Islander1.093(0.933, 1.253) *2.984
Household Income (log)−0.714(−0.718, −0.710) *0.490
Bachelor’s Degree (log)−0.247(−0.255, −0.239) *0.781
Urban−1.110(−1.146, −1.074) *0.330
COVID-19 Infection−0.574(−0.606, −0.542) *0.563
Moderna (dose 2)−0.527(−0.543, −0.511) *0.590
Johnson & Johnson (primary dose)0.161(0.055, 0.267) *1.175
Shape Parameter (α)8.180(8.058, 8.302) *
Error Correlation (φ)0.215(0.187, 0.243) *
Log Likelihood−388,295
Observations (n)74,352
Notes: * p < 0.05. CI = Confidence Interval.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Huang, Y.; Lee, J. Delay in COVID-19 Vaccinations: The Role of Travel Time to Vaccine Sites. COVID 2025, 5, 70. https://doi.org/10.3390/covid5050070

AMA Style

Huang Y, Lee J. Delay in COVID-19 Vaccinations: The Role of Travel Time to Vaccine Sites. COVID. 2025; 5(5):70. https://doi.org/10.3390/covid5050070

Chicago/Turabian Style

Huang, Yuxia, and Jim Lee. 2025. "Delay in COVID-19 Vaccinations: The Role of Travel Time to Vaccine Sites" COVID 5, no. 5: 70. https://doi.org/10.3390/covid5050070

APA Style

Huang, Y., & Lee, J. (2025). Delay in COVID-19 Vaccinations: The Role of Travel Time to Vaccine Sites. COVID, 5(5), 70. https://doi.org/10.3390/covid5050070

Article Metrics

Back to TopTop