Experimental Study on the Time-Dependent Resistance of Open-Ended Steel Piles in Sand
Abstract
1. Introduction
1.1. Soil Plugging
- Pile properties: inner diameter, outer diameter, wall thickness, embedded pile length, surface roughness.
- Type of loading: jacking/quasi-static loading, impact driving/dynamic loading, vibratory driving.
- Granulometric properties and state: grain size distribution, grain shape, grain mineral, relative density, degree of saturation, stress state.
- The lower the relative density of the sand, the lower the height of the soil column inside the pile, and, thus, the lower the value of the .
- The larger the diameter of the pile, the greater the height of the soil column inside the pile, and the higher the associated value of the .
1.2. Pile Ageing
- The variability of the natural subsoil and differences in the pile installation process, pile loading tests, and instrumentation. For this reason, even tests on similarly installed, instrumented, and loaded piles, tested at the same time after installation, can show a significant scatter of the compressive resistance as well as tensile resistance.
- In some cases, different types of pile loading tests are used to evaluate ageing (static/dynamic, tension/compression), leading to influences from the different test methods themselves, as well as from the test data evaluation and interpretation.
- Different boundary conditions related to the pile geometry, pile installation process, and soil conditions will most likely have an effect on the setup effect.
- For the evaluation of the pile ageing, different empirical functions describing the resistance as a function of time have been proposed in the literature. In most cases, the results are presented in semi-logarithmic plots. In these plots, a linear regression curve corresponds to an exponential function of type,. The underlying assumption here is that the pile ageing decays exponentially. A slightly different approach is described in [23], which proposed a hyperbolic function, . The latter is based on the assumption that the ageing will cease after a certain period of time (according to [23], 12–24 months).
2. Description of the Large-Scale Pile Tests
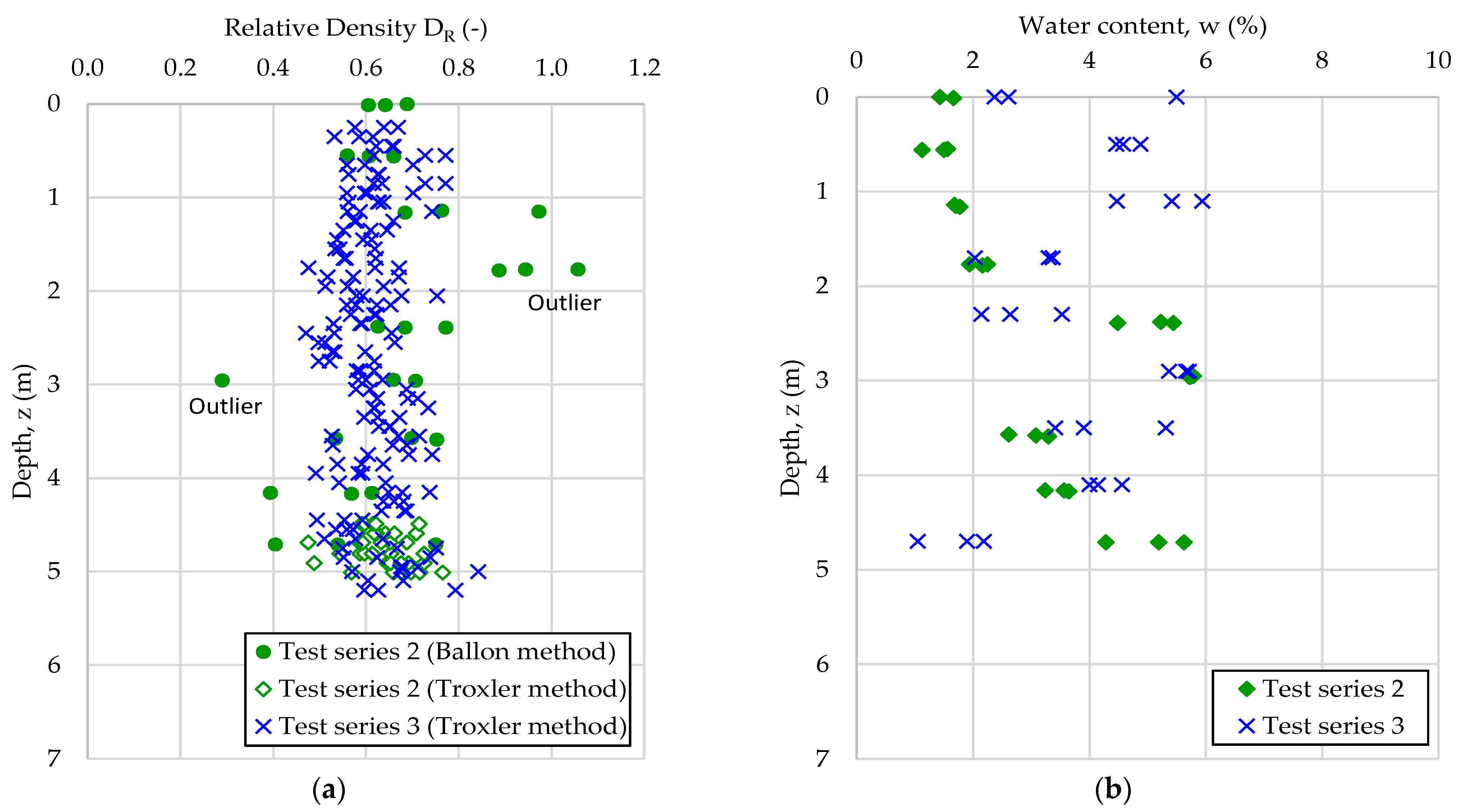
2.1. Soil Characterization
2.2. Pile Driving Hammer
2.3. Static Pile Load Testing
3. Test Results
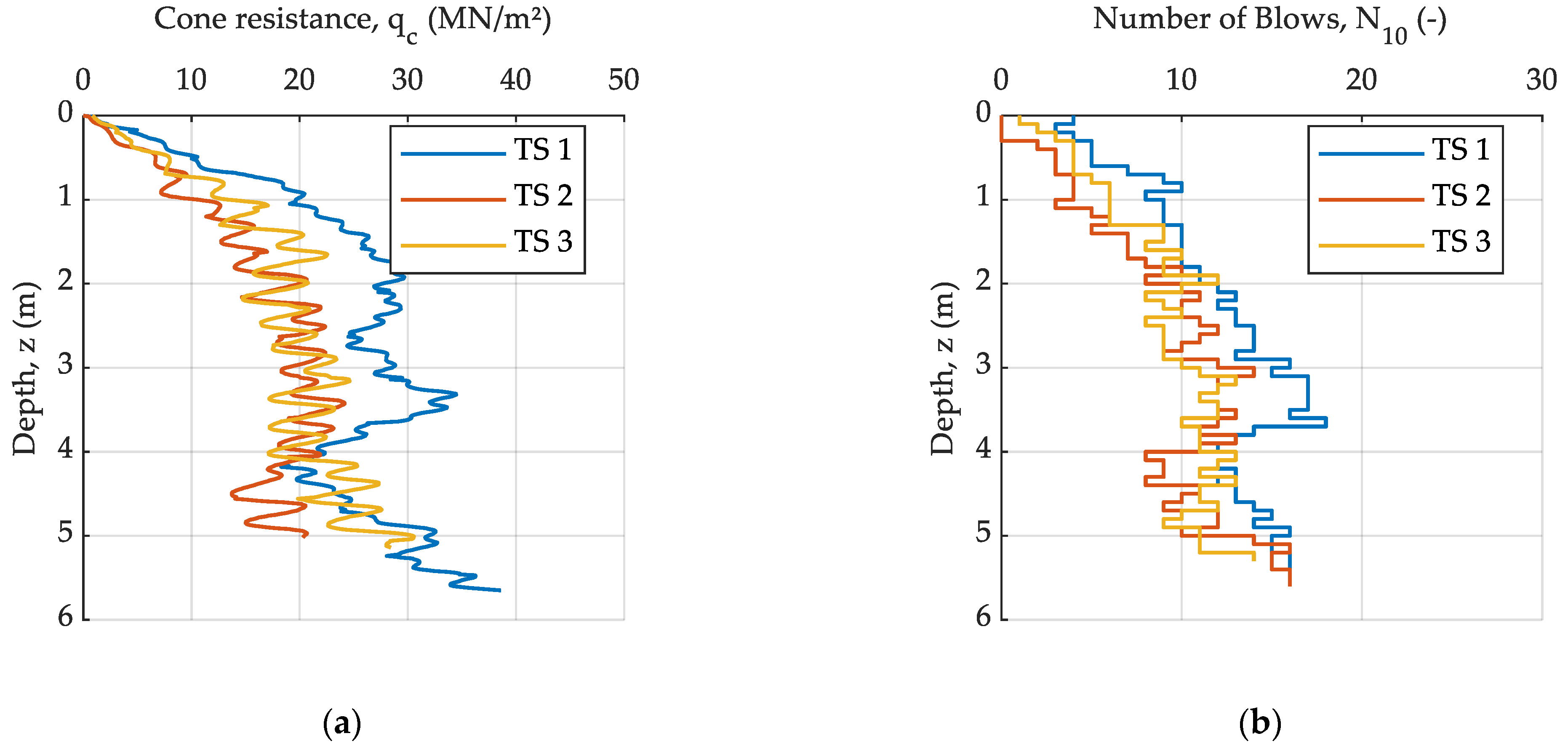
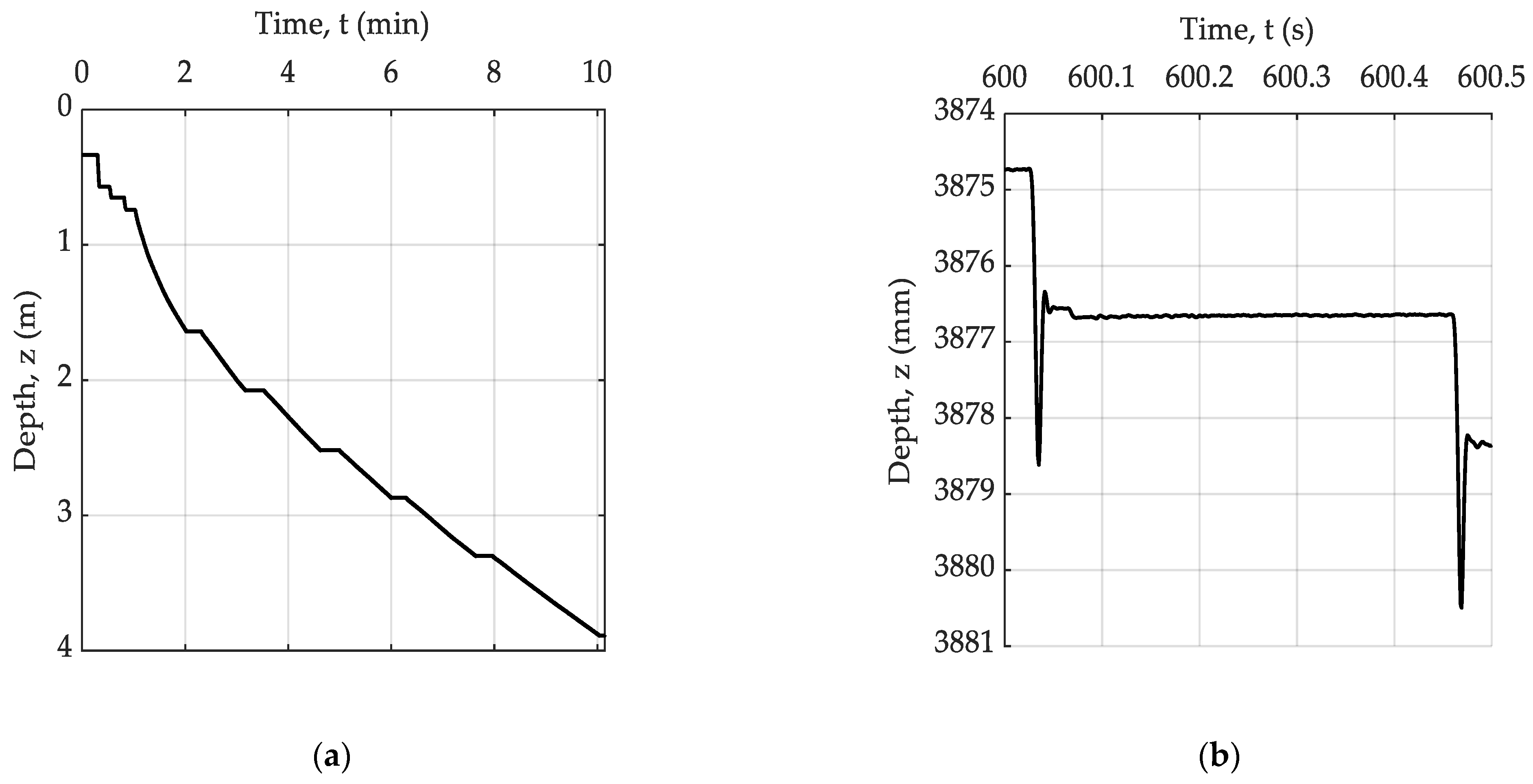
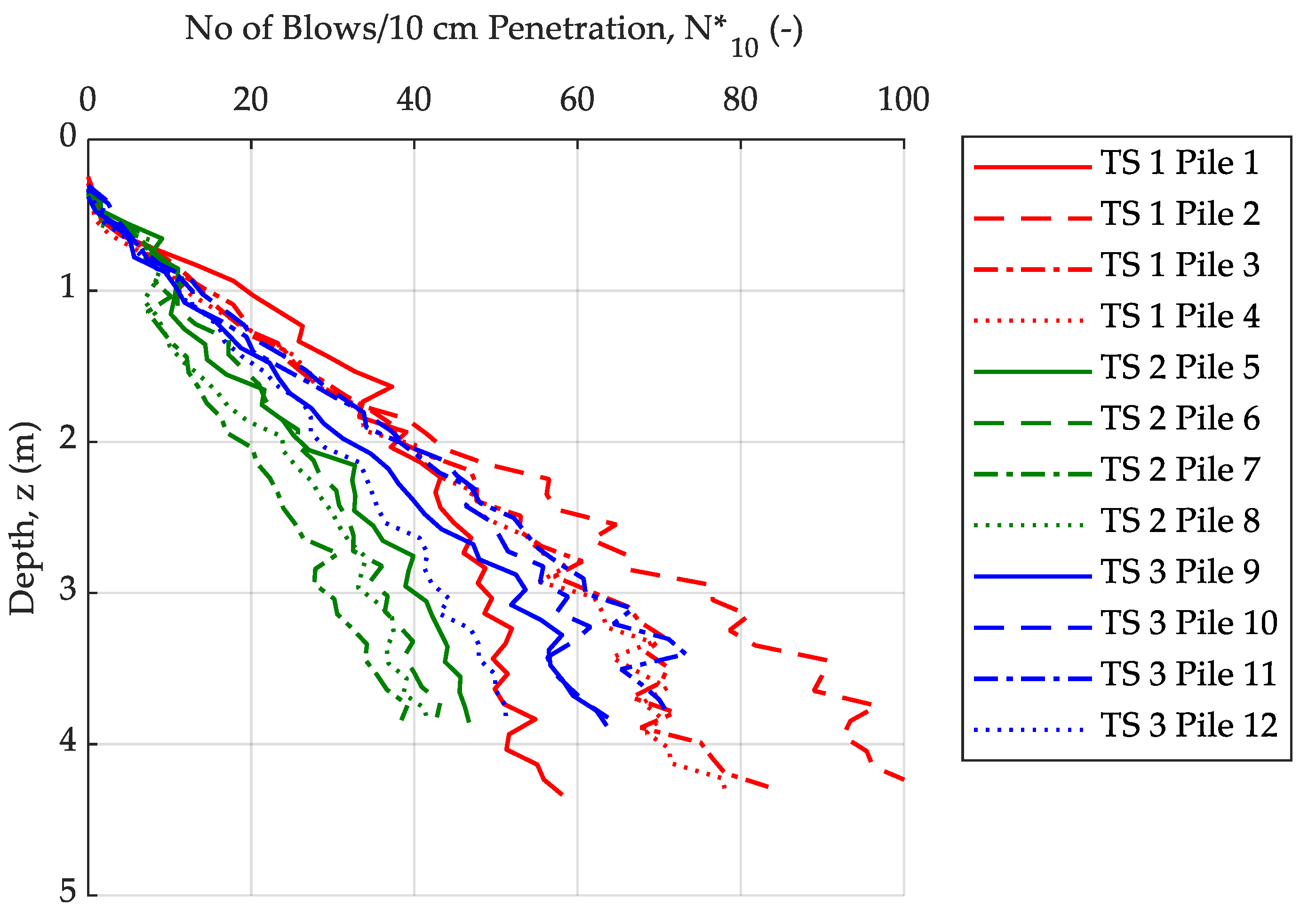
3.1. Pile Installation
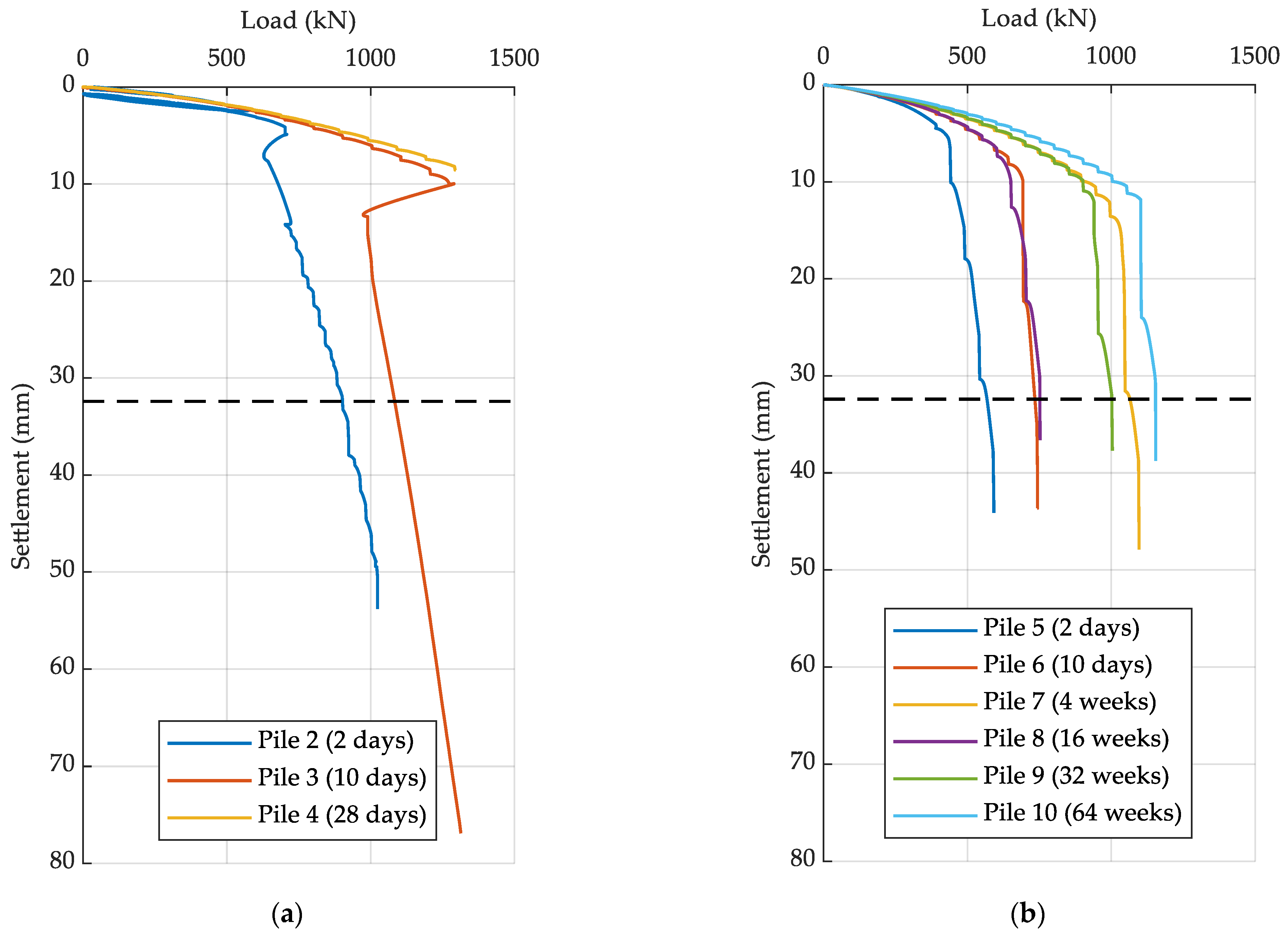
3.2. Static Compression Pile Load Testing
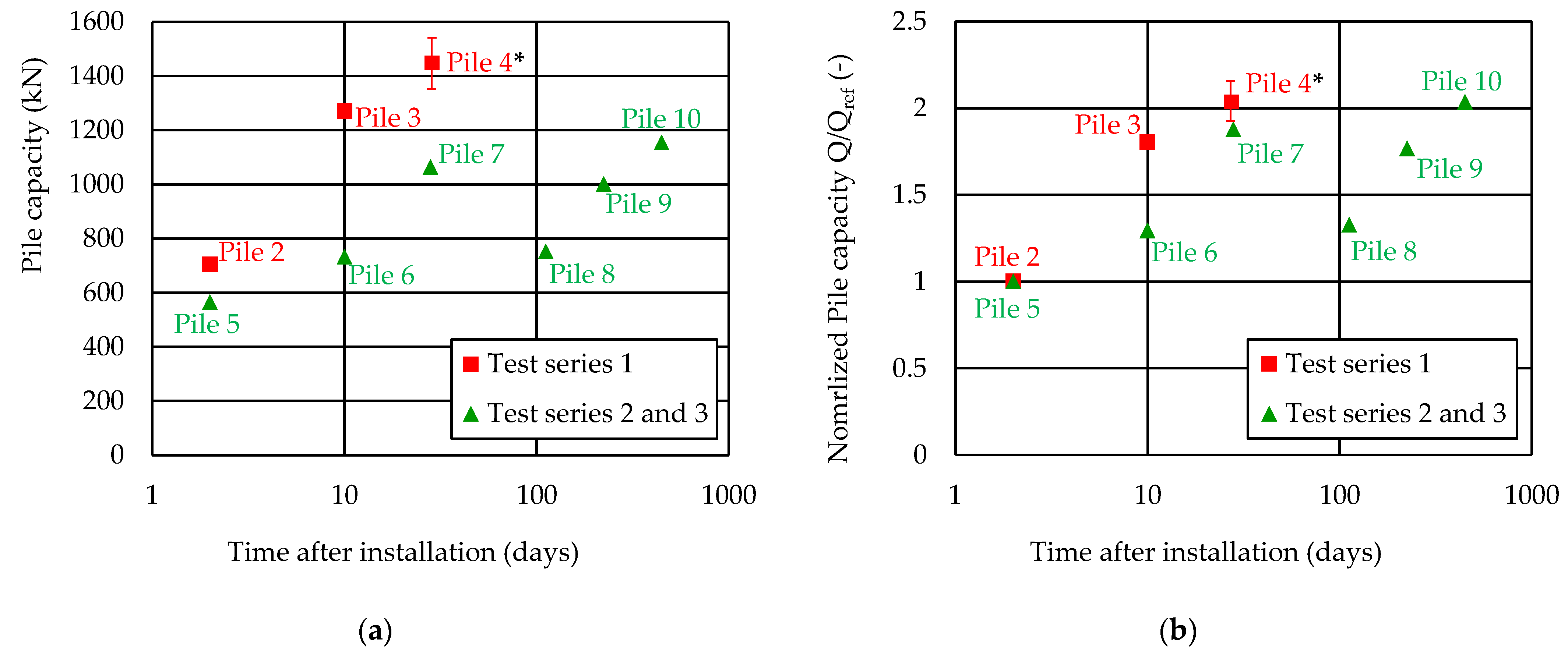
- The application of a regression line of type using all of the data shown in Figure 8 would correspond to an exponential decrease in the rate at which pile setup evolves with time. By this interpretation, pile 7 (28 days/weeks) is then a clear upward outlier, and pile 8 (16 weeks) is a corresponding downward outlier.
- Following the suggested second interpretation, the data of pile 7 have a more significant weight. Similar to the approach in [23], it is assumed that after a certain period of time, the rate at which pile ageing evolves with time comes to an almost complete standstill. From this point on, no further increase in the pile resistance was observed. Pile 8 (16 weeks) would still be a blatant downward outlier, whereas pile 10 (64 weeks) would be an upward outlier.
- Figure 9 shows a comparison of the test data from this study with test data from field tests reported in the literature [7,27,29]. All the tests involved steel pipe piles installed in sandy soils. All the pile load tests are first-time tests. Unlike the first-time compression tests performed in this study, all the other piles were tested under tension only. Again, the absolute pile capacities have been normalized to the initial pile capacity two days after installation. For the tests from the literature, the reference compressive resistance was determined by extrapolation.
- Design method according to Lüking published in the recommendations on piling (EAP) from the German Geotechnical Society [39];
- Imperial College pile design methods for driven piles in sands and clays (ICP) [40];
- University of Western Australia’s design method for open- and closed-ended driven piles in siliceous sand (UWA) [13];
- Unified CPT-based axial pile capacity design method for driven piles in sand (unified) [41].
3.3. Static Tension Pile Load Testing
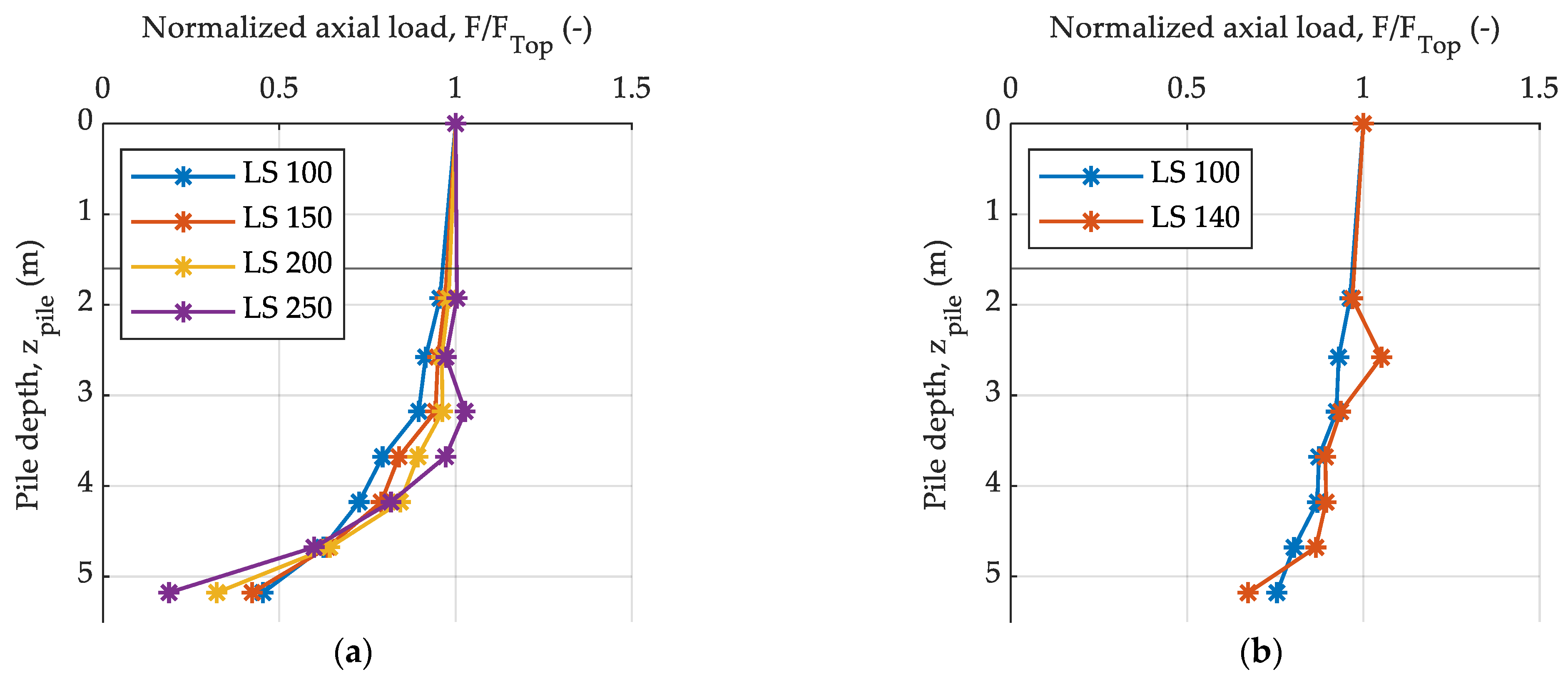
3.4. Macroscopic Analysis of Piles after Extraction
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lehane, B.M.; Jardine, R.J.; Bond, A.J.; Frank, R. Mechanisms of Shaft Friction in Sand from Instrumented Pile Tests. J. Geotech. Eng. 1993, 119, 19–35. [Google Scholar] [CrossRef]
- Altaee, A.; Evgin, E.; Fellenius, B.H. Axial load transfer for piles in sand. II. Numerical analysis. Can. Geotech. J. 1992, 29, 21–30. [Google Scholar] [CrossRef]
- Bullock, P.J.; Schmertmann, J.H.; McVay, M.C.; Townsend, F.C. Side Shear Setup. I: Test Piles Driven in Florida. J. Geotech. Geoenviron. Eng. 2005, 131, 292–300. [Google Scholar] [CrossRef]
- Bowman, E.T.; Soga, K. Mechanisms of setup of displacement piles in sand: Laboratory creep tests. Can. Geotech. J. 2005, 42, 1391–1407. [Google Scholar] [CrossRef]
- Åstedt, B.; Weiner, L.; Holm, G. Increase in bearing capacity with time for friction piles in silt and sand. In Proceedings of the Nordic Geotechnical Meeting, Lyngby, Denmark, 28–30 May 1992. [Google Scholar]
- Zhang, Z.; Wang, Y.H. Examining Setup Mechanisms of Driven Piles in Sand Using Laboratory Model Pile Tests. J. Geotech. Geoenviron. Eng. 2015, 141, 04014114. [Google Scholar] [CrossRef]
- Jardine, R.J.; Standing, J.R.; Chow, F.C. Some observations of the effects of time on the capacity of piles driven in sand. Géotechnique 2006, 56, 227–244. [Google Scholar] [CrossRef]
- Jardine, R.J.; Chow, F.C. Some Recent Developments In Offshore Pile Design. In Proceedings of the Offshore Site Investigation and Geotechnics Conference, London, UK, 11–13 September 2007. [Google Scholar]
- Paikowsky, S.G.; Whitman, R.V. The effects of plugging on pile performance and design. Can. Geotech. J. 1990, 27, 429–440. [Google Scholar] [CrossRef]
- Isemoto, N.; Kishida, H. Behavior of Sand Plugs in Open-End Steel Pipe Piles. In Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1977; pp. 601–604. [Google Scholar]
- Seo, H.; Kim, M. Soil plug behaviour of open-ended pipe piles during installation. DFI J. J. Deep. Found. Inst. 2017, 11, 128–136. [Google Scholar] [CrossRef]
- Lüking, J. Tragverhalten von offenen Verdrängungspfählen unter Berücksichtigung der Pfropfenbildung in nichtbindigen Böden. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2010. [Google Scholar]
- Lehane, B.M.; Schneider, J.A.; Xu, X. Development of the UWA-05 Design Method for Open and Closed Ended Driven Piles in Siliceous Sand. In Contemporary Issues in Deep Foundations; Laefer, D.F., Camp, W., Castelli, R., Paikowsky, S., Eds.; Geo-Denver: Denver, CO, USA, 2007; pp. 1–10. ISBN 978-0-7844-0902-2. [Google Scholar]
- Henke, S.; Grabe, J. Field measurements regarding the influence of the installation method on soil plugging in tubular piles. Acta Geotech. 2013, 8, 335–352. [Google Scholar] [CrossRef]
- Paik, K.-H.; Lee, S.-R. Behavior of soil plugs in open—Ended model piles driven into sands. Mar. Georesour. Geotechnol. 1993, 11, 353–373. [Google Scholar] [CrossRef]
- Brucy, F.; Meunier, J.; Nauroy, J.-F. Behaviour of a pile plug in sandy soils during and after driving. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1991; pp. 145–154. [Google Scholar]
- Henke, S. Untersuchungen zur Pfropfenbildung infolge der Installation Offener Profile in Granularen Böden. Habilitation; Technische Universität Hamburg-Harburg: Hamburg, Germany, 2013. [Google Scholar]
- Randolph, M.F.; Leong, E.C.; Houlsby, G.T. One-dimensional analysis of soil plugs in pipe piles. Géotechnique 1991, 41, 587–598. [Google Scholar] [CrossRef]
- Ko, J.; Jeong, S. Plugging effect of open-ended piles in sandy soil. Can. Geotech. J. 2015, 52, 535–547. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, X.B. Design and analyses of open-ended pipe piles in cohesionless soils. Int. J. Geo-Eng. 2016, 10, 22–29. [Google Scholar] [CrossRef]
- Liu, J.; Duan, N.; Cui, L.; Zhu, N. DEM investigation of installation responses of jacked open-ended piles. Acta Geotech. 2019, 14, 1805–1819. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Morikawa, Y.; Sato, T. Plugging mechanism of open-ended piles. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; pp. 1370–1373, ISBN 9781607505082. [Google Scholar]
- Karlsrud, K. Time Effects on Pile Capacity: Summary and Evaluation of Pile Test Results; Final report; Norwegian Geotechnical Institute: Oslo, Norway, 2013. [Google Scholar]
- Ng, K.W.; Roling, M.; AbdelSalam, S.S.; Suleiman, M.T.; Sritharan, S. Pile Setup in Cohesive Soil. I: Experimental Investigation. J. Geotech. Geoenviron. Eng. 2013, 139, 199–209. [Google Scholar] [CrossRef]
- Chow, F.; Jardine, R.J.; Brucy, F.; Nauroy, J. Effects of Time on Capacity of Pipe Piles in Dense Marine Sand. J. Geotech. Geoenviron. Eng. 1998, 124, 254–264. [Google Scholar] [CrossRef]
- Axelsson, G. Long-Term Set-Up of Driven Piles in Sand. Ph.D. Thesis, Kungliga Tekniska Högskolan, Stockholm, Schweden, 2000. [Google Scholar]
- Gavin, K.G.; Igoe, D.; Kirwan, L. The effect of ageing on the axial capacity of piles in sand. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 122–130. [Google Scholar] [CrossRef]
- Anusic, I.; Lehane, B.M.; Eiksund, G.R.; Liingaard, M.A. Evaluation of installation effects on set-up of field displacement piles in sand. Can. Geotech. J. 2019, 56, 461–472. [Google Scholar] [CrossRef]
- Bittar, E. Design and Optimization of Displacement Piles for Onshore and Offshore Application. Ph.D. Thesis, The University of Western Australia, Perth, Australia, 2022. [Google Scholar]
- Busch, A.V. Principles of the Axial Pile Setup. Ph.D. Thesis, University of Bremen, Bremen, Germany, 2022. [Google Scholar]
- Bhattacharya, S.; Carrington, T.; Aldridge, T. Observed increases in offshore pile driving resistance. Proc. Inst. Civ. Eng. Geotech. Eng. 2009, 162, 71–80. [Google Scholar] [CrossRef]
- Kirwan, L. Investigation into Ageing Mechanisms for Axially Loaded Piles Driven in Sand. Ph.D. Thesis, University College Dublin, Dublin, Ireland, 2015. [Google Scholar]
- Jessen, B.A.-M.; Cudmani, R.; Vogt, S. Creep and ageing of granular materials under isotropic pressure. Acta Geotech. 2024, 19, 1999–2012. [Google Scholar] [CrossRef]
- Levin, F.; Vogt, S.; Cudmani, R. Time-dependent behaviour of sand with different fine contents under oedometric loading. Can. Geotech. J. 2019, 56, 102–115. [Google Scholar] [CrossRef]
- Gavin, K.; Igoe, D. A Field Investigation into the Mechanisms of Pile Ageing in Sand. Géotechnique 2021, 71, 120–131. [Google Scholar] [CrossRef]
- Lehane, B.M.; Schneider, J.A.; Lim, J.K.; Mortara, G. Shaft Friction from Instrumented Displacement Piles in an Uncemented Calcareous Sand. J. Geotech. Geoenviron. Eng. 2012, 138, 1357–1368. [Google Scholar] [CrossRef]
- DIN 18126:2022-10; Baugrund, Untersuchung von Bodenproben—Bestimmung der Dichte Nicht Bindiger Böden bei Lockerster und Dichtester Lagerung. Beuth Verlag GmbH: Berlin, Germany, 2022.
- Liu, J.; Guo, Z.; Han, B. Load Transfer of Offshore Open-Ended Pipe Piles Considering the Effect of Soil Plugging. J. Mar. Sci. Eng. 2019, 7, 313. [Google Scholar] [CrossRef]
- Moormann, C.; Kempfert, H.-G. Jahresbericht 2014 des Arbeitskreises “Pfähle” der Deutschen Gesellschaft für Geotechnik (DGGT). Bautechnik 2014, 91, 922–932. [Google Scholar] [CrossRef]
- Jardine, R. ICP Design Methods for Driven Piles in Sands and Clays; Thomas Telford Ltd.: London, UK, 2005; ISBN 9780727732729. [Google Scholar]
- Lehane, B.M.; Liu, Z.; Bittar, E.; Nadim, F.; Lacasse, S.; Jardine, R.; Carotenuto, P.; Rattley, M.; Gavin, K.; Haavik, J. A New ‘Unified’ CPT-Based Axial Pile Capacity Design Method for Driven Piles in Sand. In Proceedings of the Fourth International Symposium on Frontiers in Offshore Geotechnics, Austin, TX, USA, 28–31 August 2022; Deep Foundations Institute, Ed.; Deep Foundations Institute: Hawthorne, NJ, USA, 2022; pp. 462–477. [Google Scholar]







| Test Series | Pile | Time after Pile Installation | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 Days | 10 Days | 4 Weeks | 16 Weeks | 32 Weeks | 48 Weeks | 64 Weeks | ||
| 1 | 1 * | SC | ST | |||||
| 1 * | DHS | |||||||
| 2 | SC | ST | ||||||
| 3 | SC | ST | ||||||
| 4 | SC ST | |||||||
| 2 | 5 | SC | ST | |||||
| 6 | SC | ST | ||||||
| 7 | SC | ST | ||||||
| 8 | SC ST | |||||||
| 3 | 9 | SC | ST | |||||
| 10 | SC ST | |||||||
| 11 | DHS | DHS | DHS | SC | ST | |||
| 12 | DHS | DHS | DHS | DHS | DHS | SC ST | ||
| Mean grain size | 0.40 mm | |
| Coefficient of uniformity | 2.45 | |
| 0.46) | 34.5° | |
| 0.97) | 37.8° | |
| Roundness of grains | 0.58 | |
| Particle sphericity | 0.78 | |
| Minimum void ratio | 0.477 | |
| Maximum void ratio | 0.738 | |
| Grain density | 2.63 g/cm3 |
| Total weight | 1875 kg |
| Height | 1835 mm |
| Piston weight | 390 kg |
| Maximum energy per blow | 5.89 kJ |
| Maximum number of blows | 175 blows/minute |
| Air pressure | 6–7 bar |
| Air consumption | 7 m3/min |
| Test Series | Pile | (m) | (m) | (-) |
|---|---|---|---|---|
| 1 | 1 | 4.34 | 4.24 | 0.98 |
| 2 | 4.34 | 4.19 | 0.97 | |
| 3 | 4.30 | 4.14 | 0.96 | |
| 4 | 4.31 | 4.17 | 0.97 | |
| 2 | 5 | 3.90 | 3.46 | 0.89 |
| 6 | 3.90 | 3.39 | 0.87 | |
| 7 | 3.90 | 3.64 | 0.93 | |
| 8 | 3.90 | 3.27 | 0.84 | |
| 3 | 9 | 3.88 | 3.72 | 0.96 |
| 10 | 3.90 | 3.74 | 0.96 | |
| 11 | 3.88 | 3.67 | 0.95 | |
| 12 | 3.89 | 3.69 | 0.95 |
| Test Series | |||||||
|---|---|---|---|---|---|---|---|
| (m2) | (m) | (-) | (-) | (-) | (m) | (-) | |
| 1 | 0.0717 | 4.3 | 0.68 | 0.568 | 0.477 | 4.15 | 0.96 |
| 2 | 3.9 | 0.65 | 0.567 | 3.74 | 0.96 | ||
| 3 | 3.9 | 0.66 | 0.566 | 3.75 | 0.96 |
| Dunkirk [7] | Blessington [27] | Shenton Park 168 [29] | Shenton Park 89 [29] | Shenton Park 450 [29] | Piles 2 and 3 | Piles 5–10 | |
|---|---|---|---|---|---|---|---|
| (kN) | 613 | 376 | 58 | 48 | 98 | 705 | 567 |
| (-) | 1.97 | 0.64 | 0.33 | 0.21 | 0.56 | 1.15 | 0.35 |
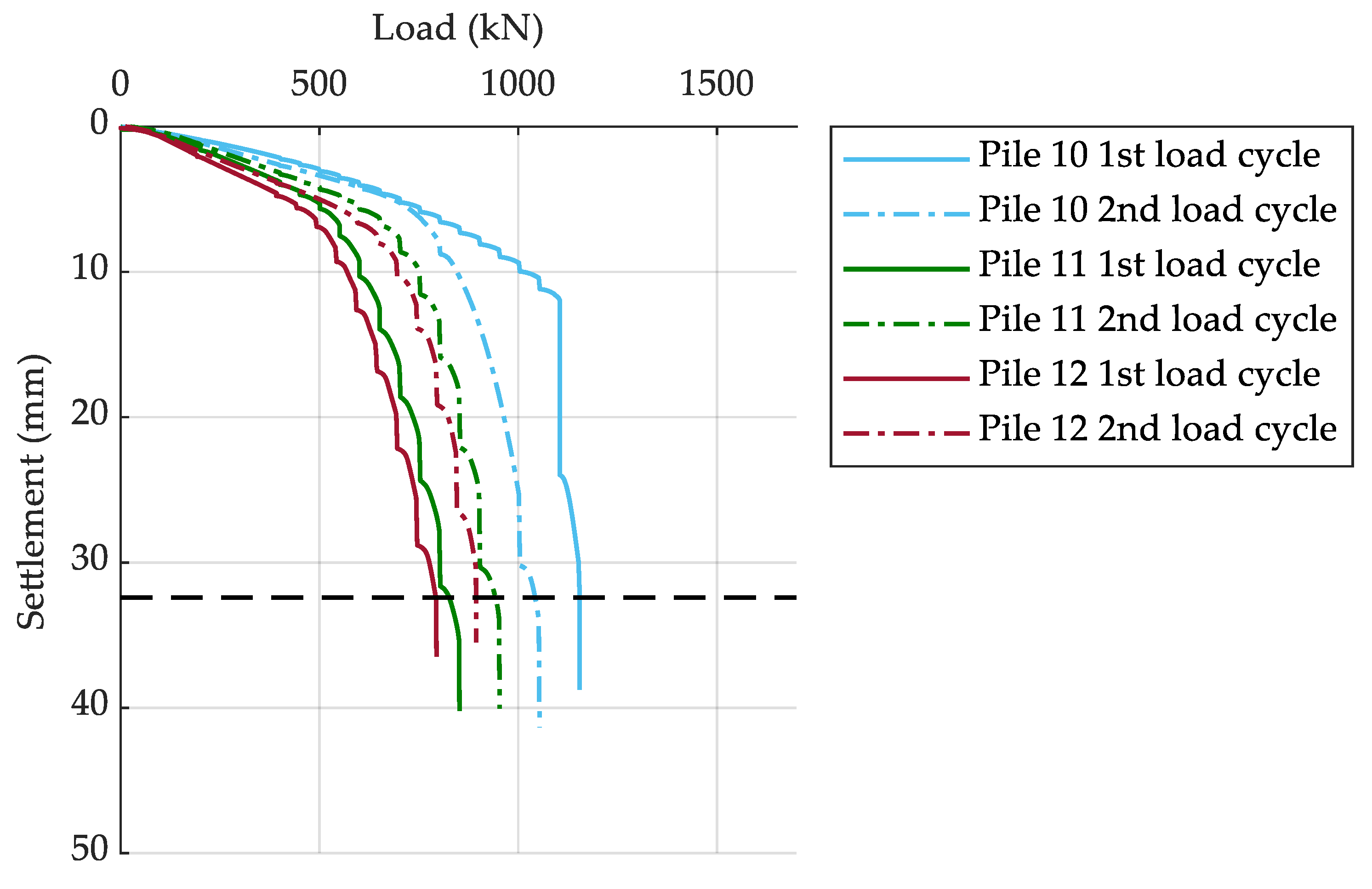
| Pile 5 (2 Days) | Pile 6 (10 Days) | Pile 7 (4 Weeks) | Pile 8 (16 Weeks) | Pile 9 (32 Weeks) | Pile 10 (64 Weeks) | |
|---|---|---|---|---|---|---|
| First load cycle | 567 kN | 734 kN | 1065 kN | 753 kN | 1003 kN | 1155 kN |
| Second load cycle | 642 kN | 694 kN | 992 kN | 753 kN | 938 kN | 1043 |
| Change | +13% | −5% | −7% | 0% | −6% | −10% |
| Pile | Time Since Installation (Days) | Time Since Static Compression Test (Days) | Compressive Resistance (kN) | Tensile Resistance (kN) | |
|---|---|---|---|---|---|
| 1 | 141 | 90 | 864 | 210 | 24% |
| 1 | 70 | - | - | 325 | - |
| 2 | 9 | 7 | 903 | 603 | 67% |
| 3 | 30 | 20 | 1273 | 594 | 47% |
| 4 | - | - | - | - | - |
| 5 | 116 | 114 | 567 | 243 | 43% |
| 6 | 116 | 106 | 734 | 248 | 34% |
| 7 | 114 | 86 | 1065 | 241 | 23% |
| 8 | 115 | 2 | 753 | 141 | 19% |
| 9 | 455 | 232 | 1003 | 231 | 23% |
| 10 | 455 | 1 | 1155 | 227 | 20% |
| 11 | 458 | 345 | 828 | 208 | 25% |
| 12 | 457 | 6 | 794 | 171 | 22% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manthey, S.; Vogt, S.; Cudmani, R.; Kidane, M. Experimental Study on the Time-Dependent Resistance of Open-Ended Steel Piles in Sand. Geotechnics 2024, 4, 985-1006. https://doi.org/10.3390/geotechnics4040050
Manthey S, Vogt S, Cudmani R, Kidane M. Experimental Study on the Time-Dependent Resistance of Open-Ended Steel Piles in Sand. Geotechnics. 2024; 4(4):985-1006. https://doi.org/10.3390/geotechnics4040050
Chicago/Turabian StyleManthey, Sven, Stefan Vogt, Roberto Cudmani, and Mussie Kidane. 2024. "Experimental Study on the Time-Dependent Resistance of Open-Ended Steel Piles in Sand" Geotechnics 4, no. 4: 985-1006. https://doi.org/10.3390/geotechnics4040050
APA StyleManthey, S., Vogt, S., Cudmani, R., & Kidane, M. (2024). Experimental Study on the Time-Dependent Resistance of Open-Ended Steel Piles in Sand. Geotechnics, 4(4), 985-1006. https://doi.org/10.3390/geotechnics4040050






