Non-Anatomical Identification and Compositional Profiling of Processed Wood Using ATR-FTIR and Chemometric Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Characterization of Wood Samples by Chemical Methods
2.3. Collection and Pre-Processing of Spectral Data
2.4. Multivariate Analysis Methods (Data Analysis, Discrimination, and Model Development)
3. Results
3.1. Characterization of Wood Samples
3.2. Principal Component Analysis on Chemical Data
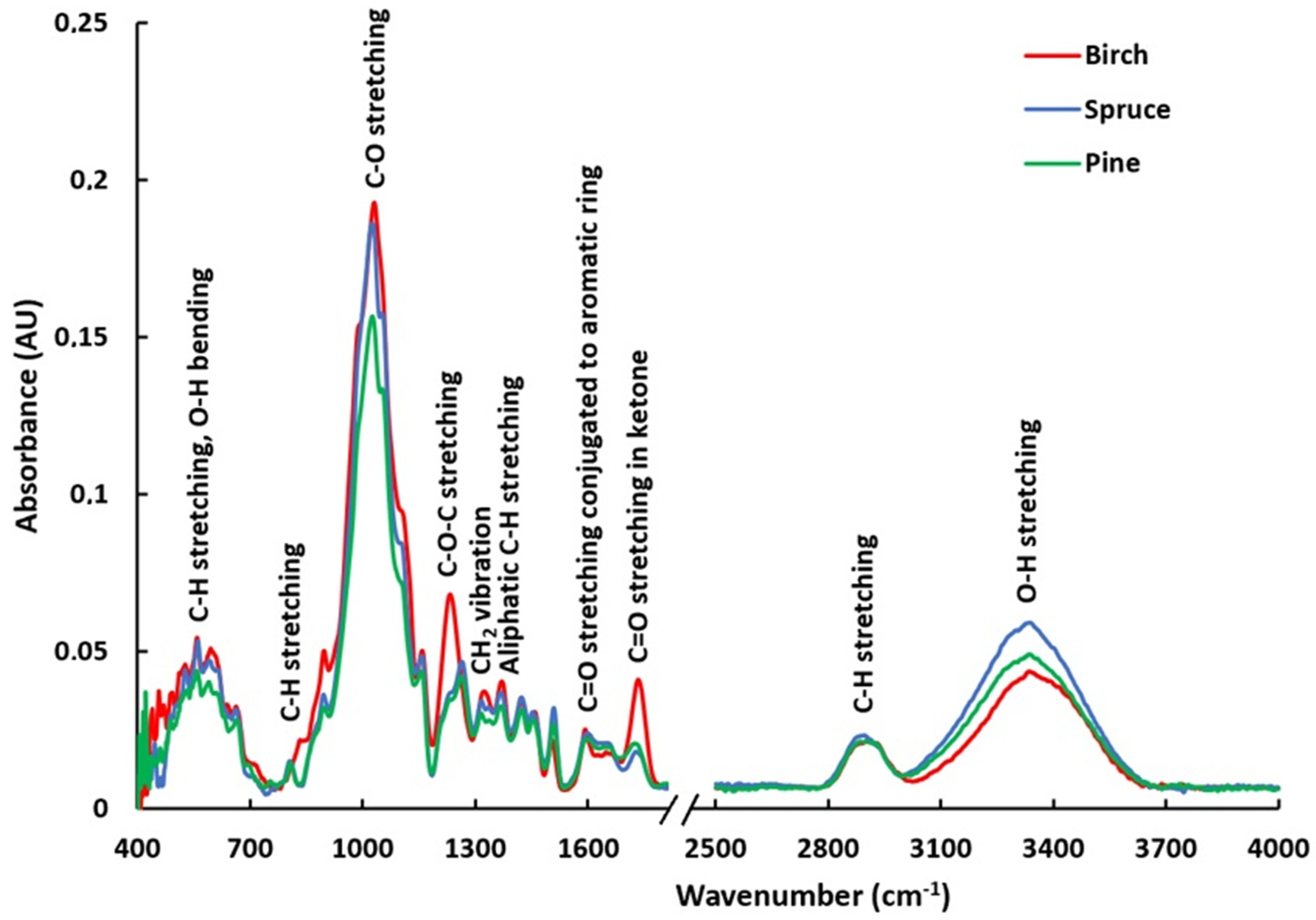
3.3. Characteristic Bands in the FTIR Absorption Spectra of Wood Samples
3.4. Principal Component Analysis on Spectral Data
3.5. PLS-DA Modeling Results
3.6. PLS Modeling Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PLS | Partial Least Squares |
| ATR-FTIR | Attenuated total reflection Fourier-transform infrared spectroscopy |
| Bi-PLS | Backward interval Partial Least Squares |
| RPD | Residual Predictive Deviation |
| PCA | Principal Component Analysis |
| PLS-DA | Partial Least Squares Discriminant Analysis |
| ASL | Acid-soluble lignin |
| TL | Total lignin |
| EA | Extractives |
References
- Sulis, D.B.; Lavoine, N.; Sederoff, H.; Jiang, X.; Marques, B.M.; Lan, K.; Cofre-Vega, C.; Barrangou, R.; Wang, J.P. Advances in lignocellulosic feedstocks for bioenergy and bioproducts. Nat. Commun. 2025, 16, 1244–1253. [Google Scholar] [CrossRef]
- Keskkonnaportaal. Metsamaa, sh Kaitsealuse Metsamaa Osakaal Eestis. Available online: https://keskkonnaportaal.ee/et/metsamaa-sh-kaitsealuse-metsamaa-osakaal-eestis (accessed on 10 September 2025).
- Zhou, N.; Thilakarathna, W.P.D.W.; He, Q.S.; Rupasinghe, H.P.V. A Review: Depolymerization of Lignin to Generate High-Value Bio-Products: Opportunities, Challenges, and Prospects. Front. Energy Res. 2022, 9, 2021–2027. [Google Scholar] [CrossRef]
- Ruffinatto, F.; Crivellaro, A.; Wiedenhoeft, A.C. Review of Macroscopic Features for Hardwood and Softwood Identification and a Proposal for a New Character List. IAWA J. 2015, 36, 208–241. [Google Scholar] [CrossRef]
- Sharma, V.; Yadav, J.; Kumar, R.; Tesarova, D.; Ekielski, A.; Mishra, P.K. On the rapid and non-destructive approach for wood identification using ATR-FTIR spectroscopy and chemometric methods. Vib. Spectrosc. 2020, 110, 103097. [Google Scholar] [CrossRef]
- Miaw, C.S.W.; Assis, C.; Silva, A.R.C.S.; Cunha, M.L.; Sena, M.M.; de Souza, S.V.C. Determination of main fruits in adulterated nectars by ATR-FTIR spectroscopy combined with multivariate calibration and variable selection methods. Food Chem. 2018, 254, 272–280. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Jin, S.; Bao, C.; Sun, Y.; Li, W. Rapid determination of lignocellulose in corn stover based on near-infrared reflectance spectroscopy and chemometrics methods. Bioresour. Technol. 2021, 321, 124449. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.N.; Ferdous, T.; Islam, Z.; Jahan, M.S.; Quaiyyum, M. Development of chemometric model for characterization of non-wood by FT-NIR data. J. Bioresour. Bioprod. 2020, 5, 196–203. [Google Scholar] [CrossRef]
- Pastore, T.C.M.; Braga, J.W.B.; Coradin, V.T.R.; Magalhães, W.L.E.; Okino, E.Y.A.; Camargos, J.A.A.; Muñiz, G.I.B.D.; Bressan, O.A.; Davrieux, F. Near infrared spectroscopy (NIRS) as a potential tool for monitoring trade of similar woods: Discrimination of true mahogany, cedar, andiroba, and curupixá. Holzforschung 2011, 65, 73–80. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Z.-G. Application of genetic simulated annealing algorithm in detection of corn straw cellulose. Chin. J. Anal. Chem. 2019, 47, 1987–1994. [Google Scholar]
- Alves, A.; Santos, A.; da Silva Perez, D.; Rodrigues, J.; Pereira, H.; Simões, R.; Schwanninger, M. NIR PLSR model selection for Kappa number prediction of maritime pine Kraft pulps. Wood Sci. Technol. 2007, 41, 491–499. [Google Scholar] [CrossRef]
- Kothiyal, V.; Jaideep; Bhandari, S.; Ginwal, H.S.; Gupta, S. Multi-species NIR calibration for estimating holocellulose in plantation timber. Wood Sci. Technol. 2015, 49, 769–793. [Google Scholar] [CrossRef]
- Fišerová, M.; Gigac, J.; Russ, A.; Maholányiová, M. Using niranalysis for determination of hardwood kraft pulp properties. Wood Res. 2012, 57, 121–130. [Google Scholar]
- Poke, F.S.; Raymond, C.A. Predicting Extractives, Lignin, and Cellulose Contents Using Near Infrared Spectroscopy on Solid Wood in Eucalyptus globulus. J. Wood Chem. Technol. 2006, 26, 187–199. [Google Scholar] [CrossRef]
- Herrera, R.; Hermoso, E.; Labidi, J.; Fernandez-Golfin, J.I. Non-destructive determination of core-transition-outer wood of Pinus nigra combining FTIR spectroscopy and prediction models. Microchem. J. 2022, 179, 107532. [Google Scholar] [CrossRef]
- Toscano, G.; Maceratesi, V.; Leoni, E.; Stipa, P.; Laudadio, E.; Sabbatini, S. FTIR spectroscopy for determination of the raw materials used in wood pellet production. Fuel 2022, 313, 123017. [Google Scholar] [CrossRef]
- Müller, G.; Schöpper, C.; Vos, H.; Kharazipour, A.; Polle, A. FTIR-ATR spectroscopic analyses of changes in wood properties during particleand fibreboard production of hardand softwood trees. BioResources 2009, 4, 49–71. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, W.; Via, B.K.; Fasina, O.; Han, G. Prediction of mixed hardwood lignin and carbohydrate content using ATR-FTIR and FT-NIR. Carbohydr. Polym. 2015, 121, 336–341. [Google Scholar] [CrossRef]
- Chen, H.; Ferrari, C.; Angiuli, M.; Yao, J.; Raspi, C.; Bramanti, E. Qualitative and quantitative analysis of wood samples by Fourier transform infrared spectroscopy and multivariate analysis. Carbohydr. Polym. 2010, 82, 772–778. [Google Scholar] [CrossRef]
- Schultz, T.; Burns, D. Rapid secondary analysis of lignocellulose: Comparison of near infrared (NIR) and Fourier transform infrared (FTIR). Tappi J. 1990, 73, 209–212. [Google Scholar]
- Andersen, C.M.; Bro, R. Variable selection in regression—A tutorial. J. Chemom. 2010, 24, 728–737. [Google Scholar] [CrossRef]
- Norgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval partial least-squares regression (iPLS): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- EN ISO 3884:2025; Solid Recovered Fuels—Methods for the Determination of the Content of Elements (Al, Ca, Fe, K, Mg, Na, P, S, Si, Ti, As, Ba, Be, Cd, Co, Cr, Cu, Hg, Mo, Mn, Ni, Pb, Sb, Se, Sn, Tl, V, Zn). European Comitee for Standardization: Brussels, Belgium, 2025.
- EN ISO 21663:2020; Solid Recovered Fuels—Methods for the Determination of Carbon (C), Hydrogen (H), Nitrogen (N) and Sulphur (S) by the Instrumental Method. European Comitee for Standardization: Brussels, Belgium, 2020.
- ASTM D1107-96; Standard Test Method for Ethanol-Toluene Solubility of Wood. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D1106-21; Standard Test Method for Acid-Insoluble Lignin in Wood. ASTM International: West Conshohocken, PA, USA, 2024.
- NREL/TP-510-42618; Determination of Structural Carbohydrates and Lignin in Biomass. U.S. Department of Energy: Denver, CO, USA, 2012.
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Brereton, R.G. Chemometrics: Data Analysis for the Laboratory and Chemical Plant; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Leardi, R.; Nørgaard, L. Sequential application of backward interval partial least squares and genetic algorithms for the selection of relevant spectral regions. J. Chemom. 2004, 18, 486–497. [Google Scholar] [CrossRef]
- Fernández Pierna, J.A.; Abbas, O.; Baeten, V.; Dardenne, P. A Backward Variable Selection method for PLS regression (BVSPLS). Anal. Chim. Acta 2009, 642, 89–93. [Google Scholar] [CrossRef]
- Napa, Ü.; Ostonen, I.; Kabral, N.; Kriiska, K.; Frey, J. Biogenic and contaminant heavy metal pollution in Estonian coniferous forests. Reg. Environ. Change 2017, 17, 2111–2120. [Google Scholar] [CrossRef]
- Ots, K.; Mandre, M. Monitoring of heavy metals uptake and allocation in Pinus sylvestris organs in alkalised soil. Environ. Monit. Assess. 2012, 184, 4105–4117. [Google Scholar] [CrossRef]
- Michopoulos, P.; Bourletsikas, A.; Kaoukis, K.; Daskalakou, E.; Karetsos, G.; Kostakis, M.; Thomaidis, N.; Pasias, I.; Kaberi, H.; Iliakis, S. The distribution and variability of heavy metals in a mountainous fir forest ecosystem in two hydrological years. Glob. NEST J. 2018, 20, 188–197. [Google Scholar]
- Korca, B.; Jusufi, K.; Citaku, V.; Kuka, X. Determination of heavy metals in wooden trees and ash residues in Kosovo. Appl. Ecol. Environ. Res. 2019, 17, 2931–2941. [Google Scholar] [CrossRef]
- Yasuda, S.; Fukushima, K.; Kakehi, A. Formation and chemical structures of acid-soluble lignin I: Sulfuric acid treatment time and acid-soluble lignin content of hardwood. J. Wood Sci. 2001, 47, 69–72. [Google Scholar] [CrossRef]
- Imamura, H. Contribution of Extractives to Wood Characteristics. In Natural Products of Woody Plants: Chemicals Extraneous to the Lignocellulosic Cell Wall; Rowe, J.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 843–860. [Google Scholar]
- Roffael, E. Significance of wood extractives for wood bonding. Appl. Microbiol. Biotechnol. 2016, 100, 1589–1596. [Google Scholar] [CrossRef]
- Rowell, R.M. (Ed.) Handbook of Wood Chemistry and Wood Composites; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Evans, P. Differentiating “hard” from “soft” woods using Fourier transform infrared and Fourier transform spectroscopy. Spectrochim. Acta Part A Mol. Spectrosc. 1991, 47, 1441–1447. [Google Scholar] [CrossRef]
- Yang, H.; Bao, L.; Liu, Y.; Luo, S.; Zhao, F.; Chen, G.; Liu, F. Identification and quantitative analysis of salt-adulterated honeysuckle using infrared spectroscopy coupled with multi-chemometrics. Microchem. J. 2021, 171, 106829. [Google Scholar] [CrossRef]
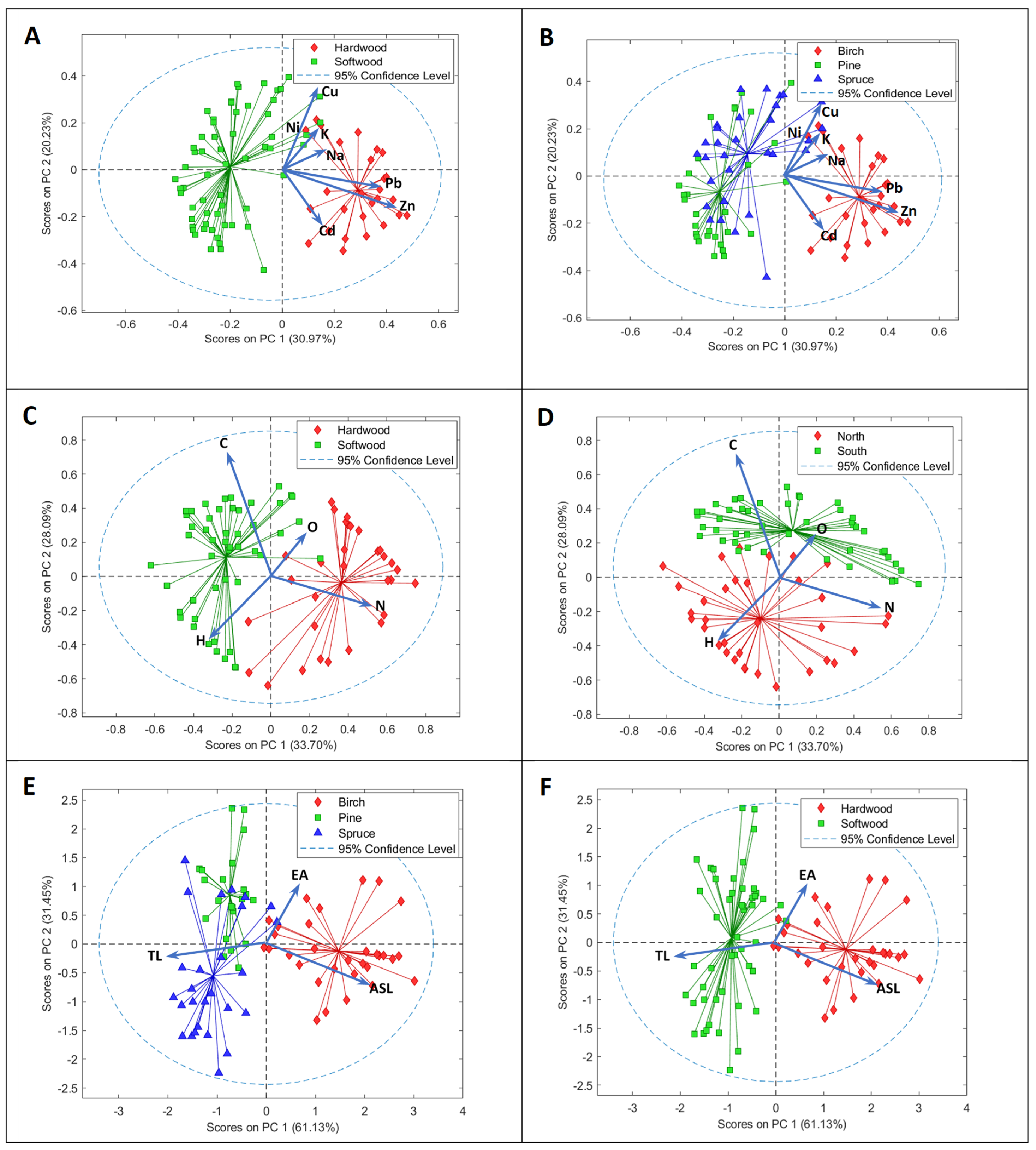
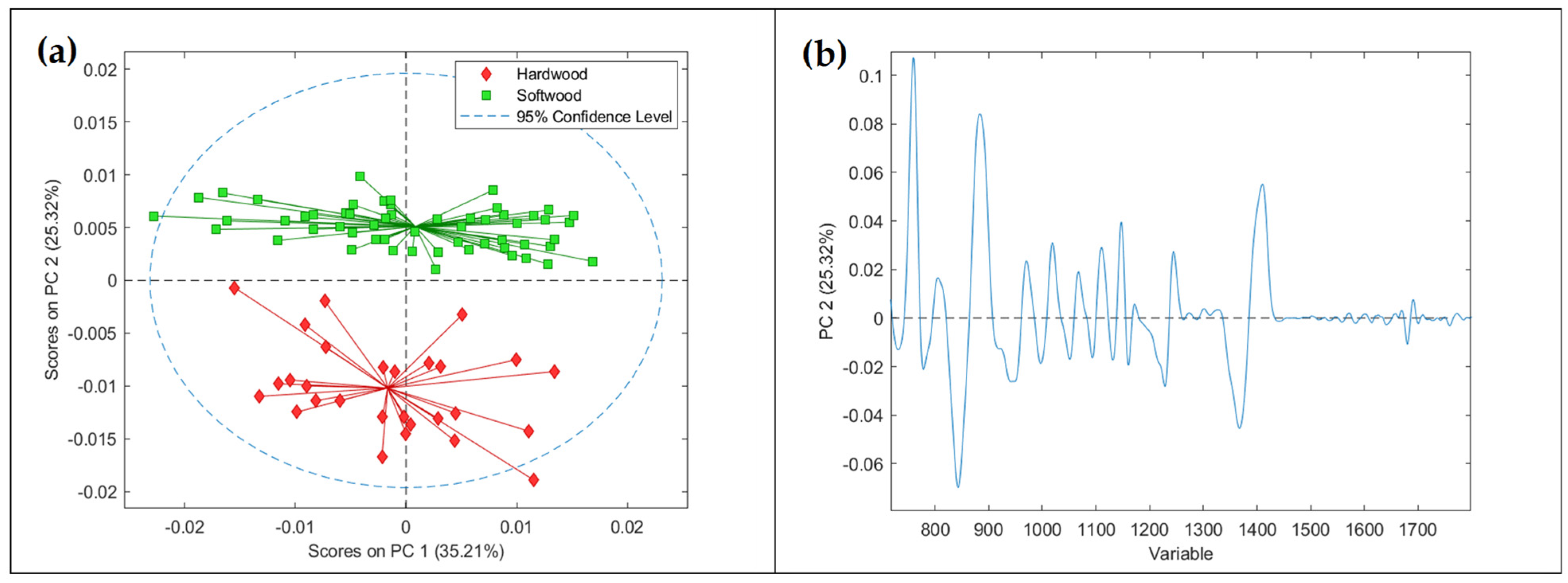

| Class | Sub-Class | Number of Samples |
|---|---|---|
| Wood species | Birch | 32 |
| Pine | 30 | |
| Spruce | 30 | |
| Wood type | Hardwood | 32 |
| Softwood | 60 | |
| Place of growth | Northern Estonia | 45 |
| Southern Estonia | 47 |
| Birch | Pine | Spruce | ||||
|---|---|---|---|---|---|---|
| Average ± SD (n = 32) | Range (Min–Max) | Average ± SD (n = 30) | Range (Min–Max) | Average ± SD (n = 30) | Range (Min–Max) | |
| Zn, mg/kg | 22.5 ± 10.7 | 9.0–44 | 5.1 ± 2.4 | 3.0–12 | 6.8 ± 4.1 | 3.0–21.3 |
| Na, mg/kg | 4.6 ± 2.5 | 2.9–12.2 | 3.2 ± 1.0 | 3.0–8.2 | 3.3 ± 0.9 | 3.0–7.5 |
| K, mg/kg | 349 ± 140 | 182–777 | 225 ± 118 | 109–504 | 456 ± 458 | 158–1760 |
| Cu, mg/kg | 0.88 ± 0.22 | 0.44–1.39 | 0.79 ± 0.35 | 0.34–2.11 | 0.94 ± 0.30 | 0.45–1.73 |
| Pb, mg/kg | 0.69 ± 0.46 | 0.19–2.20 | 0.07 ± 0.02 | 0.05–0.28 | 0.22 ± 0.14 | 0.05–0.58 |
| Cd, mg/kg | 0.08 ± 0.04 | 0.02–0.19 | 0.07 ± 0.04 | 0.01–0.16 | 0.05 ± 0.03 | 0.003–0.15 |
| Ni, mg/kg | 0.05 ± 0.02 | 0.02–0.11 | 0.07 ± 0.03 | 0.04–0.35 | 0.07 ± 0.06 | 0.02–0.28 |
| C %dw | 47.7 ± 1.7 | 43.2–49.2 | 49.6 ± 2.7 | 42.3–52.6 | 48.1 ± 3.3 | 37.4–50.4 |
| H %dw | 6.5 ± 0.3 | 5.5–6.8 | 6.7 ± 0.3 | 6.0–7.1 | 6.5 ± 0.3 | 5.6–6.9 |
| N %dw | 0.10 ± 0.02 | 0.1–0.2 | 0.07 ± 0.02 | 0.03–0.13 | 0.06 ± 0.02 | 0.04–0.12 |
| O %dw | 46.8 ± 0.8 | 44.9–48.3 | 44.7 ± 1.6 | 40.4–46.9 | 45.9 ± 2.1 | 39.0–48.3 |
| ASL %dw | 2.3 ± 0.7 | 1.3–3.6 | 0.45 ± 0.11 | 0.33–0.67 | 0.40 ± 0.10 | 0.32–0.60 |
| TL %dw | 26.1 ± 2.4 | 21.1–30.5 | 32.1 ± 2.2 | 28.5–36.4 | 31.0 ± 2.2 | 26.4–35.7 |
| EA %dw | 3.5 ± 0.8 | 2.1–5.0 | 6.1 ± 2.9 | 2.8–11.5 | 2.0 ± 0.7 | 0.9–4.0 |
| Wavenumber, cm−1 | Band Assignments |
|---|---|
| 3335 | OH stretching in hydroxyl, hydrogen bonding |
| 2927 | CH stretching in methyl and methylene groups |
| 1735–1725 | C=O stretching in unconjugated ketone, carbonyl, and aliphatic groups of xylan |
| 1640 | C=O stretching conjugated to aromatic ring |
| 1592 | Aromatic skeletal vibration typical for S units plus C=O stretch |
| 1508–1503 | C=C stretching in the aromatic ring |
| 1457 | CH2 deformation stretching |
| 1421 | Aromatic skeletal combined with C–H in-plane deforming and stretching |
| 1370 | Aliphatic CH stretching in methyl group and phenol |
| 1323 | Condensation of guaiacyl and syringyl units, CH2 bending stretching |
| 1232 | C-O-C stretching of phenol-ether bond in lignin |
| 1158 | C-O-C stretching in pyranose rings, C=O stretching in aliphatic groups |
| 1030 | C=O deformation in alcohols, C-O stretch conjugation |
| 895 | C-H stretching out of plane of aromatic ring |
| 595 | C-H stretching, O-H bending |
| Data | Cap. Var. % | Modeled Class | Sensitivity (cal)/(pred) | Specificity (cal)/(pred) | Class Error * (cal)/(pred) | RMSEC | RMSECV | RMSEP |
|---|---|---|---|---|---|---|---|---|
| FTIR, 3 LVs | 66.5 | Hardwood | 1.0/1.0 | 1.0/1.0 | 0/0 | 0.04 | 0.05 | 0.04 |
| Softwood | 1.0/1.0 | 1.0/1.0 | 0/0 | 0.04 | 0.05 | 0.04 | ||
| FTIR, 3 LVs | 62.7 | Birch | 1.0/1.0 | 1.0/1.0 | 0/0 | 0.05 | 0.06 | 0.06 |
| Pine | 0.90/0.50 | 0.93/0.57 | 0.08/0.46 | 0.30 | 0.44 | 0.50 | ||
| Spruce | 1.0/0.70 | 0.93/0.71 | 0.04/0.29 | 0.29 | 0.44 | 0.48 | ||
| Organic elements, 3 LVs | 76.9 | Hardwood | 1.0/0.88 | 0.96/1.0 | 0.02/0.06 | 0.26 | 0.27 | 0.28 |
| Softwood | 0.96/1.0 | 1.0/0.88 | 0.02/0.06 | 0.26 | 0.27 | 0.28 | ||
| Organic elements, 3 LVs | 77.6 | North | 0.98/1.0 | 0.97/1.0 | 0.03/0.0 | 0.23 | 0.25 | 0.25 |
| South | 0.98/1.0 | 0.97/1.0 | 0.03/0.0 | 0.23 | 0.25 | 0.25 | ||
| Metals, 4 LVs | 72.7 | Hardwood | 0.86/0.91 | 0.93/1.0 | 0.11/0.04 | 0.24 | 0.26 | 0.25 |
| Softwood | 0.93/1.0 | 0.86/0.91 | 0.11/0.04 | 0.24 | 0.26 | 0.25 | ||
| Metals, 4 LVs (split Onion) | 73.3 | Birch | 0.91/0.91 | 0.95/0.91 | 0.07/0.09 | 0.23 | 0.25 | 0.25 |
| Pine | 0.85/0.90 | 0.81/0.67 | 0.17/0.21 | 0.34 | 0.38 | 0.37 | ||
| Spruce | 0.80/0.60 | 0.71/0.86 | 0.24/0.27 | 0.39 | 0.44 | 0.38 | ||
| Biocomposition, 3 LVs | 100 | Hardwood | 1.0/1.0 | 1.0/1.0 | 0/0 | 0.11 | 0.12 | 0.27 |
| Softwood | 1.0/1.0 | 1.0/1.0 | 0/0 | 0.11 | 0.12 | 0.27 | ||
| Biocomposition, 3 LVs | 100 | Birch | 1.0/1.0 | 1.0/1.0 | 0/0.0 | 0.11 | 0.11 | 0.29 |
| Pine | 0.98/0.50 | 0.83/0.78 | 0.04/0.25 | 0.24 | 0.26 | 0.46 | ||
| Spruce | 0.90/0.90 | 0.75/0.72 | 0.07/0.50 | 0.30 | 0.31 | 0.57 |
| Parameter | Model | NLV | Interval (Variables) | R2cal | RMSEC | RMSECV | R2pred | RMSEP | RPD |
|---|---|---|---|---|---|---|---|---|---|
| Klason lignin | Full PLS | 5 | [1:3734] | 0.94 | 0.83 | 1.35 | 0.85 | 0.97 | 2.58 |
| BiPLS | 6 | [1:100 301:500 601:800 901:1000 1101:1400 2101:2200 2401:2800 3001:3100 3201:3500 3601:3734] | 0.94 | 0.98 | 1.19 | 0.87 | 0.88 | 2.78 | |
| Acid- soluble lignin | Full PLS | 7 | [1:3734] | 0.98 | 0.15 | 0.24 | 0.84 | 0.32 | 2.50 |
| BiPLS | 7 | [1:100 401:500 701:800 1001:1100 1201:1300 1701:1800 2401:2500 3101:3200 3301:3400 3701:3734] | 0.99 | 0.14 | 0.29 | 0.86 | 0.30 | 2.67 | |
| Extractives | Full PLS | 6 | [1:3734] | 0.99 | 0.17 | 1.51 | 0.80 | 0.98 | 2.24 |
| BiPLS | 7 | [301:400 901:1400 2201:2300 2401:2500 2601:2700 3701:3734] | 0.99 | 0.19 | 0.71 | 0.85 | 0.65 | 2.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salm, O.-S.; Kers, J.; Kulp, M. Non-Anatomical Identification and Compositional Profiling of Processed Wood Using ATR-FTIR and Chemometric Modeling. Analytica 2025, 6, 46. https://doi.org/10.3390/analytica6040046
Salm O-S, Kers J, Kulp M. Non-Anatomical Identification and Compositional Profiling of Processed Wood Using ATR-FTIR and Chemometric Modeling. Analytica. 2025; 6(4):46. https://doi.org/10.3390/analytica6040046
Chicago/Turabian StyleSalm, Olivia-Stella, Jaan Kers, and Maria Kulp. 2025. "Non-Anatomical Identification and Compositional Profiling of Processed Wood Using ATR-FTIR and Chemometric Modeling" Analytica 6, no. 4: 46. https://doi.org/10.3390/analytica6040046
APA StyleSalm, O.-S., Kers, J., & Kulp, M. (2025). Non-Anatomical Identification and Compositional Profiling of Processed Wood Using ATR-FTIR and Chemometric Modeling. Analytica, 6(4), 46. https://doi.org/10.3390/analytica6040046






