A Dyson Brownian Motion Model for Weak Measurements in Chaotic Quantum Systems

Abstract

We consider a toy model for the study of monitored dynamics in many-body quantum systems. We study the stochastic Schrödinger equation resulting from continuous monitoring with a rate $\Gamma$ of a random Hermitian operator, drawn from the Gaussian unitary ensemble (GUE) at every time t. Due to invariance by unitary transformations, the dynamics of the eigenvalues ${\left\{{\lambda }_{\alpha }\right\}}_{\alpha =1}^n$ of the density matrix decouples from that of the eigenvectors, and is exactly described by stochastic equations that we derive. We consider two regimes: in the presence of an extra dephasing term, which can be generated by imperfect quantum measurements, the density matrix has a stationary distribution, and we show that in the limit of large size $n\to \infty$ it matches with the inverse-Marchenko–Pastur distribution. In the case of perfect measurements, instead, purification eventually occurs and we focus on finite-time dynamics. In this case, remarkably, we find an exact solution for the joint probability distribution of $\lambda$’s at each time t and for each size n. Two relevant regimes emerge: at short times $t\Gamma =O\left(1\right)$, the spectrum is in a Coulomb gas regime, with a well-defined continuous spectral distribution in the $n\to \infty$ limit. In that case, all moments of the density matrix become self-averaging and it is possible to exactly characterize the entanglement spectrum. In the limit of large times $t\Gamma =O\left(n\right)$, one enters instead a regime in which the eigenvalues are exponentially separated $\log ({\lambda }_{\alpha }/{\lambda }_{\beta })=O(\Gamma t/n)$, but fluctuations $\sim O\left(\sqrt{\Gamma t/n}\right)$ play an essential role. We are still able to characterize the asymptotic behaviors of the entanglement entropy in this regime.

1. Introduction

In recent years, the study of quantum many-body systems in the presence of continuous monitoring of its local degrees of freedom has received much attention. The motivations for this case are of various kinds: first, from a practical point of view, the combinations of measurements and quantum gates are essential ingredients of quantum computation [1,2]. In addition to this fact, recent studies have shown that quantum measurements (both projective and weak) can induce peculiar phase transitions, denominated measurement-induced phase transitions (MIPTs) [3,4,5], which arise exclusively by looking at the statistics of trajectories via nonlinear observables [6,7,8,9]. Prime examples are transitions in entanglement dynamics [3,4,5] or purification time [10] induced by increasing the strength of the measurements (e.g., the probability with which each site is measured in the case of projective measurements or the rate of measurements in the case of weak measurements). In this case, it was found that going from weak to strong measurements, one can move from a volume-law entangled phase [11,12,13] to an area-law one [14,15,16,17,18]. Results along these lines were initially obtained by using random circuits [19], in which quantum evolution occurs through unitary gates chosen from a uniform distribution (Haar) possibly within an appropriate subset of the unitary group. Then, in the limit of a large local Hilbert space dimension, it has been shown that a phase transition is present, and the corresponding critical point lies in the directed percolation universality class. However, it has been clarified that this simplification is not accurate in general [20]: the critical point is described by a peculiar conformal (scale invariant) theory not exactly solvable in general [21,22,23]. Following these results, much theoretical [24,25] and numerical [26,27,28,29] work has been devoted to thoroughly characterizing MIPTs by linking them to various other phenomena, such as quantum error correction [30], purification [31,32,33], state preparation, quantum communication [34], and the complexity of classical simulation of quantum systems [35,36]. Recent results have attempted to study this phenomenology in simplified toy models [37,38]. However, in the case of noninteracting systems (e.g., free fermions), it has been shown that the transition has a radically different nature: the volume-law phase is immediately unstable for arbitrarily weak quantum measurements [39,40,41,42,43,44,45], and yet, in some cases, a subvolume phase can survive before the onset of the area-law phase [46,47,48,49,50], with a universality class more akin to problems of Anderson localization and disordered conductors, studied in the context of nonlinear sigma models [51,52]. In the interacting case, one of the main difficulties in studying individual trajectories of monitored systems lies in the fact that the probability of each trajectory depends on the state itself, in accordance with Born’s rule. This aspect produces an inevitable nonlinearity when considering statistical averages over measurement outcomes, similar to that faced in disordered systems. In analogy to that approach, it is possible to proceed through the replica trick, thus studying N identical copies of the system and eventually considering the relevant $N\to 1$ limit (in contrast with the more common $N\to 0$ limit relevant in disordered systems [53,54]). The fundamental ingredient for the replica limit is the possibility of performing an analytic continuation in N by means of an exact formula. Some studies avoid this problem by replacing the $N\to 1$ limit with the simpler and more explicit $N=2$ case, where in fact two copies are considered. Alternatively, recent results have been obtained using mean-field models [55,56,57,58], where analytical progress can be achieved. In particular, in [59], a discrete fully connected model was introduced in which the dynamics in the presence of measurements can be mapped onto a variant of branching Brownian motion and then studied in terms of the Fisher and Kolmogorov–Petrovsky–Piskunov reaction-diffusion Equation [60,61,62]. However, the nature of these results in more general problems is not completely clear. More recently, a model of spin in the presence of noise and weak measurements has been introduced in which it is possible to study the dynamics in the presence of measurements analytically and in particular explicitly consider the $N\to 1$ limit [63]: this showed that the replica limit can be highly nontrivial, with a MIPT present for any integer $N>1$, but disappearing in the $N\to 1$ limit.

Beyond the study of the transition, it becomes interesting to characterize the specific behavior of the two phases. In particular, the volume-law phase is hard to simulate from the classical point of view because of the strong presence of entanglement surviving very long times. In this paper, we focus on the characterization of the dynamics in the presence of weak measurements far from the critical point, within the volume-law phase. To do so, we introduce a model of the evolution of the density matrix of the system purely based on random matrices, akin to the one considered in Ref. [64]. We choose a dynamics based on the stochastic Schrödinger Equation [65], invariant under unitary rotations in the n-dimensional Hilbert space, such that the dynamics of the eigenvalues of the density matrix decouples from that of the eigenvectors, as is the case in Dyson Brownian motion (DBM). In this way, unitary dynamics becomes inessential since it does not affect the eigenvalues. Once we have derived a stochastic equation for the evolution of the eigenvalues, we study two relevant limits of it: in the first case, we consider dynamics induced by “imperfect” measurements, i.e., a case in which a fraction of the measurement results is unknown. This is effectively equivalent to introducing a dephasing term that on each trajectory tends to bring the density matrix closer to the identity. In this case, we prove the existence of a steady state that describes the distribution of the eigenvalues: at large n, the resulting ensemble is described by an inverse-Wishart matrix. Next, we explore the dynamics for perfect measures: in this case, the steady state at long times reduces trivially to a pure random state uniformly distributed in the steady state; however, this happens with a characteristic transient at small and intermediate times. We present the exact solution for the joint distribution of eigenvalues at all times and analyze its effects on the entanglement entropy.

2. Preliminaries on Unravelings and Trajectories

The combined dynamics of a quantum system undergoing both unitary evolution and measurements can always be modeled as a quantum channel [66], whose output contains both the state of the quantum system and the classical encoding of the results of the measurements. According to Choi’s theorem [67], a quantum channel $\mathsf{\Phi }\left(\rho \right)$ can always be expressed in terms of a set of Kraus operators ${\left\{{\mathcal{K}}_{\mathbf{a}}\right\}}_{\mathbf{a}}$, first discussed in Ref. [68]. Those provide an explicit operator-sum decomposition of the quantum channel as $\mathsf{\Phi }\left(\rho \right)={\sum }_{\mathbf{a}}{\mathcal{K}}_{\mathbf{a}}\rho {\mathcal{K}}_{\mathbf{a}}^{†}$, and describe the dynamics by means of linear maps from the system’s Hilbert space to itself. Because of trace-norm conservation, Kraus operators satisfy the condition ${\sum }_{\mathbf{a}}{\mathcal{K}}_{\mathbf{a}}^{†}{\mathcal{K}}_{\mathbf{a}}=\mathbb{1}$, with $\mathbb{1}$ the identity operator in the Hilbert space of the quantum system. However, the specific decomposition of $\mathsf{\Phi }$ in terms of the Kraus operators is not unique as ${\left\{{\mathcal{K}}_{\mathbf{a}}^{\prime }\right\}}_{\mathbf{a}}$ with ${\mathcal{K}}_{\mathbf{a}}^{\prime }={\sum }_{\mathbf{b}}{U}_{\mathbf{a},\mathbf{b}}{\mathcal{K}}_{\mathbf{b}}$, for an arbitrary unitary transformation $U_{\mathbf{a},\mathbf{b}}$, define the same quantum channel $\mathsf{\Phi }\left(\rho \right)$. Different decompositions of the same quantum channel are referred to as unravelings. In the context of repeated measurement, the Kraus operators are factorized ${\mathcal{K}}_{\mathbf{a}}=K_{a_1}{K}_{a_2}\dots K_{a_T}$ where $\mathbf{a}=(a_1,a_2,\dots ,a_T)$ labels the collection of all measurement outcomes performed at each time step. For MIPTs, one is interested in the single trajectory where the initial density matrix $\rho \left(0\right)$ evolves as

$${\rho }_{\mathbf{a}}=p_{\mathbf{a}}^{-1}{\tilde{\rho }}_{\mathbf{a}},{\tilde{\rho }}_{\mathbf{a}}\equiv {\mathcal{K}}_{\mathbf{a}}\rho \left(0\right){\mathcal{K}}_{\mathbf{a}}^{†},$$

(1)

where the probability of a specific trajectory has been introduced according to Born’s rule as $p_{\mathbf{a}}=\mathrm{tr}\left[{\tilde{\rho }}_{\mathbf{a}}\right]$. Given any functional of the state $F\left[\rho \right]$, we define the average over trajectories as

$$⟨F\left[\rho \right]⟩=\sum _{\mathbf{a}}{p}_{\mathbf{a}}F\left[{\rho }_{\mathbf{a}}\right],\mathrm{Born}\mathrm{rule}.$$

(2)

If the results of the measurements are not known, one only has access to linear functionals of the state, such as the quantum expectation of any observable, e.g., $⟨\mathrm{tr}\left[\widehat{O}\rho \right]⟩=\mathrm{tr}\left[\widehat{O}\mathsf{\Phi }\left[\rho \left(0\right)\right]\right]$, which depends solely on the quantum channel $\mathsf{\Phi }\left[\rho \right]$ and is independent on the specific unraveling. However, this is not true for nonlinear functionals such as the Renyi’s entropies, where one considers the functionals

$$S_k\left[\rho \right]:=\frac{1}{1-k}\ln \mathrm{tr}\left[{\rho }^k\right],$$

(3)

and in particular, the Von Neumann entropy defined as the limit $k\to 1$, or, explicitly,

$$S_1\left[\rho \right]:=-\mathrm{tr}\left[\rho \log \rho \right]=-\sum _{\alpha }{\lambda }_{\alpha }\log {\lambda }_{\alpha },$$

(4)

where ${\left\{{\lambda }_{\alpha }\right\}}_{\alpha =1}^n$ denotes the eigenvalues of $\rho$. Quantities like $⟨S_1\left[\rho \right]⟩$ can be used as order parameters for MIPTs. By discarding the Born’s weight for trajectories, one can define a different average

$${⟨F\left[\rho \right]⟩}_0=\frac{{\sum }_{\mathbf{a}}F\left[{\rho }_{\mathbf{a}}\right]}{{\sum }_{\mathbf{a}}1},\mathrm{Unbiased}\mathrm{outcomes},$$

(5)

where all measurement outcomes have equal weight and are statistically independent at different times. Unbiased outcomes can be obtained via post-selection by artificially attributing the same probability to each trajectory. In some contexts, ${⟨\dots ⟩}_0$ is used as an approximation for the more physical $⟨\dots ⟩$. We will see that both cases emerge naturally in our framework.

3. The Model

We consider a toy model for continuous monitoring in a quantum system with a Hilbert space of dimension n. Let us explain the model by splitting the unitary evolution and the monitoring parts. For the unitary evolution, we have the Hamiltonian increment

$$dH=J\sum _{\alpha ,\beta =1}^{n}d{h}_{\alpha \beta }\left(t\right)|\alpha ⟩⟨\beta |,$$

(6)

where hermiticity is ensured requiring that $d{h}_{\alpha \beta }=d{h}_{\beta \alpha }^{*}$. Otherwise, the increments are chosen as a Hermitian Brownian motion with covariance $d{h}_{\alpha \beta }d{h}_{\gamma \delta }^{*}={\delta }_{\alpha \gamma }{\delta }_{\beta \delta }dt/n$. Equivalently, in the limit $dt\to 0$, we can write $d{h}_{\alpha \beta }=\sqrt{dt}{h}_{\alpha \beta }$, where $h_{\alpha \beta }$ is an $n\times n$ Hermitian matrix, drawn from the Gaussian unitary ensemble (GUE)

$$P\left(h\right)=\frac{1}{Z}{e}^{-\frac{n}{2}\mathrm{tr}\left[h{h}^{†}\right]},$$

(7)

and the measure is over the independent entries of a Hermitian matrix (with a semi-circle spectrum of support $[-2,2]$ in the large n limit). A crucial property of the GUE distribution is its invariance under unitary conjugation, $P\left(h\right)=P\left(uh{u}^{†}\right)$ for any unitary $u\in U\left(n\right)$. The dynamics induced by such a unitary evolution is simply described by $\rho +d\rho =e^{-idH}\rho e^{idH}$, where the Itô calculus conventions are implied. For measurements, let us first introduce the standard form of the stochastic Schrödinger Equation [65,69,70] for an imperfect monitoring of a Hermitian operator $\widehat{O}$. Within a small time step $\mathsf{\Delta }t$, the system is evolved coupling the operator $\widehat{O}$ with an extra spin $1/2$ (ancilla) whose value along a reference direction is projectively measured with an outcome $a=\pm 1$. As explained in the previous section, this evolution can be encoded into the Kraus operators $K_a=(1-a\sqrt{\Gamma \mathsf{\Delta }t}\widehat{O}+\gamma \mathsf{\Delta }t{\widehat{O}}^2/2)/\sqrt{2}$ (see Appendix A in Ref. [63] for a summary of this derivation), where $\Gamma$ is a rate quantifying the measurement strength. In the limit $\mathsf{\Delta }t\to 0$, the collection of measurements $\mathbf{a}$ can be used to define a standard Wiener process $Y\left(t\right)$ ($d{Y}^2=dt$) and one obtains the stochastic evolution equation

$$d\rho =(1+x)\Gamma dt{\mathcal{D}}_O\left[\rho \right]+\sqrt{\Gamma }dY\{\widehat{O}-{⟨\widehat{O}⟩}_t,\rho \}$$

(8)

with the dephasing superoperator ${\mathcal{D}}_O\left[\rho \right]\equiv \widehat{O}\rho \widehat{O}-\frac{1}{2}\{{\widehat{O}}^2,\rho \}$. The parameter $x\ge 0$ quantifies an extra source of dephasing. It can be seen as due to a fraction of measurements whose outcomes are not known or more generally to a coupling with an external dephasing bath. The limit $x=0$ corresponds to perfect measurements. In our model, within each infinitesimal time step $dt$, we choose $\widehat{O}\left(t\right)={\sum }_{\alpha ,\beta =1}^n{o}_{\alpha \beta }\left(t\right)|\alpha ⟩⟨\beta |$ to be a random operator, with components $o_{\alpha \beta }$ drawn from the GUE distribution (7). We can thus introduce a Hermitian Brownian motion setting $d{o}_{\alpha \beta }=o_{\alpha \beta }\left(t\right)dY$, satisfying $d{o}_{\alpha \beta }d{o}_{\gamma \delta }^{*}={\delta }_{\alpha \gamma }{\delta }_{\beta \delta }dt/n$. Using this, according to the rules of stochastic calculus, we can rewrite the dephasing part as ${\mathcal{D}}_O\left[\rho \right]dt={\mathcal{D}}_O\left[\rho \right]d{Y}^2=d\widehat{O}\rho d\widehat{O}-\frac{1}{2}\{d{\widehat{O}}^2,\rho \}=-(\rho -\frac{\mathbb{1}}{n})dt$, where $d\widehat{O}={\sum }_{\alpha ,\beta =1}^{n}d{o}_{\alpha \beta }|\alpha ⟩⟨\beta |$. Note that at finite $\mathsf{\Delta }t$, $o_{\alpha \beta }\left(t\right)dY$ is the product of two Gaussian distributions that is not Gaussian. However, this is irrelevant in the $\mathsf{\Delta }t\to 0$ limit, where only the covariance is relevant to define a Wiener process.

In the following, we will assume that the density matrix is initially prepared in the infinite-temperature state $\rho =\mathbb{1}/n$. Thus, because both the Hamiltonian increment and the observable $\widehat{O}$ are always chosen from the GUE, the distribution of the density matrix at any time is itself invariant under unitary transformation. In other words, diagonalizing $\rho =u\Lambda u^{†}$, u will be Haar distributed in the unitary group $U\left(n\right)$ and will completely decouple from the dynamics of $\Lambda =\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_n)$. In the following, we will focus on the dynamics and the distribution of the eigenvalues ${\left\{{\lambda }_{\alpha }\right\}}_{\alpha =1}^n$. As they are unaffected by the unitary dynamics, in the following we will ignore the latter.

4. The $\mathit{n}=\mathbf{2}$ Case

Before dealing with the general n case, it is worth considering specifically the $n=2$ case as an instructive warm-up. We can parameterize the density matrix in terms of a vector $\overrightarrow{r}=\{r_1,r_2,r_3\}$, within the Bloch sphere ($\left|\overrightarrow{r}\right|\le 1$), as

$$\rho =\frac{1}{2}(\mathbb{1}+\overrightarrow{r}·\overrightarrow{\sigma })=\frac{1}{2}(\mathbb{1}+r_{\alpha }{\sigma }_{\alpha }),$$

(9)

where $\overrightarrow{\sigma }=\{{\sigma }_1,{\sigma }_2,{\sigma }_3\}$ denotes the set of Pauli matrices. The modulus $r=|\overrightarrow{r}|$ coincides with the difference $|{\lambda }_1-{\lambda }_2|$ between the two eigenvalues of $\rho$, whereas the normalization of the trace, forcing ${\lambda }_1+{\lambda }_2=1$, is implicit in the parameterization. It is also convenient to similarly parameterize the measurement operator as $O=o_0\mathbb{1}+\overrightarrow{o}·\overrightarrow{\sigma }$. We can assume $\widehat{O}$ to be traceless so that $o_0=(o_{11}+o_{22})/2=0$, as this contribution would be inessential in either case. The three remaining one-indexed random variables $o_1=\mathrm{Re}\left(o_{12}\right)$, $o_2=-\mathrm{Im}\left(o_{12}\right)$, $o_3=(o_{11}-o_{22})/2$ are real-valued and satisfy $o_{\alpha }{o}_{\beta }={\delta }_{\alpha \beta }/4$. In terms of these variables, the infinitesimal variation $d{r}_{\alpha }=\mathrm{tr}\left(d\rho {\sigma }_{\alpha }\right)$ reads

$$d{r}_{\alpha }=-\Gamma dt(1+x)r_{\alpha }+2\sqrt{\Gamma }(d{o}_{\alpha }-d{o}_{\beta }{r}_{\beta }{r}_{\alpha }).$$

(10)

This can be recast into a closed stochastic equation for the modulus $r=|\overrightarrow{r}|$ (as required by unitary invariance), which takes the form

$$dr=\Gamma dt\left(\frac{1-r^2}{r}-xr\right)+\sqrt{\Gamma }dY(1-r^2),$$

(11)

$dY$ being the standard Wiener process satisfying $d{Y}^2=dt$ defined before Equation (8). In order to recast the previous equation into the standard Langevin form, let us perform the change in variables $r=\tanh \left(\omega \right)$, $\omega \in {\mathbb{R}}^{+}$. In terms of $\omega$, we indeed have $d\omega =-\Gamma V^{\prime }\left(\omega \right)dt+\sqrt{\Gamma }dY$, where the potential is given by the following:

$$V\left(\omega \right)=-\frac{x}{2}{\cosh }^2\left(\omega \right)-\log \left[\sinh \left(2\omega \right)\right].$$

(12)

As a consequence, the evolution of the probability distribution $P(\omega ,t)$ can be described through the associated Fokker–Planck (FP) equation

$${\partial }_{t}P(\omega ,t)=\frac{\Gamma }{2}{\partial }_{\omega }\left[\left({\partial }_{\omega }+2V^{\prime }\left(\omega \right)\right)P(\omega ,t)\right].$$

(13)

which admits a stationary probability distribution $P_{\mathrm{stat}}\left(\omega \right)=\frac{1}{Z}{e}^{-2V\left(\omega \right)}$. Coming back to the original coordinate, one has

$$P_{\mathrm{stat}}\left(r\right)=\frac{1}{Z}\frac{r^2}{{(1-r^2)}^3}{e}^{-x{(1-r^2)}^{-1}},$$

(14)

a result already derived in [63] in the context of mean-field approximation. Since $\mathrm{tr}\left({\rho }^2\right)=(1+r^2)/2$, it follows that the purity has a nontrivial stationary distribution as well for any $x>0$. As $x\to 0$, the distribution becomes more and more peaked around $r=1$, eventually collapsing to $P_{\mathrm{stat}}\left(r\right)=\delta (r-1)$ for $x=0$: this is consistent with the fact that perfect measurements eventually lead to purification. For $x=0$, the finite-time solution of Equation (13) can be explicitly worked out as follows:

$$P(\omega ,t)=\frac{\omega \sinh \left(2\omega \right)e^{-\frac{{\omega }^2}{2\Gamma t}-2\Gamma t}}{\sqrt{2\pi }{(\Gamma t)}^{3/2}},$$

(15)

normalized in $\omega \in {\mathbb{R}}^{+}$. The origin of this form will be clarified for general n in Section 7.1.

We can use these results to compute the Von Neumann entropy (4). In particular, on each trajectory, it can be related to the variable r

$$S_1=S_{\max }-\frac{1}{2}\left[(1+r)\log (1+r)+(1-r)\log (1-r)\right],$$

(16)

with $S_{\max }=\log n=\log 2$, the entropy of the maximally mixed state. We can compute the behavior of $⟨S_1⟩$ in different regimes; in the stationary state at $x>0$, one has

$${⟨S_1⟩}_{\mathrm{stat}}=\left\{\begin{array}{cc}\log 2-\frac{3}{4x}+O\left(x^{-2}\right),\hfill & x\gg 1\hfill \\ -\frac{1}{4}x\log x,\hfill & x\ll 1\hfill \end{array}\right..$$

(17)

For $x=0$, the system purifies, and $⟨S_1⟩\to 0$. For large times, we have

$$⟨S_1⟩=\frac{e^{-2\Gamma t}}{2}\left(1+\frac{{(\Gamma t)}^{-\frac{1}{2}}}{\sqrt{2\pi }}-\frac{{\pi }^2+6}{24}\frac{{(\Gamma t)}^{-\frac{3}{2}}}{\sqrt{2\pi }}+O\left(t^{-\frac{5}{2}}\right)\right).$$

(18)

See Appendix B for the details of the derivation and for the higher orders.

5. Dynamics of the Spectrum

5.1. Stochastic Evolution of the Eigenvalues

In order to derive an evolution equation for the eigenvalues in the general case, we follow the standard approach [71] and make use of second-order perturbation theory, as follows:

$$d{\lambda }_{\alpha }=d{\rho }_{\alpha \alpha }+\sum _{\beta \ne \alpha }\frac{|d{\rho }_{\alpha \beta }{|}^2}{{\lambda }_{\alpha }-{\lambda }_{\beta }}.$$

(19)

Now, one has to substitute the infinitesimal variations ${\rho }_{\alpha }$ as determined in Equation (8). To further simplify the calculation, we take advantage of unitary rotational invariance, so that $\rho$ at time t is assumed to be diagonal in an appropriate basis ${\rho }_{\alpha \beta }={\lambda }_{\alpha }{\delta }_{\alpha \beta }$ (no sum over $\alpha$). Thus, we have

$$d{\rho }_{\alpha \alpha }=-\Gamma dt(1+x)\left({\lambda }_{\alpha }-\frac{1}{n}\right)+2\sqrt{\Gamma }{\lambda }_{\alpha }\left[d{o}_{\alpha \alpha }-\sum _{\beta }{\lambda }_{\beta }d{o}_{\beta \beta }\right],$$

(20)

whereas for the off-diagonal elements, we simply have $d{\rho }_{\alpha \ne \beta }=\sqrt{\Gamma }d{o}_{\alpha \beta }({\lambda }_{\alpha }+{\lambda }_{\beta })$. We can consider the diagonal elements of $d\widehat{O}$ and rescale them as $d{B}_{\alpha }=\sqrt{n}d{o}_{\alpha \alpha }$, so that $d{B}_{\alpha }d{B}_{\beta }={\delta }_{\alpha \beta }dt$ are standard Wiener increments. Then, one finally finds

$$d{\lambda }_{\alpha }=\gamma dt\left[-(1+x)(n{\lambda }_{\alpha }-1)+\sum _{\beta \ne \alpha }\frac{{({\lambda }_{\alpha }+{\lambda }_{\beta })}^2}{{\lambda }_{\alpha }-{\lambda }_{\beta }}\right]+2\sqrt{\gamma }{\lambda }_{\alpha }\left(d{B}_{\alpha }-\sum _{\beta }{\lambda }_{\beta }d{B}_{\beta }\right),$$

(21)

where we rescaled $\gamma =\Gamma /n$. Let us notice that, as it should be, the evolution of Equation (21) preserves the trace, as ${\sum }_{\alpha }d{\lambda }_{\alpha }=d\mathrm{tr}\left(\rho \right)=0$. Additionally, for $x=0$, the configuration ${\lambda }_{\alpha }=1$, ${\lambda }_{\beta \ne \alpha }=0$ is a fixed point, since as expected, in the absence of any dephasing ($x=0$), measurements eventually lead to purification and the density matrix reduces to a rank-1 projector. It is useful to further manipulate Equation (22) by rewriting ${\lambda }_{\alpha }-1/n=\frac{1}{n}{\sum }_{\beta \ne \alpha }({\lambda }_{\alpha }-{\lambda }_{\beta })$, where we used ${\sum }_{\beta }{\lambda }_{\beta }=1$. In such a way, we obtain

$$d{\lambda }_{\alpha }=\gamma dt\sum _{\beta \ne \alpha }\left[4\frac{{\lambda }_{\alpha }{\lambda }_{\beta }}{{\lambda }_{\alpha }-{\lambda }_{\beta }}+x({\lambda }_{\beta }-{\lambda }_{\alpha })\right]+2\sqrt{\gamma }{\lambda }_{\alpha }\left(d{B}_{\alpha }-\sum _{\beta }{\lambda }_{\beta }d{B}_{\beta }\right).$$

(22)

For $x=0$, Equation (22) presents some analogy with the eigenvalue flow studied in [72], see Equation (28) therein with $(1+m{\lambda }_i)dt\to 0$, ${\sigma }^2=4\gamma$ and $\beta =2$. The sum over $\beta \ne \alpha$ is clearly a manifestation of the typical Coulombic repulsion between eigenvalues. On top of that, the form of the noise is non-diagonal, as a combined effect of exactly preserving the trace and attributing Born’s probability to trajectories. Then, in order to simplify the dynamics, we introduce a new set of unconstrained variables.

5.2. Mapping to Unconstrained Variables

As the dynamics of the eigenvalues exactly preserves the traces, it is useful to write them as ${\lambda }_{\alpha }\equiv y_{\alpha }/\left({\sum }_{\beta =1}^n{y}_{\beta }\right)$ in terms of a new set of variables ${\left\{y_{\alpha }\right\}}_{\alpha =1}^n$. Of course, the mapping between the $\lambda$’s and the y’s is not one-to-one, as a global rescaling of all the y’s does not affect the mapping. This freedom can be used to simplify the evolution of the y’s, in particular, by writing

$$d{y}_{\alpha }=4\gamma dt{F}_{\alpha }\left(\overrightarrow{y}\right)+\sqrt{4\gamma }{y}_{\alpha }d{B}_{\alpha },$$

(23)

we can look for a force term $F_{\alpha }\left(\overrightarrow{y}\right)$ which is homogeneous of degree 1. From standard Itô calculus, one can verify that

$$F_{\alpha }\left(\overrightarrow{y}\right)=\frac{x}{4}\sum _{\beta }{y}_{\beta }+\frac{y_{\alpha }^2}{{\sum }_{\beta }{y}_{\beta }}+\sum _{\beta \ne \alpha }\frac{y_{\alpha }{y}_{\beta }}{y_{\alpha }-y_{\beta }}+g\left(\overrightarrow{y}\right)y_{\alpha },$$

(24)

where $g\left(\overrightarrow{y}\right)$ is an arbitrary homogeneous function ($g\left(c\overrightarrow{y}\right)=g\left(\overrightarrow{y}\right)$), which correctly reproduces Equation (22) for the evolution of the $\lambda$’s. Equation (23) has the advantage of involving only a diagonal noise term, which is nonetheless multiplicative. We can further simplify its form setting $w_{\alpha }=\log y_{\alpha }$, which leads to

$$d{w}_{\alpha }=4\gamma {\tilde{F}}_{\alpha }\left(\overrightarrow{w}\right)dt+\sqrt{4\gamma }d{B}_{\alpha },$$

(25)

where ${\tilde{F}}_{\alpha }\left(\overrightarrow{w}\right)=e^{-w_{\alpha }}{F}_{\alpha }\left(e^w\right)$. Setting $g\left(\overrightarrow{y}\right)=(n-1)/2$, one can express

$${\tilde{F}}_{\alpha }=-{\partial }_{\alpha }V\left(\overrightarrow{w}\right)+\frac{x}{4}{\mathsf{f}}_{\alpha }\left(\overrightarrow{w}\right),$$

(26)

where ${\partial }_{\alpha }=\partial /{\partial }_{w_{\alpha }}$, the potential $V\left(\overrightarrow{\omega }\right)$ is

$$V\left(\overrightarrow{\omega }\right)=-\frac{1}{2}\sum _{\alpha \ne \beta }\log \sinh \frac{|w_{\alpha }-w_{\beta }|}{2}-\log \sum _{\beta }{e}^{w_{\beta }}$$

(27)

whereas the non-conservative force is given by ${\mathsf{f}}_{\alpha }={\sum }_{\beta }{e}^{w_{\beta }-w_{\alpha }}$. We will now explain how the dynamics induced by Equation (25) can be solved in different regimes.

6. Stationary State at $\mathit{x}>\mathbf{0}$ and $\mathit{n}\to \infty$

We now consider the dynamics induced by imperfect measurements at finite $x=O\left(1\right)$ in the large n limit. When the dephasing term dominates the right-hand side of Equation (22), the eigenvalue distribution is expected to be peaked around $\lambda =1/n$. Therefore, it is convenient to rescale the eigenvalues via

$${\tilde{\lambda }}_{\alpha }=\frac{2n{\lambda }_{\alpha }}{x},$$

(28)

with the trace condition becoming ${\sum }_{\alpha }{\tilde{\lambda }}_{\alpha }=2n/x$. With this scaling, we can analyze the noise term in Equation (22), which is proportional to ${\tilde{\lambda }}_{\alpha }(d{B}_{\alpha }-x/\left(2n\right){\sum }_{\beta }{\tilde{\lambda }}_{\beta }d{B}_{\beta })\sim {\tilde{\lambda }}_{\alpha }d{B}_{\alpha }$. Indeed, by summing the last term in quadrature, we see it scales like $n^{-1/2}$ and can thus be neglected for $n\gg 1$. This can be understood as the sum ${\sum }_{\alpha }{\tilde{\lambda }}_{\alpha }$ being extensive and in the $n\to \infty$ limit its fluctuations are subleading with respect to its average. In this scaling, Equation (22) becomes

$$d{\tilde{\lambda }}_{\alpha }=4\gamma dt\left[\sum _{\beta \ne \alpha }\frac{{\tilde{\lambda }}_{\alpha }{\tilde{\lambda }}_{\beta }}{{\tilde{\lambda }}_{\alpha }-{\tilde{\lambda }}_{\beta }}+\frac{n}{2}\left(1-\frac{x}{2}{\tilde{\lambda }}_{\alpha }\right)\right]+\sqrt{4\gamma }{\tilde{\lambda }}_{\alpha }d{B}_{\alpha }.$$

(29)

This associated stochastic dynamics is exactly solvable even at finite n. Indeed, by introducing again logarithmic variables ${\tilde{w}}_{\alpha }=\log {\tilde{\lambda }}_{\alpha }$, we can reduce this to a Langevin equation, analogous to Equation (25), as follows:

$$d{\tilde{w}}_{\alpha }=4\gamma dt(-{\partial }_{\alpha }{V}_x\left(\overrightarrow{\tilde{w}}\right))+\sqrt{4\gamma }d{B}_{\alpha }.$$

(30)

We stress that this equation involves a completely conservative force where the potential $V_x\left(\overrightarrow{\tilde{w}}\right)$ now reads as follows:

$$V_x\left(\overrightarrow{\tilde{w}}\right)=-\frac{1}{2}\sum _{\alpha \ne \beta }\log \sinh \frac{|{\tilde{w}}_{\alpha }-{\tilde{w}}_{\beta }|}{2}+\frac{n}{2}\sum _{\alpha }\left[e^{-{\tilde{w}}_{\alpha }}+\left(1+\frac{x}{2}\right){\tilde{w}}_{\alpha }\right].$$

(31)

It is helpful to comment between the relation of the variables ${\tilde{w}}_{\alpha }$ introduced here and $w_{\alpha }$ in Section 5.2. We can see that they match, up to an inessential shift of the center of mass. The initial value of the sum ${\sum }_{\alpha }{e}^{w_{\alpha }}$ can be chosen arbitrarily and in the limit $n\to \infty$ it becomes a conserved quantity. Since we implicitly chose ${\sum }_{\alpha }{e}^{{\tilde{w}}_{\alpha }}={\sum }_{\alpha }{\tilde{\lambda }}_{\alpha }=2n/x$, we can rewrite ${\lambda }_{\alpha }=e^{{\tilde{w}}_{\alpha }}/{\sum }_{\alpha }{e}^{{\tilde{w}}_{\alpha }}$ coherently with Section 5.2.

Thanks to the Langevin form of Equation (30), we can easily deduce the joint distribution

$$P_{\mathrm{stat}}\left(\overrightarrow{\tilde{w}}\right)=\frac{1}{Z}{e}^{-2V\left(\overrightarrow{\tilde{w}}\right)}=\frac{1}{Z}\prod _{\alpha >\beta }\sinh {\left(\frac{{\tilde{w}}_{\alpha }-{\tilde{w}}_{\beta }}{2}\right)}^2\prod _{\alpha }{e}^{-{\tilde{w}}_{\alpha }n(1+\frac{x}{2})}{e}^{-n{e}^{-{\tilde{w}}_{\alpha }}},$$

(32)

which is the stationary solution to the associated FP equation. In terms of the rescaled eigenvalues ${\tilde{\lambda }}_{\alpha }$

$$P_{\mathrm{stat}}\left(\overrightarrow{\tilde{\lambda }}\right)=\frac{1}{Z}\frac{{\prod }_{\alpha >\beta }{({\tilde{\lambda }}_{\alpha }-{\tilde{\lambda }}_{\beta })}^2}{{\prod }_{\alpha }{\tilde{\lambda }}_{\alpha }^{n(2+x/2)}}{e}^{-n{\sum }_{\alpha }{\tilde{\lambda }}_{\alpha }^{-1}},$$

(33)

which is, upon rescaling ${\tilde{\lambda }}_{\alpha }\to {\tilde{\lambda }}_{\alpha }/2n={\lambda }_{\alpha }/x$, the joint distribution function for the eigenvalues of a matrix in the inverse-Wishart ensemble, with $m=n(1+x/2)$. We refer to Appendix C for a brief discussion of such an ensemble.

Let us now introduce the one-particle density function

$$f\left(\tilde{\lambda }\right)=\frac{1}{n}\sum _{\alpha }\delta (\tilde{\lambda }-{\tilde{\lambda }}_{\alpha }),$$

(34)

satisfying $\int d\tilde{\lambda }f\left(\tilde{\lambda }\right)=1$, $\int d\tilde{\lambda }f\left(\tilde{\lambda }\right)\tilde{\lambda }=2/x$. For matrices in the inverse-Wishart ensemble, the eigenvalue density takes the inverse-Marchenko–Pastur (IMP) expression reported in Equation (A12) of Appendix C. It is thus immediate to verify that the distribution for the rescaled eigenvalues defined above reads

$$f(\tilde{\lambda },x)\equiv f_{\mathrm{IMP}}(\tilde{\lambda },x)=\frac{x}{4\pi {\tilde{\lambda }}^2}\sqrt{(\tilde{\lambda }-{\tilde{\lambda }}_{-})({\tilde{\lambda }}_{+}-\tilde{\lambda })},$$

(35)

and it is shown in Figure 1. The endpoints ${\tilde{\lambda }}_{\pm }$ are given by

$${\tilde{\lambda }}_{\pm }=\frac{4}{x^2}{\left(\sqrt{1+\frac{x}{2}}\pm 1\right)}^2.$$

(36)

The distribution in Equation (35) is valid in the $n\to \infty$ limit which is also needed for Equation (29) to become a valid approximation of the original Equation (22). The behavior of $f_{\mathrm{IMP}}(\tilde{\lambda },x)$ as x is varied and defines a sharply peaked distribution around $2/x$ for $x\gg 1$, as the interval ${\tilde{\lambda }}_{+}-{\tilde{\lambda }}_{-}=\frac{16}{x^2}\sqrt{1+\frac{x}{2}}$ collapses to a point. Conversely, in the limit of nearly perfect measurements $x\ll 1$, the rescaled eigenvalues spread on the positive semi-axis between ${\tilde{\lambda }}_{-}\to 1/4$ and ${\tilde{\lambda }}_{+}\to \infty$, whereas $f\left(\tilde{\lambda }\right)$ remains peaked around $\tilde{\lambda }=1/3$. As this corresponds to $\lambda \to 0$, this signals the purification dynamics induced by perfect measurements. For any finite n, it is important to notice, however, that even in this regime, one has to assume $x\gg n^{-1}$ for our approximation to be valid, so that the limits $x\to 0$, $n\to \infty$ do not commute.

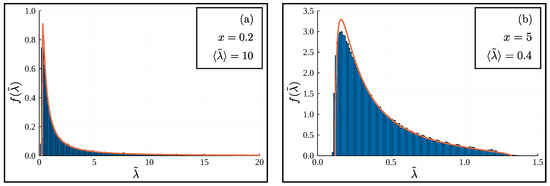
Figure 1. Inverse-Marchenko–Pastur distribution. The spectral density $f\left(\tilde{\lambda }\right)$ for the rescaled eigenvalues $\tilde{\lambda }$ defined in Equation (28) is shown. In the large n limit, it takes the inverse-Marchenko–Pastur form given in Equation (35). In both plots, the orange line displays the theoretical curve, whereas the blue histogram bars are computed after a numerical simulation (with $n=50$) of the weak measurement protocol. (a) The spectral density at $x=0.2$ in the range $[0,4/x]$. At small x, most eigenvalues are located in vicinity of ${\tilde{\lambda }}_{-}\to 1/4$, as an effect of purification. (b) The spectral density at $x=5.0$ in its domain $[{\tilde{\lambda }}_{-},{\tilde{\lambda }}_{+}]$. For larger values of x, the rescaled eigenvalues take finite values around their average $⟨\tilde{\lambda }⟩=2/x$.

The Von Neumann entropy, defined in Equation (4), can be computed in the stationary state, in terms of the inverse-Marchenko–Pastur eigenvalue distribution above, as follows:

$${⟨S_1⟩}_{\mathrm{stat}}=S_{\max }-\log \frac{x}{2}-\frac{x}{2}\int d\tilde{\lambda }{f}_{\mathrm{IMP}}\left(\tilde{\lambda }\right)\tilde{\lambda }\log \tilde{\lambda },$$

(37)

with $S_{\max }=\log n$ the entropy of the maximally mixed state. The last integral on the right-hand side can be evaluated by means of contour integration

$$-\frac{x}{2}\frac{x}{4\pi }{\int }_{{\tilde{\lambda }}_{-}}^{{\tilde{\lambda }}_{+}}d\tilde{\lambda }\frac{\log \tilde{\lambda }}{\tilde{\lambda }}\sqrt{(\tilde{\lambda }-{\tilde{\lambda }}_{-})({\tilde{\lambda }}_{+}-\tilde{\lambda })}=1+\left(2+\frac{x}{2}\right)\log \frac{x}{2}-\left(1+\frac{x}{2}\right)\log \left(1+\frac{x}{2}\right),$$

(38)

so that one has the remarkably simple exact formula, as follows:

$${⟨S_1⟩}_{\mathrm{stat}}-S_{\max }=1-\left(1+\frac{x}{2}\right)\log \left(1+\frac{2}{x}\right).$$

(39)

In particular, this allows us to evaluate its asymptotic behavior in the opposite regimes $x\gg 1$ and $n^{-1}\ll x\ll 1$, as follows:

$${⟨S_1⟩}_{\mathrm{stat}}-S_{\max }=\left\{\begin{array}{cc}-\frac{1}{x}+O\left(x^{-2}\right),\hfill & x\gg 1\hfill \\ -\log \left(x\right)+O\left(1\right),\hfill & x\ll 1\hfill \end{array}\right..$$

(40)

6.1. Finite Time Dynamics

The finite time evolution of the set of unconstrained ${\left\{{\tilde{w}}_{\alpha }\right\}}_{\alpha =1}^n$ used in this section has been studied in detail by one of the authors in Ref. [72]. Our Langevin Equation (30) indeed reduces to Equation (42) of Ref. [72] upon the identification $t\to \Gamma xt$, $m=-1$, $\sigma =\sqrt{4/xn}$, $\beta =2$. Consistent with our result in Equation (35), a stationary inverse-Wishart distribution was also obtained there. Here, we briefly summarize the procedure and the results with our notation and parameters. The associated FP equation can be mapped to an imaginary time quantum problem via the transformation

$$P(\overrightarrow{\tilde{w}},t)={\left[P_{\mathrm{stat}}\left(\overrightarrow{\tilde{w}}\right)\right]}^{1/2}\mathsf{\Psi }(\overrightarrow{\tilde{w}},t),$$

(41)

with $P_{\mathrm{stat}}\left(\overrightarrow{\tilde{w}}\right)$ given in Equation (32) (we better discuss the quantum mapping from FP to Schrödinger in Section 7.1). The ensuing Schrödinger equation reads

$${\partial }_t\mathsf{\Psi }=-2\gamma [\mathcal{H}-E_0]\mathsf{\Psi },$$

(42)

with the Hermitian Hamiltonian

$$\mathcal{H}=\sum _{\alpha }\left[-\frac{{\partial }^2}{\partial {\tilde{w}}_{\alpha }^2}+U\left({\tilde{w}}_{\alpha }\right)\right],$$

(43)

and the finite energy shift $E_0$, which is the n-particle ground state of H. As the trajectories of the n particles are non-crossing, the problem is mapped onto fermions. The one-particle potential $U\left({\tilde{w}}_{\alpha }\right)$ is of Morse type:

$$U\left({\tilde{w}}_{\alpha }\right)=\frac{{\left(xn\right)}^2}{4}\left[\frac{e^{-2{\tilde{w}}_{\alpha }}}{4}-\left(\frac{2}{x}+\frac{1}{2}\right)e^{-{\tilde{w}}_{\alpha }}\right].$$

(44)

The single-particle spectrum of the Morse potential features a finite number of bound states ${\psi }_k\left(\tilde{w}\right)$ at eigenenergy $E_k=-{[k+1/2-n(1+x/4)]}^2$, with $k\in \mathbb{N}$, $k<k_{\max }$, $k_{\max }<\lfloor n(1+x/4)-1/2\rfloor$, and a continuum of scattering states ${\varphi }_p\left(\tilde{w}\right)$, such that $E_p=p^2$, with $p\in \mathbb{R}$. Let us notice that the number of bound states is always greater than the number of particles, i.e., $\lfloor n(1+x/4)+1/2\rfloor >n\forall x>0$, and the scattering states are empty. The n-fermion ground state is thus $E_0={\sum }_k{E}_k$. Consequently, the n-fermion energy states of the original FP operator are simply given by

$$\epsilon \left(n\right)=\frac{2}{xn}[E\left(n\right)-E_0],$$

(45)

so that the lowest eigenvalue is ${\epsilon }_0\left(n\right)=0$. The single-particle finite time evolution from an initial $w_0$ to a final w coordinate is determined by the Euclidean propagator $G_{\mathrm{M}}$ using the spectral decomposition over the bound and the scattering states

$$G_{\mathrm{M}}\left(\tilde{w},{\tilde{w}}^0,\tau \right):=\sum _{k=0}^{k_{\max }}{\psi }_k\left(\tilde{w}\right){\psi }_k\left({\tilde{w}}^0\right)e^{-E_k\tau }+{\int }_{\mathbb{R}}\frac{dp}{2\pi }{\varphi }_p\left(\tilde{w}\right){\varphi }_p\left({\tilde{w}}^0\right)e^{-p^2\tau }.$$

(46)

Then, the n-fermion propagator is obtained in terms of the Karlin–McGregor determinant formula [73] for the probability evolution of n non-intersecting particles from ${\overrightarrow{\tilde{w}}}^0$ to $\overrightarrow{\tilde{w}}$. From the quantum Euclidean propagator, one can write the solution to the original FP problem using Equation (41) as

$$P\left(\overrightarrow{\tilde{w}},t;{\overrightarrow{\tilde{w}}}^0,t=0\right)=e^{E_0\Gamma xt}\frac{P_{\mathrm{stat}}^{1/2}\left(\overrightarrow{\tilde{w}}\right)}{P_{\mathrm{stat}}^{1/2}\left({\overrightarrow{\tilde{w}}}^0\right)}\underset{1\le \alpha ,\beta \le n}{\det }{G}_{\mathrm{M}}({\tilde{w}}_{\alpha },{\tilde{w}}_{\beta }^0,\Gamma xt),$$

(47)

given the initial condition $P(\overrightarrow{\tilde{w}},t=0)={\prod }_{\alpha }\delta ({\tilde{w}}_{\alpha }-{\tilde{w}}_{\alpha }^0)$.

7. The Perfect Measurement Dynamics

In this section, we present the full solution of the joint eigenvalue distribution for the measurement problem at arbitrary n and time t, setting $x=0$.

7.1. Exact Solution at Finite Time

The stochastic Equation (25) takes the Langevin form

$$d{w}_{\alpha }=4\gamma dt(-{\partial }_{\alpha }V)+\sqrt{4\gamma }d{B}_{\alpha },$$

(48)

with the potential in Equation (27). The joint distribution $P(\overrightarrow{w},t)$ for the variables w’s satisfies the FP equation

$${\partial }_{t}P(\overrightarrow{w},t)=2\gamma \sum _{\alpha }{\partial }_{\alpha }\left[\left({\partial }_{\alpha }+2{\partial }_{\alpha }V\right)P(\overrightarrow{w},t)\right].$$

(49)

Formally, one can obtain a stationary solution to the FP equation, taking $P_{\mathrm{stat}}=e^{-2V}$. Of course, this is not normalizable, consistent with the fact that at $t\to \infty$ the density matrix simply purifies. Nonetheless, it can once again be used to convert the FP into a quantum problem, similarly to what was conducted in Section 6.1 with Equation (41). One has

$$P=\mathsf{\Psi }{P}_{\mathrm{stat}}^{1/2}\Rightarrow {\partial }_t\mathsf{\Psi }=-2\gamma \mathcal{H}\mathsf{\Psi },$$

(50)

which does satisfy a Schrödinger evolution with Hamiltonian operator

$$\mathcal{H}=\sum _{\alpha }\left[-{\partial }_{\alpha }^2+{\left({\partial }_{\alpha }V\right)}^2-{\partial }_{\alpha }^{2}V\right].$$

(51)

Remarkably, after using some algebra (see Appendix A and also [74,75]), one can show that

$$E_n\equiv {\left({\partial }_{\alpha }V\right)}^2-{\partial }_{\alpha }^{2}V=\frac{1}{12}\left(n^3+11n\right),$$

(52)

implying that the Schrödinger evolution in Equation (50) amounts to free diffusion with the additional non-crossing constraint when two w’s collide, which maps on free fermions, as the external Morse potential Equation (44) present in [72], see Equation (47), is absent here. The propagator for such dynamics can be obtained using the Karlin–McGregor determinant formula [73], also used in Equation (47). For a given initial condition $P(\overrightarrow{w},t=0)={\prod }_{\alpha }\delta (w_{\alpha }-w_{\alpha }^0)$, we can obtain the solution

$$P\left(\overrightarrow{w},t;{\overrightarrow{w}}^0,t=0\right)=\frac{P_{\mathrm{stat}}^{1/2}\left(\overrightarrow{w}\right)}{P_{\mathrm{stat}}^{1/2}\left({\overrightarrow{w}}_0\right)}{\left(e^{-2\gamma Ht}\right)}_{\overrightarrow{w},{\overrightarrow{w}}^0},$$

(53)

which leads to

$$P\left(\overrightarrow{w},t;{\overrightarrow{w}}^0,t=0\right)=e^{-2\gamma E_{n}t}\frac{{\sum }_{\alpha }{e}^{w_{\alpha }}}{{\sum }_{\alpha }{e}^{w_{\alpha }^0}}\prod _{\alpha <\beta }\frac{\sinh \frac{|w_{\alpha }-w_{\beta }|}{2}}{\sinh \frac{|w_{\alpha }^0-w_{\beta }^0|}{2}}\underset{1\le \alpha ,\beta \le n}{\det }{G}_0(w_{\alpha },w_{\beta }^0,2\gamma t).$$

(54)

In this expression, we introduced the free diffusion propagator, namely $G_0(w,w^{\prime },\tau )=\exp [-\frac{{(w-w^{\prime })}^2}{4\tau }]/\sqrt{4\pi \tau }$. In the following, we focus on the case of the infinite-temperature initial state, where all the initial conditions coincide ${\overrightarrow{w}}^0\to 0$ (the specific value is inessential). In that limit, Equation (54) further simplifies as $P(\overrightarrow{w},t)\to \frac{1}{Z_t}{P}_0(\overrightarrow{w},t)\left({\sum }_{\alpha }{e}^{w_{\alpha }}\right)$, where

$$P_0(\overrightarrow{w},t)=\frac{1}{Z_t^0}\prod _{\alpha <\beta }\sinh \frac{|w_{\alpha }-w_{\beta }|}{2}\prod _{\alpha <\beta }|w_{\alpha }-w_{\beta }|e^{-{\sum }_{\alpha }\frac{w_{\alpha }^2}{8\gamma t}},$$

(55)

and the time dependent constants $Z_t^0,Z_t$ are both determined by enforcing the normalization of $P_0(\overrightarrow{w},t)$ and $P(\overrightarrow{w},t)$, respectively.

7.2. Relation between the Two Averages

The distribution $P_0(\overrightarrow{w},t)$ has appeared in [75,76] in studying the dynamics of the so-called isotropic Brownian motion in the context of May-Wigner instability. In contrast, the expression for $P(\overrightarrow{w},t)$ has the extra factor ${\sum }_{\alpha }{e}^{w_{\alpha }}$, whose origin can be traced back to Born’s rule, expressing (up to an irrelevant normalization) the probability in Equation (1) as $p_{\mathbf{a}}\propto {\sum }_{\alpha }{e}^{w_{\alpha }}$. It is useful to identify the

$$\mathrm{spectrum}\left[\tilde{\rho }\right]={\left\{e^{w_{\alpha }}\right\}}_{\alpha =1}^n,$$

(56)

where $\tilde{\rho }$ is the unnormalized density matrix introduced in Equation (1). In analogy with other problems of a multiplicative process involving random matrices [77,78,79,80], we will refer to the variables $w_{\alpha }$ as the Lyapunov exponents. In the following, consistent with the definition in Equation (5), we will add a subscript 0 to the averages computed with $P_0$, with the general relation

$$⟨F\left(\overrightarrow{w}\right)⟩=\frac{{⟨F\left(\overrightarrow{w}\right)\left({\sum }_{\alpha }{e}^{w_{\alpha }}\right)⟩}_0}{{⟨{\sum }_{\alpha }{e}^{w_{\alpha }}⟩}_0}$$

(57)

for an arbitrary function $F\left(\overrightarrow{w}\right)$. For instance, for the Renyi’s entropies we can write the following:

$$\begin{array}{cc}\hfill & ⟨S_k⟩=\frac{{⟨\mathrm{tr}\tilde{\rho }⟩}_0^{-1}}{1-k}{⟨\log \left[\frac{\mathrm{tr}{\tilde{\rho }}^k}{{\left(\mathrm{tr}\tilde{\rho }\right)}^k}\right]\mathrm{tr}\tilde{\rho }⟩}_0,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill & ⟨S_1⟩=-{⟨\mathrm{tr}\tilde{\rho }⟩}_0^{-1}{⟨\left[\frac{\tilde{\rho }}{\mathrm{tr}\tilde{\rho }}\log \frac{\tilde{\rho }}{\mathrm{tr}\tilde{\rho }}\right]\mathrm{tr}\tilde{\rho }⟩}_0.\hfill \end{array}$$

(59)

Then, using Equation (56), we can rewrite the Von Neumann entropy as

$$⟨S_1⟩=\frac{{⟨{\sum }_{\alpha }{e}^{w_{\alpha }}\ln {\sum }_{\beta }{e}^{w_{\beta }}⟩}_0}{{⟨{\sum }_{\alpha }{e}^{w_{\alpha }}⟩}_0}-\frac{{⟨{\sum }_{\alpha }{e}^{w_{\alpha }}{w}_{\alpha }⟩}_0}{{⟨{\sum }_{\alpha }{e}^{w_{\alpha }}⟩}_0}.$$

(60)

In particular, introducing the moments of the eigenvalues and of the trace as

$$\begin{array}{cc}\hfill & M\left(m\right):={⟨\sum _{\alpha }{e}^{m{w}_{\alpha }}⟩}_0,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & \mathsf{\Omega }\left(m\right):={⟨{\left(\sum _{\alpha }{e}^{w_{\alpha }}\right)}^m⟩}_0,\hfill \end{array}$$

(62)

we can express Equation (60) as

$$⟨S_1⟩=\frac{1}{M\left(1\right)}{\partial }_m{\left.\left(\mathsf{\Omega }\right(m)-M(m\left)\right)\right|}_{m=1}={\left.{\partial }_m\log \frac{\mathsf{\Omega }\left(m\right)}{M\left(m\right)}\right|}_{m=1}.$$

(63)

Thus, below we will study these moments with the measure $P_0$. We observe that in Equation (55), one can recognize two Vandermonde determinants, since

$$\begin{array}{cc}\hfill & \mathsf{\Delta }\left(\overrightarrow{w}\right)\equiv \prod _{\alpha <\beta }(w_{\alpha }-w_{\beta })=\det {\left(w_{\alpha }^{k-1}\right)}_{k,\alpha =1}^n,\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill & \prod _{\alpha <\beta }\left[2\sinh \left(\frac{w_{\alpha }-w_{\beta }}{2}\right)\right]=\det {\left(e^{{\delta }_k{w}_{\alpha }}\right)}_{k,\alpha =1}^n,\hfill \end{array}$$

(65)

where we set ${\delta }_k=(n+1)/2-k$. This implies that $P_0$ describes a determinantal point process, which allows us to obtain several exact results, as discussed below.

8. Exact Results for the Unbiased Ensemble

8.1. Average of Schur’s Polynomials

The calculation of several quantities, including Renyi’s entropies (3), requires the expressions of correlation functions of the Lyapunov exponents w’s. Here, we explain how they can be expressed systematically. First, because of the symmetry under exchange in the w’s, we can restrict to symmetric functions. Then, because of the determinantal structure in Equation (63), following [81] a complete and useful basis of symmetric functions is given by Schur’s polynomials and each correlation function can be expressed once the expectation of Schur’s polynomials is known. To a partition $\kappa =({\kappa }_1,\dots ,{\kappa }_n)$ of the integer $m={\sum }_j{\kappa }_j$, with ${\kappa }_1\ge {\kappa }_2\ge \dots \ge {\kappa }_n\ge 0$, one associates the corresponding Schur polynomial via [82]

$$s_{\kappa }\left(y\right)=\frac{\det {\left(y_{\alpha }^{{\kappa }_j+n-j}\right)}_{j,\alpha =1}^n}{\det {\left(y_{\alpha }^{k-1}\right)}_{k,\alpha =1}^n}.$$

(66)

Setting $y_{\alpha }=e^{w_{\alpha }}$ and denoting $h_j={\kappa }_j+n-j$, we can now express the average

$${⟨s_{\kappa }\left(y\right)⟩}_0=C{A}_t^m\int d\overrightarrow{w}\mathsf{\Delta }\left(\overrightarrow{w}\right)\det \left(e^{h_j{w}_{\alpha }}\right)e^{-{\sum }_{\alpha }\frac{w_{\alpha }^2}{8\gamma t}},$$

(67)

where C is the normalization and the constant $A_t$ raised to the power m accounts for the shift of the center of mass and will be fixed below. We can use Andreief identity [83] to express it in terms of a single determinant

$${⟨s_{\kappa }\left(y\right)⟩}_0=C{A}_t^m\det {\left(I_{k,h_j}\right)}_{k,j=1}^n,$$

(68)

where we defined

$$I_{k,h}={\int }_{-\infty }^{\infty }\frac{dw}{\sqrt{8\pi t\gamma }}{w}^{k-1}{e}^{hw-\frac{w^2}{8\gamma t}}={\left.{\partial }_{\mu }^{k-1}\left[e^{2t\gamma {\mu }^2}\right]\right|}_{\mu =h}.$$

(69)

We can thus express the coefficients $I_{k,h}$ in terms of the Hermite polynomials $H_n\left(x\right)={(-1)}^n{e}^{x^2}{\partial }_x^n\left[e^{-x^2}\right]$ as

$$I_{k,h}=e^{2h^2\gamma t}{H}_{k-1}\left(i\sqrt{2t\gamma }h\right).$$

(70)

where again we absorbed some extra constants by redefining C. The fact that at large x, $H_{\ell }\left(x\right)=2^{\ell }{x}^{\ell }+O\left(x^{\ell -1}\right)$ can be used to express the determinant

$$\det {\left[I_{k,{\kappa }_j+j}\right]}_{k,j=1}^n\propto \exp \left[2\gamma t\sum _j{h}_j^2\right]\det \left[h_j^{k-1}\right].$$

(71)

This last determinant is once again a Vandermonde one which can be expressed via (64). We can now plug this back into Equation (67) and fix the constant C using $s_{\kappa =0}\left(y\right)=1$, where $h_j\to n-j$. We finally obtain

$${⟨s_{\kappa }\left(y\right)⟩}_0=A_t^m{e}^{2\gamma t{\sum }_{j=1}^n(h_j^2-{(j-1)}^2)}{s}_{\kappa }\left(1\right),$$

(72)

where we recognized the equality

$$\prod _{1\le j<j^{\prime }\le n}\frac{h_j-h_{j^{\prime }}}{j^{\prime }-j}=s_{\kappa }(y_1=1,\dots ,y_n=1),$$

(73)

which expresses the number of semistandard Young diagram of shape $\kappa$ and n entries [82]. We can now use ${\sum }_{j=1}^n{h}_j^2-{(j-1)}^2=(2n-1)m+2\nu \left(\kappa \right)$ [82], with

$$\nu \left(\kappa \right)=\sum _j\left(\genfrac{}{}{0pt}{}{{\kappa }_j}{2}\right)-\left(\genfrac{}{}{0pt}{}{{\kappa }_j^{\prime }}{2}\right),$$

(74)

where ${\kappa }^{\prime }=({\kappa }_1^{\prime },{\kappa }_2^{\prime },\dots )$ denotes the partition dual to $\kappa$, with ${\kappa }_i^{\prime }=\#\left\{{\kappa }_j\right|{\kappa }_j\ge i\}$. The above average can then be expressed as follows:

$${⟨s_{\kappa }\left(y\right)⟩}_0=A_t^m{e}^{2\gamma tm(2n-1)}{e}^{4\gamma t\nu \left(\kappa \right)}{s}_{\kappa }(y_{\alpha }=1).$$

(75)

8.2. Power-Law Symmetric Polynomials

For later convenience, we also introduce the power-law symmetric polynomials

$$p_j\left(y\right)=\sum _{\alpha }{y}_{\alpha }^j,$$

(76)

and additionally, for any integer partition $\mu =({\mu }_1,\dots ,{\mu }_n)$, we can set

$$p_{\mu }\left(y\right)=\prod _j{p}_{{\mu }_j}\left(y\right),$$

(77)

which form a complete linear basis for symmetric polynomials. For instance, we can express

$$p_{1^m}\left(y\right)={\left(\sum _{\alpha }{y}_{\alpha }\right)}^m.$$

(78)

Since Schur’s polynomials are also a complete basis, one can find a change in basis between the two. It is given as (see Equation (3.10) in [81,84])

$$p_{\mu }\left(y\right)=\sum _{\kappa ⊢m}{\chi }_{\mu }^{\kappa }{s}_{\kappa }\left(y\right),$$

(79)

where ${\chi }_{\mu }^{\kappa }$ represents a character of the symmetric group $S_m$, with $m={\sum }_{\alpha }{\kappa }_{\alpha }$, on the irreducible representation and the conjugacy class labeled, respectively, by the integer partitions $\kappa$ and $\mu$.

8.3. Calculation of the Moments

Thanks to the relation between power-law symmetric polynomials and Schur’s ones, given in Equation (79), we can use the previous result to express the moments of eigenvalues, c.f. Equation (61) with $y_{\alpha }=e^{w_{\alpha }}$:

$$M\left(m\right)=\sum _{r=0}^{m-1}{(-1)}^r{⟨s_{(m-r,1^r)}\left(y\right)⟩}_0,$$

(80)

which corresponds to Equation (79) in the case $\mu =\left(m\right)$, i.e., a single cycle of length m. In this case, the only non-vanishing characters ${\chi }_{\left(m\right)}^{\kappa }$ are those related to L-shaped partitions $\kappa =(m-r,1^r)=({\kappa }_1=m-r,{\kappa }_2=1,\dots ,{\kappa }_{r+1}=1)$, with $r=0,\dots ,m-1$. In particular, one has ${\chi }_{\left(m\right)}^{(m-r,1^r)}={(-1)}^r$. Therefore, from Equation (74), we obtain $2\nu \left(\kappa \right)=m(m-2r-1)$, and

$$s_{(m-r,1^r)}\left(1\right)=\frac{\Gamma (m+n-r)}{m\Gamma (r+1)\Gamma (m-r)\Gamma (n-r)}.$$

(81)

The sum in Equation (80) thus becomes

$$M\left(m\right)=e^{2\gamma tm(m+n)}\sum _{r=0}^{m-1}{(-1)}^r{s}_{(m-r,1^r)}\left(1\right)e^{-2\gamma tm(2r+1)},$$

(82)

which can be expressed for integer n in terms of the hypergeometric function ${}_{2}F_1(a,b;c;z)$ [85], obtaining the following:

$$M\left(m\right)=\left(\genfrac{}{}{0pt}{}{m+n-1}{n-1}\right)e^{2\gamma tm(m+n-1)}{}_{2}F_1(1-m,1-n;1-m-n;z).$$

(83)

In both expressions, we have fixed the value of $A_t=e^{-2\gamma t(n-1)}$ using ${\partial }_{m}M\left(0\right)={⟨{\sum }_{\alpha }{w}_{\alpha }⟩}_0=0$ in our conventions. Note that $M\left(0\right)=n$ as required, and that the lowest moments have simple expressions, e.g., one has $M\left(1\right)={⟨{\sum }_{\alpha }{e}^{w_{\alpha }}⟩}_0=n{e}^{2n\gamma t}$.

Moreover, it is also possible to compute the moments of the trace defined in Equation (62), with $y_{\alpha }=e^{w_{\alpha }}$, by making use of the same relation. We can express

$$\mathsf{\Omega }\left(m\right)=\sum _{\kappa ⊢m}{\chi }_{1^m}^{\kappa }{⟨s_{\kappa }\left(y\right)⟩}_0=e^{2t\gamma n}\sum _{\kappa ⊢m}{e}^{4\gamma t\nu \left(\kappa \right)}{\chi }_{1^m}^{\kappa }{s}_{\kappa }\left(1\right),$$

(84)

where the sum is over the partition $\kappa$ of the integer m.

8.4. Equivalent Formulations

Equation (55) can appear in different contexts that provide interesting interpretations. Following [86,87,88], and using (64) and (65), at a fixed time t, one can identify the Lyapunov exponents w’s with the spectrum of the matrix

$$W=\sqrt{4\gamma tn}H+\left(4\gamma t\right)D,$$

(85)

where H is drawn from the GUE distribution (7) and $D=\mathrm{diag}(\frac{n-1}{2},\frac{n-3}{2},\dots ,-\frac{n-1}{2})=\mathrm{diag}({\delta }_1,\dots ,{\delta }_n)$, see also [89]. The scaled distribution of the largest eigenvalue of W was computed at large n in [90], see Section III there, and found to be GUE Tracy-Widom, since no localization transition takes place when the elements of D are equispaced; see also [91]. Besides, Equation (85) is particularly effective for numerical sampling from the distribution Equation (55).

Equivalently, the w’s can be seen as performing a DBM with $\beta =2$ in inverse time $\sim 1/t$. For time inversion of the DBM we refer to, e.g., Appendix B in [90] with equally spaced initial condition. Indeed, one can rewrite (85) as

$$W=4\gamma tnX,X=\mathrm{diag}\left(\frac{{\delta }_i}{n}\right)+\sqrt{s}H,$$

(86)

with $s=1/\left(4\gamma tn\right)$, and the eigenvalues $\overrightarrow{x}\left(s\right)$ of X have the same joint law as a DBM at time s with initial condition $\overrightarrow{x}\left(0\right)=\overrightarrow{\delta }/n$. This correspondence is given in Appendix D. Note that the $\overrightarrow{x}\left(s\right)$ form a determinantal point process [88], whose kernel is given in Appendix E. The interpretation of Equation (85) already indicates a qualitative behavior for the spectrum of the w’s: at initial times, the first term dominates and the distribution will resemble the one of a GUE in with eigenvalues in the support $[-4\sqrt{t\Gamma },4\sqrt{t\Gamma }]$. At larger times, the second term becomes more important and the distribution becomes uniformly spread in $[-2t\Gamma ,2t\Gamma ]$. It is also useful to write the distribution $P_0\sim e^{-n^2{\mathcal{E}}_t\left(f\right)}$ as a functional of the single particle density

$$f\left(w\right)=\frac{1}{n}\sum _{\alpha }\delta (w-w_{\alpha }),$$

(87)

with the functional

$${\mathcal{E}}_t\left(f\right)=\frac{1}{8\Gamma t}\int dw{w}^{2}f\left(w\right)-\frac{1}{2}\int dwd{w}^{\prime }f\left(w\right)f\left(w^{\prime }\right)\left(\log \sinh \frac{|w-w^{\prime }|}{2}+\log |w-w^{\prime }|\right).$$

(88)

One can interpret this as the energy of gas particles in the presence of an external harmonic trap that repel each other. When $\Gamma t=O\left(1\right)$, the different terms are of the same order: at large n, the particles will have a separation $\propto t\gamma /n$ and a continuous description emerges. We will analyze this regime in the next section. We will then discuss the long-time regime which emerges when $t\sim n/\Gamma =1/\gamma$.

8.5. Coulomb Gas Regime $\Gamma t\sim O\left(1\right)$

To quantitatively analyze the crossover between the semicircle and the uniform distribution predicted by the form Equation (85), we rescale the time in the following way

$$t=\frac{\tau }{4\gamma n}=\frac{\tau }{4\Gamma },$$

(89)

and consider the limit $n\to \infty$ at fixed $\tau$. The above correspondence in (86) shows that $s=1/\tau$, and $W=\tau X$. The interpretation as a DBM in inverse time allows us to compute the limiting resolvent

$$g(z,\tau ):=\underset{\underset{t=\tau /\left(4\gamma n\right)\to 0}{n\to +\infty }}{\lim }\frac{1}{n}\sum _i\frac{1}{z-w_i\left(t\right)},$$

(90)

using the complex Burgers equation (see details in Appendix D). One finds that $g=g(z,\tau )$ satisfies the parametric equation

$$z=\tau g+\frac{\tau }{2}\coth \left(\frac{\tau g}{2}\right).$$

(91)

We can set $z=w-i{0}^{+}$ and $g=g_r+i\pi f$, where f is the spectral density. Eliminating the real part $g_r=\mathrm{Re}\left(g\right)$ one finds (see Appendix D) that the density $f=f_{\tau }\left(w\right)$ is the solution of

$$\begin{array}{cc}\hfill & w=\pm \left[\log +\left(b_{\tau }\left(f\right)+\sqrt{b_{\tau }{\left(f\right)}^2-1}\right)+\frac{\pi \tau f}{\sin \left(\pi \tau f\right)}\sqrt{b_{\tau }{\left(f\right)}^2-1}\right],\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill & b_{\tau }\left(f\right)=\cos \pi \tau f+\frac{\sin \pi \tau f}{2\pi f}.\hfill \end{array}$$

(93)

Its support is an interval with edges at $w=\pm w_e=\pm \left[\mathrm{arccosh}(1+\frac{\tau }{2})+\sqrt{{(1+\frac{\tau }{2})}^2-1}\right]$. As anticipated from the qualitative analysis of Equation (85), the density interpolates (see Figure 2) between a semi-circle at small $\tau$, with $w_e\simeq 2\sqrt{\tau }+\frac{{\tau }^{3/2}}{12}$, and a square distribution at large $\tau$ with $w_e=\frac{\tau }{2}+\log \left(e\tau \right)+\frac{1}{\tau }+O(1/{\tau }^2)$. At all times $\tau >0$ the density vanishes at the edges as a square root $f\left(w\right)\sim B_{\tau }{|w_e-w|}^{1/2}$, with $B_{\tau }=\sqrt{2}/\left[\pi {\tau }^{3/4}{(4+\tau )}^{1/4}\right]$, and Wigner–Dyson gap statistics near the edges.

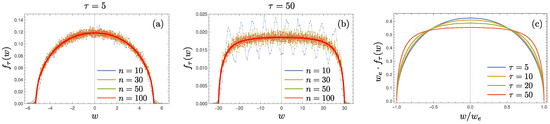
Figure 2. Short time behavior. The density $f_{\tau }\left(w\right)$ in the short time $t=\tau /4\Gamma \sim 1/\Gamma$ regime, with $\tau$ finite. $f_{\tau }\left(w\right)$ features a crossover between a semi-circle at small $\tau$ and a square distribution at larger $\tau$. (a) The small-$\tau$ semi-circle distribution is displayed for $\tau =5$ and increasing n from $n=10$ to $n=100$. The red solid line shows the theoretical $n\to \infty$ curve. (b) The large-$\tau$ square distribution is shown for $\tau =50$ and increasing n, with the red solid line showing the $n\to \infty$ curve. (c) The crossover from semi-circle towards square distribution is shown for increasing $\tau$ from $\tau =5$ to $\tau =50$. All solid lines represent the theoretical density $w_{e}w·f_{\tau }\left(w\right)$ on the rescaled $w/w_e$ axis, where $w_e$ is the edge coordinate for $f_{\tau }\left(w\right)$ in the $n\to \infty$ limit.

Although the density is known in parametric form, one can also use Equation (82) to extract the exponential moments. After some manipulation on the hypergeometric function, we find

$$\mu \left(m\right)=\underset{\begin{array}{c}n\to \infty \\ t=\tau /n\end{array}}{\lim }\frac{M\left(m\right)}{n}=\frac{e^{m\tau /2}{L}_{m-1}^{\left(1\right)}(-m\tau )}{m},$$

(94)

where $L_m^{\left(\alpha \right)}\left(x\right)$ denotes the generalized Laguerre polynomial, with ${\lim }_{m\to 0}\mu \left(m\right)=1$. A numerical check confirms that the density implicitly defined in Equation (92) satisfies

$$\mu \left(m\right)={\int }_{-w_e}^{w_e}dwf\left(w\right)e^{mw}.$$

(95)

The fact that the variables become dense and described by a continuous distribution ensures that $\mathsf{\Omega }\left(1\right)/n\to \mu \left(1\right)$ in Equation (62) is self-averaging and thus

$$\underset{n\to \infty }{\lim }{n}^{-m}\mathsf{\Omega }\left(m\right)=\mu {\left(1\right)}^m=e^{\tau m/2}.$$

(96)

8.6. Universal Regime $\Gamma t=O\left(n\right)$

8.6.1. Scaling of the Edge

Now, we consider the situation where time is scaled as $t=O(n/\Gamma )$. Using the rescaled rate $\gamma$, we can equivalently say that $\gamma t=O\left(1\right)$ whereas $n\to \infty$. In this regime the repulsion due to the $\log \sinh$ term in becomes more relevant. As a result, the Lyapunov exponents w are well separated one from the other. More precisely, assuming the ordering $w_1<w_2<\dots <w_n$, one expects that the separation between two consecutive variables $w_{\alpha +1}-w_{\alpha }=O\left(\gamma t\right)$, so that the position of the edge ${\overline{w}}_e={⟨w_n⟩}_0=O\left(t\gamma n\right)$. However, each variable $w_{\alpha }$ will have fluctuations of $O\left(\sqrt{\gamma t}\right)$ so that the interactions are relevant and complicate the analysis. A similar lattice structure was already demonstrated in a related model involving a $\log \sinh$-potential [92]. Here, the Coulombic repulsion $\log |w-w^{\prime }|$ is an additional ingredient that modifies that short-distance behavior. We can obtain a preliminary understanding of this regime by taking the $n\to \infty$ limit from the general formula of moments (83). In this limit, the moments are dominated by the largest $w_{\alpha }\sim {\overline{w}}_e$ near the edge. We can determine their value expanding $\Gamma (n+m-r)/\Gamma (n-r)\simeq n^m$ in Equations (81) and (82) and performing the sum, obtaining

$$\mathfrak{M}\left(m\right):=\underset{n\to \infty }{\lim }{e}^{-m{\overline{w}}_e}M\left(m\right)=\frac{2^{m-1}\sinh {\left(2m\gamma t\right)}^{m-1}}{m!},$$

(97)

where we also fixed ${\overline{w}}_e=2n\gamma t+\log n$. This formula suggests the existence of non-trivial statistics governing the fluctuations of the Lyapunov exponents w’s at the edge. However, we note that it does not define a normalized distribution since $\mathfrak{M}(m\to 0)=\infty$. This is due to a crossover at small m between a regime dominated by the bulk with $M(m\to 0)=n$ and one dominated by the edge $M\left(m\right)\stackrel{n\gg 1}{=}O\left({\overline{w}}_e^m\right)$. An identical formula can be obtained in the analogous long-time limit considering the product of Wishart random matrices (see Equation (3.41) in [93]). This is a manifestation of universality expected at large times in monitored systems and more generally in products of random matrices [94].

The calculation of the moments of the trace in this regime is much more involved, but it can be expressed as in Equation (84). Indeed, in the limit of large n, we can replace $s_{\kappa }\left(1\right)\to n^m{\chi }_{1^m}^{\kappa }/m!$ [82]. One can understand this using $s_{\kappa }(y_1=1,\dots ,y_n=1)$ counts the number of semistandard Young tableau of shape $\kappa$ and involving n entries, whereas ${\chi }_{1^m}^{\kappa }$ counts the number of standard Young tableau with entries $1,\dots ,m$. At large n, the difference between semistandard and standard Young tableau becomes irrelevant and $s_{\kappa }\left(1\right)/{\chi }_{1^m}^{\kappa }\sim \left(\genfrac{}{}{0pt}{}{n}{m}\right)\sim n^m/m!$. We thus obtain

$$\mathfrak{O}\left(m\right):=\underset{n\to \infty }{\lim }{e}^{-m{\overline{w}}_e}\mathsf{\Omega }\left(m\right)=\frac{1}{m!}\sum _{\kappa ⊢m}{e}^{4\gamma t\nu \left(\kappa \right)}{\left({\chi }_{1^m}^{\kappa }\right)}^2$$

(98)

which was obtained in [94] in a different model as an additional manifestation of the universality.

8.6.2. Asymptotics at Large $\gamma t$

When $\gamma t\gg 1$, the separations are $|w_{\alpha }-w_{\beta }|\gg 1$$\forall \alpha ,\beta$. Additionally, their fluctuations are much smaller than their separation. In this regime, we can approximate in the potential

$$\log \sinh |\frac{w_{\alpha }-w_{\beta }}{2}|\sim |\frac{w_{\alpha }-w_{\beta }}{2}|,$$

(99)

which is the 1-dimensional Coulombic repulsion. This kind of potential was recently studied in [95] in the context of ranked diffusion. This potential induces a force $f_{\alpha }=\frac{1}{2}{\sum }_{\beta \ne \alpha }\mathrm{sign}(w_{\alpha }-w_{\beta })$, which simply counts the number of slower particles in the back of $w_{\alpha }$, minus the faster ones in its front. Assuming a given ordering $w_1\ll w_2\ll \dots \ll w_n$, we obtain the simple dynamics

$$d{w}_{\alpha }\sim 4\gamma v_{\alpha }dt+\sqrt{4\gamma }d{B}_{\alpha }.$$

(100)

where the drift velocity $v_{\alpha }:=\frac{1}{2}(2\alpha -n-1)$. This equation is an example of ranked diffusion (RD), namely, a diffusion process in one dimension where the n particles undergo a drift term proportional to their respective rank [95,96]. In the RD problem, however, the particles can cross freely, whereas here they cannot cross, which leads to different types of fluctuations at finite t. Nevertheless, in both models in the regime $\gamma t\gg 1$, the equations decouple and can be solved separately, namely

$$w_{\alpha }\left(t\right)\sim 4\gamma v_{\alpha }t+\sqrt{4\gamma }{B}_{\alpha }\left(t\right),$$

(101)

where we recall that the $B_{\alpha }\left(t\right)$’s are n independent standard Brownian motions, each of variance t at time t. Equation (101) gives some characterization of the joint probability distribution of the Lyapunov exponents w in this large time $\gamma t\gg 1$ regime. It is not complete however, as there are $O\left(1\right)$ contributions of the joint cumulants of the $w_{\alpha }$ which persist at infinite time. These were computed in Section III-D of Ref. [95] by a saddle point method, and that calculation is easily extended to the present model in Appendix F. As a result, Equation (101) must be treated with care when computing exponential moments.

9. Entanglement Entropies for Continuous Monitoring

Now, we make use of the results obtained in the previous section for the unbiased ensemble ${⟨\dots ⟩}_0$ to characterize the behavior of the entanglement entropies.

9.1. Short Time Regime

First of all, let us consider the Coulomb gas regime. In this case, we can use the fact that the moments are self-averaging, i.e., $n^{-1}\mathrm{tr}{\tilde{\rho }}^k\stackrel{inlaw}{\to }\mu \left(k\right)$. Thus, from Equation (58), we obtain

$$⟨S_k⟩=S_{\max }+\frac{1}{1-k}\log \left[\frac{\mu \left(k\right)}{\mu {\left(1\right)}^k}\right]=\log n+\frac{1}{1-k}\log \left[\frac{L_{k-1}^{\left(1\right)}(-k\tau )}{k}\right],$$

(102)

where the Von Neumann entropy can be recovered in the limit $k\to 1$. Using $L_{k-1}^{\left(1\right)}(-k\tau )/k=1+k(k-1)\tau /2+O\left({\tau }^2\right)$ for $\tau \ll 1$, and $L_{k-1}^{\left(1\right)}(-k\tau )/k=k^{k-2}{\tau }^{k-1}/(k-1)!+O\left({\tau }^{k-2}\right)$ for $\tau \gg 1$, we also obtain the asymptotic expansions

$$⟨S_k⟩=\left\{\begin{array}{cc}{S}_{\max }-\frac{k\tau }{2}+O\left({\tau }^2\right),\hfill & \tau \ll 1\hfill \\ \log \frac{n}{\tau }+\frac{\log k!}{k-1}-\log \left(k\right),\hfill & \tau \gg 1\hfill \end{array}\right.$$

(103)

from which we can extract the $k\to 1$ limit

$$⟨S_1⟩=\left\{\begin{array}{cc}{S}_{\max }-\frac{\tau }{2}+O\left({\tau }^2\right),\hfill & \tau \ll 1\hfill \\ \log \frac{n}{\tau }-{\gamma }_E+1,\hfill & \tau \gg 1\hfill \end{array}\right.,$$

(104)

where ${\gamma }_E$ is the Euler–Mascheroni constant (not to be confused with the rescaled rate $\gamma$). Note that in this regime, the Born rule (2) and unbiased outcomes (5) give the same result, since the weight of each trajectory factorizes from the rest.

9.2. Universal Regime

As we discussed in Section 8.6, this regime is much harder to address as the w’s are strongly correlated but the moments $M\left(m\right)$ and $\mathsf{\Omega }\left(m\right)$ are not independent: they are dominated by the behavior around the edge (see Equations (97) and (98)). However, we can still access the Von Neumann entropy by making use of Equation (63). Equation (97) admits a simple analytic continuation for $m\to 1$ and we obtain

$${\mathfrak{M}}^{\prime }\left(1\right)=\log \left(2\sinh \left(2\gamma t\right)\right)+\gamma -1.$$

(105)

Unfortunately, the dependence on m in Equation (98) is much less transparent. A way to perform the analytic continuation was developed in [94]. Here, we analyze the asymptotic behavior. At small $\gamma t$’s, because of the symmetry $\nu \left({\kappa }^{\prime }\right)=\nu (-\kappa )$, where ${\kappa }^{\prime }$ is the integer partition dual to $\kappa$, it is clear that $\mathsf{\Omega }\left(m\right)$ is an even function of time for every m. Thus, at small $\gamma t\ll 1$, we can conclude that $\mathsf{\Omega }\left(m\right)=O{\left(\gamma t\right)}^2$. Up to this order, the dynamics of Von Neumann entanglement is fully captured by Equation (105). Thus, we have

$$⟨S_1⟩=-{\mathfrak{M}}^{\prime }\left(1\right)+O{\left(t\gamma \right)}^2=-\log \left(4\gamma t\right)-{\gamma }_E+1+O{\left(t\gamma \right)}^2$$

(106)

which connects nicely with the behavior for $\tau \gg 1$ obtained in Equation (104), recalling that $\tau =4\gamma nt$.

Although the regime of intermediate times is hard to access, we can still estimate the asymptotic expansion $\gamma t\gg 1$. As discussed in Section 8.6.2, the Lyapunov exponents separate linearly in time because of the drift Equation (101). Returning to the eigenvalues ${\lambda }_{\alpha }=e^{w_{\alpha }}/{\sum }_{\beta }{e}^{w_{\beta }}$, it is evident that if $w_n\gg w_{\beta \ne n}$, then ${\lambda }_{\alpha }\sim e^{w_{\alpha }-w_n}\sim {\delta }_{\alpha ,n}$, and the first $n-1$ eigenvalues are suppressed by purification. In particular, using Equation (101), we also have that

$$⟨{\lambda }_{\alpha \ne n}\left(t\right)⟩=\frac{{⟨e^{w_{\alpha }}⟩}_0}{{⟨{\sum }_{\beta }{e}^{w_{\beta }}⟩}_0}\sim \frac{{⟨e^{4\gamma t{v}_{\alpha }+\sqrt{4\gamma }{B}_{\alpha }\left(t\right)}⟩}_B}{{⟨e^{4\gamma t{v}_n+\sqrt{4\gamma }{B}_n\left(t\right))}⟩}_B}\sim e^{(\alpha -n)4\gamma t},$$

(107)

where $v_{\alpha }$ are the drift velocities in Equation (100) and ${⟨\cdots ⟩}_B$ denotes the average over the independent Brownians. The sum of the first $n-1$ averages gives ${\sum }_{\alpha <n}⟨{\lambda }_{\alpha }\left(t\right)⟩\sim e^{-4\gamma t}$, yielding

$$1-⟨{\lambda }_n\left(t\right)⟩\sim e^{-4\gamma t}.$$

(108)

Moreover, the ratio between any two eigenvalues $⟨{\lambda }_{\alpha \ne n}\left(t\right)⟩$, $⟨{\lambda }_{\beta \ne n}\left(t\right)⟩$

$$\frac{⟨{\lambda }_{\alpha }\left(t\right)⟩}{⟨{\lambda }_{\beta }\left(t\right)⟩}\sim e^{(\alpha -\beta )4\gamma t},$$

(109)

which is independent of number n of diffusing particles, and indicates that the first $n-1$ eigenvalues are logarithmically equispaced, as we show in Figure 3.

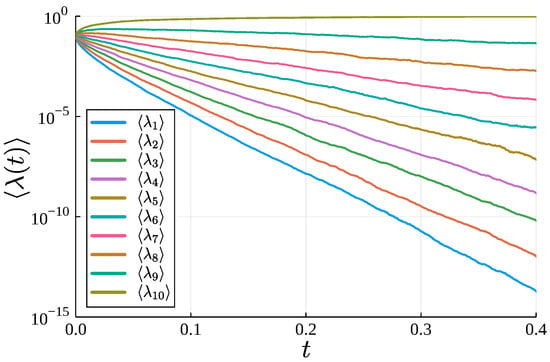
Figure 3. Long-time ranked diffusion. Long-time dynamics of the averaged eigenvalues $\lambda \left(t\right)$ for $x=0$, $\gamma =1$, $n=10$, whereas the maximum eigenvalue tends to one as $⟨{\lambda }_{10}\left(t\right)⟩\sim 1-e^{-4t}$ as time increases, the first $n-1$ eigenvalues are equispaced in logarithmic scale, i.e., $⟨{\lambda }_{\alpha }\left(t\right)⟩/⟨{\lambda }_{\beta }\left(t\right)⟩=e^{4(\alpha -\beta )t}$.

Because of the exponential separation of the eigenvalues, from Equation (108), we obtain the estimate for the Von Neumann entropy

$$\begin{array}{cc}\hfill ⟨S_1⟩& \sim -\frac{{⟨e^{w_n}\log (e^{w_n}/\sum e^{w_{\alpha }})⟩}_0}{{⟨e^{w_n}⟩}_0}=\frac{{⟨e^{w_n}\log (1+{\sum }_{\alpha <n}{e}^{w_{\alpha }-w_n})⟩}_0}{{⟨e^{w_n}⟩}_0}\approx \hfill \\ \hfill & \approx \frac{{⟨e^{w_{n-1}}⟩}_0}{{⟨e^{w_n}⟩}_0}=O\left(e^{-4\gamma t}\right),\hfill \end{array}$$

(110)

which is in agreement with the $n=2$ result of Equation (18) if one replaces $\Gamma =2\gamma$. A more detailed discussion of this approximation is given in Appendix F.

Although this suggests that for any n only the two largest eigenvalues matter for the calculations, the prefactor of the asymptotic expression of $⟨S_1⟩$ does not reduce to the one from the $n=2$ model. Indeed, a more careful calculation (see Appendix G) shows that the saddle-point evaluation of the numerator of $⟨S_1⟩$ is shifted with respect to the one of the normalization, so that the two prefactors do not cancel out. In particular, we have

$$⟨S_1⟩=\frac{n-1}{n}{e}^{-4\gamma t}\left(1+\frac{1}{\sqrt{4\pi \gamma t}}+O\left(t^{-1}\right)\right),$$

(111)

which once again agrees with the result of the $n=2$ case, whereas the prefactor $(n-1)/n$ tends to 1 in the $n\to \infty$ limit.

10. Conclusions

In this work, we studied the purification dynamics induced by weak measurement, where the measurement operators are random matrices drawn from the GUE. The ensuing is written in terms of a stochastic Schrödinger equation, invariant under unitary transformation. Because of rotational invariance, we were able to determine the evolution of the density matrix eigenvalues ${\left\{{\lambda }_{\alpha }\right\}}_{\alpha =1}^n$, both for imperfect and perfect monitoring. In both cases, no MIPT takes place, as the system is far away from the critical point and is characterized by volume-law scaling of the entanglement entropy.

In the former case of imperfect measurements $x>0$, we were able to thoroughly characterize the stationary distribution of the density matrix in the limit $n\to \infty$. There, the stationary joint probability distribution of the eigenvalues of the density matrix takes the typical expression of matrices from the inverse-Wishart ensemble, and the spectral density attains the corresponding inverse-Marchenko–Pastur form. Anyway, we showed that a solution for the finite-time stochastic dynamics also exists via a mapping to a quantum problem in imaginary time. In this context, the eigenvalue evolution at $x>0$ and for finite n is still unknown. The relevant $n=2$ case seems to suggest that the stationary state does not belong to the inverse-Wishart ensemble, and that a more sophisticated stratagem must be sought in order to treat the non-conservative forces due to additional dephasing.

In the case of perfect measurements $x=0$, we were able to fully determine the joint distribution function for the eigenvalues, at both finite time and finite n. Again, this can be conducted by mapping the stochastic dynamics onto fermions in imaginary time. Surprisingly, those undergo free diffusion as the external potential due to weak measurement disappears. Moreover, this allows us to factorize the joint probability distribution with respect to the $\mathrm{tr}\rho =1$ constraint, thus making the computation of average quantities accessible. We identify two different regimes. The first is a short-time one, where a Coulomb gas distribution appears with a time-dependent continuous density characterizing the spectrum of Lyapunov exponents. The density exhibits a characteristic crossover between the GUE semicircle and the uniform distribution. At later times, the Lyapunov exponents separate further and a continuous description is not possible anymore. Our calculations are perfectly consistent with the prediction of [94] and provide a new example supporting the universality of this regime. Subsequently, the Lyapunov exponents separate linearly over time, and the interactions between them become less important. In this regime, the dynamics resemble that of a ranked diffusion. We use this information to characterize the dynamics of entanglement in the various time regimes.

Some comments are important. It would certainly be intriguing to characterize the crossover at $x\to 0$ small and large times. Furthermore, from a technical point of view, it would be interesting to tie the regime emerging at long times with the spectral distribution of Lyapunov exponents near the edge.

Finally, interesting questions endure, characterizing the differences induced by studying the problem within other random matrix models, such as the Gaussian orthogonal ensemble.