Excitation Spectra and Edge Singularities in the One-Dimensional Anisotropic Heisenberg Model for Δ = cos(π/n), n = 3,4,5
Abstract
:1. Introduction
2. Bethe Ansatz Equations for the Anisotropic Heisenberg Ring for
3. Excitation Energies in Non-Zero Magnetic Field
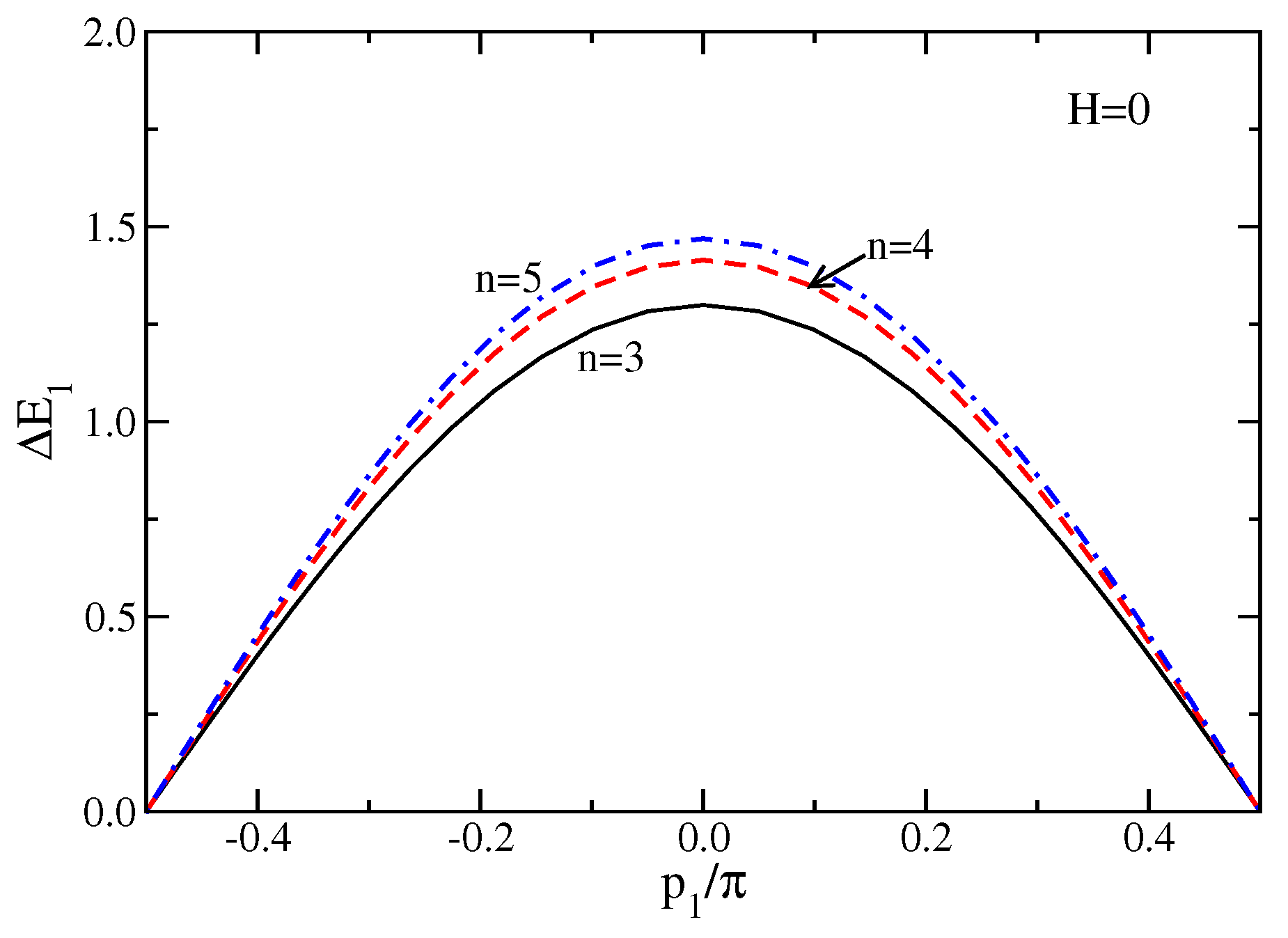
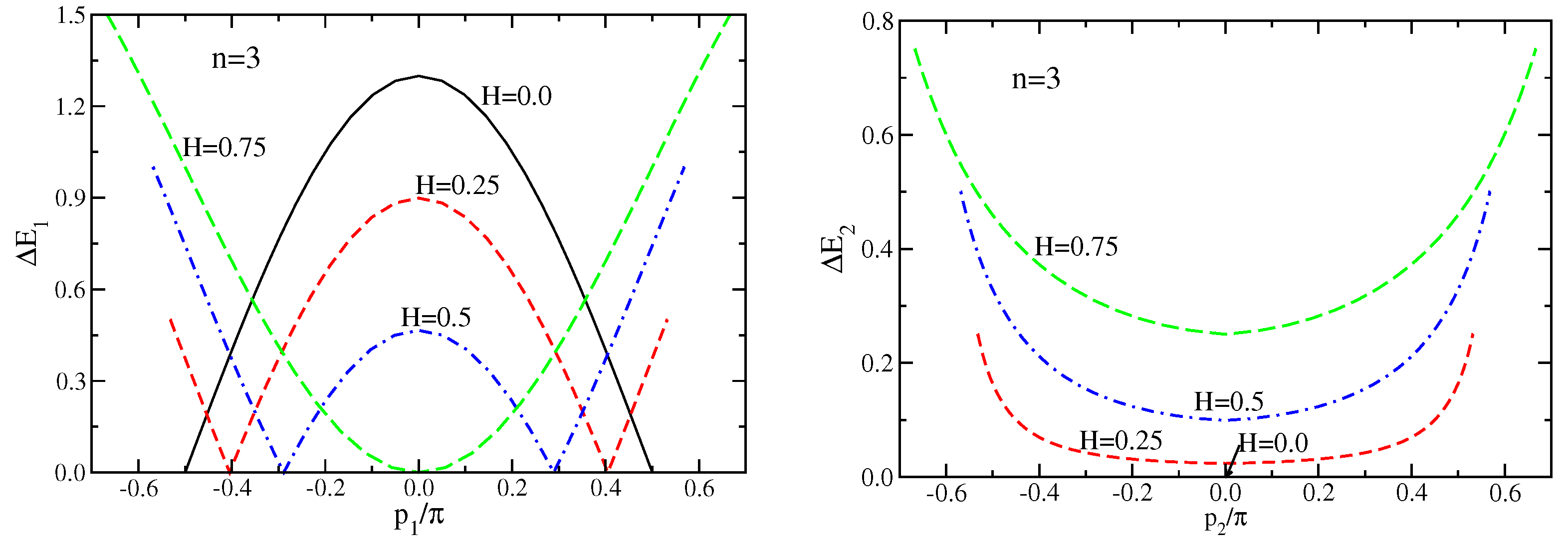
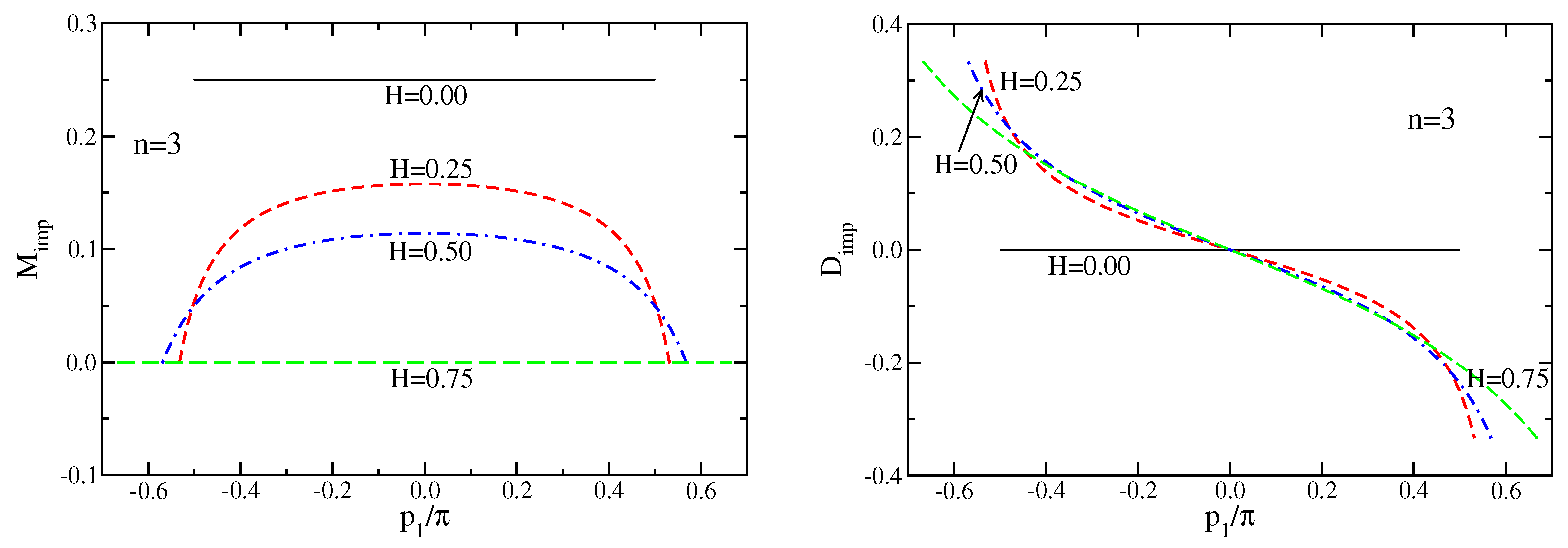
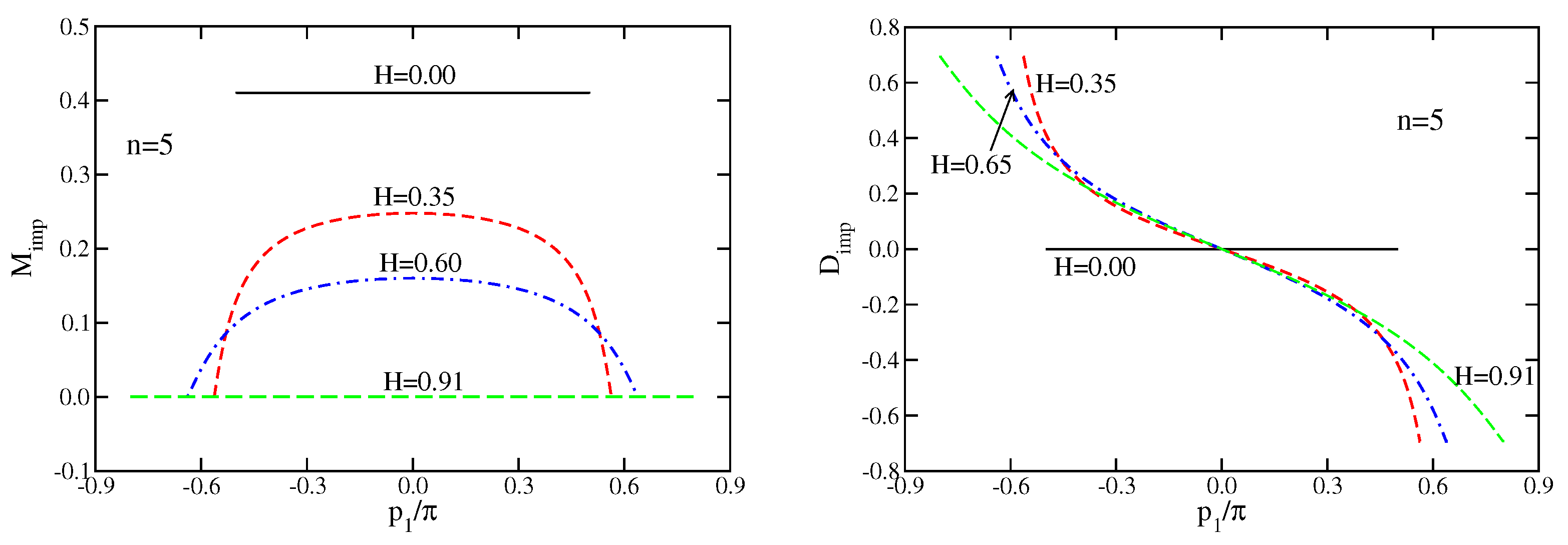
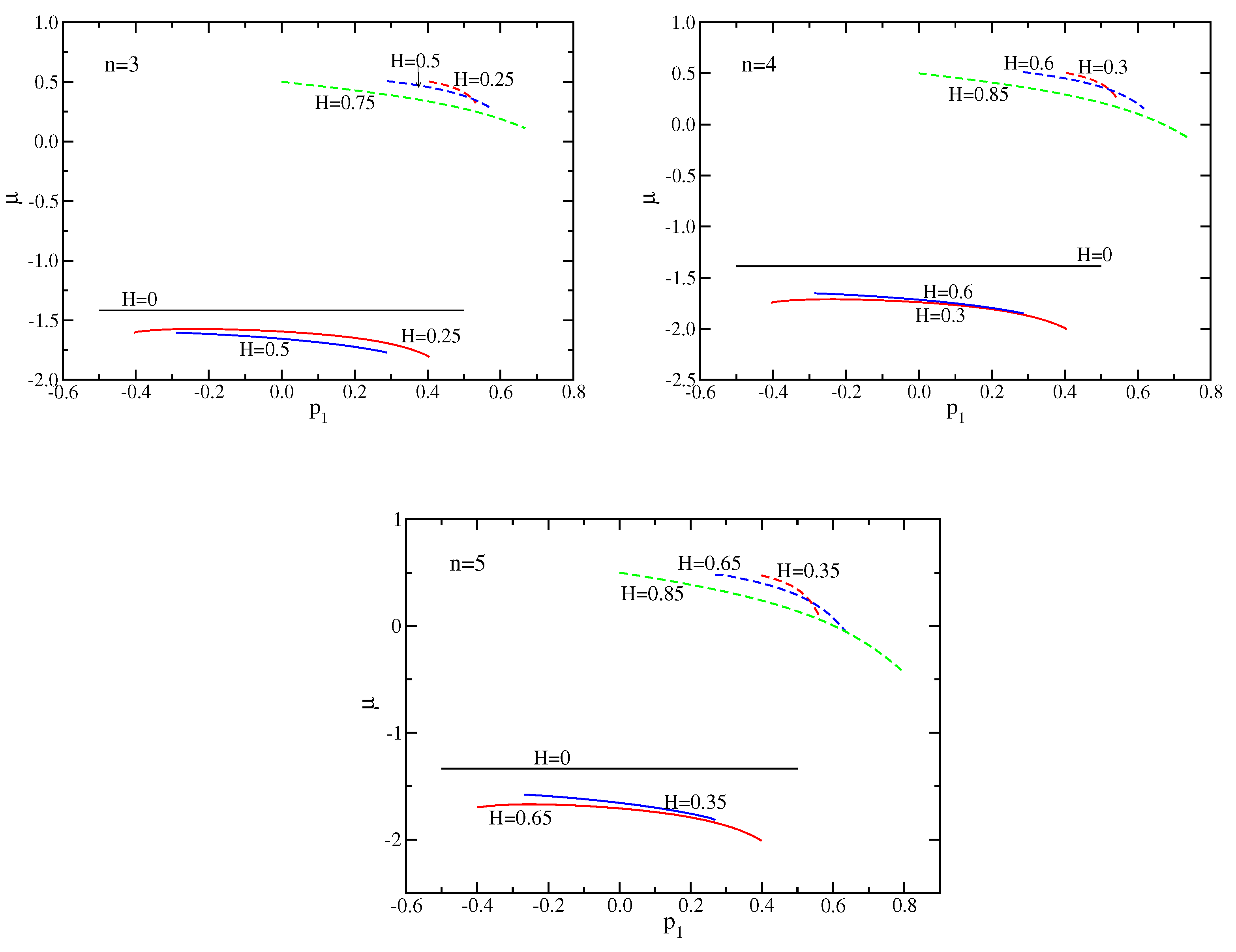
3.1. Case
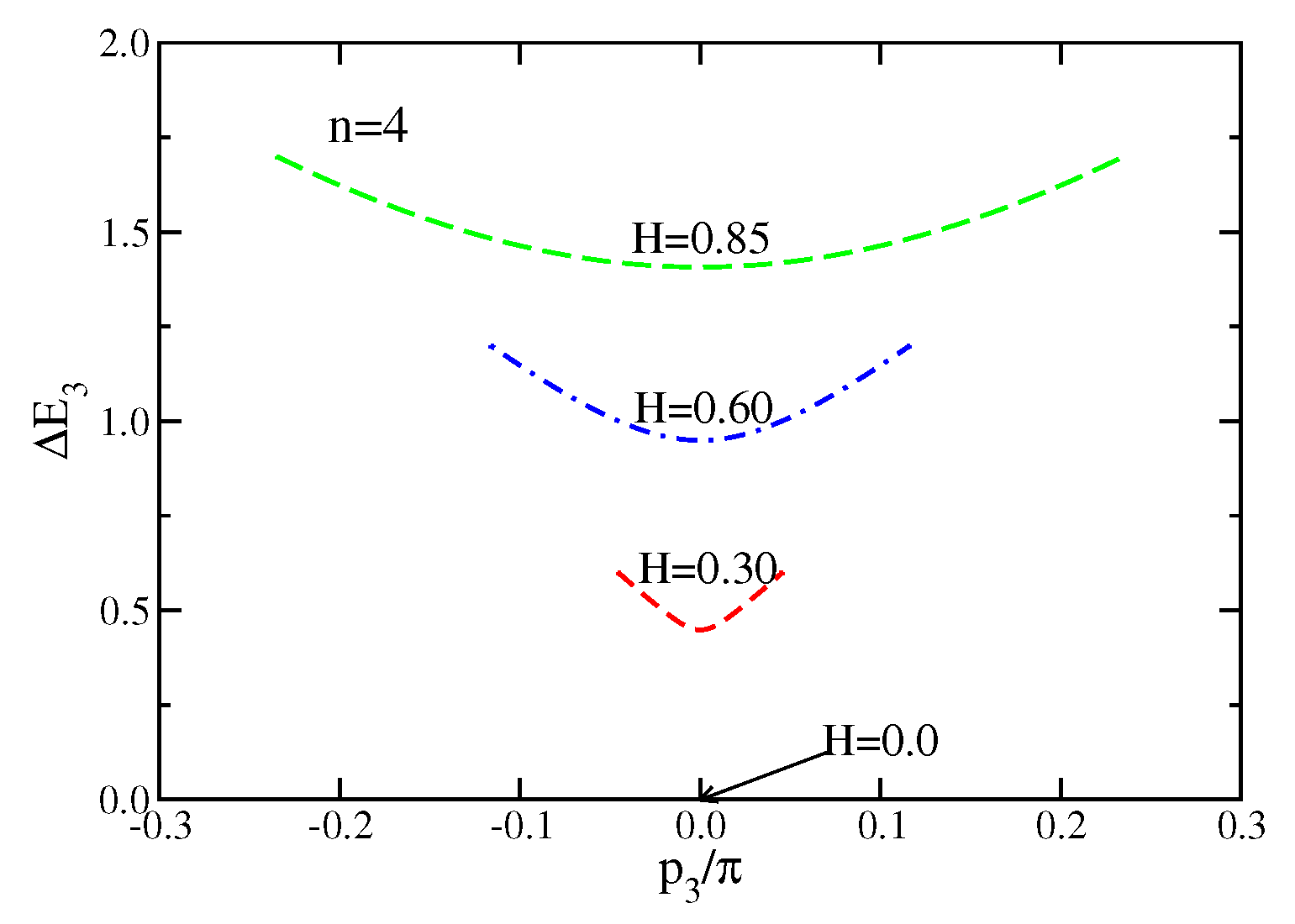
3.2. Case
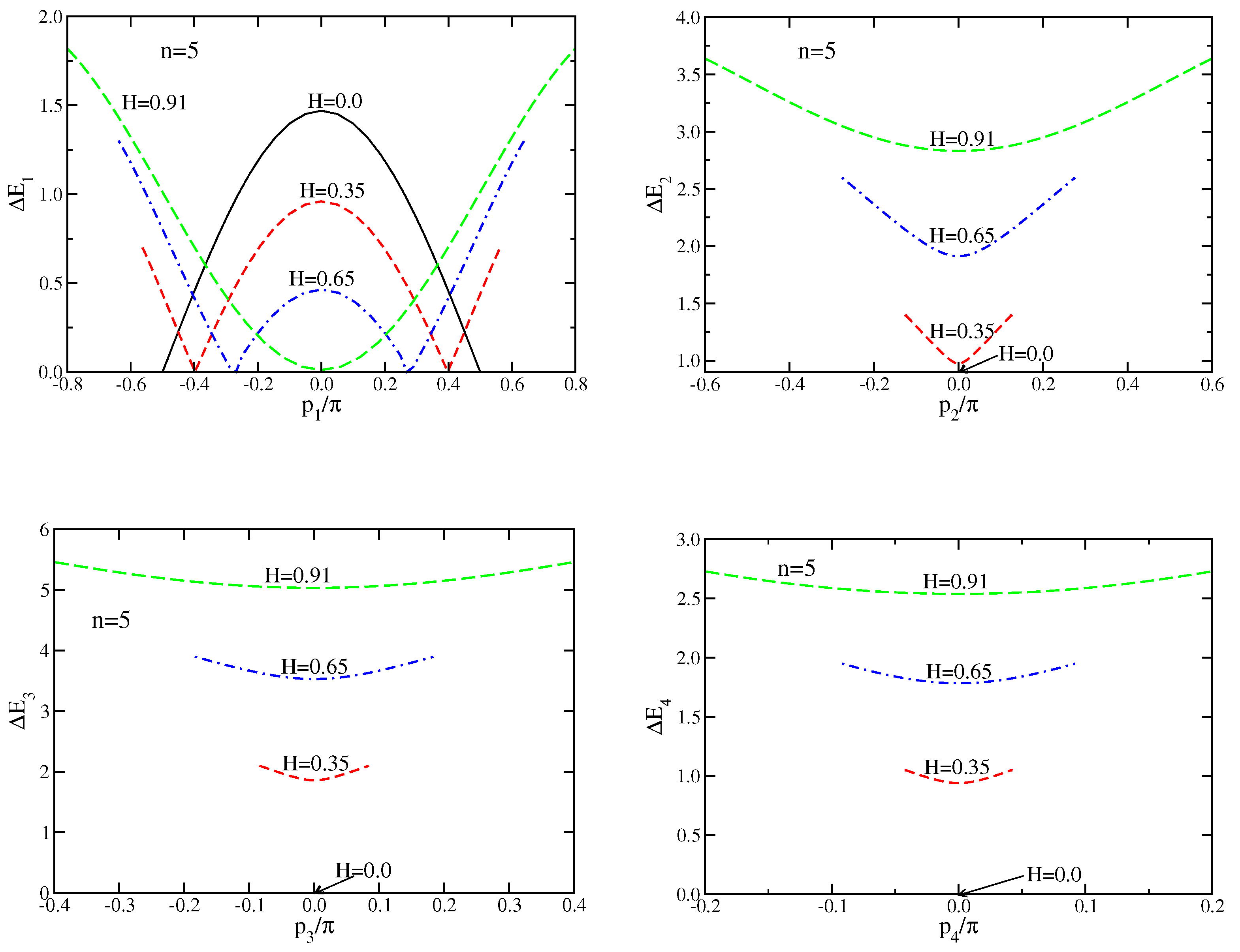
3.3. Case
3.4. Luttinger Liquid
3.5. Group Velocities
3.6. Conformal Towers
4. Field Theory Model for the Luttinger Liquid with Mobile Impurity
5. Relation to the Bethe Ansatz Results
5.1. Densities
5.2. Energy
5.3. Integration Limits
5.4. Relation of to Quantum Numbers
5.5. Luttinger Parameter
5.6. Relation of the Bethe Ansatz with the Field Theoretical Quantities
6. Conclusions
Funding
Conflicts of Interest
References
- Orbach, R. Linear antiferromagnetic chain with anisotropic coupling. Phys. Rev. 1958, 112, 309. [Google Scholar] [CrossRef]
- des Cloizeaux, J.; Gaudin, M. Anisotropic linear magnetic chain. J. Math. Phys. 1966, 7, 1384. [Google Scholar] [CrossRef]
- Yang, C.N.; Yang, C.P. One-dimensional chain of anisotropic spin-spin interactions. I. Proof of Bethe’s hypothesis for ground state in a finite system. Phys. Rev. 1966, 150, 321. [Google Scholar] [CrossRef]
- Yang, C.N.; Yang, C.P. One-dimensional chain of anisotropic spin-spin interactions. II. Properties of the ground-state energy per lattice site for an infinite system. Phys. Rev. 1966, 150, 327. [Google Scholar] [CrossRef]
- Yang, C.N.; Yang, C.P. One-dimensional chain of anisotropic spin-spin interactions. III. Applications. Phys. Rev. 1966, 151, 258. [Google Scholar] [CrossRef]
- Burkhardt, T.W.; Schlottmann, P. Edge pinning and internal phase transitions in a system of domain walls. Z. Phys. B 1984, 54, 151. [Google Scholar] [CrossRef]
- Burkhardt, T.W. Localisation-delocalisation transition in a solid-on-solid model with a pinning potential. J. Phys. A 1981, 14, L63. [Google Scholar] [CrossRef]
- Burkhardt, T.W.; Schlottmann, P. Unbinding transition in a many-string system. J. Phys. A 1993, 26, L501. [Google Scholar] [CrossRef]
- Caux, J.-S.; Maillet, J.M. Computation of dynamical correlation functions of Heisenberg chains in a magnetic field. Phys. Rev. Lett. 2005, 95, 077201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pereira, R.G.; Sirker, J.; Caux, J.-S.; Hagemans, R.; Maillet, J.M.; White, S.R.; Affleck, I. Dynamical spin structure factor for the anisotropic spin-1/2 Heisenberg chain. Phys. Rev. Lett. 2006, 96, 257202. [Google Scholar] [CrossRef] [PubMed]
- Pereira, R.G.; Sirker, J.; Caux, J.-S.; Hagemans, R.; Maillet, J.M.; White, S.R.; Affleck, I. Dynamical structure factor at small q for the XXZ spin-1/2 chain. J. Stat. Mech. 2007, P08022. [Google Scholar]
- Pereira, R.G.; White, S.R.; Affleck, I. Exact edge singularities and dynamical correlations in spin-1/2 chains. Phys. Rev. Lett. 2008, 100, 027206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pereira, R.G.; White, S.R.; Affleck, I. Spectral function of spinless fermions on a one-dimensional lattice. Phys. Rev. B 2009, 79, 165113. [Google Scholar] [CrossRef] [Green Version]
- Caux, J.-S.; Konno, H.; Sorrell, M.; Weston, R. Tracking the effects of interactions on spinons in gapless Heisenberg chains. Phys. Rev. Lett. 2011, 106, 217203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caux, J.-S.; Konno, H.; Sorrell, M.; Weston, R. Exact form-factor results for the longitudinal structure factor of the massless XXZ model in zero field. J. Stat. Mech. 2012, P01007. [Google Scholar] [CrossRef]
- Gaudin, M. Thermodynamics of the Heisenberg-Ising ring for δ≥1. Phys. Rev. Lett. 1971, 26, 1301. [Google Scholar] [CrossRef]
- Caux, J.-S.; Mossel, J.; Pérez Castillo, I. The two-spinon transverse structure factor of the gapped Heisenberg antiferromagnetic chain. J. Stat. Mech. 2008, P08006. [Google Scholar] [CrossRef] [Green Version]
- Carmelo, J.M.P.; Sacramento, P.D. The role of q-spin singlet pairs of physical spins in the dynamical properties of the spin-1/2 Heisenberg-Ising XXZ chain. Nucl. Phys. B 2022, 974, 115610. [Google Scholar] [CrossRef]
- Yang, W.; Wu, J.; Xu, S.; Wang, Z.; Wu, C. One-dimensional quantum spin dynamics of Bethe string states. Phys. Rev. B 2019, 100, 184406. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, M.; Suzuki, M. One-dimensional anisotropic Heisenberg model at finite temperature. Prog. Theor. Phys. 1972, 48, 2187. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, M. One-dimensional Heisenberg model at finite temperature. Prog. Theor. Phys. 1971, 46, 401. [Google Scholar] [CrossRef]
- Takahashi, M. Low-temperature specific heat of spin-1/2 anisotropic Heisenberg ring. Prog. Theor. Phys. 1973, 50, 1519. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, M. Numerical calculation of thermodynamic quantities of spin-1/2 anisotropic Heisenberg ring. Prog. Theor. Phys. 1974, 51, 1348. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, M.; Yamada, M. Spin-1/2 one-dimensional Heisenberg ferromagnet at low-temperature. J. Phys. Soc. Jpn. 1985, 54, 2808. [Google Scholar] [CrossRef]
- Yamada, M.; Takahashi, M. Critical behavior of spin-1/2 one-dimensional Heisenberg ferromagnet at low-temperature. J. Phys. Soc. Jpn. 1986, 55, 2024. [Google Scholar] [CrossRef]
- Schlottmann, P. Critical behavior of the isotropic ferromagnetic quantum Heisenberg chain. Phys. Rev. Lett. 1985, 54, 2131. [Google Scholar] [CrossRef]
- Schlottmann, P. Low temperature behavior of the S = 1/2 ferromagnetic Heisenberg chain. Phys. Rev. B 1986, 33, 4880. [Google Scholar] [CrossRef]
- Imambekov, A.; Glazman, L.I. Phenomenology of One-Dimensional Quantum Liquids Beyond the Low-Energy Limit. Phys. Rev. Lett. 2009, 102, 126405, Universal Theory of Nonlinear Luttinger Liquids. Science 2009, 323, 228.. [Google Scholar] [CrossRef] [Green Version]
- Essler, F.H.L. Threshold singularities in the one-dimensional Hubbard model. Phys. Rev. B 2010, 81, 205120. [Google Scholar] [CrossRef] [Green Version]
- Schlottmann, P.; Zvyagin, A.A. Threshold singularities in a Fermi gas with attractive potential in one dimension. Nucl. Phys. B 2015, 2015 892, 269. [Google Scholar] [CrossRef] [Green Version]
- Ovchinnikov, A.A. Threshold singularities in the correlators of the one-dimensional models. J. Stat. Mech. Theory Exp. 2016, 2016, 063108. [Google Scholar] [CrossRef]
- Schlottmann, P. Exponents of the spectral functions in the one-dimensional Bose gas. Condens. Matter 2018, 3, 35. [Google Scholar] [CrossRef] [Green Version]
- Lieb, E.H.; Schultz, T.D.; Mattis, D.C. Two soluble models of an antiferromagnetic chain. Ann. Phys. 1961, 16, 407. [Google Scholar] [CrossRef]
- Katsura, S. Statistical Mechanics of the Anisotropic Linear Heisenberg Model. Phys. Rev. 1962, 127, 1508. [Google Scholar] [CrossRef]
- Haldane, F.D.M. ‘Luttinger liquid theory’ of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C Solid State Phys. 1981, 14, 2585. [Google Scholar] [CrossRef]
- Khodas, M.; Pustilnik, M.; Kamenev, A.; Glazman, L.I. Dynamics of excitations in a one-dimensional Bose liquid. Phys. Rev. Lett. 2007, 99, 110405. [Google Scholar] [CrossRef] [Green Version]
- Khodas, M.; Pustilnik, M.; Kamenev, A.; Glazman, L.I. Fermi-Luttinger liquid: Spectral function of interacting one-dimensional fermions. Phys. Rev. B 2007, 76, 155402. [Google Scholar] [CrossRef] [Green Version]
- Cheianov, V.V.; Pustilnik, M. Threshold Singularities in the Dynamic Response of Gapless Integrable Models. Phys. Rev. Lett. 2008, 100, 126403. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, T.L.; Imambekov, A.; Glazman, L.I. Fate of 1D Spin-Charge Separation Away from Fermi Points. Phys. Rev. Lett. 2010, 2010 104, 116403. [Google Scholar] [CrossRef] [Green Version]
- Imambekov, A.; Schmidt, T.L.; Glazman, L.I. One-dimensional quantum liquids: Beyond the Luttinger liquid paradigm. Rev. Mod. Phys. 2012, 84, 1253. [Google Scholar] [CrossRef] [Green Version]
- Schlottmann, P. Threshold singularities in the one-dimensional supersymmetric boson -fermion gas mixture. Int. J. Mod. Phys. B 2018, 32, 1850221. [Google Scholar] [CrossRef]
- Schlottmann, P. Edge singularities in the one-dimensional Bariev model. Nucl. Phys. B 2019, 949, 114808. [Google Scholar] [CrossRef]
- Noziéres, P.; de Dominicis, C.T. Singularities in the X-Ray Absorption and Emission of Metals. III. One-Body Theory Exact Solution. Phys. Rev. 1969, 178, 1097. [Google Scholar] [CrossRef]
- Schotte, K.D.; Schotte, U. Tomonaga’s Model and the Threshold Singularity of X-Ray Spectra of Metals. Phys. Rev. 1969, 182, 479. [Google Scholar] [CrossRef]
- Ogawa, T.; Furusaki, A.; Nagaosa, N. Fermi-edge singularity in one-dimensional systems. Phys. Rev. Lett. 1992, 68, 3638. [Google Scholar] [CrossRef]
- Castella, H.; Zotos, X. Exact calculation of spectral properties of a particle interacting with a one-dimensional fermionic system. Phys. Rev. B 1993, 47, 16186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sorella, S.; Parola, A. Spectral Properties of One Dimensional Insulators and Superconductors. Phys. Rev. Lett. 1996, 76, 4604. [Google Scholar] [CrossRef] [Green Version]
- Castro Neto, A.H.; Fisher, M.P.A. Dynamics of a heavy particle in a Luttinger liquid. Phys. Rev. B 1996, 53, 9713. [Google Scholar] [CrossRef] [Green Version]
- Tsukamoto, Y.; Fujii, T.; Kawakami, N. Critical behavior of Tomonaga-Luttinger liquids with a mobile impurity. Phys. Rev. B 1998, 58, 3633. [Google Scholar] [CrossRef]
- Schlottmann, P.; Zvyagin, A.A. Integrable supersymmetric t-J model with magnetic impurity. Phys. Rev. B 1997, 55, 5027. [Google Scholar] [CrossRef]
- Schlottmann, P.; Zvyagin, A.A. Exact solution for a degenerate Anderson impurity in the U→∞ limit embedded into a correlated host. Eur. Phys. J. B 1998, 5, 325. [Google Scholar] [CrossRef]
- Balents, L. X-ray-edge singularities in nanotubes and quantum wires with multiple subbands. Phys. Rev. B 2000, 61, 4429. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, A.; Kolezhuk, A.K.; McCulloch, I.P.; Schollwöck, U. Edge singularities in high-energy spectra of gapped one-dimensional magnets in strong magnetic fields. Phys. Rev. B 2007, 75, 094414. [Google Scholar] [CrossRef] [Green Version]
- Burovski, E.; Cheianov, V.; Gamayun, O.; Lychkovskiy, O. Momentum relaxation of a mobile impurity in a one-dimensional quantum gas. Phys. Rev. A 2014, 89, 041601. [Google Scholar] [CrossRef] [Green Version]
- Lieb, E.H. Exact analysis of an interacting Bose gas. II. The excitation spectrum. Phys. Rev. 1963, 130, 1616. [Google Scholar] [CrossRef]
- Izergin, A.G.; Korepin, V.E.; Reshetikhin, N.Y. Conformal dimensions in Bethe ansatz solvable models. J. Phys. A Math. Gen. 1989, 22, 2615. [Google Scholar] [CrossRef]
- Schlottmann, P. Exact Results for Highly Correlated Electron Systems in One Dimension. Int. J. Mod. Phys. B 1997, 11, 355. [Google Scholar] [CrossRef]
- Frahm, H.; Korepin, V.E. Critical exponents for the one-dimensional Hubbard model. Phys. Rev. B 1990, 42, 10553. [Google Scholar] [CrossRef] [PubMed]
- Woynarovich, F. Finite-size effects in a non-half-filled Hubbard chain. J. Phys. A Math. Gen. 1989, 22, 4243. [Google Scholar] [CrossRef]
- Pustilnik, M.; Khodas, M.; Kamenev, A.; Glazman, L.I. Dynamic Response of One-Dimensional Interacting Fermions. Phys. Rev. Lett. 2006, 96, 196405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zvonarev, M.B.; Cheianov, V.V.; Giamarchi, T. Spin Dynamics in a One-Dimensional Ferromagnetic Bose Gas. Phys. Rev. Lett. 2007, 99, 240404. [Google Scholar] [CrossRef] [PubMed]
- Imambekov, A.; Glazman, L.I. Exact Exponents of Edge Singularities in Dynamic Correlation Functions of 1D Bose Gas. Phys. Rev. Lett. 2008, 100, 206805. [Google Scholar] [CrossRef] [Green Version]
- Frahm, H.; Palacios, G. Correlation functions of one-dimensional Bose-Fermi mixtures. Phys. Rev. A 2005, 72, 061604. [Google Scholar] [CrossRef] [Green Version]
- Cazalilla, M.A. Bosonizing one-dimensional cold atomic gases. J. Phys. B At. Mol. Opt. Phys. 2004, 37, S1. [Google Scholar] [CrossRef]
- Anderson, P.W. Infrared catastrophe in Fermi gases with local scattering potentials. Phys. Rev. Lett. 1967, 18, 1049. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlottmann, P. Excitation Spectra and Edge Singularities in the One-Dimensional Anisotropic Heisenberg Model for Δ = cos(π/n), n = 3,4,5. Quantum Rep. 2022, 4, 442-461. https://doi.org/10.3390/quantum4040032
Schlottmann P. Excitation Spectra and Edge Singularities in the One-Dimensional Anisotropic Heisenberg Model for Δ = cos(π/n), n = 3,4,5. Quantum Reports. 2022; 4(4):442-461. https://doi.org/10.3390/quantum4040032
Chicago/Turabian StyleSchlottmann, Pedro. 2022. "Excitation Spectra and Edge Singularities in the One-Dimensional Anisotropic Heisenberg Model for Δ = cos(π/n), n = 3,4,5" Quantum Reports 4, no. 4: 442-461. https://doi.org/10.3390/quantum4040032




