Statistical Scrutiny of Particle Spectra in ep Collisions

Abstract

Charged particle multiplicity distributions in positron–proton deep inelastic scattering at a centre-of-mass energy $\sqrt{s}$ = 300 GeV, measured in the hadronic centre-of-mass frames and in different pseudorapidity windows are studied in the framework of two statistical distributions, the shifted Gompertz distribution and the Weibull distribution. Normalised moments, normalised factorial moments and the H-moments of the multiplicity distributions are determined. The phenomenon of oscillatory behaviour of the counting statistics and the Koba-Nielsen-Olesen (KNO) scaling behaviour are investigated. This is the first such analysis using these data. In addition, projections of the two distributions for the expected average charged multiplicities obtainable at the proposed future ep colliders.

1. Context and Introduction

Ever since the discovery of quarks and gluons, the search for their composites forming new particles in the form of leptons and hadrons has driven high energy physicists to strive for higher and higher energy regimes in pursuit of new exotic particles. Unprecedented and cutting edge technological developments, combined with scientific expertise have pushed the energy frontier to new levels. This made possible the discovery of Higgs boson at the Large Hadron Collider (LHC) [1] at CERN in recent years. During the past four decades, beam accelerators of mammoth sizes have been built for delivering the highest possible collision energies, necessary for discovering new physics. Some of the extraordinary particle accelerators include LHC, the Large Electron–Positron Collider (LEP) [2], the Hadron–Electron Ring Accelerator (HERA) [3], the Proton–Antiproton Collider (Tevatron) [4] and the Relativistic Heavy-Ion Collider (RHIC) [5]. While colliders make the collisions of a given kind of particles possible, the collision energy results into producing a large number of particles of different types. In order to record the outcome of the particle collisions, the most complex high energy particle detectors have been designed. These giant particle detectors are engaged to track and record these particles produced in collisions. Interestingly, the information of the output of a collision, which can be obtained from the detector is rather limited in terms of directly observable quantities. Some directly measurable quantities include the number of particles produced, the charge of a particle, the angle at which a particle is produced and its momentum and energy. All other properties of the particle have to be inferred by indirect methods.

The first and foremost physical observable in any high energy interaction is a count of the particles produced. Charged particles are directly observable. Neutral particles must be detected from their decay products. Charged particles are measured in full or sliced phase space. Majority of the charged particles produced are pions, protons and kaons. The distribution of charged particles is studied systematically to probe into the production dynamics and any embedded correlations. Definite trends of the average number of particles produced, dependence on collision energy and phase space, form an interesting subject of study. Several theoretical, phenomenological and statistics-inspired approaches are adopted to understand and explain the observations of the experiments. One of the earliest efforts to understand the behaviour of probability of particle production led to the observation of a scaling behaviour, known as the Koba–Nielsen–Olesen (KNO) scaling [6,7]. Efforts to use probability distribution functions (PDF) in terms of statistical discrete distributions, such as binomial, Poisson, Bernoulli, negative binomial and multinomial [8] etc. have produced results applicable at different collision-energies. One of the most consistent description of particle production has been provided by the negative binomial distribution (NBD) [9]. Some of the statistical distributions and their modified forms which have been widely used are NBD [9,10], Gamma distribution [11], Lognormal distribution [12], Tsallis distribution [13,14] and the Weibull distribution (WD) [15,16,17]. Biró et al. [18] and Shen et al. [19] have studied particle production in heavy-ion collisions in terms of Tsallis non-extensive entropy in relation to the temperature T, and the non-extensivity parameter q. It has been extensively used to study the particle spectra produced in different types of collisions, from e${}^{+}$e${}^{-}$, pp, pA to AA to understand the mechanism of particle production [20,21,22,23,24,25,26].

In the present study, investigation of the charged hadronic multiplicity in e${}^{+}$p collisions at HERA is made in terms of the shifted Gompertz distribution (SGD) and the Weibull distribution. The application of these distributions are made to study multiplicity distributions of charged particles produced in e${}^{+}$e${}^{-}$, pp, $\overline{\mathrm{p}}$p and the hadron−nucleus (hA) collisions at different center-of-mass (c.m.) energies in full phase space and also in restricted phase space windows. The results of the study are published in [27,28,29,30,31,32]. The present work is the first attempt to analyse the data from different hadronic energy regions in the deep inelastic scattering (DIS) at the HERA.

To date, only one collider namely HERA was built to provide ep collisions at different energies. Number of future high energy ep colliders are being planned to extend the kinematic reach of an electron to probe the inner structure of a proton. Using the SGD, the behaviour of average charged multiplicity at HERA is studied and utilised to make predictions for the particle production at energies achievable at the future accelerators.

2. The Data from HERA and Kinematical Variables

The first ever constructed electron–proton storage ring, the HERA, was located at the DESY laboratory in Hamburg, Germany. It was 6.3 km in circumference and had four interaction regions which housed the experiments H1, ZEUS, HERMES, and HERA-B. Of the four experiments, H1 and ZEUS recorded the collisions of e${}^{\pm }$ and proton beams. At the interaction points, beam of positrons having 27.5 GeV energy were collided with 820 GeV protons at a c.m. energy of 300 GeV. HERA was an asymmetric accelerator and its unique kinematics made it possible to observe the hadronic recoil, in addition to the access to weak neutral-and-charged currents. Two of the detectors H1 and Zeus, recorded the outcome of positron collisions with protons, at the HERA storage ring at DESY. The H1 data [33] under scrutiny were collected during the 1994 running period, corresponding to an integrated luminosity of 1.3 pb${}^{-1}$.

In the present study, corrected multiplicity distributions are studied in different intervals of pseudo-rapidity, ${\eta }^{\ast }$, and in the intervals of the c.m. energy of hadronic system, W. Multiplicity distributions analysed are in the kinematic regions of W: 80 → 115, 115 → 150, $150\to 185$ and $185\to 220$ GeV for charged hadrons with pseudo-rapidity in different domains $1\le {\eta }^{\ast }\le {\eta }_c^{\ast }$ with ${\eta }_c^{\ast }$ = 2, 3, 4, 5, i.e., in increasing size of pseudo-rapidity window. Pseudo-rapidity is defined as $\eta =-\frac{1}{2}lntan\frac{\theta }{2}$, where $\theta$ is the angle between the hadron momentum and the positive direction of the beam axis. For this analysis, $\eta$ is measured in the current hemisphere and denoted as ${\eta }^{\ast }$, with $\theta$ being the angle between the hadron momentum and the direction of the virtual photon in the ${\gamma }^{\ast }$p rest system.

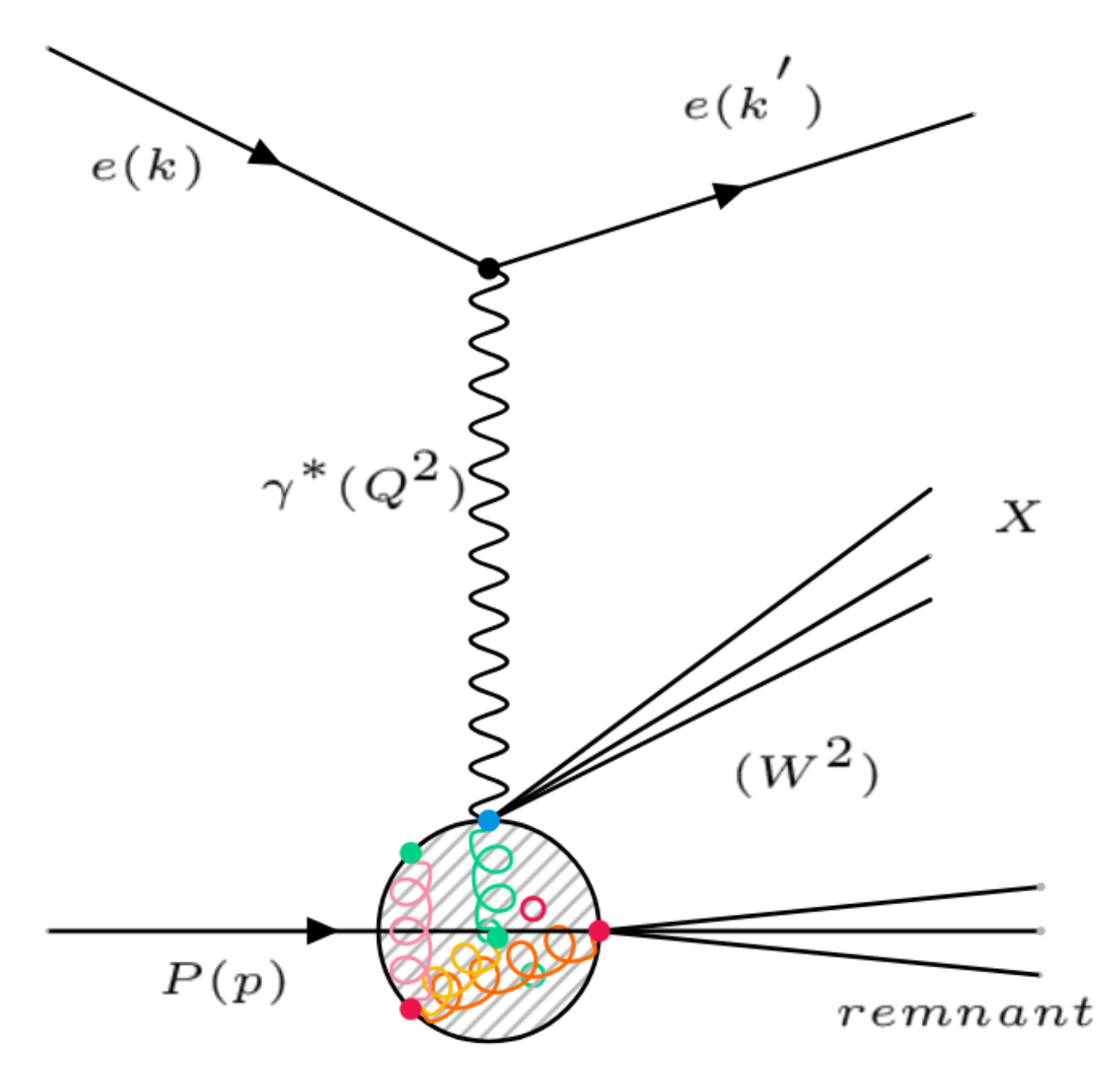
Scattering of a lepton from a proton can be viewed as the elastic scattering of the lepton from a quark or anti-quark inside the proton, as illustrated in Figure 1.

Denoting the initial four-momentum of the lepton as k, final four-momentum of the lepton as $k^{\prime }$, initial four-momentum of the proton as p, fraction of the proton-momentum carried by the struck quark as x and the final four-momentum of the hadronic system as $p^{\prime }$, following invariant variables can be defined:

$$s={(p+k)}^2,$$

(1)

$$t={(p-p^{\prime })}^2,$$

(2)

$$Q^2=-q^2=-{(k^{\prime }-k)}^2,$$

(3)

$$y=\frac{p·q}{p·k},$$

(4)

$$W^2={\left(p^{\prime }\right)}^2={(p+q)}^2,$$

(5)

where s is the center-of-mass energy squared, t is the four-momentum transfer squared between the proton and the final state hadronic system, y is the inelasticity of the scattered lepton and $W^2$ is the invariant mass squared of the final state hadrons. The energy momentum conservation demands are:

$$x=\frac{Q^2}{2p·q},$$

(6)

$$y=\frac{Q^2}{sx},$$

(7)

$$W^2=Q^2\frac{1-x}{x}.$$

(8)

The multiplicity distributions are studied in the virtual-boson proton (${\gamma }^{\ast }$p) rest system, the hadronic centre-of-mass frame. Data for probability distributions in different ${\eta }^{\ast }$ and W bins, have been taken from H1 experiment [33]. As reported in this paper, for each multiplicity, n, the statistical uncertainties were taken into account for the finite number of events in the data and in the samples generated by using several Monte Carlo (MC) event generators which include the DJANGO and the LEPTO programs to model the hadronic final states [34,35]. They were calculated by using the Monte Carlo sampling procedure to ensure the propagation of sampling fluctuations and statistical correlations, described therein.

3. Statistical Methods of Analysis

3.1. Scaling

In order to establish the energy-independence of multiplicity distribution, Koba et al. [6,7] proposed that at very high energy the probability $P\left(n\right)$ of producing n particles in a certain collision process should exhibit the scaling relation:

$$P\left(n\right)=\frac{1}{\langle n\rangle }\psi (z,s)=\underset{s\to \infty }{lim}\frac{1}{\langle n\rangle }\psi \left(z\right),\mathrm{where}z=\frac{n}{\langle n\rangle },$$

(9)

with $\langle n\rangle$ the average multiplicity of particles produced at collision energy $\sqrt{s}$. This behaviour was known as KNO-scaling. This hypothesis has been widely studied and confirmed in different types of collisions. Deviation from KNO-scaling was first observed in proton−proton collisions at the Intersecting Storage Ring (ISR) energies [36]: $\sqrt{s}$ = 30.4 to 62.2 GeV. With more data becoming available from different collider experiments at different energies, in varying intervals of phase space and for different types of collisions, the scaling behaviour is still being studied. After the observation of KNO-scaling violation, NBD became the most widely used distribution to describe the multiplicities. Almost every experiment, designed to study collisions of any kind: e${}^{+}$e${}^{-}$, e${}^{\pm }$p, $\overline{\mathrm{p}}$p, pp, hA and AA used NBD to understand the mechanism of particle production.

3.2. Parametric Distributions

Study of the multiplicity distributions by the H1 collaboration [33], showed that the Log-normal distribution (LND) [37,38] gives a reasonably accurate description of the data, in particular in the smallest ${\eta }^{\ast }$ domain. However, the quality of the fits deteriorated in larger domains. The NBD fits were acceptable in the smallest ${\eta }^{\ast }$ domain but became progressively worse for larger intervals. The two distributions were found to differ strongly for low multiplicities.

The success of NBD remained unchallenged by showing its ability to describe almost all the data available at different energies until, the multiplicity measurements from the UA1 collaboration [39] and the UA5 collaboration [40,41] on the $\overline{\mathrm{p}}$p collisions at 540 GeV revealed the NBD violation. The multiplicity distribution showed a shoulder structure in the probability $P\left(n\right)$ versus n dependence at this energy. In e${}^{+}$e${}^{-}$ annihilation at $\sqrt{s}$ = 91 GeV at the LEP, the multiplicity distribution also exhibited a prominent shoulder structure at intermediate n values. Thus, LND and NBD both were unable to describe the distributions. The shoulder was the most prominent in single hemisphere distributions [42,43]. However, the H1 measurements showed no evidence for a shoulder structure of the type. Nevertheless, these parametric forms continued to be useful for phenomenological studies. Since then, several new probability functions have been proposed and used for the description of multiplicities.

The SGD [27] is the distribution of the largest of two independent random variables one of which has an exponential distribution with parameter b and the other has a Gumbel distribution, also known as log-Weibull distribution with parameters t and b. In its original formulation the distribution was expressed referring to the Gompertz distribution instead of the Gumbel distribution but, the Gompertz distribution is a reverted Gumbel distribution. SGD finds application to problems in statistics, mathematics, computer science, social networks, in the market research, diffusion theory, and forecasting etc. A possibility to apply this distribution to the statistical phenomena in high energy physics, motivated us to use it for the description of multiplicity distributions. SGD with two non-negative fit parameters is thus proposed to be used for understanding the particle production in sub-nuclear particle collisions.

Let N be a random variable following SGD with parameters b and t, where $b>0$ is a scale parameter and $t>0$ is a shape parameter. The probability density function (PDF) of N is

$$P_N\left(n\right)=b{e}^{-bn}{e}^{-\left(t{e}^{-bn}\right)}\left[1+t(1-e^{-bn}\right)],n>0.$$

(10)

The distribution can be characterised by the maximum of two independent random variables with Gompertz distribution (parameters $b>0$ and $t>0$) and exponential distribution (parameter $b>0$). For ${lim}_{t\to 0}{P}_N\left(n\right)=b{e}^{-bn}$, the SGD approximates to an exponential distribution with mean = $1/b$. A thorough interpretation of SGD is detailed in references [44,45]. In the paper by Jiméne Torres and Jodrá [46], it is emphasised that the computation of moments is rather complicated. Even for the first and second moment, the integrals involved to obtain $E\left[X\right]$ to calculate mean and variance do not have closed-form solution in terms of simple functions. However, explicit expressions for the moments of orders 1 and 2 were obtained by the authors. Furthermore, Bemmaor [44] gave implicit formulae to compute the expectation and variance of the distribution. The following expressions for mean and the moments are thus adopted from these references.

Mean of the distribution:

$$\left(-\frac{1}{b}\right)\left[E\left(ln\zeta \right)-lnt\right]\mathrm{with}\zeta =t{e}^{-bn},$$

(11)

and

$$E\left(ln\zeta \right)=\left(1+\frac{1}{t}\right){\int }_0^{\infty }{e}^{-\zeta }ln\zeta d\zeta -\frac{1}{t}{\int }_0^{\infty }\zeta e^{-\zeta }ln\zeta d\zeta ,$$

(12)

where E is the expectation function. SGD has been recently studied in hadronic and leptonic interactions. The aim of this paper is to extend its applicability to high energy deep inelastic scattering in different regimes of W and ${\eta }^{\ast }$. The mean of the distribution as given in Equation (11) is expected to approximate the mean of the experimental distribution, $\langle n\rangle ={\displaystyle \sum _{n=0}^{n_{max}}}nP\left(n\right)$.

Another distribution was used by S. Dash et al. [16,17] for the description of multiplicity data in e${}^{+}$e${}^{-}$ and $\overline{\mathrm{p}}$p collisions at different energies. WD is a continuous probability distribution which can take many shapes. It can also be fitted to non-symmetrical data. WD has two parameters. The characteristic value $\lambda >0$ in a standard Weibull function is known as scale parameter. The second parameter of the distribution $k>0$, is the shape parameter.

The probability density function of a Weibull random variable is

$$P\left(n\right)=\frac{k}{\lambda }{\left(\frac{n}{\lambda }\right)}^{(k-1)}ex{p}^{-{\left(\frac{n}{\lambda }\right)}^k},n\ge 0.$$

(13)

Mean of the distribution $\overline{n}$ can be calculated from the following equation:

$$\overline{n}=\lambda \Gamma (1+1/k).$$

(14)

Various steps to obtain the Equation (14) are given in Appendix A.

For a multiplicity distribution, the normalised moments $C_q$, normalised factorial moments $F_q$, normalised factorial cumulants $K_q$ and ratio of the two, $H_q$ moments are defined as

$$C_q=\frac{{\sum }_{n=1}^{\infty }{n}^{q}P\left(n\right)}{{\left({\sum }_{n=1}^{\infty }nP\left(n\right)\right)}^q},$$

(15)

$$F_q=\frac{{\sum }_{n=q}^{\infty }n(n-1)\cdots (n-q+1)P\left(n\right)}{{\left({\sum }_{n=1}^{\infty }nP\left(n\right)\right)}^q},$$

(16)

$$K_q=F_q-\sum _{m=1}^{q-1}\frac{(q-1)!}{m!(q-m-1)!}{K}_{q-m}{F}_m,$$

(17)

$$H_q=K_q/F_q,$$

(18)

where $P\left(n\right)$ is the $n$-charged particle probability and q is the rank of the moment.

In the specific case of SGD, normalized moments ($C_q$) and normalized factorial moments ($F_q$) are defined below, with n as values of X:

$$C_q=\frac{E\left[X^q\right]}{{\left(E\left[X\right]\right)}^q}and{F}_q=\frac{E\left[\right(X\left)\right(X-1\left)\right(X-2)\cdots (X-(q-1)\left)\right]}{{\left(E\left[X\right]\right)}^q},$$

(19)

where q is a natural number ranging from 1 to ∞. The mean value (E[X]) of SGD is given by

$$E\left[X\right]=\frac{1}{b}\left(\gamma +lnt+\frac{1-e^{-t}}{t}+\Gamma \left[0,t\right]\right),$$

(20)

$$E\left[X^2\right]=\frac{2}{b^{2}t}\left(\gamma +\Gamma [0,t]+t^2{}_3{F}_3[\{1,1,1\},\{2,2,2\},-t]+lnt\right).$$

(21)

The higher order moments ($C_q$) can be found by using the moment generating function of the SGD [[b,t],m]

$$e^{-t}-\left(1+\frac{m}{bt}\right)t^{\frac{m}{b}}\left(\Gamma \left[1-\frac{m}{b}\right]-\Gamma \left[1-\frac{m}{b},t\right]\right),$$

(22)

$$\begin{array}{cc}\hfill E\left[\right(X\left)\right(X-1\left)\right]=& \frac{2}{b^{2}t}\left(\gamma +\Gamma [0,t]+t^2{}_3{F}_3[\{1,1,1\},\{2,2,2\},-t]+lnt\right)-\hfill \\ \hfill & \frac{\left(1-e^{-t}+t(\gamma +\Gamma [0,t]+lnt)\right)}{bt}.\hfill \end{array}.$$

(23)

Higher order factorial moments ($F_q$) can be found by using the generating function of SGD [[b,t],m]

$$e^{-t}-t^{\frac{lnm}{b}}\left(\Gamma \left[1-\frac{lnm}{b}\right]-\Gamma \left[1-\frac{lnm}{b},t\right]\right)\left(1+\frac{lnm}{bt}\right),$$

(24)

where:

(i)

$\gamma$ ≈ 0.5772156 is the Euler–Mascheroni constant.

(ii)

$\Gamma$[s] the Euler Gamma function and $\Gamma [s,n]$ the incomplete Gamma function are defined as

$$\Gamma \left[s\right]={\int }_0^{\infty }{m}^{s-1}{e}^{-m}dm\Gamma [s,n]={\int }_n^{\infty }{m}^{s-1}{e}^{-m}dm.$$

(25)

(iii)

${}_3{F}_3$ is a Generalized Hyper-geometric function.

$${}_3{F}_3\left[\{1,1,1\},\{2,2,2\},-t\right]=\sum _{k=1}^{\infty }\frac{{(-1)}^{k+1}{t}^{k+1}}{k!k^2}.$$

(26)

SGD and WD both are continuous distributions. The question arises, are this type of distributions suitable to describe discrete multiplicity data? The usage of continuous distributions such as, e.g., Gamma, lognormal, Weibull distributions to study the multiplicity data in high energy physics has been adopted in several studies. Tsallis distribution, a statistical distribution based on q-exponential and q-logarithm functions has also been widely used. Recently Weibull distribution has been introduced and used for the multiplicity data from several experiments. Multiplicity data constitute discrete data sets. In order for any continuous distribution to be used to describe the discrete data, a continuity correction may be used. In a high energy experiment, one observes the number of particles produced in a collision. This number varies between 0 and a maximum value, n. Suppose one needs to compute the probability of obtaining 10 particles. While the discrete random variable can have only specified value (10 in this case), a continuous random variable used to approximate it could take on any values within an interval around this value. In this case it varies by one unit, $9.5<10<10.5$. With a continuous distribution, the probability of obtaining a particular value of a random variable is zero. But when it is used to approximate a discrete distribution, a continuity correction can be employed so that one can approximate the probability of a specific value of the discrete distribution. As shown in [47,48], for an underlying continuous random variable X, the discrete analogue Y is given by:

$$P(\mathrm{Y}=m)=F_{\mathrm{X}}(m+\delta )-F_{\mathrm{X}}(m-(1-\delta )),$$

(27)

where the parameter $0<\delta <1$ is so chosen that the first two raw moments of X and Y remain close.

4. Analysis of the Data

The two distributions SGD and WD, described in Section 2, are fitted to the e${}^{+}$p collision data collected by the H1 detector. The best fits are obtained by using the minimisation of ${\chi }^2$ technique from the CERN’s analysis framework, ROOT6.18.

4.1. The SGD and WD Fits

Figure 2, Figure 3, Figure 4 and Figure 5 show the multiplicity distributions fitted with SGD, Equation (11), in different ${\eta }^{\ast }$ and W intervals and for W in the intervals, 80 < W < 115 GeV, 115 < W < 150 GeV, 150 < W < 185 GeV, 185 < W < 220 GeV. The figures also show the data versus SGD-fit ratio plots enabling an understanding of the goodness of the fit. Parameters of the fits and ${\chi }^2/$ndf (number of degrees of freedom) for all the fits are given in

Table 1. Shifted Gompertz distribution, Equation (10), fit parameters $b,t$, the normalisation constant c, and ${\chi }^2$/ndf (number of degrees of freedom) for the multiplicity distributions for $n>$ 0 in different W ranges of the H1 data [33].

${\mathit{\eta }}^{\ast }$	c	b	t	${\mathit{\chi }}^2/$ndf
80 $<W<$ 115 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.92 ± 0.04	0.57 ± 0.03	1.31 ± 0.33	0.67/10
1.0 $<{\eta }^{\ast }<$ 3.0	0.98 ± 0.04	0.38 ± 0.02	2.56 ± 0.30	4.26/14
1.0 $<{\eta }^{\ast }<$ 4.0	1.00 ± 0.04	0.36 ± 0.02	5.03 ± 0.65	5.63/15
1.0 $<{\eta }^{\ast }<$ 5.0	0.98 ± 0.04	0.37 ± 0.01	6.29 ± 0.69	15.23/15
115 $<W<$ 150 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.90 ± 0.03	0.56 ± 0.02	1.37 ± 0.19	2.95/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.98 ± 0.03	0.34 ± 0.02	2.20 ± 0.26	3.09/15
1.0 $<{\eta }^{\ast }<$ 4.0	0.98 ± 0.03	0.32 ± 0.01	4.81 ± 0.39	13.72/17
1.0 $<{\eta }^{\ast }<$ 5.0	0.94 ± 0.03	0.36 ± 0.01	8.50 ± 0.79	35.25/18
150 $<W<$ 185 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.90 ± 0.04	0.56 ± 0.03	1.62 ± 0.29	1.15/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.98 ± 0.03	0.33 ± 0.01	2.28 ± 0.28	5.17/17
1.0 $<{\eta }^{\ast }<$ 4.0	0.95 ± 0.04	0.30 ± 0.01	4.89 ± 0.66	9.97/19
1.0 $<{\eta }^{\ast }<$ 5.0	1.01 ± 0.04	0.30 ± 0.01	6.95 ± 0.95	7.42/19
185 $<W<$ 220 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.90 ± 0.04	0.56 ± 0.03	1.58 ± 0.30	1.29/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.96 ± 0.04	0.33 ± 0.01	2.16 ± 0.22	4.23/18
1.0 $<{\eta }^{\ast }<$ 4.0	0.95 ± 0.03	0.28 ± 0.01	4.05 ± 0.40	14.42/19
1.0 $<{\eta }^{\ast }<$ 5.0	0.93 ± 0.04	0.33 ± 0.01	9.48 ± 1.34	24.74/20

. The parameters measured from the distributions relate to the scale and shape of the distributions. The tail of the distribution determines the maximum number of particles produced in an interaction. The scale of each distribution is studied in different phase space regions and its dependence on the energy. Similarly, shape parameter affects the shape of the distribution. It connects to the higher moments such as 3rd moment (skewness) and 4th moment (Kurtosis) of the distribution. If the distribution is left skewed, the probability of producing events with small multiplicity decreases and vice versa for the case when it is right skewed. This affects the mean of the distribution, the average charged particle multiplicity in this analysis.

Figure 6, Figure 7, Figure 8 and Figure 9 show the WD defined in Equation (A1) fitted to the data in different ${\eta }^{\ast }$ and W intervals. The figures also show the data versus WD-fit ratio plots which help in understanding the goodness of the fit. Parameters of the fits and ${\chi }^2$/ndf are given in

Table 2. Weibull distribution, Equation (A1), fit parameters $k,\lambda$ with C as the normalisation constant for the multiplicity distributions for n > 0 in different W ranges of the H1 data [33].

${\mathit{\eta }}^{\ast }$	C	k	$\mathit{\lambda }$	${\mathit{\chi }}^2/$ndf
80 $<W<$ 115 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.92 ± 0.04	1.35 ± 0.08	2.93 ± 0.12	0.67 / 10
1.0 $<{\eta }^{\ast }<$ 3.0	0.98 ± 0.04	1.67 ± 0.06	5.57 ± 0.16	1.08 / 14
1.0 $<{\eta }^{\ast }<$ 4.0	0.98 ± 0.04	2.13 ± 0.09	7.27 ± 0.20	0.85 / 15
1.0 $<{\eta }^{\ast }<$ 5.0	0.99 ± 0.04	2.38 ± 0.08	7.72 ± 0.17	1.97 / 15
115 $<W<$ 150 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.90 ± 0.03	1.38 ± 0.04	3.05 ± 0.08	0.46/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.98 ± 0.03	1.61 ± 0.06	5.81 ± 0.16	1.40 /15
1.0 $<{\eta }^{\ast }<$ 4.0	0.98 ± 0.03	2.09 ± 0.06	7.97 ± 0.15	2.01/17
1.0 $<{\eta }^{\ast }<$ 5.0	1.00 ± 0.03	2.39 ± 0.08	8.59 ± 0.14	3.18/18
150 $<W<$ 185 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.89 ± 0.03	1.44 ± 0.07	3.22 ± 0.10	1.26/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.97 ± 0.03	1.61 ± 0.06	6.10 ± 0.15	0.86/17
1.0 $<{\eta }^{\ast }<$ 4.0	0.99 ± 0.04	2.06 ± 0.09	8.46 ± 0.21	1.37/19
1.0 $<\eta <$ 5.0	0.98 ± 0.04	2.45 ± 0.11	9.33 ± 0.23	3.60/19
185 $<W<$ 220 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	0.89 ± 0.04	1.42 ± 0.07	3.24 ± 0.12	0.53/11
1.0 $<{\eta }^{\ast }<$ 3.0	0.97 ± 0.04	1.62 ± 0.05	6.15 ± 0.18	0.95/18
1.0 $<{\eta }^{\ast }<$ 4.0	0.97 ± 0.03	2.02 ± 0.07	8.77 ± 0.19	2.03/19
1.0 $<{\eta }^{\ast }<$ 5.0	0.99 ± 0.04	2.48 ± 0.11	9.92 ± 0.21	2.00/20

. Optimised values of the parameters determine the fit between the data and the function.

Some experimental distributions are studied by using the continuous form of SGD and WD and also by calculating the continuity correction of $\delta$ = 0.5 as shown in Equation (27). No appreciable differences in the data versus distributions fits are found. A detailed study of this comparison by using data from several collider experiments will soon be published. Generating discrete analogues of continuous distributions is well explained in the references [47,48].

4.2. Normalised and Factorial Moments of Multiplicity Distributions

Evaluation of successive moments of a multiplicity distribution relates to the shape and scale of the distribution. The moments can be studied as a function of the collision energy and to check the validity of KNO scaling. Multiplicity distribution is expected to demonstrate the scaling property. So that the Multiplicity distribution is expected to lead to a common scaled behaviour when calculated as $\langle n\rangle P\left(n\right)$ as a function of $n/\langle n\rangle$. Higher-order moments and the cumulants are the precise tools for predicting the correlations amongst the charged particles produced in a collision. Deviation w.r.t. independent and uncorrelated production of particles can be observed effectively by measuring factorial moments. Broadening of the distribution beyond the expectation of Poisson distribution, indicates the presence of particle correlations, with the $F_q$ values becoming greater than unity.

Figure 10 and Figure 11 show the normalized moments $C_q$ for q = 2, 3, 4, 5 calculated from the SGD and WD fits for different W ranges in four pseudorapidity intervals, 1 < ${\eta }^{\ast }$ < 2, 1 < ${\eta }^{\ast }$ < 3, 1 < ${\eta }^{\ast }$ < 4 and 1 < ${\eta }^{\ast }$ < 5. Corresponding values obtained from the fits are given in

Table 3. Normalised moments and normalised factorial moments calculated from the SGD fits to the data [33] for different W ranges.

${\mathit{\eta }}^{\ast }$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$
80 $<W<$ 115 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.446 ± 0.040	2.76 ± 0.15	6.47 ± 0.54	17.57 ± 1.96	1.104 ± 0.033	1.51 ± 0.09	2.42 ± 0.22	4.20 ± 0.53
1.0 $<{\eta }^{\ast }<$ 3.0	1.366 ± 0.021	2.33 ± 0.07	4.64 ± 0.22	10.40 ± 0.66	1.169 ± 0.018	1.59 ± 0.05	2.42 ± 0.12	3.92 ± 0.27
1.0 $<{\eta }^{\ast }<$ 4.0	1.249 ± 0.022	1.85 ± 0.07	3.11 ± 0.16	5.79 ± 0.41	1.097 ± 0.020	1.33 ± 0.05	1.73 ± 0.09	2.36 ± 0.18
1.0 $<{\eta }^{\ast }<$ 5.0	1.217 ± 0.021	1.73 ± 0.06	2.79 ± 0.15	4.94 ± 0.35	1.073 ± 0.019	1.25 ± 0.04	1.55 ± 0.08	2.00 ± 0.15
115 $<W<$ 150 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.448 ± 0.022	2.78 ± 0.08	6.55 ± 0.31	18.05 ± 1.16	1.115 ± 0.018	1.55 ± 0.05	2.55 ± 0.14	4.63 ± 0.35
1.0 $<{\eta }^{\ast }<$ 3.0	1.391 ± 0.022	2.43 ± 0.08	4.97 ± 0.25	11.43 ± 0.77	1.202 ± 0.019	1.71 ± 0.06	2.72 ± 0.14	4.61 ± 0.33
1.0 $<{\eta }^{\ast }<$ 4.0	1.257 ± 0.014	1.88 ± 0.04	3.21 ± 0.10	6.07 ± 0.27	1.118 ± 0.012	1.39 ± 0.03	1.89 ± 0.06	2.71 ± 0.12
1.0 $<{\eta }^{\ast }<$ 5.0	1.189 ± 0.016	1.64 ± 0.04	2.56 ± 0.10	4.43 ± 0.23	1.060 ± 0.014	1.21 ± 0.03	1.50 ± 0.06	1.97 ± 0.11
150 $<W<$ 185 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.430 ± 0.035	2.68 ± 0.13	6.15 ± 0.47	16.43 ± 1.72	1.108 ± 0.029	1.51 ± 0.08	2.40 ± 0.21	4.22 ± 0.51
1.0 $<{\eta }^{\ast }<$ 3.0	1.394 ± 0.022	2.45 ± 0.08	5.09 ± 0.25	11.97 ± 0.78	1.214 ± 0.020	1.76 ± 0.06	2.91 ± 0.15	5.20 ± 0.36
1.0 $<{\eta }^{\ast }<$ 4.0	1.258 ± 0.019	1.89 ± 0.06	3.24 ± 0.14	6.17 ± 0.37	1.128 ± 0.017	1.43 ± 0.04	1.99 ± 0.09	2.95 ± 0.19
1.0 $<{\eta }^{\ast }<$ 5.0	1.203 ± 0.019	1.68 ± 0.05	2.64 ± 0.12	4.55 ± 0.28	1.088 ± 0.017	1.29 ± 0.04	1.64 ± 0.08	2.20 ± 0.14
185 $<W<$ 220 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.433 ± 0.042	2.70 ± 0.16	6.21 ± 0.58	16.66 ± 2.10	1.110 ± 0.034	1.52 ± 0.10	2.43 ± 0.25	4.29 ± 0.61
1.0 $<{\eta }^{\ast }<$ 3.0	1.408 ± 0.026	2.52 ± 0.10	5.36 ± 0.32	12.98 ± 1.04	1.228 ± 0.023	1.82 ± 0.07	3.11 ± 0.19	5.80 ± 0.49
1.0 $<{\eta }^{\ast }<$ 4.0	1.282 ± 0.018	1.97 ± 0.06	3.46 ± 0.15	6.71 ± 0.39	1.153 ± 0.016	1.51 ± 0.04	2.16 ± 0.10	3.27 ± 0.20
1.0 $<{\eta }^{\ast }<$ 5.0	1.175 ± 0.023	1.59 ± 0.06	2.41 ± 0.15	4.05 ± 0.33	1.062 ± 0.021	1.22 ± 0.05	1.50 ± 0.09	1.96 ± 0.16

and

Table 4. Normalised moments and normalised factorial moments calculated from the WD fits to the data [33] for different W ranges.

${\mathit{\eta }}^{\ast }$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$
80 $<W<$ 115 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.437 ± 0.038	2.69 ± 0.15	6.08 ± 0.51	15.83 ± 1.80	1.094 ± 0.031	1.45 ± 0.09	2.17 ± 0.21	3.47 ± 0.49
1.0 $<{\eta }^{\ast }<$ 3.0	1.352 ± 0.020	2.23 ± 0.07	4.27 ± 0.20	9.07 ± 0.60	1.153 ± 0.018	1.51 ± 0.05	2.14 ± 0.11	3.18 ± 0.24
1.0 $<{\eta }^{\ast }<$ 4.0	1.240 ± 0.022	1.78 ± 0.06	2.86 ± 0.16	5.00 ± 0.37	1.085 ± 0.019	1.25 ± 0.05	1.51 ± 0.09	1.85 ± 0.15
1.0 $<{\eta }^{\ast }<$ 5.0	1.199 ± 0.020	1.63 ± 0.06	2.45 ± 0.13	3.97 ± 0.29	1.053 ± 0.018	1.15 ± 0.04	1.28 ± 0.07	1.44 ± 0.11
115 $<W<$ 150 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.434 ± 0.021	2.67 ± 0.08	6.01 ± 0.28	15.61 ± 1.04	1.101 ± 0.017	1.46 ± 0.05	2.20 ± 0.13	3.60 ± 0.31
1.0 $<{\eta }^{\ast }<$ 3.0	1.375 ± 0.021	2.33 ± 0.07	4.57 ± 0.23	10.02 ± 0.70	1.185 ± 0.019	1.62 ± 0.05	2.42 ± 0.13	3.83 ± 0.29
1.0 $<{\eta }^{\ast }<$ 4.0	1.248 ± 0.013	1.81 ± 0.04	2.95 ± 0.10	5.23 ± 0.24	1.107 ± 0.012	1.32 ± 0.03	1.67 ± 0.06	2.16 ± 0.11
1.0 $<{\eta }^{\ast }<$ 5.0	1.198 ± 0.015	1.63 ± 0.04	2.45 ± 0.09	3.97 ± 0.20	1.067 ± 0.013	1.19 ± 0.03	1.38 ± 0.05	1.61 ± 0.09
150 $<W<$ 185 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.414 ± 0.033	2.56 ± 0.13	5.58 ± 0.43	13.91 ± 1.49	1.092 ± 0.027	1.41 ± 0.08	2.03 ± 0.19	3.16 ± 0.43
1.0 $<{\eta }^{\ast }<$ 3.0	1.380 ± 0.021	2.36 ± 0.07	4.68 ± 0.22	10.42 ± 0.69	1.199 ± 0.019	1.67 ± 0.05	2.59 ± 0.13	4.27 ± 0.31
1.0 $<{\eta }^{\ast }<$ 4.0	1.254 ± 0.018	1.83 ± 0.05	3.01 ± 0.13	5.41 ± 0.34	1.121 ± 0.016	1.37 ± 0.04	1.78 ± 0.08	2.40 ± 0.16
1.0 $<{\eta }^{\ast }<$ 5.0	1.190 ± 0.019	1.60 ± 0.05	2.36 ± 0.11	3.77 ± 0.25	1.069 ± 0.017	1.20 ± 0.04	1.38 ± 0.07	1.63 ± 0.11
185 $<W<$ 220 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.422 ± 0.039	2.60 ± 0.15	5.72 ± 0.52	14.41 ± 1.82	1.102 ± 0.032	1.44 ± 0.09	2.13 ± 0.23	3.38 ± 0.52
1.0 $<{\eta }^{\ast }<$ 3.0	1.379 ± 0.025	2.35 ± 0.09	4.69 ± 0.28	10.48 ± 0.87	1.200 ± 0.022	1.68 ± 0.07	2.61 ± 0.17	4.36 ± 0.40
1.0 $<{\eta }^{\ast }<$ 4.0	1.261 ± 0.018	1.86 ± 0.05	3.08 ± 0.14	5.57 ± 0.34	1.132 ± 0.016	1.41 ± 0.04	1.86 ± 0.09	2.56 ± 0.16
1.0 $<{\eta }^{\ast }<$ 5.0	1.185 ± 0.021	1.58 ± 0.06	2.32 ± 0.13	3.66 ± 0.27	1.071 ± 0.019	1.20 ± 0.04	1.40 ± 0.08	1.66 ± 0.13

. Furthermore, values of the moments derived from the data are given in

Table 5. Normalised moments and normalised factorial moments calculated from the data [33] for different W ranges.

${\mathit{\eta }}^{\ast }$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$	${\mathit{C}}_5$	${\mathit{F}}_2$	${\mathit{F}}_3$	${\mathit{F}}_4$	${\mathit{F}}_5$
80 $<W<$ 115 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.440 ± 0.095	2.72 ± 0.39	6.26 ± 1.47	16.59 ± 5.53	1.098 ± 0.078	1.48 ± 0.25	2.28 ± 0.68	3.76 ± 1.68
1.0 $<{\eta }^{\ast }<$ 3.0	1.353 ± 0.059	2.24 ± 0.20	4.28 ± 0.62	9.09 ± 1.88	1.155 ± 0.051	1.52 ± 0.15	2.16 ± 0.36	3.20 ± 0.81
1.0 $<{\eta }^{\ast }<$ 4.0	1.239 ± 0.058	1.79 ± 0.17	2.89 ± 0.43	5.12 ± 1.07	1.084 ± 0.051	1.26 ± 0.12	1.54 ± 0.25	1.94 ± 0.46
1.0 $<{\eta }^{\ast }<$ 5.0	1.201 ± 0.052	1.65 ± 0.15	2.52 ± 0.34	4.18 ± 0.79	1.056 ± 0.045	1.17 ± 0.10	1.35 ± 0.19	1.58 ± 0.32
115 $<W<$ 150 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.435 ± 0.050	2.68 ± 0.22	6.10 ± 0.89	16.13 ± 3.65	1.101 ± 0.042	1.47 ± 0.16	2.27 ± 0.47	3.87 ± 1.34
1.0 $<{\eta }^{\ast }<$ 3.0	1.376 ± 0.072	2.34 ± 0.26	4.60 ± 0.83	10.06 ± 2.54	1.187 ± 0.062	1.63 ± 0.19	2.45 ± 0.48	3.86 ± 1.10
1.0 $<{\eta }^{\ast }<$ 4.0	1.245 ± 0.040	1.80 ± 0.12	2.93 ± 0.31	5.19 ± 0.76	1.104 ± 0.036	1.32 ± 0.09	1.65 ± 0.18	2.14 ± 0.35
1.0 $<{\eta }^{\ast }<$ 5.0	1.195 ± 0.039	1.63 ± 0.11	2.46 ± 0.26	4.04 ± 0.59	1.065 ± 0.035	1.20 ± 0.08	1.40 ± 0.15	1.69 ± 0.28
150 $<W<$ 185 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.431 ± 0.079	2.68 ± 0.34	6.17 ± 1.41	16.61 ± 5.85	1.111 ± 0.067	1.51 ± 0.24	2.44 ± 0.78	4.39 ± 2.32
1.0 $<{\eta }^{\ast }<$ 3.0	1.383 ± 0.062	2.37 ± 0.23	4.72 ± 0.72	10.56 ± 2.32	1.203 ± 0.054	1.69 ± 0.17	2.62 ± 0.45	4.35 ± 1.12
1.0 $<{\eta }^{\ast }<$ 4.0	1.256 ± 0.054	1.84 ± 0.16	3.04 ± 0.44	5.51 ± 1.15	1.124 ± 0.048	1.38 ± 0.13	1.81 ± 0.28	2.48 ± 0.60
1.0 $<{\eta }^{\ast }<$ 5.0	1.192 ± 0.051	1.62 ± 0.14	2.43 ± 0.33	3.97 ± 0.78	1.074 ± 0.046	1.22 ± 0.11	1.46 ± 0.21	1.79 ± 0.41
185 $<W<$ 220 GeV
1.0 $<{\eta }^{\ast }<$ 2.0	1.427 ± 0.100	2.63 ± 0.41	5.84 ± 1.47	14.84 ± 5.35	1.110 ± 0.083	1.48 ± 0.27	2.22 ± 0.71	3.56 ± 1.72
1.0 $<{\eta }^{\ast }<$ 3.0	1.376 ± 0.078	2.35 ± 0.29	4.68 ± 0.95	10.52 ± 3.13	1.197 ± 0.069	1.67 ± 0.22	2.61 ± 0.59	4.39 ± 1.57
1.0 $<{\eta }^{\ast }<$ 4.0	1.264 ± 0.058	1.87 ± 0.18	3.09 ± 0.47	5.61 ± 1.19	1.135 ± 0.052	1.41 ± 0.14	1.86 ± 0.30	2.57 ± 0.59
1.0 $<{\eta }^{\ast }<$ 5.0	1.187 ± 0.057	1.60 ± 0.16	2.37 ± 0.36	3.82 ± 0.79	1.074 ± 0.051	1.22 ± 0.12	1.44 ± 0.22	1.77 ± 0.38

.

Figure 12 and Figure 13 show the normalized factorial moments $F_q$ for q = 2, 3, 4, 5 calculated from the SGD and WD fits to the distributions at different W and in different pseudorapidity intervals. Corresponding values obtained from the fits are given in Table 3 and Table 4. The values of the moments derived from the data are given in Table 5.

4.3. $H_q$ Moments of Multiplicity Distributions

The first results on the $H_q$ moments are presented in this section. Figure 14 shows the $H_q$ moments versus q variation calculated from the data and compared with SGD and WD distributions in different ${\eta }^{\ast }$ bins. A good agreement with the data can be observed. Results are shown for three ${\eta }^{\ast }$ bins: $1<{\eta }^{\ast }<3$, $1<{\eta }^{\ast }<4$ and $1<{\eta }^{\ast }<5$. The bin with $1<{\eta }^{\ast }<2$ has very low statistics and hence is not included.

4.4. Average Charged Particle Multiplicity

The average charged particle multiplicities for the $ep$ interactions at $\sqrt{s}$ of 300 GeV have been calculated using the $P\left(n\right)$ distributions obtained from the SGD and WD fit models, for all $n>0$. These values obtained are found to be in good agreement with the H1 experimental values, as shown in

Table 6. Comparison of experimental average multiplicity $\langle n\rangle$ with the corresponding values obtained from SGD and WD fits to the data [33] at various W and ${\eta }^{\ast }$ intervals.

	${\mathit{\eta }}^{\ast }$	Exp. Value	SGD Fit	WD Fit
(GeV)		$<\mathit{n}>$	$<\mathit{n}>$	$<\mathit{n}>$
80 $<W<$ 115	1.0 $<{\eta }^{\ast }<$ 2.0	2.92 ± 0.17	2.93 ± 0.07	2.91 ± 0.07
	1.0 $<{\eta }^{\ast }<$ 3.0	5.06 ± 0.28	5.06 ± 0.08	5.03 ± 0.09
	1.0 $<{\eta }^{\ast }<$ 4.0	6.49 ± 0.37	6.61 ± 0.11	6.44 ± 0.13
	1.0 $<{\eta }^{\ast }<$ 5.0	6.91 ± 0.36	6.92 ± 0.11	6.85 ± 0.14
115 $<W<$ 150	1.0 $<{\eta }^{\ast }<$ 2.0	3.00 ± 0.14	3.01 ± 0.04	3.00 ± 0.05
	1.0 $<{\eta }^{\ast }<$ 3.0	5.30 ± 0.32	5.27 ± 0.09	5.27 ± 0.09
	1.0 $<{\eta }^{\ast }<$ 4.0	7.08 ± 0.29	7.17 ± 0.08	7.07 ± 0.09
	1.0 $<{\eta }^{\ast }<$ 5.0	7.75 ± 0.35	7.78 ± 0.09	7.62 ± 0.11
150 $<W<$ 185	1.0 $<{\eta }^{\ast }<$ 2.0	3.13 ± 0.18	3.11 ± 0.07	3.11 ± 0.08
	1.0 $<{\eta }^{\ast }<$ 3.0	5.54 ± 0.31	5.56 ± 0.08	5.53 ± 0.09
	1.0 $<{\eta }^{\ast }<$ 4.0	7.58 ± 0.44	7.71 ± 0.11	7.50 ± 0.13
	1.0 $<{\eta }^{\ast }<$ 5.0	8.46 ± 0.47	8.69 ± 0.13	8.27 ± 0.16
185 $<W<$ 220	1.0 $<{\eta }^{\ast }<$ 2.0	3.15 ± 0.23	3.10 ± 0.09	3.13 ± 0.09
	1.0 $<{\eta }^{\ast }<$ 3.0	5.57 ± 0.39	5.56 ± 0.10	5.58 ± 0.11
	1.0 $<{\eta }^{\ast }<$ 4.0	7.73 ± 0.43	7.77 ± 0.11	7.77 ± 0.12
	1.0 $<{\eta }^{\ast }<$ 5.0	8.82 ± 0.49	8.88 ± 0.16	8.80 ± 0.17

. The $\langle n\rangle$ values obtained from the SGD and WD models in the pseudorapidity interval $1<{\eta }^{\ast }<5$ are fitted with a linear function of ln$\left(W^2\right)$ using the relation

$$\langle n\rangle =\alpha +\beta ln\left(W^2\right)$$

(28)

Values of the parameters $\alpha$ and $\beta$, obtained for the SGD model are $-6.40\pm 1.166$, $1.455\pm 0.119$, and for the WD model are $-5.406\pm 1.357,1.335\pm 0.138$, respectively. The ${\chi }^2/$ndf for SGD and WD fits are 3.35/2 and 0.1/2, respectively.

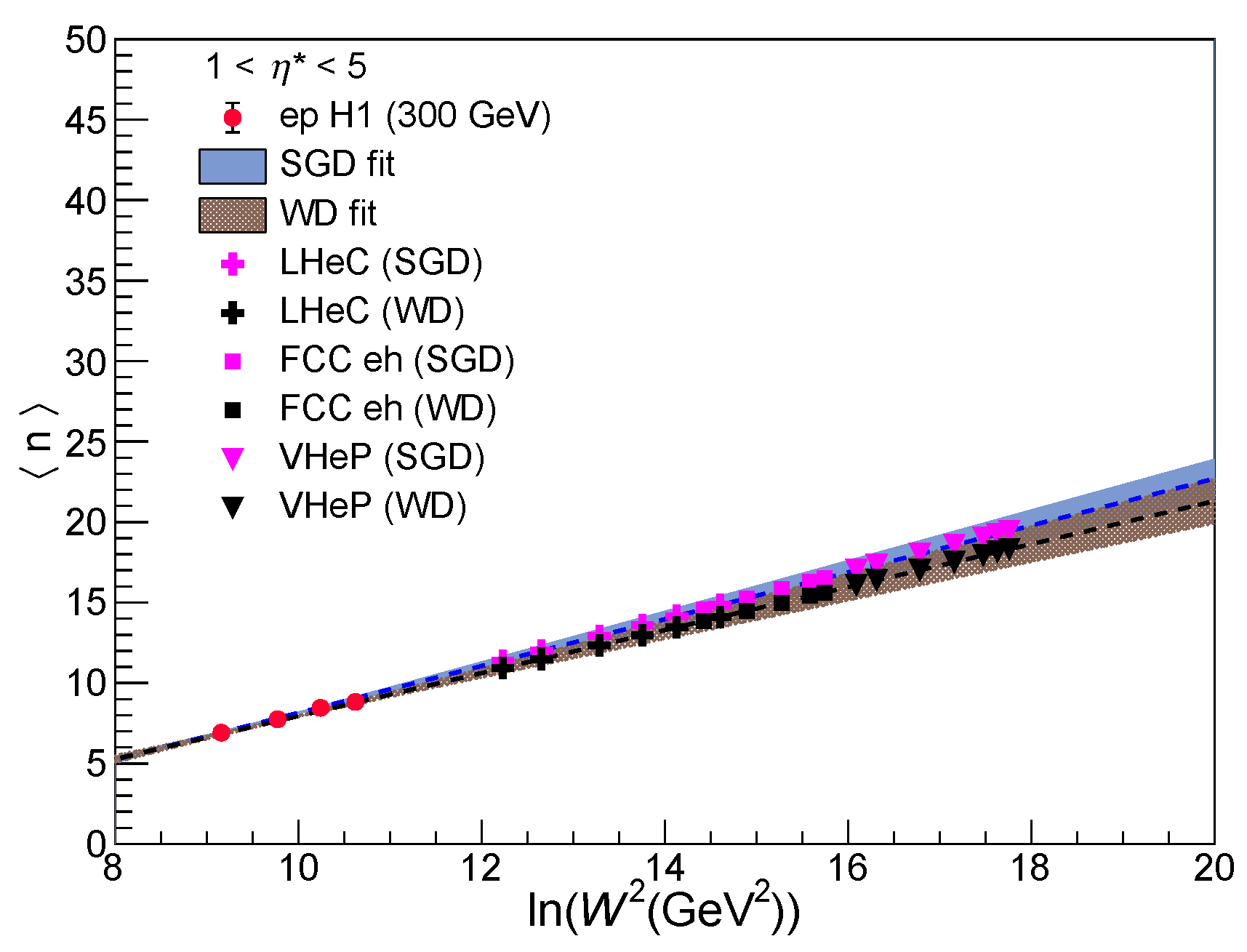
5. Projections of $\langle \mathit{n}\rangle$ for the Proposed Future $\mathit{ep}$ Colliders

The proposed future high energy ep colliders, the Large Hadron Electron Collider LHeC [49], Future Circular Collider (FCC)-eh [50] and a Very High energy electron–proton collider (VHep) [51,52] aim to extend the kinematic reach of electron probe inside the proton. The colliding beam energies and c.m. energies expected from these colliders are listed in

Table 7. The energies of electron (Ee) and proton (Ep) beams and the center-of-mass energy ($\sqrt{s}$) at HERA and at the future ep colliders.

	HERA-I	LHeC	FCC-eh	VHep
Ee (GeV)	27.5	60–140	60	3000
Ep (TeV)	0.9	7	50	7
$\sqrt{s}$ (TeV)	0.3	1.2–1.9	3.5	9

.

The increased c.m. energies that can be achieved at the proposed future ep colliders, are projected to be many orders higher than the HERA energies. This will facilitate to probe precisely the structure of proton, perform other standard tests of quantum chromodynamics (QCD) and to look for the signatures of physics beyond Standard Model (BSM) in a whole new kinematic region currently non-achievable.

Figure 15 shows the $\langle n\rangle$ expected from SGD and WD models, calculated from Equation (28), at different W for the interval $1<{\eta }^{\ast }<5$, covering the ranges offered in the past by the H1 detector at HERA and all the other three proposed future high energy ep colliders. The blue and grey bands are $68\%$ uncertainty bands on the SGD and WD central fit values, respectively. Reach of the proposed future ep colliders in terms of W are depicted in Figure 15 and also shown are the values of $\langle n\rangle$ expected at these very high energies.

Figure 16 shows the $\langle n\rangle$ dependence on $lns$ for four different types of collisions: e${}^{+}$e${}^{-}$ [53,54,55,56,57] in the full $\eta$ range, $\overline{\mathrm{p}}$p [41,58] in two phase space windows (the full $\left|\eta \right|$ and $\left|\eta \right|<3$), pp [59,60,61] collisions in the $\left|\eta \right|<2$ and $\left|\eta \right|<2.4$ windows and ep in different $\eta$ ranges. Square of c.m. energy available for particle production s is represented by $W^2$ in case of ep collisions. In each of the three cases, dashed lines represent the SGD predictions. For these collisions the analyses in terms of SGD were presented in our earlier publications. However the $\langle n\rangle$ versus $lns$ dependence was not studied. From Figure 16 it may be observed that the data agree with the SGD predictions, and ${\langle n\rangle }_{\mathrm{ee}}$ is more than ${\langle n\rangle }_{\mathrm{pp}}$ at full width in the common $\sqrt{s}$. It is also observed that in the region $\left|\eta \right|<2$ for pp and corresponding $1<{\eta }^{\ast }<5$ region for ep, the $\langle n\rangle$ is very large for the pp/$\overline{\mathrm{p}}$p collisions as compared to the ep collisions. Roy et al. [62], in a recent publication, studied $\langle n\rangle$ dependence on energy for e${}^{+}$e${}^{-}$, e${}^{\pm }$p, and $\overline{\mathrm{p}}$p collisions, to search for scaling properties of average multiplicity and pseudorapidity density. They made a similar observation that ${\langle n\rangle }_{\mathrm{ee}}$ > ${\langle n\rangle }_{\mathrm{pp}}$ > ${\langle n\rangle }_{\mathrm{ep}}$ at each value of $\sqrt{s}$. Their analysis led to a common fit to the data from all different types of collisions, as shown in Figure 1 of the paper [62]. In e${}^{+}$p data at HERA, the $\langle n\rangle$ dependence on $ln\left(W^2\right)$ increases linearly with the increasing size of pseudorapidity window.

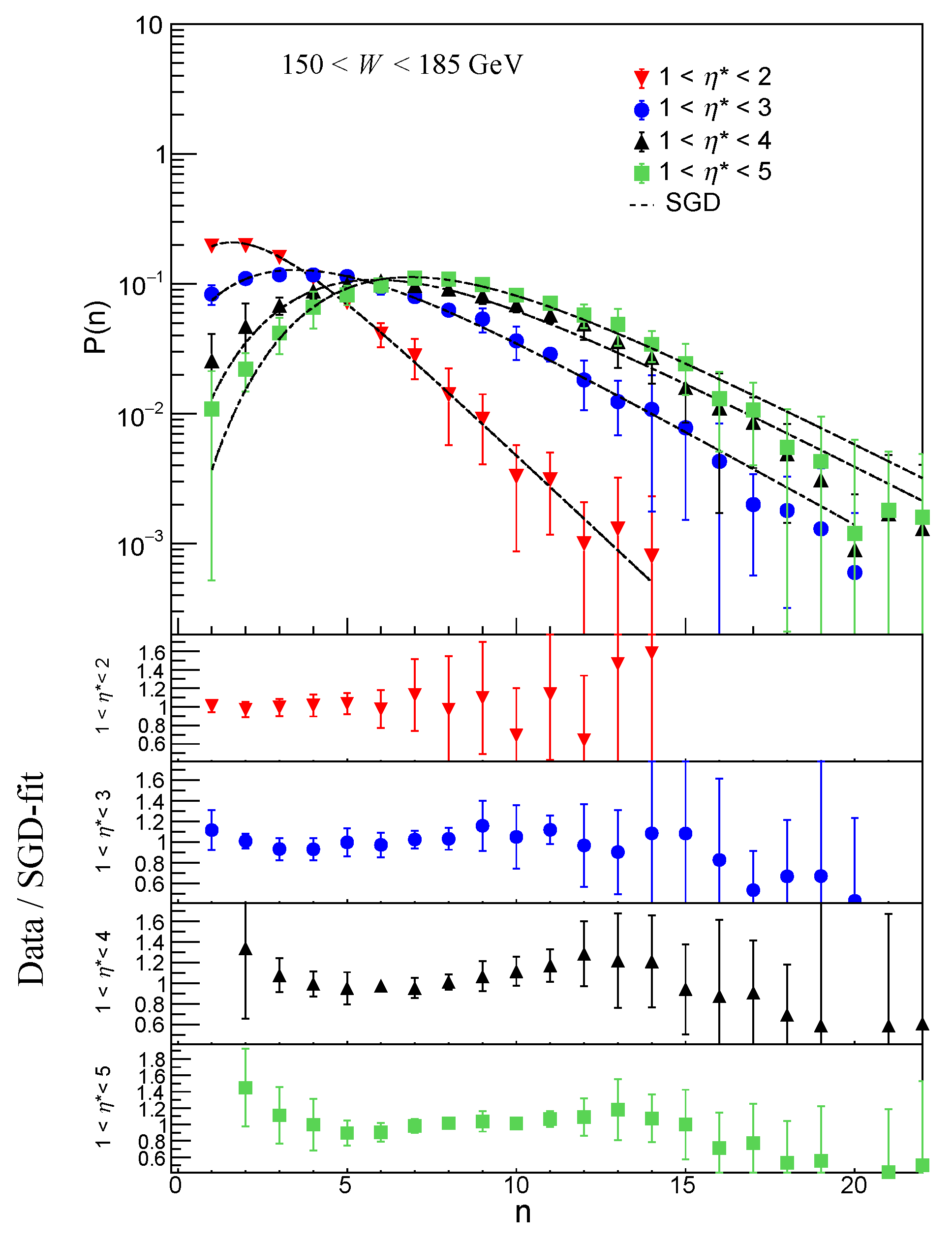
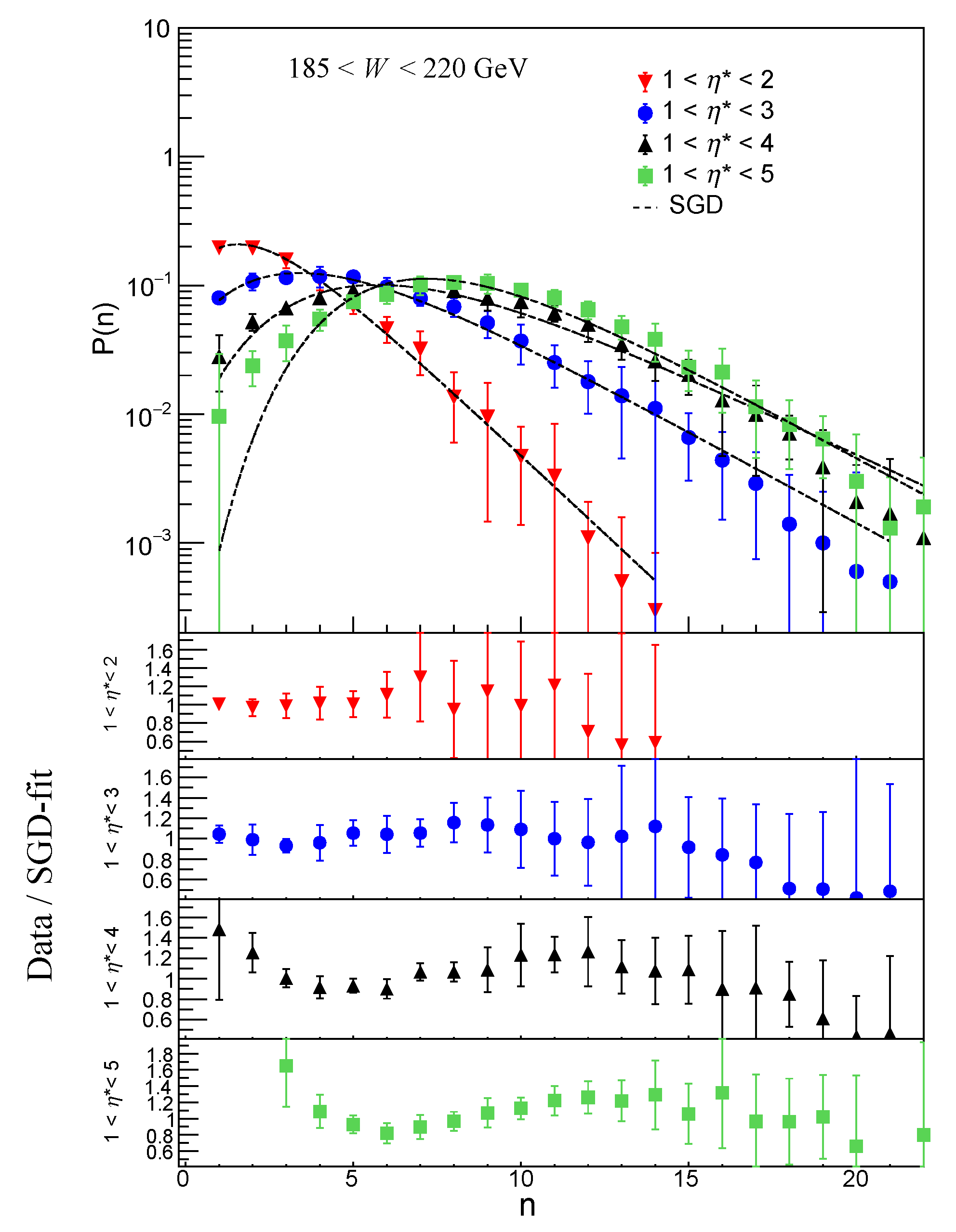
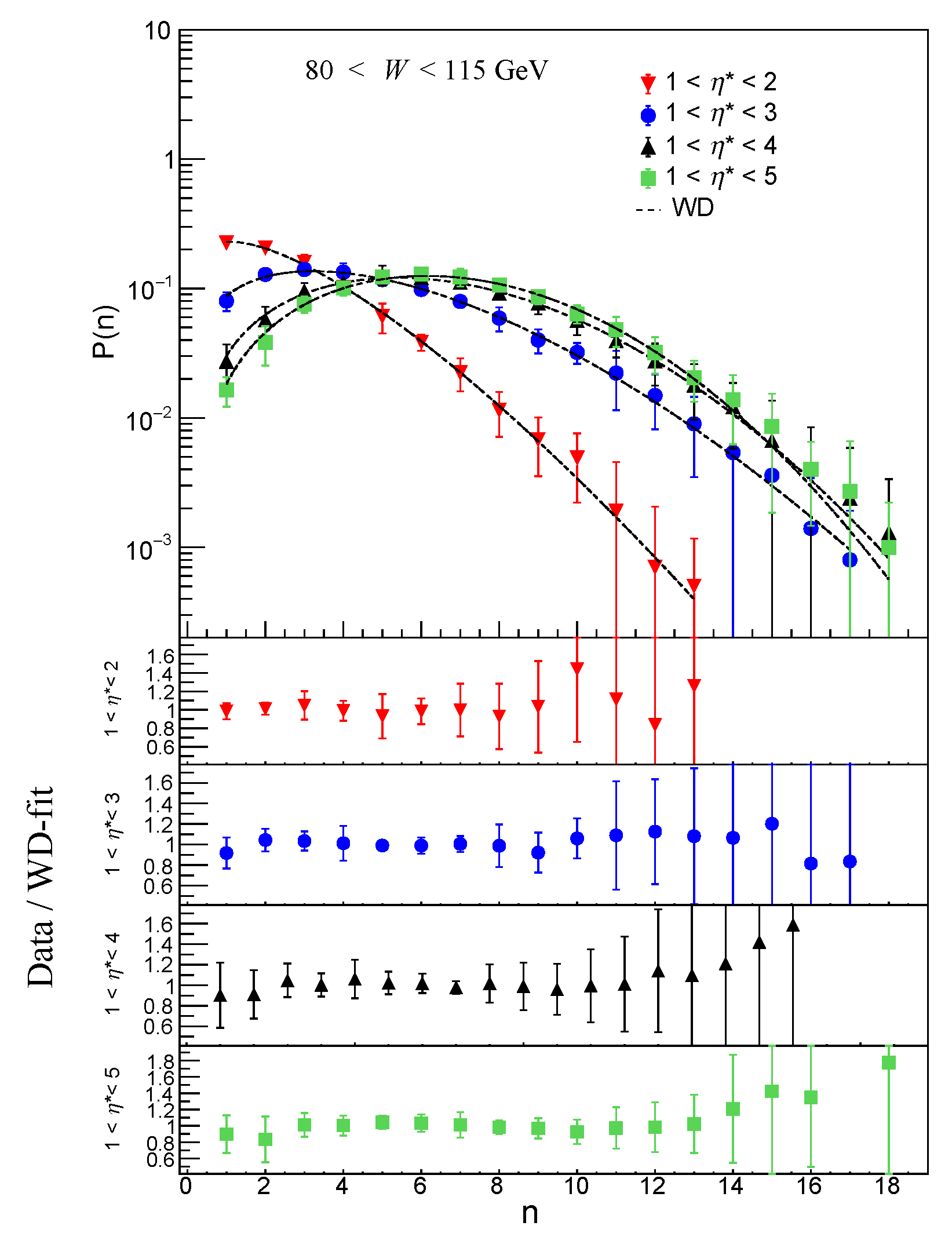
6. Results and Conclusions

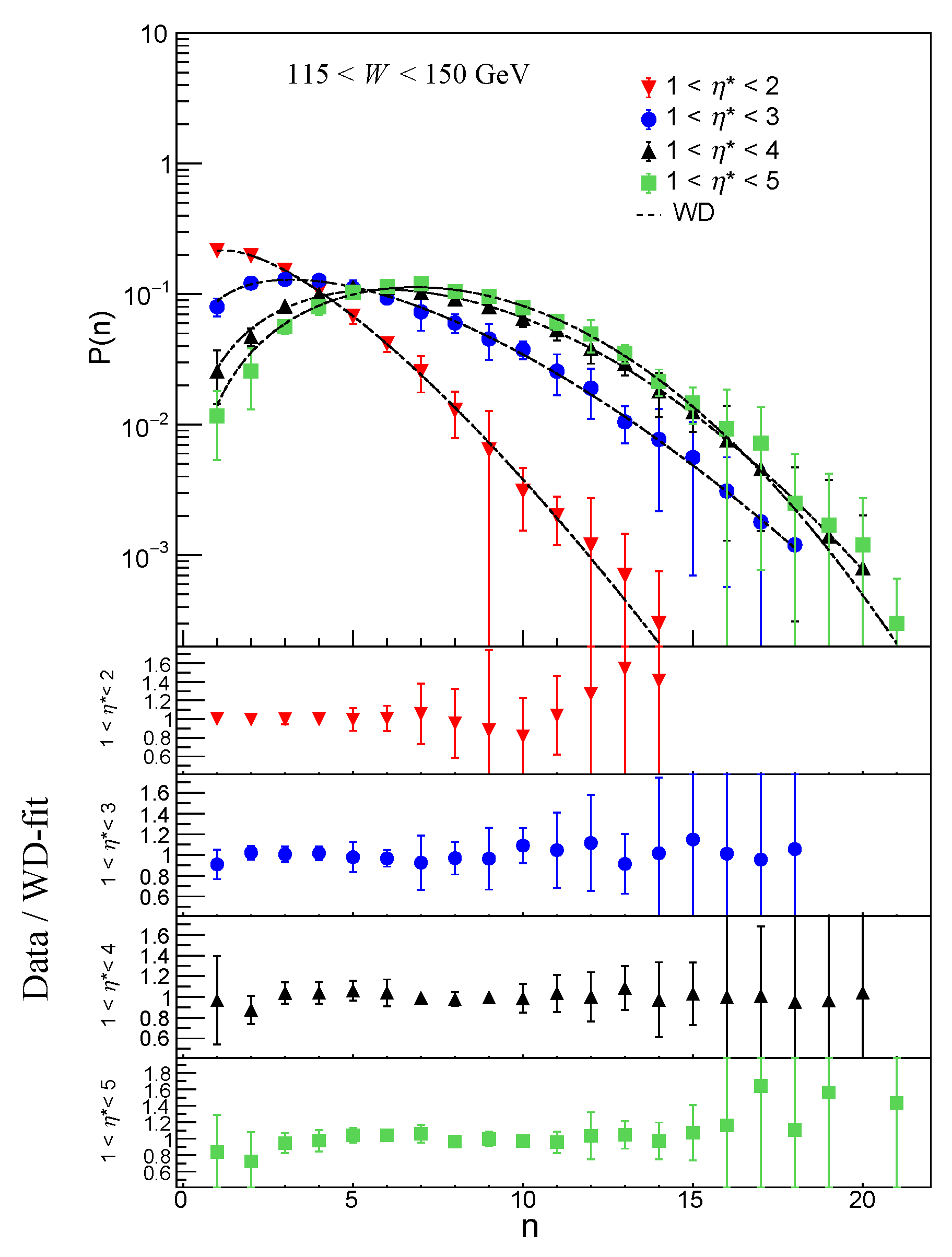
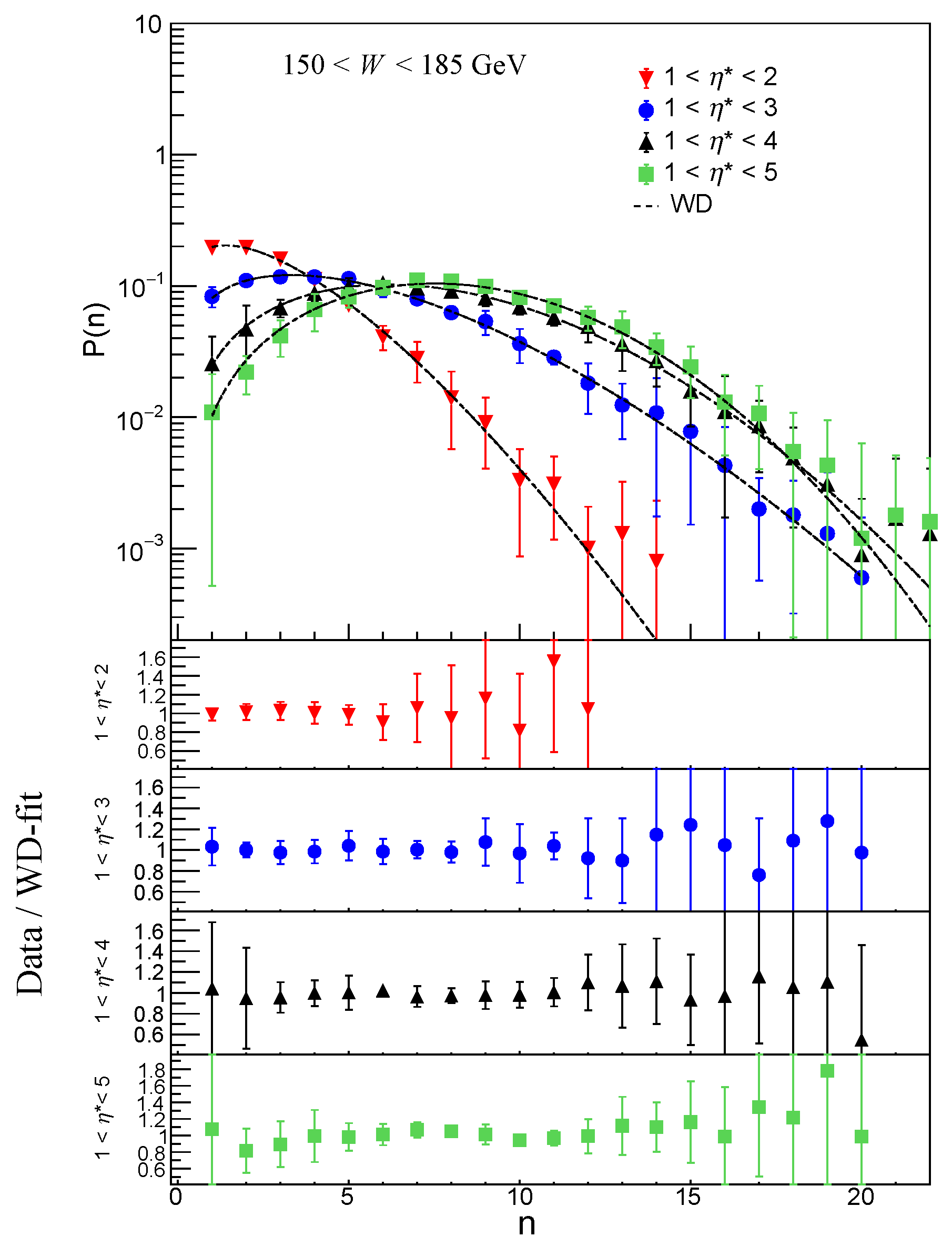
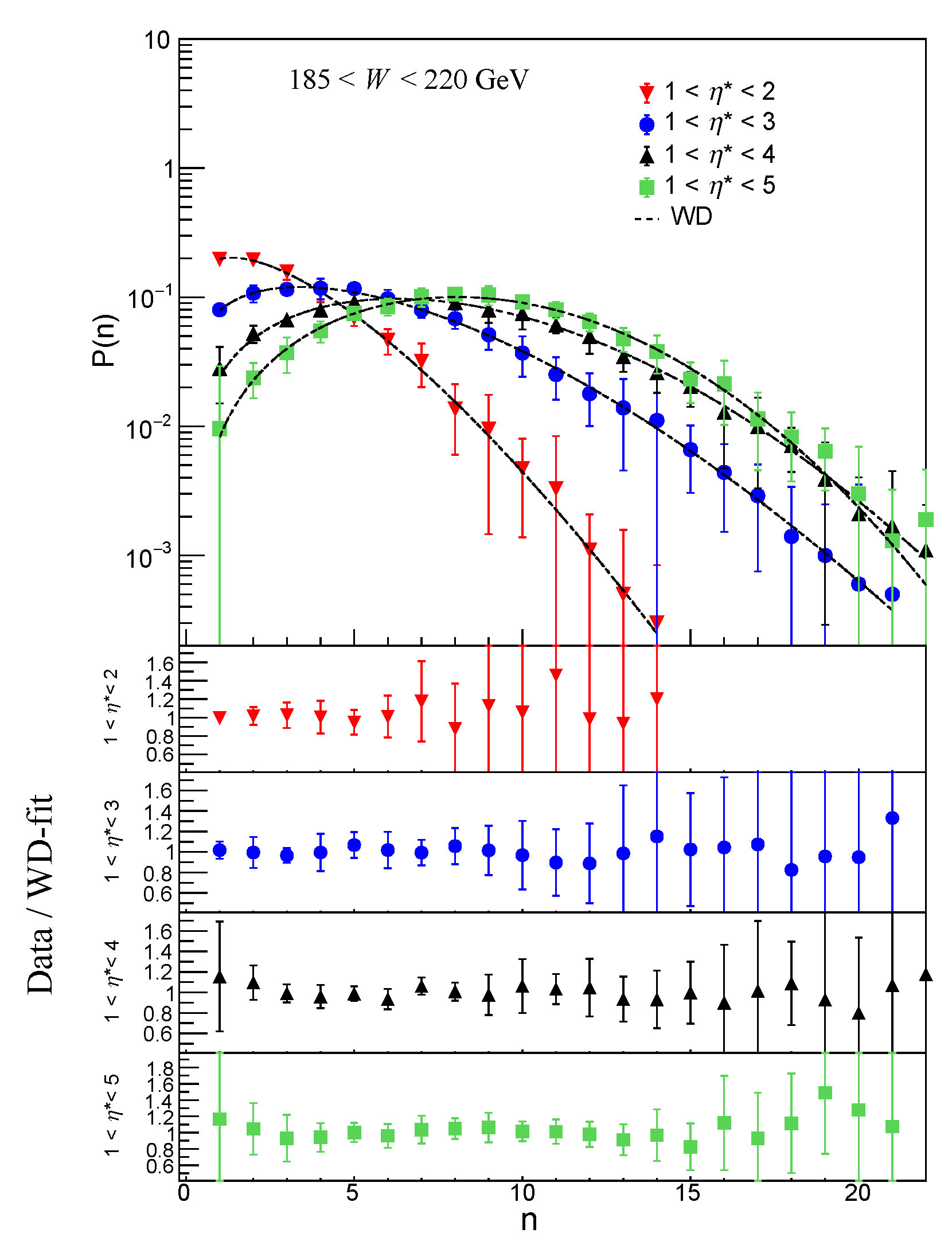
The statistical behavior of charged particle multiplicity in the hadronic final state of deep inelastic e${}^{+}$p scattering in the ${\gamma }^{\ast }$p c.m. energy range, 80< W< 220 GeV is investigated. From the shapes of the Multiplicity distributions in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, it may be observed that for both SGD and WD the high-multiplicity tails of the distributions increase faster with increasing energy than the low-multiplicity part. The same trend can be observed with broadening of pseudorapidity interval. This feature points towards a possible beginning of the KNO scaling violation in high energy region. An investigation of multiplicity distribution in reference [33], also concluded that the property of KNO scaling remains valid in DIS at HERA for small and for large pseudorapidity intervals, but not for intermediate size intervals.

The data/fit ratio plots show disagreement between the data and the SGD fit values in lower multiplicity region, particularly for $n<5$ in the two largest ${\eta }^{\ast }$ intervals: 1 < ${\eta }^{\ast }$ < 4 and 1 < ${\eta }^{\ast }$ < 5 for all $Ws$. Comparison of ratio plots in the WDs in Figure 6, Figure 7, Figure 8 and Figure 9 show good agreement with the data within the limits of error. SGD shows some disagreement in the low multiplicity region. This is because the data suffers from low statistics in this region. Similar observation was reported in the paper by H1 collaboration [33]. With LND and NBD functions it was found that large n tail of the experimental distributions is well described but deviations occur for small multiplicities.

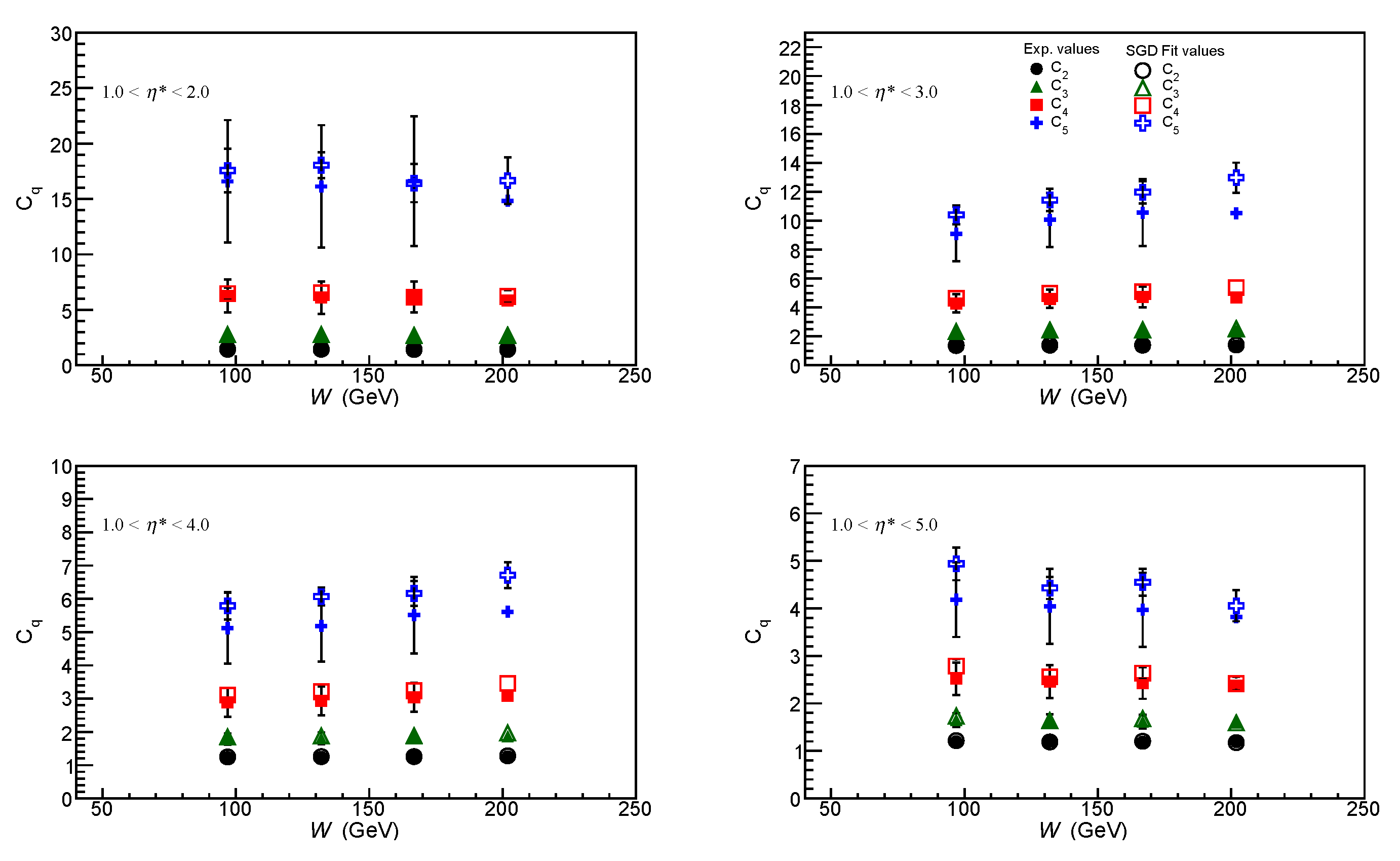
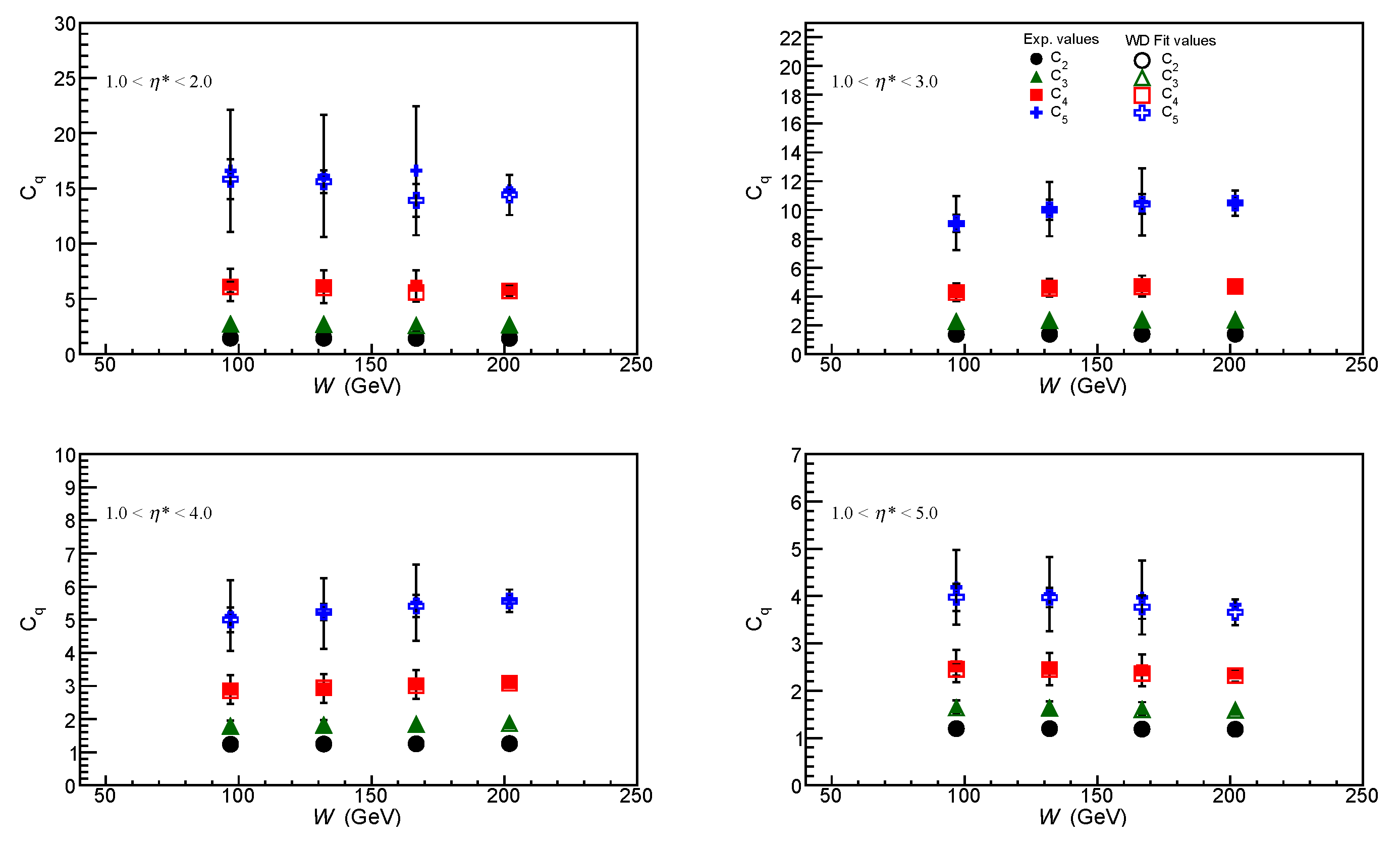
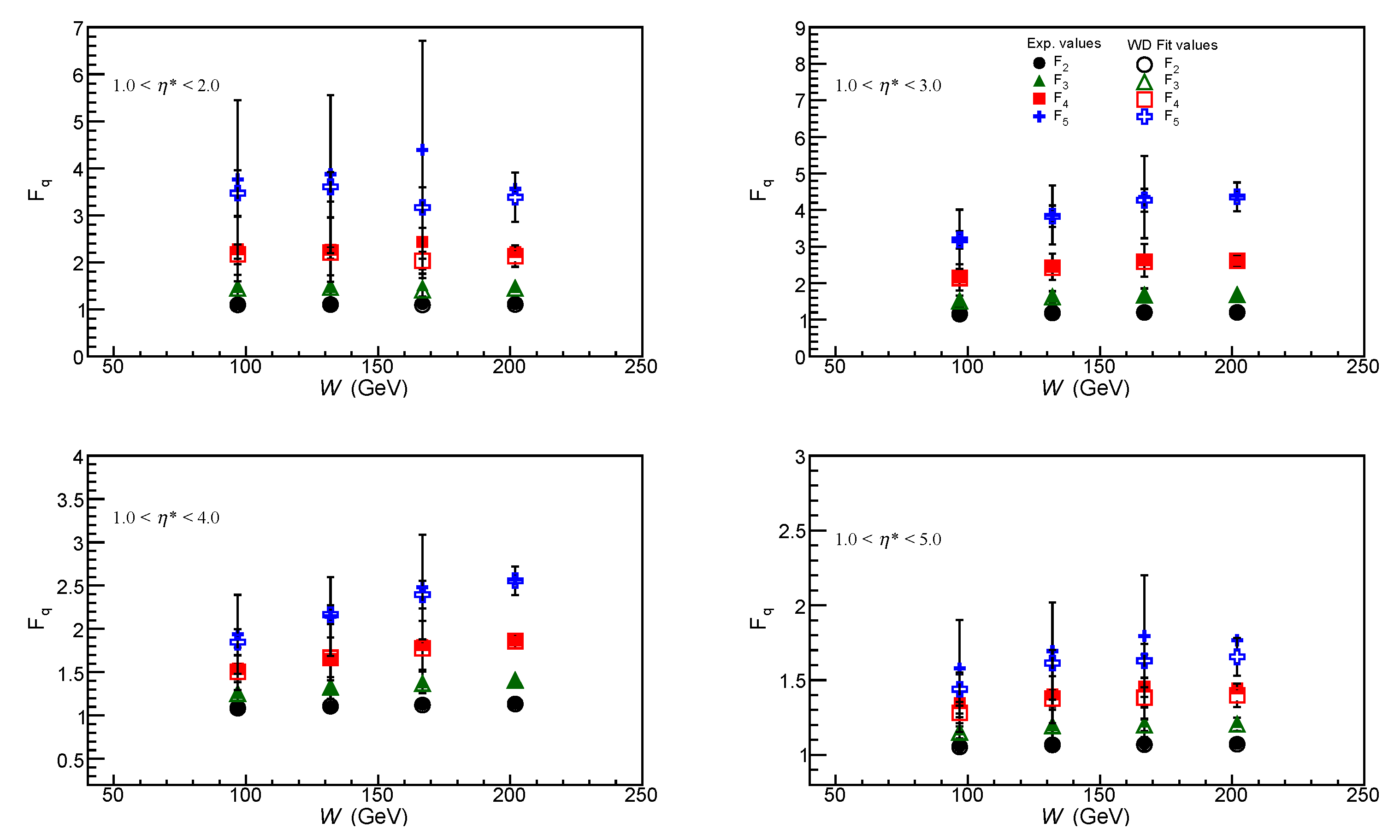
It may be observed that both normalised moments, $C_q$, and normalised factorial moments, $F_q$, computed from the SGD and WD fits, agree well with the values obtained from the data. However, due to limited statistics, values calculated from the data have large errors. At fixed W the moments decrease as ${\eta }^{\ast }$ window increases in size from 1 < ${\eta }^{\ast }$ < 2 to 1 < ${\eta }^{\ast }$ < 5. This implies widening of multiplicity distribution in the KNO form. Broadening of the distribution results in the $F_q$ values becoming greater than unity. Thus, beyond the expectation of KNO distribution, it indicates the presence of particle correlations.

From the Figure 10, Figure 11, Figure 12 and Figure 13 and the values given in the Table 3, Table 4 and Table 5, it is observed that $C_2$ and $C_3$ remain roughly constant over the W range between 80 GeV and 220 GeV, for the same pseudorapidity windows. $C_4$ and $C_5$ show a marginal increase with increasing W.

Exact KNO scaling implies that moments $C_q$, are independent of W. Thus, moments in the smallest and the largest pseudorapidity windows show little dependence on energy, thus exhibiting approximate KNO scaling. The intermediate size windows point towards the violation of KNO scaling. This observation is consistent with observation at HERA in DIS data on multiplicity distributions [63,64].

The factorial moments $F_2$, $F_5$ show little W-dependence, within limits of errors, while $F_3$, $F_4$ show a small increase with increasing W. Uniform constancy of the factorial moments establishes KNO scaling.

In the earlier paper [32], the moments of e${}^{+}$e${}^{-}$, pp and $\overline{\mathrm{p}}$p collisions were studied by us and the violation of KNO scaling was shown, as observed for higher moments in the measured data. At higher energies, particularly at the LHC energies, the moments strongly are dependent on the energy. It was observed that the values for both the normalised moments, $C_q$, as well as normalised factorial moments, $F_q$, computed from the SGD fits were in agreement with the values obtained from the data. Both types of moments were found to decrease with widening of the pseudorapidity window for both pp (for $0.5<\left|\eta \right|<2.4$) and $\overline{\mathrm{p}}$p (for $0.5<\left|\eta \right|<5.0$).

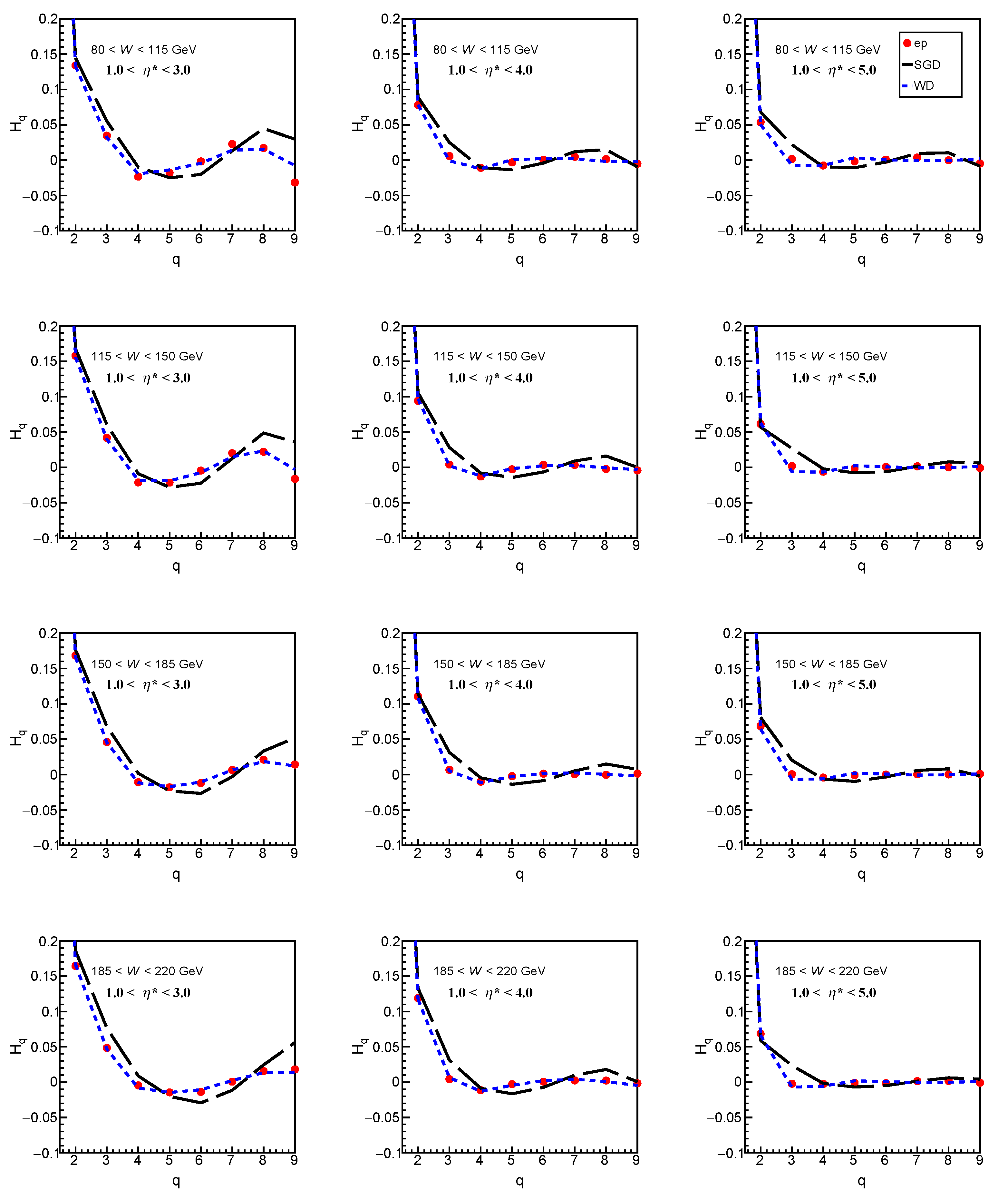
The ratio of cumulants to factorial moments is defined as $H_q$ moments. A special oscillation pattern is observed in the shape of multiplicity distribution, when analysed in terms of $H_q$ moments varying with the rank of the moment q. Moments grow very rapidly with q, but the growth cancels in their ratio. This makes the graphical representation of $H_q$ better understood. Details are well described in references [65,66,67,68].

Study of dependence of $H_q$ moments on the rank of moment q, shows the oscillatory behaviour, with first minimum occurring around $q_{min}\simeq$ 5. This behaviour was explained well within the theory of perturbative QCD [69,70,71]. In the earlier paper by us [29], hadronic multiplicities in e${}^{+}$e${}^{-}$, pp and $\overline{\mathrm{p}}$p collisions and $H_q$ moments were studied, by using SGD. For different species of the colliding particles, similar oscillations in the $H_q$ moments were observed in different pseudorapidity windows and also in the forward region. Furthermore, the shape of the multiplicity distributions analyzed in terms of the $H_q$ moments was found to reveal quasi-oscillations.

In the present study, analysis of multiplicity distributions in e${}^{+}$p data, using SGD and WD, shows similar oscillations in $H_q$ moments. The behaviour of $H_q$ moments in different ${\eta }^{\ast }$ and in different W ranges is studied. The shape of the multiplicity distribution (in every W range) analyzed in terms of the $H_q$ moments was found to show the quasi-oscillations in the regime of large q values. The perturbative QCD also predicts, a negative first minimum near $q\simeq$ 5 and expected quasi-oscillations of about zero for larger values of q.

Overall, the results from analysis of different types of moments are compatible with the results obtained earlier from e${}^{+}$e${}^{-}$, pp and $\overline{\mathrm{p}}$p collisions at different energies and in different phase space windows.

It may be observed that SGD and WD both describe the data well and with a minimum around $q\simeq$ 5, although WD reproduces the data more closely. The dependence of $H_q$ on the rank of moment, q in all ${\eta }^{\ast }$ windows shows a steep descent to a minimum value around q = 4–5. Beyond the minimum it tends to flatten out for higher q. A more regular quasi-oscillations about zero can be seen in the pseudorapidity windows $1<{\eta }^{\ast }<3$ and $1<{\eta }^{\ast }<4$. These observations follow closely the predictions from QCD and also the next-to-next-to-leading logarithm approximation (NNLLA) of perturbative QCD.

The mean charged multiplicity $\langle n\rangle$, calculated from the e${}^{+}$p data, SGD and WD fits in different intervals of W and different pseudorapidity windows, are in agreement within errors. The $\langle n\rangle$ dependence on W follows a linear dependence as ln$W^2$. Using this dependence, $\langle n\rangle$ values at the future, very high energy ep colliders are predicted.

The dependence of $\langle n\rangle$ on $lns$ for three different types of collisions: e${}^{+}$e${}^{-}$ in the full $\eta$ range, $\overline{\mathrm{p}}$p in two phase space windows (the full $\left|\eta \right|$ and $\left|\eta \right|<3$), and pp collisions in the $\left|\eta \right|<2$ and $\left|\eta \right|<2.4$ windows has been studied. It may be observed that the data agree with the SGD predictions and ${\langle n\rangle }_{\mathrm{ee}}$ is more than ${\langle n\rangle }_{\mathrm{pp}}$ at full width in the common $\sqrt{s}$. It is also observed that in the pseudorapidity region $\left|\eta \right|<2$ for pp and corresponding $1<{\eta }^{\ast }<5$ region for ep, the $\langle n\rangle$ is very large for the pp/$\overline{\mathrm{p}}$p collisions as compared to the ep collisions. This observation agrees with the observation made in a paper by Roy et al. [62] that ${\langle n\rangle }_{\mathrm{ee}}$ > ${\langle n\rangle }_{\mathrm{pp}}$ > ${\langle n\rangle }_{\mathrm{ep}}$ at each value of $\sqrt{s}$. The $\langle n\rangle$ increases linearly with $ln\left(W^2\right)$ with the increasing size of pseudorapidity window in ep data at HERA.