Displacement Analyses for a Natural Slope Considering Post-Peak Strength of Soils
Abstract
:1. Introduction
2. Methodology
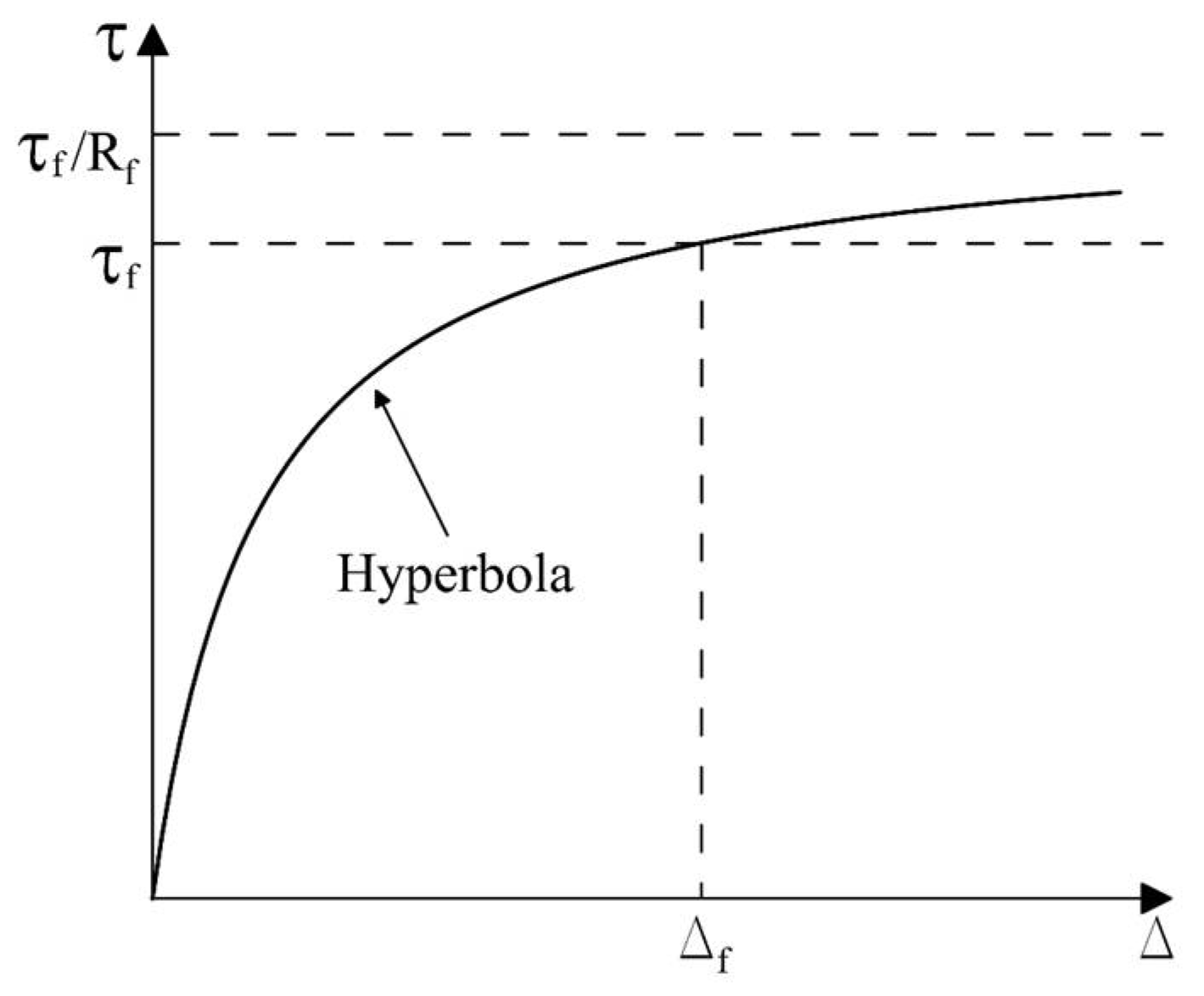
2.1. Constitutive Law for Stress-Displacement Relationship
- kinitial: initial shear stiffness
- Rf: ratio between failure strength and asymptotic shear strength
- τult: asymptotic strength at infinite displacement
- τf: failure shear strength expressed using the M-C failure criterion
- K: stiffness number (an experimental constant)
- PA: atmospheric pressure (=101.3 kPa)
- G: reference shear stiffness (=101.3 kPa/m)
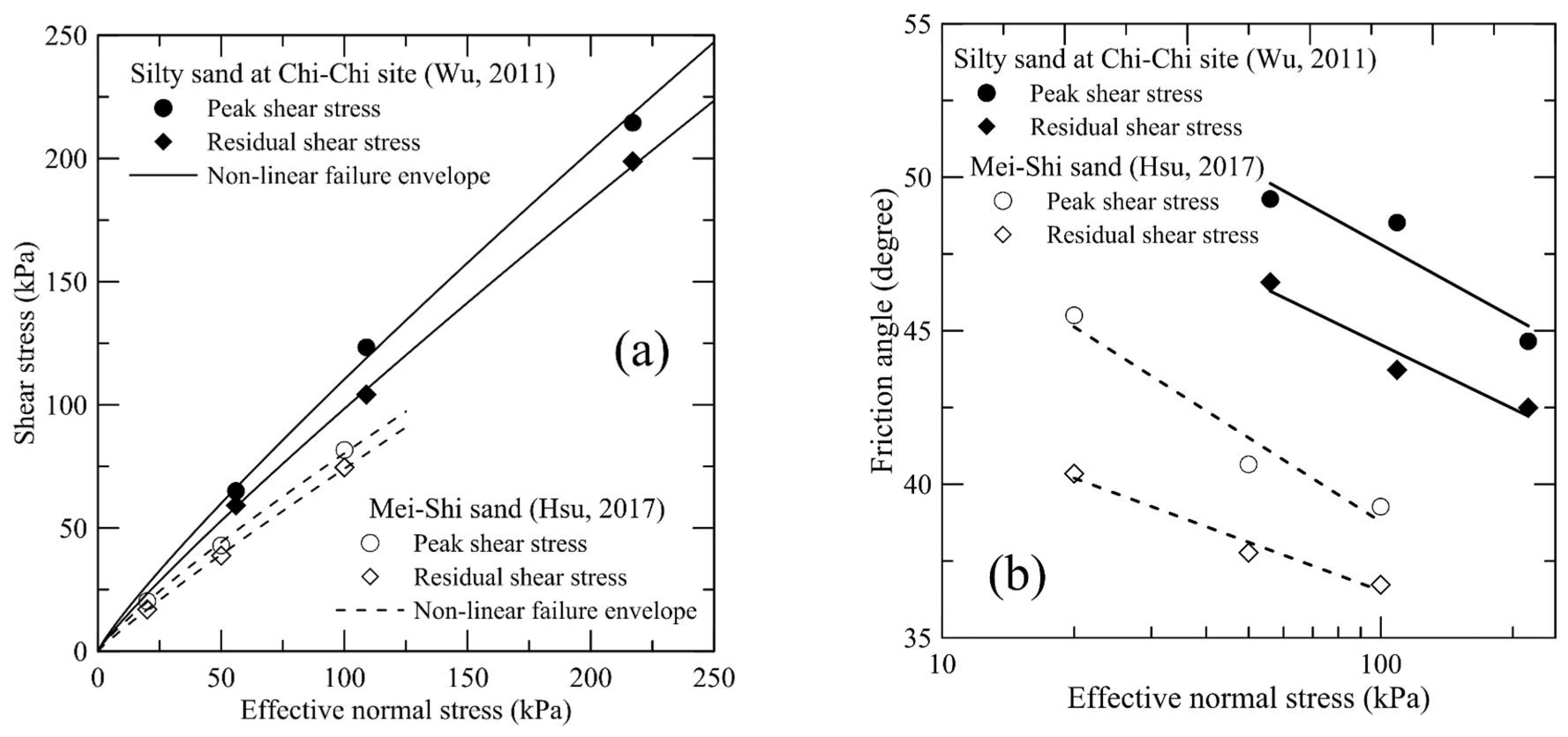
2.2. Internal Friction Angle of Soils
- σn: effective normal pressures
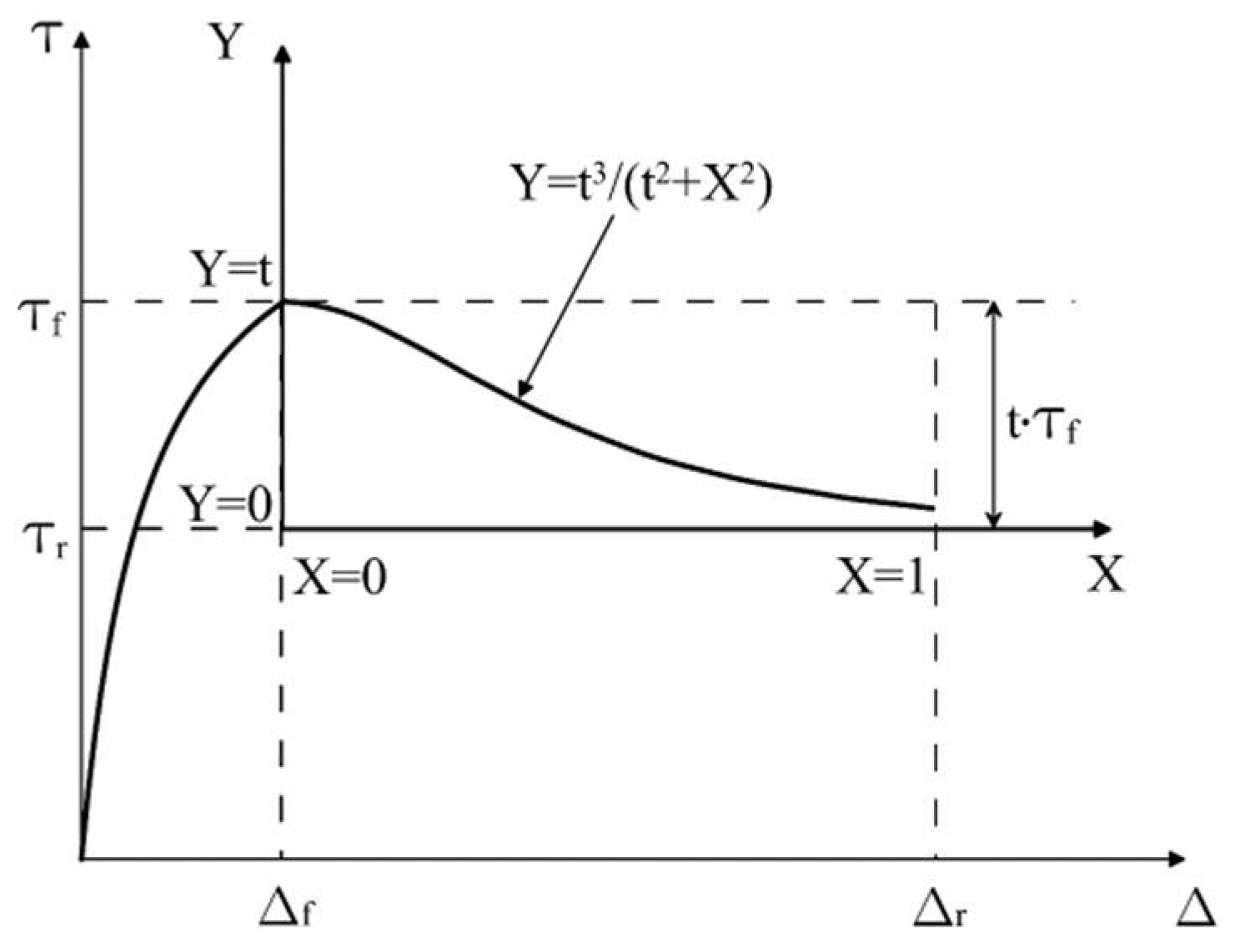
2.3. Post-Peak Stress-Displacement Relationship
- t: normalized strength deterioration from peak to residual states
- Y: normalized post-peak shear stress
- X: normalized post-peak shear displacement parameter
- Δf: shear displacement at peak stress states
- Δratio(100): value of Δratio under reference confining pressure of σn = 100 kPa
- R: experimental parameter (ranging from 0 to 0.013)

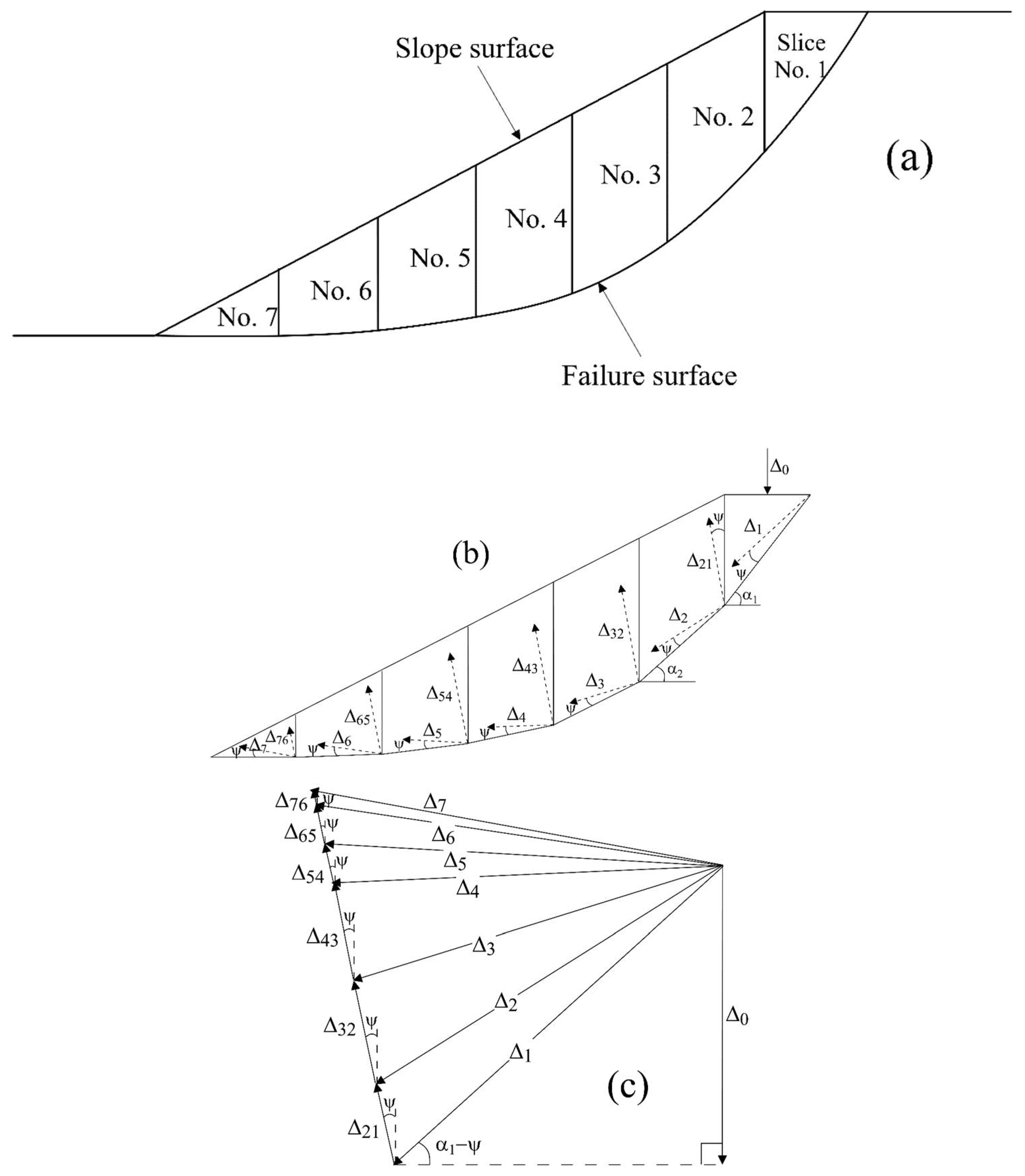
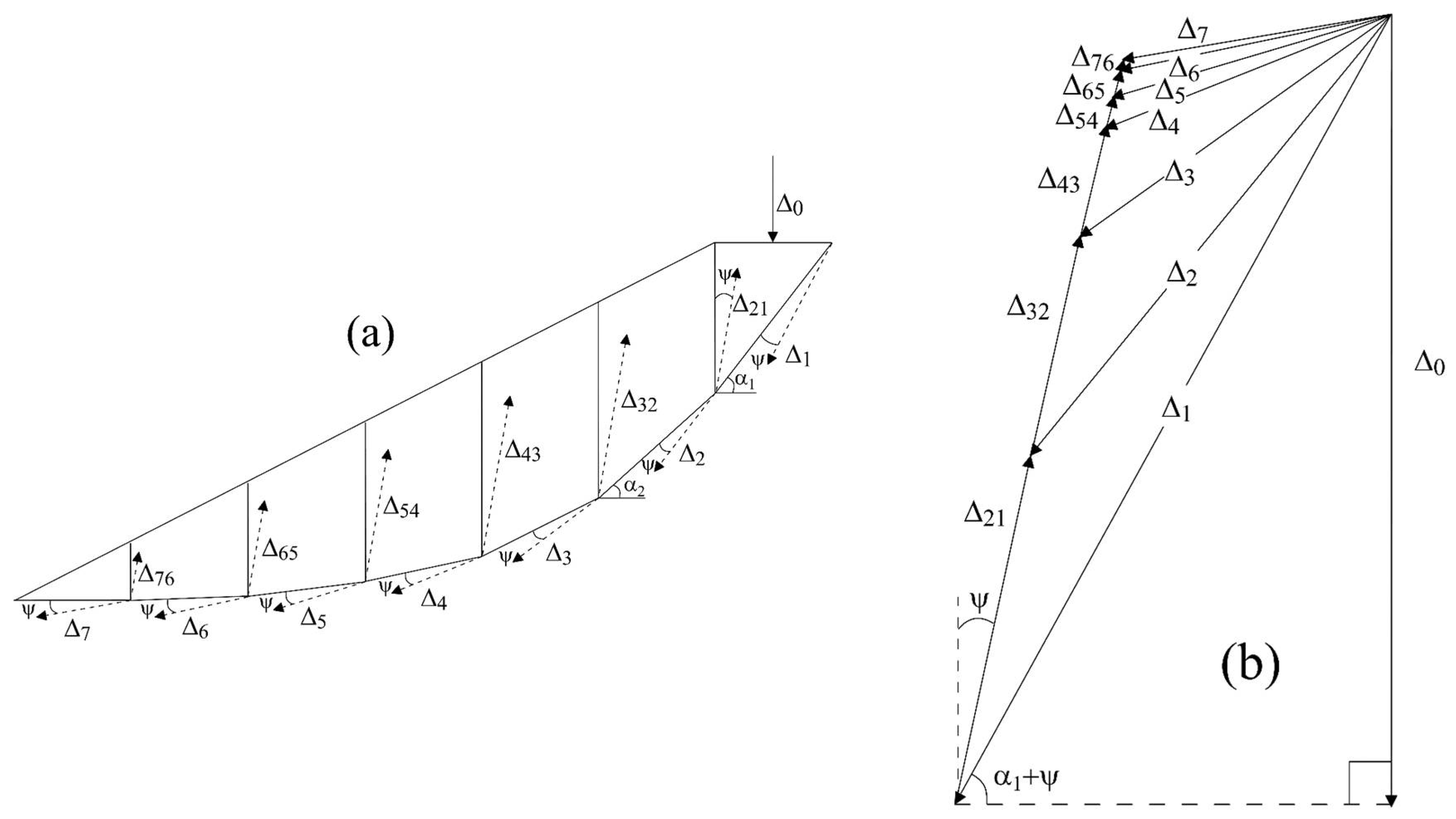
2.4. Displacement Compatibility Requirements
- Δ0: vertical displacement at the crest of slice 1;
- α1, αi: inclination angles for slices 1 and i, respectively
- Ψ: angle of dilation.
2.5. Calculating Safety Factors Using Method of Slices
- Wi: self-weight of slice i (i = 1−n)
- αi: base inclination of slice i
- ΔXi: differential vertical inter-slice force for slice i (=Xi−Xi−1)
- Sfi: ultimate shear strength at the base of slice i based on the M-C failure criterion.

2.6. Force-Equilibrium-Based Finite Displacement Method
- τfi, τi: ultimate (or peak) shear strength and shear stress, respectively, at the base of slice i (i = 1−n)
- Sfi, Si: ultimate (or peak) shear resistance and shear force, respectively, at the base of slice i
- li: length of the base of slice i.
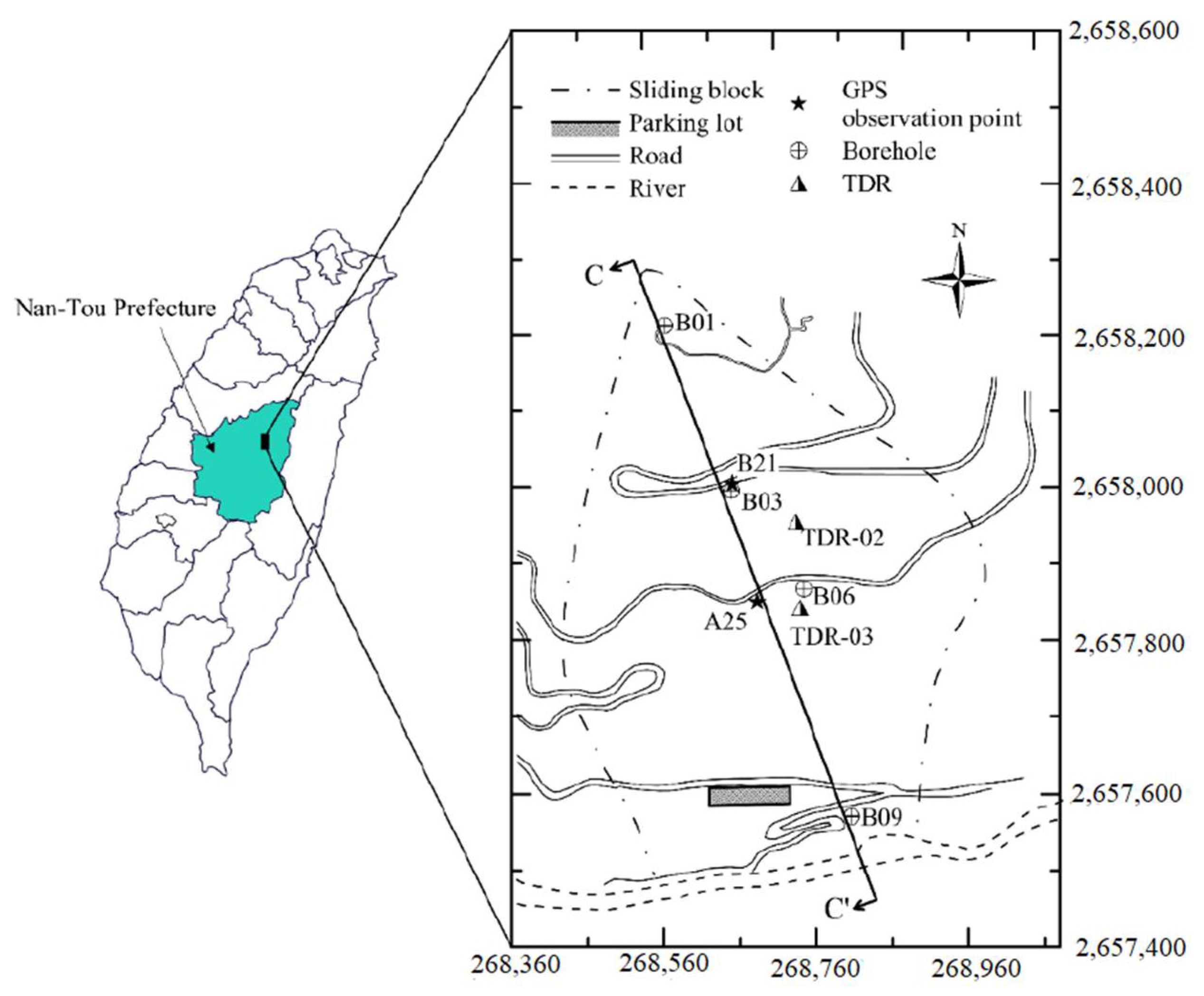
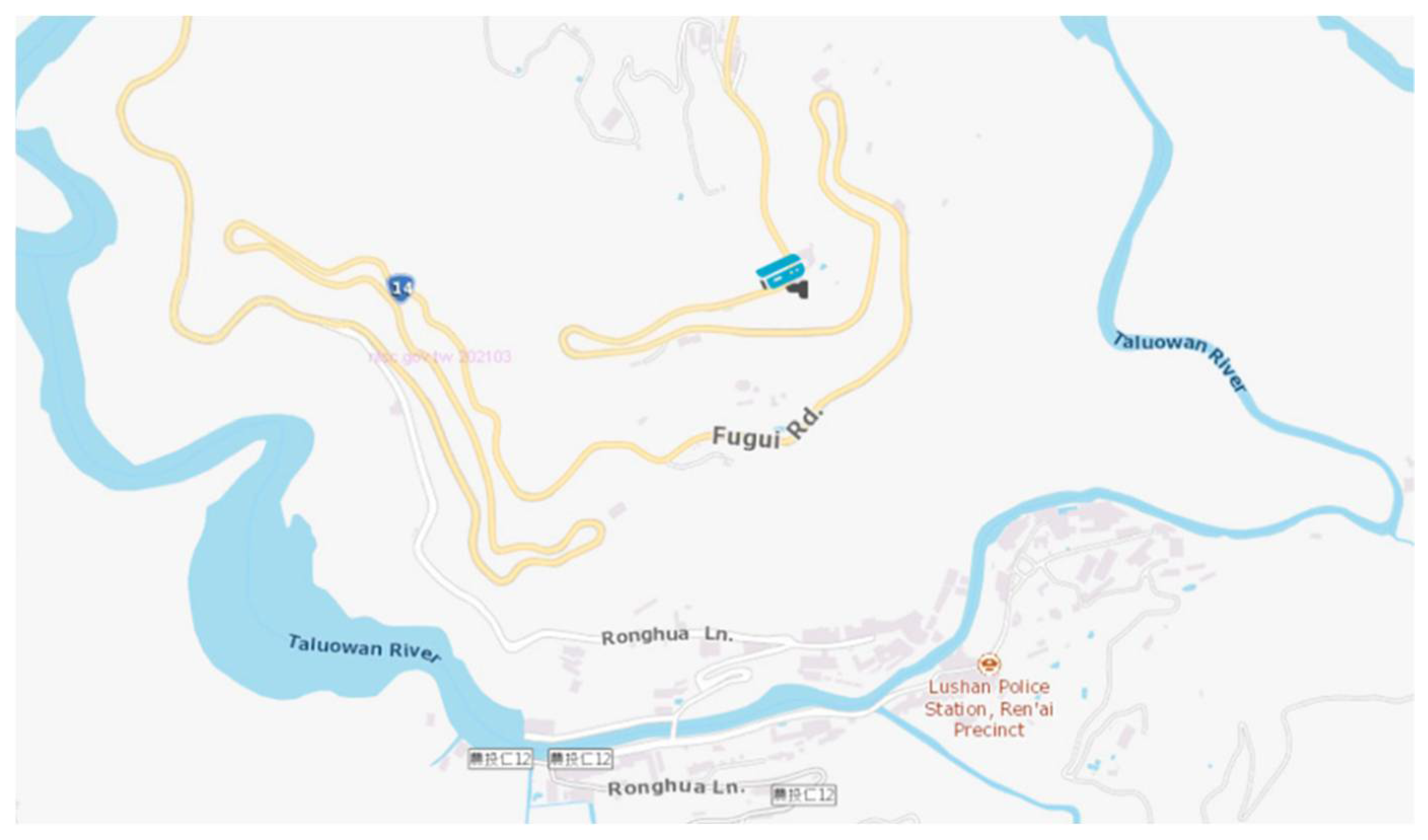
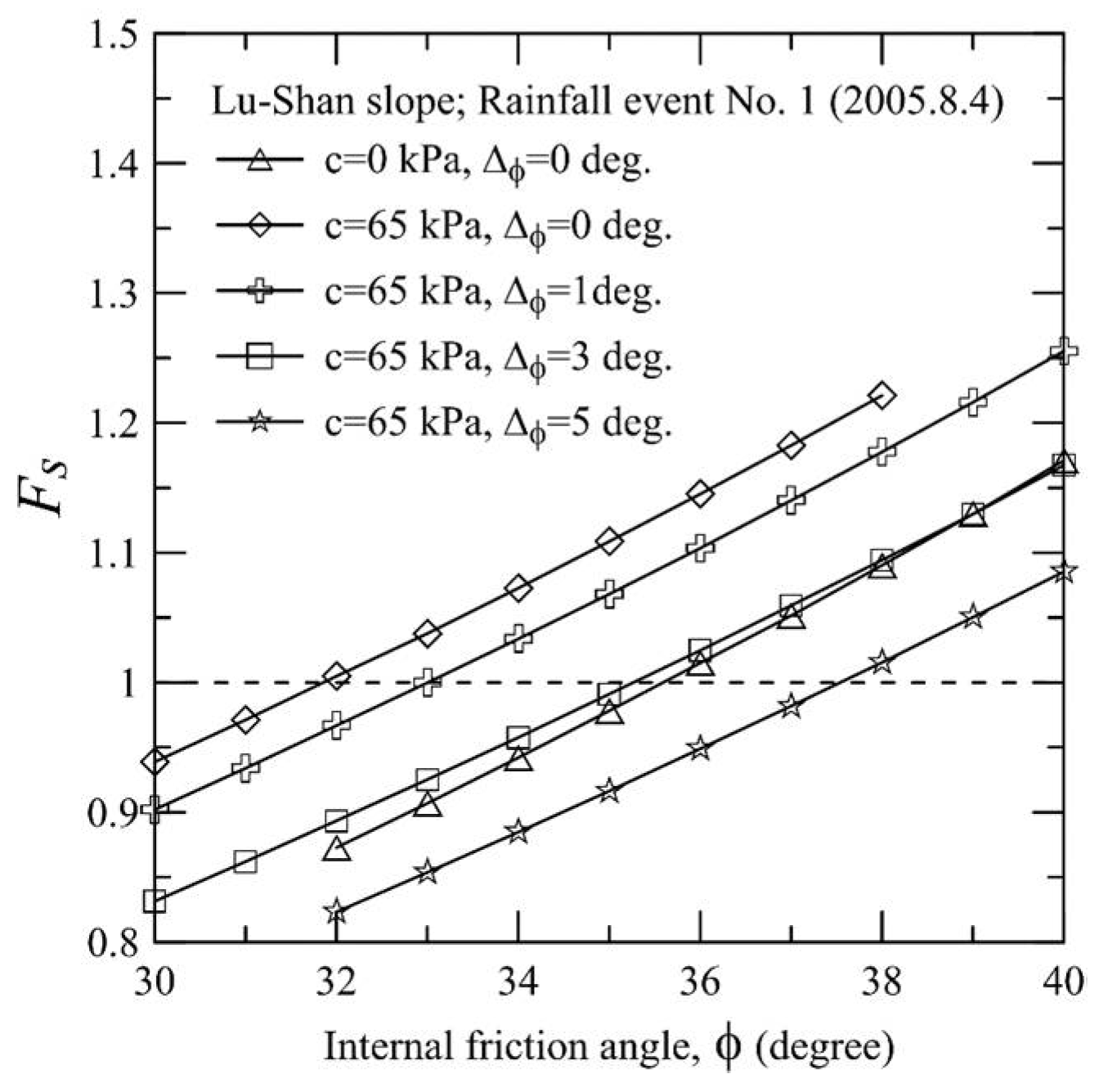
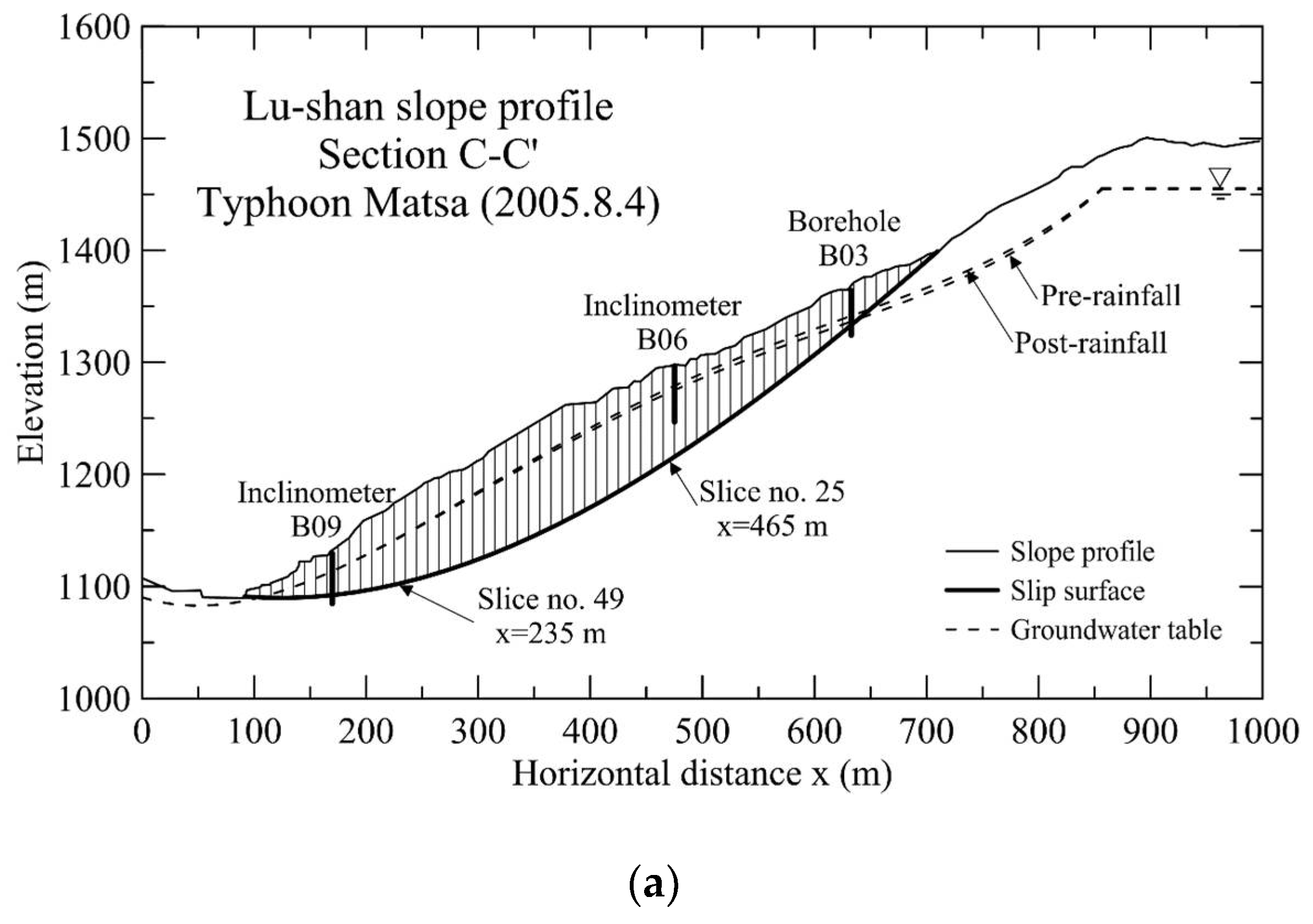
3. Case Study: Lu-Shan Slope
- c: cohesion intercept (kPa)
- z: depth (m).
4. Results and Discussion
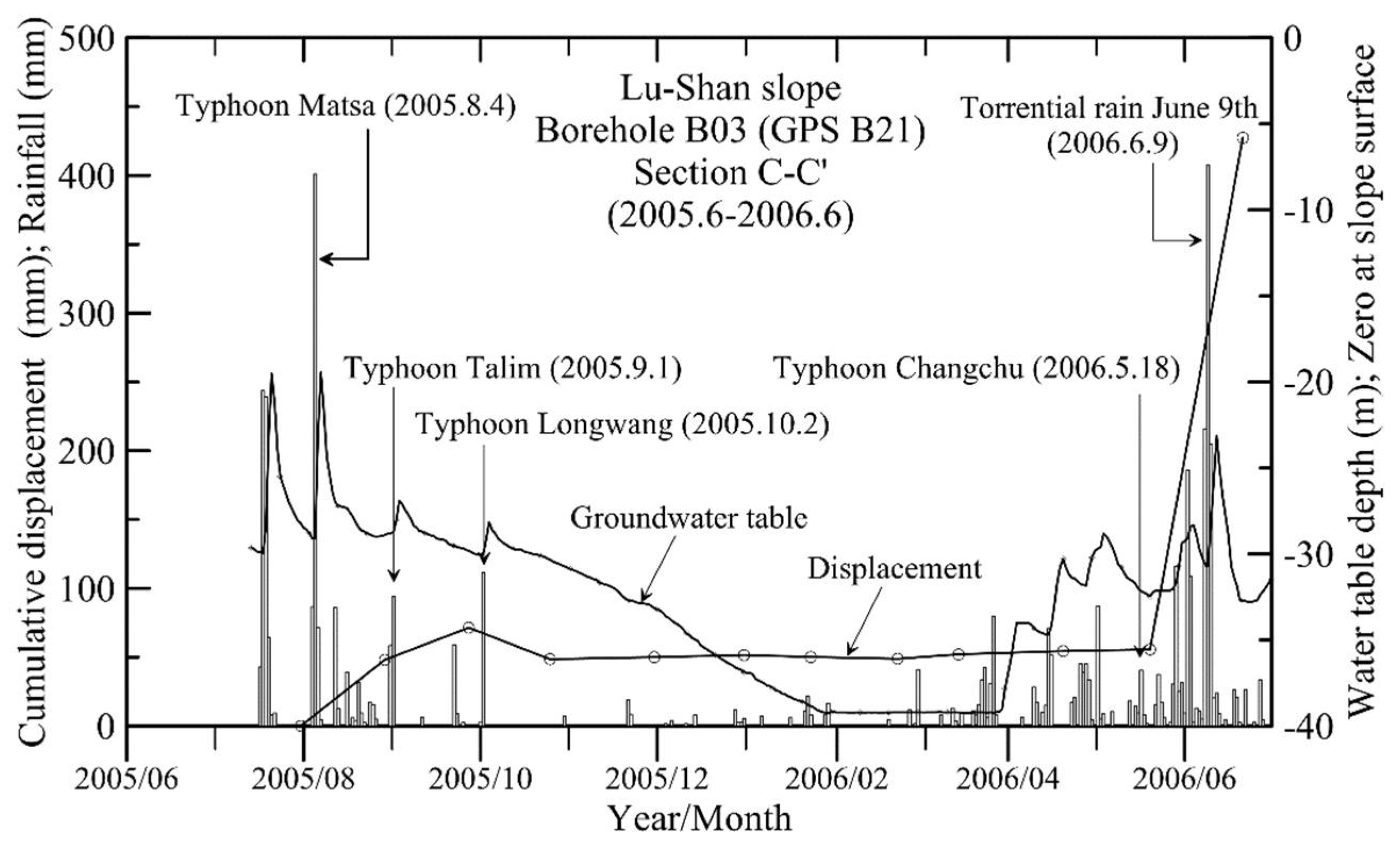
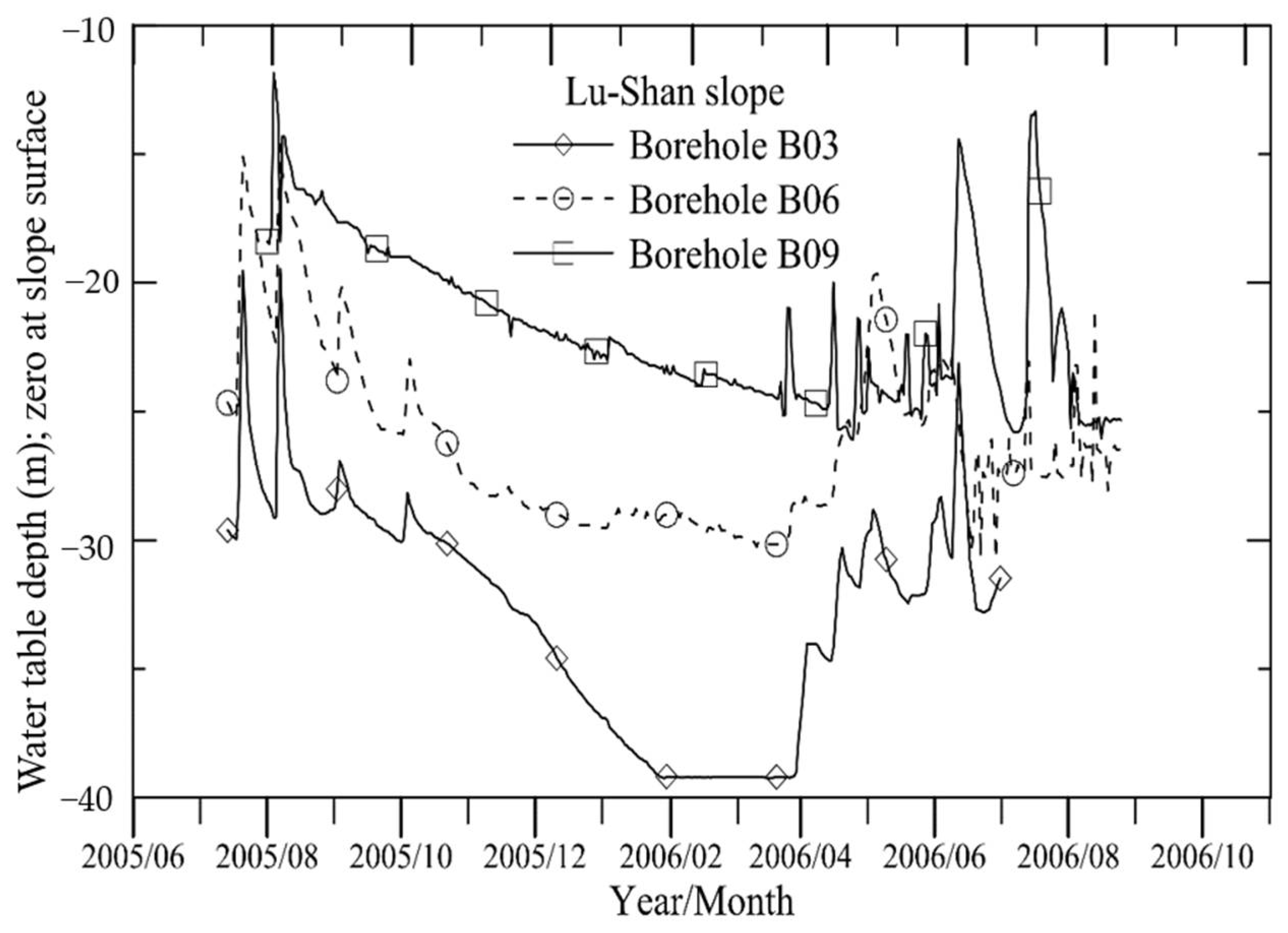
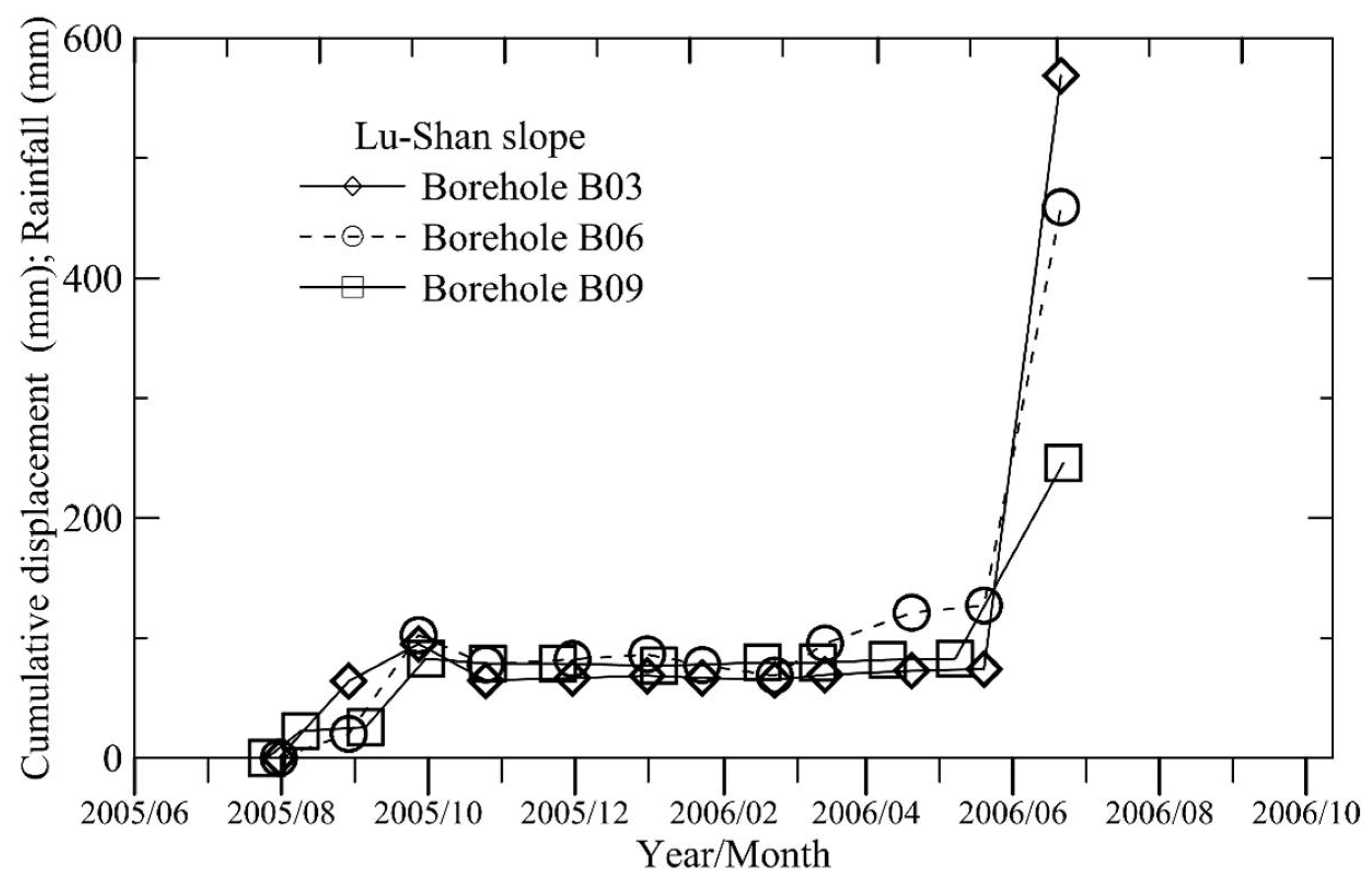
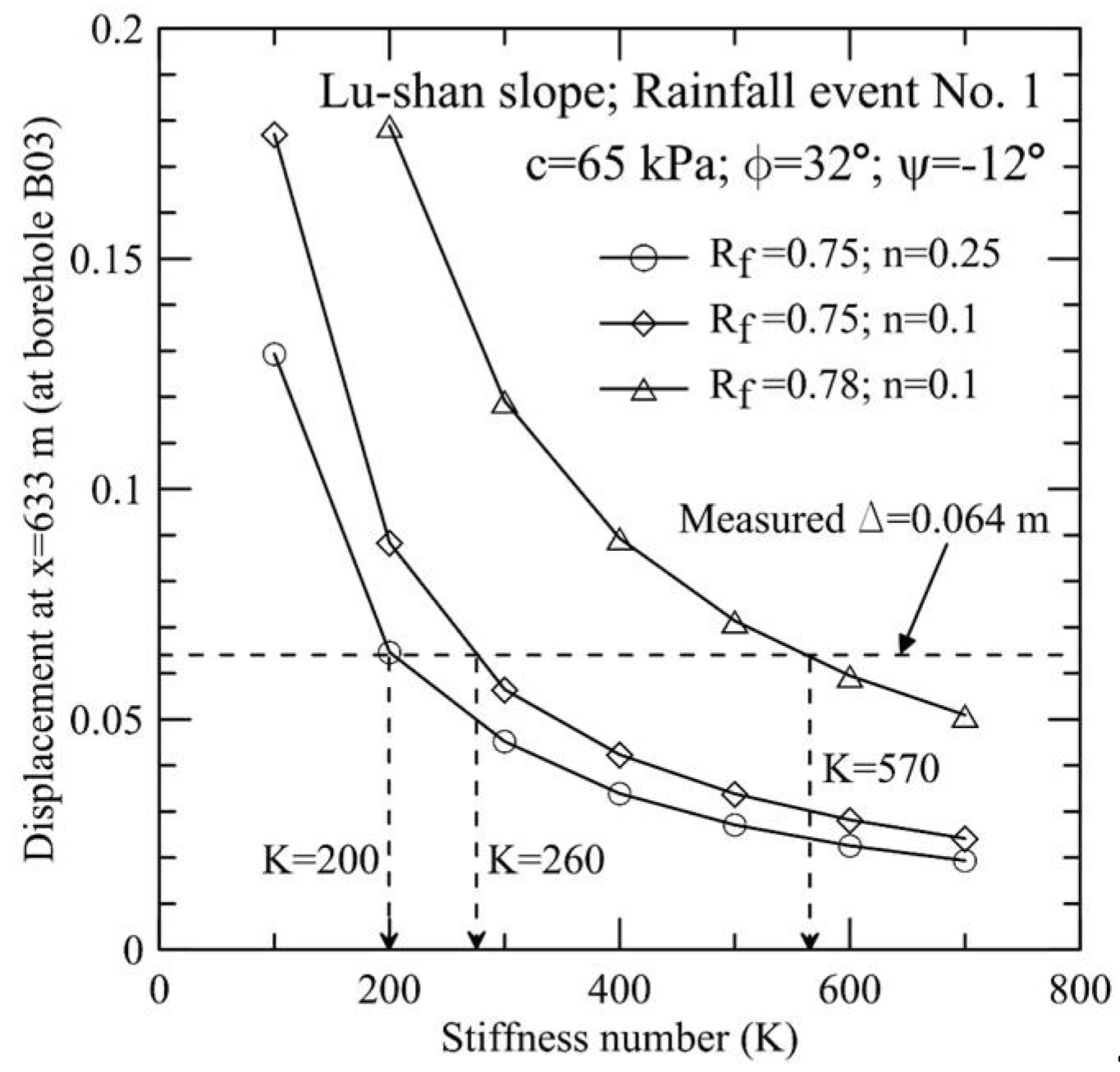
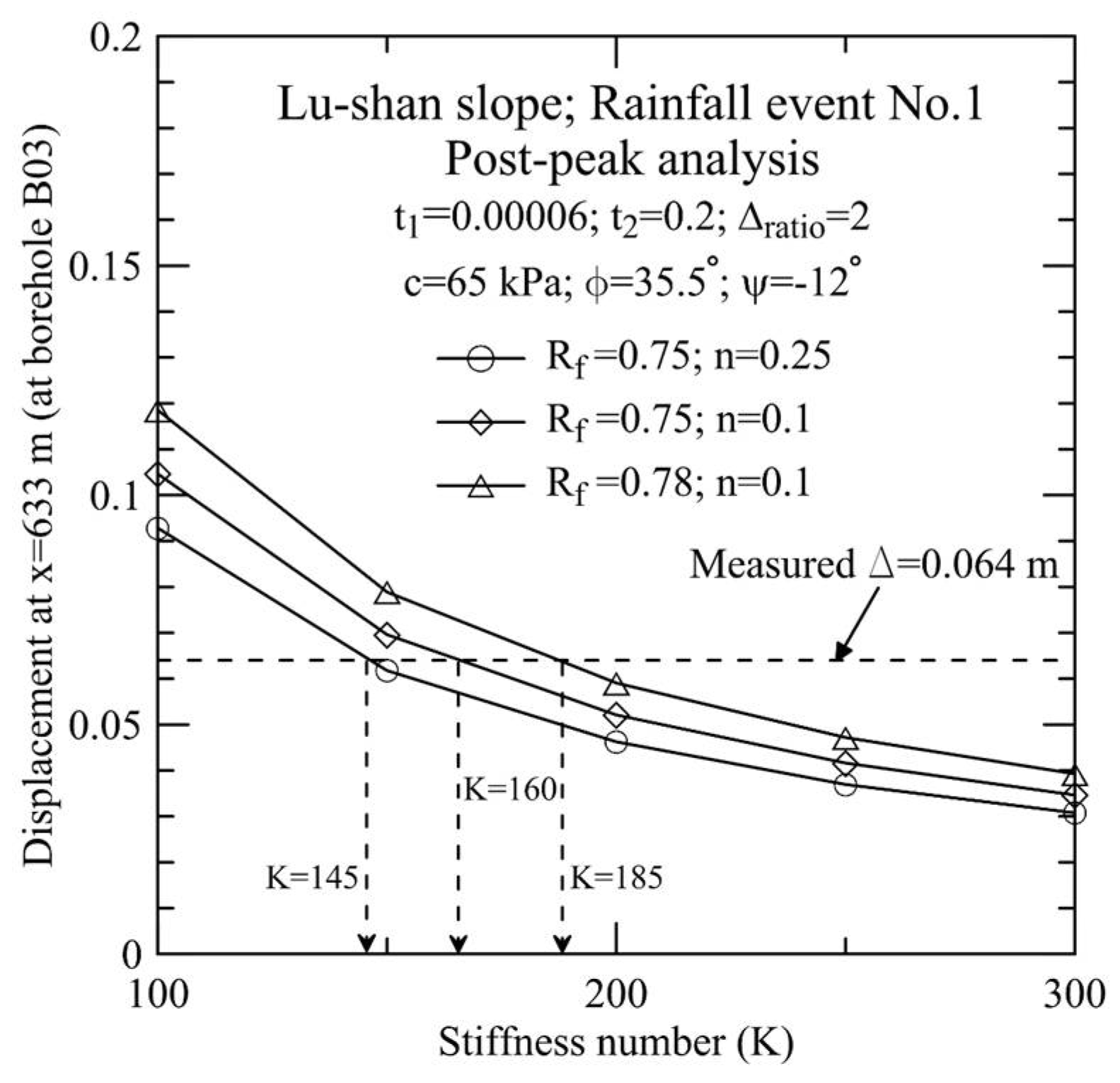
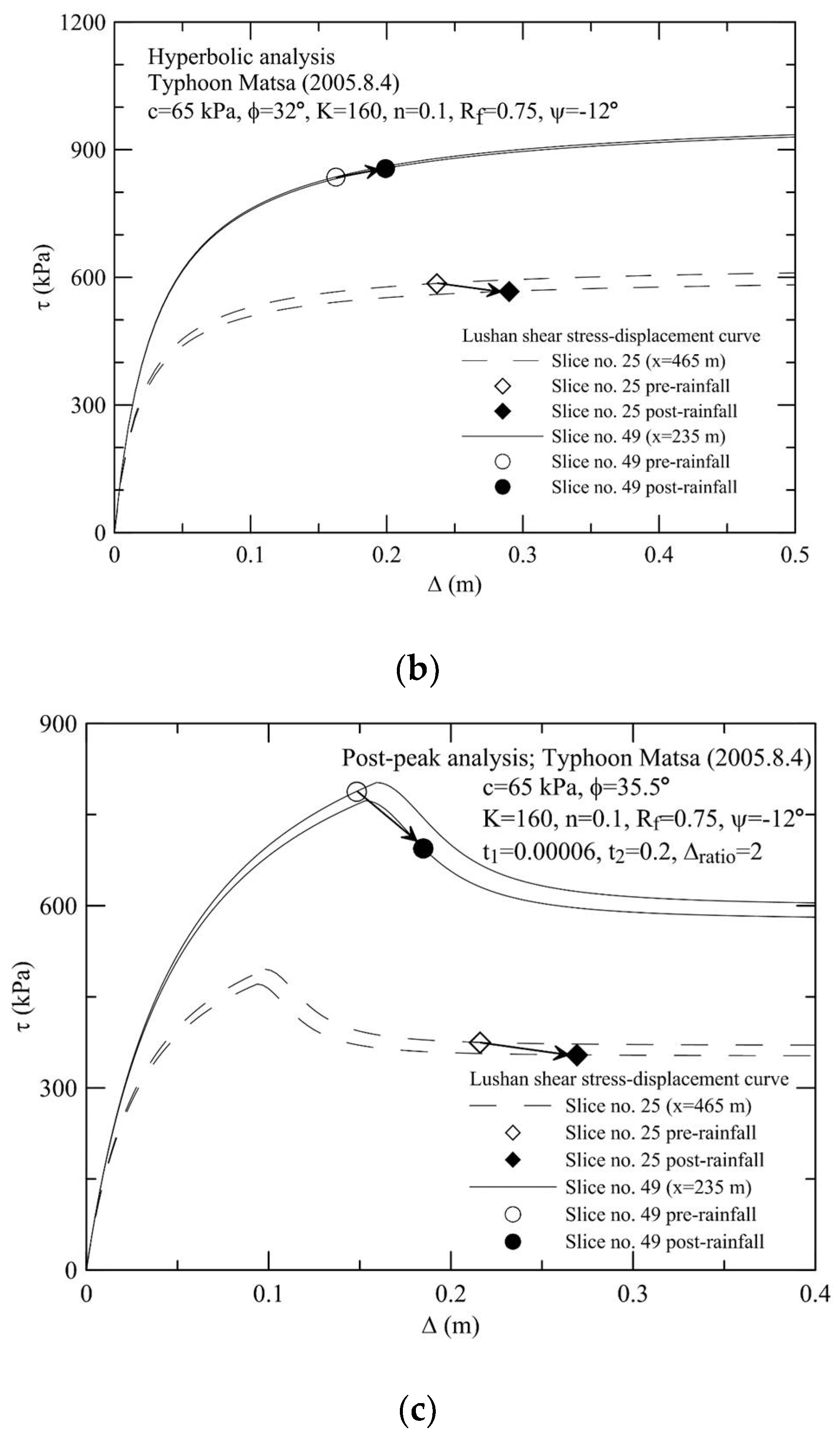
4.1. Results of Back-Analysis
4.2. Influence of Post-Peak Softening on Slope Displacements
5. Conclusions
- (1)
- The accuracy of slope displacement predictions was not influenced by the curvature of the M-C failure envelope used in the back-analyses and displacement analyses.
- (2)
- Post-peak soil strength softening was successfully described by the proposed stress-displacement relationship model. New parameters, including normalized post-peak strength deterioration (t) and residual displacement ratio (Δratio), were studied using direct shear tests on various soil types. Good agreements between the experimental and simulated post-peak stress vs. displacement relationships were obtained.
- (3)
- The accuracy of the slope displacement computations can be improved by incorporating the post-peak stress-displacement relationship in the analysis. The results of a case study on the Lu-Shan slope revealed that a transition from pre-peak to post-peak states for the slip surface near the slope toe may have taken place during the first rainfall event in the monitoring period. This critical feature may be overlooked when post-peak strength deterioration is not taken into account in the displacement analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, C.-C. Caussian-distribution-based hyetographs and their relationships with debris flow initiation. J. Hydrol. 2011, 41, 251–265. [Google Scholar] [CrossRef]
- Huang, C.-C. Critical rainfall for typhoon-induced debris flows in the Western Foothills, Taiwan. Geomorphology 2013, 185, 87–95. [Google Scholar] [CrossRef]
- Huang, C.-C.; Lo, C.-L. Simulation of subsurface flows associated with rainfall-induced shallow slope failures. J. GeoEng. 2013, 8, 101–111. [Google Scholar]
- Yu, G.; Zhang, M.; Cong, K.; Pei, L. Critical rainfall thresholds for debris flows in Sanyanyu, Zhouqu County, Gansu Province, China. Q. J. Eng. Geol. Hydrogeol. 2015, 48, 224–233. [Google Scholar] [CrossRef]
- Tu, G.; Huang, R. Infiltration in two types of embankments and the effects of rainfall time on the stability of slopes. Q. J. Eng. Hydrogeol. 2016, 49, 286–297. [Google Scholar] [CrossRef]
- Burland, J.B. On the compressibility and shear strength of natural clays. Rankine Lecture. Geotechnique 1990, 40, 329–378. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tatsuoka, F. Stability analysis for footings on reinforced sandy slopes. Soils Found. 1994, 34, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Leshchinsky, B.; Ambauen, S. Limit equilibrium and limit analysis: Comparison of benchmark slope stability problems. J. Geotech. Geoenviron. Eng. 2016, 141, 04015043. [Google Scholar] [CrossRef]
- Yin, Y.; Huang, B.; Wang, W.; Wei, Y.; Ma, X.; Zhao, C. Reservoir-induced landslides and risk control in Three Gorges project on Yangtze river, China. J. Rock Mech. Geotech. Eng. 2016, 8, 577–595. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-C. Developing a new slice method for slope displacement analyses. Eng. Geol. 2013, 157, 39–47. [Google Scholar] [CrossRef]
- Huang, C.-C.; Yeh, S.-W. Predicting periodic rainfall-induced slope displacements using force-equilibrium-based finite displacement method. J. GeoEng. 2015, 10, 83–89. [Google Scholar]
- Kondner, R.L. Hyperbolic stress-strain response: Cohesive soils. J. Soil Mech. Found. Div. 1963, 89, 115–144. [Google Scholar] [CrossRef]
- Duncan, J.M.; Chang, C.-Y. Nonlinear analysis of stress and strain in soil. J. Soil Mech. Found. Div. Proc. 1970, 96, 1629–1653. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Siddiquee, M.S.A.; Park, C.-C.; Sakamoto, M.; Abe, F. Modelling stress-strain relations of sand. Soils Found. 1993, 33, 60–81. [Google Scholar] [CrossRef] [Green Version]
- Mesri, G.; Huvaj-Sarihan, N. Residual shear strength measured by laboratory tests and mobilized in landslides. J. Geotech. Geoenviron. Eng. 2012, 138, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Eid, H.; Rabie, K. Fully softened shear strength for soil slope stability analyses. Int. J. Geomech. 2017, 17, 04016023. [Google Scholar] [CrossRef]
- Huang, C.-C. Back-calculating strength parameters and predicting displacements of deep-seated sliding surface comprising weathered rocks. Int. J. Rock Mech. Min. Sci. 2016, 88, 98–104. [Google Scholar] [CrossRef]
- Wu, K.-W. Applying Results of True Direct Shear Tests to the Stability Analysis for Integrated Road-Dyke Structures. Master’s Thesis, Feng-Chia University, Taichung City, Taiwan, 2011. (In Chinese). [Google Scholar]
- Hsu, H.-Y. Modeling on the Behavior of Soils Subjected to Cyclic Direct Shear. Master’s Thesis, National Cheng Kung University, Tainan City, Taiwan, 2017. (In Chinese). [Google Scholar]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Eng. Div. ASCE 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Duncan, J.M.; Wright, S.G. Soil Strength and Slope Stability; Wiley: Ney York, NY, USA, 2005. [Google Scholar]
- Lienhard, J.H. The Engines of Our Ingenuty: An Engineer Looks at Technology and Culture; Oxford University Press: Oxford, UK, 2003; p. 272. [Google Scholar]
- Chu, B.-L.; Huang, C.-R.; Jeng, S.-Y. Study on Terrace Sedimentary and Tou-ka-san Gravelly Strata Using In-Situ Direct Shear Tests. In Proceedings of the 3rd National Geotechnical Conference, Taichung City, Taiwan, 11–13 September 1989; pp. 695–706. [Google Scholar]
- Davoudi, M.H. Influence of willow root density on shear resistance paramters in fine grain soils using in situ direct shear tests. Res. J. Environ. Sci. 2011, 5, 157–170. [Google Scholar]
- Qiu, J.-Y.; Tatsuoka, F.; Uchimura, T. Constant pressure and constant volume direct shear tests on reinforced sand. Soils Found. 2000, 40, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C. Influences of the Slit Size on the Direct Shear Strength of Gravelly Soils. In Proceedings of the National Conference on Rock Engineering, Tainan City, Taiwan, 26 June 2006; pp. 31–40. [Google Scholar]
- Hsu, W. Simulating Physical Properties of Gravelly Strata Using Three-Dimensional Discrete Element Method. Master’s Thesis, Chaoyang University of Technology, Taichung City, Taiwan, 2009. (In Chinese). [Google Scholar]
- Ziaie Moayed, R.; Alibolandi, M.; Alizadeh, A. Specimen size effects on direct shear test of silty sands. Int. J. Geotech. Eng. 2017, 11, 198–205. [Google Scholar] [CrossRef]
- Janbu, N. Slope Stability Computations. Embankment-Dam Engineering; Hirschfeld, R.C., Poulos, S.J., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1973; pp. 47–86. [Google Scholar]
- Japanese Highway Association. Guidelines for Cut Slopes and Slope Stabilization Engineering; Japanese Highway Association: Tokyo, Japan, 1986. (In Japanese) [Google Scholar]
- Japanese Geotechnical Society. Strength Parameters in Design—c, φ and N values. Soil Foudnation Eng. Libr. 1988, 32, 127. (In Japanese) [Google Scholar]

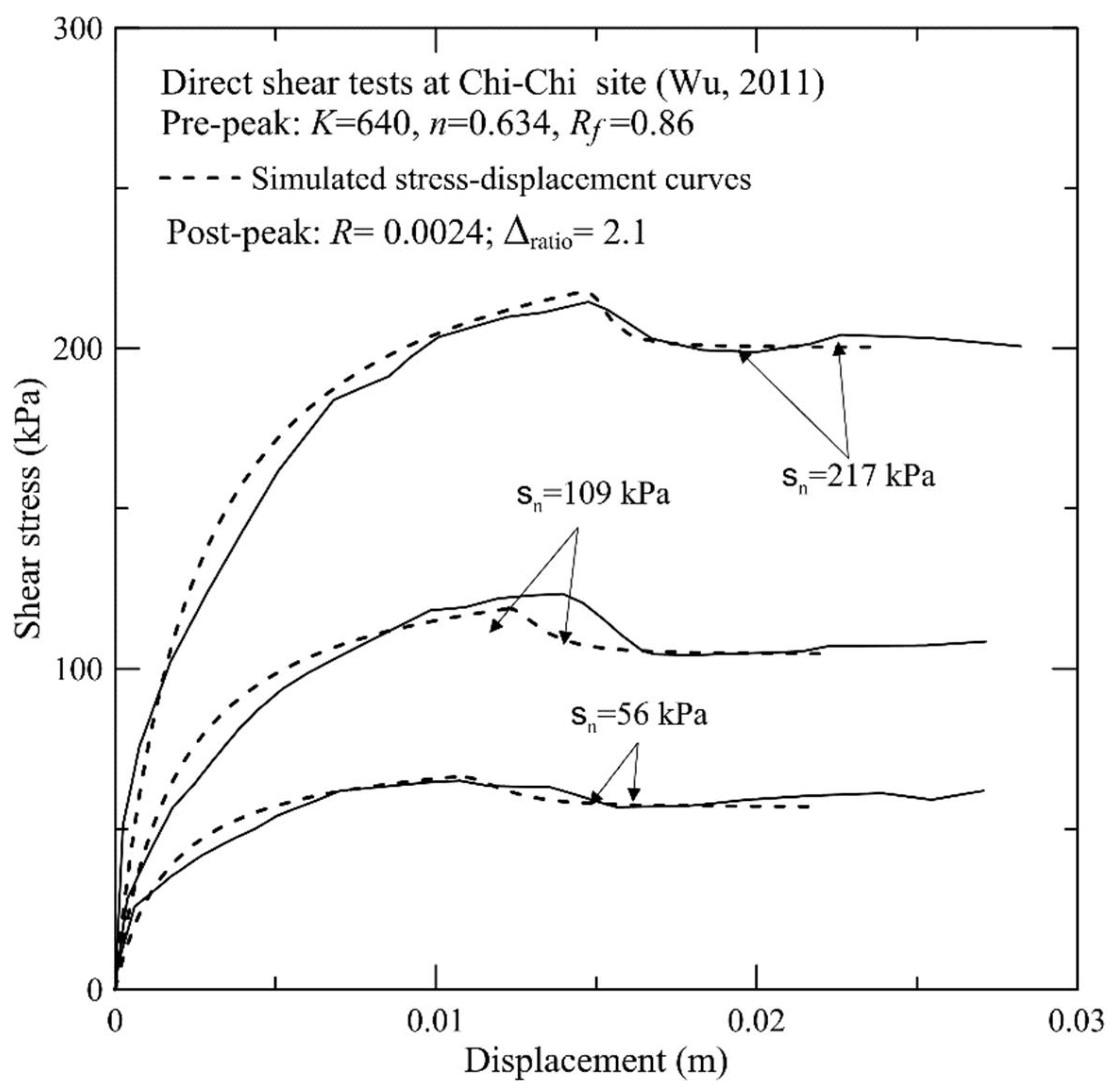
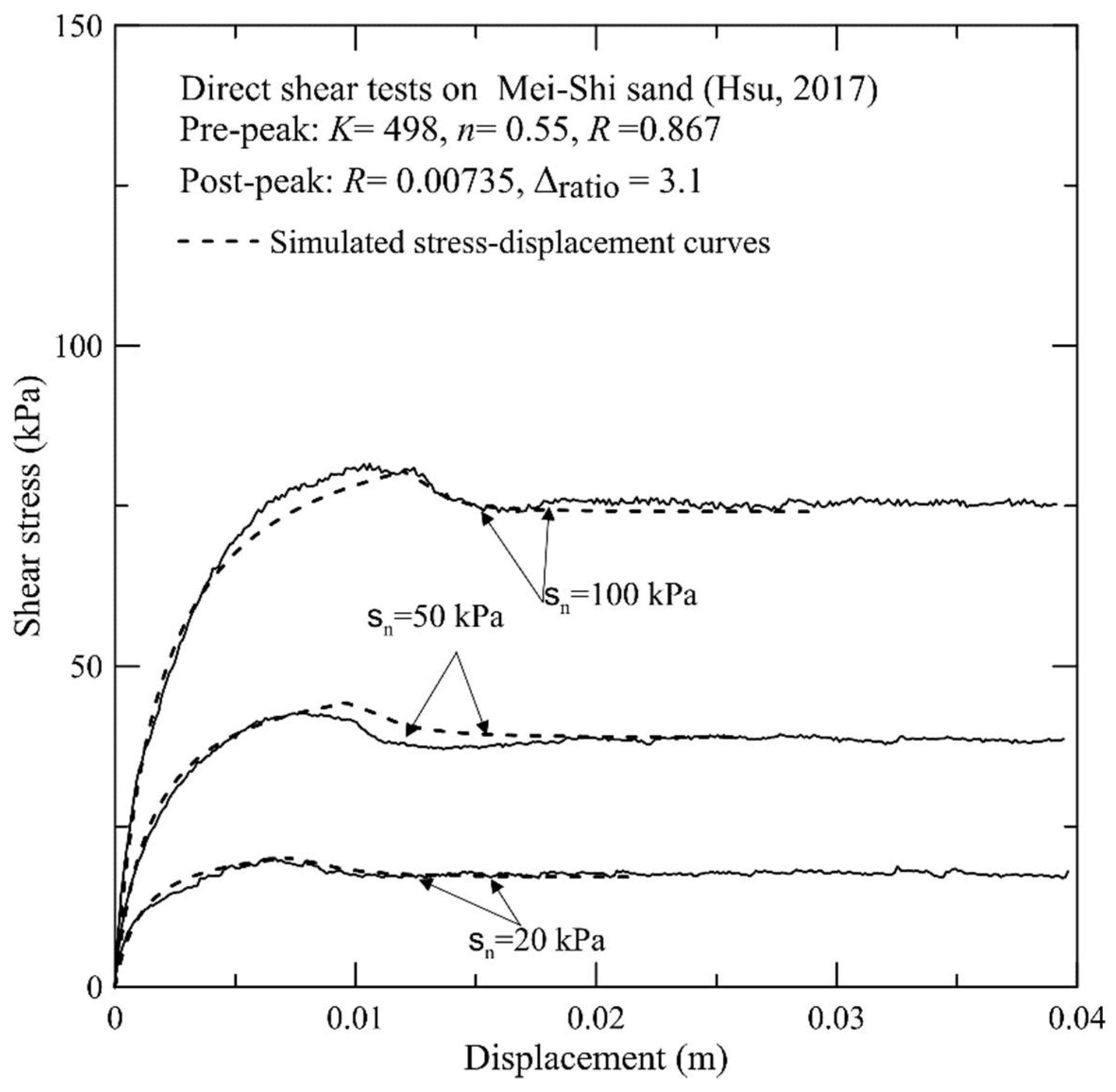






| σn (kPa) | a | b | K | n | Rf | Measured | Simulated | ||
|---|---|---|---|---|---|---|---|---|---|
| Δratio | t | Δratio | t | ||||||
| 56 | 2.3 × 10−5 | 0.013 | 640 | 0.634 | 0.86 | 2 | 0.121 | 1.97 | 0.142 |
| 109 | 1.5 × 10−5 | 0.007 | 1.8 | 0.155 | 1.844 | 0.122 | |||
| 217 | 9.5 × 10−6 | 0.004 | 1.6 | 0.073 | 1.586 | 0.082 | |||
| σn (kPa) | a | b | K | n | Rf | Measured | Simulated | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Δratio | t | Δratio | t | |||||||
| 20 | 4.8 × 10−5 | 0.043 | 498 | 0.55 | 0.867 | 3 | 0.165 | 2.97 | 0.149 | |
| 50 | 2.9 × 10−5 | 0.0196 | 2.7 | 0.098 | 2.74 | 0.123 | ||||
| 100 | 2.0 × 10−6 | 0.0108 | 2.4 | 0.088 | 2.38 | 0.078 | ||||
| Location of Bore Hole Rainfall Event | Measured Cumulative Displacement (mm) | ||
|---|---|---|---|
| B03 x = 633 m | B06 x = 475 m | B09 x = 170 m | |
| Event no. 1 (4 August 2005, Typhoon Matsa) | 48 | 17 | 22 |
| Event no. 2 (1 September 2004, Typhoon Talim) | 71 | 88 | 25 |
| Event no. 3 (2 October 2005, Typhoon Longwang) | 49 | 67 | 78 |
| Event no. 4 (22 February 2006) | 49 | 59 | 79 |
| Event no. 5 (17 April 2006) | 55 | 103 | - |
| Event no. 6 (30 April 2005) | 57 | 109 | 82 |
| Event no. 7 (30 May 2006) | - | - | 104 |
| Event no. 8 (9 June 2006) | 427 | 392 | 244 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo, C.-L.; Huang, C.-C. Displacement Analyses for a Natural Slope Considering Post-Peak Strength of Soils. GeoHazards 2021, 2, 41-62. https://doi.org/10.3390/geohazards2020003
Lo C-L, Huang C-C. Displacement Analyses for a Natural Slope Considering Post-Peak Strength of Soils. GeoHazards. 2021; 2(2):41-62. https://doi.org/10.3390/geohazards2020003
Chicago/Turabian StyleLo, Chien-Li, and Ching-Chuan Huang. 2021. "Displacement Analyses for a Natural Slope Considering Post-Peak Strength of Soils" GeoHazards 2, no. 2: 41-62. https://doi.org/10.3390/geohazards2020003






