Ellipsoidal Design of Robust Secure Frequency Control in Smart Cities Under Denial-of-Service Cyberattack
Abstract
Highlights
- The denial-of-service threat is modeled by the Bernoulli stochastic variable.
- A new sufficient condition is developed to design the controller in terms of linear matrix inequalities.
- A microgrid frequency norm-bounded model representing parameter uncertainty and cyberattack is developed.
- Various testing scenarios demonstrate the suggested controller’s efficacy.
Abstract
1. Introduction
1.1. Brief Survey and Motivation
- FDI attacks have been extensively studied, including the development of attack models and analysis of their impact on microgrid stability [17].
- Robust control techniques such as H∞ control have been investigated to improve system robustness against FDI and DoS attacks in multi-area systems [18].
- Sampled-data systems have been considered, with controllers designed to address the effects of sampling, time delays, and demand response [19].
- Distributed event-triggered control has been proposed to mitigate the consequences of FDI attacks in secondary frequency control systems [20].
- Attack detection and identification have been addressed by the development of observers capable of detecting attacks within the system [21].
- Time-varying delays have been tackled by implementing decentralized limited bandwidth event-triggered LFC in multi-area power systems [22].
- Sliding mode control has been utilized in conjunction with event-triggering mechanisms to enhance resilience against periodic DoS attacks in multi-area systems [23].
1.2. Paper Contribution
- The invariant ellipsoid technique is employed to enhance robustness against system uncertainties and ensure security against DoS cyberattacks.
- The development of robust and secure invariant-set control is based on quadratic boundedness of uncertainties in the state-input and disturbances matrices.
1.3. Paper Organization
- Fact 1—Bounding Inequality [24]:
- Fact 2—Schur Complement [24]:
2. Renewable Microgrid Modeling and Problem Formulation
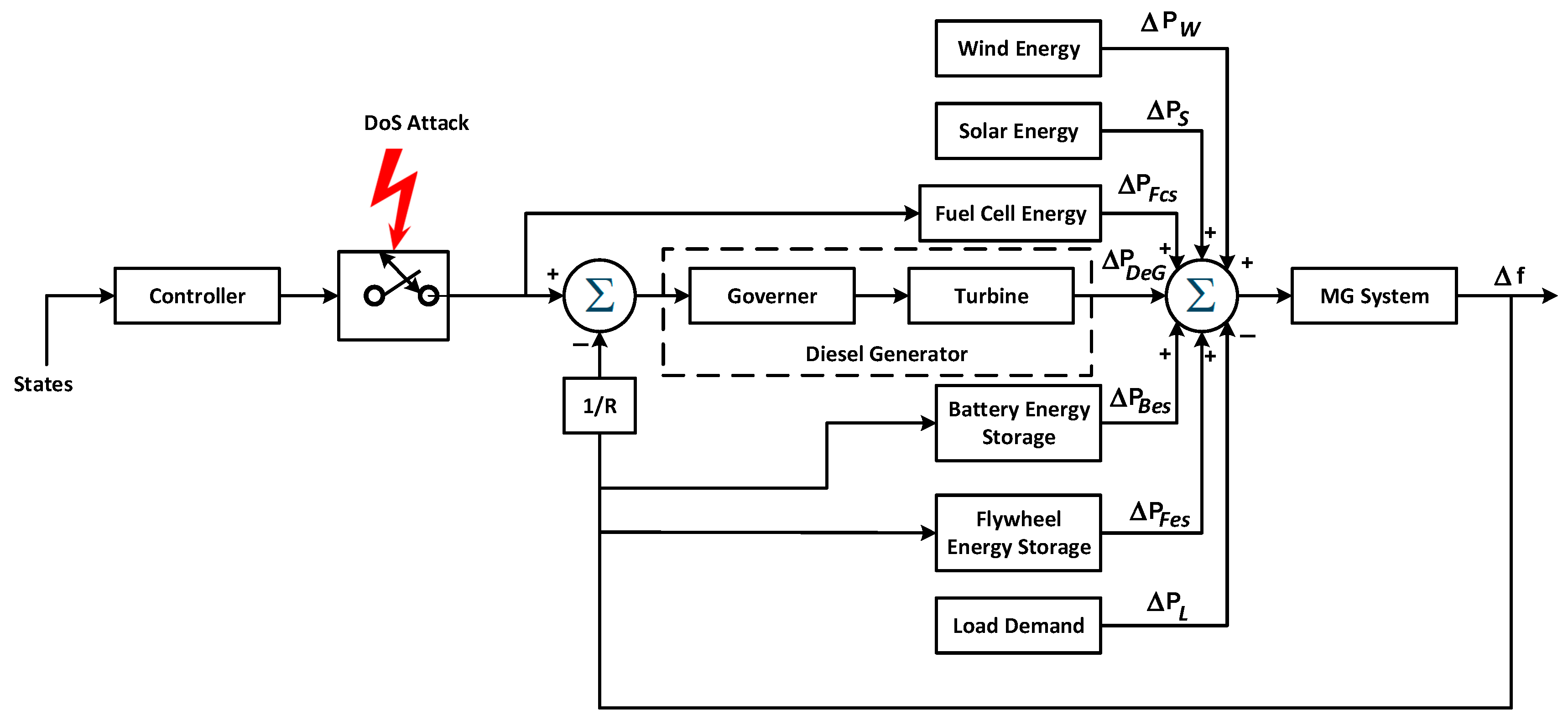
2.1. MG Continuous-Time Model
2.2. MG Discrete-Time Model
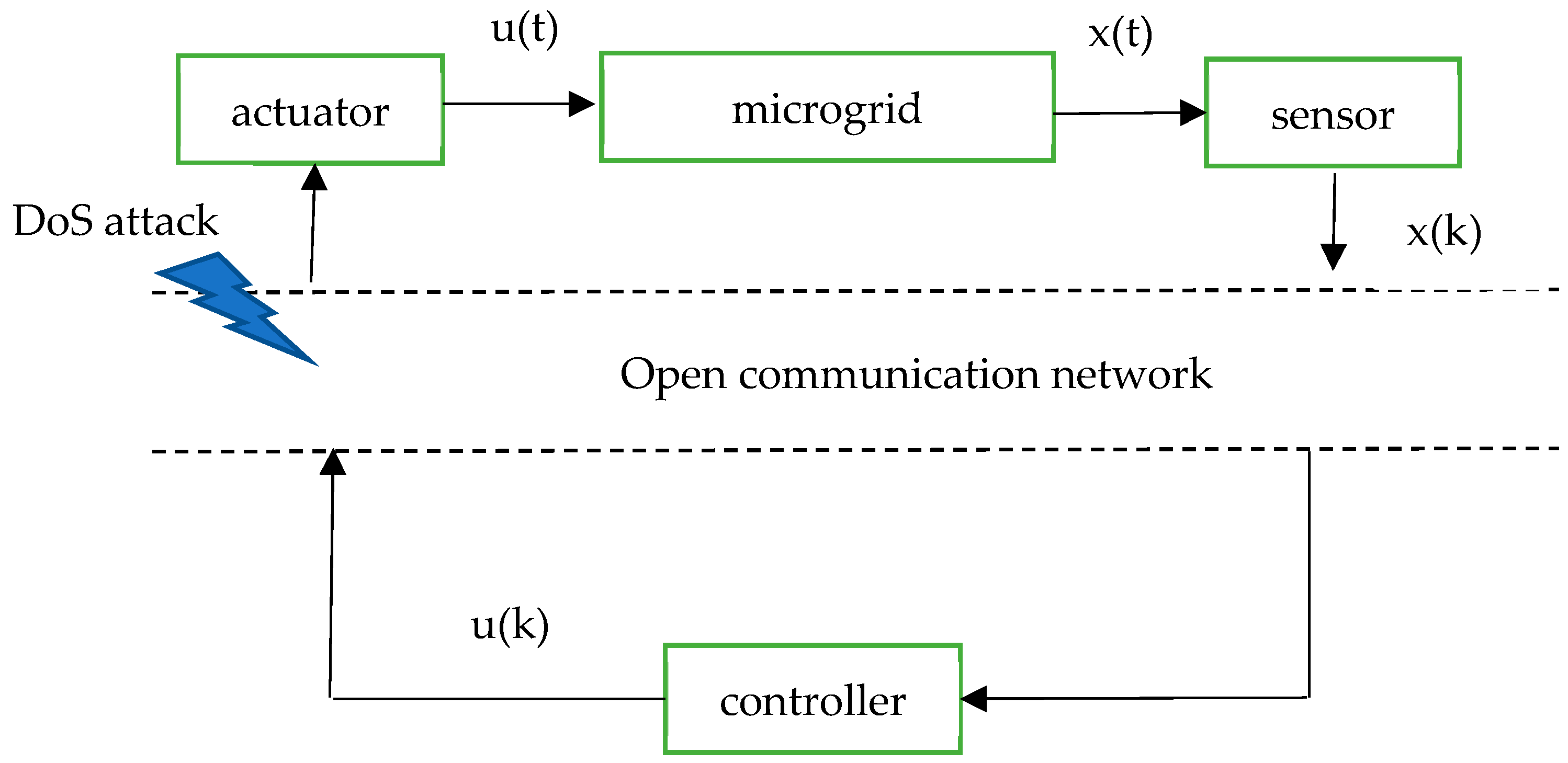
2.3. MG Uncertain Stochastic Discrete-Time Model Under DoS Attack
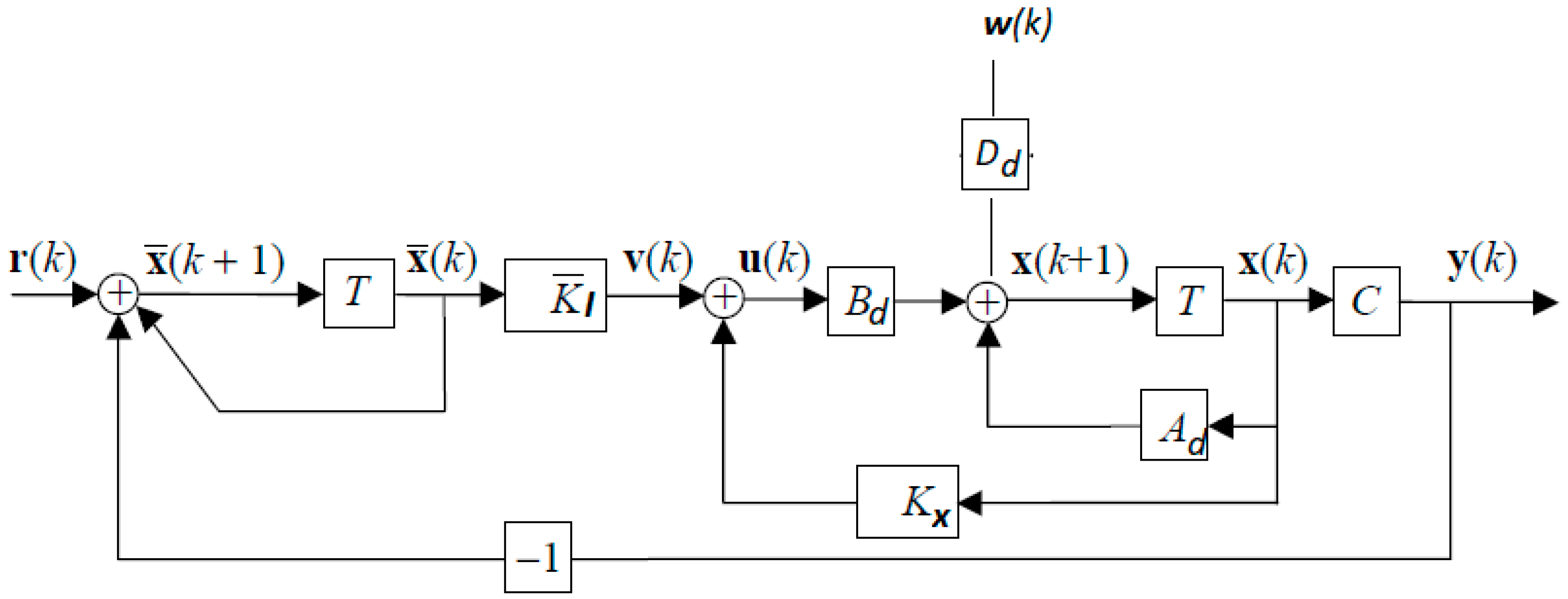
3. Ellipsoidal Design of Secure MG Control
3.1. The Proposed Control
3.2. Comparison with Control
4. Results and Discussion
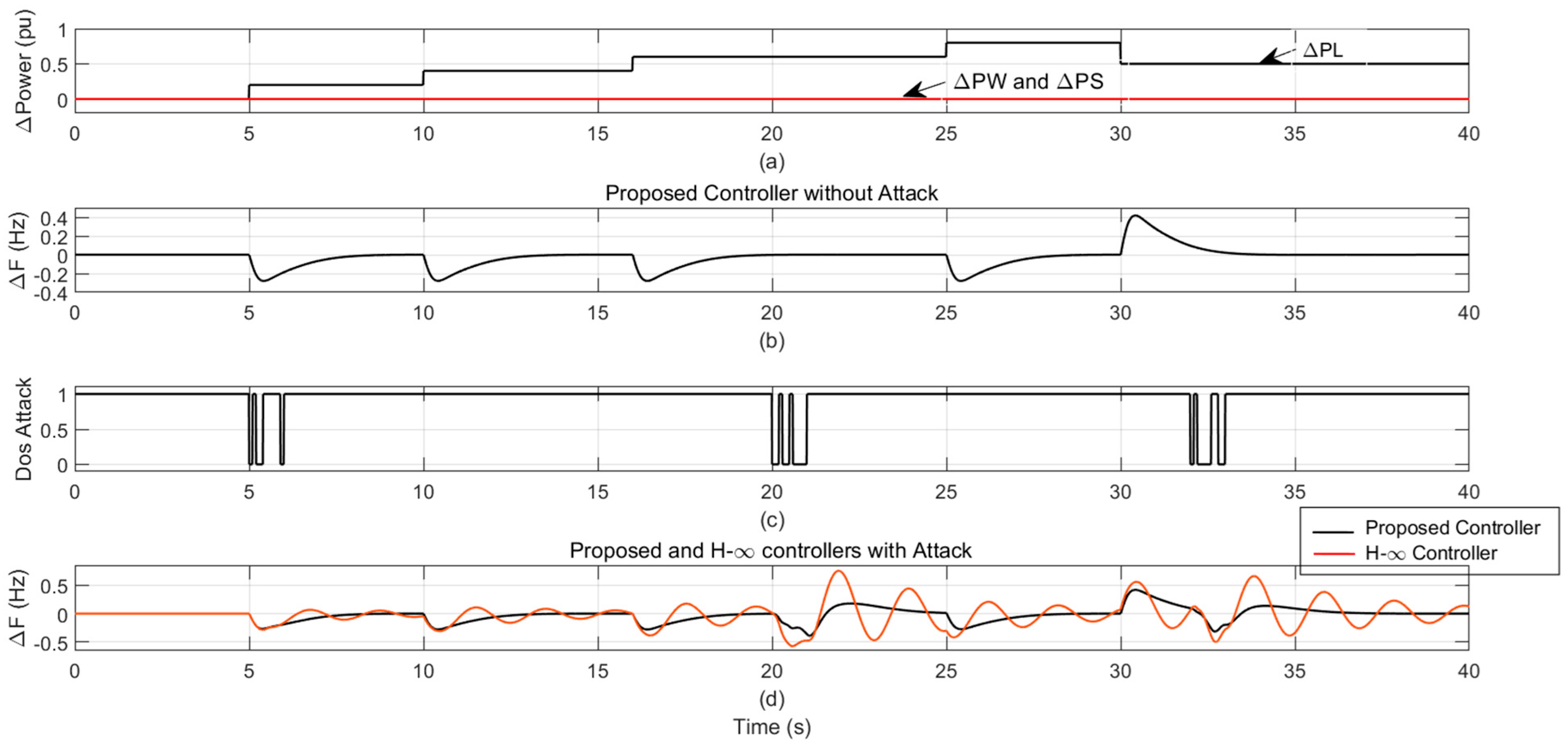
4.1. Scenario 1: Deterministic Disturbance with and Without DoS Attack
4.1.1. Case 1: Multiple Disturbance Steps in Load Power
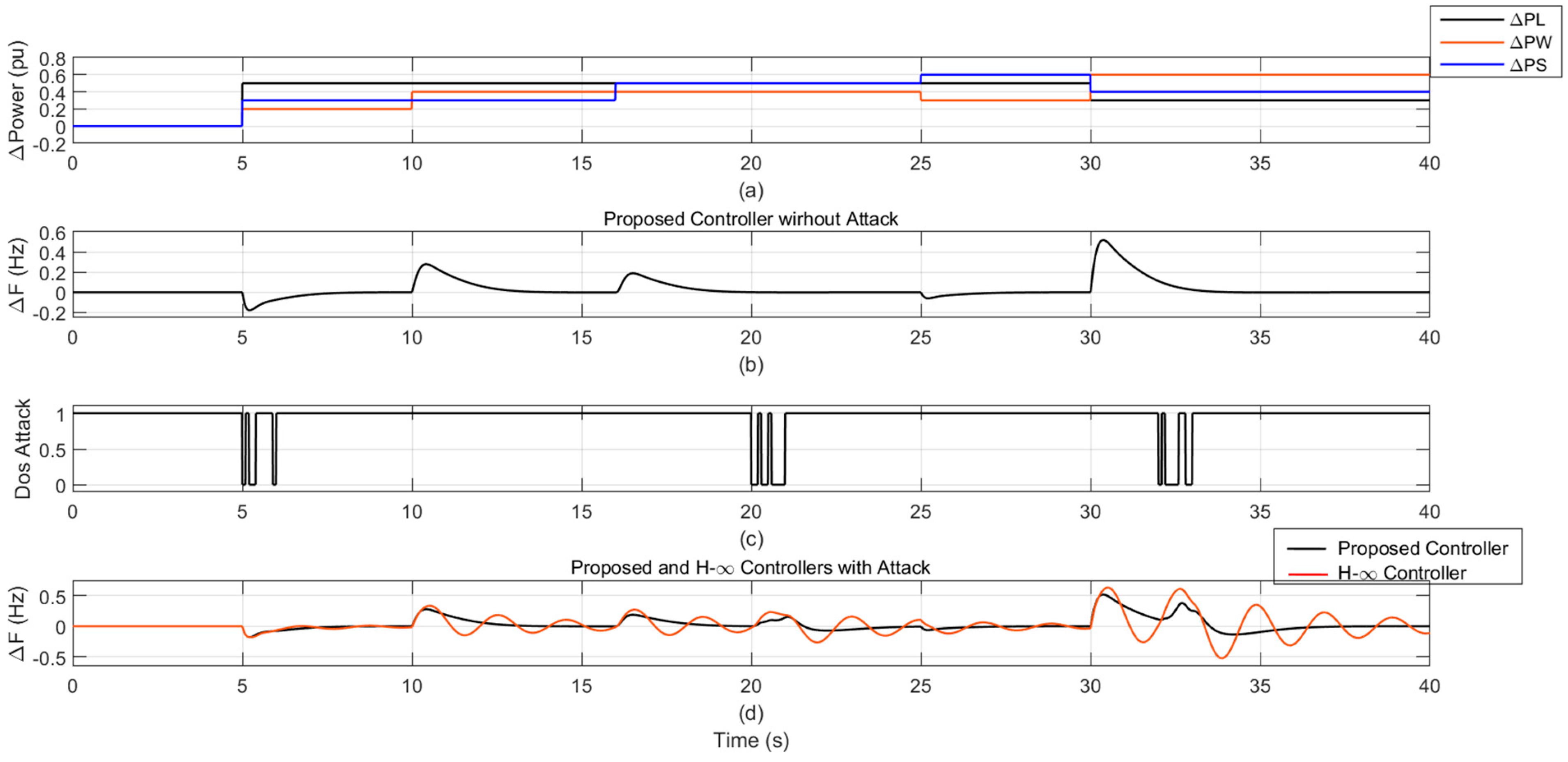
4.1.2. Case 2: Multiple-Step Disturbances in Wind Power, Solar Power and Load Power
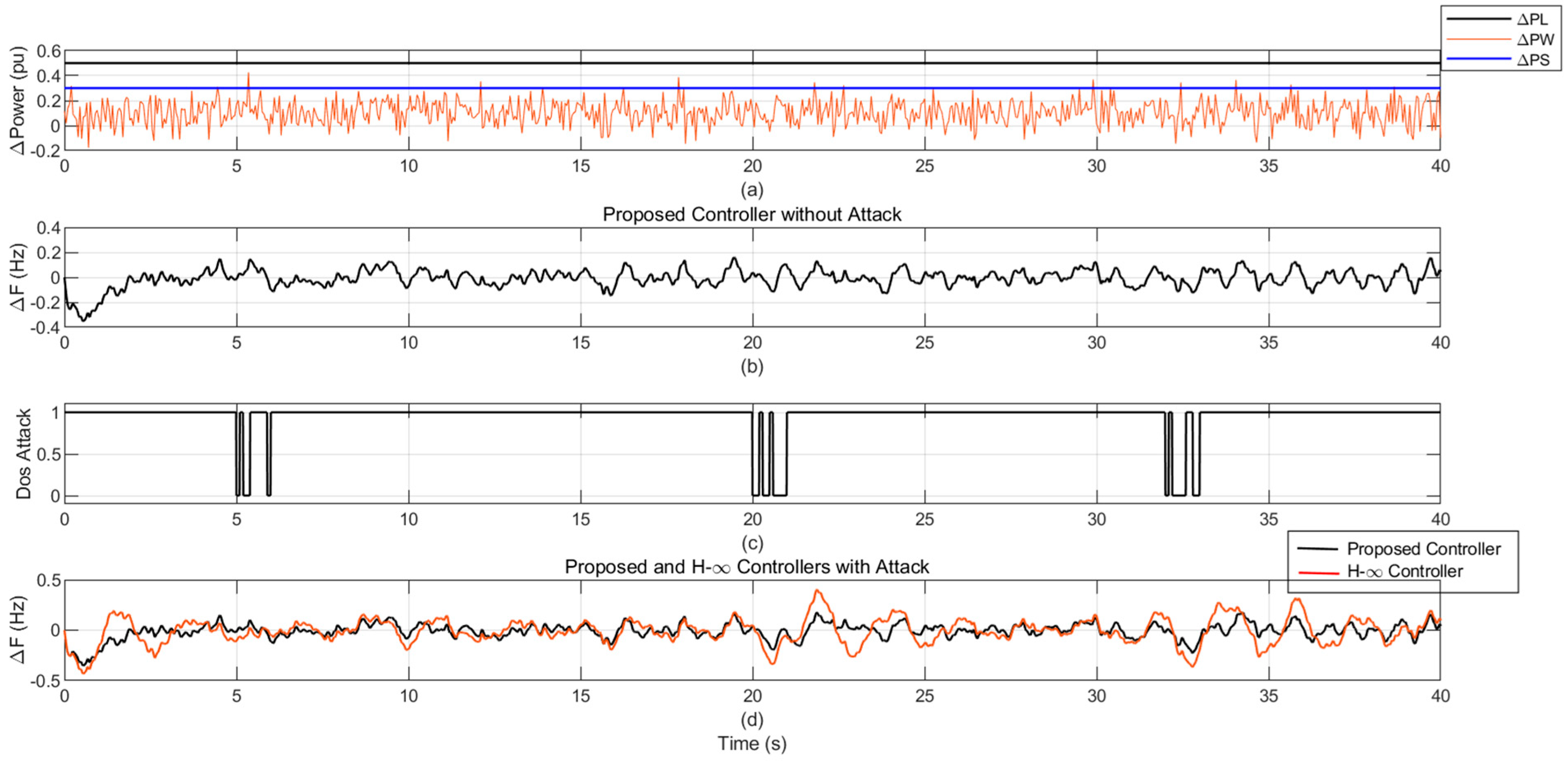
4.2. Scenario 2: Stochastic Disturbance in Wind Power
4.3. Scenario 3: Robustness Against Parameter Variation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| DoS | Denial of service |
| LMI | Linear matrix inequality |
| LFC | Load frequency control |
| AC-MG | Alternating current microgrid |
| DC-MG | Direct current microgrid |
| AC-DC MG | Hybrid microgrid |
| FC | Fuel cell |
| DeG | Diesel generator |
| CPS | Cyber-physical system |
| TDA | Time delay attack |
| FDI | False data injection |
| H | Inertia constant of rotating part in microgrid |
| D | Damping coefficient of microgrid |
| Tfc | Time constant of the fuel cell |
| Tinv | Time constant of the inverter |
| Tfilt | Time constant of the filter |
| Tg | Time constant of the governor |
| Tt | Time constant of the turbine |
| Tb | Time constant of batteries |
| R | Droop frequency |
Appendix A. Proof Sketch of Theorem 2
References
- Bevrani, H.; François, B.; Ise, T. Microgrid Dynamics and Control, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 435–486. [Google Scholar]
- Mahmoud, M.S.; AL-Sunni, F.M. Control and Optimization of Distributed Generation Systems, 2015th ed.; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Bayoumi, E.H.E.; Soliman, H.M.; Albadi, M.; Soliman, M. Invariant set design of decentralized control for islanded microgrids under plug-and-play operation. Int. J. Electr. Power Energy Syst. 2021, 128, 106678. [Google Scholar] [CrossRef]
- Kammer, C.; Karimi, A. Advanced Droop Control in Islanded Microgrids Using Dynamic Phasor Models. IFAC-Pap. Online 2017, 50, 6642–6647. [Google Scholar] [CrossRef]
- Soliman, H.M.; Bayoumi, E.H.E.; El-Sheikhi, F.A.; Ibrahim, A.M. Ellipsoidal-Set Design of the Decentralized Plug and Play Control for Direct Current Microgrids. IEEE Access 2021, 9, 96898–96911. [Google Scholar] [CrossRef]
- Awad, H.; Bayoumi, E.H.E.; Soliman, H.M.; De Santis, M. Robust tracker of hybrid microgrids by the invariant-ellipsoid set. Electronics 2021, 10, 1794. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Microgrid: Advanced Control Methods and Renewable Energy System Integration, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Soliman, H.M.; Saleem, A.; Bayoumi, E.H.E.; De Santis, M. Harmonic Distortion Reduction of Transformer-Less Grid-Connected Converters by Ellipsoidal-Based Robust Control. Energies 2023, 16, 1362. [Google Scholar] [CrossRef]
- Awad, H.; Soliman, H.M.; Bayoumi, E.H.E. Disturbance-Rejection Control for Unbalanced Operation of Microgrids: Invariant-Set Approach. ISA Trans. 2024, 153, 334–349. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Khalid, H.M.; Hamdan, M.M. Cyber-physical infrastructures in power systems: Architectures and Vulnerabilities. In Aca, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Veronica, A.J.S.J.; Kumar, N.S.; Longatt, F.G. Robust PI controller design for frequency stabilization in a hybrid microgrid system considering parametric uncertainties and communication time delay. IET Gener. Transm. Distrib. 2019, 13, 3048–3056. [Google Scholar] [CrossRef]
- Duo, W.; Zhou, M.; Abusorrah, A. A Survey of Cyber Attacks on Cyber Physical Systems: Recent Advances and Challenges. IEEE/CAA J. Autom. Sin. 2022, 9, 784–800. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W.; Liang, H.; Ahrabi, R.R. Cyber-security of smart microgrids: A survey. Energies 2021, 14, 27. [Google Scholar] [CrossRef]
- Xiahou, K.S.; Liu, Y.; Wu, Q.H. Robust load frequency control of power systems against random time-delay attacks. IEEE Trans. Smart Grid 2020, 12, 909–911. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, Y.; Sun, Z.; Chen, D. Networked and Event-Triggered Control Approaches in Cyber-Physical Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Sahoo, S.; Yang, Y.; Blaabjerg, F. Resilient synchronization strategy for AC microgrids under cyber-attacks. IEEE Trans. Power Electron. 2021, 36, 3–77. [Google Scholar] [CrossRef]
- Bi, J.; Luo, F.; He, S.; Liang, G.; Meng, W.; Sun, M. False data injection and propagation aware game: Theoretical approach for microgrids. IEEE Trans. Smart Grid 2022, 13, 3342–3353. [Google Scholar] [CrossRef]
- Chen, X.; Hu, S.; Li, Y.; Yue, D.; Dou, C.; Ding, L. Co-estimation of state and FDI attacks and attack compensation control for multi-area load frequency control systems under FDI and DoS attacks. IEEE Trans. Smart Grid 2022, 13, 2357–2368. [Google Scholar] [CrossRef]
- Lin, C.; Hu, B.; Shao, C.; Li, W.; Li, C.; Xie, K. Delay-dependent optimal load frequency control for sampling systems with demand response. IEEE Trans. Power Syst. 2022, 37, 4310–4324. [Google Scholar] [CrossRef]
- Khalili, J.; Dehkordi, N.M.; Hamzeh, M. Distributed event-triggered secondary frequency control of islanded AC microgrids under cyber attacks with input time delay. Int. J. Electr. Power Energy Syst. 2022, 143, 108506. [Google Scholar] [CrossRef]
- Hu, S.; Ge, X.; Chen, X.; Yue, D. Resilient load frequency control of islanded AC microgrid under concurrent false data injection and denial-of-service attacks. IEEE Trans. Smart Grid 2023, 14, 690–700. [Google Scholar] [CrossRef]
- Zhao, X.; Zou, S.; Wang, P.; Ma, Z. Bandwidth-aware event-triggered load frequency control for power systems under time-varying delays. IEEE Trans. Power Syst. 2023, 38, 4530–4541. [Google Scholar] [CrossRef]
- Qiao, S.; Liu, X.; Liang, Y.; Xiao, G.; Kang, Y.; Ge, S.S. Event-triggered sliding mode load frequency control of multiarea power systems under periodic denial-of-service attacks. IEEE Syst. J. 2023, 17, 2803–2814. [Google Scholar] [CrossRef]
- Poznyak, A. Robust Control: Supplementary Topics, 1st ed.; Cambridge Scholars Publishing: Cambridge, MA, USA, 2024. [Google Scholar]
- Tudu, A.K.; Naguru, N.; Dey, S.H.N.; Paul, S. Load frequency control of an isolated microgrid using optimized model predictive control by GA. Electr. Eng. 2024, 106, 4171–4183. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Hamdan, M.M.; Baroudi, U.A. Modeling and control of Cyber-Physical Systems subject to cyber attacks: A survey of recent advances and challenges. Neurocomputing 2019, 338, 101–115. [Google Scholar] [CrossRef]
- Khlebnikov, M.V.; Polyak, B.T.; Kuntsevich, V.M. Optimization of Linear Systems Subject to Bounded Exogenous Disturbances: The Invariant Ellipsoid Technique. Autom. Remote Control. 2011, 72, 2227–2275. [Google Scholar] [CrossRef]
- Werner, H.; Korba, P.; Yang, T.C. Robust Tuning of Power System Stabilizers Using LMI-Techniques. IEEE Trans. Control. Syst. Technol. 2003, 11, 147–152. [Google Scholar] [CrossRef]
- The MathWorks, Inc. MATLAB Version: 9.13.0 (R2023b). 2023. Available online: https://www.mathworks.com (accessed on 11 December 2024).
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar] [CrossRef]
- Löfberg, J. Modeling and solving uncertain optimization problems in YALMIP. IFAC Proc. Vol. 2008, 41, 1337–1341. [Google Scholar] [CrossRef]
- Labit, Y.; Peaucelle, D.; Henrion, D. SEDUMI INTERFACE 1.02: A tool for solving LMI problems with SEDUMI. In Proceedings of the IEEE International Symposium on Computer Aided Control System Design, Glasgow, UK, 18–20 September 2002; pp. 272–277. [Google Scholar] [CrossRef]
- Henrion, D.; Lasserre, J.-B. GloptiPoly: Global optimization over polynomials with Matlab and SeDuMi. In Proceedings of the 41st IEEE Conference on Decision and Control 2002, Las Vegas, NV, USA, 10–13 December 2002; Volume 1, pp. 747–752. [Google Scholar] [CrossRef]
- Wong, W.K.; Yin, Y.; Zhou, J. Using SeDuMi to find various optimal designs for regression models. Stat Pap. 2019, 60, 1583–1603. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| D (p.u. MW/Hz) | 0.015 | Tg(s) | 0.08 |
| 2H(s) | 0.1667 | Tt | 0.4 |
| Tfc(s) | 0.26 | Tb(s) | 0.1 |
| Tinv(s) | 0.04 | R (Hz/p.u. MW) | 3 |
| Tfilt(s) | 0.004 |
| Attack # | Time | Status |
|---|---|---|
| 1 | t = 5 s | During step change |
| 2 | t = 20 s | At normal operation |
| 3 | t = 32 s | During frequency settling |
| Attack # | Time | Load Power | Wind Power | Solar Power |
|---|---|---|---|---|
| 1 | t = 5 s | 0.50 pu | 0.20 pu | 0.30 pu |
| 2 | t = 10 s | 0.50 pu | 0.40 pu | 0.30 pu |
| 3 | t = 16 s | 0.50 pu | 0.40 pu | 0.50 pu |
| 5 | t = 25 s | 0.50 pu | 0.30 pu | 0.60 pu |
| 6 | t = 30 s | 0.30 pu | 0.60 pu | 0.40 pu |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soliman, H.; Bayoumi, E.; Lee, S. Ellipsoidal Design of Robust Secure Frequency Control in Smart Cities Under Denial-of-Service Cyberattack. Smart Cities 2025, 8, 39. https://doi.org/10.3390/smartcities8020039
Soliman H, Bayoumi E, Lee S. Ellipsoidal Design of Robust Secure Frequency Control in Smart Cities Under Denial-of-Service Cyberattack. Smart Cities. 2025; 8(2):39. https://doi.org/10.3390/smartcities8020039
Chicago/Turabian StyleSoliman, Hisham, Ehab Bayoumi, and Sangkeum Lee. 2025. "Ellipsoidal Design of Robust Secure Frequency Control in Smart Cities Under Denial-of-Service Cyberattack" Smart Cities 8, no. 2: 39. https://doi.org/10.3390/smartcities8020039
APA StyleSoliman, H., Bayoumi, E., & Lee, S. (2025). Ellipsoidal Design of Robust Secure Frequency Control in Smart Cities Under Denial-of-Service Cyberattack. Smart Cities, 8(2), 39. https://doi.org/10.3390/smartcities8020039






