Gauge Dependence of the Gauge Boson Projector
Abstract
:1. Introduction
2. The Gauge Boson Projector
2.1. Construction of the Fermion Propagator
2.2. Construction of the Gauge Boson Propagator
2.3. The Issue of Dispersion
2.4. A Pragmatic Solution
3. Green’s Function of the Photon
3.1. Solution for the Green’s Function of the Photon
3.2. Going Back to Historical Approaches
4. The Photon Propagator
4.1. The Gupta–Bleuler Quantisation
4.2. The Photon Projector on the Light Cone
5. The Gauge Boson Propagator
5.1. Goldstone Bosons and Mass Terms
5.2. Green’s Functions of Massive Gauge Bosons
6. Gauge Independence of Processes
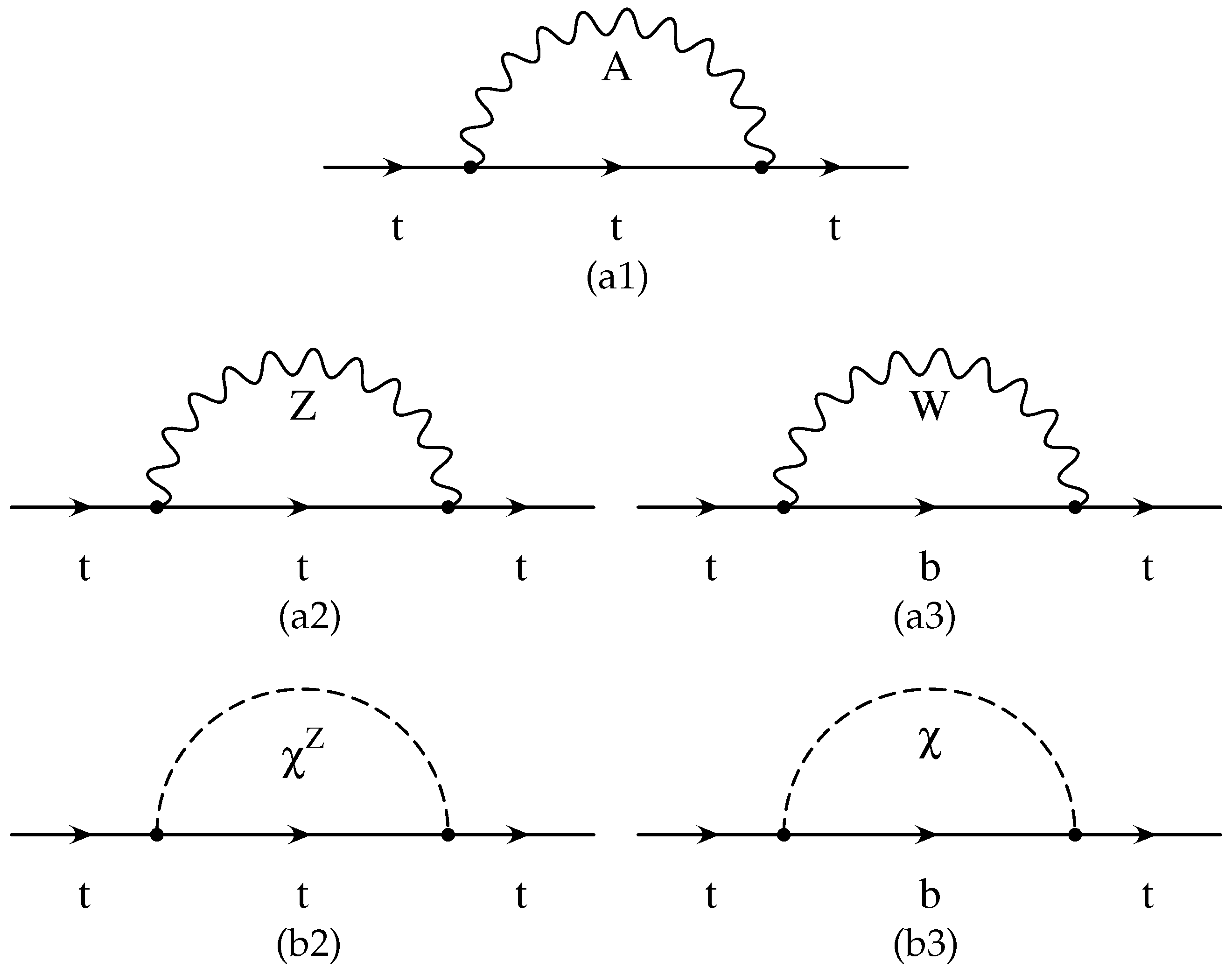
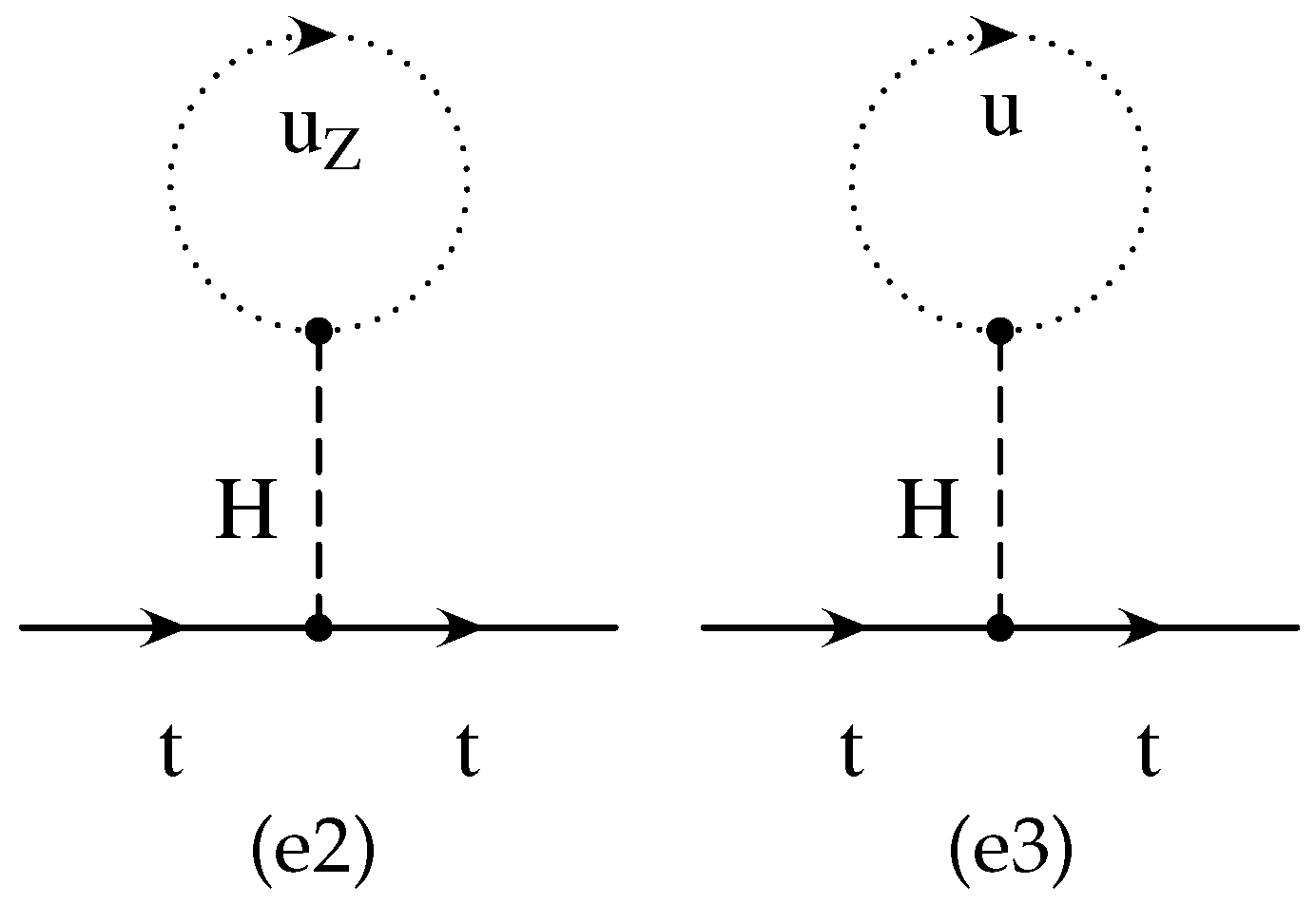
6.1. Fermion Self Energy Contribution
6.2. The Role of Unitarity
7. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Landau, L.; Lifshitz, E. The Classical Theory of Fields, 4th ed.; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Greiner, W.; Reinhardt, J. Quantum Electrodynamics, 4th ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory, 5th ed.; Addison-Wesley: Reading, PA, USA, 1995. [Google Scholar]
- Böhm, M.; Denner, A.; Joos, H. Gauge Theories of the Strong and Electroweak Interaction, 3rd ed.; B.G. Teubner: Stuttgart, Germany, 2001. [Google Scholar]
- Pavel, H.P.; Pervushin, V.N. Reduced phase space quantization of massive vector theory. Int. J. Mod. Phys. A 1999, 14, 2285. [Google Scholar] [CrossRef] [Green Version]
- Körner, J.G. Helicity Amplitudes and Angular Decay Distributions. In Proceedings of the Helmholtz International Summer School on Physics of Heavy Quarks and Hadrons (HQ 2013): JINR, Dubna, Russia, 15–28 July 2013; pp. 169–184. [Google Scholar]
- Berge, S.; Groote, S.; Körner, J.G.; Kaldamäe, L. Lepton-mass effects in the decays H → ZZ* → ℓ+ℓ−τ+τ− and H → WW* → ℓντντ. Phys. Rev. D 2015, 92, 033001. [Google Scholar] [CrossRef] [Green Version]
- Czarnecki, A.; Groote, S.; Körner, J.G.; Piclum, J.H. NNLO QCD corrections to the polarized top quark decay t(↑) → Xb + W+. Phys. Rev. D 2018, 97, 094008. [Google Scholar] [CrossRef] [Green Version]
- Faddeev, L.D.; Popov, V.N. Feynman Diagrams for the Yang-Mills Field. Phys. Lett. 1967, 25B, 29–30. [Google Scholar] [CrossRef]
- Lorenz, L. On the identity of the vibrations of light with electrical currents. Philos. Mag. Ser. 4 1867, 34, 287–301. [Google Scholar] [CrossRef]
- Kleinert, H. Particles and Quantum Fields; World Scientific: Singapore, 2016. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 3rd ed.; Oxford University Press: Oxford, UK, 1947. [Google Scholar]
- Leibbrandt, G. Introduction to Noncovariant Gauges. Rev. Mod. Phys. 1987, 59, 1067. [Google Scholar] [CrossRef] [Green Version]
- Fermi, E. Quantum Theory of Radiation. Rev. Mod. Phys. 1932, 4, 87. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures in Quantum Field Theory; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Heisenberg, W.; Pauli, W. Zur Quantentheorie der Wellenfelder. Teil II. Z. Phys. 1930, 59, 168–190. [Google Scholar] [CrossRef]
- Bleuler, K. Eine neue Methode zur Behandlung der longitudinalen und skalaren Photonen. Helv. Phys. Acta 1950, 23, 567–586. [Google Scholar]
- Gupta, S.N. Theory of longitudinal photons in quantum electrodynamics. Proc. Phys. Soc. A 1950, 63, 681. [Google Scholar] [CrossRef]
- Chisholm, J.S.R. Change of variables in quantum field theories. Nucl. Phys. 1961, 26, 469–479. [Google Scholar] [CrossRef]
- Kamefuchi, S.; O’Raifeartaigh, L.; Salam, A. Change of variables and equivalence theorems in quantum field theories. Nucl. Phys. 1961, 28, 529–549. [Google Scholar] [CrossRef]
- Salam, A.; Strathdee, J.A. Equivalent formulations of massive vector field theories. Phys. Rev. D 1970, 2, 2869–2876. [Google Scholar] [CrossRef]
- Keck, B.W.; Taylor, J.G. On the equivalence theorem for S-matrix elements. J. Phys. A 1971, 4, 291. [Google Scholar] [CrossRef]
- Kallosh, R.E.; Tyutin, I.V. The Equivalence theorem and gauge invariance in renormalizable theories. Yad. Fiz. 1973, 17, 190–209, reprinted in Sov. J. Nucl. Phys. 1973, 17, 98. [Google Scholar]
- Wu, T.T.; Wu, S.L. Comparing the Rξ gauge and the unitary gauge for the standard model: An example. Nucl. Phys. B 2017, 914, 421–445. [Google Scholar] [CrossRef]
- Gegelia, J.; Meißner, U.G. Once more on the Higgs decay into two photons. Nucl. Phys. B 2018, 934, 1–6. [Google Scholar] [CrossRef]
- Lee, T.D.; Nauenberg, M. Degenerate systems and mass singularities. Phys. Rev. 1964, 133, B1549. [Google Scholar] [CrossRef]
- Kleiss, R. Hard bremsstrahlung amplitudes for e+e- collisions with polarized beams at LEP/SLC energies. Z. Phys. 1987, C33, 433–443. [Google Scholar] [CrossRef]
- Jadach, S.; Kühn, J.H.; Stuart, R.G.; Was, Z. QCD and QED corrections to the longitudinal polarization asymmetry. Z. Phys. 1988, C38, 609–617, Erratum in 1990, C45, 528. [Google Scholar] [CrossRef] [Green Version]
- Contopanagos, H.F.; Einhorn, M.B. Is there a radiative background to the search of right-handed charged currents? Nucl. Phys. 1992, B377, 20. [Google Scholar] [CrossRef] [Green Version]
- Contopanagos, H.F.; Einhorn, M.B. Physical cnsequences of mass singularities. Phys. Lett. 1992, B277, 345–352. [Google Scholar] [CrossRef] [Green Version]
- Smilga, A.V. Quasiparadoxes of massless QED. Comments Nucl. Part. Phys. 1991, 20, 69–84. [Google Scholar]
- Falk, B.; Sehgal, L.M. Helicity flip bremsstrahlung: An equivalent particle description with applications. Phys. Lett. 1994, B325, 509–516. [Google Scholar] [CrossRef]
- Körner, J.G.; Pilaftsis, A.; Tung, M.M. One loop QCD mass effects in the production of polarized bottom and top quarks. Z. Phys. 1994, C63, 575–579. [Google Scholar] [CrossRef] [Green Version]
- Groote, S.; Körner, J.G.; Tung, M.M. Polar angle dependence of the alignment polarization of quarks produced in e+e- annihilation. Z. Phys. 1997, C74, 615–629. [Google Scholar]
- Groote, S.; Körner, J.G.; Leyva, J.A. O(αs) corrections to longitudinal spin–spin correlations in e+e− → qq. Phys. Lett. 1998, B418, 192. [Google Scholar] [CrossRef] [Green Version]
- Dittmaier, S.; Kaiser, A. Photonic and QCD radiative corrections to Higgs boson production in μ+μ− → ff. Phys. Rev. 2002, D65, 113003. [Google Scholar] [CrossRef] [Green Version]
- Groote, S.; Körner, J.G.; Leyva, J.A. O(αs) corrections to the polar angle dependence of the longitudinal spin-spin correlation asymmetry in e+e− → qq. Eur. Phys. J. C 2009, 63, 391–406, Erratum in 2014, 74, 2789. [Google Scholar] [CrossRef] [Green Version]
- Saar, R.; Groote, S. Mass, zero mass and ... nophysics. Adv. Appl. Clifford Algebras 2017, 27, 2739–2768. [Google Scholar] [CrossRef] [Green Version]
- Choi, T.; Cho, S.Y. Spin operators and representations of the Poincaré group. arXiv 2018, arXiv:1807.06425. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallagher, P.; Groote, S.; Naeem, M. Gauge Dependence of the Gauge Boson Projector. Particles 2020, 3, 543-561. https://doi.org/10.3390/particles3030037
Gallagher P, Groote S, Naeem M. Gauge Dependence of the Gauge Boson Projector. Particles. 2020; 3(3):543-561. https://doi.org/10.3390/particles3030037
Chicago/Turabian StyleGallagher, Priidik, Stefan Groote, and Maria Naeem. 2020. "Gauge Dependence of the Gauge Boson Projector" Particles 3, no. 3: 543-561. https://doi.org/10.3390/particles3030037




