Effects of Electrical and Electromechanical Parameters on Performance of Galloping-Based Wind Energy Harvester with Piezoelectric and Electromagnetic Transductions
Abstract
:1. Introduction
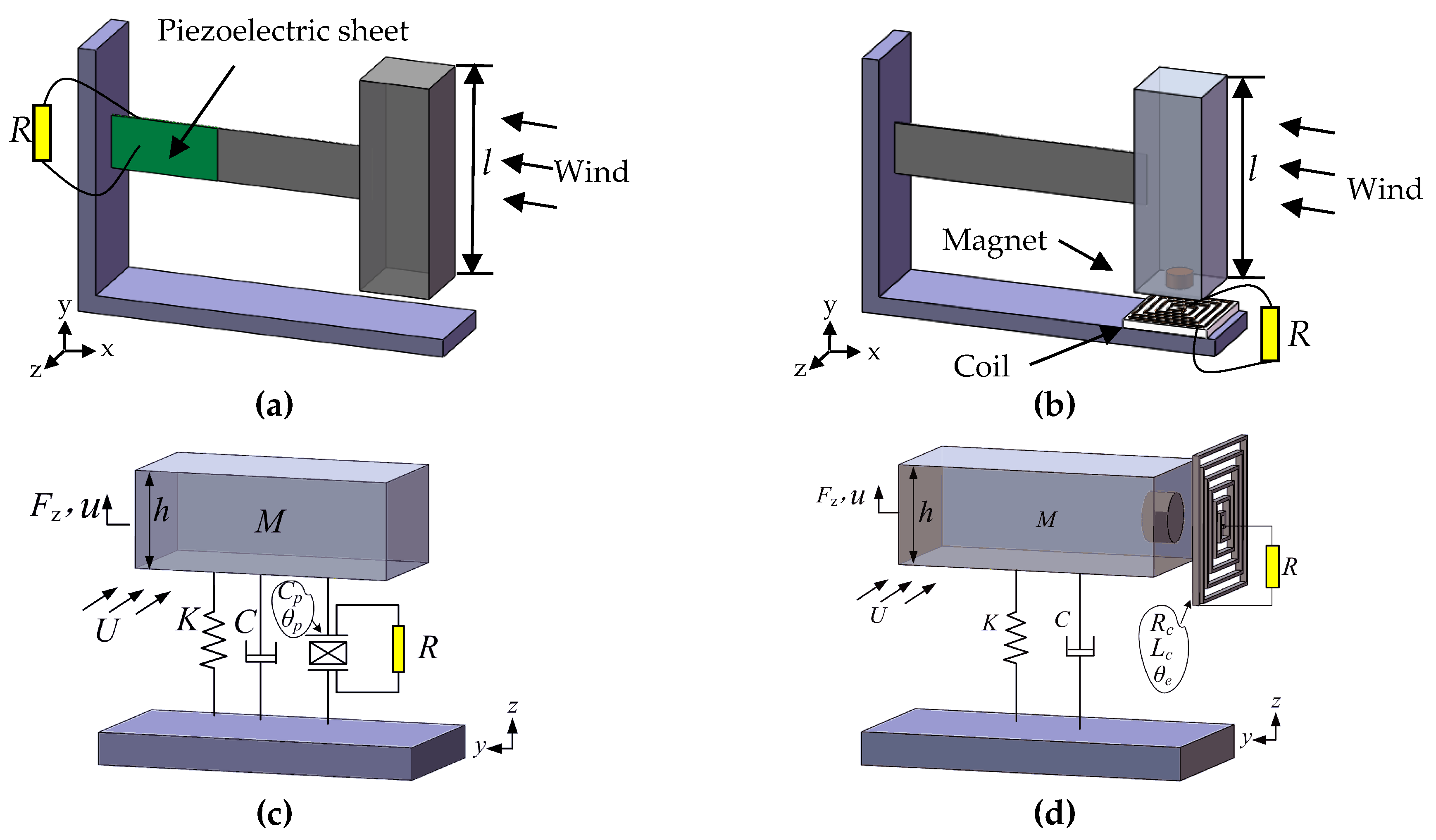
2. Configurations of GPEH and GEMEH
3. Numerical Model
3.1. GPEH
3.2. GEMEH
4. Approximate Analytical Solution
4.1. GPEH
4.2. GEMEH
5. Results
5.1. Validation of Approximate Analytical Solution
5.1.1. GPEH
5.1.2. GEMEH
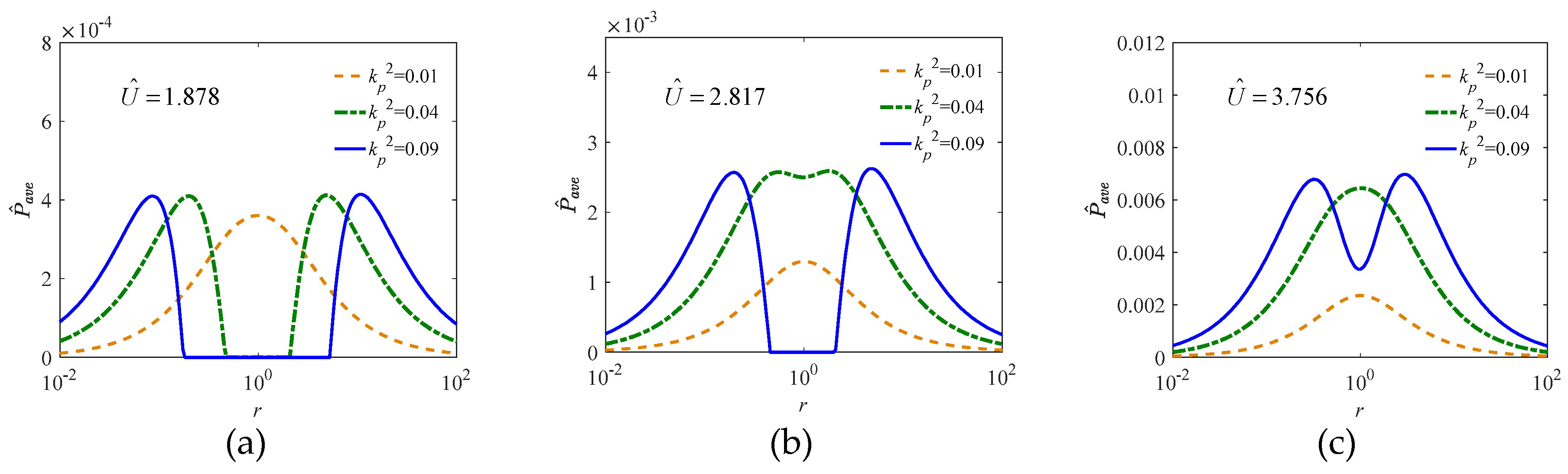
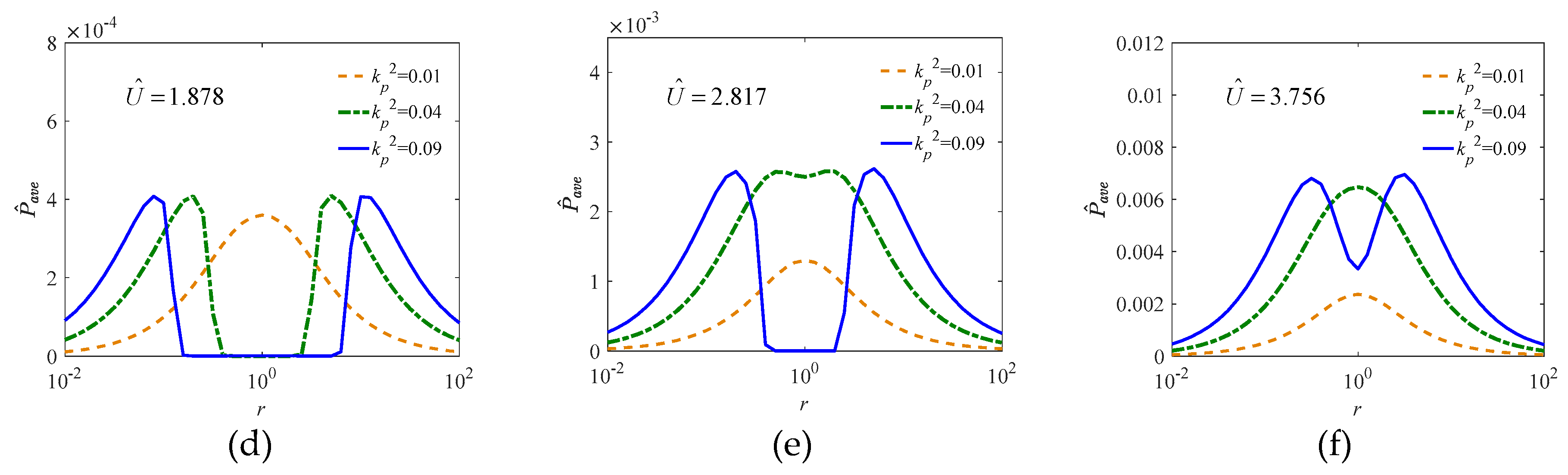
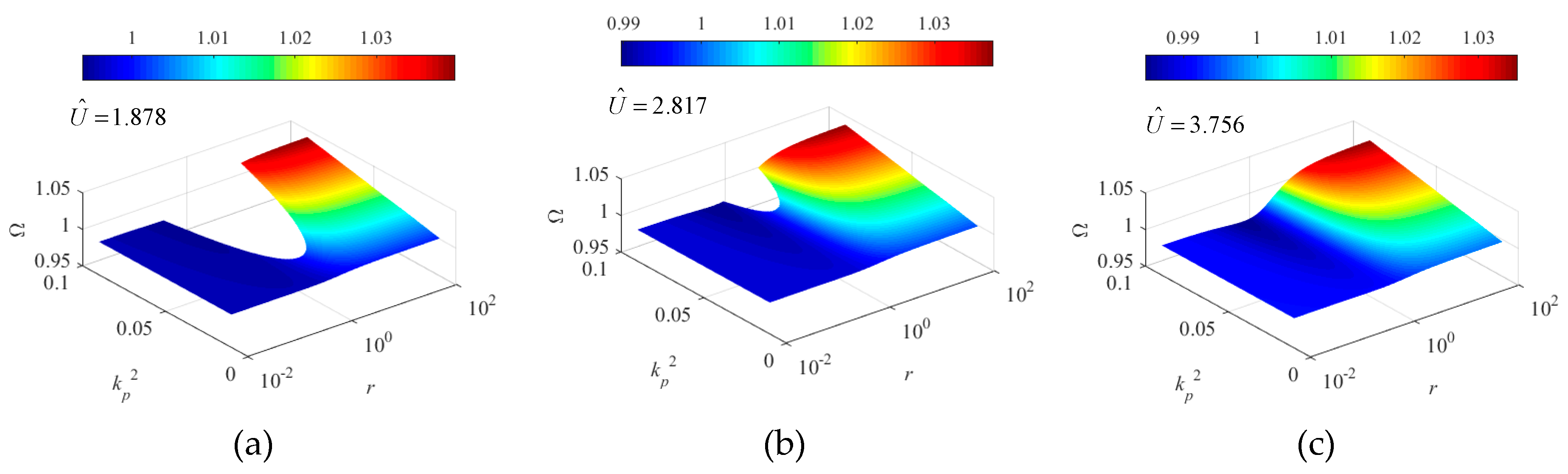
5.2. Parametric Study on Load Resistance and EMCS
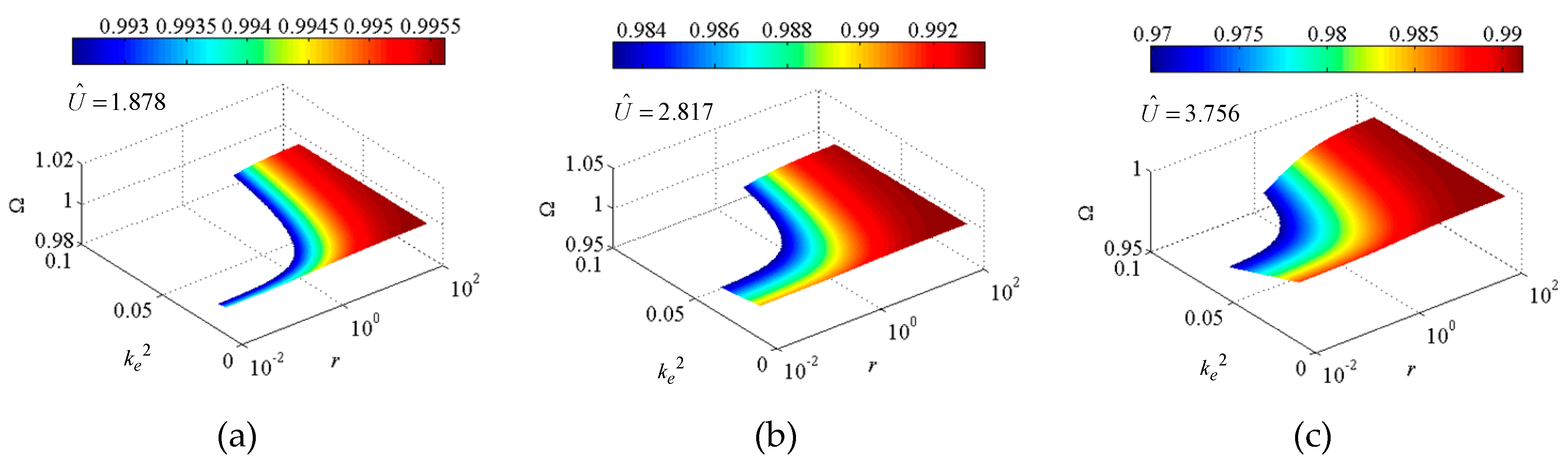
5.2.1. Effects on Dimensionless Oscillating Frequency Ω
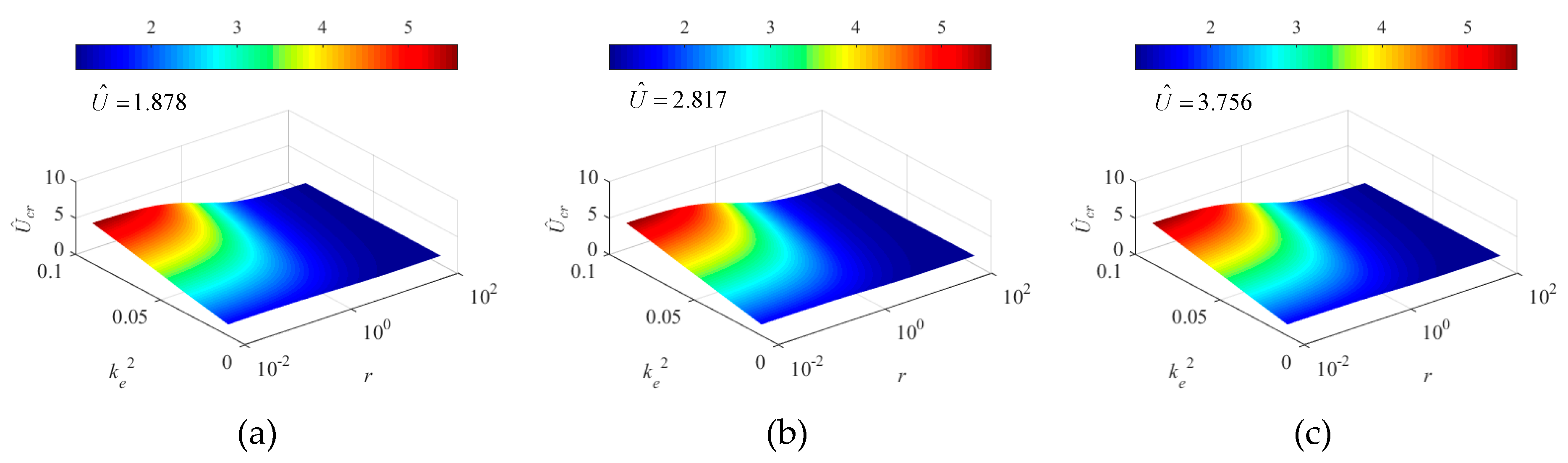
5.2.2. Effects on Dimensionless Cut-In Wind Speed,
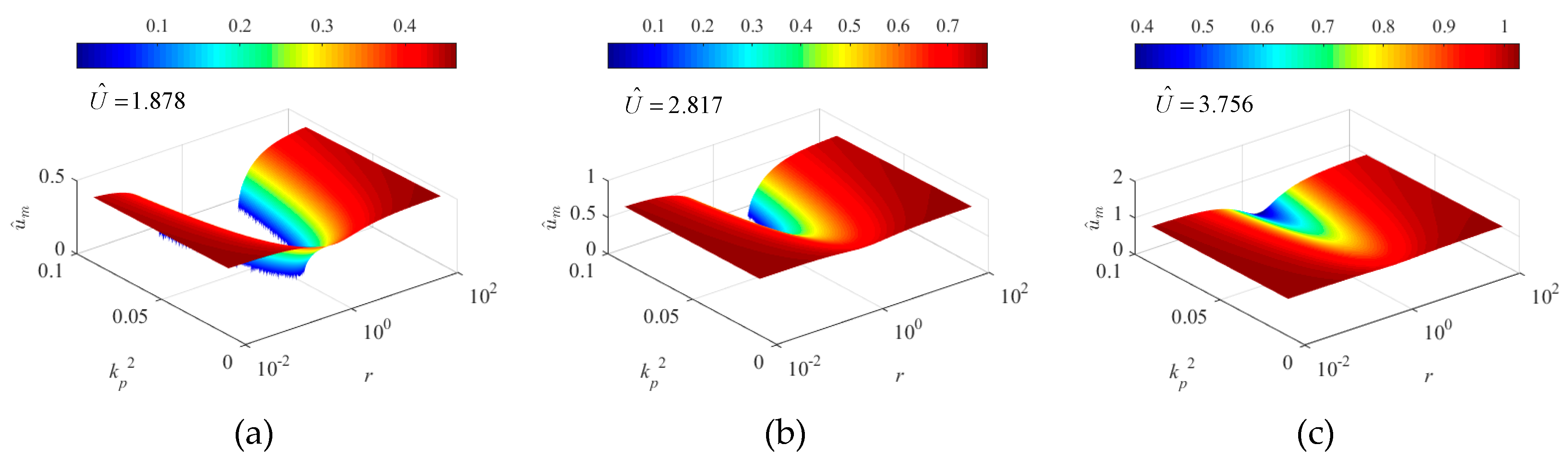
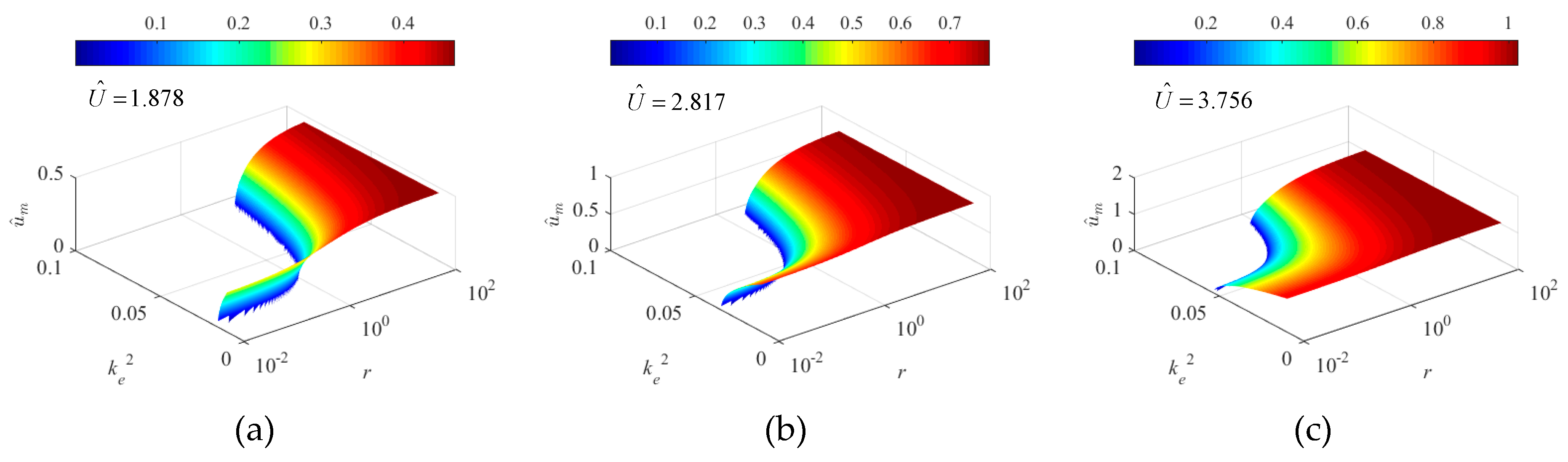
5.2.3. Effects on Dimensionless Displacement,
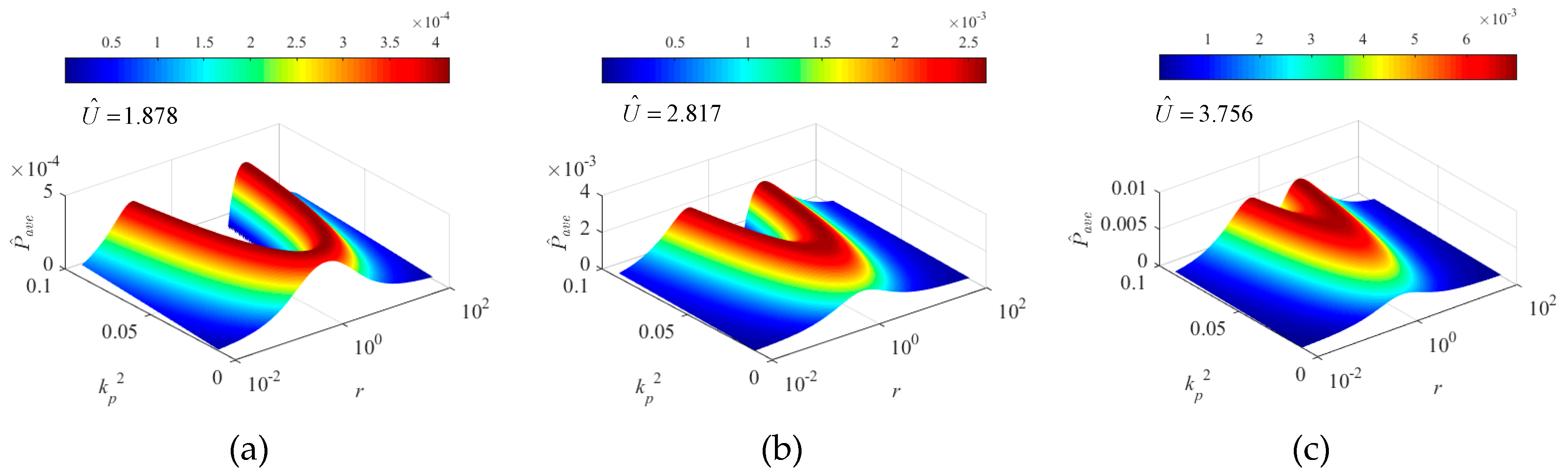
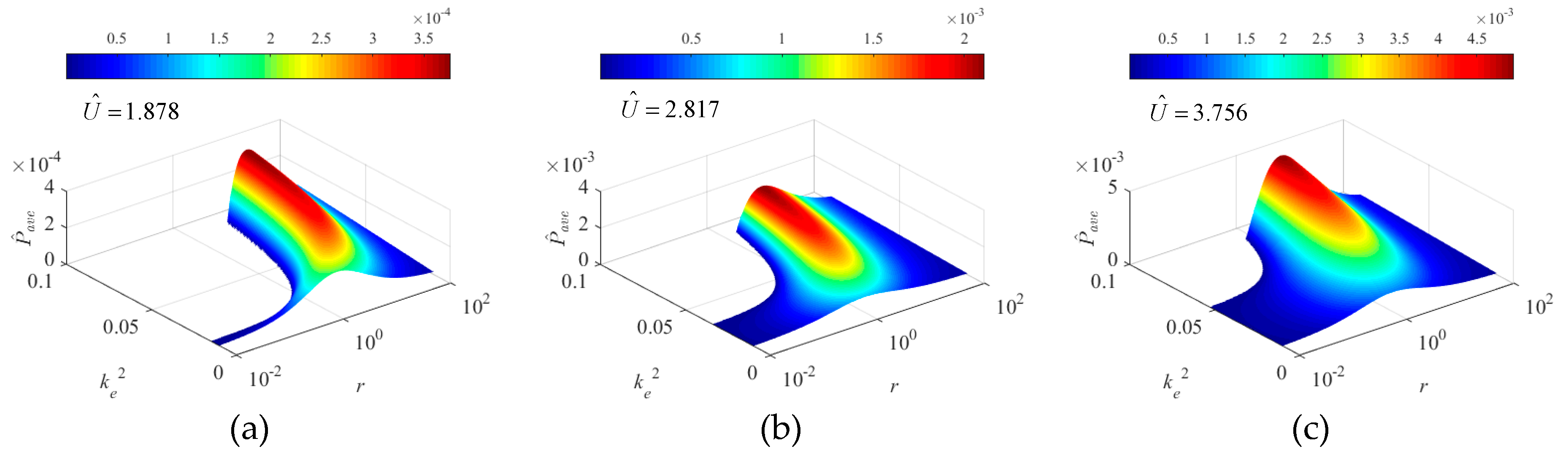
5.2.4. Effects on Dimensionless Power,
5.2.5. Optimal Power Outputs
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy Harvesting Vibration Sources for Microsystems Applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, Z.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.H.; Shin, H.J.; Lee, H.; Jeong, C.K.; Park, H.; Hwang, G.-T.; Lee, H.-Y.; Joe, D.J.; Han, J.H.; Lee, S.H.; et al. In Vivo Self-Powered Wireless Transmission Using Biocompatible Flexible Energy Harvesters. Adv. Funct. Mater. 2017, 27, 1700341. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. A Review on Mechanisms for Piezoelectric-based Energy Harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef]
- Abdelkefi, A. Aeroelastic Energy Harvesting: A review. Int. J. Eng. Sci. 2016, 100, 112–135. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. Design and Performance Evaluation of a Piezoelectric Aeroelastic Energy Harvester based on the Limit Cycle Oscillation Phenomenon. Acta Astronaut. 2019, 157, 233–240. [Google Scholar] [CrossRef]
- Aquino, A.I.; Clautit, J.K.; Hughes, B.R. Evaluation of the Integration of the Wind-Induced Flutter Energy Harvester (WIFEH) into the Built Environment: Experimental and Numerical analysis. Appl. Energy 2017, 207, 61–77. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, H.; Abdelkefi, A.; Wang, L. Improving the Performance of Aeroelastic Energy Harvesters by an Interference Cylinder. Appl. Phys. Lett. 2017, 111, 073904. [Google Scholar] [CrossRef]
- Javed, U.; Abdelkefi, A. Characteristics and Comparative Analysis of Piezoelectric-Electromagnetic Energy Harvesters from Vortex-induced Oscillations. Nonlinear Dyn. 2019. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations, 1st ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Naudascher, E.; Rockwell, D. Flow-Induced Vibrations: An Engineering Guide, 1st ed.; Dover Publications: New York, NY, USA, 1994. [Google Scholar]
- Novak, M. Aeroelastic Galloping of Prismatic Bodies. ASCE J. Eng. Mech. Div. 1969, 96, 115–142. [Google Scholar]
- Barrero-Gil, A.; Alonso, G.; Sanz-Andres, A. Energy Harvesting from Transverse Galloping. J. Sound Vib. 2010, 329, 2873–2883. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H. Power Harvesting from Transverse Galloping of Square Cylinder. Nonlinear Dyn. 2012, 70, 1355–1363. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Piezoelectric Wind Energy Harvester for Low-power Sensors. J. Intell. Mater. Syst. Struct. 2011, 22, 2215–2228. [Google Scholar] [CrossRef]
- Ewere, F.; Wang, G. Performance of Galloping Piezoelectric Energy Harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 1693–1704. [Google Scholar] [CrossRef]
- Sirohi, J.; Mahadik, R. Harvesting Wind Energy using a Galloping Piezoelectric Beam. J. Vib. Acoust. 2011, 134, 011009. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Yan, Z.; Hajj, M.R. Performance Analysis of Galloping-based Piezoaeroelastic Energy Harvesters with Different Cross-Section Geometries. J. Intell. Mater. Syst. Struct. 2014, 25, 246–256. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, L.; Yang, Y. Comparison of Modeling Methods and Parametric Study for a Piezoelectric Wind Energy Harvester. Smart Mater. Struct. 2013, 22, 125003. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, L.; Yang, Y.; Lefeuvre, E. Equivalent Circuit Representation and Analysis of Galloping-Based Wind Energy Harvesting. IEEE-ASME Trans. Mech. 2015, 20, 834–844. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Hajj, M.R.; Nayfeh, A.H. Piezoelectric Energy Harvesting from Transverse Galloping of Bluff Bodies. Smart Mater. Struct. 2013, 22, 015014. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Tang, L. Comparative Study of Tip Cross-Sections for Efficient Galloping Energy Harvesting. Appl. Phys. Lett. 2013, 102, 064105. [Google Scholar] [CrossRef]
- Vicente-Ludlam, D.; Barrero-Gil, A.; Velazquez, A. Optimal Electromagnetic Energy Extraction from Transverse Galloping. J. Fluid. Struct. 2014, 51, 281–291. [Google Scholar] [CrossRef]
- Dai, H.L.; Abdelkefi, A.; Javed, U.; Wang, L. Modeling and Performance of Electromagnetic Energy Harvesting from Galloping Oscillations. Smart Mater. Struct. 2015, 24, 045012. [Google Scholar] [CrossRef]
- Tan, T.; Yan, Z. Electromechanical Decoupled Model for Cantilever-Beam Piezoelectric Energy Harvesters with Inductive-Resistive Circuits and Its Application in Galloping Mode. Smart Mater. Struct. 2017, 26, 035062. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y. Analytical Solutions for Galloping-based Piezoelectric Energy Harvesters with Various Interfacing Circuits. Smart Mater. Struct. 2015, 24, 075023. [Google Scholar] [CrossRef]
- Wacharasindhu, T.; Kwon, J.W. A Micromachined Energy Harvester from a Keyboard using Combined Eectromagnetic and Piezoelectric Conversion. J. Micromech. Microeng. 2008, 18, 104016. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic Energy Harvesting from Vibrations of Multiple Frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.; Kee, W.L.; Lim, S.P. Hybrid Energy Harvester based on Piezoelectric and Electromagnetic Mechanisms. J. Micro/Nanolithogr. MEMS MOEMS 2010, 9, 023002. [Google Scholar] [CrossRef]





| Properties | Values | Properties | Values |
|---|---|---|---|
| Effective mass, M (kg) | 0.002783 | Cross section of bluff body, h × h (m) | 0.02 × 0.02 |
| Effective stiffness, K (N m−1) | 31.5638 | Length of bluff body, L (m) | 0.1 |
| Damping ratio, ζ | 0.011 | Fluid density, ρ (kg m−3) | 1.2041 |
| Coefficient, β | 10.55 | Aerodynamic coefficients, A1, A3 | 2.3, −18 |
| Capacitance, Cp (nF) | 25.7 | Coil resistance, Rc (Ω) | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, L.; Tang, L. Effects of Electrical and Electromechanical Parameters on Performance of Galloping-Based Wind Energy Harvester with Piezoelectric and Electromagnetic Transductions. Vibration 2019, 2, 222-239. https://doi.org/10.3390/vibration2020014
Wang H, Zhao L, Tang L. Effects of Electrical and Electromechanical Parameters on Performance of Galloping-Based Wind Energy Harvester with Piezoelectric and Electromagnetic Transductions. Vibration. 2019; 2(2):222-239. https://doi.org/10.3390/vibration2020014
Chicago/Turabian StyleWang, Hongyan, Liya Zhao, and Lihua Tang. 2019. "Effects of Electrical and Electromechanical Parameters on Performance of Galloping-Based Wind Energy Harvester with Piezoelectric and Electromagnetic Transductions" Vibration 2, no. 2: 222-239. https://doi.org/10.3390/vibration2020014





