Next Article in Journal
Effects of Electrical and Electromechanical Parameters on Performance of Galloping-Based Wind Energy Harvester with Piezoelectric and Electromagnetic Transductions
Previous Article in Journal
Experimental and Signal Processing Techniques for Fault Diagnosis on a Small Horizontal-Axis Wind Turbine Generator †
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Vibration
Volume 2
Issue 2
10.3390/vibration2020013
vibration-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams

by
Mergen H. Ghayesh
1,*,
Ali Farajpour
1 and
Hamed Farokhi
2
1
School of Mechanical Engineering, University of Adelaide, South Australia 5005, Australia
2
Department of Mechanical and Construction Engineering, Northumbria University, Newcastle upon Tyne NE1 8ST, UK
*
Author to whom correspondence should be addressed.
Vibration 2019, 2(2), 201-221; https://doi.org/10.3390/vibration2020013
Submission received: 3 May 2019 / Revised: 3 June 2019 / Accepted: 4 June 2019 / Published: 14 June 2019
Browse Figures
Versions Notes

Abstract

:
A nonlinear vibration analysis is conducted on the mechanical behavior of axially functionally graded (AFG) microscale Timoshenko nonuniform beams. Asymmetry is due to both the nonuniform material mixture and geometric nonuniformity. Using the Timoshenko beam theory, the continuous models for translation/rotation are developed via an energy balance. Size-dependence is incorporated via the modified couple stress theory and the rotation via the Timoshenko beam theory. Galerkin’s method of discretization is applied and numerical simulations are conducted for a size-dependent vibration of the AFG microscale beam. Effects of material gradient index and axial change in the cross-sectional area on the force and frequency diagrams are investigated.

1. Introduction

Vibrating [1] standard structural continuous elements (plates, shells, and beams) are the building blocks in many civil structures and machines even at small-scale levels [2,3,4,5,6,7]. The micro/nanoscale version of these structural elements are the building blocks of micro/nanomachines [8,9,10,11]. In some of these microscale devices, high thermal resistance in addition to mechanical resistance is required. One such a way to fabricate such a structure is powder metallurgy, where two materials (usually ceramics and metal) are mixed to fabricate so-called functionally graded (FG) materials [12,13,14,15,16,17,18,19,20]. If the material properties alter in an in-plane/axial direction, the beam/plate structure is called axially functionally graded (AFG).
At microscales and nanoscales, the mechanical response has been indicated to be size-dependent [21,22,23,24,25,26,27,28,29,30,31] and thus classical models of elasticity must be modified so as to include size influences [32,33,34,35,36,37,38,39,40,41,42]. A number of modification procedures based on the nonlocal elasticity [43,44,45,46], couple stress model [47,48,49,50,51,52], and strain gradient theory [53,54] have been proposed. More recently, a significant number of size-dependent models with microstructure-dependent deformational and nonlocal stress influences have been proposed [55,56]. The practicality and validity of nonlocal strain gradient models have been also tested and demonstrated for describing different physical phenomena at ultrasmall levels [57]. These models have been also developed for small-scale FG beams [58,59]. In this analysis, according to a modified version of the couple stress theory (CST), size influences are described.
The motion behavior of AFG microscale beams has been investigated in a limited number of papers. Akgoz and Civalek [60] employed a linear vibration theory for the analysis of nonuniform AFG microscale beams via a modified version of the CST for determination of mode-shapes and natural frequencies. Simsek [61] conducted a nonlinear analysis on a single degree of freedom (DOF) model of AFG microscale beams employing the modified CST. Shafiei et al. [62] applied a single-mode-truncation for the axial/transverse oscillation analysis of AFG tapered microscale beams.
The asymmetric scale-dependent vibrations of AFG microscale Timoshenko nonuniform beams is investigated incorporating rotation using the Timoshenko beam theory; this is for the first time. The translational motions are also formulated coupled with the rotational motion. The size-dependence is incorporated using the modified CST. An energy method is used to derive the coupled continuous model. Galerkin’s method for discretization is used and the resultant model is solved numerically for frequency/force diagrams.

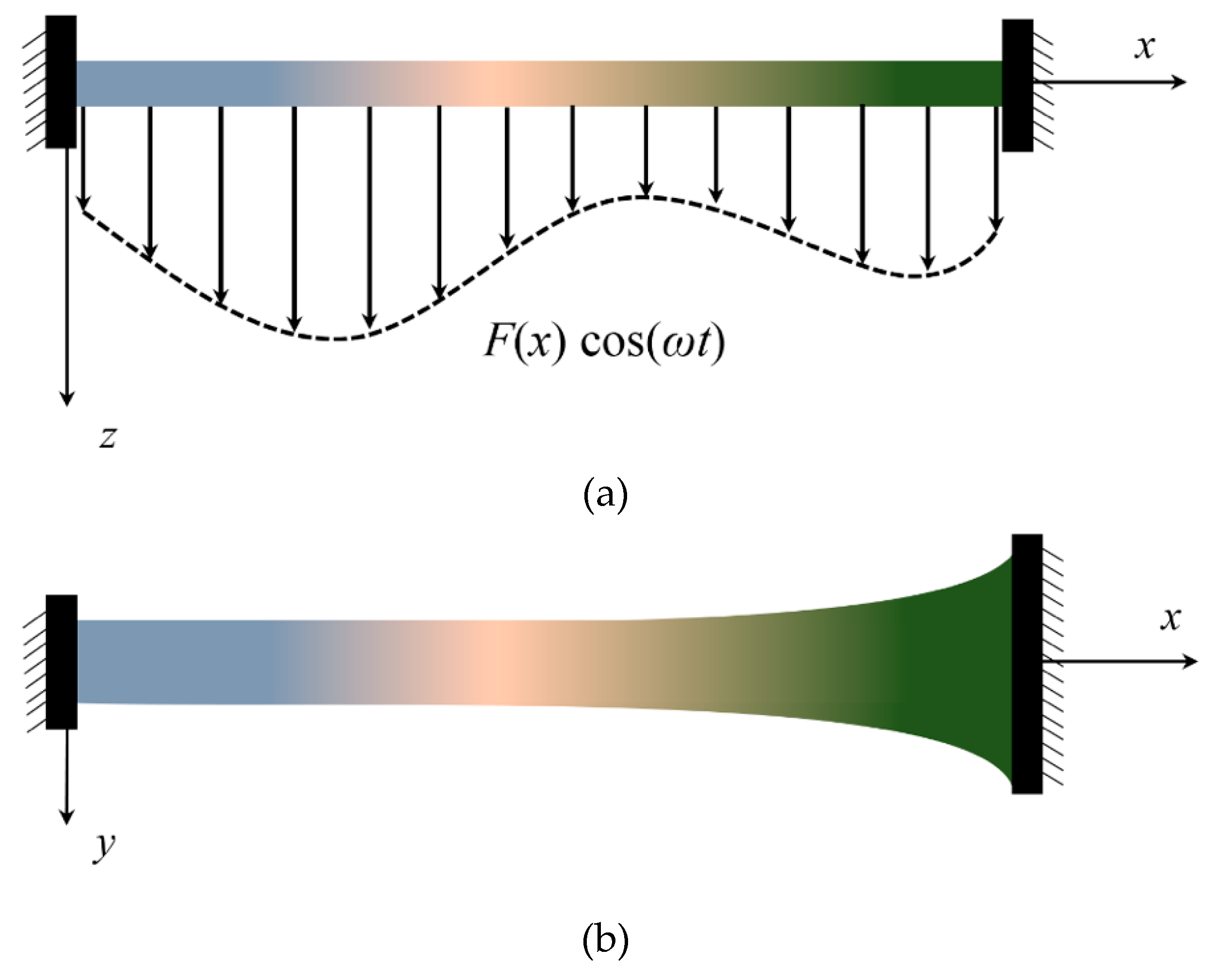
2. Model Development

A two-phase (ceramics–metal) nonuniform AFG microscale Timoshenko beam with all ends clamped is shown in Figure 1; the length, thickness, and width are shown by L, h, and b, where the latter one varies with x (as the axial coordinate). Also, [ϕ; w; u] are [rotation; transverse-displacement; axial-displacement]. The microscale beam is subject to F(x)cos(ωt) transversely. It is assumed that the microbeam is thick and short, therefore the Timoshenko beam theory is utilized, which is more appropriate than the Euler–Bernoulli one in this case. In addition, it is assumed that size influences are induced only by couple stresses. Another assumption is that the geometrical nonlinearity is induced only by the stretch of the microbeam centerline. This assumption is reasonable since the effects of curvature-type nonlinearity can be neglected when the boundary conditions are clamped.
The axial variations for nonuniformity in geometry and material properties are defined as [63]:
Χ ( x ) = ( x L ) n ( Χ R − Χ L ) + Χ L ,   with Χ ≡ [ E ; b ; ρ ; l ; ν ] μ ( x ) = E ( x ) / [ 2 ( ν ( x ) + 1 ) ] h R = h , h L = h ,     A ( x ) = h b ( x ) ,
with [L; R] as [left-end; right-end] of the microbeam. Also [μ; E; l; ρ; ν] are [shear modulus; Young’s modulus; length-scale parameter; mass density; Poisson’s ratio]; the length scale parameter is the representative of the modified CST employed in the modeling of the AFG microsystem; A is the area of cross-section. It should be noticed that the mechanical behaviors of macroscale structures are scale-free, namely the non-dimensional mechanical characteristics are not dependent on the size of the structure [64,65,66,67]. In contrast, size influences have an important impact on the mechanics of microscale structures. For instance, the dimensionless natural frequency of a microscale beam alters when its length is changed. For a Timoshenko beam [68]:
θ y = 1 2 ( ϕ − ∂ w ∂ x ) , θ x = θ z = 0 ,
χ x y = χ y x = 1 4 ( ∂ ϕ ∂ x − ∂ 2 w ∂ x 2 ) ,
ε x z = 1 2 ( ϕ + ∂ w ∂ x ) = ε z x , ε x x = ∂ u ∂ x + 1 2 ( ∂ w ∂ x ) 2 + z ∂ ϕ ∂ x ,
defining Ks as shear correction, the potential energy becomes (when Equations (3) and (4) are considered) [69]:
  U = 1 2 ∫ 0 L [ E ( x ) A ( x ) ( ∂ u ∂ x + 1 2 ( ∂ w ∂ x ) 2 ) 2 + E ( x ) I ( x ) ( ∂ ϕ ∂ x ) 2 + K s μ ( x ) A ( x ) ( ϕ + ∂ w ∂ x ) 2 + μ ( x ) A ( x ) ( l ( x ) ) 2 4 ( ∂ ϕ ∂ x − ∂ 2 w ∂ x 2 ) 2 ] d x .
In the above relations, large deformations are also incorporated since large deformations happen in many engineering problems at both ultrasmall and large-scale levels [70,71,72,73,74,75,76,77,78]. An internal-damping-related work is:
δ W D = − c d ∫ 0 L ( δ u ∂ u ∂ t + δ w ∂ w ∂ t ) d x − c r ∫ 0 L ( δ ϕ ∂ ϕ ∂ t ) d x .
Where cr and cd denote the damping coefficient related to rotation and displacements, respectively. The external-force one becomes:
δ W T = ∫ 0 L F ( x ) cos ( ω t ) δ w         d x .
The motion energy, incorporating rotary inertia, is [69]:
  T   = 1 2 ∫ 0 L { ρ ( x ) A ( x ) ( ∂ u ∂ t ) 2 + ρ ( x ) I ( x ) ( ∂ ϕ ∂ t ) 2 + ρ ( x ) A ( x ) ( ∂ w ∂ t ) 2 } d x .
Hamilton’s principle as [79,80,81,82,83]:
∫ t 1 t 2 ( δ T − δ U + δ W T + δ W D )   d t = 0 ,
for Equations (5)–(8) gives the following dimensionless continuous model:
ρ ( x ) A ( x ) ∂ 2 w ∂ t 2 − 12 ∂ ∂ x { E ( x ) A ( x ) [ η ∂ u ∂ x + 1 2 ( ∂ w ∂ x ) 2 ] ( ∂ w ∂ x ) } − 12 ∂ ∂ x { K s μ ( x ) A ( x ) ( η 3 ϕ + η 2 ∂ w ∂ x ) } − 12 ∂ 2 ∂ x 2 [ μ ( x ) A ( x ) ( l s ( x ) ) 2 4 ( η ∂ ϕ ∂ x − ∂ 2 w ∂ x 2 ) ] − f ( x ) cos ( Ω   t ) + c d ∂ w ∂ t = 0 ,
ρ ( x ) A ( x ) ∂ 2 u ∂ t 2 − 12 ∂ ∂ x { E ( x ) A ( x ) [ η 2 ∂ u ∂ x + η 2 ( ∂ w ∂ x ) 2 ] } + c d ∂ u ∂ t = 0 ,
ρ ( x ) I ( x ) ∂ 2 ϕ ∂ t 2 − 12 η 2 ∂ ∂ x { E ( x ) I ( x ) ∂ ϕ ∂ x } + 144 K s μ ( x ) A ( x ) ( η 4 ϕ + η 3 ∂ w ∂ x ) − 144 ∂ ∂ x [ μ ( x ) A ( x ) ( l s ( x ) ) 2 4 ( η 2 ∂ ϕ ∂ x − η ∂ 2 w ∂ x 2 ) ] + c r ∂ ϕ ∂ t = 0.
with the dimensionless quantities given (asterisk is ignored for briefness):
x ∗ = x L ,         ( u ∗ , w ∗ ) = ( u , w ) h ,         E ∗ ( x ) = E ( x ) E L ,         ρ ∗ ( x ) = ρ ( x ) ρ L ,       μ ∗ ( x ) = μ ( x ) E L ,         l s ∗ ( x ) = l ( x ) h , A ∗ ( x ) = A ( x ) A L ,         I ∗ ( x ) = I ( x ) I L ,         η = L h ,         f = F   L 4 E L I L   h ,         t ∗ = t E L I L ρ L A L     L 4 ,         Ω = ω ρ L A L     L 4 E L I L ,       c d ∗ = c d   L 4 E L I L ρ L A L = c r A L I L   L 4 E L I L ρ L A L ,      

3. Discretized Equations of Motion and Solution Procedure

The continuous model of the AFG microscale nonuniform Timoshenko beam is discretized using Galerkin’s technique [84,85,86,87]. As such:
w ( x , t ) = ∑ j = 1 8 φ j ( x ) q j ( t ) , ϕ ( x , t ) = ∑ j = 1 8 ψ j ( x ) p j ( t ) , u ( x , t ) = ∑ j = 1 8 ξ j ( x ) r j ( t ) ,
with time-dependent terms as generalized coordinates and x dependent as basis functions of a clamped-clamped non-AFG beam. The basis functions depend on the boundary conditions of the beam regardless of its material [88,89,90]. Since the boundary conditions are clamped-clamped, the basis functions of a non AFG clamped-clamped beam can be used in this analysis. They are normalized using the non-dimensional parameters given by Equation (13). These basis functions make a good approximation because of two reasons: (1) They satisfy the boundary conditions of the beam, and (2) a high number of them are used in the solution procedure, which leads to a good approximation. Taking f(x) = f1, inserting Equation (14) into Equations (10)–(12) gives:
∑ j = 1 8 [ ∫ 0 1 φ i ( ρ A ) φ j     d x ]   q ¨ j − 12 { η ∑ j = 1 8 ∑ k = 1 8 [ ∫ 0 1 φ i ( E ′ A + E A ′ ) ξ j ′ φ k ′     d x ] r j q k + 1 2 ∑ j = 1 8 ∑ k = 1 8 ∑ l = 1 8 [ ∫ 0 1 φ i ( E ′ A + E A ′ ) φ j ′ φ k ′ φ l ′     d x ]   q j q k q l } − 12 { η ∑ j = 1 8 ∑ k = 1 8 [ ∫ 0 1 φ i ( E A ) ξ j ′ φ k ″     d x + ∫ 0 1 φ i ( E A ) ξ j ″ φ k ′     d x ] r j q k + 3 2 ∑ j = 1 8 ∑ k = 1 8 ∑ l = 1 8 [ ∫ 0 1 φ i ( E A ) φ j ′ φ k ′ φ l ″     d x ]   q j q k q l } − 12 K s [ η 2 ∑ j = 1 8 ( ∫ 0 1 φ i ( μ ′ A + μ A ′ ) φ j ′     d x )   q j + η 3 ∑ j = 1 8 ( ∫ 0 1 φ i ( μ ′ A + μ A ′ ) ψ j     d x )   p j ] − 12 K s [ η 2 ∑ j = 1 8 ( ∫ 0 1 φ i ( μ A ) φ j ″     d x )   q j + η 3 ∑ j = 1 8 ( ∫ 0 1 φ i ( μ A ) ψ j ′     d x )   p j ] − 3 { η ∑ j = 1 8 { ∫ 0 1 φ i [ μ ″ A l s 2 + 2 μ ′ A ′ l s 2 + μ A ″ l s 2 + 4 μ ′ A l s l s ′ + 4 μ A ′ l s l s ′ + 2 μ A ( l s ′ ) 2 + 2 μ A l s l s ″ ] ψ j ′     d x } p j − ∑ j = 1 8 { ∫ 0 1 φ i [ μ ″ A l s 2 + 2 μ ′ A ′ l s 2 + μ A ″ l s 2 + 4 μ ′ A l s l s ′ + 4 μ A ′ l s l s ′ + 2 μ A ( l s ′ ) 2 + 2 μ A l s l s ″ ] φ j ″     d x } q j } − 6 { η ∑ j = 1 8 ( ∫ 0 1 φ i ( μ ′ A l s 2 + μ A ′ l s 2 + 2 μ A l s l s ′ ) ψ j ″     d x )   p j − ∑ j = 1 8 ( ∫ 0 1 φ i ( μ ′ A l s 2 + μ A ′ l s 2 + 2 μ A l s l s ′ ) φ j ‴     d x )   q j } − 3 { η ∑ j = 1 8 ( ∫ 0 1 φ i ( μ A l s 2 ) ψ j ‴       d x )   p j − ∑ j = 1 8 ( ∫ 0 1 φ i ( μ A l s 2 ) φ j ′ ′ ′ ′   d x )   q j } − ∫ 0 1 f 1 φ i cos ( Ω   t )     d x + c d ∑ j = 1 8 ( ∫ 0 1 φ i φ j     d x )   q ˙ j = 0 ,                                           i = 1 ,   2 ,   … ,   8 ,
∑ j = 1 8 [ ∫ 0 1 ξ i ( ρ A ) ξ j     d x ]   r ¨ j − 12 [ η 2 ∑ j = 1 8 ( ∫ 0 1 ξ i ( E ′ A + E A ′ ) ξ j ′     d x )   r j + η 2 ∑ j = 1 8 ∑ k = 1 8 ( ∫ 0 1 ξ i ( E ′ A + E A ′ ) φ j ′ φ k ′     d x ) q j q k ] − 12 [ η 2 ∑ j = 1 8 ( ∫ 0 1 ξ i ( E A ) ξ j ″     d x )   r j + η ∑ j = 1 8 ∑ k = 1 8 ( ∫ 0 1 ξ i ( E A ) φ j ′ φ k ″     d x ) q j q k ] + c d ∑ j = 1 8 ( ∫ 0 1 ξ i ξ j     d x )   r ˙ j = 0                   i = 1 ,   2 ,   … ,   8 ,
∑ j = 1 8 ( ∫ 0 1 ψ j ( ρ   I )   ψ i   d x )   p ¨ j − 12 η 2 { ∑ j = 1 8 [ ∫ 0 1 ψ i ( E I ′ + E ′ I ) ψ j ′     d x ] p j } − 12 { η 2 ∑ j = 1 8 [ ∫ 0 1 ψ i ( E I ) ψ j ″     d x ] p j } + 144 K s [ η 3 ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ A ) φ j ′     d x )   q j + η 4 ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ A ) ψ j     d x )   p j ] − 36 { η 2 ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ ′ A l s 2 + μ A ′ l s 2 + 2 μ A l s l s ′ ) ψ j ′     d x )   p j − η ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ ′ A l s 2 + μ A ′ l s 2 + 2 μ A l s l s ′ ) φ j ′ ′       d x )   q j } − 36 { η 2 ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ A l s 2 ) ψ j ″       d x )   p j − η ∑ j = 1 8 ( ∫ 0 1 ψ i ( μ A l s 2 ) φ j ‴         d x )   q j } + c r ∑ j = 1 8 ( ∫ 0 1 ψ i ψ j     d x )   q ˙ j = 0 ,                                               i = 1 ,   2 ,   … ,   8 ,
Employing a 24 DOF model (with equal dimensions for each motion) ensures converged results. The pseudo-arclength continuation method is used for numerical simulations.

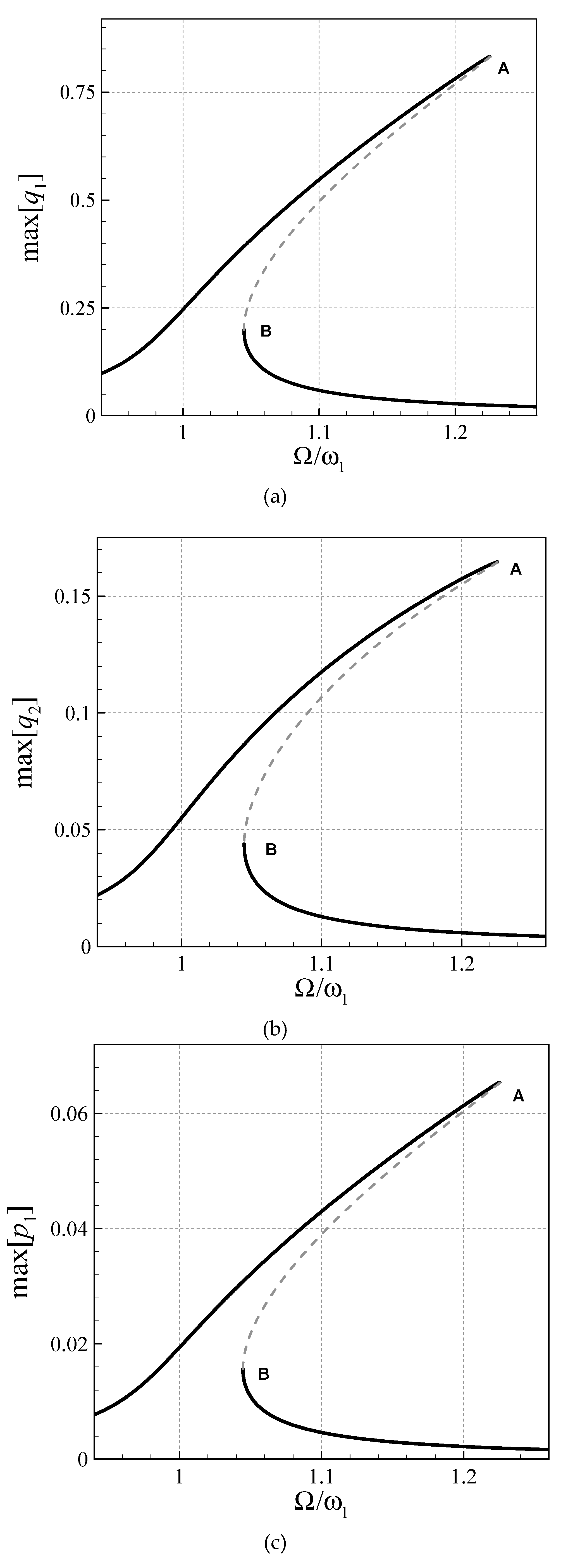
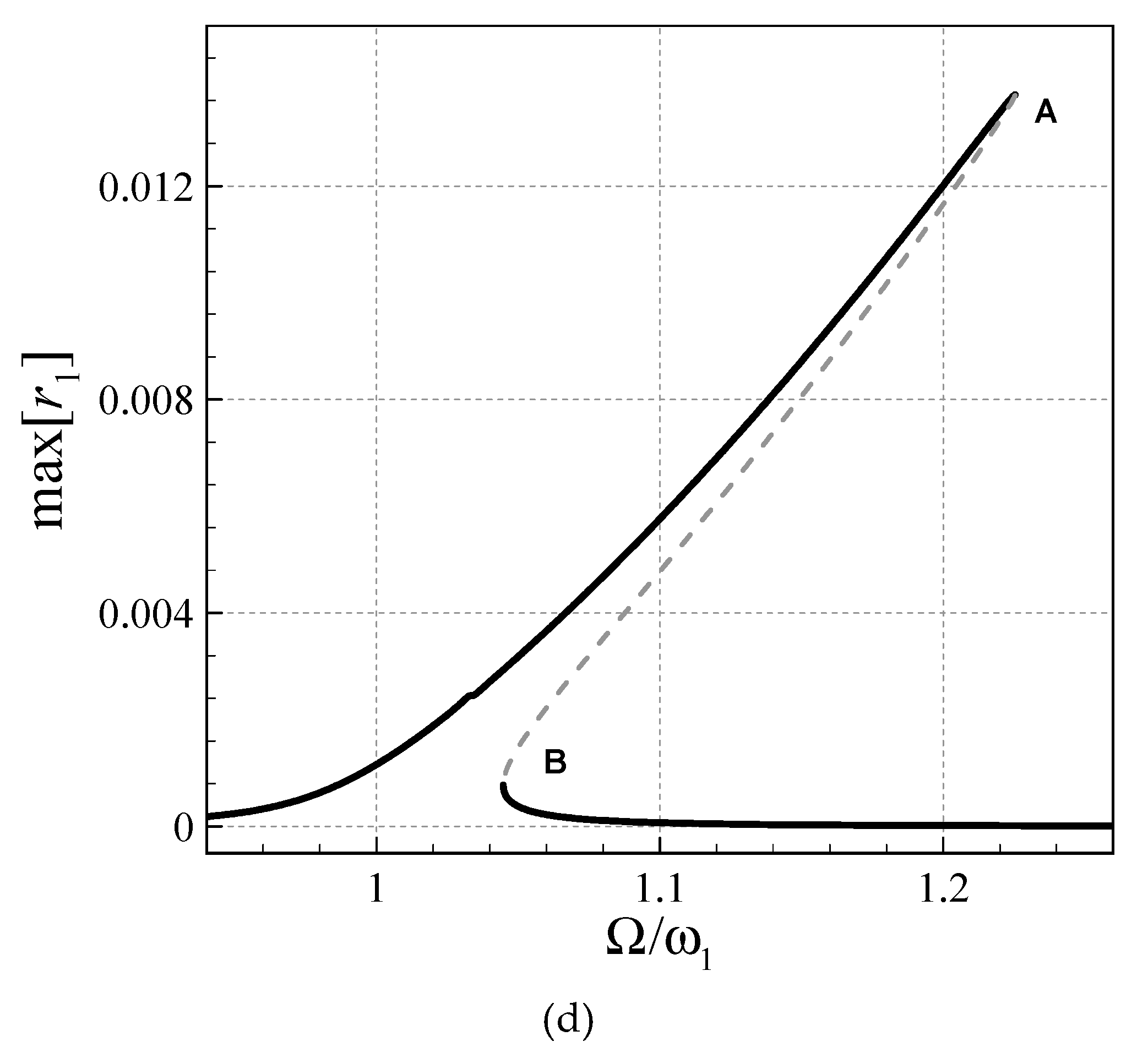
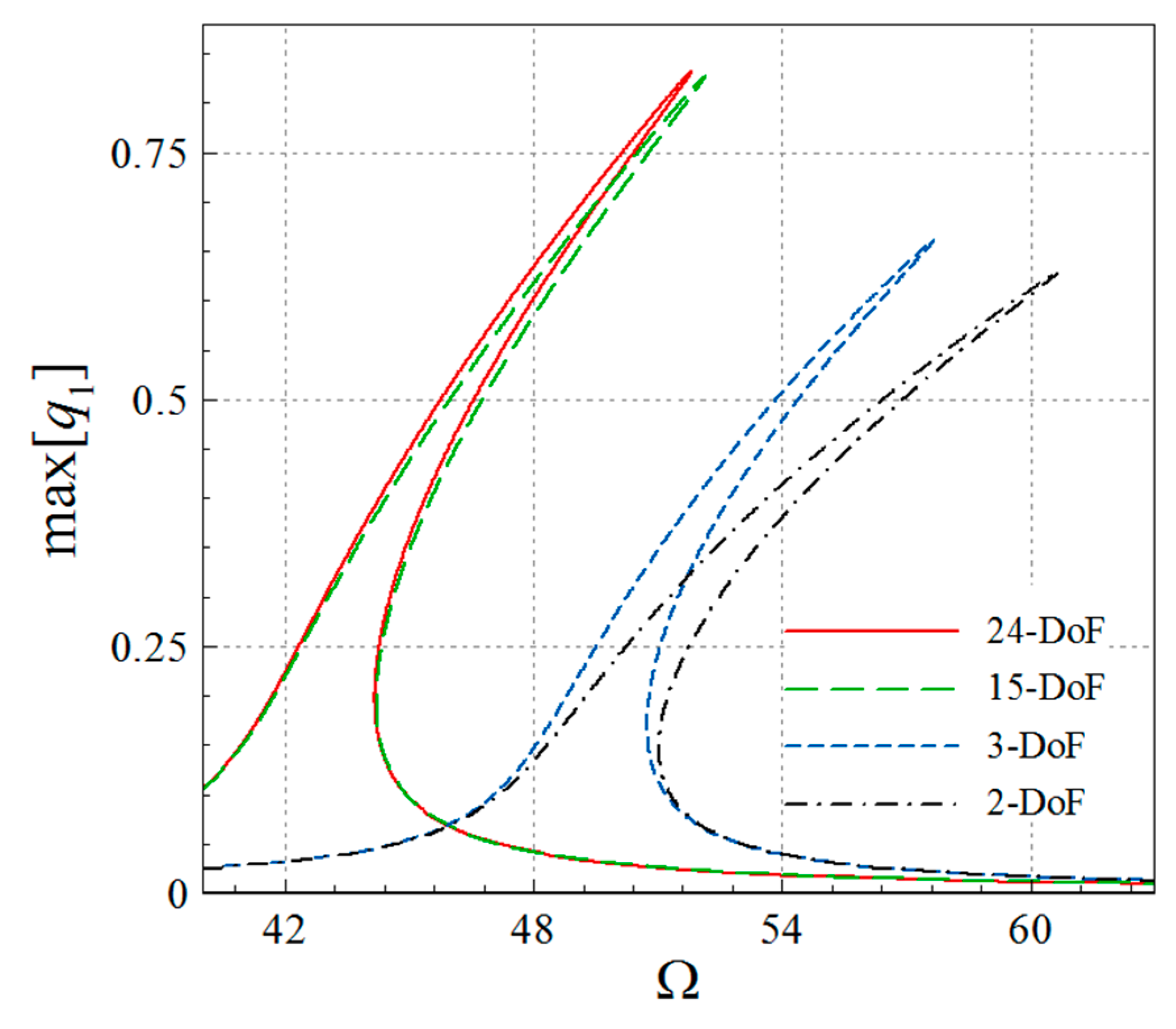
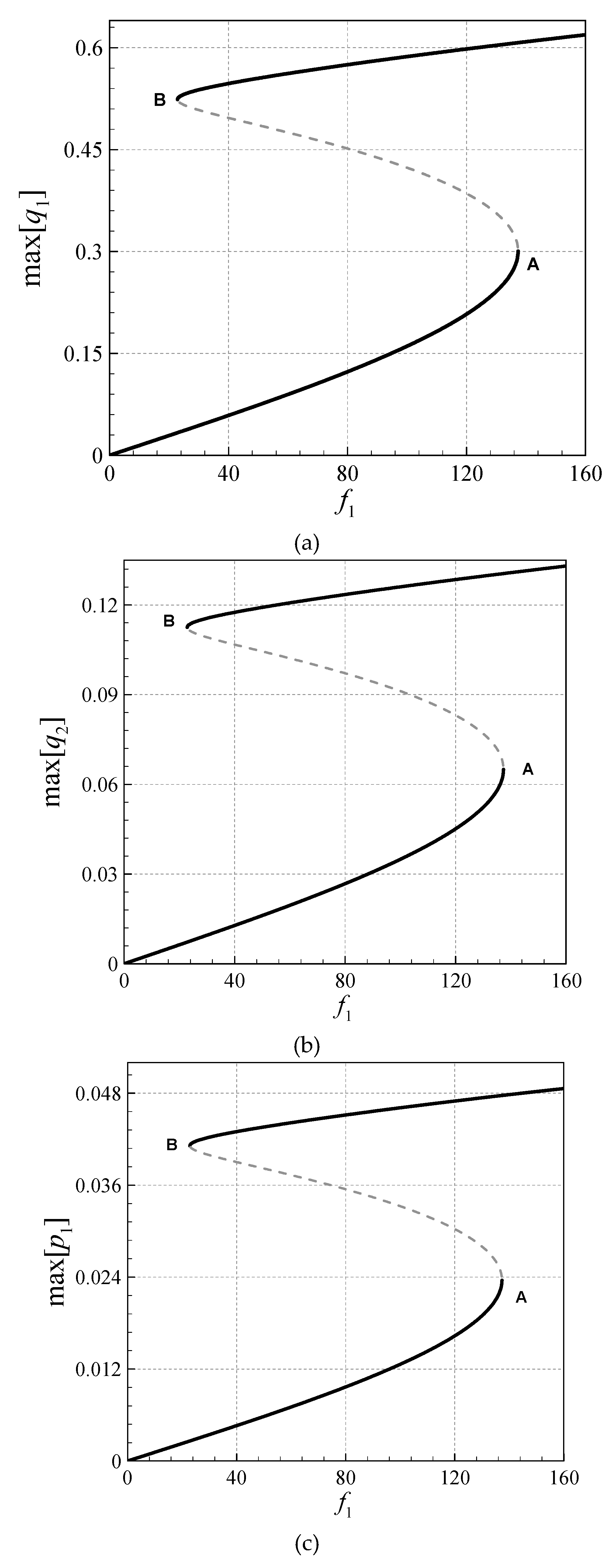
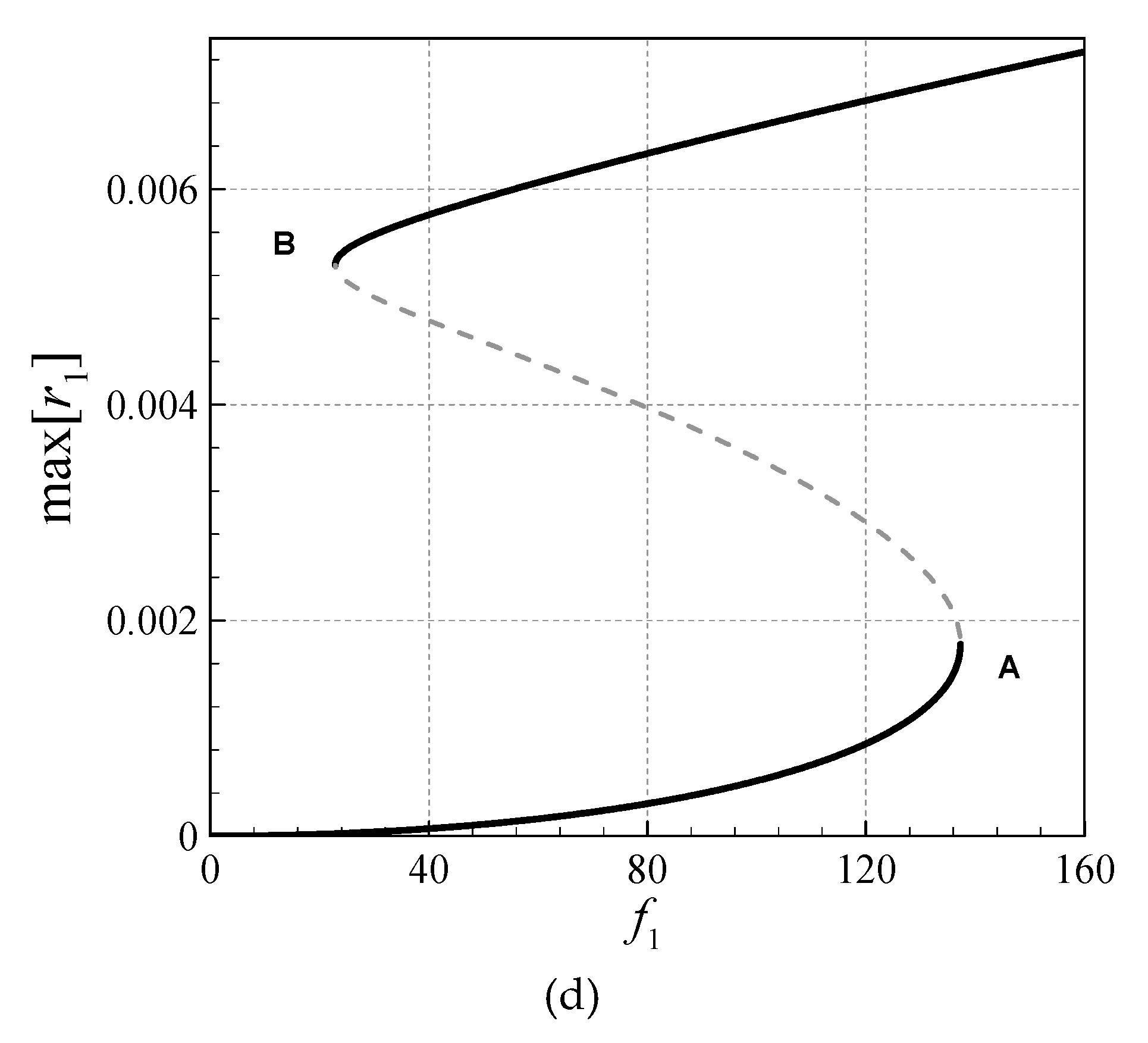
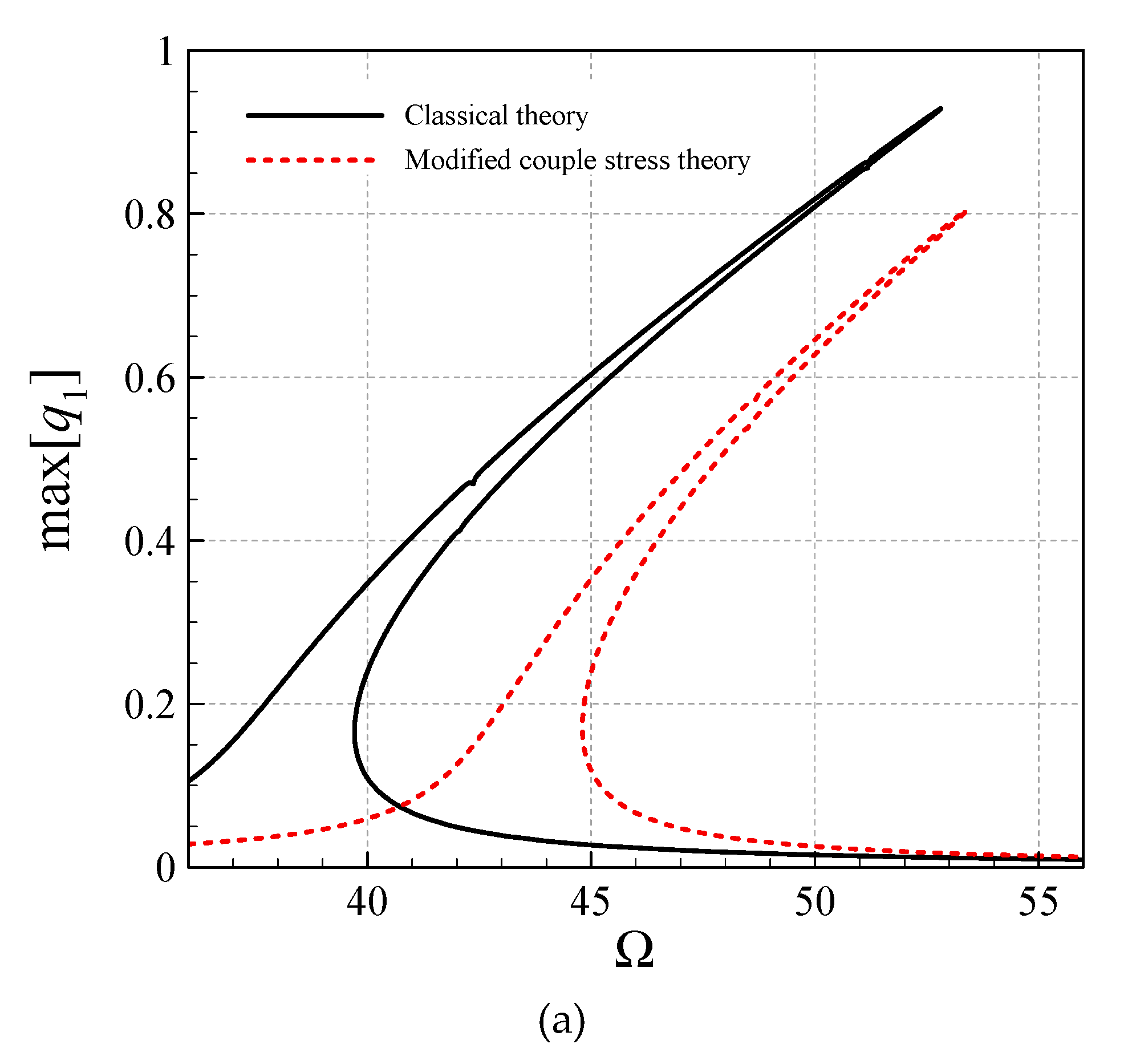
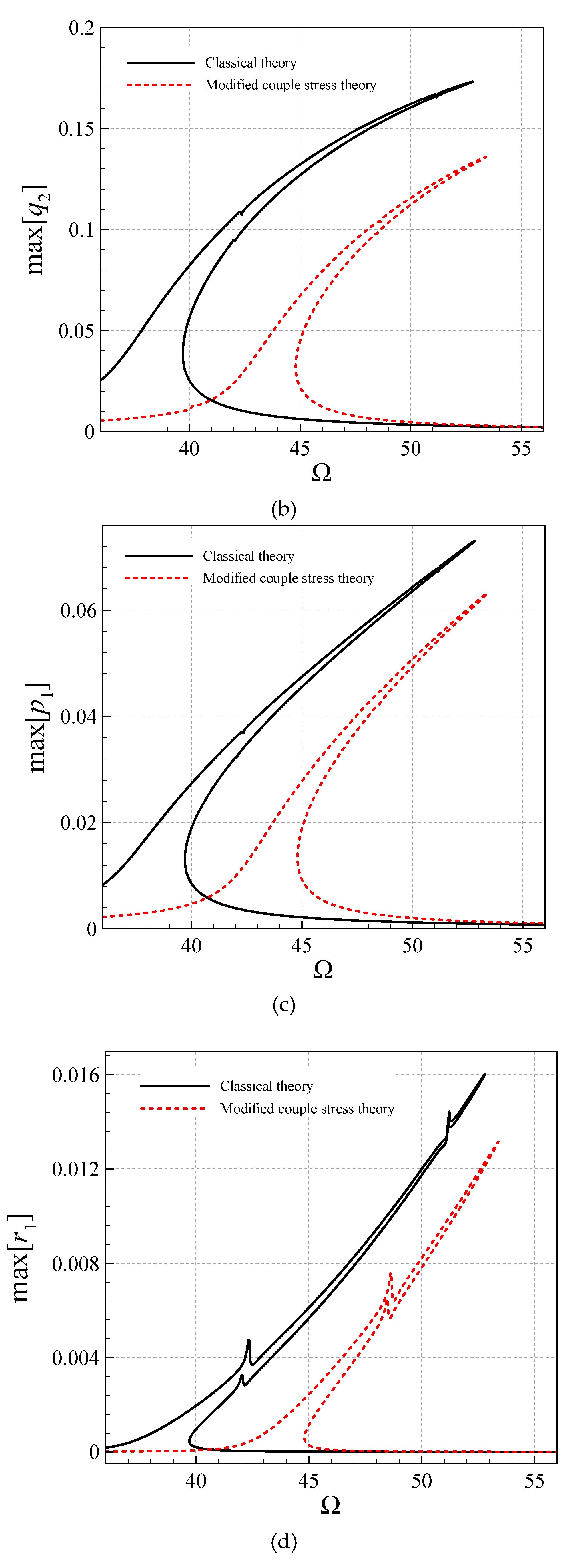
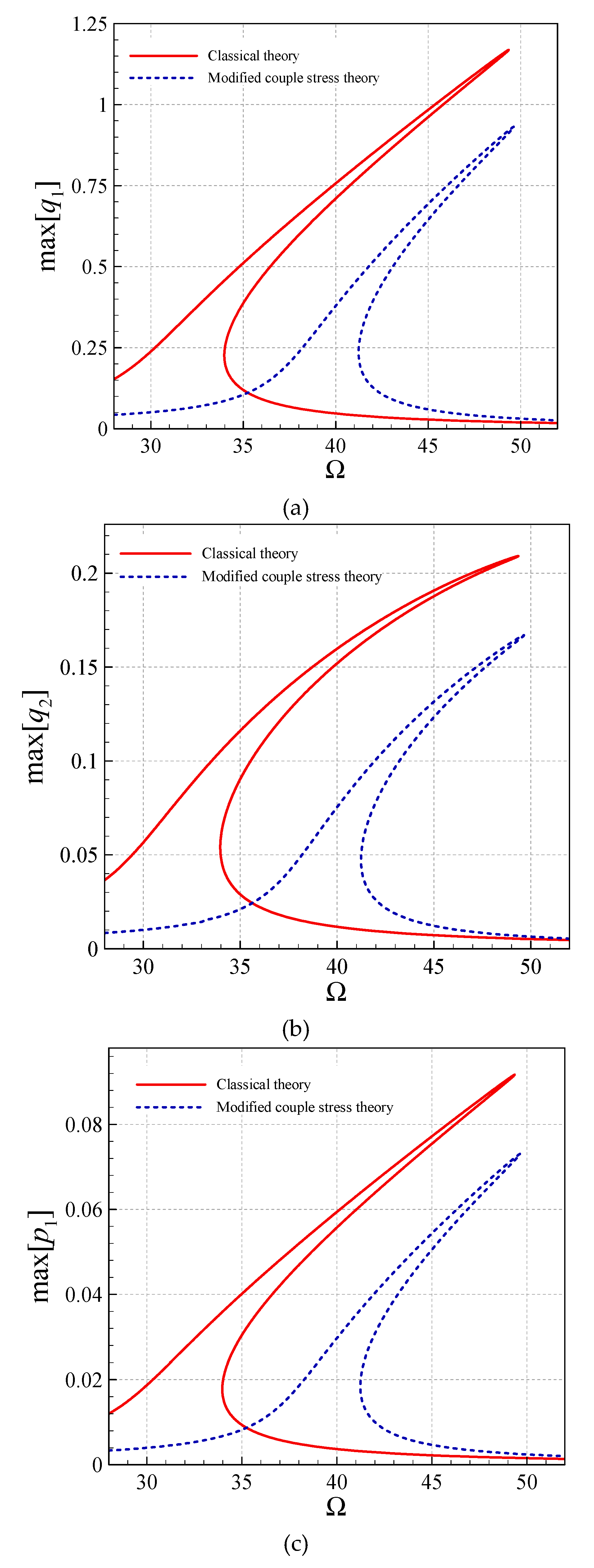
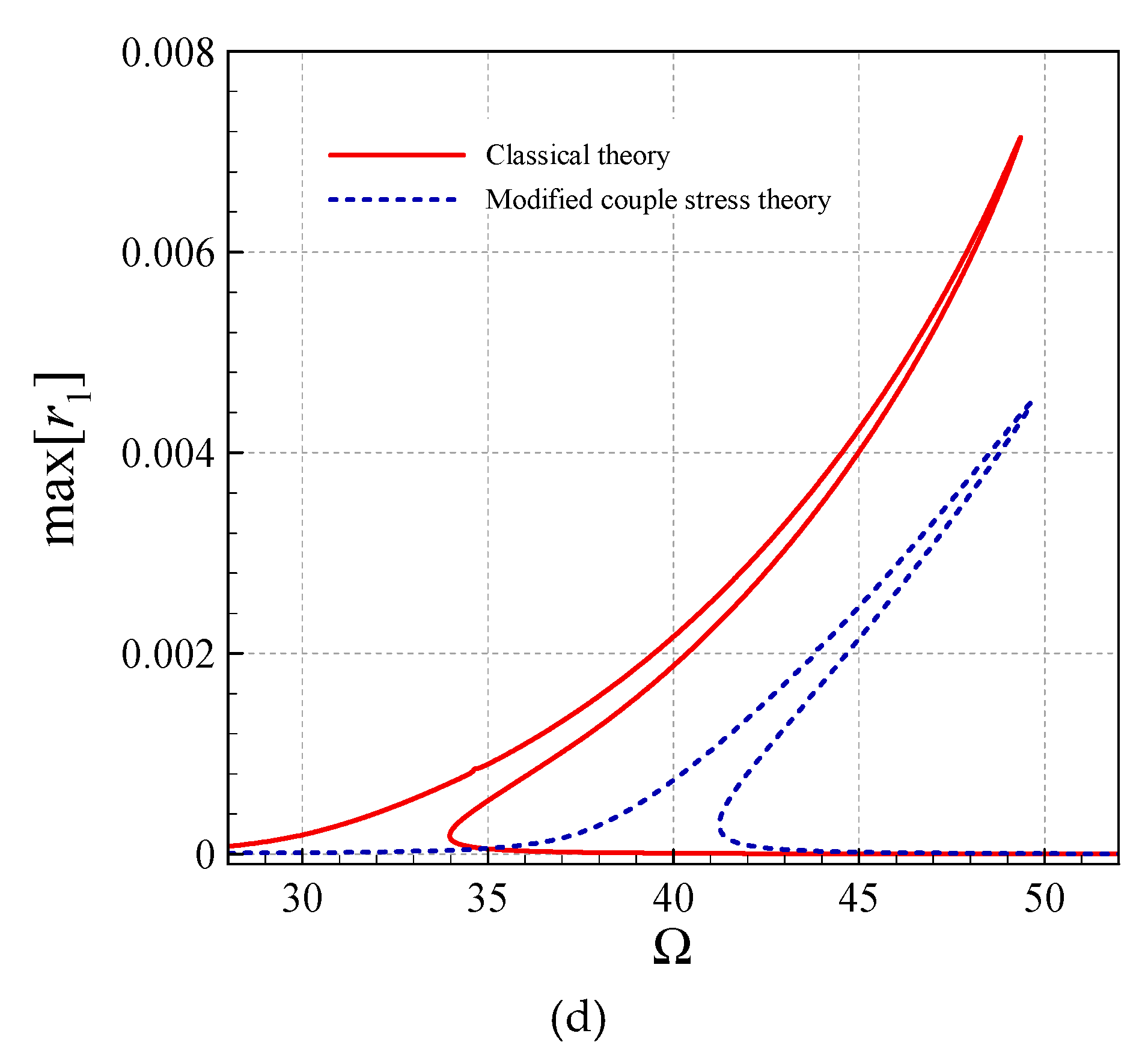
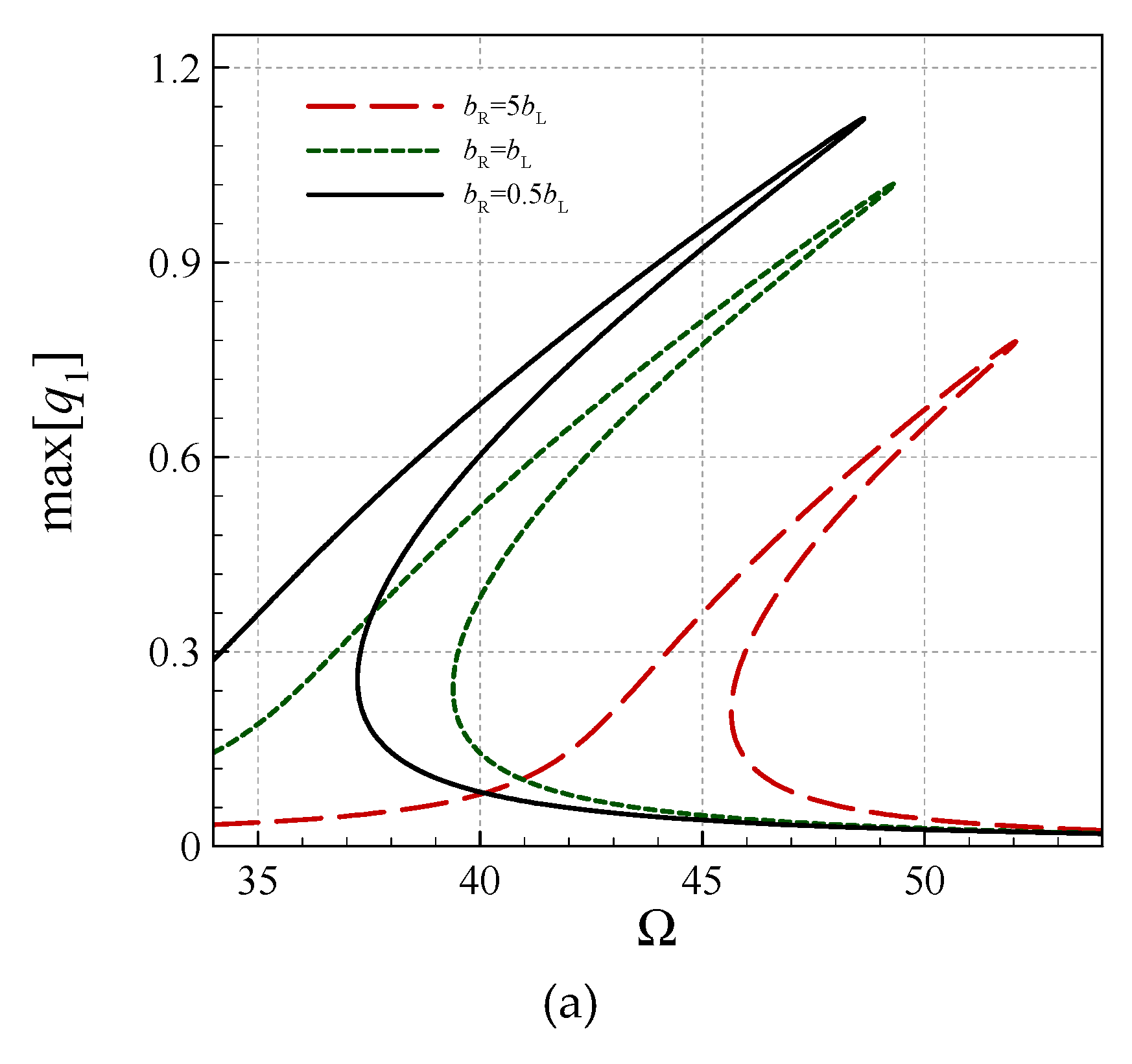
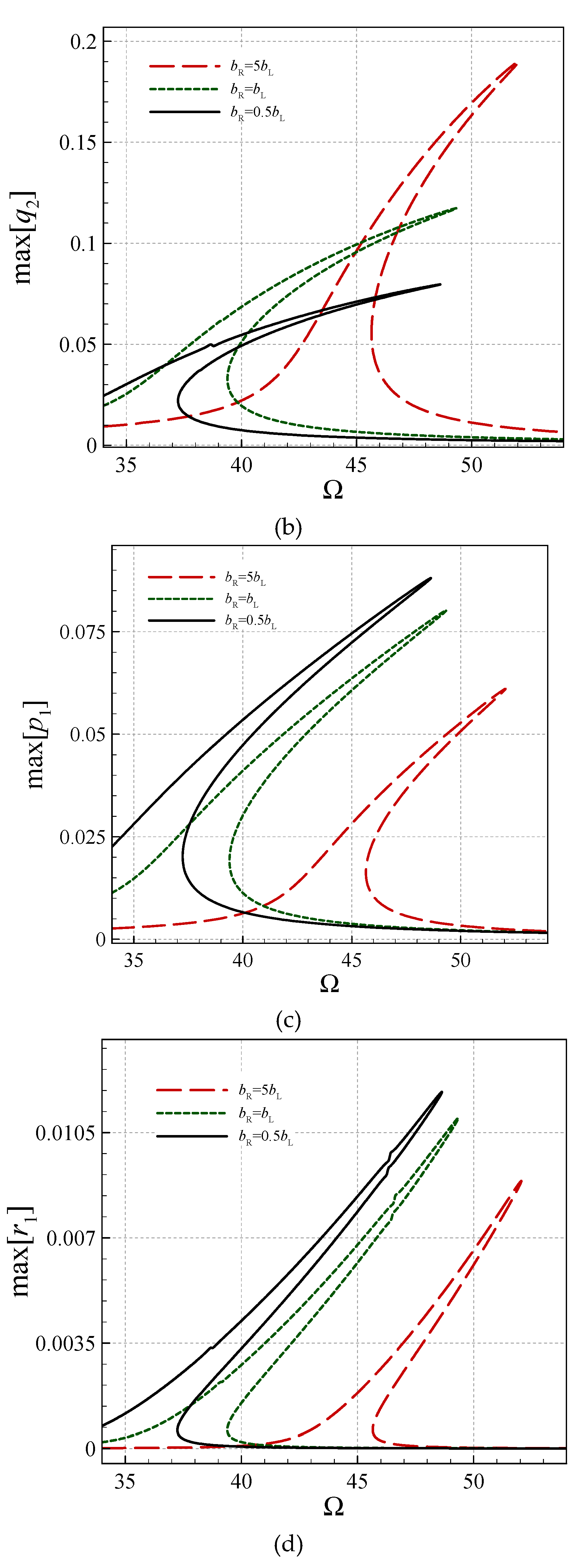
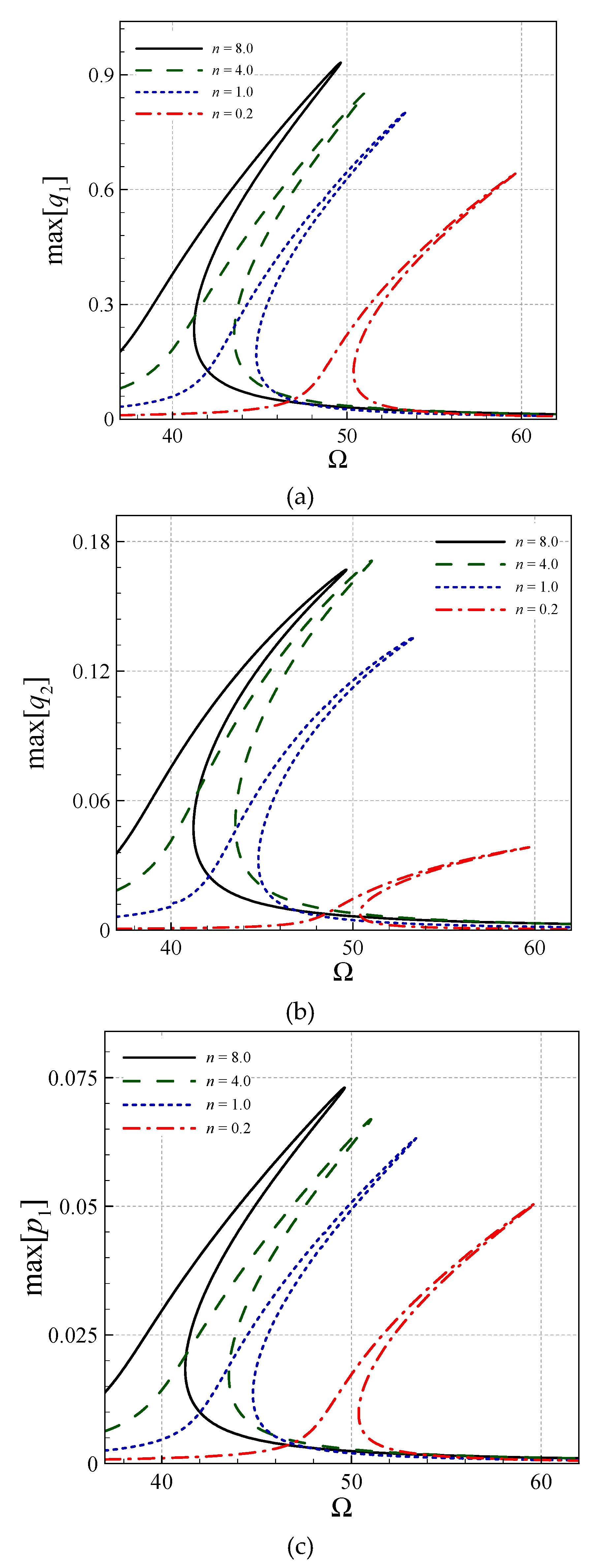
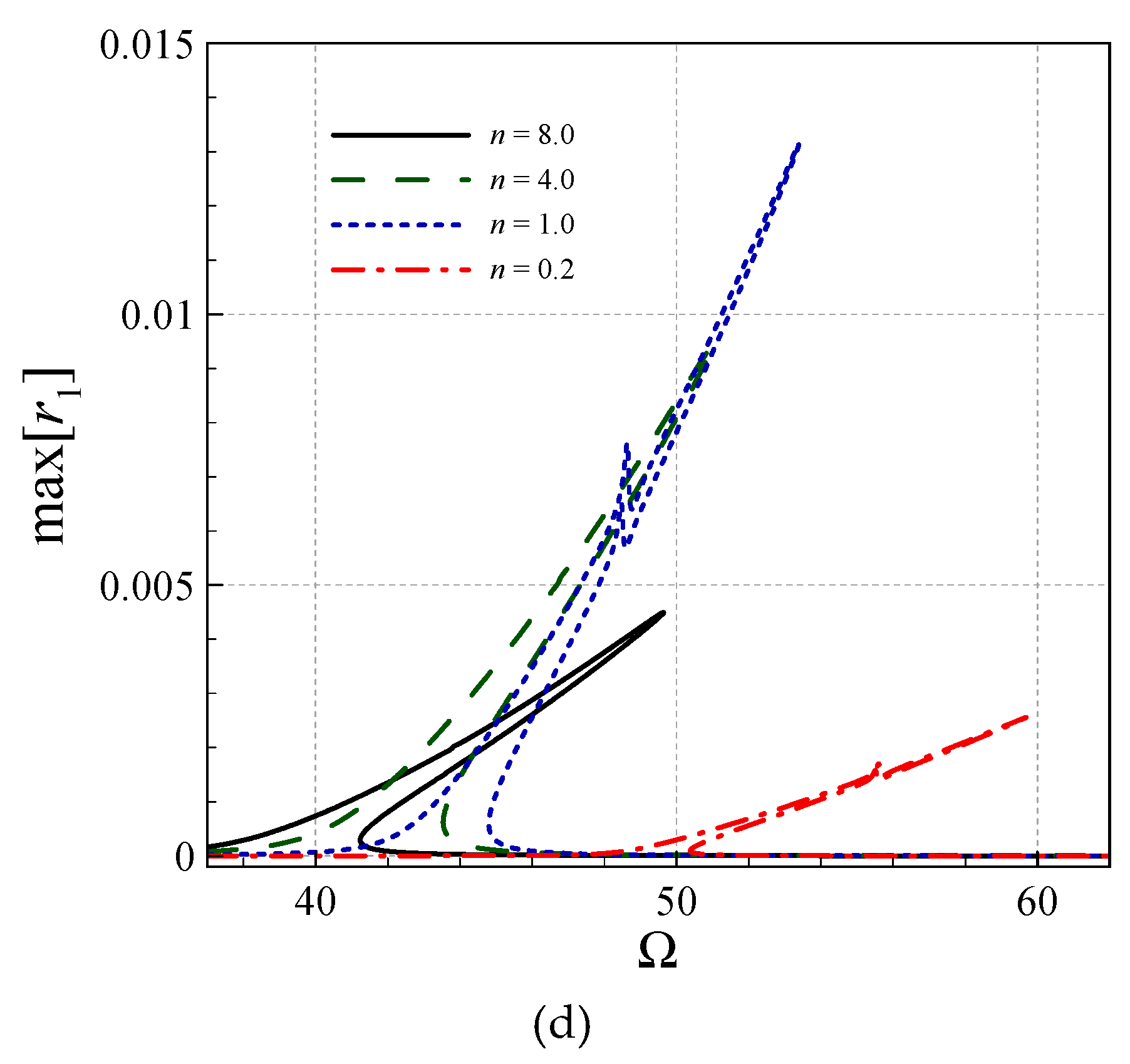
4. Asymmetric Size-Dependent Vibrations

Consider an AFG microscale nonuniform Timoshenko beam with [h = hR = hL= 2 μm; lR = 0.2 μm; lL = 0.8 μm; L/h = 60; bL/h = 1; bR/h = 3]; a modal damping ratio of ζ=0.009 is used throughout; ζ is defined as the ratio of damping coefficient (c) to critical damping coefficient (ccr). The AFG microsystem is made of Aluminium at the left end and ceramics (SiC) at the right end; [ρL = 2700 kg/m3; EL = 69 GPa; νL = 0.33], and [ρR = 3100 kg/m3; ER = 427 GPa; νR = 0.17]; Ks =5/6. These values have been used unless otherwise stated.
Figure 2 shows the asymmetric and symmetric vibrations (in frequency diagrams) where ω1 = 42.2806. The asymmetry in material distribution and nonuniform geometry give rise to asymmetric modes of vibration. The peak amplitude in the q1 motion is almost 5 times that of the q2 motion; the contribution of the q2 motion is quite strong. The motion (in all the symmetric/asymmetric modes) is hardening with two saddle-type bifurcations at Ω/ω1 = 1.2254 and 1.0447. The number of stable branches is two and that of unstable is one; as the frequency is increased, the response amplitudes in the frequency diagrams increase until hitting point A, where practically a jump occurs to a lower motion amplitude, then the asymmetric/symmetric vibration amplitudes decrease with further frequency increment. A decrease in the frequency from the upper-bound in the figure, the AFG system shows a reverse scenario characterized by an amplitude jump at point B.
A convergence test is performed to ensure the reliability of the results; the results are plotted in Figure 3. Asymmetry as well as nonlinearity in the system makes it necessary to consider high dimensions. This figure highlights that neglecting higher modes in the analysis results in both linear and nonlinear results.
The force diagrams are shown in Figure 4 for both asymmetric and symmetric vibration modes for ω1 = 42.2806. For all the symmetric and asymmetric components of axial/rotational/transverse motions, there are two bifurcations at f1 = 137.3 and 22.9, representing the jumps. For sufficiently small forces, the vibration motion is stable with increasing asymmetric/symmetric for larger forces; this scenario is violated when hitting point A, where mathematically speaking, there is a jump for both asymmetric/symmetric modes; bifurcation point B plays the same role but for decreasing forces when there is a reverse sweep.
Figure 5 and Figure 6 highlight the importance of employing the modified CST, for n = 1.0 and 8.0 (i.e., for a linear and nonlinear material and width variations, respectively), respectively. For both the gradient indices, a reduction in the peak amplitude is observed according to the modified CST for all the asymmetric and symmetric motions owing to the fact that at microscales, the structural stiffness is increased when the modified CST is utilized; a shift to the right is also observed, which shows the effect of the MCS theory in the linear regime. In addition, capturing scale influences leads to an increase in the frequency parameter of AFG microbeam since scale influences associated with couple stresses increase the structural stiffness at microscales. Size effects are very significant at nanoscales and microscales [91,92,93,94,95,96,97,98]. A comparison between Figure 5 and Figure 6 reveals that, in the presence of a larger gradient index, the size-dependence is more significant. The nature of hardening nonlinearity remains the same for both the theories and for both the asymmetric/symmetric vibration modes.
The taper ratio effect on the frequency diagrams is highlighted in Figure 7; the motion is hardening for all the cases. The largest peak amplitude is for the ratio of 0.5. The asymmetric transverse mode is weakened as the taper ratio is decreased. The larger the taper ratio is (i.e., the right end is thicker than that of the left end), the linear natural frequency increases and the transverse fundamental nonlinear peak-amplitude decreases; nevertheless, this is reverse for the secondary transverse mode. Moreover, the asymmetric axial mode and the rotation follow the scenario of the fundamental transverse mode.
Figure 8 shows that how the gradient index alters the coupled frequency diagrams. In the symmetric transverse modes, increasing n increases the peak-amplitude; the same-scenario happens for the symmetric rotation. Moreover, increasing the gradient index decreases the natural frequency in both the linear and nonlinear regimes for the transverse and rotation motions; this is not necessarily valid for the axial motion in the nonlinear regime.

5. Concluding Remarks

This study aimed at conducting an analysis on the nonlinear asymmetric vibrations of AFG microscale nonuniform Timoshenko beams. All the asymmetric and symmetric components of the coupled transverse/rotational/longitudinal motion (displacement/velocity/acceleration) were retained in the analysis. The modified CST is used to incorporate size dependence. Beam’s width and material properties were assumed to be functions of the axial coordinate. An energy method was utilized for the coupled equations. Galerkin’s method was applied and the resultant high-dimensional system was integrated numerically. From the numerical results, the following new findings were concluded:
  • Asymmetry and stretching-type nonlinearity in the AFG microsystem cause necessity for a high DOF analysis.
  • The size effect is more significant for larger gradient indices.
  • For larger gradient indices, the symmetric transverse and rotational-mode peak-amplitudes are larger.
  • All the asymmetric and symmetric modes in the coupled transverse/axial/rotational motion display hardening motions.
  • The modified CST, in all the asymmetric and symmetric modes, reduces the peak-amplitude and shifts the frequency diagrams to the right.

Author Contributions

Conceptualization, M.H.G.; Methodology, A.F., H.F. and M.H.G.; Software, H.F. and M.H.G.; Writing–Original Draft Preparation, A.F. and M.H.G.; Writing–Review & Editing, M.H.G.; Supervision, M.H.G. and H.F.

Funding

This research received no funding.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Tophøj, L.; Grathwol, N.; Hansen, S.O. Effective mass of tuned mass dampers. Vibration 2018, 1, 192–206. [Google Scholar] [CrossRef]
  2. Zaghari, B.; Rustighi, E.; Ghandchi-Tehrani, M. Improved modelling of a nonlinear parametrically excited system with electromagnetic excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
  3. Martínez-Ayuso, G.; Haddad Khodaparast, H.; Zhang, Y.; Bowen, C.R.; Friswell, M.I.; Shaw, A.D.; Madinei, H. Model validation of a porous piezoelectric energy harvester using vibration test data. Vibration 2018, 1, 123–137. [Google Scholar] [CrossRef]
  4. Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.F.; Sáez, A. Motion-based design of passive damping devices to mitigate wind-induced vibrations in stay cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef]
  5. Farokhi, H.; Ghayesh, M.H. Nonlinear mechanics of electrically actuated microplates. Int. J. Eng. Sci. 2018, 123, 197–213. [Google Scholar] [CrossRef]
  6. Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent electro-elasto-mechanics of MEMS with initially curved deformable electrodes. Int. J. Mech. Sci. 2015, 103, 247–264. [Google Scholar] [CrossRef]
  7. Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear behaviour of electrically actuated MEMS resonators. Int. J. Eng. Sci. 2013, 71, 137–155. [Google Scholar] [CrossRef]
  8. Bognash, M.; Asokanthan, S.F. Stochastic stability of a class of mems-based vibratory gyroscopes under input rate fluctuations. Vibration 2018, 1, 69–80. [Google Scholar] [CrossRef]
  9. Ghayesh, M.H.; Farokhi, H. Bistable nonlinear response of MEMS resonators. Nonlinear Dyn. 2017, 90, 1627–1645. [Google Scholar] [CrossRef]
  10. Farokhi, H.; Ghayesh, M.H.; Hussain, S. Pull-in characteristics of electrically actuated MEMS arches. Mech. Mach. Theory 2016, 98, 133–150. [Google Scholar] [CrossRef]
  11. Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
  12. Shen, H.S.; Wang, Z.X. Nonlinear analysis of shear deformable fgm beams resting on elastic foundations in thermal environments. Int. J. Mech. Sci. 2014, 81, 195–206. [Google Scholar] [CrossRef]
  13. Li, Y.; Meguid, S.A.; Fu, Y.; Xu, D. Nonlinear analysis of thermally and electrically actuated functionally graded material microbeam. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2013, 470, 20130473. [Google Scholar] [CrossRef] [PubMed]
  14. Oskouie, M.F.; Ansari, R.; Rouhi, H. Bending analysis of functionally graded nanobeams based on the fractional nonlocal continuum theory by the variational legendre spectral collocation method. Meccanica 2018, 53, 1115–1130. [Google Scholar] [CrossRef]
  15. Huynh, T.A.; Luu, A.T.; Lee, J. Bending, buckling and free vibration analyses of functionally graded curved beams with variable curvatures using isogeometric approach. Meccanica 2017, 52, 2527–2546. [Google Scholar] [CrossRef]
  16. Yang, B.; Yang, J.; Kitipornchai, S. Thermoelastic analysis of functionally graded graphene reinforced rectangular plates based on 3D elasticity. Meccanica 2017, 52, 2275–2292. [Google Scholar] [CrossRef]
  17. Tang, Y.; Lv, X.; Yang, T. Bi-directional functionally graded beams: Asymmetric modes and nonlinear free vibration. Compos. Part B Eng. 2019, 156, 319–331. [Google Scholar] [CrossRef]
  18. Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
  19. Attia, M.A.; Abdel Rahman, A.A. On vibrations of functionally graded viscoelastic nanobeams with surface effects. Int. J. Eng. Sci. 2018, 127, 1–32. [Google Scholar] [CrossRef]
  20. Zenkour, A.M.; Radwan, A.F. Compressive study of functionally graded plates resting on winkler–pasternak foundations under various boundary conditions using hyperbolic shear deformation theory. Arch. Civ. Mech. Eng. 2018, 18, 645–658. [Google Scholar] [CrossRef]
  21. Ghayesh, M.H. Viscoelastically coupled dynamics of FG timoshenko microbeams. Microsyst. Technol. 2019, 25, 651–663. [Google Scholar] [CrossRef]
  22. Ghayesh, M.H. Mechanics of tapered AFG shear-deformable microbeams. Microsyst. Technol. 2018, 24, 1743–1754. [Google Scholar] [CrossRef]
  23. Ghayesh, M.H. Stability and bifurcation characteristics of viscoelastic microcantilevers. Microsyst. Technol. 2018, 24, 4739–4746. [Google Scholar] [CrossRef]
  24. Ghayesh, M.H.; Farajpour, A. Vibrations of shear deformable FG viscoelastic microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
  25. Ghayesh, M.H.; Farokhi, H. Parametric vibrations of imperfect timoshenko microbeams. Microsyst. Technol. 2017, 23, 4917–4929. [Google Scholar] [CrossRef]
  26. Ghayesh, M.H.; Farokhi, H. Parametric instability of microbeams in supercritical regime. Nonlinear Dyn. 2016, 83, 1171–1183. [Google Scholar] [CrossRef]
  27. Ghayesh, M.H.; Farokhi, H. Nonlinear dynamics of doubly curved shallow microshells. Nonlinear Dyn. 2018, 92, 803–814. [Google Scholar] [CrossRef]
  28. Farokhi, H.; Ghayesh, M.H. Size-dependent parametric dynamics of imperfect microbeams. Int. J. Eng. Sci. 2016, 99, 39–55. [Google Scholar] [CrossRef]
  29. Farokhi, H.; Ghayesh, M.H. On the dynamics of imperfect shear deformable microplates. Int. J. Eng. Sci. 2018, 133, 264–283. [Google Scholar] [CrossRef]
  30. Farokhi, H.; Ghayesh, M.H. Nonlinear mechanical behaviour of microshells. Int. J. Eng. Sci. 2018, 127, 127–144. [Google Scholar] [CrossRef]
  31. Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
  32. Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
  33. Rashvand, K.; Rezazadeh, G.; Mobki, H.; Ghayesh, M.H. On the size-dependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter. Int. J. Mech. Sci. 2013, 77, 333–342. [Google Scholar] [CrossRef]
  34. Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
  35. Farokhi, H.; Ghayesh, M.H. Nonlinear resonant response of imperfect extensible timoshenko microbeams. Int. J. Mech. Mater. Des. 2017, 13, 43–55. [Google Scholar] [CrossRef]
  36. Farajpour, A.; Farokhi, H.; Ghayesh, M.H.; Hussain, S. Nonlinear mechanics of nanotubes conveying fluid. Int. J. Eng. Sci. 2018, 133, 132–143. [Google Scholar] [CrossRef]
  37. Farokhi, H.; Ghayesh, M.H.; Gholipour, A. Dynamics of functionally graded micro-cantilevers. Int. J. Eng. Sci. 2017, 115, 117–130. [Google Scholar] [CrossRef]
  38. Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Motion characteristics of bilayered extensible timoshenko microbeams. Int. J. Eng. Sci. 2017, 112, 1–17. [Google Scholar] [CrossRef]
  39. Farajpour, M.; Shahidi, A.; Farajpour, A. A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Mater. Res. Express 2018, 5, 035026. [Google Scholar] [CrossRef]
  40. Farajpour, M.R.; Shahidi, A.; Farajpour, A. Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electro-magnetic field: A theoretical study. Micro Nano Lett. 2018, 13, 1627–1632. [Google Scholar] [CrossRef]
  41. Farokhi, H.; Ghayesh, M.H.; Kosasih, B.; Akaber, P. On the nonlinear resonant dynamics of timoshenko microbeams: Effects of axial load and geometric imperfection. Meccanica 2016, 51, 155–169. [Google Scholar] [CrossRef]
  42. Ghayesh, M.H.; Farokhi, H. On the viscoelastic dynamics of fluid-conveying microtubes. Int. J. Eng. Sci. 2018, 127, 186–200. [Google Scholar] [CrossRef]
  43. Ghayesh, M.H. Nonlinear size-dependent behaviour of single-walled carbon nanotubes. Appl. Phys. A 2014, 117, 1393–1399. [Google Scholar] [CrossRef]
  44. Farajpour, A.; Rastgoo, A.; Farajpour, M. Nonlinear buckling analysis of magneto-electro-elastic cnt-mt hybrid nanoshells based on the nonlocal continuum mechanics. Compos. Struct. 2017, 180, 179–191. [Google Scholar] [CrossRef]
  45. Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Global dynamics of fluid conveying nanotubes. Int. J. Eng. Sci. 2019, 135, 37–57. [Google Scholar] [CrossRef]
  46. Farajpour, M.; Shahidi, A.; Hadi, A.; Farajpour, A. Influence of initial edge displacement on the nonlinear vibration, electrical and magnetic instabilities of magneto-electro-elastic nanofilms. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
  47. Dehrouyeh-Semnani, A.M.; Bahrami, A. On size-dependent timoshenko beam element based on modified couple stress theory. Int. J. Eng. Sci. 2016, 107, 134–148. [Google Scholar] [CrossRef]
  48. Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. A timoshenko beam element based on the modified couple stress theory. Int. J. Mech. Sci. 2014, 79, 75–83. [Google Scholar] [CrossRef]
  49. Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear stability of fluid-conveying imperfect micropipes. Int. J. Eng. Sci. 2017, 120, 254–271. [Google Scholar] [CrossRef]
  50. Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear vibrations of micropipes conveying fluid. Int. J. Eng. Sci. 2017, 117, 20–33. [Google Scholar] [CrossRef]
  51. Dehrouyeh-Semnani, A.M.; Mostafaei, H.; Dehrouyeh, M.; Nikkhah-Bahrami, M. Thermal pre-and post-snap-through buckling of a geometrically imperfect doubly-clamped microbeam made of temperature-dependent functionally graded materials. Compos. Struct. 2017, 170, 122–134. [Google Scholar] [CrossRef]
  52. Kahrobaiyan, M.H.; Asghari, M.; Hoore, M.; Ahmadian, M.T. Nonlinear size-dependent forced vibrational behavior of microbeams based on a non-classical continuum theory. J. Vib. Control 2012, 18, 696–711. [Google Scholar] [CrossRef]
  53. Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. Longitudinal behavior of strain gradient bars. Int. J. Eng. Sci. 2013, 66, 44–59. [Google Scholar] [CrossRef]
  54. Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. A strain gradient timoshenko beam element: Application to MEMS. Acta Mech. 2015, 226, 505–525. [Google Scholar] [CrossRef]
  55. Farajpour, M.; Shahidi, A.; Tabataba’i-Nasab, F.; Farajpour, A. Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. Eur. Phys. J. Plus 2018, 133, 219. [Google Scholar] [CrossRef]
  56. Zhu, X.; Li, L. Closed form solution for a nonlocal strain gradient rod in tension. Int. J. Eng. Sci. 2017, 119, 16–28. [Google Scholar] [CrossRef]
  57. Li, L.; Hu, Y.; Ling, L. Wave propagation in viscoelastic single-walled carbon nanotubes with surface effect under magnetic field based on nonlocal strain gradient theory. Phys. E Low-dimens. Syst. Nanostruct. 2016, 75, 118–124. [Google Scholar] [CrossRef]
  58. Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
  59. Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
  60. Akgöz, B.; Civalek, Ö. Free vibration analysis of axially functionally graded tapered bernoulli–euler microbeams based on the modified couple stress theory. Compos. Struct. 2013, 98, 314–322. [Google Scholar] [CrossRef]
  61. Şimşek, M. Size dependent nonlinear free vibration of an axially functionally graded (AFG) microbeam using he’s variational method. Compos. Struct. 2015, 131, 207–214. [Google Scholar] [CrossRef]
  62. Shafiei, N.; Kazemi, M.; Ghadiri, M. Nonlinear vibration of axially functionally graded tapered microbeams. Int. J. Eng. Sci. 2016, 102, 12–26. [Google Scholar] [CrossRef]
  63. Ghayesh, M.H. Viscoelastic dynamics of axially fg microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
  64. Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluid. Nanofluid. 2018, 22, 72. [Google Scholar] [CrossRef]
  65. Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Application of nanotubes in conveying nanofluid: A bifurcation analysis with consideration of internal energy loss and geometrical imperfection. Microsyst. Technol. 2019. [Google Scholar] [CrossRef]
  66. Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2015, 79, 1771–1785. [Google Scholar] [CrossRef]
  67. Farokhi, H.; Ghayesh, M.H. Nonlinear dynamical behaviour of geometrically imperfect microplates based on modified couple stress theory. Int. J. Mech. Sci. 2015, 90, 133–144. [Google Scholar] [CrossRef]
  68. Ma, H.; Gao, X.-L.; Reddy, J. A microstructure-dependent timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
  69. Reddy, J. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
  70. Gholipour, A.; Ghayesh, M.H.; Zander, A.; Mahajan, R. Three-dimensional biomechanics of coronary arteries. Int. J. Eng. Sci. 2018, 130, 93–114. [Google Scholar] [CrossRef]
  71. Gholipour, A.; Ghayesh, M.H.; Zander, A. Nonlinear biomechanics of bifurcated atherosclerotic coronary arteries. Int. J. Eng. Sci. 2018, 133, 60–83. [Google Scholar] [CrossRef]
  72. Ghayesh, M.H.; Farokhi, H. Mechanics of tapered axially functionally graded shallow arches. Compos. Struct. 2018, 188, 233–241. [Google Scholar] [CrossRef]
  73. Ghayesh, M.H. Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl. Math. Model. 2018, 59, 583–596. [Google Scholar] [CrossRef]
  74. Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluid. Nanofluid. 2019, 23, 34. [Google Scholar] [CrossRef]
  75. Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect nsgt nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
  76. Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
  77. Ghayesh, M.H.; Kazemirad, S.; Reid, T. Nonlinear vibrations and stability of parametrically exited systems with cubic nonlinearities and internal boundary conditions: A general solution procedure. Appl. Math. Model. 2012, 36, 3299–3311. [Google Scholar] [CrossRef]
  78. Ghayesh, M.H.; Moradian, N. Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 2011, 81, 781–799. [Google Scholar] [CrossRef]
  79. Ghayesh, M.H. Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. Int. J. Mech. Sci. 2018, 140, 339–350. [Google Scholar] [CrossRef]
  80. Ghayesh, M.H.; Farokhi, H. Chaotic motion of a parametrically excited microbeam. Int. J. Eng. Sci. 2015, 96, 34–45. [Google Scholar] [CrossRef]
  81. Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
  82. Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
  83. Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
  84. Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear bending and forced vibrations of axially functionally graded tapered microbeams. Int. J. Eng. Sci. 2017, 120, 51–62. [Google Scholar] [CrossRef]
  85. Farokhi, H.; Ghayesh, M.H. Size-dependent behaviour of electrically actuated microcantilever-based mems. Int. J. Mech. Mater. Des. 2016, 12, 301–315. [Google Scholar] [CrossRef]
  86. Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. On the nonlinear mechanics of layered microcantilevers. Int. J. Eng. Sci. 2017, 120, 1–14. [Google Scholar] [CrossRef]
  87. Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear oscillations of viscoelastic microplates. Int. J. Eng. Sci. 2017, 118, 56–69. [Google Scholar] [CrossRef]
  88. Ghayesh, M.H. Dynamics of functionally graded viscoelastic microbeams. Int. J. Eng. Sci. 2018, 124, 115–131. [Google Scholar] [CrossRef]
  89. Farokhi, H.; Ghayesh, M.H. Supercritical nonlinear parametric dynamics of timoshenko microbeams. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 592–605. [Google Scholar] [CrossRef]
  90. Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear resonant behavior of microbeams over the buckled state. Appl. Phys. A 2013, 113, 297–307. [Google Scholar] [CrossRef]
  91. Farajpour, A.; Farokhi, H.; Ghayesh, M.H. Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. Eur. J. Mech. A/Solids 2019, 74, 281–296. [Google Scholar] [CrossRef]
  92. Ghayesh, M.H.; Farokhi, H. Nonlinear dynamics of microplates. Int. J. Eng. Sci. 2015, 86, 60–73. [Google Scholar] [CrossRef]
  93. Farokhi, H.; Ghayesh, M.H. Thermo-mechanical dynamics of perfect and imperfect timoshenko microbeams. Int. J. Eng. Sci. 2015, 91, 12–33. [Google Scholar] [CrossRef]
  94. Farajpour, M.R.; Rastgoo, A.; Farajpour, A.; Mohammadi, M. Vibration of piezoelectric nanofilm-based electromechanical sensors via higher-order non-local strain gradient theory. Micro Nano Lett. 2016, 11, 302–307. [Google Scholar] [CrossRef]
  95. Nejad, M.Z.; Hadi, A.; Farajpour, A. Consistent couple-stress theory for free vibration analysis of euler-bernoulli nano-beams made of arbitrary bi-directional functionally graded materials. Struct. Eng. Mech. 2017, 63, 161–169. [Google Scholar]
  96. Asemi, S.R.; Farajpour, A. Vibration characteristics of double-piezoelectric-nanoplate-systems. IET Micro Nano Lett. 2014, 9, 280–285. [Google Scholar] [CrossRef]
  97. Ghayesh, M.H.; Farajpour, A. Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
  98. Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear oscillations of functionally graded microplates. Int. J. Eng. Sci. 2018, 122, 56–72. [Google Scholar] [CrossRef]
Vibration 02 00013 g001 550
Figure 1. Axially functionally graded (AFG) microscale nonuniform Timoshenko beam: (a) Side view; (b) top view.
Figure 1. Axially functionally graded (AFG) microscale nonuniform Timoshenko beam: (a) Side view; (b) top view.
Vibration 02 00013 g001
Vibration 02 00013 g002a 550Vibration 02 00013 g002b 550
Figure 2. Frequency diagrams for (a) q1, (b) q2, (c) p1 and (d) r1 (bR = 3bL, (ls)R = 0.1, f1 = 40.0, n = 2.0 (ls)L = 0.4).
Figure 2. Frequency diagrams for (a) q1, (b) q2, (c) p1 and (d) r1 (bR = 3bL, (ls)R = 0.1, f1 = 40.0, n = 2.0 (ls)L = 0.4).
Vibration 02 00013 g002aVibration 02 00013 g002b
Vibration 02 00013 g003 550
Figure 3. Frequency diagrams for different degrees of freedom (DOFs); bR = 3bL, (ls)R = 0.1, n = 2.0, f1 = 40.0, (ls)L = 0.4.
Figure 3. Frequency diagrams for different degrees of freedom (DOFs); bR = 3bL, (ls)R = 0.1, n = 2.0, f1 = 40.0, (ls)L = 0.4.
Vibration 02 00013 g003
Vibration 02 00013 g004a 550Vibration 02 00013 g004b 550
Figure 4. Force diagrams for (a) q1, (b) q2, (c) p1 and (d) r1 (bR = 3bL, (ls)R = 0.1, n = 2.0, Ω/ω1 = 1.1000, (ls)L = 0.4).
Figure 4. Force diagrams for (a) q1, (b) q2, (c) p1 and (d) r1 (bR = 3bL, (ls)R = 0.1, n = 2.0, Ω/ω1 = 1.1000, (ls)L = 0.4).
Vibration 02 00013 g004aVibration 02 00013 g004b
Vibration 02 00013 g005a 550Vibration 02 00013 g005b 550
Figure 5. Frequency diagrams for classical ((ls)L = 0.0; (ls)R = 0.0) and modified couple stress theory (CST) for (a) q1, (b) q2, (c) p1 and (d) r1; ((ls)L = 0.4; (ls)R = 0.1): f1 = 40.0, bR = 3bL, n = 1.0.
Figure 5. Frequency diagrams for classical ((ls)L = 0.0; (ls)R = 0.0) and modified couple stress theory (CST) for (a) q1, (b) q2, (c) p1 and (d) r1; ((ls)L = 0.4; (ls)R = 0.1): f1 = 40.0, bR = 3bL, n = 1.0.
Vibration 02 00013 g005aVibration 02 00013 g005b
Vibration 02 00013 g006a 550Vibration 02 00013 g006b 550
Figure 6. Frequency diagrams for classical ((ls)R = 0.0; (ls)L = 0.0) and modified CST ((ls)R = 0.1; (ls)L = 0.4) for (a) q1, (b) q2, (c) p1 and (d) r1; f1 = 40.0, bR = 3bL, n = 8.0.
Figure 6. Frequency diagrams for classical ((ls)R = 0.0; (ls)L = 0.0) and modified CST ((ls)R = 0.1; (ls)L = 0.4) for (a) q1, (b) q2, (c) p1 and (d) r1; f1 = 40.0, bR = 3bL, n = 8.0.
Vibration 02 00013 g006aVibration 02 00013 g006b
Vibration 02 00013 g007a 550Vibration 02 00013 g007b 550
Figure 7. Frequency diagrams for different tapered status and for (a) q1, (b) q2, (c) p1 and (d) r1; n = 4.0, (ls)R = 0.1, (ls)L = 0.4, f1 = 40.0.
Figure 7. Frequency diagrams for different tapered status and for (a) q1, (b) q2, (c) p1 and (d) r1; n = 4.0, (ls)R = 0.1, (ls)L = 0.4, f1 = 40.0.
Vibration 02 00013 g007aVibration 02 00013 g007b
Vibration 02 00013 g008a 550Vibration 02 00013 g008b 550
Figure 8. Frequency diagrams for different n and for (a) q1, (b) q2, (c) p1 and (d) r1; bR = 3bL, f1 = 40.0, (ls)R = 0.1, (ls)L = 0.4.
Figure 8. Frequency diagrams for different n and for (a) q1, (b) q2, (c) p1 and (d) r1; bR = 3bL, f1 = 40.0, (ls)R = 0.1, (ls)L = 0.4.
Vibration 02 00013 g008aVibration 02 00013 g008b

Share and Cite

MDPI and ACS Style

Ghayesh, M.H.; Farajpour, A.; Farokhi, H. Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams. Vibration 2019, 2, 201-221. https://doi.org/10.3390/vibration2020013

AMA Style

Ghayesh MH, Farajpour A, Farokhi H. Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams. Vibration. 2019; 2(2):201-221. https://doi.org/10.3390/vibration2020013

Chicago/Turabian Style

Ghayesh, Mergen H., Ali Farajpour, and Hamed Farokhi. 2019. "Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams" Vibration 2, no. 2: 201-221. https://doi.org/10.3390/vibration2020013

Article Metrics

Back to TopTop