A Realistic Approach of the Maximum Work Extraction from Solar Thermal Collectors
Abstract
:1. Introduction
2. Review up Today
2.1. Maximum Work Extraction from Solar Energy
2.2. Maximum Work Extraction Using Solar Collectors
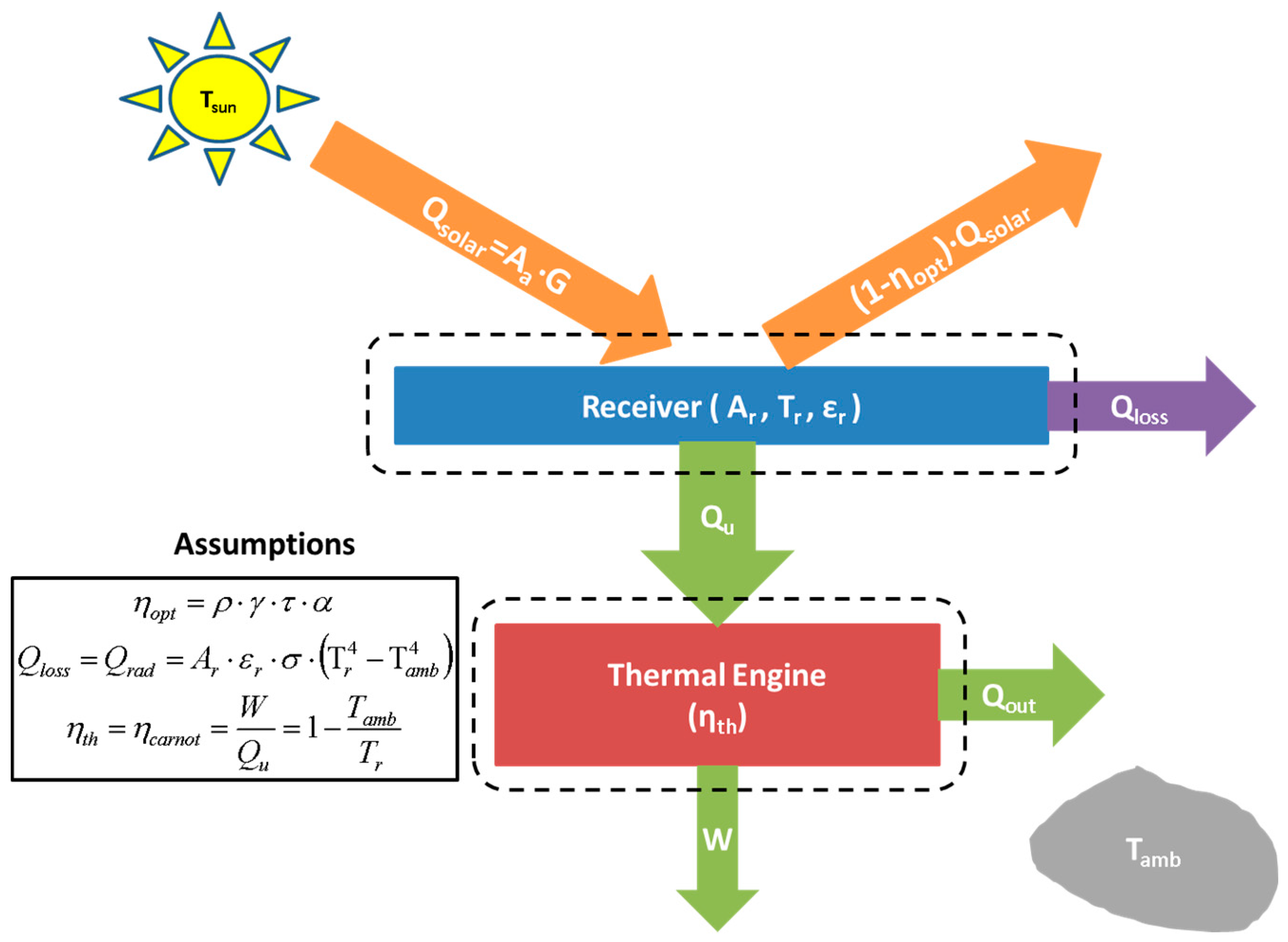
3. Suggested Model
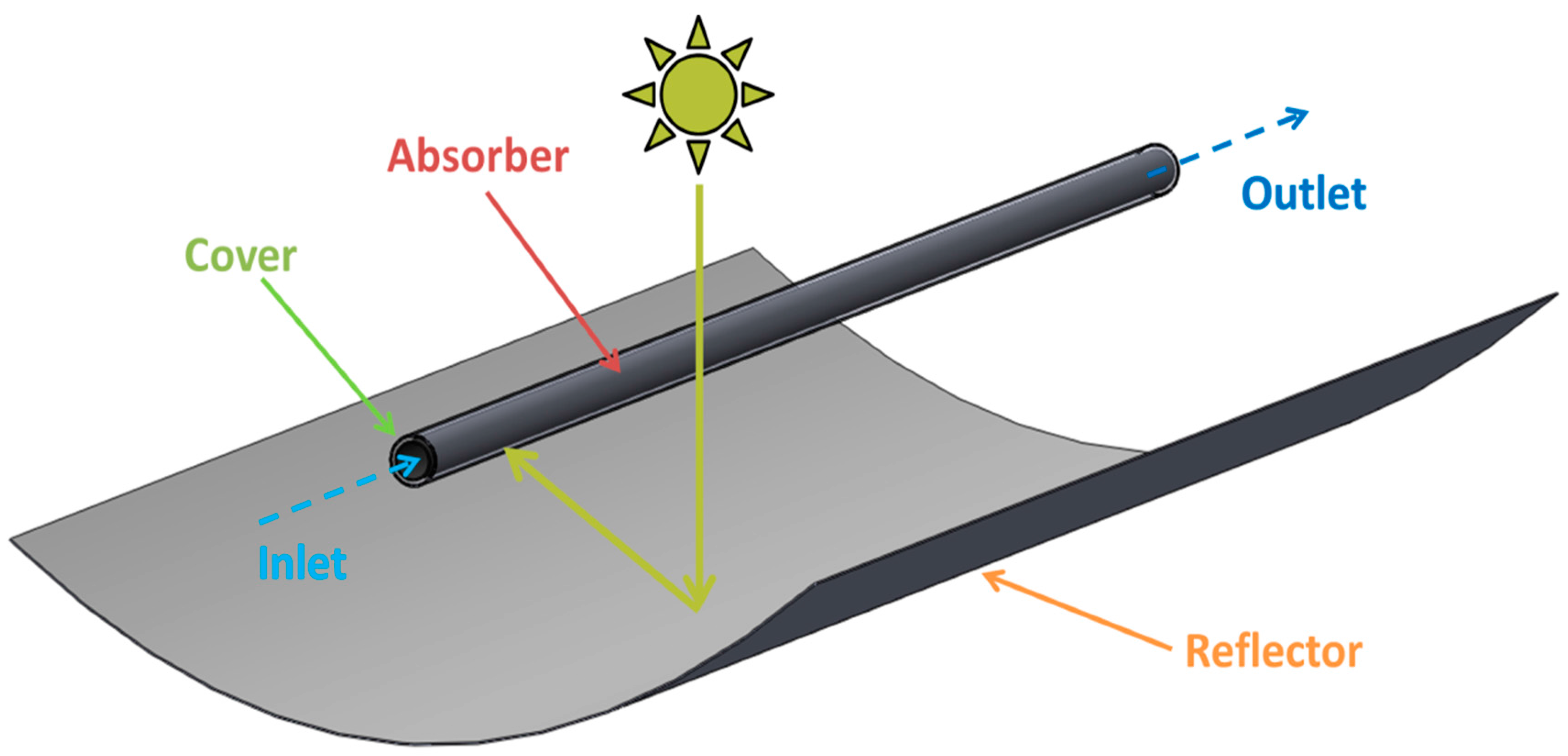
3.1. General Description
- -
- The optical efficiency of the collector (ηopt), which is the product of the receiver absorbance, the cover transmittance, the concentrator reflectance; it also includes the impact of the incident angle.
- -
- The radiation thermal losses of the receiver are taken into account using the emittance of the receiver (εr). This parameter usually takes low values (close to 0.05~0.10) for high-quality collectors. It has been assumed the collector exchanges irradiation with the ambient and not with the sky.
- -
- The solar irradiation is considered as heat and not irradiation in the model, something that is not performed in similar studies [13].
- -
- The convection losses are neglected because by using vacuum between glass cover and absorber (in parabolic trough collectors, for instance), these thermal losses become negligible. This assumption is reasonable because the present work aims to determine the maximum work extraction using a real concentrating solar collector. So, this assumption corresponds to a high quality concentrating collector. In any case, an increase in the emittance (about 0.1) can be performed in order to take into account the convection thermal losses.
3.2. Mathematical Description
3.2.1. Energy Balance in the Receiver
3.2.2. Energy Balance in the Thermal Engine
3.2.3. Total System Energy Balance
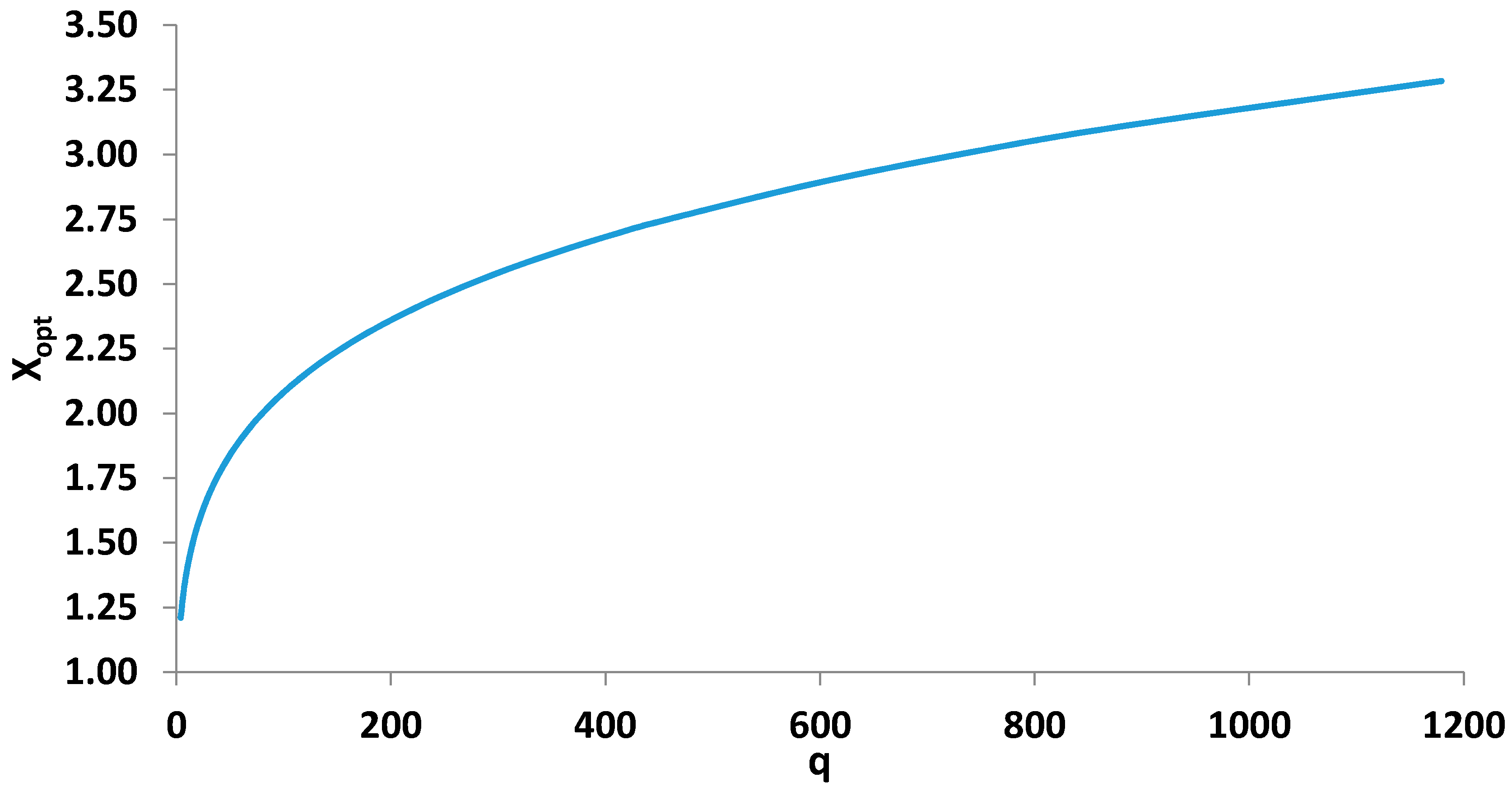
3.2.4. Optimum Operation Temperature
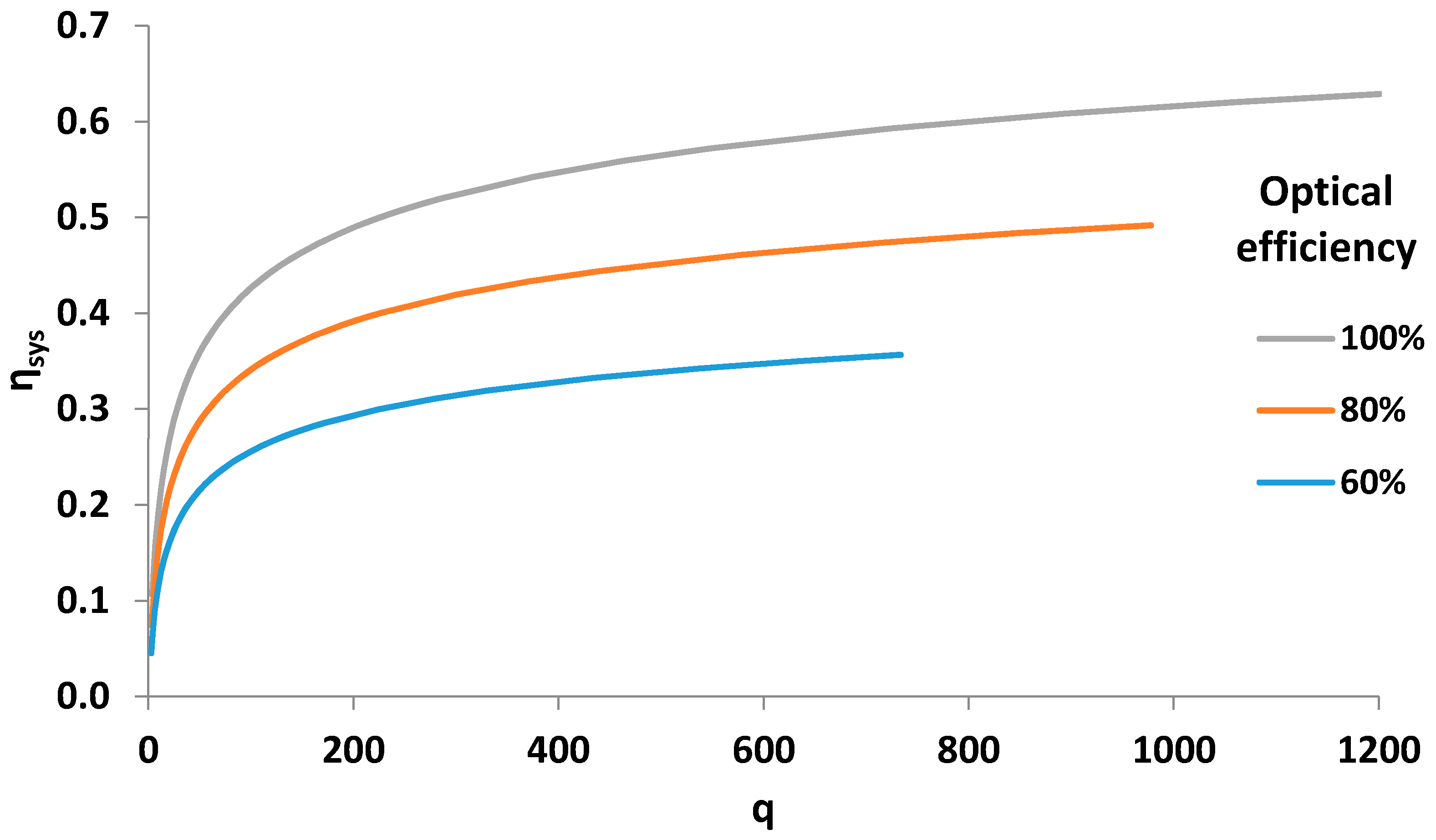
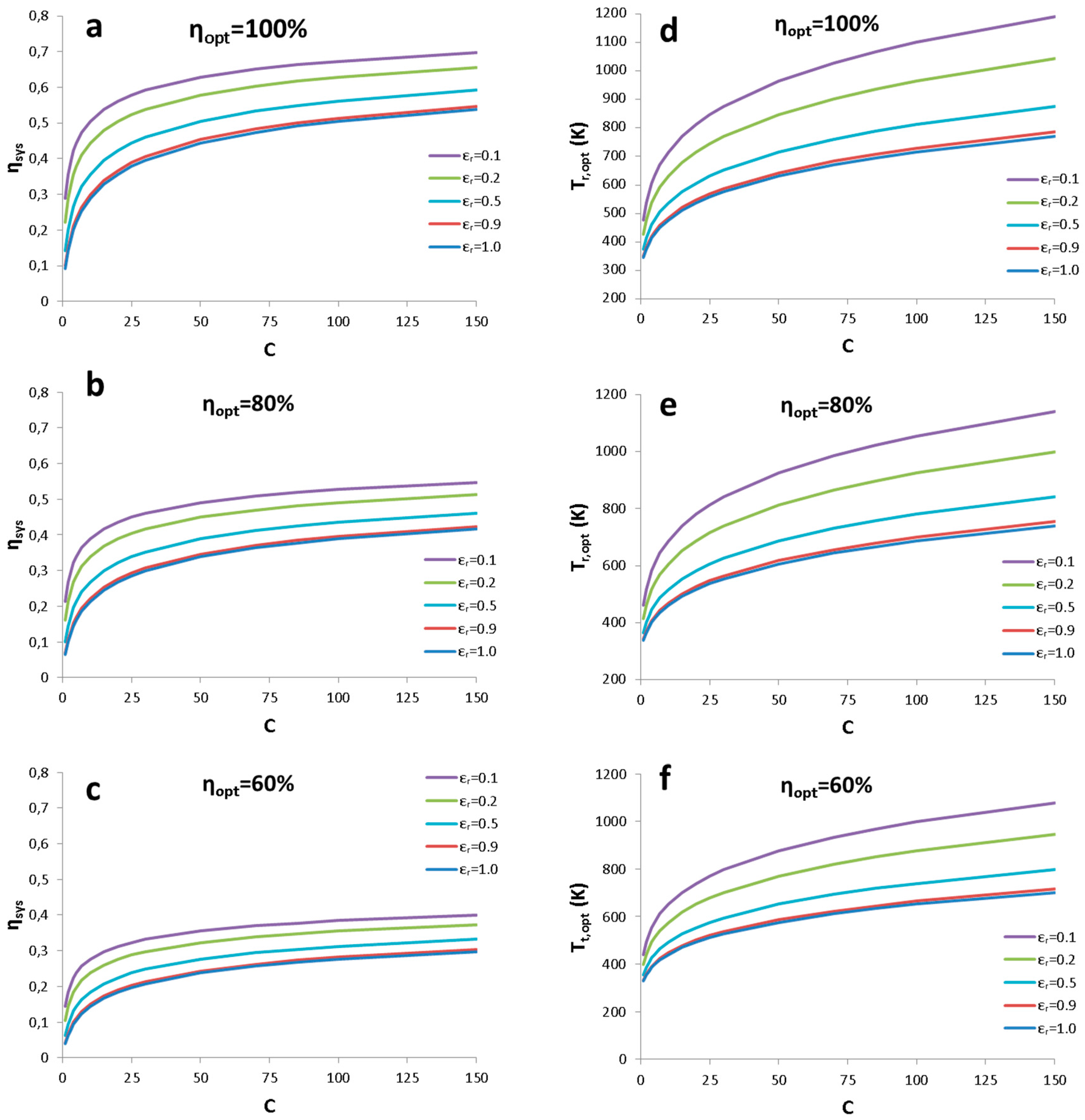
4. Results—Discussion
4.1. Solution of the Optimization Polynomial
4.2. Impact of Design Parameters in the System Performance
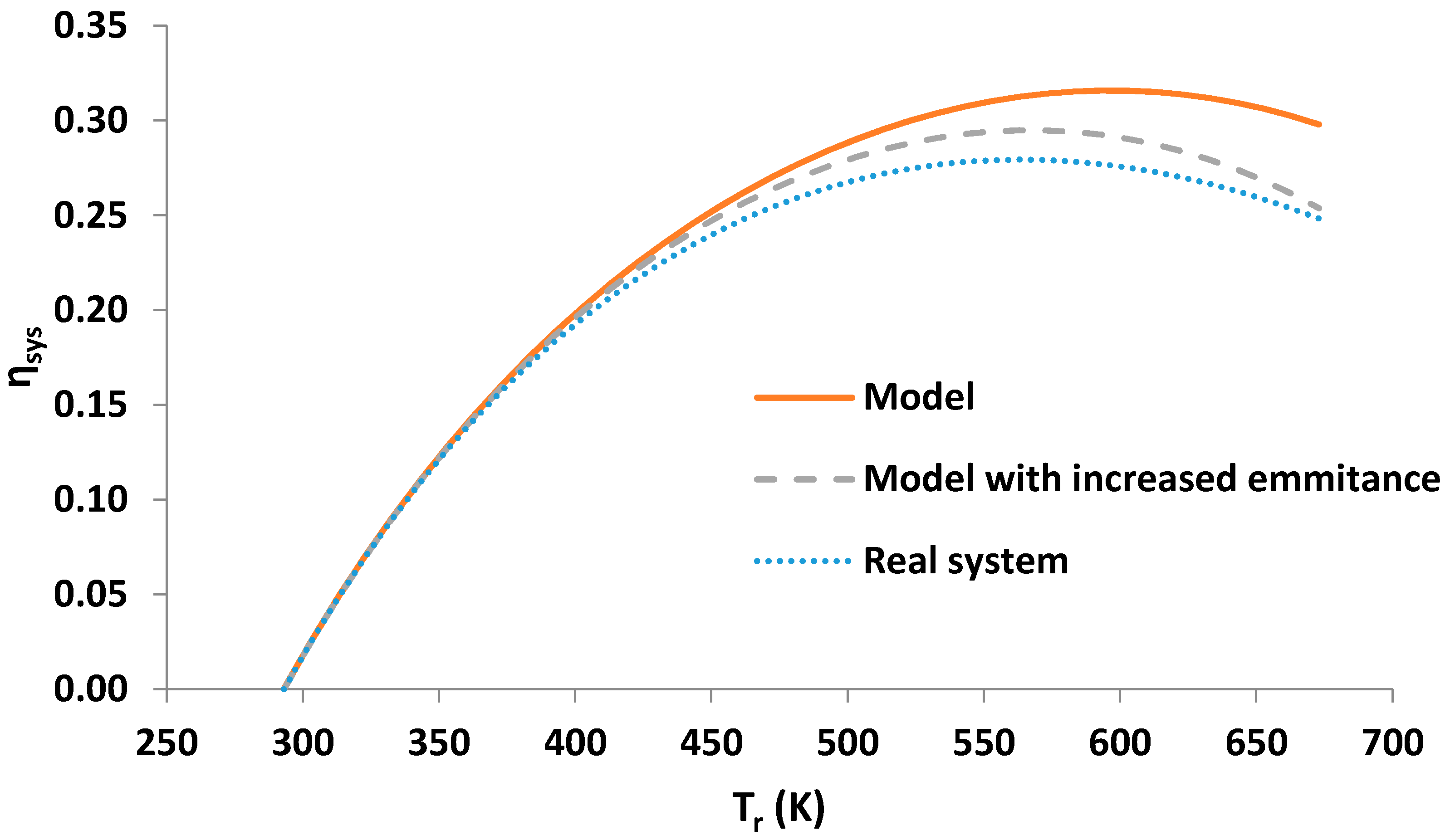
4.3. The Application of the Model in a Real Solar Collector
4.4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Area, m2 |
| C | Concentration ratio, - |
| f | Geometric factor, - |
| G | Solar irradiation, W/m2 |
| p | Efficiency parameter, - |
| q | Polynomial parameter, - |
| Q | Heat or radiant energy, W |
| T | Temperature, K |
| UL | Thermal loss coefficient, W/m2 K |
| W | Work, W |
| X | Ratio of receiver temperature to ambient temperature, - |
| Z | Collector quality parameter, - |
| Greek symbols | |
| α | Absorbance, - |
| γ | Intercept factor, - |
| δ | Cone half-angle, ° |
| ε | Emittance, - |
| η | Efficiency, - |
| θ | Incident angle, ° |
| ρ | Reflectance, - |
| σ | Stefan–Boltzmann constant, [=5.67 × 10−8 W/m2 K4] |
| τ | Transmittance, - |
| Subscripts and Superscripts | |
| a | Aperture |
| amb | Ambient |
| carnot | Carnot cycle |
| coll | Collector |
| ex | exergy |
| loss | Thermal losses |
| max | Maximum |
| opt | Optimum |
| out | Output heat |
| r | Receiver |
| r,opt | Optimum receiver |
| solar | Solar energy |
| sun | Sun |
| sys | System |
| th | Thermal |
| u | Useful |
References
- Modi, A.; Kærn, M.R.; Andreasen, J.G.; Haglind, F. Thermoeconomic optimization of a Kalina cycle for a central receiver concentrating solar power plant. Energy Convers. Manag. 2016, 115, 276–287. [Google Scholar] [CrossRef] [Green Version]
- Larrouturou, F.; Caliot, C.; Flamant, G. Influence of receiver surface spectral selectivity on the solar-to-electric efficiency of a solar tower power plant. Solar Energy 2016, 130, 60–73. [Google Scholar] [CrossRef]
- Boukelia, T.E.; Mecibah, M.S.; Kumar, B.N.; Reddy, K.S. Optimization, selection and feasibility study of solar parabolic trough power plants for Algerian conditions. Energy Convers. Manag. 2015, 101, 450–459. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Xu, E.; Ma, G.; An, Q. Analysis and Optimization of the Start-up Process based on Badaling Solar Power Tower Plant. Energy Proced. 2015, 69, 1688–1695. [Google Scholar] [CrossRef]
- Guédez, R.; Topel, M.; Spelling, J.; Laumert, B. Enhancing the Profitability of Solar Tower Power Plants through Thermoeconomic Analysis Based on Multi-objective Optimization. Energy Proced. 2015, 69, 1277–1286. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Korres, D.; Antonopoulos, K.A. Thermal analysis of a flat plate collector with Solidworks and determination of convection heat coefficient between water and absorber. In Proceedings of the 28th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Pau, France, 29 June–3 July 2015. [Google Scholar]
- Bellos, E.; Tzivanidis, C.; Tsifis, G. Energetic, Exergetic, Economic and Environmental (4E) analysis of a solar assisted refrigeration system for various operating scenarios. Energy Convers. Manag. 2017, 148, 1055–1069. [Google Scholar] [CrossRef]
- Krüger, D.; Pandian, Y.; Hennecke, K.; Schmitz, M. Parabolic trough collector testing in the frame of the REACT project. Desalination 2008, 220, 612–618. [Google Scholar] [CrossRef]
- Tzivanidis, C.; Bellos, E.; Korres, D.; Antonopoulos, K.A.; Mitsopoulos, G. Thermal and optical efficiency investigation of a parabolic trough collector. Case Stud. Therm. Eng. 2015, 6, 223–237. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A.; Gkinis, G. Thermal enhancement of solar parabolic trough collectors by using nanofluids and converging-diverging absorber tube. Renew. Energy 2016, 94, 213–222. [Google Scholar] [CrossRef]
- Semprini, S.; Sánchez, D.; De Pascale, A. Performance analysis of a micro gas turbine and solar dish integrated system under different solar-only and hybrid operating conditions. Solar Energy 2016, 132, 279–293. [Google Scholar] [CrossRef]
- Montes, M.J.; Rubbia, C.; Abbas, R.; Martínez-Val, J.M. A comparative analysis of configurations of linear Fresnel collectors for concentrating solar power. Energy 2014, 73, 192–203. [Google Scholar] [CrossRef]
- Petela, R. Exergy of undiluted thermal radiation. Solar Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- Parrott, J.E. Theoretical upper limit to the conversion efficiency of solar energy. Solar Energy 1978, 21, 227–229. [Google Scholar] [CrossRef]
- Badescu, V. How much work can be extracted from a radiation reservoir? Phys. A 2014, 410, 110–119. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley Interscience: New York, NY, USA, 1988. [Google Scholar]
- Torres-Reyes, E.; Cervantes-de Gortari, J.G.; Ibarra-Salazar, B.A.; Picon-Nuñez, M. A design method of flat-plate solar collectors based on minimum entropy generation. Exergy Int. J. 2001, 1, 46–52. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar thermal collectors and applications. Prog. Energy Combust. Sci. 2004, 30, 231–295. [Google Scholar] [CrossRef]
- Souliotis, M.; Quinlan, P.; Smyth, M.; Tripanagnostopoulos, Y.; Zacharopoulos, A.; Ramirez, M.; Yianoulis, P. Heat retaining integrated collector storage solar water heater with asymmetric CPC reflector. Solar Energy 2011, 85, 2474–2487. [Google Scholar] [CrossRef]
- Dudley, V.E. SANDIA, Report Test Results for Industrial Solar Technology Parabolic Trough Solar Collector; SAND94-1117; Sandia National Laboratory: Albuquerque, NM, USA, 1995.
| Collector | C | ηopt | εr | Tr,opt (K) | ηsys |
|---|---|---|---|---|---|
| Flat plate collector | 1 | 0.8 | 0.25 | 401 | 0.1449 |
| Evacuated tube collector | 1 | 0.7 | 0.10 | 451 | 0.1777 |
| Compound parabolic collector | 3 | 0.6 | 0.10 | 527 | 0.2079 |
| Parabolic trough collector | 30 | 0.75 | 0.10 | 884 | 0.4400 |
| Solar dish collector | 100 | 0.75 | 0.10 | 1110 | 0.5011 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, E.; Tzivanidis, C. A Realistic Approach of the Maximum Work Extraction from Solar Thermal Collectors. Appl. Syst. Innov. 2018, 1, 6. https://doi.org/10.3390/asi1010006
Bellos E, Tzivanidis C. A Realistic Approach of the Maximum Work Extraction from Solar Thermal Collectors. Applied System Innovation. 2018; 1(1):6. https://doi.org/10.3390/asi1010006
Chicago/Turabian StyleBellos, Evangelos, and Christos Tzivanidis. 2018. "A Realistic Approach of the Maximum Work Extraction from Solar Thermal Collectors" Applied System Innovation 1, no. 1: 6. https://doi.org/10.3390/asi1010006






